Изобретение относится к промысловой геофизике, а также к геофизическим исследованиям скважин, и может быть использовано при определении и уточнении пространственного положения забоя обсаженных и необсаженных скважин.
Известен способ определения координат центра забоя скважины с помощью источника света, в качестве которого используют лазер с устройством, автоматически удерживающим его рабочий луч по отвесной прямой. Контейнер с лазером и контейнер со светочувствительным экраном и телекамерой опускают последовательно ходами в прямолинейные участки скважины. В каждой точке отмечают на экране отклонения луча относительно оси скважины. Телекамера при этом посылает изображение со светочувствительного экрана на экран телевизора, установленного на дневной поверхности. Далее контейнеры перемещают в следующую точку, замеряя глубину ствола скважины. Координаты центра забоя скважины и ее искривление в пределах каждой заходки определяют либо аналитическим способом, по известным алгоритмам, либо графически по сумме и направлению векторов на экране после каждой передвижки контейнеров на очередную заходку (авт. св. СССР N 927986, кл. E 21 B 47/022, 1982).
Недостатком этого технического решения является неприемлемость его при исследовании промысловых скважин.
Кроме того, этот способ трудоемок и требует дорогостоящей лазерной и телевизионной аппаратуры. Он также технически трудно осуществим (особенно при изучении глубоких скважин со сложным профилем) ввиду большого числа замеров, которые приводят к накоплению погрешности и возможного многократного отражения светового луча от стенок скважины.
Наиболее близким (по технической сущности) является способ определения координат забоя скважины путем регистрации времени распространения акустических сигналов, возбуждаемых импульсным источником, до сейсмоприемника (патент США N 4003017, E 21 B 47/02, 1977).
Недостатком способ является необходимость использования (для возбуждения акустических сигналов) бура с вмонтированным в него датчиком, что неприемлемо при определении координат забоя у ранее пробуренных скважин.
Другим недостатком этого способа является высокая вероятность повреждения дорогостоящего бурового инструмента при ударах о забой скважины.
Изобретение направлено на решение задачи, заключающейся в обеспечении высокой точности определения координат забоя скважин.
Для решения задачи в известном способе определения координат забоя скважины путем регистрации времени распространения акустических сигналов, возбуждаемых импульсным источником, до сейсмоприемника, акустические сигналы возбуждают на дневной поверхности в районе устья скважины как минимум четырех точках с заданными координатами, сейсмоприемник устанавливают в забой скважины и регистрируют время распространения акустических сигналов от каждой точки возбуждения до забоя, после проведения измерений времени распространения акустических сигналов до забоя от всех заданных точек результаты измерений, представляют в виде аппроксимирующего гиперболоида
(x-x0)2/q2 + (y-y0)2/q2 + 1 = t2/t
преобразуют его в уравнение:
x2 + y2 + a1x + a2y + a3t2 + a4 = 0,
из которого вычисляют координаты забоя скважины по формуле:
x0 = -a1/2; y0 = -a2/2,
где x, y - координаты точек возбуждения акустических сигналов;
t - время прохождения акустического сигнала от точки возбуждения до забоя;
q - масштабный коэффициент;
a1, a2, a3, a4 - параметры гиперболоида;
a1= -x0/2, a2= -y0/2, a3= -q2/t
(x0,y0) - искомые координаты забоя;
t0 - минимальное время распространения акустического сигнала от дневной поверхности до забоя.
Способ основан на том, что между глубиной расположения забоя, смещением точки возбуждения сейсмических сигналов от проекции точки забоя на дневную поверхность, скоростью распространения акустических сигналов и временем распространения последних от точки возбуждения на дневной поверхности до забоя скважины существует зависимость
x2 = (vt)2 - h2,
где
x - смещение точки возбуждения акустических волн от проекции точки забоя на дневную поверхность;
v - скорость распространения акустических сигналов;
t - время распространения акустических сигналов от точки возбуждения до забоя;
h - глубина расположения забоя.
Уравнение (1) приведем к гиперболической зависимости вида
t2 = ax2 + bx + c
Минимуму этой функции соответствует проекция точки забоя на ось X. Это значит, что, проводя сейсмические воздействия по линейному профилю, проходящему через проекцию точки забоя на дневную поверхность, и измерив время распространения сигналов до забоя, математическим путем можно получить координаты точки забоя скважины.
В связи с тем, что при определении местоположения забоя скважины достаточно сложно проложить профиль, проходящий через проекцию точки забоя на дневную поверхность, способ рассмотрен для трехмерного пространства и функция времени распространения сейсмических сигналов от заданных точек на дневной поверхности с известными и искомыми координатами забоя аппроксимируется двухполосным гиперболоидом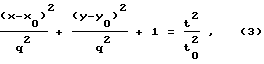 ,
,
где
x, y - координаты точки возбуждения акустических сигналов на дневной поверхности;
x0, y0 - искомые координаты забоя;
q - масштабный коэффициент.
t0 - минимальное время распространения акустического сигнала от дневной поверхности до забоя.
Таким образом, вычисление координат забоя скважины сводится к вычислению параметров аппроксимирующего гиперболоида, для однозначного определения которого достаточно четырех точек, не лежащих на одной прямой.
Способ поясняется рисунком, на котором приведена функциональная схема осуществления способа.
Способ осуществляется следующим образом.
На дневной поверхности около устья 1 скважины 2 в заданной точке I с известными реальными координатами (x1, y1) размещают импульсный сейсмический источник 3. Сейсмоприемник 4 опускают в забой скважины 2.
После спуска сейсмоприемника в забой скважины по радиоканалу 5 в определенный момент времени с вычислительного комплекса 6, который одновременно служит пунктом управления проведения измерений и включает в свой состав универсальную микроЭВМ 7, дополнительно оснащенную аналого-цифровым преобразователем 8, на сейсмоисточник передают сигнал готовности, по приходу которого посредством сейсмоисточника 3 производят импульсное сейсмическое воздействие в точке I. Одновременно с сейсмовоздействием по радиоканалу 5 на вычислительный комплекс 6 с сейсмоисточника 3 передают синхроимпульс, который является сигналом запуска микроЭВМ 7 для измерения времени прохождения акустического сигнала (t1) от точки I на поверхности земли до сейсмоприемника 4.
Акустический сигнал достигает сейсмоприемника 4, где он преобразуется в электрический. Выходной сигнал сейсмоприемника поступает на аналого-цифровой преобразователь 8.
При поступлении синхроимпульса начинается считывание сигнала с аналого-цифрового преобразователя в микроЭВМ 7, где происходит определение времени распространения акустических сигналов (t1) от точки I до сейсмоприемника 4 в забое скважины 2.
После проведения цикла измерений в точке I сейсмоисточник 3 перемещают в следующую заданную на поверхности земли точку II с известными реальными координатами (x2, y2), где весь цикл от сейсмовоздействия до измерения времени распространения (t2) сигнала до сейсмоприемника 4 повторяется вновь.
Далее последовательно выполняют весь цикл работ в точках III и IV (на дневной поверхности) с известными координатами (x3, y3) и (x4, y4), в результате которых получают времена распространения акустических сигналов от точек III и IV до сейсмоприемника 4 - t3 и t4 соответственно.
Таким образом, после проведения измерений во всех заданных точках микроЭВМ 7 располагает информацией о временах распространения акустических сигналов (t1, t2, t3, t4) до сейсмоприемника 4, а также графическими изображениями этих сигналов, данными о дате, времени и месте проведения измерений. Одновременно на вычислительном комплексе 6 проводят контроль качества проведенных измерений с отображением результатов в виде таблиц и графиков.
Полученной информации достаточно, чтобы на вычислительном комплексе 6 определить параметры гиперболоида, который оптимальным образом описывает результаты измерений. Параметры гиперболоида, а следовательно, и координаты забоя скважины вычисляют следующим образом.
Уравнение (3) приводим к виду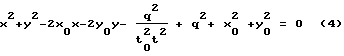 .
.
Введем обозначения:
a1 = -2x0; a2 = -2y0;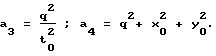 .
.
Тогда уравнение (4) приобретает вид
x2 + y2 + a1x + a2y + a3t2 + a4 = 0
Поиск a1, a2, a3, a4 и тем самым x0, y0, t0, q по совокупности экспериментальных точек xi, yi, ti, где i = 1,...,m. производим по методу наименьших квадратов, m - число точек (m ≥ 4).
Введем функцию вида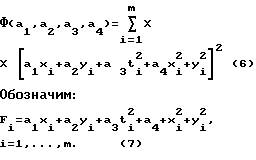 .
.
Значения a1, a2, a3, a4 выбираем при условии минимизации функции Φ. . Для этого частные производные 7 ∂φ/∂aj, , где j = 1,...4 приравняем нулю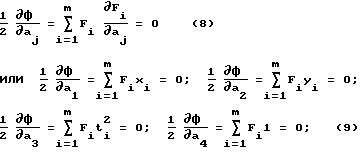 ;
;
Подставим соотношение (7) в уравнения (9) и получим систему уравнений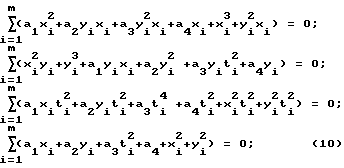 ;
;
Проссумируем слагаемые в системе уравнений (10) так, чтобы выделить коэффициенты при неизвестных a1, a2, a3, a4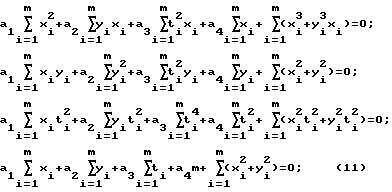 ;
;
Представим систему (11) в стандартном виде:
b11a1 + b12a2 + b13a3 + b14a4 = c1;
b21a1 + b22a2 + b23a3 + b24a4 = c2;
b31a1 + b32a2 + b33a3 + b34a4 = c3;
b41a1 + b42a2 + b43a3 + b44a4 = c4;
где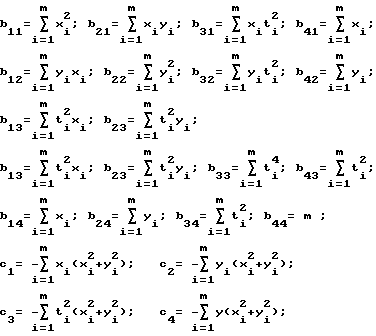 ;
;
Преобразуем систему уравнений (12) и приведем ее к следующему виду:
b11a1 + b12a2b13a3 + b14a4 = c1;
(b11b22 - b12)a2 + (b11b23 - b13b21)a3 + (b11b24 - b14b21)a4 = c2b11 - c1b21;
(b11b23 - b31b12)a2 + (b11b33 - b13)a3 + (b11b34 - b31b14)a4 = c3b11 - c1b31;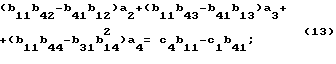 ;
;
Последние три уравнения системы (13) не содержат a1 и являются самостоятельными. Перепишем их в более наглядном виде
d12a2 + d13a3 + d14a4 = D2;
d22a2 + d23a3 + d24a4 = D3;
d32a2 + d33a3 + d34a4 = D4;
где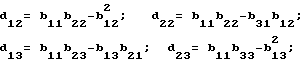 ;
;
d14 = b11b24 - b14b21; d24 = b11b34 - b31b14;
d32 = b11b42 - b41b12; D2 = c2b11 - c1b21;
d33 = b11b43 - b41b13; D3 = c3b11 - c1b31;
d34= b11b44-b
Решая систему уравнений (14), получим a2, a3, a4. После этого из первого уравнения системы (13) находим a1: .
.
Таким образом, найденные значения a1, a2, a3, a3 являются параметрами аппроксимирующего гиперболоида и, учитывая замену в уравнении (4), получим координаты забоя скважины: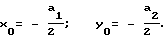 .
.
Способ опробован в Тюменской области на Мортымья-Тетеревском месторождении нефти на 4 контрольных скважинах в 4 и 6 точках импульсного воздействия.
Для всех примеров координаты устья и забоя скважины, а также координаты точек возбуждения акустического сигнала на дневной поверхности определяют в метрах (м) в системе координат СК-42 в прямоугольной проекции Гаусса-Крюгера с погрешностью для устья и точек возбуждения не более ±5 м, для забоя не более ±10 м. Время распространения акустического сигнала от точки возбуждения до забоя измеряют в миллисекундах (мс) с погрешностью ±1 мс.
Теоретическим и экспериментальным путем установлено, что для уверенной регистрации распространения акустического сигнала (на фоне помех) на глубину до 3000 м достаточно использовать груз (P) весом в 2000 кг при высоте (h) его подъема на 1 м.
Пример 1. Скважина N 1356.
Параметры скважины:
координаты забоя: x
координаты устья: x = 6703791; y = 591215.
На дневной поверхности вокруг устья скважины выбирают четыре точки импульсного воздействия и определяют их координаты. Сейсмоприемник 4 опускают в забой скважины.
На дневной поверхности груз P перемещают в точку I импульсного воздействия. Поднимают груз P на высоту h и сбрасывают его вертикально на землю в точке I.
Одновременно с сейсмовоздействием по радиоканалу 5 с сейсмоисточника 3 на вычислительный комплекс 6 передают синхроимпульс для запуска микроЭВМ и измерения времени распространения акустического сигнала от точки I до сейсмоприемника.
Далее, последовательно производят перемещение груза P, подъем его на высоту h, сбрасывание его и регистрацию времени распространения акустического сигнала (t) в точках II, III, IV. В итоге для каждой из четырех точек получают следующие данные:
точка I x1 = 6703133, y1 = 591045, t1 = 853,0;
точка II x2 = 6702817, y2 = 590699, t2 = 947,3;
точка III x3 = 6704163, y3 = 590518, t3 = 804,6;
точка IV x4 = 6703936, y4 = 591559, t4 = 746,4.
Полученные данные обрабатывают по предложенному в способе алгоритму и рассчитывают координаты забоя, которые равны
x0 = 6704122, y0 = 591298.
Из анализа полученных данных следует, что координаты забоя соответствуют контрольным значениям. Отклонение по x составляет 1 м, по y - 2 м, что не превышает заданной погрешности измерений.
Пример 2. Скважина та же, только сейсмовоздействия производят в 6 точках. Дополнительно к точкам примера 1 выбирают еще две точки с известными координатами, в них также последовательно производят перемещение груза, его подъем и сбрасывание, регистрацию времени распространения акустического сигнала в забой, дополнительно получают следующие данные:
точка V x5 = 6703224, y5 = 592198, t5 = 908,8;
точка VI x6 = 6703360, y6 = 591867, t6 = 829,4.
По параметрам 6 точек рассчитывают координаты забоя скважины.
Координаты забоя равны
x0 = 6704126, y0 = 591297.
Из анализа полученных данных следует, что координаты, рассчитанные по 4 и 6 точкам, в пределах допустимой погрешности совпадают с контрольными координатами забоя.
Пример 3. Скважина N 382, импульсное воздействие выполняют в 4 точках. Параметры скважины
координаты устья: x = 6703995, y = 586952;
координаты забоя: x
Результаты (координаты точек и время распространения акустического сигнала в забой), полученные по 4 точкам, следующие:
точка I x1 = 6703916, y1 = 587341, t1 = 722,2;
точка II x2 = 6705090, y2 = 587553, t2 = 919,5;
точка III x3 = 6704556, y3 = 587885, t3 = 859,3;
точка IV x4 = 6703630, y4 = 587500, t4 = 747,0.
По этим данным рассчитывают координаты забоя скважины
x0 = 6703842, y0 = 587009.
Сравнение значений координат забоя с контрольными показывает, что они в пределах допустимой погрешности совпадают.
Пример 4. Условия проведения экспериментов те же, что и в примере 3, только к 4 точкам сейсмического воздействия добавляют еще 2.
Координаты дополнительных точек и время распространения акустического сигнала в забой следующие:
точка V x5 = 6703456, y5 = 587839, t5 = 809,6;
точка VI x6 = 6704794, y6 = 586533, t6 = 843,3.
Вычисленные по 6 точкам координаты забоя в пределах допустимой погрешности совпадают с координатами, рассчитанными по 4 точкам, и с контрольными координатами забоя:
x0 = 6703846, y0 = 587007.
Пример 5. Скважина N 1319.
Поскольку при вычислении координат забоя по 4 и 6 точкам результаты в пределах допустимой погрешности совпадают, дальнейшие эксперименты проводят только по 4 точкам.
Параметры скважины:
координаты устья: x = 6695441, y = 592274,
координаты забоя: x
Координаты точек (на дневной поверхности в районе устья скважины) возбуждения акустических сигналов и время их распространения от этих точек до забоя следующие:
точка I x1 = 6695569, y1 = 593729, t1 = 851,2;
точка II x2 = 6695239, y2 = 593912, t2 = 899,1;
точка III x3 = 6694867, y3 = 593597, t3 = 851,8;
точка IV x4 = 6695253, y4 = 591939, t4 = 805,8.
Координаты забоя, вычисленные по значениям этих точек, в пределах погрешности совпадают с координатами забоя контрольной скважины и имеют следующие значения
x0 = 6695399, y0 = 592730.
Пример 6. Скважина N 1312. Сейсмовоздействия проводят в 4 точках на дневной поверхности в районе устья скважины.
Параметры скважины:
координаты устья: x = 6697770, y = 590737,
координаты забоя: x
Координаты точек возбуждения акустических сигналов и время распространения от точки возбуждения до забоя следующие:
точка I x1 = 6696877, y1 = 590315, t1 = 913,3;
точка II x2 = 6697143, y2 = 590541, t2 = 834,6;
точка III x3 = 6697467, y3 = 590627, t3 = 796,1;
точка IV x4 = 6698553, y4 = 591924, t4 = 869,9.
Вычисленные координаты забоя в пределах погрешности совпадают с контрольными координатами забоя и имеют следующие значения
x0 = 6697750, y0 = 591213.
Преимуществами способа являются:
- возможность определения координат забоя обсаженных и необсаженных скважин независимо от сложности их профиля и глубины;
- высокая устойчивость алгоритма и простота его реализации на микроЭВМ;
- высокая точность определения координат забоя: отклонение расчетных их значений от контрольных не превышает заданной погрешности ± 10 м;
- простота реализации способа в полевых условиях;
- применение маломощных импульсных невзрывных и экологически чистых источников возбуждения акустических сигналов.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ТРАЕКТОРИИ СКВАЖИНЫ | 2007 |
|
RU2357078C2 |
| СПОСОБ КОНТРОЛЯ МЕСТОПОЛОЖЕНИЯ БУРОВОГО ДОЛОТА В ПРОЦЕССЕ БУРЕНИЯ | 2006 |
|
RU2305298C1 |
| СПОСОБ ТРИАНГУЛЯЦИИ ЦЕЛЕЙ | 2010 |
|
RU2423720C1 |
| СПОСОБ АНАЛОГО-ЦИФРОВОГО ПРЕОБРАЗОВАНИЯ | 1993 |
|
RU2097866C1 |
| КОМПОНОВКА НИЗА БУРИЛЬНОЙ КОЛОННЫ | 1997 |
|
RU2135731C1 |
| Способ определения местоположения забоя скважины | 1989 |
|
SU1698865A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ С КОСМИЧЕСКОГО АППАРАТА КООРДИНАТ ИСТОЧНИКА КОЛЬЦЕВЫХ ВОЛН НА ВОДНОЙ ПОВЕРХНОСТИ | 2016 |
|
RU2640944C2 |
| СПОСОБ СКВАЖИННОЙ СЕЙСМОРАЗВЕДКИ | 1996 |
|
RU2101733C1 |
| СЕЙСМОПРИЕМНИК | 1993 |
|
RU2092873C1 |
| СПОСОБ БУРЕНИЯ СКВАЖИНЫ | 1997 |
|
RU2135730C1 |
Изобретение относится к промысловой геофизике, а также к геофизическим исследованиям скважин и может быть использовано при определении и уточнении пространственного положения забоя обсаженных и необсаженных скважин. Координаты забоя определяют на основе регистрации времени распространения акустических сигналов от точек их возбуждения на дневной поверхности в районе устья скважины до забоя скважины. Регистрацию времени распространения акустических сигналов проводят сейсмоприемником, расположенным в забое скважины. Измерения времени распространения акустических сигналов производят не менее чем в четырех точках возбуждения, не лежащих на одной прямой. По полученным данным (времени распространения акустических сигналов и координатам точек их возбуждения) на вычислительном комплексе определяют параметры двухполостного гиперболоида, на основе которых вычисляют координаты забоя скважины. 1 ил.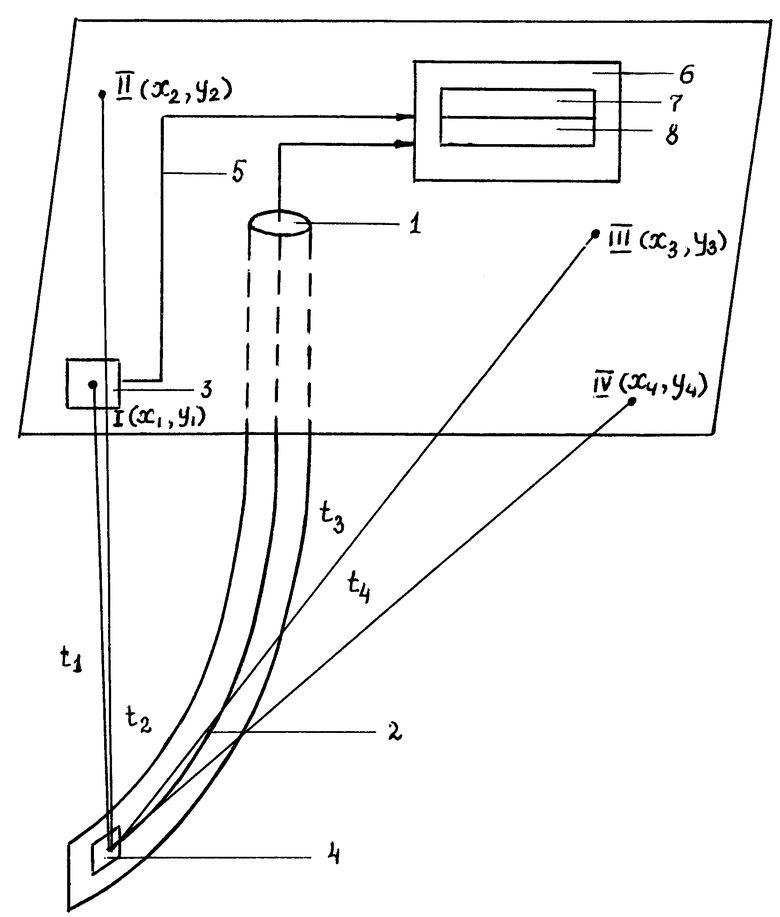
Способ определения координат забоя скважины путем регистрации времени распространения акустических сигналов, возбуждаемых импульсным источником, до сейсмоприемника, отличающийся тем, что акустические сигналы возбуждают на дневной поверхности в районе устья скважины, как минимум, в четырех точках с заданными координатами, сейсмоприемник устанавливают в забой скважины и регистрируют время распространения акустических сигналов от каждой точки возбуждения до забоя, после проведения измерений времени распространения акустических сигналов до забоя от всех заданных точек результаты измерений представляют в виде аппроксимирующего гиперболоида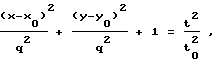
преобразуют его в уравнение
x2 + y2 + a1x + a2y + a3t2 + a4 = 0,
из которого вычисляют координаты забоя скважины по формуле
x0 = - a1/2; y = - a2/2,
где x, y - координаты точек возбуждения акустических сигналов;
t - время прохождения акустического сигнала от точки возбуждения до забоя;
q - масштабный коэффициент;
a1, a2, a3, a4 - параметры гиперболоида;
a1 = - x0/2; a2 = - y0/2; 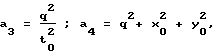
(x0, y0) - искомые координаты забоя;
t0 - минимальное время распространения акустического сигнала от дневной поверхности до забоя.
Авторы
Даты
1998-06-10—Публикация
1996-05-22—Подача