Изобретение относится к космической технике и касается способов и устройств по определению положения центра масс космических аппаратов (КА) при управлении их угловым движением с помощью силовых приводов в условиях космического полета.
Наукой "Геометрия масс", включающей в себя и определение местоположения центра масс различных физических объектов, человечество занималось с незапамятных времен. Одно из наиболее полных описаний как по истории этой науки, так и по практическому использованию результатов ее исследований, представлено в монографии "Определение моментов инерции" [1]. В указанной монографии рассматриваются классические работы, связанные с наукой "геометрии масс", начиная с сочинений Галилея, Ньютона, Гюйгенса и др.
Естественно, что за столь продолжительное время разработано много различных способов определения положения центра масс любых объектов. К числу таких объектов можно отнести, например КА, проходящий наземные испытания.
В качестве одного из предложенных является классический способ определения центра масс (тяжести) с помощью динамометра (см. там же, стр.21). Для этого к объекту, подвешенному на острие призмы, прикладывают управляющий момент, равный произведению силы на плечо ее действия (расстояния от точки подвеса объекта до точки приложения силы). Измеряют величину силы при помощи динамометра. Измеряют также угол отклонения объекта от равновесного положения. По указанным измеренным значениям, а также по заранее известным весу объекта и длине плеча силы определяют расстояние от точки подвеса до центра масс. Указанные действия могут быть повторены при различных положениях тела, при этом каждый раз определяются конкретные расстояния до центра масс (например, расстояния от центра масс до места установки двигателя ориентации на конструкции КА).
Известны и другие способы определения положения центра масс с использованием управляющего момента, например: "...качания на параллельных осях" (см. там же стр.23-29); "...качание двойного маятника" (способ, используемый для исследования инерционно-массовых характеристик самолетов в ЦАГИ, см. там же, стр.51-66) и др.
Указанные, хорошо отработанные на Земле способы определения положения центра масс непригодны для условий космического полета. Это связано с тем, что отсутствие силы тяжести в условиях космического полета приводит к отсутствию силового воздействия на тело через реакцию опор в виде призм, поверхностей качания, нитей подвеса и т.д.
Для определения массы КА и положения его центра масс (в условиях космического полета) на него необходимо воздействовать несбалансированными силами или моментами сил. В качестве прототипа предлагаемого изобретения выбирается известный способ определения положения центра масс КА с помощью создающих моменты силовых приводов [2].
Суть способа-прототипа заключается в измерении параметров движения КА под воздействием управляющих моментов силовых приводов и в определении по измеренным параметрам положения центра масс.
В качестве силовых приводов рассматриваются силовые гироскопы. А в качестве измеряемых параметров рассматриваются угловые ускорения отдельных точек КА (определенных смещением акселерометров относительно центра масс) и угловая скорость аппарата.
Подставляя измеренные параметры в известные динамические уравнения (14)-(19)(см. стр. 31 описания способа-прототипа), включающие члены, обусловленные как поступательным, так и вращательным движением аппарата, рассчитывают положение центра масс через определение смещений акселерометров. Для этого разрабатывается специальный математический алгоритм, задействующий фильтр Калмана, который, в свою очередь, включает в себя пересчет после каждого цикла измерений ковариационной матрицы ошибок. Таким образом, математический процесс носит итерационный характер и сам по себе имеет определенную ошибку. В лучшем случае указанная "...ошибка не превышала 1,3% по каждой координате" (см. там же, стр.33).
Однако, если проводить общую оценку точности "определения положения центра масс, то необходимо учитывать и ошибки, которые вносят приборы, измеряющие параметры. Авторы способа-прототипа понимают сложность получения таких инструментальных измерений и отмечают, что "... современные средства измерения углового ускорения не обеспечивают точности, необходимой для определения инерционных характеристик КА. В связи с этим положение центра масс определяется не в процессе действия управляющего момента, а в результате оценки изменения угловой скорости аппарата под воздействием импульса управляющего момента" (см. там же, стр.31).
В данном случае рассматриваются микроускорения отдельных точек КА и, чтобы выделить полезный сигнал из шумов, вносимых работающей бортовой аппаратурой, необходимо запретить любое постороннее движение внутри КА. Для больших орбитальных станций типа орбитальной пилотируемой научной станции (ОПНС) "Мир" это проблематично, так как системы обеспечения жизнедеятельности экипажа должны работать непрерывно.
Кроме этого, необходимо планировать специальную динамику КА, т.е. тестовый, продолжительный режим работы силовых гироскопов, предполагающий выдачу тарированных импульсов управляющих моментов по всем осям управления.
Предварительные оценки относительной погрешности определения положения центра масс при помощи способа-прототипа проводились для ОПНС "Мир". В лучшем случае суммарная относительная погрешность при определении каждой его координаты составляла ~8%.
На получение более высокого технического результата, связанного с увеличением точности определения положения центра масс при одновременном упрощении используемого математического аппарата, направлено предлагаемое изобретение.
Для достижения указанного технического результата в известном способе определения положения центра масс КА в процессе его управления с помощью силовых приводов, включающем измерение параметров движения КА под действием тарированных управляющих моментов, прилагаемых к корпусу КА от силовых моментных приводов, и определение по измеренным параметрам положения центра масс КА, стабилизируют угловое движение КА с помощью силовых приводов подвеса двигательной установки в процессе коррекции его орбиты, измеряют по окончании первичного режима стабилизации углы поворота выходных валов силовых приводов подвеса корректирующей двигательной установки, повторно после приложения тарированного управляющего момента к корпусу КА от моментного силового привода по одной из осей стабилизации стабилизируют угловое движение КА с помощью вращения силовых приводов подвеса двигательной установки с учетом приложенного момента, измеряют угол поворота выходного вала силового привода подвеса корректирующей двигательной установки по этой же оси стабилизации, определяют угол отклонения двигательной установки между первой и второй стабилизацией как разность соответственно измеренных угловых значений поворота выходного вала силового привода подвеса двигательной установки, по определенному углу отклонения двигательной установки между первой и второй стабилизацией, а также по тарированным значениям величин силы тяги корректирующей двигательной установки и управляющего момента определяют расстояние от точки подвеса корректирующей двигательной установки до физического центра масс КА, а по указанному расстоянию и по измеренным после первой стабилизации космического аппарата углам поворота выходных валов приводов подвеса корректирующей двигательной установки определяют положение физического центра масс относительно расчетного, связанного со строительными осями КА.
В предлагаемом способе технический результат достигается за счет двух основных положений.
Первое: при определении искомых величин значительно упрощены расчетные зависимости, в состав которых входят значения параметров измеряемых величин. Полностью исключен итерационный процесс, а следовательно, и погрешность, которую он вносит в определение искомых величин.
Второе: выбор новых измеряемых параметров, постоянно присутствующих при проведении штатных режимов коррекции орбиты КА и не требующих специальной подготовки (условий) для их измерения.
Кроме того, приборы, с помощью которых производится измерение выбранных параметров, устойчивы к различного рода помехам. Полезный сигнал с приборов относительно легко поддается расшифровке с достаточно высокой степенью точности.
В качестве примера реализации способа рассмотрим случай коррекции ОПНС "Мир" при помощи одного из космических кораблей - транспортного корабля (ТК) "Союз-ТМ" или грузового корабля (ГК) "Прогресс-М" (см.фиг.1), где введены следующие обозначения:
1 - базовый блок ОПНС "Мир";
2 - астрофизический модуль "Квант";
3 - модуль дооснащения "Квант-2";
4 - технологический модуль "Кристалл";
5 - исследовательский модуль "Спектр";
6 - специализированный модуль "Природа";
7 - ТК "Союз-ТМ";
8 - ГК "Прогресс-М".
OXYZ - расчетное положение главных центральных осей ОПНС "Мир", совпадающих со строительными осями.
 - вектор тяги от двигательной установки (ДУ) ГК "Прогресс-М".
- вектор тяги от двигательной установки (ДУ) ГК "Прогресс-М".
ДУ ГК и ТК помещена в два кардановых подвеса, позволяющих камере сгорания поворачиваться относительно осей тангажа и рыскания.
Для реализации предлагаемого способа необходимо также иметь возможность прикладывать к корпусу станции тарированный управляющий момент. В качестве исполнительных органов, реализующих указанный момент, могут быть использованы силовые гироскопы, магнитные исполнительные органы системы ориентации и др.
На ОПНС "Мир" для получения такого момента применяются двухстепенные силовые гироскопы - гиродины.
Предлагаемый способ построен на основе анализа динамики управления угловым движением ОПНС при коррекции ее орбиты с помощью ДУ в кардановых подвесах и одновременном приложении к ее корпусу тарированного управляющего момента.
Рассмотрим подробно динамику работы системы стабилизации на примере кораблей "Союз-ТМ" и "Прогресс-М".
Поскольку динамика работы системы стабилизации в контурах тангажа и рыскания идентична, то далее ограничимся рассмотрением одного контура, например, рыскания.
Считая углы и угловые скорости кораблей малыми, запишем динамическое уравнение, описывающее угловое движение ОПНС при коррекции, в виде: ,
,
где
αy - угол рыскания ОПНС;
Iу - момент инерции ОПНС вокруг оси рыскания;
P - тяга ДУ;
l - расстояние от точки приложения тяги до центра масс ОПНС;
Ψ - угол поворота камеры ДУ по рысканию;
Мву - внешний возмущающий момент, действующий на ОПНС по оси рыскания.
Уравнение привода постоянного тока, поворачивающего камеру ДУ, имеет вид:
ε = F(U) (2) ,
где
ε - угол поворота привода;
U - управляющий сигнал на привод;
F - нелинейная функция.
Привод постоянного тока через редуктор поворачивает камеру ДУ, т.е.
Ψ = ε/n (3) ,
где
n - передаточное число редуктора.
В традиционных системах стабилизации (см., например, Колесников К.С. Жидкостная ракета как объект регулирования, М.; Машиностроение, 1969, с. 40-44) закон формирования управляющего сигнала на привод имеет вид:
U = K1αy + K2αy - K3ε (4) ,
где
K1, K2 - коэффициенты усиления по углу и угловой скорости ГК(ТК);
K3- коэффициент усиления по обратной связи с привода.
Угловая скорость αy измеряется блоком датчиков угловой скорости (БДУС), а угол αy получается путем интегрирования сигнала с БДУС.
Уравнения (1) - (4) описывают динамику работы системы стабилизации.
Если пренебречь действием Мву (как величиной более высокого порядка малости по сравнению с моментом от тяги на плече смещения центра масс), то в результате работы системы стабилизации ГК(ТК), ДУ поворачивается таким образом, чтобы вектор тяги  проходил через физический центр масс ОПНС "Мир" (см.фиг.2).
проходил через физический центр масс ОПНС "Мир" (см.фиг.2).
На фиг. 2 показано положение камеры сгорания ДУ после стабилизации углового положения ГК(ТК) по каналам рыскания и тангажа, при этом введены следующие обозначения:
9 - корпус ГК(ТК);
10 - привод камеры сгорания ДУ по оси рыскания;
11 - привод камеры сгорания ДУ по оси тангажа;
12 - камера сгорания ДУ.
OXYZ - расчетное положение главных центральных осей ОПНС "Мир", совпадающих со строительными осями;
O'X'Y'Z'- физическое положение главных центральных осей ОПНС "Мир";
O0X0Y0Z0 - строительные оси приводов камеры сгорания ДУ;
O1Х1Y1Z1 - строительные оси камеры сгорания.
Как видно из фиг.2, вектор тяги  после завершения процесса стабилизации направлен на физический центр масс O' ОПНС "Мир". При этом имеются углы разворота камеры сгорания по рысканию Ψ1 и по тангажу Q1. Центр физического базиса O' смещен относительно главных центральных осей на расстояния a, b и c соответственно по осям OX, OY и OZ.
после завершения процесса стабилизации направлен на физический центр масс O' ОПНС "Мир". При этом имеются углы разворота камеры сгорания по рысканию Ψ1 и по тангажу Q1. Центр физического базиса O' смещен относительно главных центральных осей на расстояния a, b и c соответственно по осям OX, OY и OZ.
В исходном положении (при неработающей системе стабилизации) продольные оси строительных осей ОПНС "Мир" и камеры ДУ ГК(ТК) совпадают, а остальные две - однонаправлены и соответственно параллельны друг другу.
На фиг.2 обозначены также три характерных линейных размера:
l - расстояние от O1 до O2, где O2 точка, имеющая координату (a,0,0); ,
,
Если выразить расстояние a, b и c через l, то они примут вид:
а = lк - l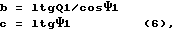
где
lк - конструктивно заданное расстояние между точками O и O1.
Значения a, b и c, записанные в (6), можно представить через 1'', подставив выражение
l = l″cosΨ1cosQ1 (7) ,
тогда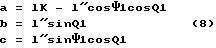
В выражениях (8) значения углов Ψ1 и Q1 известны по данным телеметрической информации. Следовательно, для окончательного определения a, b и c необходимо определить l''.
С целью определения значения 1'' после установившегося режима стабилизации углового движения корпуса ОПНС "Мир" прикладываем к корпусу, например, с помощью системы гиродинов управляющий момент  . Пусть этот момент будет направлен по оси OY (см. фиг.3), т.е.
. Пусть этот момент будет направлен по оси OY (см. фиг.3), т.е. 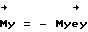 . Тогда уравнение (1) примет вид:
. Тогда уравнение (1) примет вид: ,
,
Система стабилизации космического корабля, выполняющего коррекцию орбиты, воспримет указанный управляющий момент как большой возмущающий и будет парировать его до тех пор, пока не наступит очередная стабилизация углового движения корпуса ОПНС "Мир". При этом парирование достигается за счет поворота камеры ДУ на угол Ψ2 (см. фиг.3) и образования тем самым для вектора тяги  плеча d (обозначения на фиг.3 соответствуют обозначениям на фиг.2).
плеча d (обозначения на фиг.3 соответствуют обозначениям на фиг.2).
По условию выполнения режима стабилизации: ,
,
где
Следовательно, .
.
Так как расстояние l'' физически неизменно для обоих случаев коррекции, то его можно определить из образовавшегося прямоугольника O0O'O'' по известному d и противолежащему углу 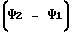 :
: .
.
Величины векторов  известны, значение угла Ψ2 также известно. Следовательно, величина l'' определена, a по ней определены и значения a, b и c:
известны, значение угла Ψ2 также известно. Следовательно, величина l'' определена, a по ней определены и значения a, b и c: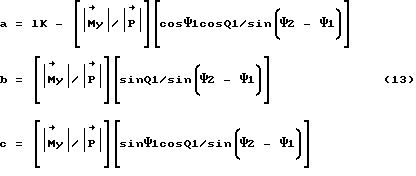 .
.
Если приложить управляющий момент 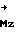 только по оси тангажа, то выражения (13) приводятся к виду:
только по оси тангажа, то выражения (13) приводятся к виду: .
.
Предлагаемый способ может быть реализован (как уже отмечалось) при помощи системы стабилизации движения ТК "Союз-ТМ" или ГК "Прогресс-М". Структурная схема устройства-аналога указанной системы представлена в монографии К. С.Колесникова "Жидкостная ракета как объект регулирования" (М.: Машиностроение, 1969) на с. 42, рис. 1.8. Корректирующий контур (КК) в ТК "Союз-ТМ" и ГК "Прогресс-М" в отличии от устройства-аналога содержит интегратор угловой скорости, два усилителя и сумматор. При этом выход гироскопического датчика указанного устройства-аналога соединен с входом интегратора КК и через первый усилитель с первым входом его же сумматора. Выход интегратора КК через второй усилитель соединен с вторым входом его сумматора. Выход сумматора является выходом КК.
Для оценки точности предлагаемого способа определения положения центра масс необходимо установить относительную погрешность величин, входящих в расчетные зависимости (13), (14).
Согласно проектным материалам на ОПНС "Мир" относительная погрешность в определении линейного размера lк составляет ~0,2%, т.е.
δlк/lк ~ 0,02 % .
Разработанные в Главной оперативной группе управления ОПНС "Мир" методики по тарировке тяги 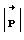 ДУ "Союз-ТМ" и "Прогресс-М", позволяют получать:
ДУ "Союз-ТМ" и "Прогресс-М", позволяют получать:
δP/P ≤ 0,35 % .
Относительная погрешность в определении углов поворота каждого привода камеры ДУ "Союз-ТМ" и "Прогресс-М" составляет:
δε/ε ~ 0,3 % .
А относительная погрешность в определении управляющего момента, выдаваемого гиродинами на корпус ОПНС "Мир", составляет
δM/M ~ 2,2 % .
Примем за малые углы Ψ и Q, так как в процессе стабилизации углового движения ТК "Союз-ТМ" и ТК "Прогресс - М" они не превышают 8o. Введем значение общего угла ε , заменяющего Ψ и Q. Тогда можно принять равносильность (⇐⇒) следующих выражений: .
.
Определим относительные погрешности величин a, b и c, преобразовав выражения (13, 14) по известным из теории ошибок правилам (см., например, Н.И. Кошкин, М.Г.Ширкевич. Справочник по элементарной физике. М., "Наука", 1972, с.242). При этом используем принятую в выражениях (15,16) равносильность.
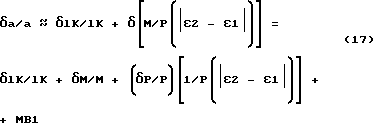 ,
,
где
МВ1- величина более высокого порядка малости, которой можно пренебречь при определении δa/a .
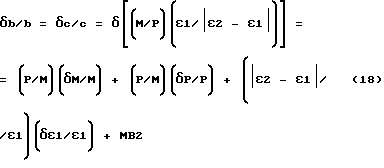 ,
,
где
МВ2- величина более высокого порядка малости, которой можно пренебречь при определении δb/b,δc/c .
Примем расчетные значения: P = 3000н; М = 1500н•м; δM/M = 0,022; .
.
Подставим эти значения в (17) и (18): .
.
Оценка точности способа произведена для случая его использования на ОПНС "Мир".
Как видно из вышеизложенного, наибольшую ошибку вносит относительная погрешность величины управляющего момента. Однако необходимо отметить, что на космических аппаратах другого назначения (например, космической астрофизической обсерватории (КАО) "Гамма") использовались гиродины с более высокой точностью выдачи управляющего момента. При этом относительная погрешность составляла ~0,25%. Более высокая точность достигалась за счет установки на приводах осей прецессии специальных шаговых двигателей.
На гиродинах, установленных на международной космической станции "Альфа", на приводах осей прецессии также будут применяться специальные шаговые двигатели. Предполагаемая точность выдачи величины управляющего момента будет не хуже, чем при помощи гиродинов на КАО "Гамма".
Если подставить δM/M ≈ 0,25% в выражения (17,18), при прочих равных значениях получим δa/a ≈ 0,5%, δb/b = δc/c ≈ 1,8 % . Следовательно, предложенный способ определения положения физического центра масс позволит решать аналогичную задачу на станции "Альфа" с относительной погрешностью по каждой координате не хуже 2%.


Изобретение относится к космической технике и касается средств определения положения центра масс космических аппаратов (КА) при управлении их угловым движением с помощью силовых приводов в условиях космического полета. В предлагаемом способе измеряют углы поворота выходных валов приводов подвеса двигательной установки при последовательных стабилизациях углового движения КА в процессе коррекции его орбиты, при этом дважды стабилизируют КА с приложением к нему во втором случае тарированных управляющих моментов со стороны моментных приводов при создании тарированной силы тяги данной двигательной установкой. С учетом величин этих моментов и силы тяги, по результирующему углу отклонения двигательной установки определяют фактическое положение центра масс КА в его строительных осях. Способ целесообразно применять на борту таких КА, как орбитальная научная станция "Мир", международная космическая станция "Альфа" и др. Относительная погрешность определения центра масс по каждой координате составляет ~ 2 %. Способ дает повышение точности и упрощение расчетной процедуры определения положения центра масс КА. 3 ил.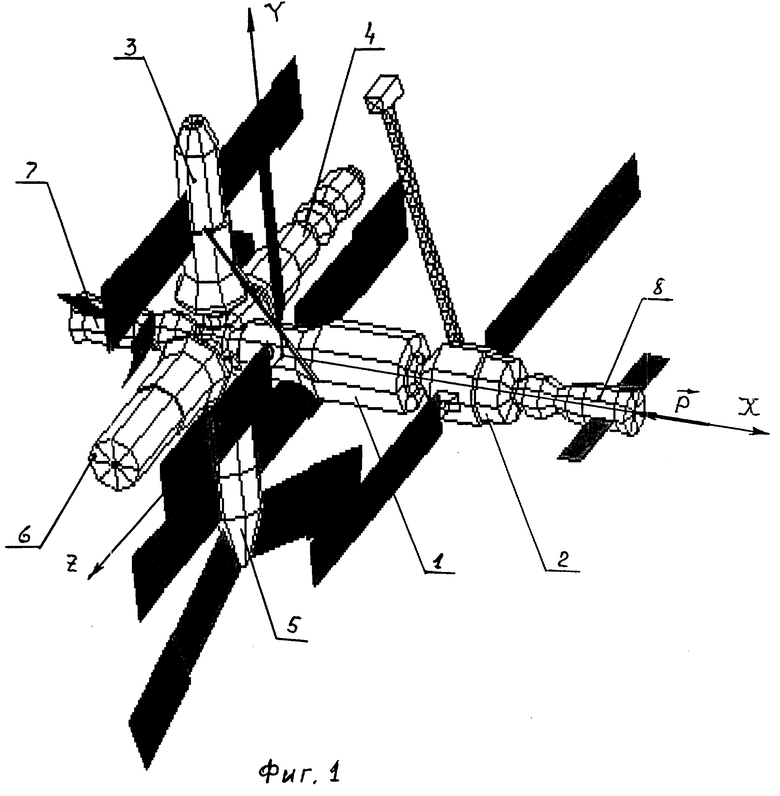
Способ определения положения центра масс космического аппарата в процессе его управления с помощью силовых приводов, включающий измерение параметров движения космического аппарата под действием тарированных управляющих моментов, прилагаемых к корпусу космического аппарата от силовых моментных приводов, и определение по измеренным параметрам положения центра масс космического аппарата, отличающийся тем, что стабилизируют угловое движение космического аппарата с помощью силовых приводов подвеса двигательной установки в процессе коррекции его орбиты, измеряют по окончании первичного режима стабилизации углы поворота выходных валов силовых приводов подвеса корректирующей двигательной установки, повторно после приложения тарированного управляющего момента к корпусу космического аппарата от моментов силового привода по одной из осей стабилизации стабилизируют угловое движение космического аппарата с помощью вращения силовых приводов подвеса двигательной установки с учетом приложенного момента, измеряют угол поворота выходного вала силового привода подвеса корректирующей двигательной установки по этой же оси стабилизации, определяют угол отклонения двигательной установки между первой и второй указанными стабилизациями как разность соответственно измеренных углов поворота выходного вала силового привода подвеса двигательной установки по определенному углу отклонения двигательной установки между первой и второй стабилизациями, а также по тарированным значениям величин силы тяги корректирующей двигательной установки и управляющего момента, определяют расстояние от точки подвеса корректирующей двигательной установки до физического центра масс космического аппарата, а по указанному расстоянию и по измеренным после первой стабилизации космического аппарата углам поворота выходных валов приводов подвеса корректирующей двигательной установки определяют положение физического центра масс относительно расчетного положения, связанного со строительными осями космического аппарата.
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Гернет М.М., Ратобыльский В.Ф | |||
| Определение моментов инерции | |||
| - М.: Маш иностроение, 1969, с | |||
| Выбрасывающий ячеистый аппарат для рядовых сеялок | 1922 |
|
SU21A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Бергменн Э., Дзиелски Дж | |||
| Опред еление инерционных характеристик КА с помощью управляющих моментов | |||
| Аэроко смическая техника | |||
| Способ приготовления консистентных мазей | 1919 |
|
SU1990A1 |
| Солесос | 1922 |
|
SU29A1 |
Авторы
Даты
1998-06-27—Публикация
1997-02-06—Подача