Изобретение относится к физике и химии поверхностных явлений и может быть использовано для определения параметров двойного электрического слоя.
Известен способ изучения поверхностных явлений, включающий регистрацию электрического сигнала, генерируемого на границе фаз (авт. свид. СССР N 966560, кл. G 01 N 13/00, 1982, Бюл. N 38).
Известен также способ исследования диффузной границы фаз, включающий изменение потенциала одной фазы относительно другой и отыскание минимума дифференциальной емкости границы фаз (Методы измерений в электрохимии. Ред. Э.Егер, А.Залкинд, т. 1. - М.: Мир, 1977, с. 106).
Во многих случаях потенциал минимума емкости расположен за пределами области поляризуемости границы фаз, что затрудняет его непосредственное определение. Кроме того, знания потенциала минимума не достаточно для определения ряда характеристик двойного слоя, в частности заряда частиц, образующих ионную обкладку границы фаз.
Предлагаемый способ позволяет получить дополнительные сведения о диффузной границе фаз благодаря тому, что он включает определение и использование точки перегиба на зависимости дифференциальной емкости от потенциала.
Измеряют значение потенциала, соответствующее точке перегиба дифференциальной емкости, а по найденному значению судят о потенциале минимума дифференциальной емкости и о составе межфазного слоя.
Через границу фаз пропускают переменный ток фиксированной амплитуды, регистрируют вторую гармонику потенциала, измеряют ее амплитуду как функцию среднего значения потенциала, а потенциал перегиба и минимума дифференциальной емкости находят из расположения экстремума и нуля этой функции.
Определяют интервал между потенциалами перегиба и минимума емкости и сравнивают найденный интервал с величиной 6RT/F, где R - газовая постоянная, F - число Фарадея, T - абсолютная температура фаз. Из результатов сравнения делают вывод о заряде n избыточного иона, участвующего в образовании двойного слоя, и о количестве дополнительных степеней свободы, соответствующих данному иону.
Предложенный способ позволяет исследовать явления испарения и конденсации двойного электрического слоя на границе фаз.
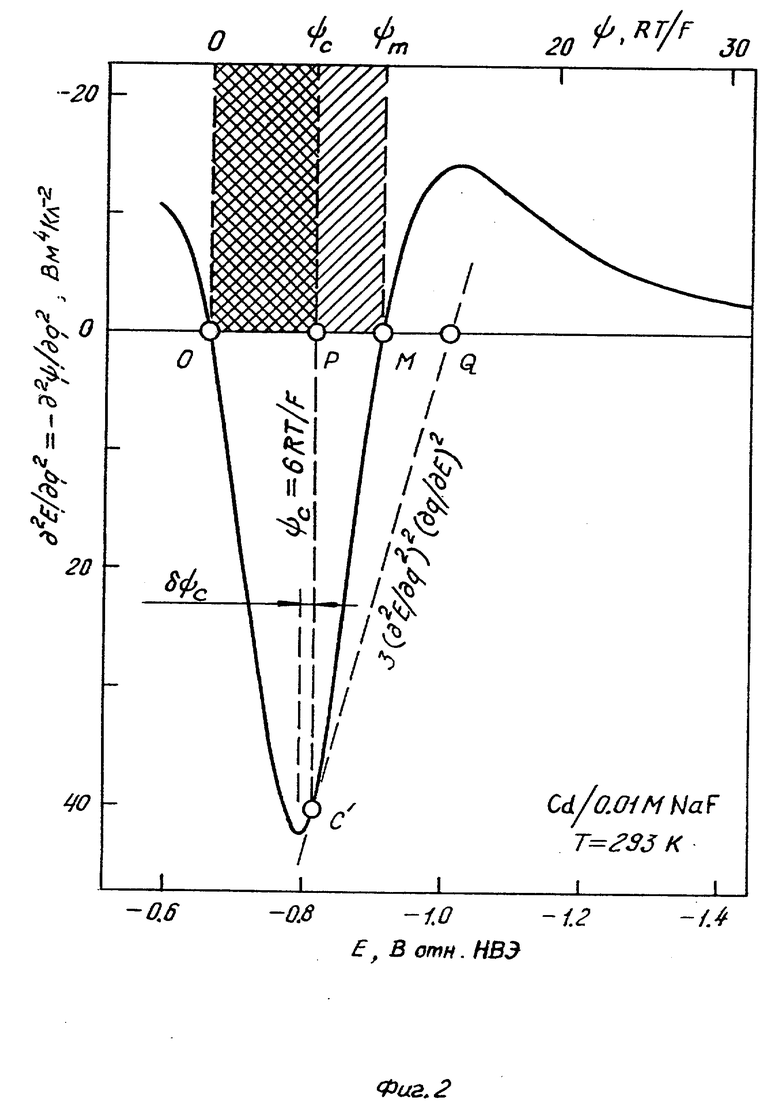
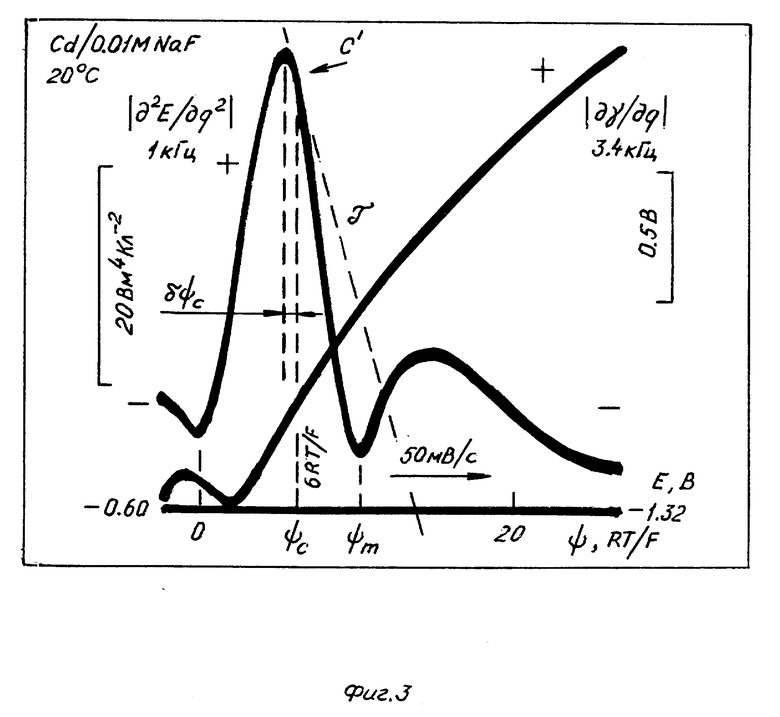
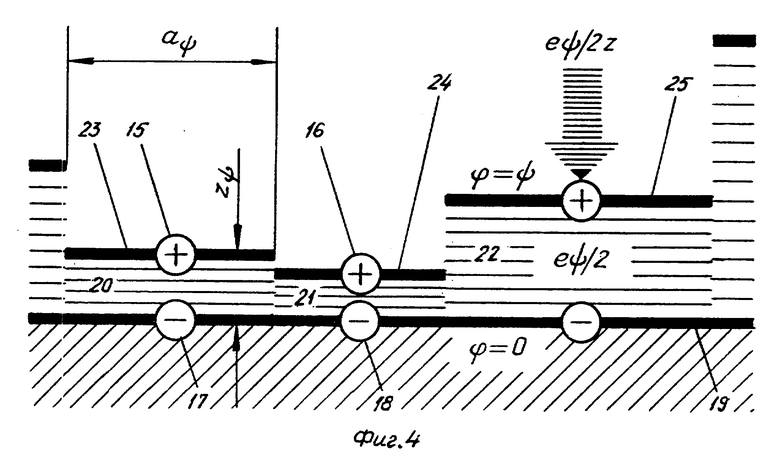
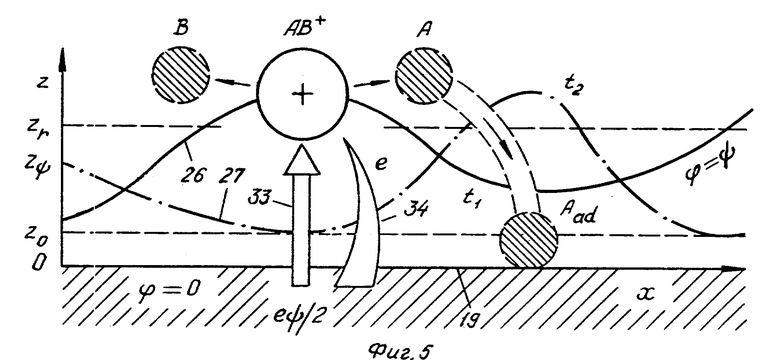
На фиг. 1 показано устройство для исследования диффузной границы фаз; на фиг. 2 - образ точки перегиба дифференциальной емкости на положительном склоне экстремума амплитуды второй гармоники потенциала; на фиг. 3 - сопоставление нулей второй гармоники потенциала и первой гармоники поверхностного натяжения при фиксированной амплитуде переменного тока через границу фаз; на фиг. 4 - сотовая модель двойного электрического слоя с распределением потенциала на границе металл-раствор; на фиг. 5 - волнообразные эквипотенциали на границе металл-раствор; на фиг. 6 - сочетание двух диффузных заряженных слоев на границе раствор-раствор; на фиг. 7 - перегиб и максимум на зависимости дифференциальной емкости диффузного слоя от потенциала; на фиг. 8 - элементарный вклад двойного слоя в снижение активационного барьера на зависимости потенциальной энергии исходных веществ и продуктов от координаты реакции в прямом и обратном процессах.
Распространены системы фаз, включающие растворы электролитов. В качестве примера ниже рассмотрено применение предлагаемого способа к системе "металлический электрод - двухкомпонентный раствор": кадмий в водном растворе 0,01 М NaF. Пластина кадмия, служащая исследуемым электродом, подвергнута предварительной электрополировке до получения фактора шероховатости 1,2. Потенциал E исследуемого электрода задан в шкале нормального водородного электрода (НВЭ), равновесный потенциал которого поддерживается реакцией 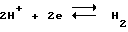 при давлении 0,1 МПа в растворе ионов водорода с активностью, равной единице.
при давлении 0,1 МПа в растворе ионов водорода с активностью, равной единице.
В определенной области потенциалов (у кадмия от -0,6 до -1,3 В) исследуемый электрод поляризуем и подобен конденсатору без утечки. Переход через потенциал E0 нулевого заряда приводит к изменению полярности металлической и ионной обкладок двойного электрического слоя на границе электрода с раствором (у кадмия в 0,01 М NaF E0 = -0,66 В). При отрицательном заряде металлической обкладки (E < E0) ионная обкладка содержит избыток катионов Na+ над анионами F-.
Исследование диффузной границы фаз проведено с помощью устройства (фиг. 1), обеспечивающего регистрацию производных потенциала E и поверхностного натяжения электрода γ по поверхностной плотности q заряда электрода, ∂2E / ∂q2 и ∂γ / ∂q .
Исследуемый электрод 1 в виде пластины приведен одной стороной в контакт с раствором электролита 2, находящимся в сосуде 3. В раствор погружены электрод сравнения 4 и вспомогательный электрод 5, служащие для задания среднего потенциала исследуемого электрода, а также дополнительный электрод 6, используемый для пропускания через исследуемый электрод 1 переменного тока заданной частоты fс. Электроды 4 и 5 подключены к потенциостату 7. Электрод 6 соединен с генератором 8 переменного напряжения, настроенного на заданную частоту fс. В цепь генератора 8 введено нагрузочное сопротивление 9, фиксирующее амплитуду переменного тока через электрод 6.
Электрод 6 подключен также к входу избирательного усилителя 10, настроенного на прием сигнала с частотой 2 fс, вдвое большей заданной частоты, что позволяет выделить вторую гармонику потенциала E, амплитуда которой пропорциональна величине ∂2E / ∂q2. После синхронного детектирования сигнал с выхода усилителя 10 поступает на вход осциллографа 11, развертка которого задана потенциалом, снимаемым с электрода 4. Это позволяет получить на экране осциллографа зависимость ∂2E / ∂q2 от E.
Кроме того, исследуемый электрод 1 приведен в механический контакт с пьезоэлементом 12, обкладки которого подключены к избирательному усилителю 13, настроенному на частоту fс переменного тока. Пьезоэлемент воспринимает колебания поверхностного натяжения γ , амплитуда которых пропорциональна ∂γ / ∂q и может быть зарегистрирована на осциллографе как функция потенциала E. Для уменьшения электрических наводок на пьезоэлемент исследуемый электрод подключен к земле 14.
На описанном устройстве получены зависимости ∂2E / ∂q2 - E и ∂γ / ∂q - E для кадмия в 0,01 М NaF при 20oC. Это достигнуто путем регистрации амплитуды второй гармоники потенциала E (1 кГц) и первой гармоники поверхностного натяжения твердого электрода γ (3,4 кГц) при фиксированной амплитуде плотности заряда q.
Из соотношения
∂2E / ∂q2 = -(∂q/∂E)-3 ∂2q / ∂E2 (1)
следует, что ∂2E / ∂q2 имеет нули при потенциалах экстремумов дифференциальной емкости Cd = ∂q / ∂E . Первый нуль, при -0,66 В (в шкале НВЭ), близкий к нулю ∂γ / ∂q , соответствует минимуму Cd в точке нулевого заряда E=E0 или Ψ = 0 , где Ψ = Eo- E . Второй нуль, при -0,91 В, соответствует максимуму Ψ = Ψm = 0,25B .
В точке C перегиба дифференциальной емкости выполнено ∂3q / ∂E3 = 0 , что соответствует наклону
∂(∂2E/∂q2)/∂E = 3(∂2E/∂q2)2(∂q/∂E)2>0 (2)
кривой ∂2E / ∂q2 - E в точке C', которая является образом точки C перегиба и расположена вблизи (δΨc = 0,02B) экстремума ∂2E / ∂q2. Этому экстремуму соответствуют значения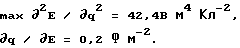
Их подстановка в (2) дает ∂(∂2E/∂q2)/∂E = 216 м4 Кл-2. Касательная τ с этим наклоном определяет точку C', измеренный потенциал ψ которой практически совпадает со значением ψc = 0,15 B, рассчитанным по уравнению
ψc = 6RT / nF (3)
при величине заряда иона n = 1 и T = 293 К (фиг. 2, 3); величина ψc - потенциал диффузионного коллапса, то есть критическое значение ψ , выше которого (по абсолютной величине) над электродом формируется уплотненная ионная атмосфера с зарядом, не зависящим от концентрации раствора электролита.
Экспериментальные результаты, полученные предложенным способом, указывают на сотовую структуру границы фаз (фиг. 4). При ψ > 0 двойной электрический слой образован избыточными катионами 15, 16 (Na+) и отрицательными зарядами 17, 18 поверхности металла 19. Среднее расстояние между ионами двойного слоя много больше среднего удаления иона от поверхности 19, разделяющей вещества фаз (zψ << aψ) . В этих условиях двойной электрический слой представляет собой систему независимых ячеек 20, 21, 22, образованных избыточными ионами и подобных элементарным конденсаторам.
В пределах своей ячейки каждый избыточный ион наделен порцией энергии
Ae = eψ / 2 , (4)
освобождаемой без одновременного участия других ионов двойного слоя, и испытывает притяжение к противоположно заряженному электроду с силой
Fe = eψ / 2(z + ze) , (5)
где
e - элементарный заряд, z - расстояние от центра иона до электрода, ze - постоянная, равная в простейшем случае нулю.
В каждой ячейке электрический потенциал ϕ изменяется от значения ϕ = 0 на поверхности 19 металла до значения ϕ = ψ на внешней обкладке 23. Обкладки 23, 24, 25 всех ячеек имеют один и тот же потенциал ϕ = ψ . Они образуют волнообразную эквипотенциаль, которая меняется со временем t и принимает различные формы 26, 27 в последовательные моменты t1, t2 (фиг. 5).
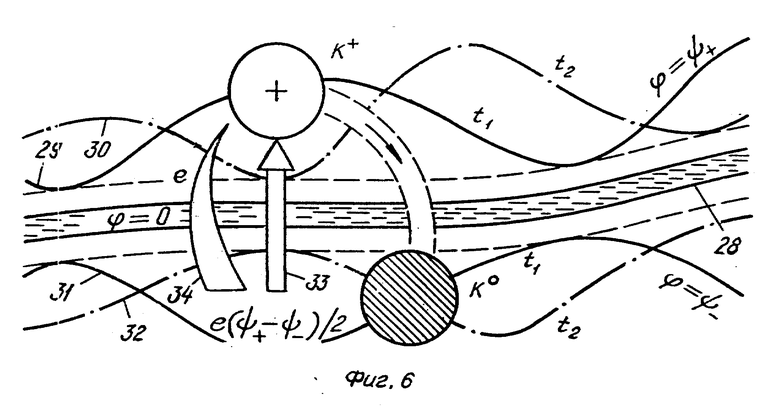
Граница двух жидкостей включает контактный слой 28, толщина которого соизмерима с размером молекул жидкостей. По обе стороны от контактного слоя расположены два диффузных двойных слоя, ограниченных эквипотенциалями ϕ = ψ+ и ϕ = ψ- , которые флуктуируют, принимая положения 29, 30 и 31, 32 в последовательные моменты времени t1 и t2 (фиг. 6).
Результаты, полученные предложенным способом, являются основной для построения единой теории двойного электрического слоя - без эмпирического разделения его на плотную и диффузную части. Резкое уменьшение диффузности в окрестности потенциала ψc - результат перехода от преобладания кинетической энергии теплового движения ионов к преобладанию потенциальной энергии взаимодействия противоположных зарядов. На оси потенциала E электрода величина ψc/ представляет собой интервал между потенциалами перегиба и минимума дифференциальной емкости. Этот интервал зависит от заряда частиц, образующих двойной электрический слой, и от количества степеней свободы этих частиц.
Это может быть показано на примере отрицательно заряженного электрода в растворе электролита сколь угодно малой концентрации. Ионная атмосфера такого электрода образована катионами. Концентрация анионов пренебрежимо мала. Диффузионный поток JD катионов от электрода направлен против потока JF, обусловленного притяжением катионов к электроду,
JD = D ∂c / ∂z ; JF = cbFe, (6)
где
c = c(z,ψ) - концентрация катионов (по их количеству в тонком слое Δz ) ;
D = D(z) - коэффициент диффузии катиона;
b = D/kT - подвижность катиона;
k - постоянная Больцмана;
Fe(z,ψ) - сила притяжения катиона электродом.
В стационарном состоянии JD + JF = 0 при любом D,
∂c/∂z + (Fe/kT)c = 0. (7)
Отсюда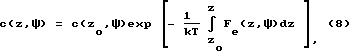
где
z0 - расстояние наибольшего притяжения центра катиона к электроду. Ионная атмосфера существует, если ее заряд qa = -q на единицу поверхности конечен,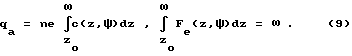
Возможность образования ионной атмосферы определяется видом функции Fe(z,ψ) . Например, сила Fe ≈ 1/z способна удержать ионную атмосферу при бесконечном разбавлении, тогда как сила Fe ≈ 1/z2 слишком слаба для этого.
В простейших условиях при заданном ψ диэлектрическая проницаемость ε раствора не оказывает значительного влияния на Fe, как и в случае взаимного притяжения пластин конденсатора.
При бесконечном разбавлении раствора величина ψc - потенциал начала образования ионной атмосферы
qa = 0 при ψ ≤ ψc; qa > 0 при ψ > ψc . (10)
В окрестности ψ c при qа>0
ψ = ψc(T) + qa/ Cm , (11)
где
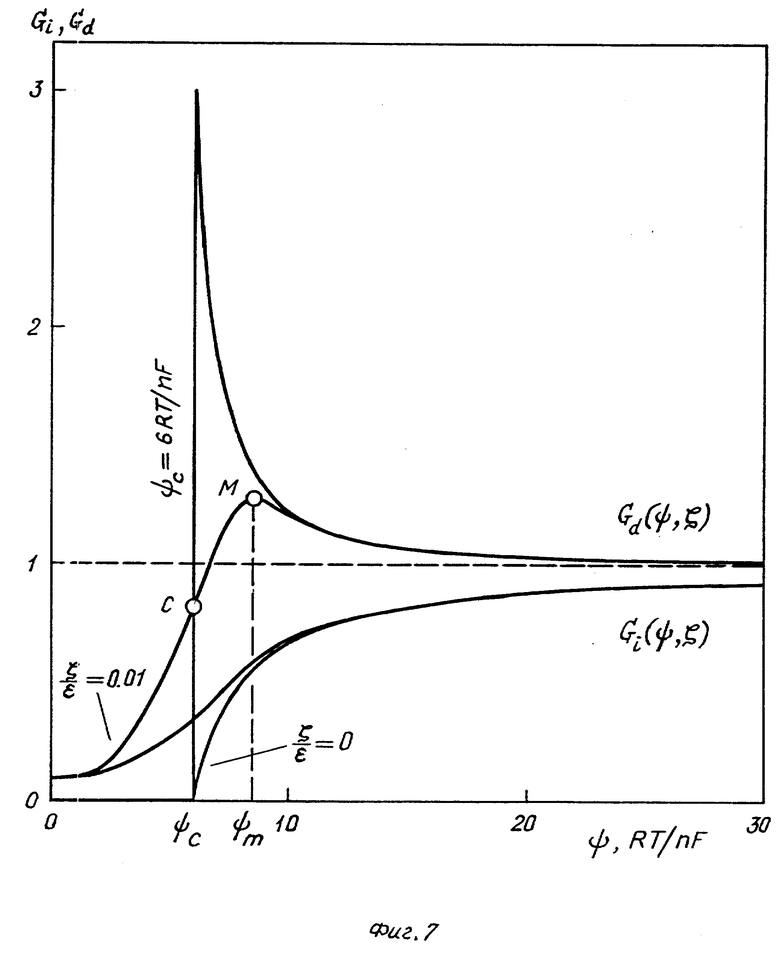
Cm = (∂qa/ ∂ψ) ψ = ψc - максимальное значение дифференциальной емкости двойного слоя (см. фиг. 7);
Gi= CiZo/ε и Gd = Cdzo/ ε - безразмерные значения интегральной емкости Ci и дифференциальной емкости Cd двойного слоя;
ζ - безразмерная концентрация раствора;
отношение ζ / ε = 0,01 соответствует приблизительно концентрации 0,01 моль/л; при увеличении концентрации раствора положение M максимума дифференциальной емкости смещается в сторону более высоких значений ψ ) .
При адиабатическом (мгновенном) разряде двойного слоя он освобождает энергию
Wc = qaψ / 2 = qaψc/ 2 + q
а при равновесном (медленном) разряде - энергию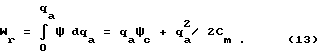
Такие же соотношения справедливы для модели автономного двойного слоя, в которой упругие шары с противоположными зарядами nk>0 (катионы, n = 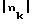 ) и na<0 (анионы либо электроны, n =
) и na<0 (анионы либо электроны, n = 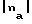 ) разделены изолирующей перегородкой и способны перемещаться в областях, размерности которых νk и νa в общем случае различны (модель на чертеже не показана). Например, νk = 3 для катионов в объеме раствора, νa = 2 для электронов в плоскости границы раздела фаз.
) разделены изолирующей перегородкой и способны перемещаться в областях, размерности которых νk и νa в общем случае различны (модель на чертеже не показана). Например, νk = 3 для катионов в объеме раствора, νa = 2 для электронов в плоскости границы раздела фаз.
Образование двойного слоя может рассматриваться как конденсация плазмы до состояния, в котором потенциальная энергия взаимодействия заряженных частиц соизмерима с их кинетической энергией. Из двух членов правой части (12) аддитивен по заряду (и, следовательно, по количеству частиц) лишь первый член qaψc/ 2 . Аддитивность указывает на тепловое происхождение этой части потенциальной энергии. При n = 1 (nk = -na = 1) в окрестности ψ = ψc , то есть при малых q, на каждую пару противоположно заряженных частиц приходится в среднем кинетическая энергия Wk = (νa + νk) kT/ 2 и потенциальная энергия Wp = eψc/ 2 .
Характерное для конденсированного состояния равенство wp = wk выполнялось бы при гармонических колебаниях частиц со всеми доступными степенями свободы. Этому условию удовлетворяют колебания вдоль границы раздела (по две степени свободы на частицу). Несколько отклоняются от него колебания в направлении нормали к границе (третья степень свободы). Поэтому указанное равенство выполняется приближенно, что может быть учтено заменой νk и νa на их эффективные значения
νke ≲ νk и νae ≲ νa ,
Wp = Wke = (νke+ νae)kT/ 2 .
Отсюда при nk = -na = 1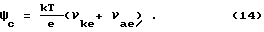
В случае любых nk и na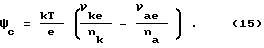
При ψ = ψc этому соответствует термо-э.д.с.
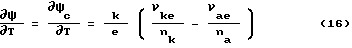
Если νke = νae = 3 и nk = -na = 1, то
ψc = 6kT/ e = 6 RT/ F ;
∂ψ/ ∂T = 6K/ e = 0,517 мВ/К .
При фиксированном q увеличение ψ с ростом T является результатом превращения тепловой энергии в электрическую. Если же фиксировано ψ , ν ν двойной слой полностью теряет заряд, то есть испаряется при температуре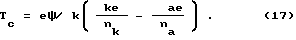
Переход через точку нулевого заряда (изменение знака q и ψ ) сопровождается перестановкой nk и na. При этом термо-э.д.с. меняет знак скачком.
Из данных, полученных предложенным способом, следует, что по сравнению с частицами электронейтральной в целом среды избыточные заряженные частицы диффузного двойного слоя аккумулируют больше тепловой энергии так, как если бы они обладали дополнительными степенями свободы, количество которых соответствует размерности их теплового движения.
В системе электрод-электролит число дополнительных степеней свободы, приходящихся на пару противоположных зарядов "катион раствора - электрон металла", превосходит 3. В примере с кадмием и ионами натрия оно близко к 6 при достаточно большом разбавлении раствора. Это возможно, если в тепловом движении наряду с ионами раствора участвуют также электроны поверхности металла, взаимодействующие с молекулами растворителя.
Классический подход к распределению положительных ионов у отрицательно заряженного электрода основан на решении уравнений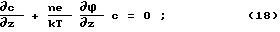

Эти уравнения однако не совместимы с условием конечности перепада потенциала ϕ в автономной ионной атмосфере,
0 ≤ ϕ(z) - ϕ (z0) ≤ ψ . (20)
Поэтому классический подход не в состоянии объяснить образование плотного двойного слоя в разбавленных растворах. Причина такого расхождения уравнений (18), (19) с опытом заключена в самоотталкивании заряда, который искусственно распределен в пространстве. Сосредоточенному заряду ne соответствует куб со стороной ac = c-1/3. Притягивающее поле электрода ослаблено в центре куба полем, которое создается половиной куба с эффективной поверхностной плотностью заряда σ = nec2/3/ 2 . Это поле должно быть добавлено к решению уравнения Пуассона (19), подставляемому в (18):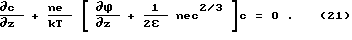
Отсюда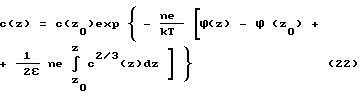
В отличие от (18) эти уравнения описывают автономную ионную атмосферу и, в частности, дают необходимую асимптотику c(z) __→ 0 при z __→ ∞ . В данном случае на ион действует сила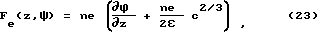
не зависящая от свойств электрода, что возможно лишь в частном случае. Исследования предложенным способом показывают, что в общем случае сила Fe, притягивающая ион диффузной атмосферы к электроду, зависит не только от заряда электрода, но и от количества дополнительных степеней свободы, вносимых этим зарядом, а, следовательно, от свойств металла и характера взаимодействия его с растворителем.
Замена половины куба зазором означает переход к модели в виде мозаики микроконденсаторов (см. фиг. 4). Зазор возникает естественным путем между электродом и монослоем диффундирующих ионов при 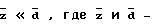 средние расстояние иона до электрода и расстояние между ионами. Для
средние расстояние иона до электрода и расстояние между ионами. Для 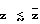 справедливо приближение плоского конденсатора Fe = neψ/ 2z . Измеренное на опыте значение ψc может быть использовано для экстраполяции Fe в сторону больших
справедливо приближение плоского конденсатора Fe = neψ/ 2z . Измеренное на опыте значение ψc может быть использовано для экстраполяции Fe в сторону больших 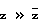 с учетом свойств электрода:
с учетом свойств электрода: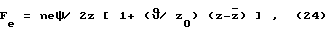
где параметр ϑ < z0 должен быть найден путем решения (7) с последующим расчетом ψc и сопоставлением найденного значения с экспериментальным. Результат проведенной таким путем экстраполяции справедлив для достаточно малых концентраций электролита (0,01 М), включающих случай бесконечно разбавленного раствора.
При определенных условиях на электроде возможен обратимый разряд некоторых ионов, например, 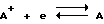 либо
либо 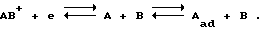 На некоторой стадии тепловой флуктуации локальная толщина двойного слоя zψ оказывается меньше эффективной дальности zr переноса заряда, например, путем туннелирования. Ток утечки, возникающий при этом в двойном слое, усиливается с ростом перенапряжения
На некоторой стадии тепловой флуктуации локальная толщина двойного слоя zψ оказывается меньше эффективной дальности zr переноса заряда, например, путем туннелирования. Ток утечки, возникающий при этом в двойном слое, усиливается с ростом перенапряжения 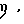 равного отклонению ψ от равновесного значения ψe . За время разряда избыточного иона диполи среды не успевают изменить ориентацию, наведенную исходным полем. Вокруг вакансии разрядившегося иона образуется пассивная зона, суммарный дипольный момент которой равен в среднем нулю (с точностью до флуктуаций): диполи, число которых не изменилось, уравновешиваются парами зарядов "катион - электрон", число которых в результате разряда уменьшилось на единицу. Вакансии соответствует локальное значение ψ = ψz ≈ 0 .
равного отклонению ψ от равновесного значения ψe . За время разряда избыточного иона диполи среды не успевают изменить ориентацию, наведенную исходным полем. Вокруг вакансии разрядившегося иона образуется пассивная зона, суммарный дипольный момент которой равен в среднем нулю (с точностью до флуктуаций): диполи, число которых не изменилось, уравновешиваются парами зарядов "катион - электрон", число которых в результате разряда уменьшилось на единицу. Вакансии соответствует локальное значение ψ = ψz ≈ 0 .
Изменение локального перепада потенциала от ψ до ψe включает две стадии ψ __→ ψz и ψz__→ ψe . В случае, если ψz< ψe < ψ , эти стадии представляют собой разряд и ионизацию с переносом элементарного заряда e, имеющего знак ψ . Освобождение энергии e (ψ - ψz) / 2 сочетается с потреблением энергии e (ψe- ψz) / 2 . В среднем по электроду это эквивалентно освобождению энергии eη/ 2 = eψ / 2 - eψe/ 2 , которая расходуется на уменьшение высоты активационного барьера. Перенос энергии (стрелка 33, фиг. 5, 6) совершается одновременно с переносом заряда (стрелка 34).
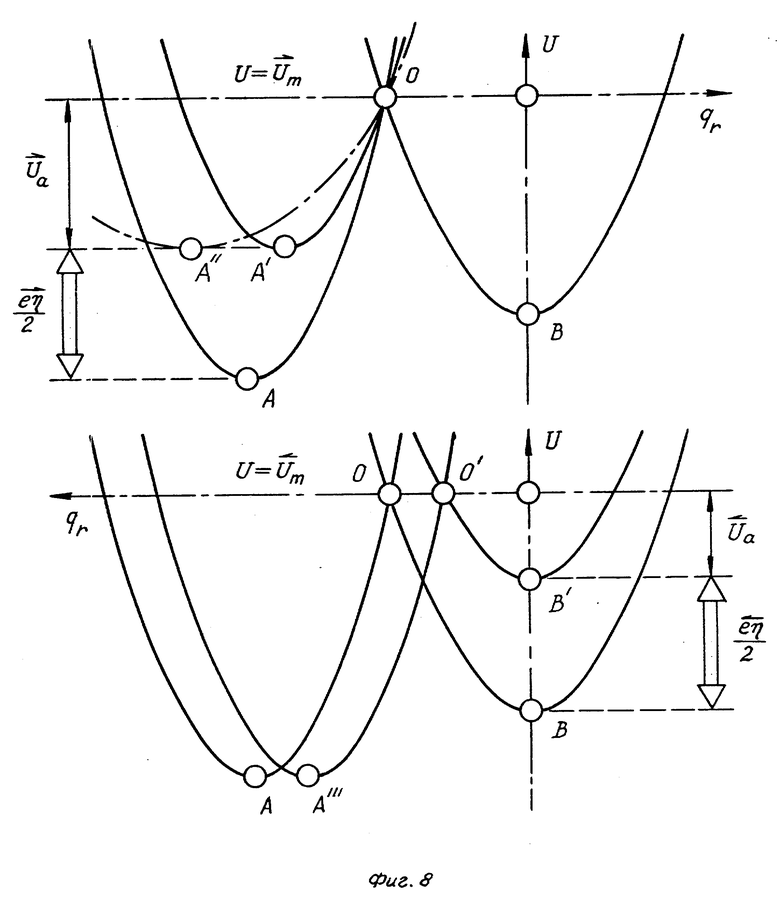
Переходный комплекс, образующийся в результате разряда иона, расположен в пассивной зоне и в простейшем случае свободен от химической связи с веществом электрода. При этом перенапряжение не влияет на состояние O переходного комплекса в координатах "Потенциальная энергия U системы - положение qr элемента системы" (фиг. 8). Сдвиг и деформация кривой потенциальной энергии исходного вещества не меняют уровня состояния 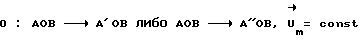 (прямая реакция)
(прямая реакция) 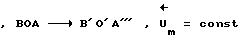 (обратная реакция). Снижение высоты активационного барьера до
(обратная реакция). Снижение высоты активационного барьера до  либо
либо  создается энергией
создается энергией 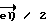 (прямая реакция) либо
(прямая реакция) либо 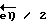 (обратная реакция). Возможно в определенных пределах различие расстояний qr(0) - qr(A′) и qr(0) - qr(A) . Равенство координат qr у состояний B и B' соответствует в данном примере локализации этих состояний на поверхности электрода (адсорбированный атом). В других случаях начальное и конечное состояния (A, A', A'', A''', B, B') участвующих в реакции веществ расположены в объеме раствора.
(обратная реакция). Возможно в определенных пределах различие расстояний qr(0) - qr(A′) и qr(0) - qr(A) . Равенство координат qr у состояний B и B' соответствует в данном примере локализации этих состояний на поверхности электрода (адсорбированный атом). В других случаях начальное и конечное состояния (A, A', A'', A''', B, B') участвующих в реакции веществ расположены в объеме раствора.
Примером переходного комплекса, образованию которого способствует нулевая поляризация пассивной зоны, является частица H3O в реакции разряда иона H3O+ в водной среде, с временем жизни не более 10-7 ... 10-10 с в объеме раствора (координатой реакции может служить положение протона относительно электрода). Из известного поведения этого переходного комплекса в электронейтральной среде с относительно малыми флуктуациями поляризации следует значительно меньшая вероятность его формирования в сильном электрическом поле двойного слоя.
Аналогичны процессы при переносе иона через границу двух несмешивающихся жидкостей. Перемещению иона предшествует его разряд с образованием промежуточной нейтральной или менее заряженной частицы, которая пересекает границу фаз и после этого восстанавливает свой заряд (переход K+ __→ K0 на фиг. 6).
Состояние заряженной ячейки границы фаз определяется плотностью расположения ячеек. Обособленность ячеек проявляется при разряде одной из них. Из классической электродинамики следует, что часть освобождаемой при разряде энергии может поступать от смежных ячеек. Эта часть, оцениваемая как 2z/d, достигает величины 0,2 при изменении ψ от 0 до 1 В. Однако равенство Ae = eψ / 2 выполнено в том же диапазоне ψ с более высокой точностью (0,02 для реакции выделения водорода на ртутном электроде). Это указывает на автономность ячейки в процессе ее разряда, что выходит за пределы классических представлений.
Наличная энергия ячейки eψ / 2 играет роль своеобразного кванта двойного слоя с фундаментальной константой, равной элементарному заряду. По аналогии эта энергия может быть названа контом (конт, cont). Как носитель элементарной энергии ячейка двойного слоя выполняет функцию квазичастицы.
При n = 1 ячейку можно рассматривать как состояние пары зарядов, созданное поглощением виртуального фотона, переносящего энергию поля двойного слоя. Поглощение чередуется с испусканием, что обеспечивает дискретную связь между ячейками и выравнивание их вклада в общее поле. В интервале времени τ между поглощением и испусканием ячейка изолирована от дополнительного влияния других ячеек. Минимальное время τ может быть оценено с использованием соотношения неопределенностей
τ ≈ 2h / eψ , (25)
где
h - постоянная Планка;
τ ≈ 10-15 с при ψ = 1B .
Элементарный акт разряда с потреблением порции энергии eψ / 2 осуществим лишь в том случае, если возможно образование переходного комплекса. Кроме того, времени τ должно быть достаточно для преодоления расстояния λ между зарядами ячейки. Согласно упрощенной оценке, для электрона без начальной скорости в направлении иона такой разряд возможен, если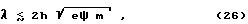
где
m - масса электрона;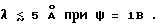
В этом одно из отличий границы фаз от макроскопического конденсатора, где за счет многократного взаимодействия с обновляющимся полем электрон способен приобрести при движении между пластинами вдвое большую энергию eψ .
Обнаруженные предложенным способом явления испарения и конденсации дискретной ионной атмосферы естественным образом объясняют основные свойства границы фаз, ранее оставшиеся непонятными: максимум дифференциальной емкости в окрестности потенциала нулевого заряда и независимость дифференциальной емкости от концентрации раствора за пределами этой окрестности. Размеры указанной окрестности определяются в предложенном способе положением точки перегиба емкости. Они содержат сведения о свойствах избыточных заряженных частиц по обе стороны границы фаз и о поверхностной теплоемкости, вносимой областью пространственного заряда. С дискретностью ионной атмосферы связана также не известная ранее лимитирующая стадия элементарного акта разряда иона:
перемещение иона вдоль границы фаз, отвлекающее значительную часть энергии внешнего источника и существенно влияющее поэтому на кинетику процесса.
Предложенный способ может быть использован для дальнейшего развития представлений о поверхностных явлениях с учетом дискретности электромагнитного поля.
Изобретение относится к физике и химии поверхностных явлений и может быть использовано для определения параметров двойного электрического слоя на границе фаз. Способ включает изменение потенциала одной фазы относительно другой и отыскание минимума дифференциальной емкости границы фаз. Определяют значение потенциала, соответствующее точке перегиба на зависимости дифференциальной емкости от потенциала, а по найденному значению судят о потенциале минимума дифференциальной емкости и о составе межфазного слоя. Через границу фаз пропускают переменный ток фиксированной амплитуды, регистрируют вторую гармонику потенциала, измеряют ее амплитуду как функцию среднего значения потенциала, а потенциалы точек перегиба и минимума дифференциальной емкости находят из расположения экстремума и нуля этой функции. Определяют интервал между потенциалами точек перегиба и минимума дифференциальной емкости, после чего сравнивают найденный интервал с величиной 6 RT/F, где R - газовая постоянная, F - число Фарадея, T - абсолютная температура фаз, и судят о заряде избыточного иона, участвующего в образовании двойного электрического слоя на границе фаз. 2 з.п.ф-лы, 8 ил.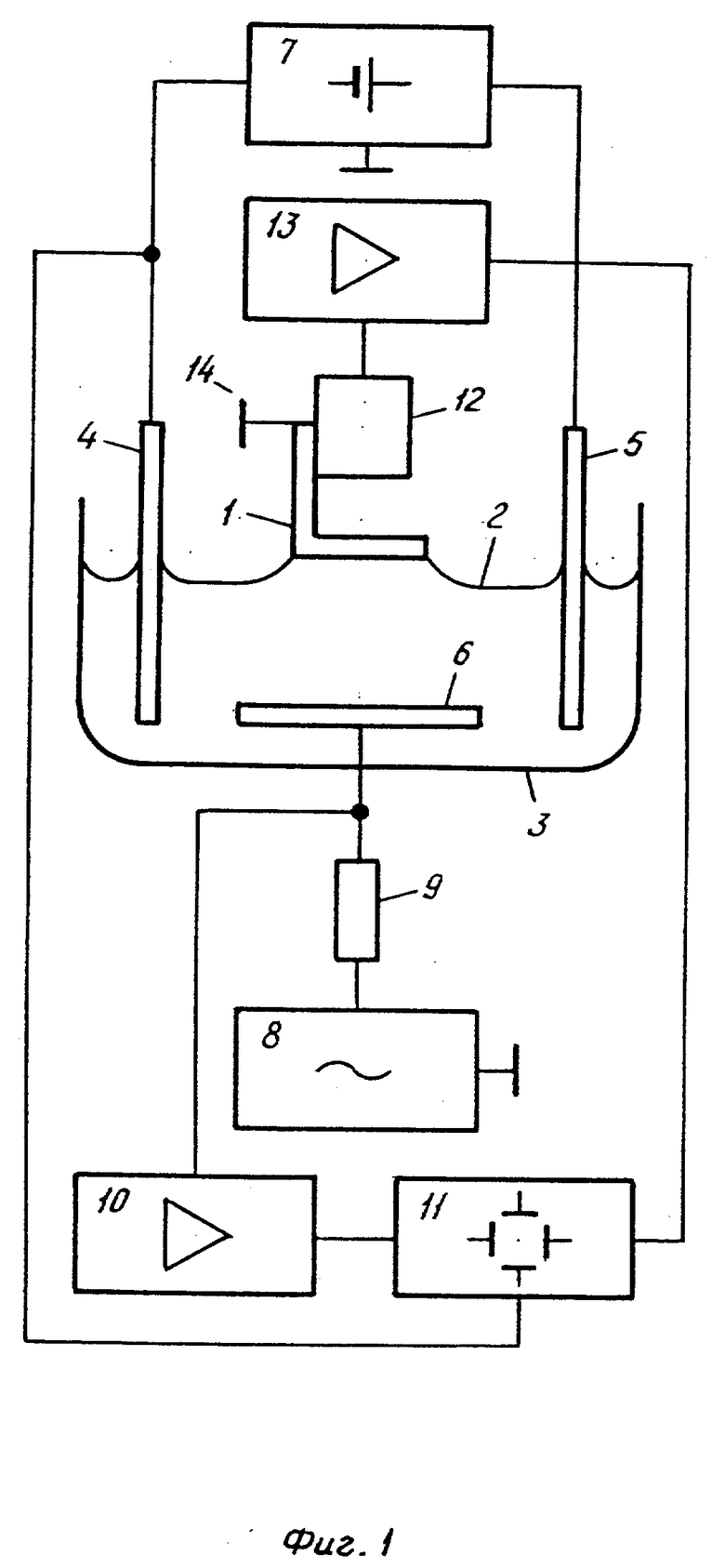
| SU, авторское свидетельство, 966560, кл | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Методы измерений в электрохимии: Ред.Э.Егер, А.Залкинд, т | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Светоэлектрический измеритель длин и площадей | 1919 |
|
SU106A1 |
Авторы
Даты
1998-09-27—Публикация
1996-06-14—Подача