Предлагаемое изобретение относится к измерительной технике и может быть использовано в электро- и радиоизмерительных устройствах, информационно-вычислительных и других (например, навигационных) системах для определения спектра электрических сигналов.
Известен способ определения спектра электрического сигнала, заключающийся в дискретизации сигнала через равные интервалы времени, с частотой дискретизации, не менее удвоенной верхней частоты сигнала, и непосредственной обработке полученных после дискретизации отсчетов по методу быстрого преобразования Фурье (БПФ) [1].
Однако указанный способ обладает низкой точностью определения спектральных составляющих анализируемого сигнала, особенно при частотах, близких к верхней частоте сигнала, что существенно сужает область рабочих частот.
Кроме того, известен способ определения спектра электрического сигнала [2], являющийся прототипом предлагаемого изобретения, заключающийся в получении N+1 цифровых отсчетов y[k] (выборок) электрического сигнала y(t) через равный интервал времени Δt, формировании N кусочно-линейных интерполирующих функций между соседними отсчетами сигнала, получении приближенной функции сигнала и нахождении Фурье-образа этой функции.
Однако и этот способ обладает низкой точностью определения спектра анализируемого сигнала при частотах, близких, равных или превышающих значение половины частоты дискретизации сигнала.
Задачей изобретения является создание способа определения спектра электрических сигналов с более высокой точностью измерения спектральных составляющих анализируемого сигнала, а также расширение рабочей области частот за частоту дискретизации сигнала.
Это достигается тем, что в способе, заключающемся в получении цифровых отсчетов y[k] сигнала через равные промежутки времени Δt и формировании интерполирующих функций между соседними отсчетами сигнала, получении приближенной функции, аппроксимирующей сигнал, и нахождении Фурье-образа этой функции, составляется оценка функции (аппроксимирующая функция) сигнала y(t) вида (1)
(1)
в которой на первом интервале дискретизации 0 ≤ t < Δt, т.е. при k = 0) интерполяционную временную функцию представляют полиномом L - степени (L≥3)
на последующих интервалах - разностью полиномов, интерполирующих анализируемый и предшествующий участки функции сигнала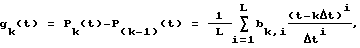
где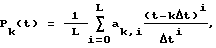
ak,i - сумма весовых коэффициентов при ti,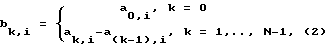 (2)
(2)
на последнем интервале дискретизации ((N-1)Δt, NΔt) используют линейный полином (L = 1)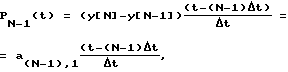
после чего спектральные коэффициенты рассчитывают по формуле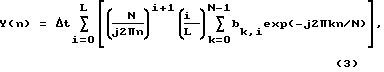 (3)
(3)
где n = 0, N-1 - порядковые номера дискретных частотных отсчетов.
Способ поясняется чертежами, где: на фиг. 1 приведена одна из возможных структурных схем устройства, поясняющая способ определения спектра электрического сигнала; на фиг.2 - графики относительных погрешностей способов определения спектральных компонентов электрического сигнала; а - для прототипа, б - для предложенного способа (L = 3), в - для предложенного способа (L = 4).
Устройство (фиг. 1) содержит последовательно соединенные датчик электрического сигнала 1 (ДЭС), аналого-цифровой преобразователь 2 (АЦП), интерфейс связи 3 (ИС), электронно-вычислительную машину 4 (ЭВМ).
Способ можно уяснить, рассмотрев работу устройства. Аналоговый электрический сигнал y(t), формируемый датчиком сигнала 1, поступает в аналого-цифровой преобразователь 2, с выхода которого код каждой k-ой дискретной выборки сигнала y(k) (где k = 0, ..., N-1) поступает через интерфейс связи 3 в электронно-вычислительную машину 4.
При составлении оценки функции сигнала (1) предварительно на каждом k-ом временном интервале (т. е. [kΔt, (k+1)Δt]) функцию интерполируют полиномом Pk(t) L-й степени (здесь L≥3), при этом на первом этапе на каждом k-ом интервале для последовательности из L+1 выборок (y[k], y[k+1], ..., y[k+L]) строят L+1 функций времени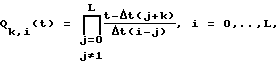
на втором этапе для каждого k-го интервала составляют интерполяционный полином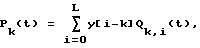
который путем объединения подобных членов при ti приводят к виду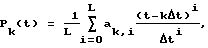
где ak,i - сумма весовых коэффициентов при ti для (k, i) последовательностей; и на последнем интервале дискретизации ((N-1)Δt, NΔt) используют линейный полином
На третьем этапе составляют оценку функции сигнала y(t)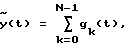
в которой на первом интервале дискретизации (0 ≤ t < Δt, т.е. при k = 0) интерполяционную временную функцию представляют полиномом L-й степени (L≥3)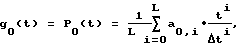
на последующих интервалах - разностью полиномов, интерполирующих анализируемый и предшествующий участки функций сигнала
где 
Затем в электронно-вычислительной машине 4 по полученным через интерфейс связи 3 дискретным выборкам сигнала y[k], в зависимости от заданной степени L полинома, вычисляются коэффициенты bk,i (используя выражение (2)), интерполяционной функции (1)). Так, значения коэффициентов bki, например, в случае интерполяции функции на интервале между отсчетами полиномом третьей степени (L = 3), вычисляют по выражениям:


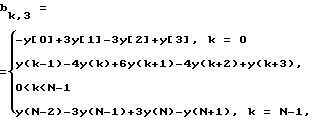
При использовании при интерполяции полинома четвертой степени значения bk,i вычисляют по выражениям




После чего по формуле (3) вычисляют спектр электрического сигнала y(t).
Сравнение погрешностей определения спектра электрического сигнала предложенного способа и способа прототипа выполним на примере аналитического экспоненциально спадающего сигнала, часто встречающегося на практике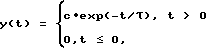
где c - масштабный множитель, τ - постоянная времени. Так, при τ = 0,1 мкс, интервале дискретизации Δt = 0,025 мкс и числе отсчетов N = 128 относительные погрешности расчета спектра d% для способов прототипа и предложенного в предлагаемом изобретении для L, равных 3 и 4, представлены соответственно на графиках фиг. 2а; фиг. 2б; фиг. 2в. Анализ приведенных на фиг. 2 относительных погрешностей показывает, что предложенный способ обеспечивает снижение погрешности определения амплитуды и фазы спектральных составляющих более чем на порядок, а также расширение области рабочих частот не менее чем в 4 раза.
Литература:
1. Макс Ж. Методы и техника обработки сигналов при физических измерениях. /Пер. с франц. -Т. 2. Основные принципы и классические методы. -М.: Мир, 1983. -312 с.
2. Шютте. Новый алгоритм быстрого преобразования Фурье для анализа линейных систем - применение к релаксационной спектроскопии с молекулярным пучком //Приборы для научных исследований, N 3, 73, (1981).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА КВАЗИПЕРИОДИЧЕСКИХ СИГНАЛОВ | 1999 |
|
RU2187838C2 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА ПОЛИГАРМОНИЧЕСКИХ СИГНАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2008 |
|
RU2363005C1 |
| ИЗМЕРИТЕЛЬ ВРЕМЕННОЙ ЗАДЕРЖКИ СИГНАЛОВ В ДИНАМИЧЕСКИХ СИСТЕМАХ | 1992 |
|
RU2118847C1 |
| СПОСОБ АКТИВНОГО КОНТРОЛЯ УРОВНЯ НЕСИНУСОИДАЛЬНОСТИ НАПРЯЖЕНИЯ И ТОКА | 2003 |
|
RU2262174C2 |
| СПОСОБ ДОПЛЕРОВСКОЙ ФИЛЬТРАЦИИ ИОНОСФЕРНЫХ СИГНАЛОВ | 2012 |
|
RU2516589C1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА ЭЛЕКТРИЧЕСКОГО СИГНАЛА | 2010 |
|
RU2431853C1 |
| СПОСОБ АНАЛИЗА МНОГОЧАСТОТНЫХ СИГНАЛОВ, СОДЕРЖАЩИХ СКРЫТЫЕ ПЕРИОДИЧНОСТИ | 2009 |
|
RU2399060C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2001 |
|
RU2189621C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2001 |
|
RU2189622C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ИСХОДНЫХ СИГНАЛОВ | 2003 |
|
RU2259591C2 |

Изобретение относится к измерительной технике и предназначено для спектрального анализа электрических сигналов. Способ определения спектра электрического сигнала y(t) заключается в получении цифровых отсчетов y[k] сигнала через равные интервалы времени Δt и формировании интерполирующих функций между соседними отсчетами сигнала, получении приближенной функции, аппроксимирующей сигнал, и нахождении Фурье-образа этой функции, составлении оценки функции сигнала y(t) вида
в которой на первом интервале дискретизации (0≤t<Δt, т.е. при k = 0) интерполяционную временную функцию представляют полиномом
на последующих интервалах - разностью полиномов, интерполирующих анализируемый и предшествующий участки функции сигнала


где ak,i - сумма весовых коэффициентов при ti, на последнем интервале дискретизации используют линейный полином, после чего спектральные коэффициенты рассчитывают по формуле
Способ обеспечивает более высокую точность определения спектра и более широкую область рабочих частот. 2 ил.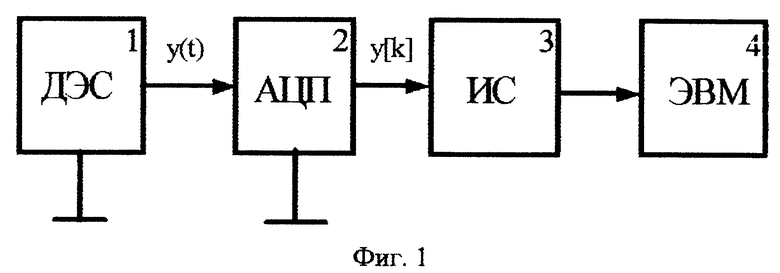
Способ определения спектра электрического сигнала y(t), заключающийся в получении цифровых отсчетов y[k] сигнала через равные интервалы времени Δt и формировании интерполирующих функций между соседними отсчетами сигнала, получении приближенной функции, аппроксимирующей сигнал, и нахождении Фурье-образа этой функции, отличающийся тем, что составляют оценку функции сигнала y(t) вида
в которой на первом интервале дискретизации (0 ≤ t < Δt, т.е. при k = о) интерполяционную временную функцию представляют полиномом
на последующих интервалах - разностью полиномов, интерполирующих анализируемый и предшествующий участки функции сигнала
где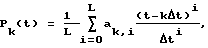
ak,i - сумма весовых коэффициентов при ti,
на последнем интервале дискретизации ((N-1)Δt, NΔt) используют линейный полином (L = 1)
после чего спектральные коэффициенты рассчитывают по формуле
где n = 0, ..., N-1 - порядковые номера дискретных частотных отсчетов.
| Шютте, Новый алгоритм быстрого преобразования Фурье для анализа линейных схем - применение к релаксационной спектроскопии с молекулярным пучком | |||
| Приборы для научных исследований, N 3.73 (1981) | |||
| Цифровой анализатор спектра | 1975 |
|
SU653575A1 |
Авторы
Даты
1999-07-10—Публикация
1997-10-30—Подача