Изобретение относится к измерительной технике и может быть использовано при дискретном гармоническом анализе полигармонических сигналов, в том числе характеризующихся быстрыми колебаниями основной частоты, например при измерении параметров электрических сетей с резкопеременной нагрузкой, исследовании виброакустических процессов в электромеханических агрегатах и т.п.
Из уровня техники известен классический способ цифрового спектрального анализа сигналов ([1] - Макс Ж. Методы и техника обработки сигналов при физических измерениях. В 2-х томах, М., Мир, 1983, т.2, стр.84-94), заключающийся в дискретизации сигнала путем аналого-цифрового преобразования и умножении последовательности дискретных отсчетов на временное окно для получения выборки дискретных отсчетов. Для уменьшения влияния конечности выборки на точность спектрального анализа, так называемого "эффекта окна", выборка умножается на плавно изменяющуюся функцию, обращающуюся в нуль за пределами окна (весовую функцию). Далее расчет спектральных составляющих спектра сигнала проводится методом дискретного преобразования Фурье.
Также известно устройство ([1], т.2, стр.87, рис.19.8) для реализации данного способа, содержащее низкочастотный фильтр, аналого-цифровой преобразователь, блок памяти, арифметическое устройство и усреднитель. Вход низкочастотного фильтра предназначен для поступления исследуемого сигнала, а выход соединен со входом аналого-цифрового преобразователя, выход которого подключен ко входу блока памяти. С памятью связано арифметическое устройство. Выход блока памяти соединен со входом усреднителя, выход которого является информационным выходом устройства.
Недостатком данных способа и устройства является то, что точность расчета спектральных составляющих полигармонического сигнала напрямую зависит от того, сколько периодов исследуемого сигнала попало во временное окно и в выборку дискретных отсчетов. Если исследуемый физический процесс носит стационарный характер и исследуемые сигналы имеют соответственно постоянную частоту основной (первой) гармоники, то достаточно подобрать ширину временного окна в зависимости от требуемой точности расчета спектра ([1], т.2, стр.90, рис.19.9) и умножить выборку дискретных отсчетов на соответствующую весовую функцию для коррекции "эффекта окна". Но если частота основной гармоники сигнала быстро изменяется по неизвестному заранее закону (колеблется), то точность расчета спектральных составляющих исследуемого сигнала резко снижается. Также при таком способе невозможно рассчитывать спектральные составляющие для каждого периода сигнала, поскольку для анализа берутся сразу несколько периодов, но результат расчета получается один для всех периодов сигнала. Помимо этого, уже полученная измерительная информация дополнительно усредняется за несколько циклов измерения, что делает невозможным получение достоверных спектров для полигармонических сигналов при быстрых колебаниях основной частоты.
Также известен способ цифрового спектрального анализа ([2] - НПП "ЭНЕРГОТЕХНИКА". Измерители показателей качества электрической энергии «PECУPC-UF2», Руководство по эксплуатации, 2005, п.4.5, [on-line] [найдено 18.12.2007] http://www.entp.ru/documentation/uf2_re.pdf), принятый в качестве прототипа, при котором для учета изменения частоты сигнала предварительно измеряется частота основной (первой) гармоники сигнала. Затем частота дискретизации аналого-цифрового преобразователя подстраивается таким образом, чтобы получить определенное число дискретных отсчетов за период измеренного значения основной частоты сигнала. Далее получают дискретные отсчеты сигнала путем аналого-цифрового преобразования и производят дискретный гармонический анализ с помощью дискретного преобразования Фурье.
Также известно устройство ([2], п.п.4.1-4.11, рис.А1) для реализации данного способа, содержащее первичный измерительный преобразователь, аналого-цифровой преобразователь и вычислительное устройство. Измеряемая физическая величина подается на вход первичного измерительного преобразователя. С его выхода исследуемый сигнал подается на вход аналого-цифрового преобразователя, с выхода которого измерительная информация поступает на вход вычислительного устройства, выход которого предназначен для выдачи спектральных составляющих исследуемого сигнала.
Недостатком данных способа и устройства является снижение точности расчета спектра в том случае, когда колебание основной частоты измеряемого сигнала происходит во время получения дискретных отсчетов. Это происходит из-за того, что аналого-цифровой преобразователь уже настроен на то значение периода основной частоты сигнала, которое имело место до возникновения колебания частоты, и возникшее изменение частоты никак не может быть учтено. Как следствие, возникает несовпадение интервала времени анализа сигнала и фактического периода его основной частоты. Кроме того, при работе устройства-прототипа нельзя обеспечить возможность расчета спектра каждого периода сигнала, что может требоваться, например, при исследовании переходных и пусковых режимов работы различного оборудования. Это происходит из-за того, что в данных способе и устройстве после предварительного измерения мгновенной частоты основной гармоники сигнала требуется определенное время на подстройку частоты дискретизации аналого-цифрового преобразователя, и за это время неизбежно происходит потеря информации об отдельных участках сигнала.
Задачей данного изобретения является повышение точности определения спектральных составляющих полигармонических сигналов при быстрых колебаниях основной частоты и обеспечение при этом возможности расчета спектральных составляющих для каждого периода сигнала.
Указанная задача решается за счет того, что в способе спектрального анализа полигармонического сигнала, заключающемся в получении последовательности дискретных отсчетов исследуемого сигнала путем аналого-цифрового преобразования и проведении дискретного гармонического анализа исследуемого сигнала с помощью дискретного преобразования Фурье, из исследуемого сигнала выделяют его основную гармонику, формируют из нее дополнительный сигнал, интервал дискретизации аналого-цифрового преобразования задают постоянным и получают последовательность дискретных отсчетов дополнительного сигнала путем его аналого-цифрового преобразования одновременно с исследуемым сигналом, далее на основании полученной последовательности дискретных отсчетов дополнительного сигнала вычисляют период частоты основной гармоники исследуемого сигнала, на основании которого определяют число интервалов дискретизации исследуемого сигнала, наиболее соответствующее величине периода частоты основной гармоники исследуемого сигнала, затем из последовательности дискретных отсчетов исследуемого сигнала производят выборку дискретных отсчетов длиной, равной числу интервалов дискретизации исследуемого сигнала, далее вычисляют корректирующий коэффициент по формуле:
R=(NΔt)/Т,
где R - корректирующий коэффициент;
N - число интервалов дискретизации исследуемого сигнала;
Δt - интервал дискретизации аналого-цифрового преобразования, с;
Т - период частоты основной гармоники исследуемого сигнала, с,
и дискретный гармонический анализ проводят над полученной выборкой дискретных отсчетов исследуемого сигнала, при этом аргументы всех тригонометрических функций, входящих в формулы для вычисления косинусных и синусных коэффициентов ряда Фурье, умножают на корректирующий коэффициент, а в устройстве для реализации данного способа, содержащем первичный измерительный преобразователь со входом для поступления измеряемой физической величины и выходом для выдачи исследуемого сигнала, аналого-цифровой преобразователь, вход которого соединен с выходом первичного измерительного преобразователя, и вычислительное устройство, вход которого сообщен с выходом аналого-цифрового преобразователя, а выход предназначен для выдачи спектральных составляющих исследуемого сигнала, введен блок выделения основной гармоники исследуемого сигнала со входом, соединенным с выходом первичного измерительного преобразователя, и выходом, а аналого-цифровой преобразователь выполнен с дополнительным входом, соединенным с выходом блока выделения основной гармоники исследуемого сигнала.
Известно, что при проведении спектрального анализа неизбежно возникают погрешности определения спектра, что является отражением общефизического принципа, согласно которому "невозможно одновременно определить частоту и время" ([1], т.2, стр.87). При цифровом спектральном анализе полигармонических сигналов, частота которых быстро колеблется, возникают дополнительные погрешности из-за невозможности учесть это изменение частоты, т.к. колебания частоты носят в общем случае случайный характер. Сущность заявленного изобретения состоит в компенсации влияния колебаний частоты на точность расчета путем определения основной частоты сигнала одновременно с получением его дискретных отсчетов. Это, во-первых, позволяет повысить точность расчета спектральных составляющих сигналов независимо от колебаний частоты основной гармоники за счет последующей коррекции расчета на основе данных измерения той мгновенной частоты сигнала, которую он имел именно во время дискретизации, и, во-вторых, обеспечить возможность расчета спектра каждого периода сигнала, так как становится возможным выбирать интервал времени анализа сигнала равным фактическому периоду его основной частоты и не требуется проводить усреднение результатов измерений.
Сущность изобретения поясняется чертежами.
На фиг.1 показана функциональная схема устройства для реализации способа спектрального анализа полигармонического сигнала;
на фиг.2 - эпюры мгновенных значений исследуемого и дополнительного сигналов;
на фиг.3 - схема расчета периода частоты основной гармоники исследуемого сигнала;
на фиг.4 - спектр амплитуд сигнала для примера расчета.
Устройство для реализации способа спектрального анализа полигармонических сигналов содержит первичный измерительный преобразователь 1, блок 2 выделения основной гармоники исследуемого сигнала, аналого-цифровой преобразователь 3 и вычислительное устройство 4. Вход первичного измерительного преобразователя 1 предназначен для поступления измеряемой физической величины, а его выход предназначен для выдачи исследуемого сигнала и сообщен со входом аналого-цифрового преобразователя 3 и со входом блока 2. Выход блока 2 сообщен с дополнительным входом аналого-цифрового преобразователя 3, выход которого сообщен со входом вычислительного устройства 4, выход которого предназначен для выдачи спектральных составляющих исследуемого сигнала.
Способ спектрального анализа полигармонических сигналов заключается в следующем.
Измеряемая физическая величина Ψ(t), являющаяся функцией времени t, подается на вход первичного измерительного преобразователя 1, выполняющего все операции по преобразованию физической величины Ψ(t) в исследуемый сигнал x(t). С выхода первичного измерительного преобразователя 1 исследуемый сигнал x(t) подается на вход аналого-цифрового преобразователя 3 и параллельно - на вход блока 2, который выделяет из исследуемого сигнала x(t) основную гармонику и формирует из нее на своем выходе дополнительный сигнал s(t). Далее дополнительный сигнал s(t) подается на дополнительный вход аналого-цифрового преобразователя 3, где подвергается дискретизации одновременно с исследуемым сигналом x(t). Интервал дискретизации аналого-цифрового преобразователя 3 задается постоянным независимо от основной частоты исследуемого сигнала x(t).
В результате дискретизации с выхода аналого-цифрового преобразователя 3 выдается единый цифровой поток данных, содержащий две согласованные по времени дискретные последовательности: дискретную последовательность h[t] исследуемого сигнала и дискретную последовательность d[t] дополнительного сигнала. Понятие "согласованные по времени" означает, что, во-первых, период Т частоты основной гармоники исследуемого сигнала и период Тдоп частоты основной гармоники дополнительного сигнала равны и, во-вторых, дискретная последовательность дополнительного сигнала смещена относительно дискретной последовательности исследуемого сигнала на время τ, необходимое для обработки исследуемого сигнала x(t) в блоке 2. Время τ является постоянным и точно учитывается в дальнейших расчетах.
Далее дискретная последовательность h[t] исследуемого сигнала и дискретная последовательность d[t] дополнительного сигнала поступают на вход вычислительного устройства 4, где определяется период Тдоп и число N интервалов дискретизации исследуемого сигнала, наиболее соответствующее величине периода Т. Для этого на основании полученной дискретной последовательности d[t] дополнительного сигнала определяются моменты перехода дополнительного сигнала s(t) через нулевое значение в одном и том же направлении. Эти моменты времени на фиг.2 обозначены точками А и В. Значение дискретного отсчета в дискретной последовательности d[t] для этих моментов должно стать равным нулю или изменить свой знак одинаковым образом: с плюса на минус, или наоборот. Подробно процедура определения моментов времени А и В поясняется схемой на фиг.3, на которой изображены ось времени t и совмещенная с ней числовая ось m, а также отмечены моменты времени А и В. По оси ординат откладываются значения дискретных отсчетов дискретной последовательности d[t] дополнительного сигнала. Поскольку при дискретизации сигналов и дискретном гармоническом анализе требуется переход от времени t к его дискретным значениям, и наоборот, то через отдельные значения m: m1, m2, m3, m4 - на фиг.3 одновременно обозначены как моменты физического времени, так и порядковые номера дискретных отсчетов в дискретной последовательности d[t] дополнительного сигнала, которые соответствуют этим моментам и для которых были получены дискретные отсчеты d[m1], d[m2], d[m3], d[m4].
Интервал между смежными моментами времени, например между моментами времени m1 и m2, является интервалом дискретизации Δt аналого-цифрового преобразования. Тогда для определения значения времени t, которому соответствует то или иное значение m, достаточно умножить число интервалов дискретизации Δt на разницу между этим значением m и значением m, соответствующим первому дискретному отсчету в выборке дискретных отсчетов, которая будет произведена далее.
Поскольку дополнительный сигнал s(t) содержит только основную гармонику и имеет гладкую форму без выбросов и помех, то участки сигнала между дискретными отсчетами d[m1] и d[m2] и между дискретными отсчетами d[m3] и d[m4] могут быть представлены кусочно-линейной интерполяцией. Момент времени m1 - это момент времени, в который был получен дискретный отсчет d[m1] с порядковым номером m1 и который предшествует пересечению оси времени t линией, интерполирующей дополнительный сигнал s(t) в точке А. Следующий дискретный отсчет d[m2] получен в момент времени m2 после пересечения оси времени t линией, интерполирующей дополнительный сигнал s(t) в точке А. Момент времени m3 - это момент времени, который предшествует пересечению оси времени линией, интерполирующей дополнительный сигнал s(t) в точке В, и в который был получен дискретный отсчет
d[m3] с порядковым номером m3. Следующий дискретный отсчет d[m4] получен в момент времени m4 после пересечения оси времени t сигналом s(t) в точке В.
На фиг.3 показаны две линии, необходимые для определения периода Тдоп: линия между дискретными отсчетами d[m1] и d[m2] пересекает ось времени t в точке А, а линия между дискретными отсчетами d[m3] и d[m4] пересекает ось времени t в точке В. Период Тдоп частоты основной гармоники дополнительного сигнала определяется по формуле:
Тдоп=t1+t2+t3,
где t1 - часть интервала дискретизации Δt между моментом времени А и моментом времени m2, с;
t2 - часть интервала дискретизации Δt между моментом времени m3 и моментом времени В, с;
t3 - сумма целых интервалов дискретизации Δt между моментами времени m2 и m3, с.
При этом часть t1 интервала дискретизации Δt находится из условия подобия треугольников, образованных пересечением оси времени t, линии, интерполирующей дополнительный сигнал s(t) и проходящей через точку А, и вертикальными линиями, проходящими через моменты времени m1 и m2, и определяется по формуле:
t1=Δt(|d[m2]|/(|d[m2]|+|d[m1]|)),
где Δt - интервал дискретизации аналого-цифрового преобразования, с;
|d[m1]| - модуль дискретного отсчета, полученного в момент времени m1;
|d[m2]| - модуль дискретного отсчета, полученного в момент времени m2.
Часть t2 интервала дискретизации Δt находится из условия подобия треугольников, образованных пересечением оси времени t, линией, интерполирующей дополнительный сигнал s(t) и проходящей через точку В, и вертикальными линиями, проходящими через моменты времени m3 и m4, и определяется по формуле:
t2=Δt(|d[m3]|/(|d[m4]|+|d[m3]|)),
где Δt - интервал дискретизации аналого-цифрового преобразования, с;
|d[m3]| - модуль дискретного отсчета, полученного в момент времени m3;
|d[m4]| - модуль дискретного отсчета, полученного в момент времени m4.
Сумма целых интервалов t3 определяется по формуле:
t3=Δt(m3-m2),
где Δt - интервал дискретизации аналого-цифрового преобразования, с;
m2 - номер дискретного отсчета в дискретной последовательности d[t] дополнительного сигнала, полученного в момент времени m2;
m3 - номер дискретного отсчета в дискретной последовательности d[t] дополнительного сигнала, полученного в момент времени m3.
Далее определяют число N интервалов дискретизации исследуемого сигнала, наиболее соответствующее величине периода Т, по формуле:
N=(T/Δt),
где T - период частоты основной гармоники исследуемого сигнала, с;
Δt - интервал дискретизации аналого-цифрового преобразования, с.
Для дальнейшего использования полученное число N округляют стандартным арифметическим округлением. Произведение числа N на интервал дискретизации Δt составляет интервал времени анализа исследуемого сигнала, при этом за счет процедуры округления максимальное несовпадение интервала времени анализа сигнала и периода его основной частоты не может превысить половину интервала дискретизации Δt. При этом число N получается произвольным, что требует отказа от использования алгоритма быстрого преобразования Фурье, так как для реализации данного алгоритма количество интервалов дискретизации должно являться степенью числа 2. Поскольку ни алгоритм быстрого преобразования Фурье, ни другие известные алгоритмы быстрых преобразований не влияют на точность расчетов, а позволяют лишь сократить объем вычислений, то за счет отказа от ограничений в выборе значений числа N достигается более полное совпадение интервала времени анализа сигнала и фактического периода его основной частоты. При этом задача сокращения объема вычислений не является актуальной для заявляемого изобретения.
После определения числа N из дискретной последовательности h[t] исследуемого сигнала производят выборку дискретных отсчетов. Для этого сначала определяют номер NА дискретного отсчета в дискретной последовательности d[t] дополнительного сигнала, соответствующий моменту времени на числовой оси m, наиболее близко расположенному к моменту времени А. Далее производят учет запаздывания дополнительного сигнала s(t) относительно исходного сигнала x(t) на время τ. Поскольку время τ является постоянной величиной, то дискретная последовательность d[t] дополнительного сигнала также запаздывает относительно дискретной последовательности h[t] исследуемого сигнала на число Nτ дискретных отсчетов, которое является постоянным и определяется по формуле:
Nτ=τ/Δt,
где Nτ - число дискретных отсчетов, на которое дискретная последовательность d[t] дополнительного сигнала запаздывает относительно дискретной последовательности h[t] исследуемого сигнала;
τ - время, необходимое для обработки исследуемого сигнала x(t) в блоке 2, с;
Δt - интервал дискретизации аналого-цифрового преобразования, с.
Для дальнейшего использования полученное число Nτ округляют также стандартным арифметическим округлением. Затем определяют номер N0 дискретного отсчета в дискретной последовательности h[t] исследуемого сигнала, соответствующий началу периода Т, по формуле:
N0=NA-Nτ,
где NА - номер дискретного отсчета в дискретной последовательности d[t] дополнительного сигнала, соответствующий моменту времени на числовой оси m, наиболее близко расположенному к моменту времени А;
Nτ - число дискретных отсчетов, на которое дискретная последовательность d[t] дополнительного сигнала запаздывает относительно дискретной последовательности h[t] исследуемого сигнала.
Выборка дискретных отсчетов для проведения дискретного гармонического анализа производится из дискретной последовательности h[t] исследуемого сигнала начиная с отсчета с номером N0 и длиной, равной числу N.
Далее проводят дискретный гармонический анализ, для чего полученную выборку дискретных отсчетов обрабатывают в соответствии с классическими формулами преобразования Фурье без использования алгоритмов быстрых преобразований. Известно, что при вычислении косинусных и синусных коэффициентов ряда Фурье для сигналов, представленных дискретными отсчетами, интегралы, входящие в формулы преобразования Фурье, вычисляются методом прямоугольников, т.е. вычисляются суммы площадей сигнала между смежными дискретными отсчетами. Из-за колебания частоты исследуемого сигнала возникает разница между каждой смежной площадью, рассчитанной при заданном фактическом интервале дискретизации, и той площадью, которая должна была получиться при точном совпадении интервала времени анализа с периодом Т частоты сигнала. Как было показано выше, за счет того что в данном способе спектрального анализа число N интервалов дискретизации определяется наиболее соответствующим величине периода частоты основной гармоники исследуемого сигнала, это несовпадение не может превысить половину интервала дискретизации Δt. Для дополнительной компенсации этого несовпадения способом, заявляемым в изобретении, вводится корректирующий коэффициент R, вычисляемый по формуле:
R=(NΔt)/T,
где N - число интервалов дискретизации исследуемого сигнала;
Δt - интервал дискретизации аналого-цифрового преобразования, с;
Т - период частоты основной гармоники исследуемого сигнала, с.
Далее, в процессе проведения дискретного преобразования Фурье, на этот корректирующий коэффициент R умножаются аргументы всех тригонометрических функций, входящих в формулы для вычисления косинусных и синусных коэффициентов ряда Фурье:
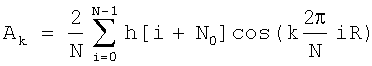 ,
,
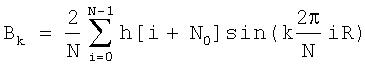 ,
,
где k - номер гармоники;
Аk - косинусный коэффициент ряда Фурье для k-ой гармоники;
Bk - синусный коэффициент ряда Фурье для k-ой гармоники;
N - число интервалов дискретизации исследуемого сигнала;
N0 - номер дискретного отсчета в дискретной последовательности h[t] исследуемого сигнала, соответствующий началу периода Т;
[i+N0] - текущий порядковый номер отсчета в дискретной выборке h[t] исследуемого сигнала при суммировании;
h[i+N0] - дискретный отсчет исследуемого сигнала для момента времени [i+N0];
R - корректирующий коэффициент.
Спектральные составляющие находятся по формулам:
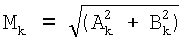 ,
,
φk=arctg(Аk/Вk),
где Мk - амплитуда k-й гармоники;
φk - фазовый угол k-й гармоники.
Предлагаемый способ спектрального анализа полигармонических сигналов и устройство для его реализации обеспечивают также возможность расчета спектра каждого периода исследуемого сигнала без пропусков участков исследуемого сигнала за счет того, что дискретная последовательность исследуемого сигнала поступает на вход вычислительного устройства 4 непрерывно и одновременно на вход вычислительного устройства 4 поступает вся информация, необходимая для определения периода частоты основной гармоники исследуемого сигнала. При этом не требуется дополнительного времени для определения этого периода и, как следствие, не происходит пропусков участков исследуемого сигнала.
В качестве примера реализации заявляемого изобретения приведен расчет спектральных составляющих полигармонического сигнала при условии возникновения колебания частоты основной гармоники сигнала. Для этого расчет произведен для двух смежных периодов сигнала с различной частотой основной гармоники сигнала. Прочие условия: спектральный состав сигнала и параметры аналого-цифрового преобразования - одинаковы для обоих периодов сигнала, что необходимо для обеспечения сопоставимости результатов расчетов, произведенных для двух периодов сигнала. Частота основной гармоники первого периода измеряемой физической величины Ψ(t) равна 50,08 Гц. Частота основной гармоники второго периода измеряемой физической величины Ψ(t) равна 49,93 Гц, что эквивалентно быстрому снижению основной частоты процесса (возникновению колебания частоты) на 0,15 Гц. На выходе первичного преобразователя 1 после преобразования измеряемой физической величины Ψ(t) получен полигармонический исследуемый сигнал x(t). Амплитуды гармоник заданы в относительных единицах (отн. ед.). Сигнал x(t) описывается, например, следующей функцией времени:
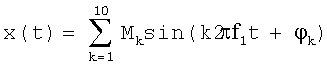 ,
,
где x(t) - исследуемый сигнал;
t - время, с;
k - номер гармоники;
Mk - амплитуда k-й гармоники, отн. ед.;
f1 - частота основной (первой) гармоники, Гц;
φk - фазовый угол k-й гармоники, градус.
Амплитуды и фазовые углы гармоник приведены в таблице 1. Амплитуда основной гармоники равна 100 отн. ед.: это позволяет получить результаты расчета спектра амплитуд, численно равные процентам.
На выходе блока 2 выделяется основная гармоника исследуемого сигнала и формируется дополнительный сигнал s(t), содержащий только основную гармонику исследуемого сигнала x(t). Сигнал s(t) описывается следующей функцией времени:
s(t)=Mssin(2πf1 (t-τ)+(φ1),
где s(t) - дополнительный сигнал;
Ms - амплитуда дополнительного сигнала, отн. ед.;
f1 - частота основной (первой) гармоники, Гц;
t - время, с;
τ - время, необходимое для обработки исследуемого сигнала x(t) в блоке 2, с;
φ1 - фазовый угол основной гармоники, градус.
Амплитуда дополнительного сигнала Ms равна 100. Динамический диапазон аналого-цифрового преобразования равен от -110 до +110 отн. ед. Интервал дискретизации Δt аналого-цифрового преобразования равен 3,9·10-5 с. Время τ равно 0,001 с. Последовательность дискретных отсчетов h[t] для исследуемого сигнала x(t) и последовательность дискретных отсчетов d[t] для дополнительного сигнала s(t) в примере получены расчетным путем. Для этого вычислены точные аналитические значения функций x(t) и s(t) для моментов времени t, отстоящих друг от друга на величину Δt. Полученные точные значения функций x(t) и s(t) преобразуют в целые числа в соответствии с порядком работы аналого-цифрового преобразователя, для чего каждое значение функций x(t) и s(t) делят на величину динамического диапазона, равного 110, умножают на 215 и округляют стандартным арифметическим округлением. Точность такого преобразования значений функций x(t) и s(t) в целые числа соответствует точности 16-битного аналого-цифрового преобразования.
Величина периода Т частоты основной гармоники для первого периода сигнала определена в соответствии с приведенной выше методикой расчета по схеме на фиг.3 и равна 0,019968 с. Величина периода Т частоты основной гармоники для второго периода сигнала определена аналогичным образом и равна 0,020028 с. При данных параметрах сигналов число N интервалов дискретизации равно 512 для первого периода сигнала и число N равно 514 для второго периода сигнала. Интервал времени анализа для первого периода сигнала включает 512 интервалов дискретизациии и равен 0,019968 с. Интервал времени анализа для второго периода сигнала включает 514 интервалов дискретизациии и равен 0,020046 с. При этом разница между интервалом времени анализа для второго периода сигнала и периодом его основной частоты равна 1,8·10-5 с, что составляет 46,154% от Δt и близко к максимально возможному для заявляемого способа спектрального анализа значению некратности интервала времени анализа сигнала периоду его основной частоты. Корректирующий коэффициент для первого периода сигнала равен R=(512·3,9·10-5)/0,019968=1,0. Корректирующий коэффициент для второго периода сигнала равен R=(514·3,9·10-5)/0,020028=1,000899.
Затем рассчитывают спектральные составляющие Мk и φk методом дискретного преобразования Фурье, при проведении которого аргументы всех тригонометрических функций, входящих в формулы для вычисления косинусных коэффициентов Аk и синусных коэффициентов Вk ряда Фурье, умножают на корректирующий коэффициент R.
Результаты расчета спектральных составляющих сигнала x(t) приведены в таблице 2.
ника k
В таблице 2 приведены также результаты, полученные при расчете спектра сигнала x(t) по прототипу при тех же исходных данных, что и по заявляемому способу. Согласно прототипу, число N интервалов дискретизации для расчета для первого и второго периодов сигнала одинаково и равно 512, а интервал дискретизации Δt аналого-цифрового преобразования для второго периода сигнала определен таким образом, чтобы за предыдущий (первый) период основной частоты производилось 512 измерений мгновенных значений исследуемого сигнала. Для значения основной частоты первого периода, равного 50,08 Гц, интервал дискретизации Δt равен 3,9·10-5 с, как и для способа, заявляемого в изобретении, что позволяет корректно сравнить результаты расчета по прототипу и по заявляемому способу. На фиг.4 показан полученный по данному способу спектр амплитуд Мk для второго периода сигнала с частотой основной гармоники, равной 49,93 Гц.
Как видно из таблицы 2, максимальная абсолютная погрешность определения амплитуды гармоник сигнала x(t) равна 0,035, что составляет 0,07%, и погрешность определения фазового угла 0,07 градуса. Для прототипа максимальная абсолютная погрешность определения амплитуды гармоник сигнала x(t) равна 0,2524, что составляет 5,048%, и погрешность определения фазового угла 5,75 градуса. Это свидетельствует о том, что заявленные способ и устройство для его реализации позволяют повысить точность определения спектральных составляющих полигармонических сигналов при быстрых колебаниях основной частоты. Кроме того, как видно из спектра амплитуд на фиг.4, полученных способом, заявляемым в изобретении, данный спектр практически не содержит гармоник, которых не было в исследуемом сигнале x(t), что свидетельствует об отсутствии проявления известных эффектов (эффекта Гиббса и др.), вызванных влиянием конечности выборки и снижающих точность спектрального анализа.
При этом из примера реализации видно, что вся информация, необходимая и достаточная для точного расчета спектральных составляющих полигармонического сигнала, получена одновременно с проведением аналого-цифрового преобразования за время, равное величине периода частоты основной гармоники сигнала. Это обеспечивает возможность расчета спектральных составляющих для каждого периода сигнала.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство измерения частотных характеристик группового времени запаздывания четырехполюсников | 1988 |
|
SU1631511A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ШИРОКОПОЛОСНОГО СИГНАЛА | 2012 |
|
RU2517799C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СПЕКТРА ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ | 1997 |
|
RU2133041C1 |
| Адаптивный спектроанализатор | 1987 |
|
SU1576867A1 |
| Способ определения наличия в сигнале гармоник, длительность которых превышает установленное значение | 2023 |
|
RU2821216C1 |
| СПОСОБ ИЗВЛЕЧЕНИЯ ИЗ ДОПЛЕРОВСКИХ ПОРТРЕТОВ ВОЗДУШНЫХ ОБЪЕКТОВ ПРИЗНАКОВ ИДЕНТИФИКАЦИИ С ИСПОЛЬЗОВАНИЕМ МЕТОДА СВЕРХРАЗРЕШЕНИЯ | 2015 |
|
RU2589737C1 |
| Способ оценки фаз многочастотных периодических сигналов в условиях наличия помех с использованием компенсации шумов преобразования | 2020 |
|
RU2740790C1 |
| СПОСОБ АНАЛОГО-ДИСКРЕТНОЙ ОБРАБОТКИ РАДИОЛОКАЦИОННЫХ ИМПУЛЬСНЫХ СИГНАЛОВ | 2004 |
|
RU2291463C2 |
| Способ оценки амплитуд многочастотного сигнала методом спектрального анализа, проводимого с различной длительностью времени анализа | 2024 |
|
RU2836461C1 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ ШУМОВЫХ ГИДРОАКУСТИЧЕСКИХ СИГНАЛОВ НА ОСНОВЕ КВАДРАТУРНОГО ПРИЕМНИКА | 2013 |
|
RU2550757C1 |
Изобретение относится к измерительной технике и может быть использовано при дискретном гармоническом анализе полигармонических сигналов, в том числе характеризующихся быстрыми колебаниями основной частоты. Способ спектрального анализа полигармонических сигналов заключается в том, что исследуемый сигнал подают на вход аналого-цифрового преобразователя, на дополнительный вход которого одновременно подают дополнительный сигнал, полученный из исследуемого сигнала при помощи блока выделения основной гармоники исследуемого сигнала. Интервал дискретизации аналого-цифрового преобразования задают постоянным и получают одновременно последовательности дискретных отсчетов исследуемого и дополнительного сигналов. Далее на основании последовательности дискретных отсчетов дополнительного сигнала вычисляют период частоты основной гармоники исследуемого сигнала и число интервалов дискретизации, наиболее соответствующее величине периода частоты основной гармоники. Затем из последовательности дискретных отсчетов исследуемого сигнала производят выборку дискретных отсчетов длиной, равной числу интервалов дискретизации исследуемого сигнала. Далее вычисляют корректирующий коэффициент, равный отношению произведения числа интервалов дискретизации исследуемого сигнала на интервал дискретизации к периоду частоты основной гармоники исследуемого сигнала, и проводят дискретный гармонический анализ, умножая аргументы всех тригонометрических функций, входящих в формулы для вычисления косинусных и синусных коэффициентов ряда Фурье, на корректирующий коэффициент. Представлено также устройство для реализации данного способа. Технический результат - повышение точности определения спектральных составляющих полигармонических сигналов при быстрых колебаниях основной частоты и обеспечение при этом возможности расчета спектральных составляющих для каждого периода сигнала. 2 н.п. ф-лы, 4 ил., 2 табл.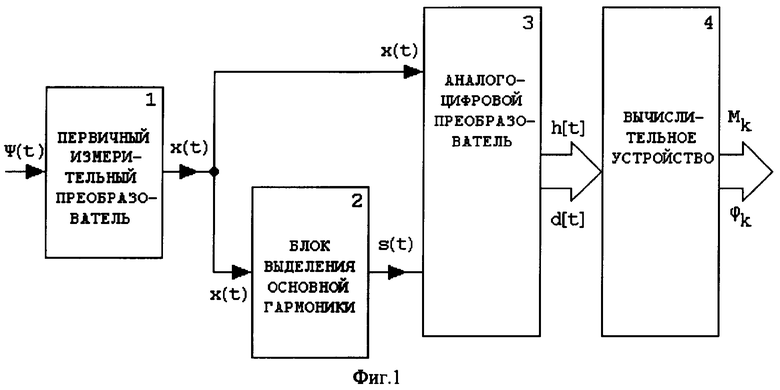
1. Способ спектрального анализа полигармонических сигналов, заключающийся в получении последовательности дискретных отсчетов исследуемого сигнала путем аналого-цифрового преобразования и проведении дискретного гармонического анализа исследуемого сигнала с помощью дискретного преобразования Фурье, отличающийся тем, что из исследуемого сигнала выделяют его основную гармонику, формируют из нее дополнительный сигнал, интервал дискретизации аналого-цифрового преобразования задают постоянным и получают последовательность дискретных отсчетов дополнительного сигнала путем его аналого-цифрового преобразования одновременно с исследуемым сигналом, далее на основании полученной последовательности дискретных отсчетов дополнительного сигнала вычисляют период частоты основной гармоники исследуемого сигнала, на основании которого определяют число интервалов дискретизации исследуемого сигнала, наиболее соответствующее величине периода частоты основной гармоники исследуемого сигнала, затем из последовательности дискретных отсчетов исследуемого сигнала производят выборку дискретных отсчетов длиной, равной числу интервалов дискретизации исследуемого сигнала, далее вычисляют корректирующий коэффициент по формуле:
R=(NΔt)/T,
где R - корректирующий коэффициент;
N - число интервалов дискретизации исследуемого сигнала;
Δt - интервал дискретизации аналого-цифрового преобразования, с;
Т - период частоты основной гармоники исследуемого сигнала, с,
и дискретный гармонический анализ проводят над полученной выборкой дискретных отсчетов исследуемого сигнала, при этом аргументы всех тригонометрических функций, входящих в формулы для вычисления косинусных и синусных коэффициентов ряда Фурье, умножают на корректирующий коэффициент.
2. Устройство для реализации способа по п.1, содержащее первичный измерительный преобразователь со входом для поступления измеряемой физической величины и выходом для выдачи исследуемого сигнала, аналого-цифровой преобразователь, вход которого соединен с выходом первичного измерительного преобразователя, и вычислительное устройство, вход которого сообщен с выходом аналого-цифрового преобразователя, а выход предназначен для выдачи спектральных составляющих исследуемого сигнала, отличающееся тем, что введен блок выделения основной гармоники исследуемого сигнала со входом, соединенным с выходом первичного измерительного преобразователя, и выходом, а аналого-цифровой преобразователь выполнен с дополнительным входом, соединенным с выходом блока выделения основной гармоники исследуемого сигнала.
| HПП "ЭНЕРГОТЕХНИКА" | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Руководство по эксплуатации | |||
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА СИГНАЛОВ | 1993 |
|
RU2090898C1 |
| Анализатор периодических сигналов | 1976 |
|
SU569964A2 |
| Анализатор спектра | 1980 |
|
SU911362A1 |
| JP 11083916 A, 26.03.1999. | |||
Авторы
Даты
2009-07-27—Публикация
2008-01-25—Подача