Изобретение относится к технической кибернетике и предназначено для идентификации линейных динамических объектов со случайным входным воздействием. Способ может быть применен для определения математической модели объекта на основе дискретной информации о сигналах на его входе и выходе и реализован с использованием ЭВМ в автоматическом режиме, в реальном масштабе времени.
Известен способ идентификации линейных объектов управления (патент RU 2079870, МПК G 05 В 23/02, опубл. 20.05.97) на основе рекуррентного оценивания в условиях неопределенности порядка модели объекта управления и при воздействии помех. Сущность аналога состоит в том, что переход от дифференциального уравнения, оценивающего динамику исследуемого объекта, к алгебраическому уравнению с непрерывно формируемыми коэффициентами осуществляется путем фильтрации входного и выходного контролируемых сигналов объекта системой линейных фильтров, причем множество сечений алгебраического уравнения образует систему линейных алгебраических уравнений, решением которой являются параметры, связанные с идентифицируемыми параметрами объекта линейным преобразованием.
Недостатками такого способа идентификации являются:
- невысокий порядок дифференциального уравнения, так как в данном способе нет правила или критерия оценки этого порядка;
- наличие систем низкочастотных линейных фильтров экспоненциального сглаживания, которые изменяют контролируемые входной и выходной сигналы объекта и приводят к неидентифицируемости вещественных и комплексно сопряженных нулей и комплексно сопряженных полюсов модели объекта управления в форме передаточной функции;
- формируемая система линейных алгебраических уравнений (так же, как и система нормальных уравнений в методе наименьших квадратов в случае переопределенности) может иметь неустойчивое решение в силу плохой их обусловленности.
Наиболее близким к предлагаемому способу является способ идентификации линейного объекта при стационарном входном воздействии (патент РФ 2146063, МПК G 05 В 17/02, опубл. 27.02.2000), сущность которого состоит в следующем: по результатам измерений входных и выходных сигналов в равноотстоящие промежутки времени с шагом дискретизации Δt в идентификаторе непрерывной дроби вычисляют детерминированные характеристики корреляции - взаимную корреляционную функцию входного и выходного сигналов Rxy(kΔt) и корреляционную функцию входного сигнала Rxx(kΔt). Далее строят дискретную передаточную функцию (ДПФ) объекта как соотношение z-преобразований взаимной корреляционной функции входного и выходного сигналов и корреляционной функции входного сигнала по формуле
Для получения ДПФ (1) идентифицируемого объекта применяют модифицированный алгоритм В. Висковатова, который позволяет с помощью непрерывных дробей автоматически определить структуру и неизвестные параметры модели, а также исключить процедуру перебора пробных моделей объекта, используя для этого последовательную обработку детерминированных характеристик корреляции значений входного и выходного сигналов объекта по формуле: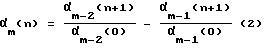
до выполнения правила останова, где α-1(n) = Rxx(nΔt) - детерминированная характеристика корреляции значений входного сигнала объекта, α0(n) = Rxy(nΔt) - детерминированная характеристика корреляции значений вход-выходного сигналов объекта, m=1,2,3,..., n=0,1,2.....
Получив ДПФ в виде непрерывной дроби, свернув ее в дробно-рациональную функцию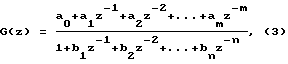
где аi, bi - параметры модели объекта, переходят от данного выражения к прогнозирующей модели в виде разностного уравнения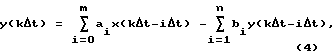
где x(kΔt) - величина сигнала на входе объекта в k-том такте; y(kΔt) - величина сигнала на выходе объекта в k-том такте. Уравнение вида (4) позволяет восстанавливать значения модельного сигнала yм(kΔt) на выходе модели.
Этот способ имеет следующие недостатки:
применяется только для стационарных случайных вход-выходных сигналов x(t) и у (t);
метод основан на использовании детерминированных характеристик корреляции, определение которых включает в себя предварительное оценивание постоянных уровней вход-выходных случайных сигналов объекта, что в случае нестационарности входного или выходного сигналов приведет к получению ошибочной модели объекта;
не предусмотрена процедура проверки стационарности вход-выходных сигналов x(t) и у(t), что может также привести к получению ошибочной модели объекта.
Предлагаемым изобретением ставится задача структурно-параметрической идентификации линейного объекта со случайным стационарным или нестационарным сигналом на входе и (или) выходе, позволяющая ввести процедуру проверки вход-выходных сигналов на стационарность с помощью структурных функций, процедуру стационаризации этих сигналов в случае их нестационарности, исключая при этом визуальный анализ стационарности реализации вход-выходных случайных сигналов и, тем самым, расширяя область применения метода идентификации для различных типов вход-выходных сигналов, значительным образом повышая степень автоматизации, точность, достоверность и быстродействие процесса идентификации, что позволяет использовать данный метод как способ текущей идентификации в реальном масштабе времени, определять изменение структуры модели и, тем самым, повышать точность, надежность и качество результатов моделирования.
Поставленная задача решается новым способом идентификации линейного объекта путем определения значений входного и выходного сигналов объекта, подачи их на идентификатор непрерывной дроби, в котором значения входного и выходного сигналов преобразуют в детерминированные характеристики корреляции значений входного и вход-выходного сигналов объекта с последующей их обработкой, и выполнением дальнейшего восстановления прогнозирующей модели объекта с определением модельных значений его выходного сигнала, что становится возможным за счет того, что перед подачей входного и выходного сигналов на идентификатор непрерывной дроби определяют стационарность каждого из этих сигналов в своем блоке определения стационарности, в котором сначала вычисляют структурную функцию сигнала, затем сглаживают ее значения с помощью фильтра низких частот и путем аппроксимации непрерывной дробью находят модель структурной функции, по которой определяют стационарность сигнала, и при наличии стационарности каждого из сигналов, входного и выходного, их направляют на идентификатор непрерывной дроби, а при отсутствии стационарности входного и/или выходного сигналов, значения каждого из них многократно подвергают разностным преобразованиям с последующим выполнением для каждого из преобразованных сигналов упомянутых операций в своем блоке определения стационарности до ее установления.
Структурная схема системы, реализующей предлагаемый способ, изображена на фиг.1.
Случайный входной сигнал x(kΔt) поступает одновременно на вход блока 1 объекта идентификации и на вход блока 2 определения стационарности входного сигнала, который включает в себя 3 подблока: 2.1 - подблок вычисления структурной функции входного сигнала, 2.2 - подблок сглаживания ее значений с помощью фильтра низких частот, 2.3 - подблок аппроксимации непрерывной дробью модели структурной функции входного сигнала с последующим определением по ней его стационарности сигнала. При наличии стационарности входной сигнал поступает на вход блока 6 - идентификатора непрерывной дроби, а при ее отсутствии на вход блока 4 взятия разностей входного сигнала, в котором значения входного сигнала подвергаются разностным преобразованиям с целью их стационаризации, после чего преобразованный входной сигнал вновь поступает на вход блока 2 с последующим выполнением упомянутых операций. Процедура прекращается при получении стационарного сигнала.
Выходной сигнал y(kΔt) поступает на вход блока 3 определения стационарности выходного сигнала, который включает в себя 3 подблока: 3.1 - подблок вычисления структурной функции выходного сигнала, 3.2 - подблок сглаживания ее значений с помощью фильтра низких частот, 3.3 - подблок аппроксимации непрерывной дробью модели структурной функции выходного сигнала с последующим определением по ней его стационарности. При наличии стационарности выходной сигнал поступает на вход блока 6 идентификатора непрерывной дроби, а при ее отсутствии на вход блока 5 взятия разностей выходного сигнала, в котором значения выходного сигнала подвергаются разностным преобразованиям с целью их стационаризации, после чего преобразованный выходной сигнал вновь поступает на вход блока 3 с последующим выполнением упомянутых операций. Процедура прекращается при получении стационарного сигнала. После стационариэации входного и выходного сигналов в блоке 6 производят их преобразования в детерминированные характеристики корреляции значений входного и вход-выходного сигналов, производят их обработку с помощью формулы (2) до выполнения правила останова, строят непрерывную дробь по преобразованным значениям сигналов и определяют ДПФ идентифицируемого объекта. Далее в блоке 7 восстановления модели объекта определяют прогнозирующую модель идентифицируемого объекта. Затем параметры прогнозирующей модели идентифицируемого объекта поступают на вход блока 8 восстановления модельных значений выходного сигнала объекта, в котором определяют модельный выходной сигнал yм(k). Процесс идентификации заканчивается, так как получена модель идентифицируемого объекта.
Предлагаемый способ осуществляется следующим образом: по результатам измерений входных и выходных сигналов в равноотстоящие промежутки времени с шагом дискретизации Δt вычисляют структурную функцию входного сигнала Cх(kΔt)
и структурную функцию выходного сигнала Cy(kΔt)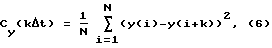
после чего пропускают значения Cх(kΔt) и Су(kΔt) через фильтры низких частот, тем самым сглаживая их, а затем применяют модифицированный метод В. Висковатова для аппроксимации непрерывными дробями моделей структурных функций входного и выходного сигналов. Для этого определяются следующие матрицы:
для структурной функции входного сигнала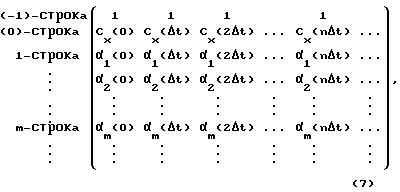
в которой (-1)-строка содержит значения единичной функции l(t), а (0)-строка - значения структурной функции входного сигнала Сх(kΔt) в моменты времени {nΔt}
для структурной функции выходного сигнала определяется аналогичная матрица, однако ее (0)-строка содержит значения структурной функции выходного сигнала Сy (k t) в моменты времени {nΔt}
t) в моменты времени {nΔt} соответственно, после чего проверяется устойчивость полученных объектов-преобразователей по их математическим моделям ДПФ с помощью любого из известных критериев устойчивости. В случае устойчивости объекта-преобразователя следует утверждать, что данный сигнал стационарен. В противном случае сигнал является нестационарным и необходима процедура его стационаризации с помощью взятия разностей:
соответственно, после чего проверяется устойчивость полученных объектов-преобразователей по их математическим моделям ДПФ с помощью любого из известных критериев устойчивости. В случае устойчивости объекта-преобразователя следует утверждать, что данный сигнал стационарен. В противном случае сигнал является нестационарным и необходима процедура его стационаризации с помощью взятия разностей:
для входного сигнала
Δdx(k) = Δd-1x(k+1)-Δd-1x(k), (8)
для выходного сигнала
Δry(k) = Δr-1y(k+1)-Δr-1y(k), (9)
где Δ - правая разность, d, r - порядки разностей для сигналов х и у соответсвенно. Порядки взятия разностей d и r определяются устойчивостью моделей структурных функций в форме ДПФ объектов-преобразователей  Если объект-преобразователь устойчив, следует прекратить процесс взятия разностей, так как стационаризация сигнала произведена.
Если объект-преобразователь устойчив, следует прекратить процесс взятия разностей, так как стационаризация сигнала произведена.
По окончании процедуры стационаризации входного и выходного сигналов находится модель идентифицируемого объекта в идентификаторе непрерывной дроби. Для этого на основании (1) расчетным путем определяется идентифицирующая матрица: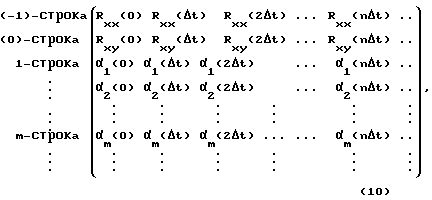
в которой (-l)-стpoкa и (0)-строка содержат значения корреляционной функции входного сигнала Rхх(kΔt) и взаимной корреляционной функции входного и выходного сигналов Rху(kΔt) в моменты времени {nΔt}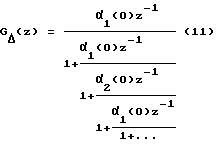
При аппроксимации дробно-рациональной функции в матрице (10) наблюдается появление нулевой строки, номер которой позволяет идентифицировать порядок функции. Если в некоторой i-той строке (i=0,1,2,...) матрицы (10) конечное число ki, первых элементов равны нулю, а последующие элементы отличны от нуля, то необходимо осуществить сдвиг влево на ki, элементов до появления в нулевом столбце ненулевого элемента и далее продолжить определение других элементов матрицы (10) по правилу (2). Для i-той строки при восстановлении правильной С-дроби (11) элемент αi(0) умножается на 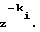
Получив ДПФ преобразователя разностей, с помощью обратных разностных преобразований переходят к ДПФ объекта и далее к прогнозирующей модели в виде разностного уравнения (4), которая позволяет восстанавливать значения модельного сигнала yм(kΔt) на выходе модели.
Таким образом, предлагаемый способ идентификации объекта отличается от известного тем, что позволяет расширить область его применения на класс нестационарных вход-выходных сигналов объекта путем введения процедур проверки стационарности сигналов и их стационаризации, исключая при этом визуальный анализ реализации вход-выходных сигналов и повышая точность, быстродействие и степень автоматизации процесса идентификации. В конечном итоге, предлагаемый способ позволяет достоверно прогнозировать состояние объекта с различными типами входных воздействий, принимать адекватные решения по управлению, диагностике и контролю этих объектов.
Пример 1.
Аналоговый объект идентификации - интегрирующий операционный усилитель с передаточной функцией
на вход которого подается случайный сигнал, дискретная модель которого имеет вид
x(k)=2a(k)+0.36788 x(k-l),
где a(k) - белый шум с математическим ожиданием Ма=0 и дисперсией Da=1, а на выходе имеется случайный сигнал, заданный разностным уравнением
y(k)=0.63212x(k-l)+y(k-l). (12)
На основании дискретных моделей входного и выходного сигналов моделировались реализации x(kΔt) и y(kΔt) объемом N=90 с шагом дискретизации Δt= 1c. По полученным реализациям вычисляются значения структурных функций Cх(kΔt) и Cy(kΔt) по формулам (5) и (6) соответственно. На фиг.2 непрерывной линией изображена структурная функция Cх(k t), а пунктиром ее вид после сглаживания фильтром низких частот. Применим модифицированный алгоритм В. Висковатова для аппроксимации непрерывной дробью модели структурной функции входного сигнала. Для этого определим матрицу (7) с учетом того, что в нулевой строке необходимо сделать сдвиг влево на один элемент, обусловленный начальным значениемCx(0)=0,
t), а пунктиром ее вид после сглаживания фильтром низких частот. Применим модифицированный алгоритм В. Висковатова для аппроксимации непрерывной дробью модели структурной функции входного сигнала. Для этого определим матрицу (7) с учетом того, что в нулевой строке необходимо сделать сдвиг влево на один элемент, обусловленный начальным значениемCx(0)=0,
в которой 2-ую строку можно считать нулевой. На основании элементов первого столбца матрицы аппроксимируем непрерывной дробью модель структурной функции входного сигнала в форме ДПФ объекта преобразователя
ДПФ объекта-преобразователя имеет один полюс zn=032913, на основании значения которого можно сделать вывод об устойчивости объекта-преобразователя и, следовательно, о стационарности входного сигнала.
На фиг. 3 непрерывной линией изображена структурная функция Сy(kΔt), а пунктиром ее вид после сглаживания фильтром низким частот. Аналогичным образом определим матрицу вида (7)
в которой 2-ую строку можно считать близкой к нулевой (при расчете элементов следующей строки их значения резко возрастают). Тогда модель структурной функции выходного сигнала в форме ДПФ объекта-преобразователя имеет вид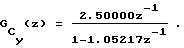
Так как полюс ДПФ объекта-преобразователя лежит вне единичной окружности, можно сделать вывод о неустойчивости объекта. Следовательно, выходной сигнал нестационарен. Применим процедуру стационаризации
Δy(k)=y(k+1)-y(k),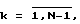
после чего вновь вычислим и сгладим структурную функцию выходного сигнала (фиг.4). Матрица (7) будет иметь вид
ДПФ объекта-преобразователя имеет вид
zn=037453, следовательно, сигнал стационарен.
По окончании процедуры стационаризации выходного сигнала находится модель идентифицируемого объекта. Для этого вычисляются детерминированные характеристики корреляции - взаимная корреляционная функция входного и выходного сигналов Rxy(kΔt) и корреляционная функция входного сигнала Rxx(kΔt), а затем расчетным путем определяется идентифицирующая матрица (10)
в которой (-1)-строка и (0)-строка содержат значения корреляционной функции входного сигнала Rxx(kΔt) и взаимной корреляционной функции входного и выходного сигналов Rxy(kΔt). Тогда ДПФ преобразователя разностей будет иметь вид
а прогнозирующая модель в разностях:
Δyм(k)=0.63306.
Заменив Δум(k)= yм(k+l)-yм(k), запишем ДПФ объекта и прогнозирующую модель в виде (4)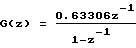
и
ум(k)=0.63306x(k-1)+yм(k-1)
соответственно.
Таким образом, по предлагаемому способу восстановлена прогнозирующая модель объекта, которая по структуре и параметрам совпадает (с точностью до погрешностей вычислений) с исходной моделью (12), что в конечном итоге позволяет получать достоверный прогноз значений выходного сигнала объекта.
Пример 2.
Объект идентификации - сильфонный датчик давления жидкости с непрерывной передаточной функцией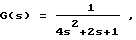
на вход которого подается давление, дискретная модель которого имеет вид
x(k)=2a(k)-0.59101 a(k-l)+ 0.59101 x(k-l)-0.08208 x(k-2),
где a(k) - белый шум с математическим ожиданием Ма=0 и дисперсией Dа=1, а на выходе имеется случайный сигнал, разностное уравнение которого задается формулой
y(k)=0,01958x(k-1)+0,012x(k-2)+ +1,73125y(k-1)-0,78818y(k-2) (13)
На основании дискретных моделей вход-выходных сигналов моделировались реализации x(kΔt) и y(kΔt) объемом N=500 с шагом дискретизации Δt=0.5с., а затем по ним вычислялись значения структурных функций Cx(kΔt) и Cy(kΔt). На фиг.5 непрерывной линией изображена структурная функция Cx(kΔt), а пунктиром ее вид после сглаживания фильтром низким частот. Затем определялась матрица вида (7)
в которой 4-ую строку можно считать нулевой. На основании элементов первого столбца матрицы можно записать модель структурной функции входного сигнала в форме ДПФ объекта-преобразователя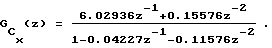
ДПФ объекта-преобразователя имеет один нуль - zн=-0.08554 и два полюса - z1 n= 03619 и z2 n=-0.31962, на основании значений которых можно сделать вывод об устойчивости объекта-преобразователя и, следовательно, о стационарности входного сигнала.
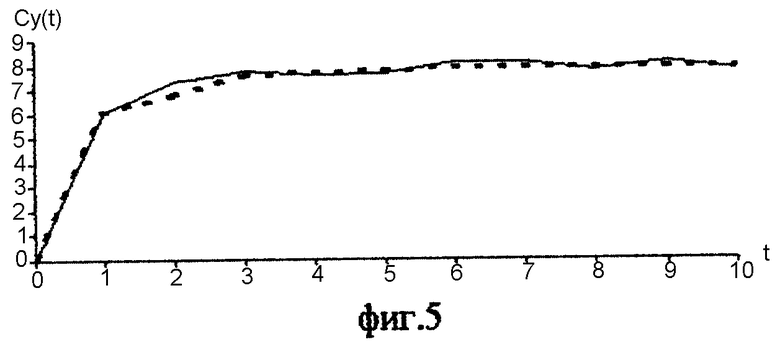
На фиг.6 пунктиром изображена сглаженная с помощью фильтра низких частот структурная функция Сy(kΔt). В соответствии с модифицированным алгоритмом В. Висковатова произведем децимацию через четыре отсчета сглаженных значений Сy(kΔt) и определим матрицу (7)
а затем модель структурной функции выходного сигнала в форме ДПФ объекта-преобразователя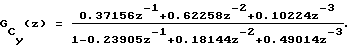
ДПФ объекта-преобразователя имеет 2 нуля - z1 н=-1.49187 и z2 н-0.18444; 3 полюса - z1 n=-0.64805 и z2,3 n=0.44355±i0.74806, на основании которых можно сделать вывод об устойчивости объекта-преобразователя и о стационарности выходного сигнала.
Далее вычисляются детерминированные характеристики корреляции - взаимная корреляционная функция входного и выходного сигналов Rxy(kΔt) и корреляционная функция входного сигнала Rxx(kΔt), а затем расчетным путем определяется идентифицирующая матрица (10). Так как Rxy(0)=-0.00116, т.е. близко к нулю, в нулевой строке необходимо сделать сдвиг влево на один элемент. Тогда идентифицирующая матрица примет вид
На основании элементов первого столбца матрицы запишем ДПФ идентифицируемого объекта
а затем прогнозирующую модель идентифицируемого объекта в виде (4)
yм(k)=0,02706x(k-l)+0,01024x(k-2)+1,73937yм(k-1)-0,79649yм(k-2),
которая по структуре и параметрам совпадает (с точностью до вычислительных погрешностей) с исходной моделью (13). В связи с этим можно говорить о том, что с помощью предлагаемого способа была восстановлена модель сильфонного датчика давления жидкости в виде разностного уравнения, которая позволяет осуществлять наилучший прогноз выходного процесса по его предыдущим значениям в смысле наименьшей среднеквадратической ошибки.
Пример 3.
Объект идентификации - термопара, которая имеет передаточную функцию
Входной сигнал объекта задается разностным уравнением:
x(k)=a(k)+x(k-l),
где a(k) - белый шум с математическим ожиданием Мa=0 и дисперсией Da=1, а на выходе имеется случайный сигнал, дискретная математическая модель которого имеет вид:
y(k)=0.221199 x(k-1)+0,7788 y(k-l). (14)
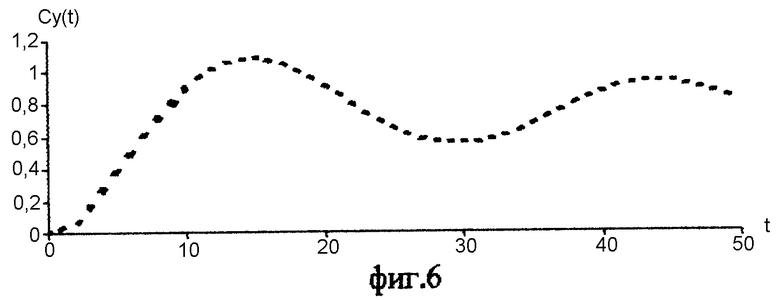
На основании дискретных моделей вход-выходных сигналов моделировались реализации x(kΔt) и y(kΔt) объемом N=300 с шагом дискретизации Δt=1c. По полученным реализациям производилось вычисление структурных функций Cx(kΔt) и Сy(kΔt) по формулам (5) и (6) соответственно. На фиг.7 изображена сглаженная кривая Cx(kΔt). Определим матрицу (7) для Cx(k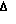 t):
t):
в которой 2-ая строка близка к нулевой. Запишем модель структурной функции Cx(kΔt) в форме ДПФ объекта-преобразователя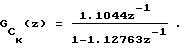
которая имеет полюс zn=1.12763. Так как zn=1.12763 лежит вне единичной окружности, объект-преобразователь неустойчив и, следовательно, входной сигнал нестационарен. Применим процедуру стационаризации
Δx(k)=x(k+l)-x(k),
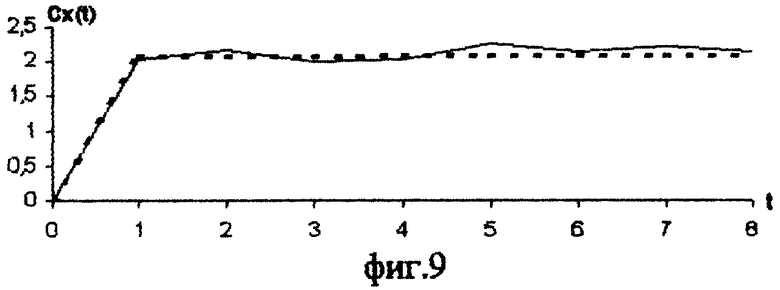
после которой вновь вычислим и сгладим структурную функцию входного сигнала. На фиг.9 непрерывной линией изображена структурная функция Cx(kΔt), пунктиром сглаженная кривая. Тогда матрица (7) имеет вид
а ДПФ объекта-преобразователя -
Следовательно, объект устойчив, а входной сигнал является стационарным.
Структурная функция Cy(kΔt) до (непрерывная линия) и после (пунктир) сглаживания изображена на фиг.8. Найдем модель Cy(kΔt) в форме ДПФ объекта-преобразователя, произведя предварительную децимацию через один отсчет значений структурной функции. Матрица (7) будет иметь вид
Тогда модель структурной функции выходного сигнала в форме ДПФ объекта-преобразователя имеет вид
Нули и полюса объекта принимают значения:
z1,2 н=-1,76836±i1,17272,
z1 п=-20,62816,
z2,3 п=9,39188±il7,42898.
Объект-преобразователь неустойчив, поэтому применим процедуру стационаризации сигнала
Δy(k)=y(k+1)-y(k),
после чего вновь вычислим и сгладим структурную функцию выходного сигнала (фиг. 10). Матрица (7) с учетом децимации значений структурной функции через один отсчет имеет следующий вид:
а модель структурной функции выходного сигнала в форме ДПФ объекта-преобразователя:
Объект-преобразователь устойчив, поэтому выходной сигнал стационарен.
После стационаризации входного и выходного сигналов находим модель идентифицируемого объекта. Вычислив взаимную корреляционную функцию входного и выходного сигналов Rxy(kΔt) и корреляционную функцию входного сигнала Rxx(kΔt), построим идентифицирующую матрицу (10) с учетом того, что Rxy(0)= 0,02851≈0:
Тогда ДПФ преобразователя разностей имеет вид
Запишем прогнозирующую модель в разностях
Δум(k)=0.2421lx(k-1)+0.7646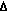 yм(k-1).
yм(k-1).
Заменив
Δyм(k)=yм(k+l)-yм(k) и Δx(k)=x(k+l)-x(k),
получим прогнозирующую модель генератора yм(k)=0,24211x(k-1)-0,24211x(k-2)+1,7746yм(k-1)-0,7746yм(k-2)
и его ДПФ
Таким образом, по предлагаемому способу восстановлена прогнозирующая модель объекта, которая по структуре и параметрам совпадает (с точностью до погрешностей вычислений) с исходной моделью (14), что на практике дает возможность делать достоверные предсказания относительно состояния термопары с последующим улучшением процесса управления, диагностики и контроля данного объекта.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 1999 |
|
RU2146063C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2002 |
|
RU2233480C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2001 |
|
RU2189621C1 |
| СПОСОБ АНАЛИЗА МНОГОЧАСТОТНЫХ СИГНАЛОВ, СОДЕРЖАЩИХ СКРЫТЫЕ ПЕРИОДИЧНОСТИ | 2009 |
|
RU2399060C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 1995 |
|
RU2097818C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕАРИЗОВАННОГО ДИНАМИЧЕСКОГО ОБЪЕКТА | 2003 |
|
RU2256950C2 |
| Способ идентификации мультисинусоидальных цифровых сигналов | 2022 |
|
RU2787309C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ МУЛЬТИСИНУСОИДАЛЬНЫХ ЦИФРОВЫХ СИГНАЛОВ | 2018 |
|
RU2703933C1 |
| Способ идентификации нелинейных систем | 2019 |
|
RU2714612C1 |
| ИЗМЕРИТЕЛЬ ВРЕМЕННОЙ ЗАДЕРЖКИ СИГНАЛОВ В ДИНАМИЧЕСКИХ СИСТЕМАХ | 1992 |
|
RU2118847C1 |





Изобретение относится к технической кибернетике и предназначено для идентификации линейных динамических объектов со случайным стационарным или нестационарным входным воздействием. Технический результат заключается в повышении точности и надежности. Способ заключается в том, что измеряют значения вход-выходных сигналов объекта, вычисляют структурные функции сигналов, сглаживают значения структурных функций с помощью фильтра низких частот, аппроксимируют непрерывной дробью модели структурных функций вход-выходных сигналов и определяют с помощью полученных моделей стационарность каждого из сигналов, причем осуществляют стационаризацию вход-выходных сигналов в случае их нестационарности с помощью разностных преобразований, подают значения вход-выходных сигналов на идентификатор непрерывной дроби с последующим восстановлением прогнозирующей модели идентифицируемого объекта и определяют по ней модельные значения выходного сигнала объекта идентификации. 10 ил.
Способ идентификации линейного объекта путем определения значений входного и выходного сигналов объекта, подачи их на идентификатор непрерывной дроби, в котором значения входного и выходного сигналов преобразуют в детерминированные характеристики корреляции значений входного и вход-выходного сигналов объекта с последующей их обработкой и выполнением дальнейшего восстановления прогнозирующей модели объекта с определением модельных значений его выходного сигнала, отличающийся тем, что перед подачей входного и выходного сигналов на идентификатор непрерывной дроби определяют стационарность каждого из этих сигналов в своем блоке определения стационарности, в котором сначала вычисляют структурную функцию сигнала, затем сглаживают ее значения с помощью фильтра низких частот и путем аппроксимации непрерывной дробью находят модель структурной функции, по которой определяют стационарность сигнала, и при наличии стационарности каждого из сигналов, входного и выходного, их направляют на идентификатор непрерывной дроби, а при отсутствии стационарности входного и/или выходного сигналов, значения каждого из них многократно подвергают разностным преобразованиям с последующим выполнением для каждого из преобразованных сигналов упомянутых операций в своем блоке определения стационарности до ее установления.
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 1999 |
|
RU2146063C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНЫХ ОБЪЕКТОВ УПРАВЛЕНИЯ | 1994 |
|
RU2079870C1 |
| Устройство для идентификации статических параметров многосвязной автоматической системы | 1986 |
|
SU1474596A1 |
| US 5043863 A, 27.08.1991. | |||
Авторы
Даты
2002-09-20—Публикация
2001-04-02—Подача