Изобретение относится к вычислительной технике, обработке данных и, в частности может быть использовано при обработке изображений в томографии (особенно медицинской), выделении сигналов из шумов.
Известно устройство определения среднего значения нестационарного случайного процесса (НСП) [3], содержащее аналогово-цифровой преобразователь (АЦП), формирователь временного интервала взаимосвязей, формирователь импульсов, распределитель импульсов, группу элементов "И", элемент "И", регистры, блок регистров, сумматор, делитель импульсов, цифроаналоговый преобразователь (ЦАП).
Недостатком данного устройства является то, что определение среднего значения НСП производится на интервале ковариации НСП, где учитываются только двумерные естественные взаимосвязи ординат НСП во времени. Последние учитывают только часть многомерных естественных (в общем случае М-мерных) взаимосвязей ординат НСП во времени, где М может быть (3 - 10) и более. В силу этого определение среднего значения НСП производится с большой погрешностью.
Задача, решаемая предполагаемым техническим решением, заключается в уменьшении погрешности определения среднего значения (математического ожидания) НСП и расширении области применения. Задача решается с помощью устройства, содержащего параллельный аналогово-цифровой преобразователь на n-разрядов, последовательно-параллельных регистров емкостью на N двоичных разрядов, регистр сдвига на N двоичных разрядов, генератор тактовых импульсов, n оперативно-запоминающих устройств с памятью 2N•Q бит, n параллельных цифроаналоговых преобразователей, n умножителей и сумматор на n входов.
Принцип работы устройства приведен на четырех чертежах. На фиг. 1 показана блок-схема устройства определения математического ожидания НСП; фиг. 2 показан принцип преобразования аналогового НСП к виду, необходимому для учета многомерных взаимосвязей по разрядам; фиг.3 показан принцип определения оценки символа двоичного кода за счет учета М-мерных взаимосвязей; фиг.4 приведены результаты моделирования и определения математического ожидания НСП на персональном компьютере.
Сущность изобретения состоит в более глубоком учете многомерных естественных взаимосвязей в матожидании НСП, реализации байесовской оценки по минимуму среднеквадратической функции потерь при определении матожидания НСП.
Представление НСП y(t) в виде параллельного двоичного кода: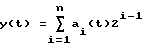 (1),
(1),
где y(t) = my(t)+ξ(t) или (2), где y(t) = my(t)ξ(t) соответственно my(t) - искомое матожидание НСП y(t), ξ(t) - шумовая составляющая, ai(t)={0, 1}, i= 1-n - число разрядов с отбрасыванием шумов квантования σкв= 1/2n при n ≥= 10 есть линейная операция относительно разрядов. Физически это означает, что взаимосвязи между символами ai(t) по разрядам в соответствующие моменты времени такие же, как и между ординатами НСП y(t) в эти же моменты времени (фиг. 2). Это позволяет проводить обработку (оценку символа ai(t)) за счет учета взаимосвязей между символами "0" и "1" по каждому разряду отдельно и одновременно по всем i разрядам, что позволяет распараллелить вычислительный процесс и значительно повышать быстродействие. Получив оценку символа ai(t) в совпадающие моменты времени в каждом разряде, далее путем известной операции код-аналог находим оценку искомого матожидания my(t) НСП: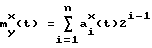 (3)
(3)
Известно, что оптимальную оценку my(t) НСП y(t) возможно получить, применив байесовскую оценку с использованием среднеквадратической функции потерь (МСК-оценку) [2, с. 19-20; 1, с. 125-128]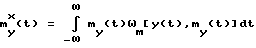 (4),
(4),
где my x(t), my(t) - соответственно оценка и истинное значение искомого матожидания y(t);
ωм[y(t)my(t)] - многомерная (М-мерная) совместная функция плотности вероятности y(t) и my(t).
Выражение (4) при традиционной обработке по огибающей y(t) реализовать практически невозможно, т. к. для оценки матожидания my(t) надо фактически иметь его. Но тогда незачем было бы проводить обработку (фильтрацию). Собственно в этом парадоксе и состоит трудность использования байесовских оценок при традиционных методах обработки (фильтрации).
Байесовскую МСК-оценку возможно реализовать при знаковой (семиотической, символьной) обработке по разрядам. В частности, выражение (4) в этом случае приобретает вид: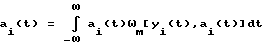 (5),
(5),
где a
ωм[yi(t),ai(t)] - совместная многомерная (М-мерная) плотность вероятности последовательности символов "0" и "1" y(t) и истинного символа ai(t).
Поскольку априорное распределение символов ai(t) известно и равно "0" или "1", то для оценки символа ai(t), согласно (5) необходимо определить ωм[yi(t),ai(t)].
На фиг.2 показан пример определения многомерной (М-мерной) плотности вероятност ωм[yi(t),ai(t)] и оценки символа ai(t) на отрезке анализа НСП Т или массиве символов N = T/Δt+1, где N ≤1/2f - интервал квантования НСП y(t), f - наибольшая частота в спектре y(t).
Соответственно многомерная (М-мерная) совместная плотность вероятности последовательности символов "0", "1" y(t) и истинного символа ai(t) на отрезке времени Т (или массиве символов N = T/Δt+1) переходит в совместную частоту появления групп символов Aji "0" и "1" длиной М (как показано на фиг.2) или p[Aji(M)], где j = 1-aм - число видогрупп Aji(M).
При этом ωм[yi(t),ai(t)] = p[Aji(M).
Как показано на фиг. 3, при подсчете групп Aji(M) идет направленный перебор символов "0" и "1", начиная с точки обработки (фильтрации) tk, т.е. частота px[Aji(M)] и оценка символов ai x(t) определяются в точке tk. Поэтому, далее везде это обозначается как ai x(tk). Общее число групп символов Aji(M) на массиве N равно СN м, где CN м - число сочетаний из N по М, M < N. При этом М или длина групп символов Aji(M) есть учет многомерных (М-мерных) взаимосвязей между символами "0" и "1". Сдвигаясь на один такт Δ вправо (фиг. 2) производим аналогичные вычисления, определяем следующее значение ai x(tk+1) и т.д. Соответственно выражение (5) принимает вид: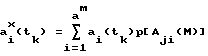 (6)
(6)
Выражение (6) есть байесовская МСК-оценка, т.е. она является ассимптотически несмещенной, состоятельной, эффективной и удовлетворяет практически всем требованиям математической статистики.
Подставляя (6) в (3) имеем: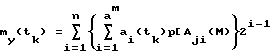 (7)
(7)
Поскольку преобразование код-аналог (7) также линейная операция (до шумов квантования), то оценка матожидания my x(tk) НСП также является байесовской МСК-оценкой. При описанном подходе возможно определять my x(tk) любых случайных (стационарных, нестационарных, эргодических, неэргодических и т.п. ) и детерминированных процессов, т.к. при преобразовании аналог-код (1) и нахождении оценки символа ai x(tk) по (6) никаких ограничений не накладывалось, кроме выбора числа разрядов n и частоты квантования Δt,, которые выбираются такими как при любых преобразованиях аналог-код для цифровой обработки информации.
Поскольку при подсчете многомерной плотности вероятности p[Aji(M)] используется символьная обработка (фиг. 3), то при этом учитывается порядок следования ординат y(t) во времени, их удаление от точки фильтрации tk. Это все в целом и позволяет учесть многомерные взаимосвязи и получить многомерную (М-мерную) плотность вероятности p[Aji(M)].
Основной вопрос при такой обработке состоит в выборе интервала времени Т (или массива символов "0", "1"), где многомерные взаимосвязи наиболее сильные и на которых необходимо находить p[Aji(M)] в каждом разряде в каждой точке tk.
В известных устройствах [3, ] указанные взаимосвязи при определении my x(t) НСП определяются на интервалах ковариации, которые определяются по нецентрированным НСП [4, с. 9] путем построения функции парной ковариации известным образом [5, с.213-226]. В известном устройстве [3], где определяются интервалы ковариации по функциям ковариации с парной ковариацией, учитываются только двумерные взаимосвязи, т.е. группы Aj (М=2) определенным образом.
В табл. 1 приведено общее количество взаимосвязей, которые возможно учесть при ковариационной (корреляционной) обработке и при использовании многомерных взаимосвязей (М-мерных).
Как видно из табл. 1, уже при массиве N ≥=10 символов число учитываемых взаимосвязей при многомерном варианте более чем на два порядка превышает число взаимосвязей, которые учитываются при ковариационном (корреляционном) подходе. Соответственно определение интервала ковариации имеет намного большую погрешность, чем если бы такой интервал взаимосвязей определялся с учетом многомерных взаимосвязей. Поскольку при определении ai(t) по (6) вначале определяется интервал (массив символов) взаимосвязей N1≤=N, а затем многомерная плотность вероятности p[Aji(M1)], где M1 ≤ N1, то погрешность определения массива Ni автоматически переносится и на погрешность определения p[Aji(M1)]. Определение интервалов ковариации через функцию ковариации высших порядков также не решает вопроса из-за самого принципа построения функций ковариации.
В предлагаемом техническом решении реализован подход, который учитывает текущий интервал (массив символов) взаимосвязей N1, определяемый через каждый интервал квантования Δt, вообще без определения каких-либо функций ковариации (парных или высших порядков).
Он состоит в том, что по выбранному массиву символов N выбирается M < N так, чтобы частота появления групп p[Аji(М)] практически не отличалась от вероятности появления p[Aji(M)] . В целом массив взаимосвязей N1 имеет сложную зависимость от N, М, p[Aji(M)], т.е.
N1 = f{p[N, M, Aji(M)]} (8)
Тем не менее оказалось возможным для каждой последовательности символов "0" и "1" длиной N найти на ЭВМ единственным образом свое значение N1 и соответственно M1 < N1, а затем ai(tk). Поскольку последовательностей 2N символов "0" и "1" при символьной обработке полностью исчерпывают все варианты, то возможно заранее каждой последовательности N определить свое значение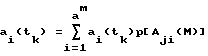
Имея заранее определенные значения ai(tk) для каждой из 2N последовательностей возможно их записать в оперативно-запоминающее устройство (ОЗУ) или постоянное запоминающее устройство (ПЗУ) с организацией памяти 2N•Q бит, где Q бит - число двоичных разрядов, необходимых для записи ai(tk), 2N - адреса последовательностей. На фиг.1 показано устройство определения my(t) НСП любого вида, реализующее данный подход.
Устройство содержит параллельный аналогово-цифровой преобразователь (АЦП) двоичного кода 1, последовательно- параллельные регистры 2, 5; оперативно-запоминающие устройства (ОЗУ) 3, 4; регистр 6 сдвига на N тактовых импульсов, генератор тактовых импульсов 7, умножители 8, 11; цифроаналоговые преобразователи 9, 10 и сумматор 12.
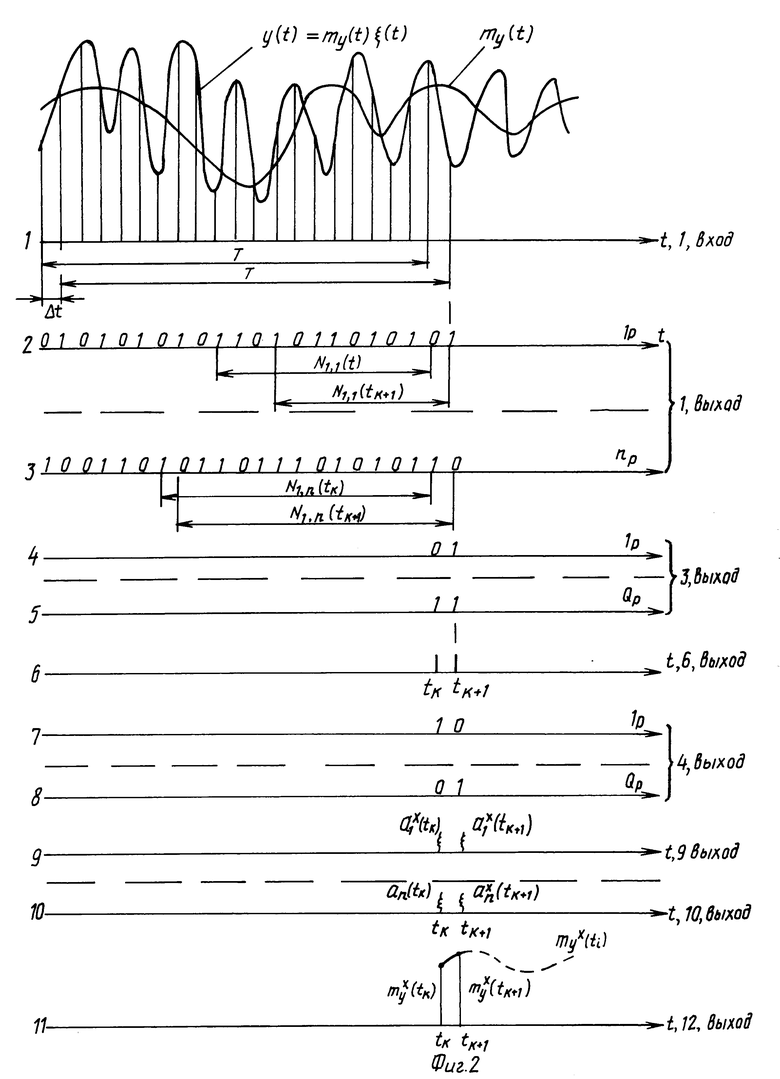
Устройство работает следующим образом. Аналоговый НСП y(t) подается на вход параллельного АЦП 1. Каждый из (1-n) разрядов АЦП соединен со входом n последовательно-параллельных регистров емкостью N двоичных символов. Одновременно с поступлением первого информационного символа с выходов 1-n разрядов АЦП 1 на входы последовательно-параллельных регистров 2, 5 (фиг.2, строки 2, 3) начинает работать регистр 6 сдвига на N тактовых импульсов.
В момент, когда регистры 2, 5 заполняются N информационными символами и поступят на N параллельных входов ОЗУ 3, 4 подается сигнал считывания (фиг. 2, строка 6). Соответственно на выходах ОЗУ 3, 4 (фиг.1) одновременно появятся Q параллельных двоичных символов, соответствующих конкретным двоичным последовательностям "0" и "1" длиной N, поступившие на входы n ОЗУ 3, 4 (фиг.2, строки 4-5, 7-8).
Каждый из Q выходов ОЗУ 3, 4 являются входами для своих n цифроаналоговых преобразователей 9, 10 (фиг.1), на выходах которых появляются оценки символов ai x(tk) (фиг.2, строки 9, 10) в аналоговом виде. Последние подаются на первые входы умножителей 8, 11 (фиг.1), а на вторые входы этих умножителей подаются напряжения, пропорциональные весам разрядов, соответственно 20 на вход умножителя 8 и так до 2n-1 на умножитель 11. Выходы n умножителей 8, 11 являются входами аналогового сумматора 12 (фиг.1), на выходе которого появляется оценка искомого матожидания my x(tk) (фиг.2, строка 11).
С поступлением следующего тактового импульса в момент tk+1 происходит сдвиг на один информационный символ во всех n регистрах 2, 5 и на входах n ОЗУ 3, 4 (фиг. 1) появляются новые последовательности "0" и "1" длиной N, которые отличаются от предыдущих только двумя символами (одним слева и одним справа). На выходе регистра 6 на N тактовых импульсов (например, 133 ИР13) появится импульс считывания в момент tk+1, который подается одновременно на входы считывания всех n ОЗУ 3, 4 (фиг. 2, строка 6 момент tk+1). Соответственно на всех выходах n ОЗУ 3, 4 появится одновременно Q двоичных параллельных символов, которые одновременно подаются на входы своих n ЦАП (фиг. 2, строки 4-5, 7-8, момент tk+1). И далее процесс повторяется как было описано выше для момента времени tk, в результате чего на выходе сумматора 12 появляется оценка искомого матожидания my x(tk+1) (фиг.2 строка 11). И так процесс повторяется с поступлением каждого тактового импульса.
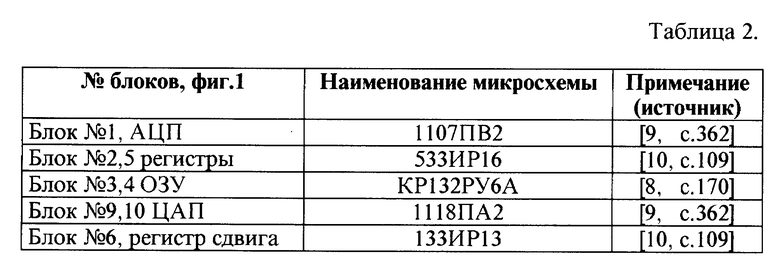
Для устройства на фиг.1 с тактовой частотой f = 10 мГц, N = 12, числа разрядов n = 8 в табл. 2 приведены наименования отечественных серийных микросхем, которые используются для функциональных блоков предлагаемого устройства.
Как видно из приведенных данных, реализация предлагаемого устройства может быть выполнена на серийных микросхемах.
На фиг. 4 даны результаты обработки НСП путем моделирования НСП и обработки по алгоритму фиг.1 при N=15 на ПЭВМ. При этом преследовалась цель:
- показать обработку НСП и детерминированного сигнала любого вида;
- возможность обработки НСП и детерминированных сигналов в различных сочетаниях;
- обработку НСП при Pс/Pш < 1.
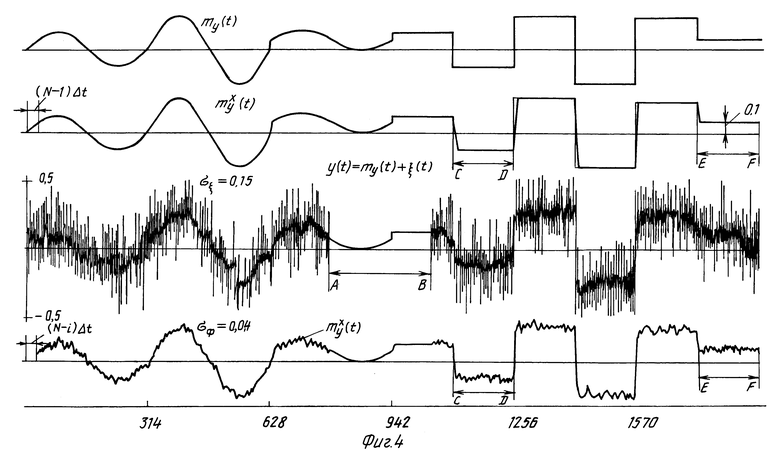
Соответственно на строке 1 приведено матожидание НСП my(t) произвольного вида, а на строке 2 результат его обработки, т.е. обработки детерминированного сигнала. Как видно из фиг. 4, строка 2 my(t) практически воспроизводится без искажений (с погрешностью до шумов квантования). "Платой" является потеря вначале (N-1) ординат предыстории. На строке 3 показан НСП с наложенными шумами в виде
y(t) = my(t)+ξ(t) с σш= 0.15
При этом имеются участки, где my(t) без шумов участок A-B и участки, где my(t)<σш, C-D, E-F. В результате обработки (строка 4) σш с 0,15 уменьшилась до σф= 0.04 или почти в σш/σф= 3,75 раза.
Видно, что никаких переходных процессов, когда фильтрация с зашумленного участка переходит на детерминированный сигнал без шума (участок A-B) и наоборот (участок B-F) не происходит. Довольно хорошо воспроизводятся фронты импульсов как при фильтрации, так и при воспроизведении чистого детерминированного сигнала (строка 2), так и зашумленного (строка 4).
Видно также (участки C-D, E-F строка 4), что и при Pс/Pш < 1 восстановление my(t) происходит удовлетворительно.
Литература
1. Василенко Г.И. Теория восстановления сигналов. М.: Сов. радио, 1979, 270 с.
2. Кулик Е.И. Методы измерения случайных процессов. - М.: Радио и связь, 1986, 271 с.
3. А. С. N 1295417 (СССР) Устройство для определения среднего значения аддитивного нестационарного случайного процесса. А.Ф. Валиулин, Ю.В. Новокшонов, В.П. Ходаковский. Опубликовано в Б.И. 1986, N 9.
4. ГОСТ 21878-76. Случайные процессы и динамические системы. М.: Госстандарт СССР, СМ СССР, 1976.
5. Мирский Г.Я. Характеристики статистической взаимосвязи и их измерение. М.: Энергоиздат, 1982, 318с.
6. Хэвлайс Дж., Тейзнер Дж. К. Ультрозвуковая визуализация в медицине: принципы и аппаратура, ТИИЭР, т. 67, N4, с. 209-234, 1979.
7. Анисимов В.В., Курганов В. Д., Злобин В. К. Распознавание и цифровая обработка изображений. М.: Высшая школа, 1983, 294 с.
8. Справочник. /Под ред. Гордонова Ю. Г., Дьякова Ю.Н. Полупроводниковые БИС запоминающих устройств. М.: Радио и связь, 1986, 359 с.
9. Якубовский С. В. и др. (под ред.). Аналоговые и цифровые интегральные микросхемы. М.: Сов. радио, 1979, 336 с.
10. Каталог интегральных микросхем. М. : Государственное центральное конструкторское бюро "Дейтон", 1993.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АНАЛИЗА НЕСТАЦИОНАРНОГО ПРОЦЕССА | 1998 |
|
RU2159956C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АЗИМУТА И ЗЕНИТНОГО УГЛА СКВАЖИНЫ И ГИРОСКОПИЧЕСКИЙ ИНКЛИНОМЕТР | 1996 |
|
RU2100594C1 |
| УСТРОЙСТВО АДАПТИВНОЙ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2004 |
|
RU2259638C1 |
| УСТРОЙСТВО ПЛАНИРОВАНИЯ ТОПОЛОГИИ ЛОГИЧЕСКИХ ИНТЕГРАЛЬНЫХ СХЕМ | 2012 |
|
RU2530275C2 |
| СПОСОБ И УСТРОЙСТВО РАСПОЗНАВАНИЯ КЛАССОВ СИГНАЛОВ | 1998 |
|
RU2133501C1 |
| ВЫЧИСЛИТЕЛЬНАЯ ОТКРЫТАЯ РАЗВИВАЕМАЯ АСИНХРОННАЯ МОДУЛЬНАЯ СИСТЕМА | 2009 |
|
RU2453910C2 |
| УСТРОЙСТВО КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2001 |
|
RU2197788C2 |
| Генератор периодических псевдослучайных двоичных последовательностей сложной структуры | 2018 |
|
RU2690765C1 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧЕЙ ШИФРОВАНИЯ/ДЕШИФРОВАНИЯ | 2023 |
|
RU2796051C1 |
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2012 |
|
RU2485575C1 |
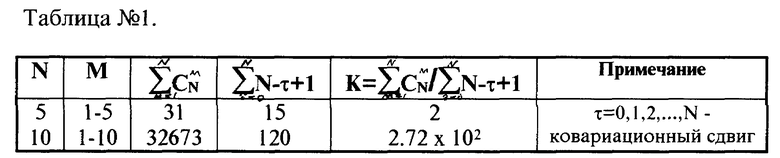

Изобретение относится к области вычислительной техники и может быть использовано при обработке экспериментальных данных, выделении сигналов из шумов, а также при обработке изображений. Цель изобретения - повышение точности. Устройство содержит аналого-цифровой преобразователь, цифроаналоговые преобразователи, сумматор, регистры, сдвигающий регистр, оперативно-запоминающие устройства. 4 ил., 2 табл.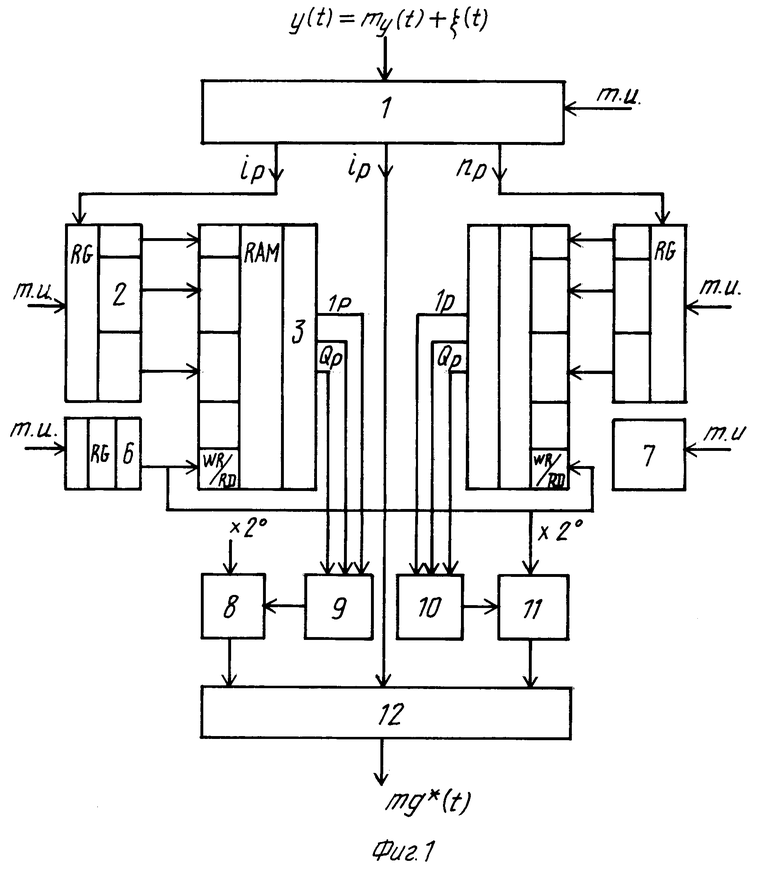
Устройство определения математического ожидания нестационарного случайного процесса (НСП) семиотического типа, содержащее регистры, генератор тактовых импульсов, параллельные цифроаналоговые преобразователи, сумматор, параллельный аналого-цифровой преобразователь, вход которого является входом устройства, отличающееся тем, что n-разрядов параллельного аналого-цифрового преобразователя подсоединены на n последовательно-параллельных регистров емкостью N двоичных разрядов, а каждый из N разрядов регистров подсоединены на N информационных входов n оперативно-запоминающих устройств с памятью 2N•Q бит, считывающие входы которых подсоединены на выход сдвигающего регистра на N тактовых импульсов, а Q выходов каждого оперативно-запоминающего устройства - на входы параллельных n цифроаналоговых преобразователей, выходы которых подсоединены на первые информационные входы n умножителей, где вторые информационные входы - с напряжением, пропорциональным весам разрядов аналого-цифрового преобразователя, а выходы подсоединены на n входов сумматора, выход которого является выходом устройства.
| Василенко Г.И | |||
| Теория восстановления сигналов.-М.:Сов.радио, 1979, с.34 | |||
| Кулик Е.И | |||
| Методы измерения случайных процессов.-М.:Радио и связь, 1986, сб.19-20, с.125-128 | |||
| Плющильный станок | 1930 |
|
SU21878A1 |
| Случайные процессы и динамические системы.-М.:Госстандарт СССР, СМ СССР, 1976, с.9 | |||
| Мирский Г.Я | |||
| Характеристики статистической взаимосвязи и их измерение.-М.:Энергоиздат, 1982, с.213-226 | |||
| Хэвлайс Дш, Тейзнер Дж.К | |||
| Ультразвуковая визуализация в медицине: принципы и аппаратура | |||
| ТИИЭР, т.67, N 4, 1979, с.209-239 | |||
| Анисимов В.В., Курганов В.Д., Злобин В.К | |||
| Распознавание и цифровая обработка изображений.-М.:Высшая школа, 1983, с.56 | |||
| Справочник под ред | |||
| Гордонова Ю.Г | |||
| и др | |||
| Полупроводниковые БИС запоминающих устройств.-М.:Радио и связь, 1986, с.19 | |||
| Якубовский С.В | |||
| и др | |||
| Аналоговые и цифровые интегральные микросхемы.-М.:Сов.радио, 1979, с.109 | |||
| Каталог интегральных микросхем.-М.:Государственное центральное конструкторское бюро, Дейтон, 1993, с.81 | |||
| SU, Авторское свидетельство, 1295417, кл | |||
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1999-07-20—Публикация
1996-09-09—Подача