Предлагаемое устройство относится к вычислительной технике и может быть использовано для достоверной параллельной реализации систем булевых функций в средствах криптографической защиты информации, искусственного интеллекта, системах автоматизированного проектирования интегральных схем и др.
Известно вычислительное устройство, включающее в себя сумматор, выход которого подключен к второму входу регистра результата, регистра для хранения булевых переменных, выход которого подключен к блоку конъюнкций, регистры для фиксации очередных строк матриц, описывающих структуру соответствующих конъюнкций, выходы которых подключены также к блоку конъюнкций, выход которого подключен к третьему входу регистра результата, выход которого является шиной выдачи результата вычислений (Малюгин, В.Д. Параллельные логические вычисления посредством арифметических полиномов. / В.Д.Малюгин. - М.: Физматлит, 1997. - С.156-157).
Недостаток известного устройства - отсутствие функциональной возможности контроля ошибок логических вычислений.
Наиболее близким по сущности технического решения заявленному устройству является вычислительное устройство, содержащее блок конъюнкций, входы которого являются входами устройства для подачи n булевых переменных, выходы подключены к первому и второму блокам памяти, предназначенным для хранения коэффициентов первого и второго полиномов избыточной модулярной числовой нормальной формы соответственно, два сумматора, блок вычисления остатка по модулю, элемент ИЛИ-НЕ, элемент И, регистр памяти, выходы которого являются выходами значений d булевых функций (пат. РФ 2417405, МПК G06F 7/57. Самопроверяемый модулярный вычислитель систем логических функций [Текст] / О.А.Финько, С.М.Сульгин, А.В.Щербаков; заявитель и патентообладатель О.А.Финько, С.М.Сульгин, А.В.Щербаков. - №2009121955; заявл. 08.06.09; зарегистр.27.04.11, - 18 с.: ил.).
Недостаток известного устройства - большая длительность вычислений.
Цель изобретения - уменьшение длительности вычислений.
Поставленная цель достигается тем, что в самопроверяемый специализированный вычислитель систем булевых функций, содержащий блоки памяти, предназначенные для хранения коэффициентов полиномов избыточной числовой нормальной формы, входы которых являются входами устройства, к которым подключена шина подачи n булевых переменных, выходы которых соединены со входами многоместных сумматоров, выходы которых соединены с информационными входами многоканальных мультиплексоров, выходы первого мультиплексора подключены к (s+1)-му, (s+2)-му, …, (d+s)-му входам (d - количество реализуемых булевых функций, составляющих информационные разряды разделенного AN-кода, s - количество избыточных булевых функций, соответствующих избыточным разрядам разделенного AN-кода) блока вычисления остатка по модулю и информационным входам регистра памяти, выходы которого являются выходами устройства выдачи значений d булевых функций, выходы второго мультиплексора подключены к 1-му, 2-му, …, s-му входам блока вычисления остатка по модулю, выходы которого подключены к входам элемента ИЛИ-НЕ, выход которого подключен к первому входу элемента И, второй вход которого подключен к входу подачи синхроимпульсов устройства, а выход подключен к синхровходу регистра памяти, с целью уменьшения длительности вычислений введены шина подачи коэффициентов полиномов избыточной числовой нормальной формы, подключенная к входам блоков памяти, многоканальные мультиплексоры выделения информационных разрядов реализуемых и избыточных булевых функций, блок памяти хранения адресов информационных разрядов, к входу которого подключена шина адреса, выход которого подключен к адресным входам мультиплексоров.
Структурная схема предлагаемого устройства дана на фиг.1.
Известно, что булеву функцию (БФ) можно представить посредством линейных числовых полиномов (ЛЧП) (Финько, О.А. Модулярная арифметика параллельных логических вычислений [Текст] / О.А.Финько. - М.: ИПУ РАН, 2003. - 224 с.).
Например: пороговая БФ  как класс булевых функций, которая определяется отношением:
как класс булевых функций, которая определяется отношением:

где  ; xi∈{0,1} - булевы переменные; i=1, 2, …, n; 1≤p≤n, р - порог функции
; xi∈{0,1} - булевы переменные; i=1, 2, …, n; 1≤p≤n, р - порог функции 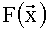 , в базисе Ω={∨,∧,¬} может быть выражена дизъюнктивной формулой:
, в базисе Ω={∨,∧,¬} может быть выражена дизъюнктивной формулой:
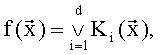
где ; Ki - элементарные конъюнкции длины р; 1≤p≤n.
; Ki - элементарные конъюнкции длины р; 1≤p≤n.
Любую пороговую БФ можно представить с помощью ЛЧП вида:
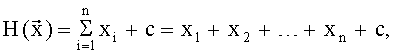
где c∈Z, Z - множество целых неотрицательных чисел, и удовлетворяет условию:
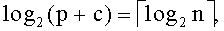
где  • - наименьшее целое число ≥•.
• - наименьшее целое число ≥•.
Большой интерес также представляет возможность реализации не только пороговых, но и БФ других классов с помощью одного ЛЧП. Однако задача представления БФ общего вида с помощью одного ЛЧП в настоящее время остается нерешенной. В то же время можно определить условие существования ЛЧП (2), с помощью которого можно реализовать БФ общего вида.
Пусть дана произвольная БФ типовых криптопримитивов, имеющая представление в виде таблицы истинности (табл.1).


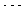

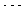







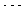

где  j=0, 1, …, 2n-1.
j=0, 1, …, 2n-1.
Данную БФ можно представить с помощью ЛЧП:

полученного посредством алгоритма проверки представимости БФ общего вида одним ЛЧП:

где |•|m - наименьший неотрицательный вычет числа • по модулю m; 0≤ai<m; i=1,2,…, n+1; m=2t, t∈Z.
Значение БФ  может быть вычислено по формуле:
может быть вычислено по формуле:

где • - наибольшее целое число, не превосходящее •.
Пусть дана система БФ:

где  ; xi∈{0,1} - булевы переменные; i=1, 2, …, n.
; xi∈{0,1} - булевы переменные; i=1, 2, …, n.
Представим таблицу истинности реализуемой системы БФ в следующем виде (табл.2), где  - значения, принимаемые j-й БФ на i-м наборе переменных,
- значения, принимаемые j-й БФ на i-м наборе переменных,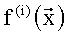 - целые неотрицательные числа:
- целые неотрицательные числа:








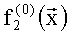





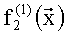

















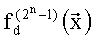

Обозначим вычисленные значения БФ (3) как y1= , y2=
, y2= , …, yd=
, …, yd= , а числом Y(i) обозначим двоичное представление:
, а числом Y(i) обозначим двоичное представление:

Представим каждую БФ системы (3) посредством ЛЧП:

где  ∈Z, i=1, 2, …, n+1, j=1, 2, …, d.
∈Z, i=1, 2, …, n+1, j=1, 2, …, d.
ЛЧП для системы (3) вычисляется по формуле:
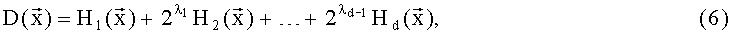
где  i=1, 2, …, n; j=1, 2, …, d.
i=1, 2, …, n; j=1, 2, …, d.
Значение  соответствует
соответствует  -му разряду двоичного представления результата вычисления
-му разряду двоичного представления результата вычисления  .
.
Однако представленный алгоритм не позволяет контролировать ошибки, которые возникают при вычислении системы БФ.
Для обеспечения контроля логических вычислений дополним реализуемую систему БФ 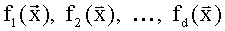 избыточными БФ
избыточными БФ  и получим избыточную систему
и получим избыточную систему  где s - количество избыточных БФ.
где s - количество избыточных БФ.
Так же как и для системы БФ  значение которой интерпретируется в виде целых неотрицательных чисел, избыточная система БФ
значение которой интерпретируется в виде целых неотрицательных чисел, избыточная система БФ 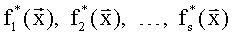 представляется как
представляется как

где  - значения, принимаемые j-и БФ на i-м наборе переменных, Y*(i) - целые неотрицательные числа.
- значения, принимаемые j-и БФ на i-м наборе переменных, Y*(i) - целые неотрицательные числа.
Рассмотрим полученную избыточную систему БФ по правилу задания разделимого AN-кода (Дадаев, Ю.Г. Арифметические коды, исправляющие ошибки / Ю.Г.Дадаев. - М.: Советское радио, 1969. - 168 с.), где кодовое слово R формируется из выражения:

где Y - исходное число, здесь - вектор значений реализуемых БФ, S=|-2aY|A - информационная часть кода, I=2aY - проверочные символы кодовой комбинации, 2 - основание системы счисления, а - количество двоичных разрядов, необходимое для записи чисел, не превосходящих генератора кода А.
Получим:
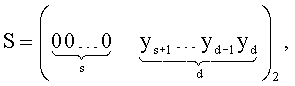

Отсюда:

где d - количество информационных символов кодового слова (количество реализуемых булевых функций), s - количество проверочных символов (количество избыточных булевых функций), причем количество проверочных символов зависит от выбора численного значения генератора и определяется следующим образом:
l=log2AY+1, s=l-d,
где l - общая длина кодовой комбинации.
Таким образом, требуется реализовать таблицу истинности, представленную в табл.3.


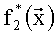


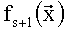

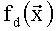

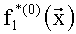
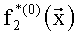


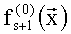



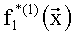



















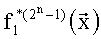


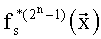
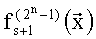


Используя преобразование (5), (6) построим полиномы избыточной числовой AN-формы:
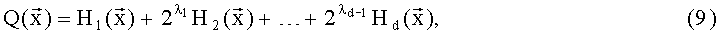

Как известно, выбор генератора А арифметического AN-кода определяет арифметическое расстояние кода D и его корректирующие свойства. Таким образом, код с D=2 гарантировано обнаруживает однократную ошибку (в одной БФ).
В процессе реализации систем БФ выполняется классическая процедура контроля ошибок в соответствии со свойствами и выбранными параметрами AN-кода.
Принцип контроля заключается в выполнении следующего правила:

что соответствует правильному результату, а выражение  является признаком ошибки.
является признаком ошибки.
Пример
Пусть дана таблица истинности системы БФ, представленная в табл.4.
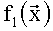


Полином (6) примет вид:
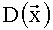 =27x1+37х2+41x3+43.
=27x1+37х2+41x3+43.
Применим арифметический разделимый AN-код с генератором А=5, построим избыточную систему БФ в соответствии с табл.3 и получим табл.5.
 и
и 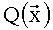



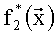


В соответствии с (6) получим полиномы (9) и (10):
 =27x1+37x2+41х3+43,
=27x1+37x2+41х3+43,
 =12x1+15x2+20x3+59.
=12x1+15x2+20x3+59.
Пример обнаружения однократной ошибки (звездочкой * обозначается функция, значение которой содержит ошибку) продемонстрируем в табл.6.
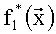
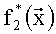




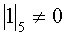
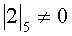





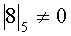











На чертежах представлено:
на фиг.1 изображен самопроверяемый специализированный вычислитель систем булевых функций;
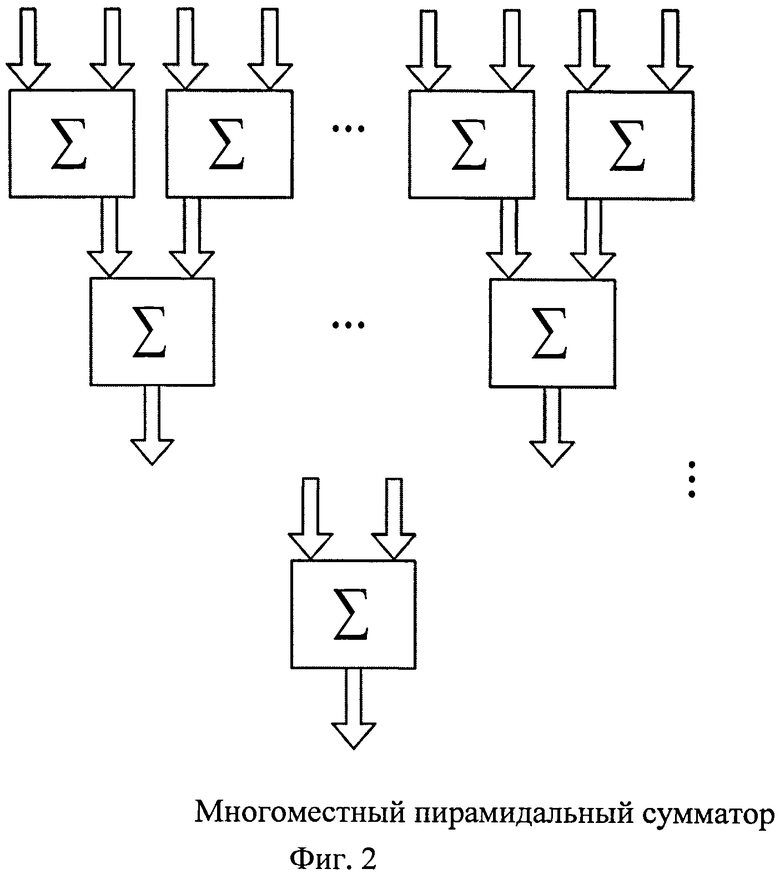
на фиг.2 изображен многоместный пирамидальный сумматор;
на фиг.3 изображен график выигрыша в скорости функционирования заявленного устройства по сравнению с прототипом;
на фиг.4 изображен график зависимости выигрыша в скорости функционирования заявленного устройства по сравнению с прототипом от возрастания количества n булевых переменных.
Предлагаемое устройство содержит: шину 9 подачи значений n булевых переменных x1, x2, …, xn шину 10 подачи коэффициентов полиномов избыточной числовой нормальной формы, блоки памяти 1.1 и 1.2, блок памяти 2 хранения адресов информационных разрядов, шину адреса 11, многоместные сумматоры 3.1 и 3.2, многоканальные мультиплексоры 4.1 и 4.2, блок 5 вычисления остатка по модулю, элемент ИЛИ-НЕ 6, регистр памяти 7, элемент И 8, выходы 12.1, …, 12.d выдачи значений булевых функций 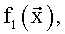 …,
…, 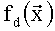 соответственно, вход 13 шины подачи синхроимпульсов.
соответственно, вход 13 шины подачи синхроимпульсов.
Шина 9 подачи значений n булевых переменных x1, x2, …, xn и шина 10 подачи коэффициентов полиномов избыточной числовой нормальной формы, являются входами блоков памяти 1.1 и 1.2, предназначенных для их хранения, выходы которых соединены со входами многоместных сумматоров 3.1 и 3.2, выходы которых соединены с информационными входами многоканальных мультиплексоров 4.1 и 4.2, выходы мультиплексора 4.1 подключены к (s+1)-му, (s+2)-му, …, (d+s}-му входам (старшие разряды слева) блока 5 вычисления остатка по модулю и информационным входам регистра памяти 7, выходы которого являются выходами устройства выдачи значений d булевых функций:  …,
…,  , выходы мультиплексора 4.2 подключены к 1-му, 2-му, …, s-му входам блока 5 вычисления остатка по модулю, выходы которого подключены к входам элемента 6 ИЛИ-НЕ, выход которого подключен к первому входу элемента 8 И, второй вход которого соединен с входом 13 подачи синхроимпульсов устройства, а выход 8 подключен к синхровходу регистра памяти 7.
, выходы мультиплексора 4.2 подключены к 1-му, 2-му, …, s-му входам блока 5 вычисления остатка по модулю, выходы которого подключены к входам элемента 6 ИЛИ-НЕ, выход которого подключен к первому входу элемента 8 И, второй вход которого соединен с входом 13 подачи синхроимпульсов устройства, а выход 8 подключен к синхровходу регистра памяти 7.
Многоместный сумматор как в случае прототипа, так и в случае предлагаемого устройства имеет наиболее типичную - пирамидальную структуру, представленную на фиг.2.
Предлагаемое устройство работает следующим образом. В исходном состоянии в блоки 1.1 и 1.2 памяти занесены по шине 10 коэффициенты: a1, a2, …, an+1;  полиномов избыточной числовой нормальной формы (9) и (10), соответственно полученных в результате преобразований (5), (6), регистр 7 памяти обнулен. В момент времени, соответствующий началу преобразования, на входы блоков 1.1 и 1.2 памяти из шины 9 поступают значения булевых переменных x1, x2,…, xn С выходов блоков 1.1 и 1.2 памяти на входы многоместных сумматоров 3.1 и 3.2 поступают произведения ai·(x1, x2, …, xn), где i=1, 2, …, n+1 и
полиномов избыточной числовой нормальной формы (9) и (10), соответственно полученных в результате преобразований (5), (6), регистр 7 памяти обнулен. В момент времени, соответствующий началу преобразования, на входы блоков 1.1 и 1.2 памяти из шины 9 поступают значения булевых переменных x1, x2,…, xn С выходов блоков 1.1 и 1.2 памяти на входы многоместных сумматоров 3.1 и 3.2 поступают произведения ai·(x1, x2, …, xn), где i=1, 2, …, n+1 и 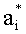 ·( x1, x2, …, xn), где i=1, 2, …, n+1. С выходов многоместных сумматоров 3.1 и 3.2 значения произведений поступают на информационные входы многоканальных мультиплексоров 4.1 и 4.2, предназначенных для выделения группы значений информационных разрядов, в зависимости от адресов, поступивших на их адресные входы с выходов блока 2 памяти адресов, к входу которого подсоединена шина 11 адреса. С выходов мультиплексора 4.1 на (s+1)-й,(s+2)-й,…,(d+s)-й входы (старшие разряды слева) блока 5 вычисления остатка по модулю и на информационные входы регистра памяти 7 поступает числовой результат вычисления полинома
·( x1, x2, …, xn), где i=1, 2, …, n+1. С выходов многоместных сумматоров 3.1 и 3.2 значения произведений поступают на информационные входы многоканальных мультиплексоров 4.1 и 4.2, предназначенных для выделения группы значений информационных разрядов, в зависимости от адресов, поступивших на их адресные входы с выходов блока 2 памяти адресов, к входу которого подсоединена шина 11 адреса. С выходов мультиплексора 4.1 на (s+1)-й,(s+2)-й,…,(d+s)-й входы (старшие разряды слева) блока 5 вычисления остатка по модулю и на информационные входы регистра памяти 7 поступает числовой результат вычисления полинома  , с выходов мультиплексора 4.2 на 1-й, 2-й, …, s-й входы (старшие разряды слева) блока 5 вычисления остатка по модулю поступает числовой результат вычисления полинома
, с выходов мультиплексора 4.2 на 1-й, 2-й, …, s-й входы (старшие разряды слева) блока 5 вычисления остатка по модулю поступает числовой результат вычисления полинома  . С выходов блока 5 вычисления остатка по модулю на входы элемента 6 ИЛИ-НЕ поступает результат вычисления
. С выходов блока 5 вычисления остатка по модулю на входы элемента 6 ИЛИ-НЕ поступает результат вычисления  . На выходе элемента 6 ИЛИ-НЕ образуется сигнал «1» при выполнении равенства (11) (ошибки нет) и «0» в противном случае. Синхроимпульс с входа 13 устройства через элемент 8 И поступает на синхровход регистра 7 памяти при отсутствии ошибок вычислений в соответствии с (11). Таким образом, при отсутствии ошибок вычислений в регистр 7 памяти записывается численный результат вычисления полинома
. На выходе элемента 6 ИЛИ-НЕ образуется сигнал «1» при выполнении равенства (11) (ошибки нет) и «0» в противном случае. Синхроимпульс с входа 13 устройства через элемент 8 И поступает на синхровход регистра 7 памяти при отсутствии ошибок вычислений в соответствии с (11). Таким образом, при отсутствии ошибок вычислений в регистр 7 памяти записывается численный результат вычисления полинома 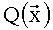 , интерпретируемый как результат реализации системы БФ, соответствующий размещению от младшего разряда справа
, интерпретируемый как результат реализации системы БФ, соответствующий размещению от младшего разряда справа  к старшим разрядам слева
к старшим разрядам слева  .
.
Предлагаемое устройство имеет глубину в 6 ступеней преобразования: 1-я ступень - блоки памяти 1.1 и 1.2, предназначенные для хранения коэффициентов полиномов 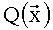 и
и  ; 2-я ступень - многоместные сумматоры 3.1 и 3.2 и блок 2 памяти, предназначенный для хранения адресов информационных разрядов; 3-я ступень - многоканальные мультиплексоры 4.1 и 4.2, предназначенные для выделения информационных разрядов; 4-я ступень - блок 5 вычисления остатка по модулю; 5-я ступень - элемент 6 ИЛИ-НЕ; 6-я ступень - элемент 8 И и регистр 7 памяти. Прототип имеет такую же глубину: 1-я ступень - блок конъюнкций; 2-я ступень - блоки памяти; 3-я ступень - сумматоры; 4-я ступень - блок вычисления остатка по модулю; 5-я ступень - элемент ИЛИ-НЕ; 6-я ступень - элемент И, регистр памяти. Однако наиболее существенный вклад в длительность преобразования как предлагаемого устройства, так и прототипа вносит многоместный арифметический сумматор, длительность его функционирования определяется глубиной его функционирования, которая определяется формулой:
; 2-я ступень - многоместные сумматоры 3.1 и 3.2 и блок 2 памяти, предназначенный для хранения адресов информационных разрядов; 3-я ступень - многоканальные мультиплексоры 4.1 и 4.2, предназначенные для выделения информационных разрядов; 4-я ступень - блок 5 вычисления остатка по модулю; 5-я ступень - элемент 6 ИЛИ-НЕ; 6-я ступень - элемент 8 И и регистр 7 памяти. Прототип имеет такую же глубину: 1-я ступень - блок конъюнкций; 2-я ступень - блоки памяти; 3-я ступень - сумматоры; 4-я ступень - блок вычисления остатка по модулю; 5-я ступень - элемент ИЛИ-НЕ; 6-я ступень - элемент И, регистр памяти. Однако наиболее существенный вклад в длительность преобразования как предлагаемого устройства, так и прототипа вносит многоместный арифметический сумматор, длительность его функционирования определяется глубиной его функционирования, которая определяется формулой:

где t - количество входов сумматора. Учитывая то, что в устройстве-прототипе сумматор содержит 2n входов, а в предлагаемом устройстве - n+1 входов, то соответственно глубина схемы в первом случае составит: log2(2n) ступеней, а во втором: log2(n+1) ступеней. Таким образом, глубина сумматора, используемого в предлагаемом устройстве в

раз меньше по сравнению с прототипом (во столько же раз выше его быстродействие), где T∑прот - длительность функционирования многоместного сумматора прототипа, а Т∑заяв - длительность функционирования многоместного сумматора предлагаемого устройства. Например, для различных значений n значения выигрыша представлены в табл.7.
В целом выигрыш в быстродействии предлагаемого устройства составит:

учитывая, что  формула (14) примет вид:
формула (14) примет вид:

Более высокое быстродействие предлагаемого устройства выгодно отличает его от прототипа.
Оценка выигрыша в скорости функционирования заявленного устройства по сравнению с прототипом представлена на фиг.3, 4.
Таким образом, полученные результаты дают научный и инженерный инструментарий для реализации гарантировано достоверной обработки логической информации и обеспечивают необходимые условия для создания перспективных средств криптографической защиты информации.
| название | год | авторы | номер документа |
|---|---|---|---|
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2579991C1 |
| ОТКАЗОУСТОЙЧИВЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2018 |
|
RU2680035C1 |
| САМОПРОВЕРЯЕМЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ ЛОГИЧЕСКИХ ФУНКЦИЙ | 2009 |
|
RU2417405C2 |
| ПОЛИНОМИАЛЬНЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ С ОБНАРУЖЕНИЕМ ОШИБОК | 2015 |
|
RU2586574C1 |
| АРИФМЕТИЧЕСКИЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2011 |
|
RU2461868C1 |
| МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2007 |
|
RU2373564C2 |
| СПОСОБ ПОВЫШЕНИЯ ДОСТОВЕРНОСТИ КРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫ КАНАЛОВ СВЯЗИ РОБОТОТЕХНИЧЕСКИХ КОМПЛЕКСОВ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ | 2023 |
|
RU2809279C1 |
| МОДУЛЯРНЫЙ ПОЛИНОМИАЛЬНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2586575C1 |
| Логический вычислитель в системе остаточных классов | 2016 |
|
RU2637488C1 |
| УСТРОЙСТВО ПАРАЛЛЕЛЬНОГО ФОРМИРОВАНИЯ q-ЗНАЧНЫХ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ НА АРИФМЕТИЧЕСКИХ ПОЛИНОМАХ | 2021 |
|
RU2762209C1 |


Изобретение относится к вычислительной технике и может быть использовано для достоверной параллельной реализации систем булевых функций в средствах криптографической защиты информации, искусственного интеллекта, системах автоматизированного проектирования интегральных схем. Техническим результатом является уменьшение длительности вычислений. Устройство содержит блоки памяти, сумматоры, мультиплексоры, блок вычисления остатка по модулю, регистр памяти, логические элементы И, ИЛИ-НЕ. 4 ил., 7 табл.
Самопроверяемый специализированный вычислитель систем булевых функций, содержащий блоки памяти, предназначенные для хранения коэффициентов полиномов избыточной числовой нормальной формы, входы которых являются входами устройства, к которым подключена шина подачи n булевых переменных, выходы которых соединены со входами многоместных сумматоров, выходы которых соединены с информационными входами многоканальных мультиплексоров, выходы первого мультиплексора подключены к (s+1)-му, (s+2)-му,…, (d+s)-му входам (d - количество реализуемых булевых функций, составляющие информационные разряды разделенного AN-кода, s - количество избыточных булевых функций, соответствующих избыточным разрядам разделенного AN-кода) блока вычисления остатка по модулю и информационным входам регистра памяти, выходы которого являются выходами устройства выдачи значений d булевых функций, выходы второго мультиплексора подключены к 1-му, 2-му,…, s-му входам блока вычисления остатка по модулю, выходы которого подключены к входам элемента ИЛИ-НЕ, выход которого подключен к первому входу элемента И, второй вход которого подключен к входу подачи синхроимпульсов устройства, а выход - подключен к синхровходу регистра памяти; отличающийся тем, что введены шина подачи коэффициентов полиномов избыточной числовой нормальной формы, подключенная к входам блоков памяти, многоканальные мультиплексоры выделения информационных разрядов реализуемых и избыточных булевых функций, блок памяти хранения адресов информационных разрядов, к входу которого подключена шина адреса, выходы которого подключены к адресным входам мультиплексоров.
| САМОПРОВЕРЯЕМЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ ЛОГИЧЕСКИХ ФУНКЦИЙ | 2009 |
|
RU2417405C2 |
| Многофункциональный логический модуль двух переменных с самоконтролем | 1984 |
|
SU1275444A1 |
| US 2008021942 A1, 24.01.2008 | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| US 6370558 B1, 09.04.2002. | |||
Авторы
Даты
2013-06-20—Публикация
2012-05-18—Подача