Изобретение относится к области контроля и диагностирования систем автоматического управления и их элементов.
Известен способ контроля линейных динамических систем, контроль параметров по которому осуществляется последовательно во времени и требует многократного переключения уровня стимулирующего входного сигнала в момент фиксации нулей сигналов с модели чувствительности. (Авторское свидетельство N 297034, М.кл. G 05 B 23/00, 1969).
Наиболее близким к предлагаемому изобретению техническим решением является способ диагностирования неисправностей динамических объектов. (Авторское свидетельство N 1462254, М.кл. G 05 B 23/02, 1987).
Недостатком этого способа является необходимость подачи нескольких гармонических тестовых сигналов и регистрации реакции системы на каждый из них, что обуславливает большие временные и аппаратные затраты на реализацию способа. Кроме того, применение способа ограничено линейными объектами.
Цель изобретения - уменьшение временных и аппаратных затрат на диагностирование, упрощение процесса диагностирования и расширение функциональных возможностей способа путем обеспечения возможности диагностирования нелинейных объектов.
Указанная цель достигается тем, что предлагается новая совокупность действий:
1. В качестве объекта диагностирования рассматривают систему, состоящую из произвольно соединенных динамических элементов. Фиксируют число m динамических элементов и число k контрольных точек объекта диагностирования.
2. Предварительно определяют время контроля Tk≥TПП, где TПП - время переходного процесса объекта. Время переходного процесса оценивают для номинальных значений параметров объекта.
3. В качестве диагностического признака наличия дефекта в i-м динамическом элементе используют интегральную меру следующего вида:
где 
 вектор отклонений временных характеристик объекта в k контрольных точках;
вектор отклонений временных характеристик объекта в k контрольных точках; структурная чувствительность (чувствительность временных характеристик объекта к изменению весовой функции i-го динамического элемента);
структурная чувствительность (чувствительность временных характеристик объекта к изменению весовой функции i-го динамического элемента);
Δi(t) - интегральное отклонение весовой функции i-го динамического элемента от номинального значения.
Рассмотрим подробнее что представляет собой интегральное отклонение весовой функции Δi(t) в выражении (1). Для этого запишем уравнение, связывающее отклонение временной характеристики объекта в j-й контрольной точке ΔFj(t) с отклонением весовой функции i-го динамического элемента: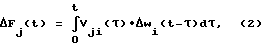
где Vji(τ) - структурная чувствительность для j-й контрольной точки и i-го динамического элемента;
Δwi(τ) - отклонение весовой функции i-го динамического элемента от номинального значения в момент времени τ.
Сигналы, численно равные структурным чувствительностям Vji(t), могут быть получены с учетом следующих соображений.
Рассмотрим вектор коэффициентов влияния i-го динамического элемента:
где  вектор передаточных функций всей системы для различных контрольных точек; Wi(p) - передаточная функция i-го динамического элемента. По определению передаточной функции для нулевых начальных условий
вектор передаточных функций всей системы для различных контрольных точек; Wi(p) - передаточная функция i-го динамического элемента. По определению передаточной функции для нулевых начальных условий
где 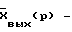 вектор изображений выходных сигналов объекта для различных контрольных точек.
вектор изображений выходных сигналов объекта для различных контрольных точек.
Тогда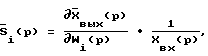
откуда
Слева в выражении (4) - вектор изображений чувствительностей выходных сигналов объекта к изменению весовой функции i-го динамического элемента. Таким образом, чтобы получить искомые чувствительности  необходимо входной тестовый сигнал подать на модель структурной чувствительности с передаточными функциями
необходимо входной тестовый сигнал подать на модель структурной чувствительности с передаточными функциями 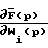 (Р. Томович, М. Вукобратович. Общая теория чувствительности. М.: Сов. радио. 1972- стр. 176-177).
(Р. Томович, М. Вукобратович. Общая теория чувствительности. М.: Сов. радио. 1972- стр. 176-177).
Модель структурной чувствительности может быть получена путем последовательного соединения двух одинаковых моделей объекта, когда выходом первой модели является входной сигнал i-го динамического элемента, а вход второй модели организуется на выходе i-го динамического элемента (там же, стр. 180).
Другими словами, две одинаковые модели объекта диагностирования должны быть включены последовательно через перемычку, идущую от входа рассматриваемого i-го блока в первой модели к выходу i-го блока второй модели. Это соединение поясняет фиг. 1.
Если подать на такое последовательное соединение двух моделей тестовое воздействие V, то на выходах контрольных точек второй модели появляются сигналы, численно равные функциям чувствительности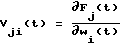 для i-го блока.
для i-го блока.
Изменение передаточной функции всей системы ΔFj(p) связано с изменением передаточной функции i-го динамического элемента ΔWi(p) при одиночном дефекте и использовании модели чувствительности первого порядка следующим соотношением:
ΔFj(p) = Vji(p)•ΔWi(p), (5)
где Vji(p) - чувствительность для i-го блока и j-й контрольной точки, определяемая выражением (4).
Формуле (5) в области оригиналов соответствует свертка (2). Запишем уравнение (2) для всех контрольных точек в векторном виде и проинтегрируем его на интервале 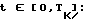
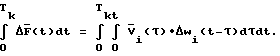
Поскольку Δwi(t) = 0 при t <0, внутренний интеграл не изменится, если его верхний предел заменить на Tk. Меняя порядок интегрирования, получим: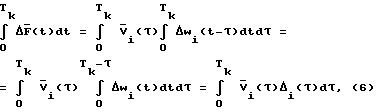
где  - интегральное отклонение весовой функции i-го динамического элемента.
- интегральное отклонение весовой функции i-го динамического элемента.
В качестве контролируемого параметра i-го блока выберем интегральное отклонение его весовой функции (7). Как видно из выражения (6), это позволяет заменить интеграл свертки (2) произведением функций 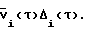
Если дефект только в i-м динамическом элементе, то
причем, чтобы квадратичный функционал (1) обратился в ноль, подынтегральное выражение должно быть равно 0 при всех t: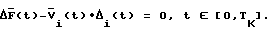
Для того, чтобы диагностический признак (1) не зависел от неизвестного и искомого на этапе поиска дефектов интегрального отклонения Δi(t), выразим это отклонение из системы уравнений: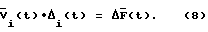
Умножение выражения (8) слева на 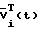 позволяет выразить скаляр Δi(t):
позволяет выразить скаляр Δi(t):
или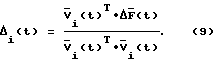
Подставляя выражение (9) в формулу (1) и, производя эквивалентные преобразования, получим:
В развернутой для элементов векторов форме это выражение примет вид: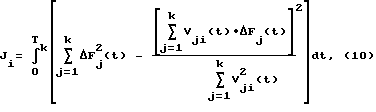
где 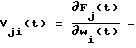 структурная чувствительность временной характеристики в j-ой контрольной точке для i-го динамического элемента.
структурная чувствительность временной характеристики в j-ой контрольной точке для i-го динамического элемента.
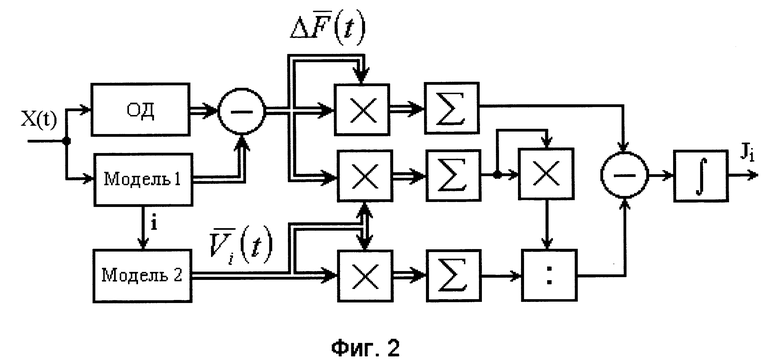
Дальнейшие операции при реализации предлагаемого способа направлены на определение интегральных диагностических признаков для каждого динамического элемента по формуле (10) и поясняются блок-схемой устройства, показанной на фиг. 2.
4. Задают модель чувствительности временных характеристик объекта в различных контрольных точках к изменению весовой функции i-го динамического элемента в виде последовательного соединения двух одинаковых эталонных моделей объекта через перемычку, соединяющую вход i-го динамического элемента в первой эталонной модели с выходом i-го динамического элемента во второй эталонной модели. В качестве первой и второй эталонных моделей используются два одинаковых аналоговых устройства, состоящих, как и объект, из m динамических элементов и реакции которых на тестовое воздействие в k контрольных точках равны реакциям исправного объекта диагностирования на то же воздействие
5. На входы динамического объекта и его первой эталонной модели подают тестовое воздействие (единичное ступенчатое, линейно возрастающее, прямоугольное импульсное и т.д.).
6. Регистрируют реакцию объекта и первой эталонной модели в k контрольных точках и определяют отклонения временных характеристик объекта от номинальных ΔFj(t), i= l,2,.,k на интервале t ∈ [0,TK]. С k выходов второй эталонной модели, соответствующих k контрольным точкам объекта диагностирования, снимают сигналы, численно равные функциям чувствительности Vji(t).
7. Каждый из сигналов Vji(t) подают на первый и второй входы соответствующих блоков перемножения первой группы. Выходные сигналы k блоков перемножения первой группы численно равные квадратам функций чувствительности Vj1 2(t), подают на входы первого сумматора. Сигнал с выхода сумматора, численно равный сумме квадратов функций чувствительности первого динамического элемента, где суммирование произведено по числу контрольных точек, подают на второй вход (делитель) блока деления.
8. Одновременно функции чувствительности первого динамического элемента для различных контрольных точек подают на первые входы второй группы блоков перемножения, на вторые входы которых, подают сигналы отклонения временных характеристик ΔFj(t). Выходные сигналы второй группы блоков перемножения подают на входы второго сумматора. Выходной сигнал второго сумматора одновременно подают на оба входа блока перемножения. Выходной сигнал блока перемножения подают на первый вход (делимое) блока деления.
9. Сигналы, равные отклонениям от номинальных значений временных характеристик ΔFj(t), подают на первый и вторые входы блоков перемножения третьей группы. Выходные сигналы блоков перемножения третьей группы подают на входы третьего сумматора.
10. Из выходного сигнала третьего сумматора вычитают выходной сигнал блока деления и разностный сигнал интегрируют на интервале [0,Tк].
11. По истечении времени контроля Тк на выходе интегратора фиксируют значение диагностического признака J1 для первого динамического элемента.
12. Затем последовательно определяют диагностические признаки остальных динамических элементов, для чего выполняют пункты 3-11 каждый раз, предварительно изменяя положение перемычки, соединяющей первую эталонную модель и вторую эталонную модель согласно номеру динамического элемента, для которого находится диагностический признак.
13. После нахождения всех m диагностических признаков по минимуму значения признака определяют неисправный динамический элемент.
Таким образом, реализация предлагаемого способа предполагает m-кратную подачу однотипного тестового воздействия на объект, где m-число рассматриваемых (т.е. контролируемых) блоков объекта.
Время поиска неисправности приближенно определяется выражением Т ≈ m • Tк, где m - число контролируемых блоков системы, и может быть значительно меньше, чем в прототипе, где измерение для каждой частоты гармонического воздействия должны производиться после завершения переходных процессов в объекте и требуется подача нескольких, различных по частоте тестовых гармонических воздействий при определении каждого диагностического признака.
Работоспособность предлагаемого способа иллюстрируется следующими примерами.
Пример 1. Рассмотрим объект диагностирования, структурная схема которого показана на фиг. 3.
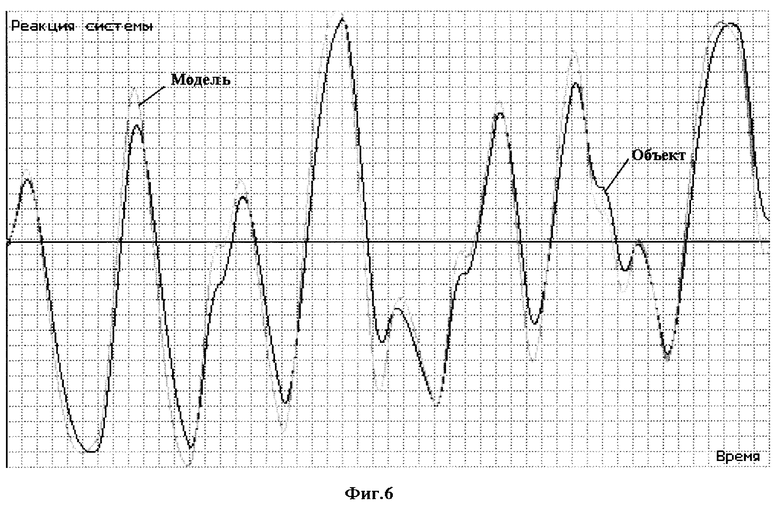
Номинальные значения параметров: T1= 5; K1=l; К2= 1; T2= 1; К3= 1; Т3= 5. При поиске дефектов использовался прямоугольный импульсный тестовый сигнал единичной амплитуды со скважностью 10 и длительностью импульса одна секунда. Моделирование объекта диагностирования, его модели и модели чувствительности проводилось на интервале 0-50 с. методом Эйлера с шагом дискретизации 0,001 с. На фиг. 4 показаны сигналы для контрольной точки КТ3 при отсутствии дефектов (кривая 1) и при наличии одиночного дефекта (кривая 2) в звене 1 (отклонение постоянной времени T1 на 50%). На фиг. 5 показана структурная функция чувствительности для динамического элемента 1 и контрольной точки КТЗ. Значения диагностических признаков при использовании контрольных точек КТ2 и КТЗ следующие: J1=1,262; J2=4,176; J3=6,605, а при использовании всех трех контрольных точек: J1=5,471; J2=63,65; J3=29,74.
Анализ значений признаков указывает на наличие дефекта в первом динамическом элементе, причем различимость состояний первого и второго динамических элементов лучше при использовании трех контрольных точек. Моделирование поиска одиночных дефектов в блоках 2 и 3 также приводит к правильным результатам.
Пример 2. Для исследования возможности применения предлагаемого способа при функциональном диагностировании было проведено моделирование процессов поиска того же дефекта при подаче на вход системы псевдослучайного двоичного двуполярного сигнала [П. Эйкхофф. Основы идентификации систем управления. М. : Мир, 1975. С. 495- 506]. Такие сигналы имеют статистические свойства, приближающиеся к свойствам белого шума. Период последовательности TП легко изменяется в соответствии с формулой TП= (2n-1)•T, где n - количество разрядов регистра сдвига, Т - период следования тактовых импульсов. При моделировании были выбраны следующие характеристики псевдослучайного сигнала: амплитуда сигнала A=1; период Т=1 с; количество разрядов регистра сдвига n=7. Время моделирования, шаг дискретизации и место дефекта были выбраны такими же, как в предыдущем тестовом примере. На фиг. 6 представлены выходные сигналы номинальной модели и объекта диагностирования в третьей контрольной точке, на фиг. 7 - структурная функция чувствительности для первого динамического элемента в этой же контрольной точке, на фиг. 8 -абсолютное отклонение реакции объекта диагностирования в третьей контрольной точке от номинальной, а на фиг. 9 - псевдослучайный двоичный двуполярный тестовый входной сигнал, которой может рассматриваться как модель реального случайного входного сигнала при функциональном диагностировании. Результаты моделирования дают следующие значения диагностических признаков: J1=1,723; J2=69,94; J3= 115,5, что показывает работоспособность разработанного алгоритма в режиме функционального диагностирования. Кроме того, производилось моделирование процессов поиска дефектов при однополярном псевдослучайном двоичном входном сигнале при различных параметрах A и n.
Пример 3. Применение предлагаемого способа для диагностирования нелинейных систем рассмотрим на примере объекта диагностирования, структурная схема которого приведена на фиг. 10.
Номинальные значения параметров: T1=9; K1=0,1; К3=1; Т3=0,1; К4=1; Т4= 0.5, нелинейный элемент "усилитель с ограничением" с ограничением на уровне
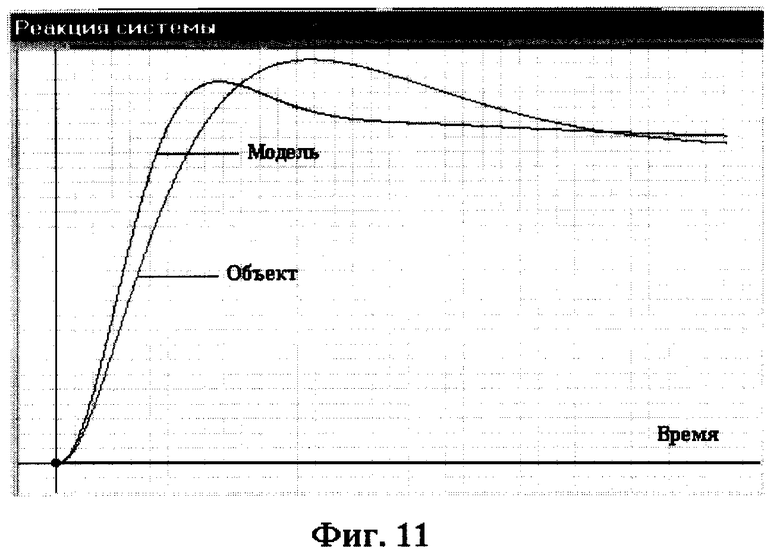
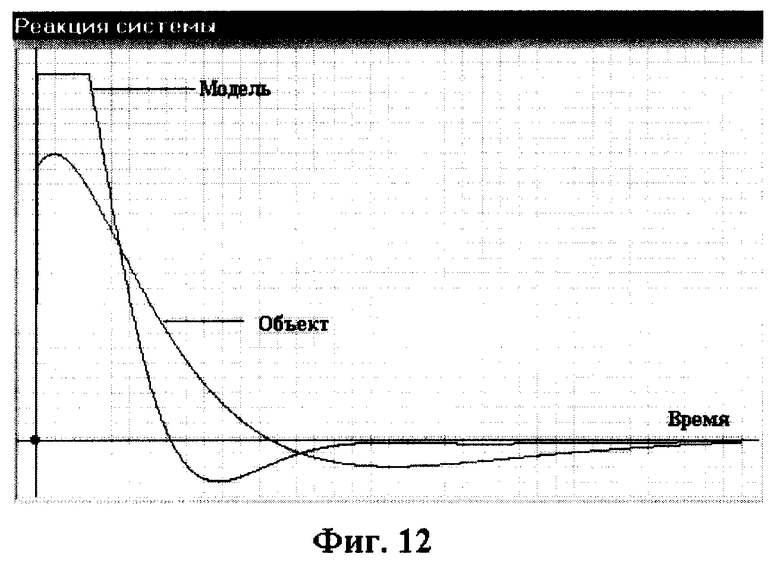
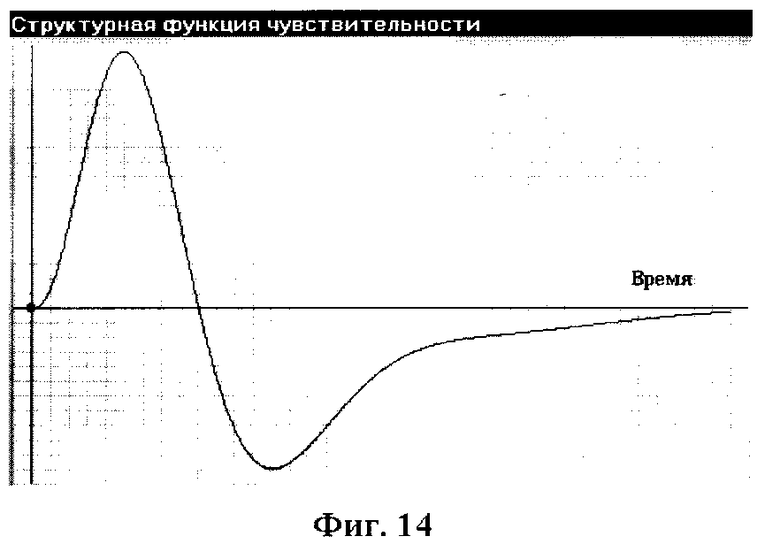
2. Для диагностирования использовалось ступенчатое воздействие с амплитудой, равной 3. Моделирование объекта диагностирования, его модели и модели чувствительности проводилось на интервале 0-15 с с шагом дискретизации 0,01 с. На фиг. 11 показаны сигналы для контрольной точки КТ4 при отсутствии дефектов (Модель) и при наличии одиночного дефекта (Объект) в звене 1 (изменение постоянной времени T1=5). На фиг. 12 показаны эти же сигналы в контрольной точке КТ2. На фиг. 13 приведено отклонение реакции объекта от номинального значения в контрольной точке КТ4. На фиг. 14 показана структурная функция чувствительности для динамического элемента 1 в контрольной точке КТ4. Значения диагностических признаков при использовании контрольных точек 1,2,3,4 следующие: J1=0,866; J2=1,55; J3=2.14, J4=2.5. Применение для диагностирования псевдослучайного двоичного сигнала с параметрами Т=0,1 с, А=3, n=7 дает следующие значения диагностических признаков J1=8,47; J2=33,2; J3=34,6, J4=22,1.
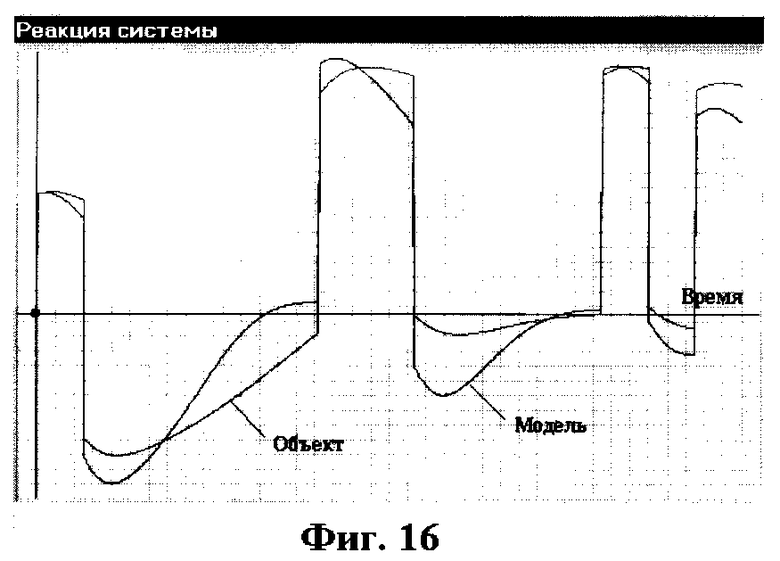
Пример 4. Для иллюстрации возможности поиска дефектов в нелинейном элементе рассмотрим объект диагностирования, приведенный в предыдущем примере. Моделировался поиск дефекта в виде изменения уровня ограничения нелинейного элемента. Для диагностирования использовался псевдослучайный двоичный сигнал с параметрами Т=1 с, А=3, n=7. Моделирование объекта диагностирования, его модели и модели чувствительности проводилось на интервале 0-15 с с шагом дискретизации 0,01 с. На фиг. 15 показаны сигналы для контрольной точки КТ4 при отсутствии дефектов (Модель) и при наличии одиночного дефекта (Объект). На фиг. 16 показаны эти же сигналы в контрольной точке КТ1. Значения диагностических признаков при использовании контрольных точек 1,2,3,4 следующие: J1=15,8; J2=4,42; J3= 18,2, J4=13.4.
Способ остается работоспособным при одновременном отклонении нескольких параметров в одном динамическом элементе и использовании других видов тестовых воздействий.









Изобретение относится к области контроля и диагностирования систем автоматического управления. Технический результат заключается в уменьшении временных и аппаратных затрат, упрощении процесса диагностирования и расширении функциональных возможностей способа. Способ заключается в том, что в качестве объекта диагностирования рассматривают систему, состоящую из произвольно соединенных m динамических элементов. Предварительно определяют время контроля Тк ≥ Тпп, где Тпп - время переходного процесса объекта. Задают модель чувствительности  временных характеристик объекта в различных контрольных точках к изменению временных характеристик i-го динамического элемента в виде последовательного соединения двух одинаковых эталонных моделей объекта через перемычку, соединяющую вход i-го в первой эталонной модели с выходом i-го элемента второй эталонной модели. В качестве динамического признака i-го динамического элемента определяют интегральную меру, для чего подают тестовый сигнал одновременно на объект и первую эталонную модель. Операции определения диагностических признаков повторяют для каждого динамического элемента. 16 ил.
временных характеристик объекта в различных контрольных точках к изменению временных характеристик i-го динамического элемента в виде последовательного соединения двух одинаковых эталонных моделей объекта через перемычку, соединяющую вход i-го в первой эталонной модели с выходом i-го элемента второй эталонной модели. В качестве динамического признака i-го динамического элемента определяют интегральную меру, для чего подают тестовый сигнал одновременно на объект и первую эталонную модель. Операции определения диагностических признаков повторяют для каждого динамического элемента. 16 ил.
Способ диагностирования динамических объектов, заключающийся в том, что фиксируют число m динамических элементов объекта диагностирования, число k контрольных точек, задают модель чувствительности динамических характеристик объекта к изменению динамических характеристик его элементов, на вход объекта и его эталонную модель подают тестовое воздействие, определяют отклонение динамических характеристик от номинальных, определяют диагностические признаки для каждого динамического элемента в виде интегральной меры рассогласования модельных и реально наблюдаемых отклонений динамических характеристик, динамический элемент, минимизирующий интегральную меру, принимают в качестве неисправного, отличающийся тем, что предварительно определяют время контроля объекта Тк ≥ Тпп, где Тпп - время переходного процесса объекта для номинальных значений параметров, задают модель чувствительности  временных характеристик объекта в различных контрольных точках к изменению весовой функции i-го динамического элемента в виде последовательно соединения двух одинаковых эталонных моделей объекта через перемычку, соединяющую вход i-го динамического элемента в первой эталонной модели с выходом i-го динамического элемента во второй эталонной модели, в качестве диагностического признака i-го динамического элемента определяют интегральную меру
временных характеристик объекта в различных контрольных точках к изменению весовой функции i-го динамического элемента в виде последовательно соединения двух одинаковых эталонных моделей объекта через перемычку, соединяющую вход i-го динамического элемента в первой эталонной модели с выходом i-го динамического элемента во второй эталонной модели, в качестве диагностического признака i-го динамического элемента определяют интегральную меру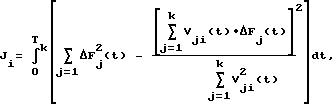
для чего подают тестовое воздействие одновременно на объект и первую эталонную модель, из выходных сигналов объекта вычитают выходные сигналы первой эталонной модели для каждой контрольной точки и получают отклонение временных характеристик ΔFj(t) объекта, выходные сигналы второй эталонной модели, численно равные функциям чувствительности Vji (t), подают на первый и второй входы j-го блока перемножения первой группы и на второй вход j-го блока перемножения второй группы, выходные сигналы блоков перемножения первой группы подают на входы первого сумматора, выходной сигнал первого сумматора подают на второй вход блока деления, сигнал ΔFj(t) отклонений временной характеристики в j-й контрольной точке подают одновременно на первый вход j-го блока перемножения второй группы и на первый и второй входы j-го блока перемножения третьей группы, выходные сигналы блоков перемножения второй группы подают на входы второго сумматора, выходной сигнал которого подают на первый и второй входы блока перемножения, выходной сигнал блока перемножения подают на первый вход блока деления, выходные сигналы блоков перемножения третьей группы подают на входы третьего сумматора, из выходного сигнала которого вычитают выходной сигнал блока деления, полученный разностный сигнал подают на интегратор и по истечении времени контроля Тк фиксируют на выходе интегратора сигнал, численно равный диагностическому признаку j-го динамического элемента, затем многократно изменяют положение перемычки между первой и второй эталонной моделью в соответствии с номером контролируемого динамического элемента, подают на вход объекта и первой эталонной модели то же самое тестовое воздействие и повторяют операции определения диагностических признаков для каждого динамического элемента объекта.
| Способ диагностирования неисправностей динамических объектов | 1987 |
|
SU1462254A1 |
| СПОСОБ КОНТРОЛЯ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ | 0 |
|
SU297034A1 |
| Устройство для определения параметров линейных динамических объектов | 1973 |
|
SU473992A1 |
| Способ контроля частотных характеристик линейных систем управления | 1977 |
|
SU661512A1 |
| US 4654582 A, 31.03.1987 | |||
| US 4851985 A, 25.07.1989. | |||
Авторы
Даты
2000-07-20—Публикация
1999-03-18—Подача