ОПТИМАЛЬНЫЙ ДЕКОДЕР ПРОГРАММИРУЕМЫХ ВЫХОДНЫХ ДАННЫХ ДЛЯ РЕШЕТЧАТЫХ КОДОВ С КОНЕЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ БИТОВ Российский патент 2002 года по МПК H03M13/25 

Область техники
Изобретение относится к декодерам, используемым для кодов с исправлением ошибок, более конкретно к декодерам для решетчатых кодов с конечными последовательностями битов.

Предшествующий уровень техники
Алгоритм Витерби представляет собой способ декодирования методом максимума правдоподобия, согласно которому определяется наиболее вероятная последовательность данных или слово для случая аддитивных белых гауссовых шумов канала, т.е. он минимизирует вероятность ошибки в декодируемом слове. Такая схема представляет собой по существу динамическую программу нахождения пути в решетке, соответствующей решетчатому коду, который наиболее близок к принятой последовательности выходных данных канала.

С другой стороны, вероятность ошибки символа или бита минимизируется с использованием так называемого декодера максимума апостериорной вероятности (MAP-декодера). MAP-декодер был впервые формально описан в работе Bahl, Cocke, Jelinek, Raviv (отсюда альтернативное название "BCJR-алгоритм"), "Optimal Decoding of Linear codes for Minimizing Symbol Error Rate, "IEEE Transactions on Information Theory, pp. 284-287, March 1976. Термины "МАР-декодер" или "BCJR-алгоритм" используются здесь для характеристики декодера данных, который выдает распределение вероятности состояний в каждом каскаде решетчатого кода и который также может использовать априорную информацию о статистике битов данных. MAP-декодер оптимален в том смысле, что он формирует эти вероятности состояния или программируемый ("мягкий") выходной результат с высокой точностью, в то время как имеются другие, хотя и более простые декодеры, которые могут формировать только аппроксимацию этих вероятностей. Варианты указанного алгоритма позволяют сформировать другую, связанную с указанной информацию, например вероятностное распределение символов данных в каждом каскаде или распределение выходных символов кодера в каждом каскаде.

MAP-декодер требует, чтобы начальное состояние в передаче решетчатого кода было известным, а в некоторых случаях требует также, чтобы было известно и конечное состояние. К сожалению, вследствие этого MAP-декодер не может быть использован для декодирования решетчатых кодов, которые используют конечную последовательность битов, т.е. кодов, для которых начальное и конечное состояния кодера не могут быть известны заранее. В частности, говорят, что передача решетчатого кода использует "конечную последовательность битов", если начальное состояние кодера идентично конечному состоянию для заданного блока входных битов. Очевидным для устройства "кодирования вперед" является знание того, каким должно быть, исходя из битов данных, конечное состояние. Это просто последние km битов блока сообщения, где k - число битов на входной символ кодера, m - размер памяти кода. Кодер с конечной последовательностью битов отличается от обычного кодера, в котором начальное состояние является предварительно конфигурированным состоянием, обычно состоянием "всех нулей". Обычные кодеры могут также завершать обработку предварительно конфигурированным состоянием путем добавления "конца" из km битов к входному блоку сообщения. Декодер с конечной последовательностью битов отличается тем, что он должен оценивать начальное состояние кодера в дополнение к его другим функциям. Если кодер с конечной последовательностью битов использует цилиндрическую решетку кодов, кодовое слово, генерируемое таким кодером, можно представить в виде круга символов. Декодер может начать обработку с любой произвольной точки круга, добиться состояния синхронизации и затем кодировать биты данных.

Был предложен ряд декодеров с конечной последовательностью битов, аналогичных декодеру, основанному на алгоритме Витерби, которые формируют оценку максимума правдоподобия кодового слова решетчатого кода. Декодер "мягкого" (программируемого) выходного результата, с другой стороны, должен оценивать вероятности состояний вокруг цилиндрической "решетки" решетчатого кода. Такой декодер в настоящее время неизвестен. В частности, как поясняется выше, MAP-декодер с программируемыми выходными данными требует, чтобы начальное состояние решетчатого кода было известным, и в некоторых случаях должно быть известным также конечное состояние. Следовательно, применение MAP-декодера ограничено обычными кодами, без конечной последовательности битов, что в свою очередь препятствует достижению преимуществ, связанных с конечной последовательностью битов, в повышении эффективности исправления ошибок в системах, осуществляющих передачи коротких блоков данных (т.е. пакетную передачу), если необходимо вырабатывать достоверные программируемые выходные данные.

Таким образом, существует потребность в разработке декодера, обеспечивающего высокую точность и в то же время относительно простого, предназначенного для формирования программируемого выходного результата при использовании решетчатых кодов с конечной последовательностью битов.

Сущность изобретения
В соответствии с настоящим изобретением циклический MAP-декодер для решетчатых кодов с исправлением ошибок, использующих конечную последовательность битов, формирует выходные данные "мягкого" решения. Циклический MAP-декодер формирует оценку вероятностей состояний первого каскада решетчатого кода, причем эти вероятности заменяют априорную информацию начального состояния обычного MAP-декодера. В соответствии с настоящим изобретением циклический MAP-декодер обеспечивает распределение вероятности начального состояния любым из двух способов. Первый из них связывает решение с задачей собственного значения, для которой результирующий собственный вектор представляет собой желательное распределение вероятности начального состояния. Зная начальное состояние, циклический MAP-декодер выполняет остальную часть декодирования в соответствии с обычным алгоритмом декодирования на основе максимума апостериорной вероятности. Второй способ основан на рекурсивной обработке для обеспечения сходимости итераций к распределению начального состояния. После достаточного количества итераций состояние циклической последовательности состояний известно с высокой вероятностью, и циклический MAP-декодер выполняет остальную часть обработки в соответствии с обычным алгоритмом декодирования по методу максимума апостериорной вероятности.

Краткое описание чертежей
Признаки и преимущества настоящего изобретения поясняются в нижеследующем детальном описании изобретения, иллюстрируемом чертежами, на которых представлено следующее:
Фиг. 1 - цилиндрическая решетка для решетчатого кода четырех состояний с конечной последовательностью битов, использующего двоичные входные символы;
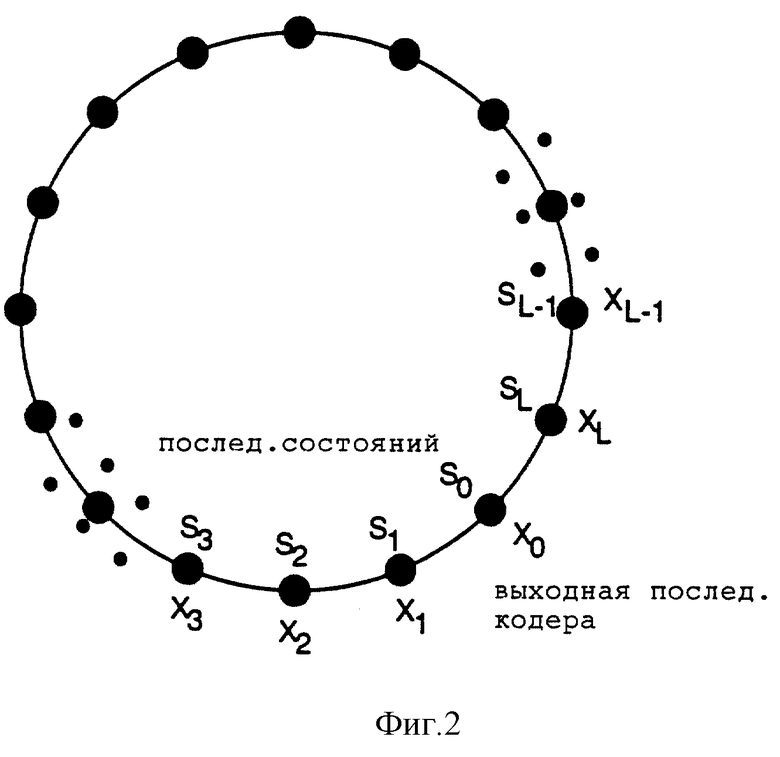
Фиг. 2 - состояние циклического кодера и последовательности выходных данных кодера для решетчатого кода с конечной последовательностью битов;
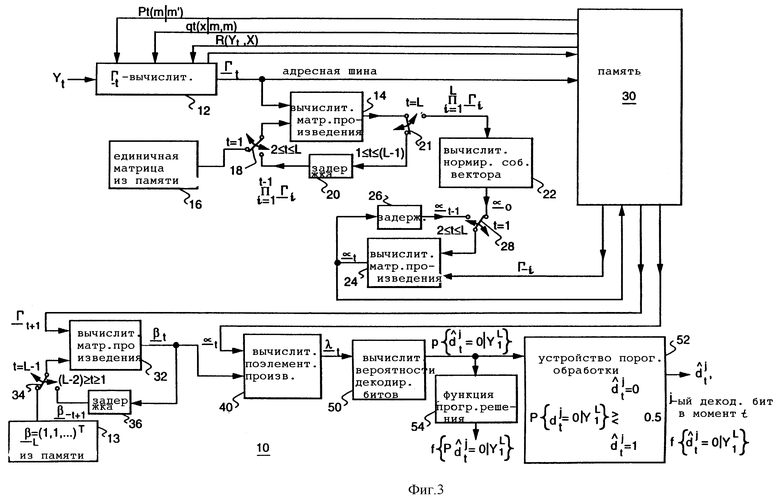
Фиг. 3 - упрощенная блок-схема, иллюстрирующая циклический MAP-декодер, согласно настоящему изобретению;
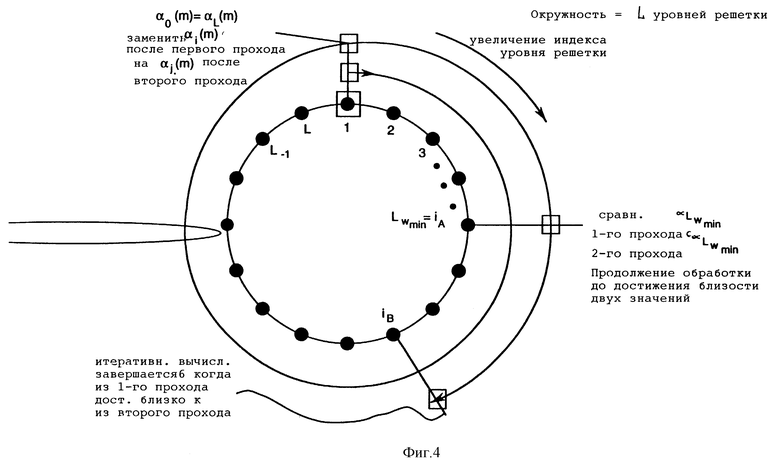
Фиг. 4 - временной цикл для циклического MAP-декодера в соответствии с настоящим изобретением;
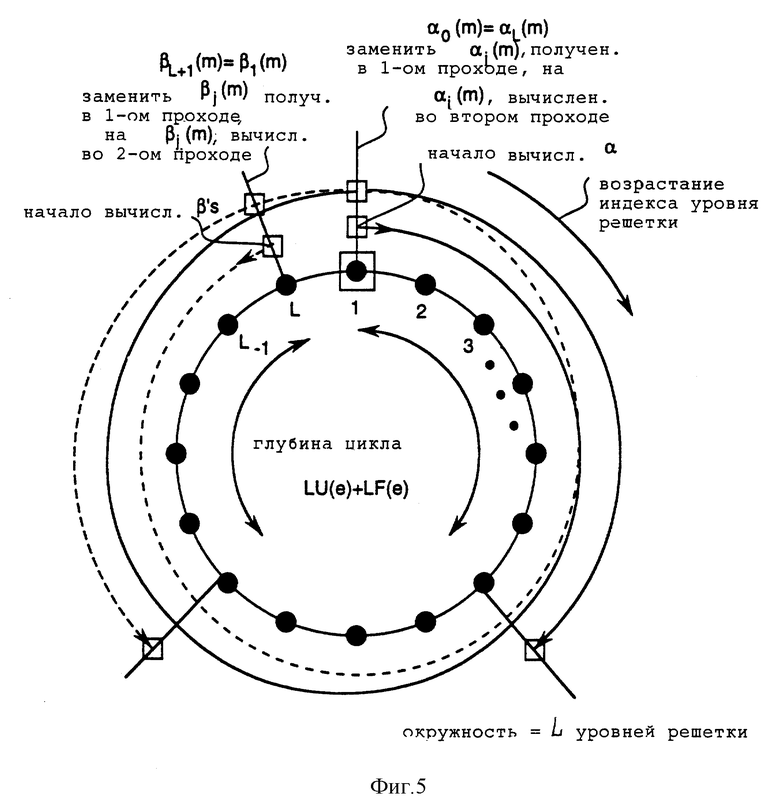
Фиг. 5 - временной цикл для предпочтительного варианта осуществления циклического MAP-декодера в соответствии с настоящим изобретением;
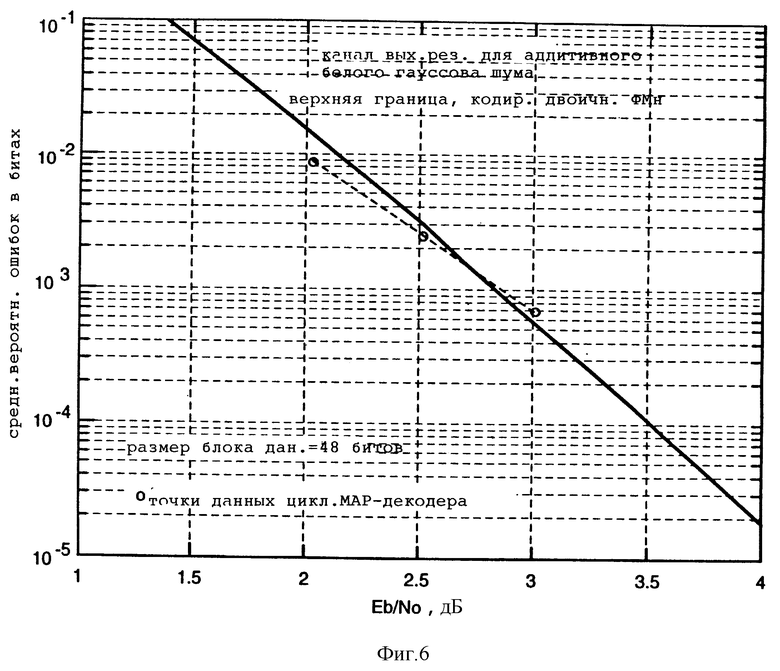
Фиг. 6 - графическое представление зависимости частоты ошибок в битах от отношения сигнал/шум для циклического MAP-декодера, использующего сверточный код с конечной последовательностью битов при скорости декодирования = 1/2 и памяти = 6, в соответствии с настоящим изобретением;
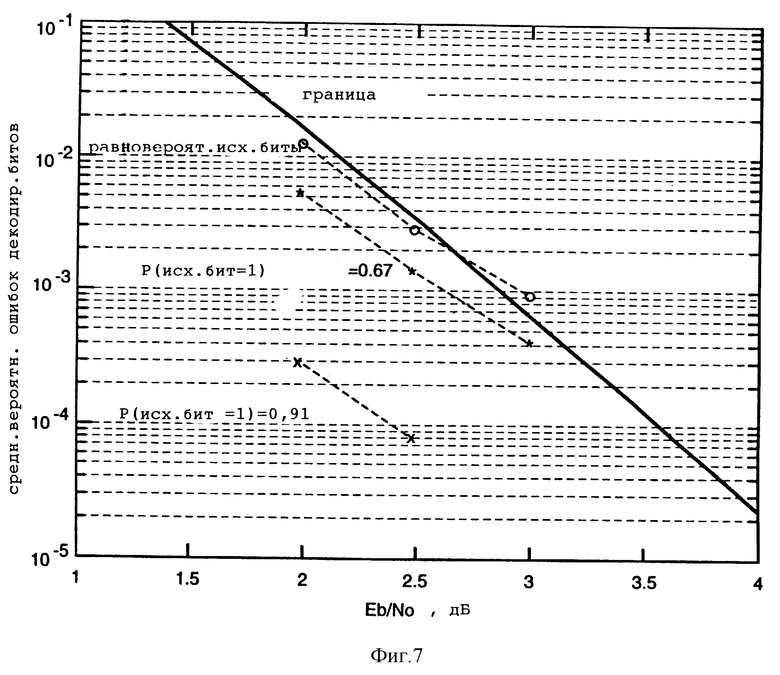
Фиг. 7 - графическое представление зависимости частоты ошибок в битах от отношения сигнал/шум при статистике со смещенным источником для циклического MAP-декодера, использующего сверточный код с конечной последовательностью битов при скорости декодирования = 1/2 и памяти = 6, в соответствии с настоящим изобретением;
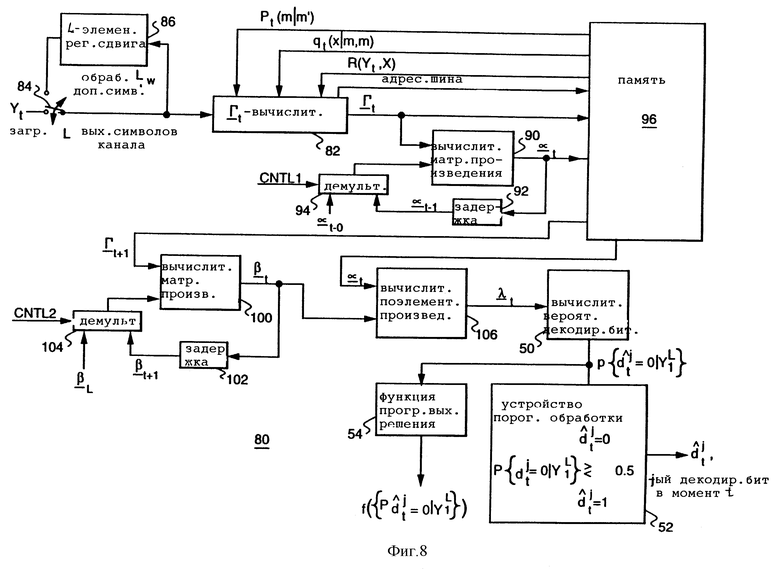
Фиг. 8 - упрощенная блок-схема, иллюстрирующая предпочтительный вариант циклического MAP-декодера, согласно настоящему изобретению.

Детальное описание изобретения
Кодер с конечной последовательностью битов использует цилиндрическую "решетку" решетчатого кода, поэтому кодовое слово, генерируемое таким кодером, можно представить как круг символов. На фиг. 1 показан пример цилиндрической решетки для кодера решетчатого кода с конечной последовательностью битов, имеющего четыре состояния и использующего двоичные входные символы. Недостаток априорной информации относительно начального состояния кодера в случае таких решетчатых кодов ухудшает надежность декодирования с использованием стандартного MAP (или BCJR) алгоритма декодирования для первой части принимаемого сообщения.

Выходная последовательность кодера для решетчатого кода с конечной последовательностью битов образует круговую диаграмму, как показано на фиг. 2. Состояния кодера показаны как упорядоченные по кругу. Если S₀ - одно из таких состояний, то кодер начинает обработку по процедуре кодирования с состояния S₀ в момент времени t₀ и после прохождения цикла по кругу через ряд переходов состояний заканчивает обработку в том же состоянии S₀. Декодер, который работает циклически с закодированной таким образом последовательностью, причем каждое состояние кодера приводит к следующему состоянию по кругу, представляет собой циклический декодер или декодер с конечной последовательностью битов.

В соответствии с настоящим изобретением циклический MAP-декодер для решетчатых кодов с исправлением ошибок, использующих конечные последовательности битов, формирует программируемые ("мягкие") выходные результаты. В противоположность этому, в обычном MAP-декодере задано начальное состояние или узел решетки. Затем такой декодер осуществляет декодирование в соответствии с путем в решетке кодера, спускающимся из указанного начального состояния. В декодере с конечной последовательностью битов, однако, декодер должен сначала идентифицировать состояние в последовательности состояний кодера, и только потом он может начать декодирование. Циклический MAP-декодер, соответствующий настоящему изобретению, обеспечивает оценку вероятностей состояний в первом каскаде решеточного кода, причем эти вероятности заменяют априорно известное начальное состояние в обычном MAP-декодере. Циклический MAP-декодер, соответствующий настоящему изобретению, обеспечивает распределение вероятности начального состояния любым из двух способов. Первый из них связывает решение с задачей собственного значения, для которой результирующий собственный вектор представляет собой желательное распределение вероятности начального состояния. Зная начальное состояние, циклический MAP-декодер выполняет остальную часть декодирования в соответствии с обычным алгоритмом декодирования на основе максимума апостериорной вероятности (или BCJR-алгоритмом). Второй способ основан на рекурсивной обработке для обеспечения сходимости итераций к распределению начального состояния. После достаточного количества итераций состояние циклической последовательности состояний известно с высокой вероятностью, и циклический MAP-декодер выполняет остальную часть обработки в соответствии с обычным алгоритмом декодирования по методу максимума апостериорной вероятности (или BCJR-алгоритмом).

Задачей обычного алгоритма максимума апостериорной вероятности (или BJCR-алгоритма) является нахождение следующих условных вероятностей:
P {состояние в момент времени t/выходные данные канала приема y₁...y_L}.

В этом выражении L представляет длину блока данных в единицах числа символов кодера. (Кодер для (n,k)-кода обрабатывает k-битовые входные символы для формирования n-битовых выходных символов.) Обозначение y_t представляет собой выходные данные (символ) канала в момент t.

Алгоритм декодирования на основе максимума апостериорной вероятности (MAP-алгоритм) прежде всего определяет вероятности
λ_t(m) = P{S_t= m; YLl

}; (1)
т. е. совместную вероятность того, что состояние S_t кодера в момент t есть m и принято множество данных каналов Y_l ^L = {y₁, ..., y_L}. Это требуемые вероятности, умноженные на постоянную (P{Y_l ^L}, вероятность приема множества выходных данных каналов {y₁, ..., y_L}).

Затем определяем элементы матрицы Г_t в следующем виде:
Г_t(i,j) = P{состояние j в момент t; y_t/состояние i в момент t-1}
Матрица Г_t вычисляется как функция вероятности перехода канала R(Y_t,X), вероятности p_t(m/m'), что кодер осуществляет переход из состояния m в состояние m' в момент времени t, и вероятности q_t(X/m',m) того, что выходной символ кодера есть X, при условии, что предыдущее состояние кодера есть m', а текущее состояние кодера есть m. В частности, каждый элемент Г_t вычисляется суммированием всех возможных выходных данных X кодера следующим образом: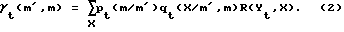

MAP-декодер вычисляет L таких матриц, по одной для каждого решетчатого кода. Они формируются из принятых выходных символов канала с учетом свойства ветвей решетки для данного кода.

Затем определяется M элементов совместной вероятности вектора-строки α_t в виде
α_t(j) = P{состояние j в момемт t; y₁,...,y_t} (3)
и M элементов условных вероятностей вектора-столбца β_t в виде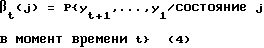

для j = 0, 1, ..., (M-1), где M - число состояний кодера. (Матрицы и вектора обозначены жирным шрифтом.) Этапы алгоритма MAP (или BCJR)-декодирования можно представить следующим образом:
(i) Вычислить α₁,...,α_L посредством прямой рекурсии:
α_t= α_t-1Г_t, t = 1,...,L (5)
(ii) Вычислить β₁,...,β_L-1 посредством обратной рекурсии:
β_t= Г_t+1β_t+1, t = L-1,...,1 (6)
(iii) Вычислить элементы λ_t согласно выражению
λ_t(i) = α_t(i)β_t(i) для всех i,t = 1,..,L (7)
(iv) Найти связанные величины, если это необходимо. Например, пусть A_t ^j - множество состояний S_t = {S_t ¹, S_t ², ..., S_t ^km}, такое, что j-й элемент S_t ^j множества S_t равен нулю. Для обычного нерекурсивного решетчатого кода S_t ^j = d_t ^j, т. е. j-й бит данных в момент t. Поэтому выходные данные программируемого решения декодера имеют вид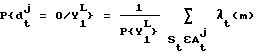

где 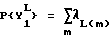и m - индекс, соответствующий состоянию S_t.

Выходные данные "жесткого" решения или декодированные биты получают с использованием выражения P{d_t ^j = 0/Y_l ^L} при следующем решающем правиле: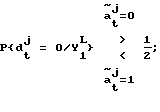

Т.е. если P{d_t ^j = 0/Y_l ^L} > 1/2, то 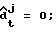если P{d_t ^j = 0/Y_l ^L} < 1/2, то 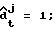в других случаях d_t ^j принимает случайным образом значения 0 или 1.

В качестве другого примера связанных значений для этапа (iv), упомянутого выше, можно привести матрицу вероятностей σ_t, содержащую элементы, как определено ниже:
σ_t(i,j) = P{S_t-1= i; S_t= j; YL1

} = α_t-1(i)γ_t(i,j)β_t(j)
Эти вероятности можно использовать, когда желательно определить апостериорную вероятность выходных битов кодера.

В стандартном применении алгоритма MAP-декодирования прямая рекурсия инициализируется вектором α₀= (1,0,...,0), а обратная рекурсия инициализируется вектором β_L= (1,0,...,0)^T. Эти начальные условия основываются на предположении, что начальное состояние кодера S₀ = 0, а его конечное состояние S_L = 0.

В соответствии с одним из вариантов осуществления настоящего изобретения циклический MAP-декодер определяет распределение вероятности начальных состояний путем решения задачи собственных значений следующим образом. Пусть α_t, β_t, Г_t, λ_t будут теми же, что и ранее, а начальные α₀ и β_L определяются следующим образом: β_L- вектор-столбец (111. . . 1)^T, а α₀- неизвестная (векторная) переменная.

Тогда
(i) Вычислить Г_t для t = 1, 2, ... L согласно уравнению (2).

(ii) Найти максимальное собственное значение матричного произведения Г₁, Г₂ ... Г_L. Нормировать соответствующий собственный вектор так, чтобы его компоненты суммировались до единицы. Этот вектор представляет собой решение для α₀. Собственное значение есть P{Y_l ^L}.

(iii) Сформировать последующее значение α_t путем прямой рекурсии согласно уравнению (5).

(iv) Начиная с β_L, инициализированного, как указано выше, сформировать β_t путем обратной рекурсии, как установлено в уравнении (6).

(v) Сформировать λ_t, как указано в уравнении (7), а также другие переменные, например выходные данные программируемого решения P{d_t ^j = 0/Y_l ^L} или матрицу вероятностей σ_t, как описано выше.

Изобретателями показано, что неизвестная переменная α₀ удовлетворяет матричному уравнению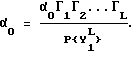

Из того факта, что эта формула выражает соотношение вероятностей, известно, что произведение Г_t матриц в правой части имеет максимальное собственное значение, равное P{Y_l ^L}, что соответствующий собственный вектор должен быть вектором вероятности.

При первоначальном β_L= (111...1)^T уравнение (6) дает β_L-1. Таким образом, повторное применение этой обратной рекурсии даст все значения β_t.
Если α₀ известно, а β_L установлено, все вычисления в циклическом MAP-декодере в соответствии с изобретением осуществляются согласно обычному алгоритму MAP-декодирования.

На фиг. 3 представлена упрощенная блок-схема, иллюстрирующая циклический MAP-декодер 10 для декодирования решетчатого кода с конечной последовательностью битов с исправлением ошибок в соответствии со способом, использующим собственный вектор, как описано выше. Декодер 10 содержит вычислитель 12 Г_t, предназначенный для приема упомянутых выходных сигналов канала, вероятности R(Y_t,X) перехода канала, вероятности p_t(m/m') того, что кодер осуществляет переход из состояния m' в состояние m в момент времени t, и вероятности q_t(X/m',m) того, что выходной символ кодера есть X при условии, что предыдущее состояние кодера есть m', а текущее состояние кодера есть m, и для определения из указанных данных скалярных элементов упомянутых матриц Г_t вероятности. Таким образом, вычислитель 12 получает на своих входах из памяти 30 вышеуказанные данные и осуществляет вычисление Г_t в функции выходных данных канала y_t. Вычислитель 12 вычисляет каждый элемент Г_t путем суммирования по всем возможным выходным данным X кодера в соответствии с уравнением (2).

Вычисленные значения Г_t подаются на вычислитель 14 произведения матриц Г_t, предназначенный для формирования произведения матриц Г₁, Г₂, ..., Г_L с использованием единичной матрицы 16, получаемой, например, из памяти, переключателя 18 и схемы задержки 20. В момент t = 1 единичная матрица подается на вход вычислителя 14 произведения матриц. Для каждого последующего момента времени с t = 2 до t = L произведение матриц 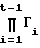подается назад через схему задержки на вычислитель произведения матриц. Затем в момент времени t = L полученное произведение матриц подается через переключатель 21 на вычислитель 22 нормированного произведения матриц подается через переключатель 21 на вычислитель 22 нормированного собственного вектора, который вычисляет нормированный собственный вектор, соответствующий максимальному собственному значению матричного произведения, введенного в него. Если таким образом инициализировано α₀, т.е. как этот нормированный собственный вектор, последующие вектора α_t определяются рекурсивно в соответствии с уравнением (5) в вычислителе 24 произведения матриц с использованием элемента задержки 26 и переключателя 28, как показано на чертеже. Соответствующие значения Г_t извлекаются из памяти 30, и полученные значения α_t запоминаются затем в памяти 30.

Значения β_t определяются в вычислителе 32 произведения матриц с использованием переключателя 34 и элемента задержки 36 в соответствии с уравнением (6). Затем с использованием значений α_tиβt вычисляются вероятности λ_t в вычислителе 40 поэлементного произведения, согласно уравнению (7). Значения λ_t подаются на вычислитель 50 вероятности значения декодированного бита, который определяет вероятность того, что j-й декодированный бит в момент времени t, т. е. d, равен нулю. Эта вероятность подается на устройство 52 пороговой обработки, которое реализует следующее решающее правило: если вероятность с вычислителя 50 превышает 1/2, то принимается решение, что декодированный бит равен нулю; если вероятность меньше 1/2, то принимается решение, что декодированный бит равен единице; если вероятность равна 1/2, то декодированному биту случайным образом присваивается значение 0 или 1. Выходное значение устройства пороговой обработки соответствует биту на выходе декодера в момент времени t.

Вероятность того, что декодированный бит равен нулю, т.е. P{d_t ^j = 0}, также подается, как показано на фиг. 3, на блок 54 определения функции "мягкого" выходного результата для определения функции вероятности, т.е. P{ d^j, = 0}, такой, например, как

в качестве выходного результата "мягкого" решения декодера. Кроме того, может быть использована другая функция P{d_t ^j = 0}

Как вариант, полезной функцией для блока 54 может быть просто единичная функция, так что программируемое выходное решение соответствует просто P{d_t ^j = 0}.

Альтернативный вариант осуществления MAP-декодера согласно настоящему изобретению, определяет распределения вероятности состояния путем рекурсивного метода. В частности, в одном из вариантов осуществления (метод динамической сходимости) рекурсия продолжает осуществляться, пока не будет обнаружена сходимость декодера. В этом рекурсивном методе (или методе динамической сходимости) этапы (ii) и (iii) метода собственного вектора, описанного выше, заменяются следующим образом:
(ii. a) Начиная с начального α₀, равного (1/M, ..., 1/M), где M - число состояний в решетчатом коде, вычислить рекурсию вперед L раз. Нормировать результаты так, чтобы элементы каждого нового α_t суммировались до единицы. Сохранить все L векторов α_t.
(ii. b) Принимая α₀ равным α_L из предыдущего этапа и начиная с момента t = 1, вычислить первые L_wmin векторов α_t. Т.е. вычислить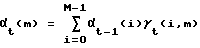

для m = 0, 1, ..., M-1 и t = 1, 2, ..., L_wmin,
где L_wmin - соответствующее минимальное число каскадов решетчатого кода. Осуществить нормировку, как описано выше. Сохранить только самое последнее множество из L векторов α, найденных путем рекурсивного вычисления согласно этапам (ii.a) и (ii.b), и α_Lwmin, найденное ранее на этапе (ii.a).

(ii. c) Сравнить α_Lwmin, полученное на этапе (ii.b), с ранее полученным множеством, полученным на этапе (ii.a). Если M соответствующих элементов их нового и старого значения α_Lwmin находятся в пределах поля допуска, то перейти к этапу (iv), как описано выше. В противном случае продолжать обработку согласно этапу (ii.d).

(ii.d) При t = t + 1 вычислить α_t= α_t-1Г_t. Осуществить нормировку, как и ранее. Сохранить только самое последнее множество из L вычисленных векторов α и α_t, полученных ранее на этапе (ii.a).

(ii. e) Сравнить новые значения α_t с ранее найденным множеством. Если M новых и старые α_t находятся в пределах поля допуска, то перейти к этапу (iv). В противном случае продолжить обработку с этапа (ii.d), если два самых последних вектора не совпадают в пределах поля допуска и если число рекурсий не превысило определенный максимум (в типовом случае 2L); в противном случае перейти к этапу (iv).

Круговой "временной цикл", показанный на фиг. 4, показывает итоги обработки на этапах (ii.a) - (ii.e) для вычисления α_t для t = 1, 2, ..., L для циклического MAP-декодера, в результате которой получены оценки всех L векторов α_t. Данный способ затем продолжается обработкой на этапах (iv) и (v), описанных выше для способа с использованием собственных векторов, для получения выходных результатов "мягкого" (программируемого) решения и декодированных выходных битов циклического MAP-декодера.

В циклическом MAP-декодере α₀ инициализируется как α₀= (1/M,...,1/M), поскольку исходное состояние кодера не известно. Также предполагается, что все M исходных состояний равновероятны. (Если это не соответствует действительности, то исходное состояние α₀(m) может быть присвоено соответственно априорной информации с учетом вероятностей исходного начального состояния. Таким образом, декодер, описанный здесь, также успешно применим для решеточных кодов с частичными конечными состояниями.)
Объяснение работы циклического MAP-декодера, соответствующего изобретению, облегчается с учетом определения α_t(m). Элемент α_t(m) представляет собой совместную вероятность того, что кодер находится в состоянии m в момент времени t и что декодер принимает последовательность символов {y₁, ..., y_t}, поступающих из канала. Анализ уравнения (5) для рекурсивного вычисления α_t выявляет влияние отсутствия априорной информации о начальном состоянии кодера решеточного кода с конечной последовательностью битов. Из уравнения (5) видно, что отсутствие информации о начальном состоянии кодера решеточного кода с конечной последовательностью битов будет приводить к смещению α₁(m) в том смысле, что вычисленная совместная вероятность того, что кодер находится в состоянии m в момент времени t = 1 и что декодер принимает выходной результат канала y₁, будет больше, чем это действительно имеет место для спусков при некорректных начальных состояниях, и меньше, чем это действительно имеет
место для спусков при корректном начальном состоянии. Хотя это смещение будет иметь тенденцию к распространению вследствие рекурсивных вычислений α_t(m), однако оно вместе с тем будет уменьшаться по мере приема большего количества выходных символов канала. Поэтому если длина L блока сообщения довольно велика, то α_L(m) будет более точным, чем α₀(m), с учетом того, что декодер уже обработал всю последовательность символов при второй итерации декодирования, как показано выше для этапа (ii.b).

Рекурсивный способ (или способ динамической сходимости), соответствующий настоящему изобретению, сравнивает значения, полученные из каждой итерации, и завершает рекурсивное вычисление α_t при обнаружении сходимости. Следовательно, данный способ уменьшает количество требуемых вычислений, поскольку зачастую не требуется повторно вычислять α_t для всех L каскадов решетчатого кода.

В другом варианте осуществления изобретения циклический MAP-декодер модифицирован таким образом, что декодеру необходимо только обрабатывать предварительно определенное фиксированное число каскадов решеточного кода во второй раз, т. е. на предварительно определенную глубину цикла. Это дает преимущества при реализации, так как количество вычислений, требуемых для декодирования, одно и то же для каждого кодированного блока сообщений. Соответственно, снижается сложность аппаратных средств и программного обеспечения.

Описываемая здесь глубина цикла определяется в контексте декодера с ограниченным кодовым расстоянием, представляющего собой декодер, который обеспечивает исправление любой комбинации e или менее ошибок, имевших место при наблюдении на уровнях решеточного кода длины L_obs. Это непосредственно применимо к декодерам, построенным для удовлетворения других критериев, например минимизации вероятности ошибки декодера.

Возможный способ оценки требуемой глубины цикла для MAP-декодирования сверточного кода с конечной последовательностью битов состоит в определении ее из экспериментов с аппаратными средствами или с программным обеспечением при условии, что необходимо осуществить циклический MAP-декодер с переменной глубиной цикла, причем эксперименты должны проводиться для измерения частоты ошибок в декодированных битах данных в зависимости от отношения E_b/N₀ для последовательно возрастающих значений глубины цикла. Минимальная глубина цикла декодера, которая обеспечивает минимальную вероятность ошибки декодированных битов данных для конкретного значения отношения E_b/N₀, находится при условии, когда дальнейшее увеличение глубины цикла не снижает вероятности ошибки.

Если частота ошибок в декодированных битах данных, которая превышает минимально достижимую при конкретном значении отношения E_b/N₀, допустима, то возможно уменьшить требуемое число каскадов решетчатого кода, обрабатываемых MAP-декодером. В частности, поиск глубины цикла, как описано выше, может быть просто завершен, когда получена желаемая вероятность ошибки в битах данных.

Другим способом определения глубины цикла для данного кода является использование свойств кодового расстояния. С этой целью необходимо определить две различные глубины для принятия решения в декодере. Как использовано в настоящем описании, термин "корректный путь" относится к последовательности состояний или к пути через решетку решетчатого кода, который вытекает из кодирования блока битов данных. Термин "некорректное подмножество узла" относится к множеству некорректных (решетчатых) ответвлений из узла корректного пути и их "спускам". Обе глубины решений, определенные ниже, зависят от сверточного кодера. (Для целей иллюстрации данный вариант осуществления настоящего изобретения описан здесь со ссылками на сверточный кодер, однако следует иметь в виду, что настоящее изобретение не ограничено сверточными кодами.)
Глубины решений определяются следующим образом.

(i) Определить глубину прямого решения для исправления e-ошибки, LF(e), в качестве первой глубины в решетчатом коде, при которой все пути в некорректном подмножестве исходного узла корректного пути, независимо от того, сливается ли этот узел с корректным путем или нет, лежат более чем на Хэмминговом расстоянии 2e от корректного пути. Важность параметра LF(e) состоит в том, что если e или менее ошибок имеется перед исходным узлом и известно, что кодирование начато в данной позиции, то декодер должен осуществлять корректное декодирование. Формальное табулирование глубин прямого решения для сверточных кодов было проведено в работе J.B.Anderson, K.Balachandran, "Decision Depth of Convolutional Codes", IEEE Transactions on Information Theory, vol. IT-35, pp.455-59, March 1989. Ряд свойств параметра LF(e) был описан в указанной работе, а также в работе J.B.Anderson, S.Mohan, "Source and Channel Coding - An Algorithmic Approach, Kluwer Academic Publishers, Norwell, MA, 1991. Главным из этих свойств является то, что существует простое линейное соотношение между LF и e, например, для кодов скорости 1/2 параметр LF примерно равен 9,08e.

(ii) Затем определить глубину решения без слияния для исправления e-ошибок, т.е. LU(e), которая определяется как первая глубина в решетчатом коде, при которой все пути в решетчатом коде, которые нигде не касаются корректного пути, лежат более чем на Хэмминговом расстоянии 2e от корректного пути.

Важность параметра LU(e) для циклического MAP-декодирования с принятием программируемого решения состоит в том, что вероятность идентификации состояния на действительно переданном пути высока после того, как декодер обработает LU(e) каскадов решетчатого кода. Поэтому минимальная глубина цикла для циклического MAP-декодирования равна LU(e). Вычисления глубины LU(e) показывают, что она всегда больше, чем LF(e), но что она подчиняется тому же самому аппроксимирующему закону. Это означает, что минимальная глубина цикла может быть оценена как глубина прямого решения LF(e), если глубина решения без слияния для кода не известна.

Путем нахождения минимальной глубины решения без слияния для данного кодера тем самым находим наименьшее число каскадов решетчатого кода, которое должно быть обработано конкретным циклическим декодером, который генерирует выходные результаты "мягкого" (программируемого) решения. Алгоритм нахождения LF(e), т.е. глубины прямого решения, был представлен в работе J.B.Anderson, K. Balachandran, "Decision Depths of Convolutional Codes", упомянутой выше. Для определения LU(e) необходимо осуществить следующую обработку:
(i) Вытянуть "решетку" кода слева направо, начиная со всех узлов решетчатого кода, за исключением нулевого состояния.

(ii) На каждом уровне исключить любые пути, которые сливаются с корректным (все нули) путем; не растягивать какие-либо пути за пределы узла корректного (нулевого) состояния.

(iii) На уровне k найти наименьшее Хэммингово расстояние или вес, среди всех путей, завершающихся в узлах на этом уровне.

(iv) Если это наименьшее расстояние превышает 2e, то прекратить обработку. Тогда LU(e) = k.

Эксперименты с использованием математического моделирования привели к двум неожиданным результатам: (1) циклическая обработка β_t привела к повышению эффективности декодера; (2) использование глубины цикла LU(e) + LF(e) ≈ 2LF(e) существенно повысило эффективность. Эти неожиданные результаты позволили модифицировать циклический MAP-декодер для решетчатых кодов с конечной последовательностью битов на основе рекурсии. Следовательно, предпочтительный вариант алгоритма для циклического MAP-декодера, основанного на рекурсивной обработке, включает следующие этапы:
(i) Вычислить Г_t для t = 1, 2, ..., L в соответствии с уравнением (2).

(ii) Начиная с исходного α₀, травного (1/M, ..., 1/M), где M - число состояний в решетчатом коде, вычислить рекурсию вперед, согласно уравнению (5), (L + L_w) раз для u = 1, 2, ... (L + L_w), где L_w - глубина цикла декодера. Индекс уровня решетчатого кода t принимает значения ((u-1)modL)+1. Когда декодер осуществляет циклическую обработку принятой последовательности символов из канала, α_L обрабатывается как α₀. Осуществить нормировку результатов так, чтобы элементы каждого нового вектора α_t суммировались до единицы. Сохранить L самых последних векторов α, найденных посредством этой рекурсивной обработки.

(iii) Начиная с исходного β_L, равного (1, ..., 1)^T, вычислить обратную рекурсию, согласно уравнению (6), (L + L_w) раз для u = 1, 2, ... (L + L_w). Индекс уровня решетчатого кода t принимает значения L - (u mod L). Когда декодер осуществляет циклическую обработку принятой последовательности, β₁ используется как β_L+1, а Г₁ используется как Г₁₊₁ при вычислении нового β_L. Осуществить нормировку результатов так, чтобы элементы каждого нового вектора β_t суммировались до единицы. Сохранить L самых последних векторов β, найденных посредством этой рекурсивной обработки.

Следующий этап этого предпочтительного способа рекурсивной обработки является тем же самым, что и этап (v), описанный выше относительно способа собственных векторов, для получения "мягких" решений и выходных декодированных битов с использованием циклического MAP-декодера.

Круговой "временной цикл", показанный на фиг. 5, показывает итоговые результаты обработки, связанной с вычислением α_t и β_t для u = 1, 2, ..., (L + L_w) для циклического MAP-декодера, соответственно этому предпочтительному варианту способа рекурсивной обработки.

Эффективность этого предпочтительного варианта обработки циклического MAP-декодера была проверена для программируемых решений для канала с аддитивным белым гауссовским шумом посредством компьютерного моделирования с использованием двоичной "антиподной" (диаметрально противоположной) сигнализации (например, двоичной фазовой манипуляции). Моделирование было осуществлено с использованием сверточного кода с наиболее известными параметрами: скорость = 1/2, память = 6. (Данный код считается наилучшим в смысле наибольшего свободного расстояния.) Все результаты моделирования, представленные здесь, были получены декодером, который использовал глубину цикла, равную удвоенной величине глубины прямого решения кода (40 каскадов решетки решеточного кода). Кроме того, в моделировании использовались короткие блоки сообщений, содержащие 48 битов.

На фиг. 6 представлен график усредненной вероятности ошибки декодированных битов в зависимости от отношения E_b/N₀. Биты источника с равной вероятностью принимали значения 0 и 1. Однако когда это моделирование было повторено для статистики смещенного источника, которая была априорно известна в декодере, то средняя вероятность ошибки в битах циклического MAP-декодера при заданном отношении E_b/N₀ значительно снизилась. На фиг. 7 представлено сравнение частоты ошибок в битах в зависимости от отношения E_b/N₀ для следующих трех случаев: исходные биты с равной вероятностью; P{сходный бит равен 1} = 0,67 и P{исходный бит равен 1} = 0,91. Во втором случае P{исходный бит равен 1} ≈ P{исходный бит равен 0}. В третьем случае P{исходный бит равен 1} ≈ 10P{исходный бит равен 0}.

На фиг. 8 представлена упрощенная блок-схема, иллюстрирующая циклический MAP-декодер 80, выполненный в соответствии с данным предпочтительным вариантом осуществления изобретения. Декодер 80 содержит вычислитель 82 Г_t, предназначенный для приема упомянутых выходных сигналов канала, вероятности R(Y_t, X) перехода канала, вероятности p_t(m/m') того, что кодер осуществляет переход из состояния m' в состояние m в момент времени t, и вероятности q_t(X/m', m) того, что выходной символ кодера есть X при условии, что предыдущее состояние кодера есть m', а текущее состояние кодера есть m, и для определения из указанных данных скалярных элементов упомянутых матриц Г_t вероятности. Таким образом, вычислитель 82 вычисляет Г_t как функцию выходных данных канала y_t. Выходные данные y₁ ..., y_L подаются на вычислитель Г_t через переключатель 84. Когда переключатель установлен в нижнее положение, L выходных символов каналов загружаются в вычислитель Г_t 82 и в регистр сдвига 86 по одному в каждый момент времени. Затем переключатель 84 устанавливается в верхнее положение, обеспечивая перемещение первых L_w принятых символов в вычислитель Г_t для обеспечения циклической обработки. Вычислитель Г_t получает на своих входах из памяти 96 вероятность перехода канала R(Y_t,X), вероятность p_t(m/m') того, что кодер осуществил переход из состояния m' в состояние m в момент t, и вероятность q_t(X/m',m) того, что выходной символ кодера есть X, при условии, что предыдущее состояние кодера есть m', а текущее состояние кодера - m. Вычислитель 82 вычисляет каждый элемент Г_t путем суммирования по всем возможным выходным данным X кодера в соответствии с уравнением (2).

Вычисленные значения Г_t подаются на вычислитель 90 произведения матриц, который умножает матрицу Г_t на матрицу α_t-1, которая рекурсивно выдается с помощью элемента задержки 92 и схемы демультиплексора 94. Управляющий сигнал CNTRL1 обеспечивает в демультиплексоре 94 выбор α₀ из памяти 96 в качестве входных данных для вычислителя матричного произведения 90 при t = 1. Когда 2 ≤ t ≤ L, управляющий сигнал CNTRL1 обеспечивает в демультиплексоре 94 выбор α_t-1 с элемента задержки 92 в качестве входных данных для вычислителя 90 произведения матриц 90. Значения Г_t и α_t запоминаются в памяти 96, если это необходимо.

Вектора β_t вычисляются рекурсивно в вычислителе 100 произведения матриц с помощью элемента задержки 102 и схемы демультиплексора 104. Управляющий сигнал CNTRL2 обеспечивает в демультиплексоре 104 выбор β_L из памяти 96 в качестве входных данных для вычислителя 100 произведения матриц при t = L - 1. Когда L - 2 ≥ t ≥ 1, управляющий сигнал CNTRL2 обеспечивает в демультиплексоре 104 выбор β_t+1 с элемента задержки 102 в качестве входных данных для вычислителя 100 произведения матриц. Полученные в результате значения β_t умножаются на значения α_t в вычислителе 106 поэлементных произведений для получения вероятностей λ_t, как описано выше. Тем же самым способом, как описано выше со ссылками на фиг. 3, значения λ_t подаются на вычислитель 50 вероятности значения декодированного бита, выходной результат которого подается на устройство 52 пороговой обработки 52, в результате чего формируются декодированные выходные биты декодера.

Условная вероятность P{d_t ^j = 0/Y_l ^L} того, что декодированный бит равен нулю, также показана на фиг. 8, как подаваемая на функциональный блок 54 программируемого выходного результата, для получения функции вероятности, т. е. fP{d_t ^j = 0/Y_l ^L}, например в виде

в качестве выходного результата программируемого решения.

Другой полезной функцией вероятности P{d_t ^j = 0/Y_l ^L} является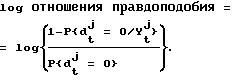

Как вариант, полезной функцией для блока 54 может быть просто единичная функция, так что программируемый выходной результат равен P{d_t ^j = 0/Y_l ^L}.

Различные практически используемые эффективные способы кодирования критически зависят от выходной программируемой информации MAP-декодера. В одном из таких способов, при котором внешний декодер использует декодирование ошибок и стираний записи, выход программируемого ("мягкого") решения внутреннего MAP-декодера может обрабатываться как индикатор надежности декодирования с использованием устройства троичного решения, которое может присваивать декодированному биту значение 0 или 1 или уведомлять о стирании информации. Кроме того, программируемый выходной результат декодера может быть с выгодой использован таким процессором, как декодер речевого сигнала или декодер изображения. Например, синтезатор речи или вокодер может использовать выходные результаты "мягкого" решения для идентификации вероятных ошибок передачи в принятом кадре речевого сигнала для инициирования использования способов компенсации ошибок для улучшения качества речи в аппаратуре, функционирующей в весьма зашумленных каналах.

До создания настоящего изобретения MAP-декодирование не возможно было применять для кодов с конечными последовательностями битов. Важность конечной последовательности битов состоит в том, что она позволяет повысить эффективность исправления ошибок для коротких кодовых слов, для которых трудно получить большой выигрыш за счет кодирования. Короткие коды естественным образом возникают в системах пакетной передачи данных и в системах речевой связи, использующих кодирование речевых сигналов с низкой скоростью.

Кроме того, настоящее изобретение полезно для использования в каналах с замираниями или с низкими отношениями мощности сигнала к шуму, что характерно для спутниковых систем связи с малоапертурными оконечными устройствами, а также в системах мобильной связи.

Хотя выше представлены и описаны предпочтительные варианты осуществления настоящего изобретения, очевидно, что такие варианты осуществления приведены только в качестве примера. Соответственно, следует иметь в виду, что изобретение определяется только в соответствии с его сущностью и объемом, как представлено в формуле изобретения.

Изобретение относится к кодерам с исправлением ошибок и обеспечивает высокую точность декодирования. Заявленный декодер максимума апостериорной вероятности (МАР-декодер) для решетчатых кодов с исправлением ошибок, использующих конечную последовательность битов, формирует выходные данные "мягкого" решения с оценкой вероятностей состояний первого каскада решетчатого кода, причем эти вероятности заменяют априорную информацию начального состояния обычного МАР-декодера. Декодер обеспечивает распределение вероятности начального состояния любым из двух способов. Первый из них связывает решение с задачей собственного значения, для которой результирующий собственный вектор представляет собой желательное распределение вероятности начального состояния. Зная начальное состояние, циклический МАР-декодер выполняет остальную часть декодирования в соответствии с обычным алгоритмом декодирования на основе максимума апостериорной вероятности. Второй способ основан на рекурсивной обработке для обеспечения сходимости итераций к распределению начального состояния. После достаточного количества итераций состояние циклической последовательности состояний известно с высокой вероятностью, и циклический МАР-декодер выполняет остальную часть обработки в соответствии с обычным алгоритмом декодирования по методу максимума апостериорной вероятности. 6 с. и 19 з.п. ф-лы, 8 ил.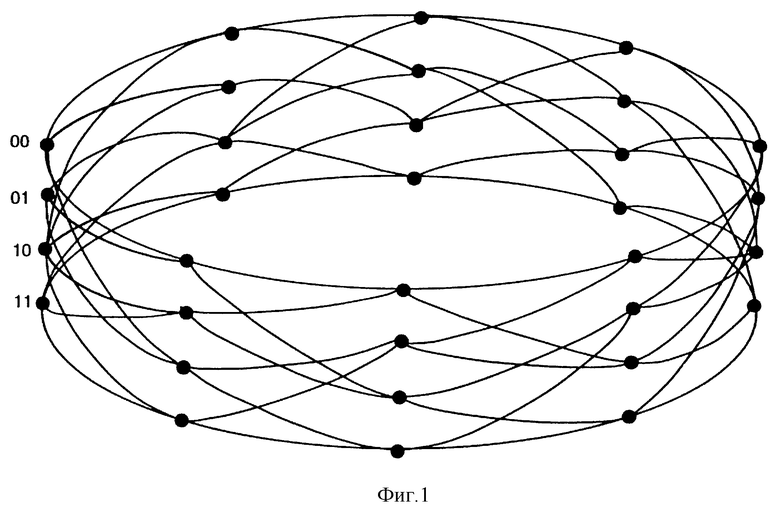

1. Декодер для решетчатого кода с конечной последовательностью битов, генерируемого кодером, причем упомянутый декодер обеспечивает декодирование путем определения совместной вероятности того, что состояние S_t кодера в момент t есть m и что принята последовательность из L выходных сигналов каналов, имеющих значения Y₁ ^L= { y₁, . . . , y_L} , что соответствует λ_t(m) = P{S_t= т; YLl

}, причем упомянутый решетчатый код имеет М состояний кодера, декодер определяет L матриц вероятности Г_t, по одной для каждого из L уровней решетчатого кода, элементы упомянутых матриц вероятности определяются соотношением
Г_t(i, j) = Р{ состояние j в момент времени t-1; y_t/состояние i в момент времени t-1} ,
путем определения векторов-строк α_t, имеющих М элементов совместной вероятности, определяемых соотношением

и путем определения векторов-столбцов β_t, имеющих М элементов условной вероятности, определяемых соотношением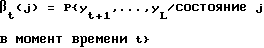
для j = 0,1, . . . , (M-1),
причем упомянутый декодер содержит вычислитель Г_t, предназначенный для приема упомянутых выходных сигналов каналов, вероятности R(У_t, X) перехода канала, вероятности p_t(m/m') того, что кодер осуществляет переход из состояния m' в состояние m в момент времени t, и вероятности q_t(X/m', m) того, что выходной символ кодера есть Х, при условии, что предыдущее состояние кодера есть m', а текущее состояние кодера есть m, и для определения из указанных данных скалярных элементов упомянутых матриц Г_t вероятности, вычислитель произведения матриц Г_t, предназначенный для приема упомянутых скалярных элементов с вычислителя Г_t и вычисления из них произведения Г₁Г₂ . . . Г_L матриц, вычислитель нормированного собственного вектора, предназначенный для приема произведения Г₁Г₂ . . . Г_L матриц и вычисления нормированного собственного вектора α₀, соответствующего наибольшему собственному значению P{ Y₁ ^L} упомянутого произведения матриц, вычислитель произведения матриц α_t, предназначенный для приема нормированного собственного вектора α₀ и формирования последующего значения α_t путем прямой рекурсии в соответствии с выражением α_t = α_t-1Г_t, t= 1, . . . , L, память для хранения матриц Г_t вероятности и векторов-строк α_t, вычислитель произведения матриц β_t, предназначенный для формирования векторов-столбцов путем инициализации β_L = (1, 1,1,...,1)^T и для формирования предыдущего β_t путем обратной рекурсии в соответствии с соотношением β_t= Г_t+1β_t+1, t = L-1, . . . , 1, вычислитель поэлементного произведения, предназначенный для формирования векторов λ_t совместной вероятности, элементы которого являются упомянутыми совместными вероятностями λ_t(i,j), путем умножения элементов векторов-строк на элементы векторов-столбцов согласно соотношению λ_t(i) = α_t(i)β_t(i) для всех i, t = 1, . . . , L, и вычислитель вероятности значения декодированного бита, предназначенный для определения из λ_t вероятности того, что заданный бит данных, введенный в кодер в момент времени t, равен нулю, причем бит данных является m-м битом из k битов данных, и для формирования программируемого выходного результата в качестве функции указанной вероятности. 2. Декодер по п. 1, отличающийся тем, что дополнительно содержит устройство пороговой обработки для приема вероятности того, что бит данных, введенный в кодер в момент времени t, равен нулю и для реализации решающего правила для формирования декодированных выходных битов. 3. Декодер по п. 1, отличающийся тем, что упомянутый решетчатый код с конечной последовательностью битов представляет собой сверточный код. 4. Декодер по п. 1, отличающийся тем, что представляет собой декодер с ограниченным кодовым расстоянием. 5. Декодер для решетчатого кода с конечной последовательностью битов, генерируемого кодером, причем упомянутый декодер обеспечивает декодирование путем определения совместной вероятности того, что состояние S_t кодера в момент t есть m и что принята последовательность из L выходных сигналов каналов, имеющих значения Y₁ ^L= { y₁, . . . , y_L} , что соответствует λ_t(m) = P{S_t= m; YLl}, причем упомянутый решетчатый код имеет М состояний кодера, декодер определяет L матриц Г_t условной вероятности, по одной для каждого из L уровней решетчатого кода, элементы упомянутых матриц вероятности определяются соотношением
Г_t(i, j) = Р{ состояние j в момент времени t; y_t/состояние i в момент времени t-1} ,
путем определения векторов-строк α_t, имеющих М элементов совместной вероятности, определяемых соотношением

и путем определения векторов-столбцов β_t, имеющих М элементов условной вероятности, определяемых соотношением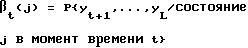
для j = 0, . . . , (M-1),
причем упомянутый декодер содержит, вычислитель Г_t, предназначенный для приема упомянутых выходных сигналов каналов вероятности R(У_t, X) перехода канала, вероятности p_t(m/m') того, что кодер осуществляет переход из состояния m' в состояние m в момент времени t, и вероятности q_t(X/m', m) того, что выходной символ кодера есть Х при условии, что предыдущее состояние кодера есть m', а текущее состояние кодера есть m, и для определения из указанных данных скалярных элементов упомянутых матриц Г_t вероятности, вычислитель произведения матриц α_t, предназначенный для приема упомянутых скалярных элементов Г_t с вычислителя Г_t и формирования векторов-строк α_t, вычислитель произведения матриц β_t, предназначенный для формирования векторов-столбцов β_t, вычислитель поэлементных произведений, предназначенный для формирования векторов совместной вероятности λ_t, элементы которого являются упомянутыми совместными вероятностями λ_t(i,j), причем упомянутые вычислитель произведения матриц α_t, вычислитель произведения матриц β_t и вычислитель поэлементных произведений формируют указанные вектора α_t, β_t, λ_t путем (1. а) вычисления, начиная с начального α₀, равного (1/М, . . . , 1/М), рекурсии вперед L раз в виде α_t = α_t-1Г_t, t = 1, . . . , L и нормирования результатов так, чтобы элементы каждого α_t суммировались до единицы, с сохранением всех L векторов α_t, (1. б) вычисления, принимая α₀ равным α_L из этапа (1. а) и начиная с момента t = 1, α_t = α_t-1Г_t, t = 1, . . . , L_wmin, где L_wmin - предварительно определенное минимальное число каскадов решетчатого кода, и нормирования результатов так, чтобы элементы каждого нового α_t суммировались до единицы, с сохранением только самого последнего множества из L векторов α_t, найденных путем рекурсивного вычисления согласно этапам (1. а) и (1. б), и α_LWmin, найденного на этапе (1. а); (1. в) сравнения α_LWmin, полученного на этапе (1. б), с α_LWmin, полученным на этапе (1. а), и перехода, при нахождении в пределах поля допуска, к этапу (2), или продолжения обработки, в противном случае, на этапе (1. г); (1. г) вычисления, при t = t+1, α_t = α_tГ_t, нормирования результатов рекурсивного вычисления так, чтобы элементы каждого α_t суммировались до единицы, с сохранением только самого последнего множества из L вычисленных векторов α_t и α_t, найденных ранее на этапе (1. а); (1. д) сравнения значений α_t с самыми последними ранее вычисленными на этапах (1. а), (1. б), (1в) значениями α_t и перехода, при нахождении в пределах поля допуска, к этапу (2), или продолжения обработки на этапе (1. г), если два самых последних вектора не совпадают в пределах поля допуска и если число рекурсий не превысило определенный максимум, и перехода к этапу (2) в противном случае; (2) инициализации β_L = (1, 1,1,...,1)^T и формирования предыдущего β_t путем обратной рекурсии в соответствии с соотношением β_t = Г_t+1β_t+1, t = L-1, . . . , 1, и нормирования результатов рекурсии так, чтобы элементы каждого β_t суммировались до единицы, с сохранением всех L векторов β_t, (3) формирования векторов совместной вероятности λ_t, элементы которых являются упомянутыми совместными вероятностями λ_t(i,j), путем умножения элементов векторов-строк на элементы векторов-столбцов согласно соотношению λ_t(i) = α_t(i)β_t(i) для всех i, t = 1, . . . , L, память для хранения упомянутых матриц вероятности и векторов-строк и вычислитель вероятности декодированного значения бита, предназначенный для определения из λ_t вероятности того, что заданный бит данных, введенный в кодер в момент времени t, равен нулю, причем бит данных является m-м битом из k битов данных, и для формирования программируемого выходного результата в качестве функции указанной вероятности. 6. Декодер по п. 5, отличающийся тем, что дополнительно содержит устройство пороговой обработки для приема значения вероятности того, что бит данных, введенный в кодер в момент времени t, равен нулю и для реализации решающего правила для формирования декодированных выходных битов. 7. Декодер по п. 5, отличающийся тем, что упомянутый решетчатый код с конечной последовательностью битов представляет собой сверточный код. 8. Декодер по п. 5, отличающийся тем, что представляет собой декодер с ограниченным кодовым расстоянием. 9. Декодер по п. 5, отличающийся тем, что кодер обеспечивает кодирование блока битов данных, причем биты данных сгруппированы в k-битовые символы для кодирования, причем предварительно определенное максимальное число рекурсий содержит двукратное число k-битовых входных символов в блоке битов данных. 10. Декодер для решетчатого кода с конечной последовательностью битов, генерируемого кодером, причем упомянутый декодер обеспечивает декодирование путем определения совместной вероятности того, что состояние S_t кодера в момент t есть m и что принята последовательность из L выходных сигналов каналов, имеющих значения Y₁ ^L= { y₁, . . . , y_L} , что соответствует λ_t(m) = P{S_t = m; YL1}, причем упомянутый решетчатый код имеет М состояний кодера, декодер определяет L матриц Г_t условной вероятности, по одной для каждого из L уровней решетчатого кода, элементы упомянутых матриц вероятности определяются соотношением
Г_t(i, j) = Р{ состояние j в момент времени t; y_t/состояние i в момент времени t-1} ,
путем определения векторов-строк α_t имеющих М элементов совместной вероятности, определяемых соотношением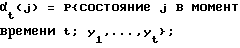

и путем определения векторов-столбцов β_t, имеющих М элементов условной вероятности, определяемых соотношением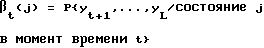
для j = 0, 1, . . . , (M-1),
причем упомянутый декодер содержит вычислитель Г_t, предназначенный для приема упомянутых выходных сигналов канала, вероятности R(Y_t, X) перехода канала, вероятности p_t(m/m') того, что кодер осуществляет переход из состояния m' в состояние m в момент времени t, и вероятности q_t(X/m', m) того, что выходной символ кодера есть Х при условии, что предыдущее состояние кодера есть m', а текущее состояние кодера есть m, и для определения из указанных данных скалярных элементов упомянутых матриц Г_t вероятности, вычислитель произведения матриц α_t, предназначенный для приема упомянутых скалярных элементов Г_t с вычислителя Г_t и формирования векторов-строк α_t,
вычислитель произведения матриц β_t, предназначенный для формирования векторов-столбцов β_t, вычислитель поэлементных произведений, предназначенный для формирования векторов совместной вероятности λ_t, причем упомянутые вычислитель произведения матриц α_t, вычислитель произведения матриц β_t и вычислитель поэлементных произведений формируют указанные вектора α_t, β_t, λ_t путем (1. а) вычисления, начиная с начального α₀, равного (1/М, . . . , 1/М), рекурсии вперед L раз в виде α_t = α_t-1Г_t, t = 1, . . . , L и нормирования результатов так, чтобы элементы каждого α_t суммировались до единицы, с сохранением всех L векторов α_t, (1. б) вычисления, принимая α₀ равным α_L из этапа (1. а) и начиная с момента t = 1, α_t = α_t-1Г_t, t = 1, 2, . . . , L_w, где глубина цикла L_w представляет собой предварительно определенное число каскадов решетчатого кода, и нормирования результатов так, чтобы элементы каждого α_t суммировались до единицы, заменяя α_t, вычисленные на этапе (1. а), на α_t, вычисленные на этапе (1. б), для t = 1, 2, . . . , L_w, (2. а) инициализации β_L = (1, 1,1,...,1)^T и формирования предыдущего β_t путем обратной рекурсии в соответствии с соотношением β_t = Г_t+1β_t+1, t = L-1, . . . , 1, и нормирования результатов рекурсии так, чтобы элементы каждого β_t суммировались до единицы, с сохранением всех L векторов β_t, (2. б) вычисления, при β_L+1, равном β₁ из этапа (2. а), и при Г_L+1, равном Г₁ начиная с t = L, β_t = Г_t+1β_t+1, t = L, L-1, . . . , L-(L_w + 1), где глубина цикла L_w представляет собой предварительно определенное число каскадов решетчатого кода, и нормирования результатов рекурсии так, чтобы элементы каждого β_t суммировались до единицы, с заменой β_t, вычисленных на этапе (2. а), значениями β_t, вычисленными на этапе (2. б), для t = L, L-1, . . . , L-(L_w+1); (3) формирования векторов совместной вероятности λ_t, элементы которой являются упомянутыми совместными вероятностями λ_t(i,j), путем умножения элементов векторов-строк на элементы векторов-столбцов согласно соотношению λ_t(i) = α_t(i)β_t(i) для всех i, t = 1, . . . , L, память для хранения упомянутых матриц вероятности и векторов-строк и вычислитель вероятности декодированного значения бита, предназначенный для определения из λ_t вероятности того, что заданный бит данных, введенный в кодер в момент времени t, равен нулю, причем бит данных является m-м битом из k битов данных, и для формирования программируемого выходного результата в качестве функции указанной вероятности. 11. Декодер по п. 10, отличающийся тем, что дополнительно содержит устройство пороговой обработки для приема значения вероятности того, что бит данных, введенный в кодер в момент времени t, равен нулю и для реализации решающего правила для формирования декодированных выходных битов. 12. Декодер по п. 10, отличающийся тем, что упомянутый решетчатый код с конечной последовательностью битов представляет собой сверточный код. 13. Декодер по п. 10, отличающийся тем, что представляет собой декодер с ограниченным кодовым расстоянием. 14. Декодер по п. 10, отличающийся тем, что кодер обеспечивает кодирование блока битов данных, причем биты данных группируются в k-битовые символы для кодирования, при этом предварительно определенное максимальное число рекурсий содержит двукратное число k-битовых входных символов в блоке битов данных. 15. Способ декодирования решетчатого кода с конечной последовательностью битов, генерируемого кодером, путем определения совместной вероятности того, что состояние S_t кодера в момент t есть m и что принята последовательность из L выходных сигналов каналов, имеющих значения Y₁ ^L= { y₁, . . . , y_L} , что соответствует λ_t(m) = P{S_t = m; YL1}, причем упомянутый решетчатый код имеет М состояний кодера, упомянутый способ включает этапы определения L матриц Г_t вероятности, по одной для каждого из L уровней решетчатого кода, элементы упомянутых матриц вероятности определяются соотношением
Г_t(i, j) = Р{ состояние j в момент времени t-1; y_t/состояние i в момент времени t-1} ,
определения векторов-строк α_t, имеющих М элементов совместной вероятности, определяемых соотношением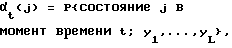

и определения векторов-столбцов β_t, имеющих М элементов условной вероятности, определяемых соотношением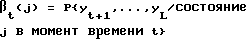
для j = 0, . . . , (M-1),
причем этапы указанного способа включают определение скалярных элементов упомянутых матриц Г_t вероятности из упомянутых выходных сигналов канала, вероятности R(Y_t, X) перехода канала, вероятности p_t(m/m') того, что кодер осуществляет переход из состояния m' в состояние m в момент времени t, и вероятности q_t(X/m', m) того, что выходной символ кодера есть Х при условии, что предыдущее состояние кодера есть m', а текущее состояние кодера есть m, вычисление произведения матриц Г₁ Г₂, . . . , Г_L из упомянутых скалярных элементов Г_t, вычисление нормированного собственного вектора α₀, соответствующего наибольшему собственному значению P{ Y^L ₁} упомянутого произведения матриц Г₁, Г₂, . . . , Г_L, формирование последующего значения α_t путем прямой рекурсии в соответствии с выражением α_t = α_t-1Г_t, t = 1, . . . , L, формирование векторов-столбцов путем инициализации β_L = (1, 1,1,...,1)^T и формирование предыдущего β_t путем обратной рекурсии в соответствии с соотношением β_t = Г_t+1β_t+1, t = L-1, . . . , 1, формирование векторов совместной вероятности λ_t, элементы которой являются упомянутыми совместными вероятностями λ_t(i,j), путем умножения элементов векторов-строк на элементы векторов-столбцов согласно соотношению λ_t(i) = α_t(i)β_t(i) для всех i, t = 1, . . . , L, и определение из λ_t вероятности того, что заданный бит данных, введенный в кодер в момент времени t, равен нулю, причем бит данных является m-м битом из k битов данных, и формирование программируемого выходного результата в качестве функции указанной вероятности. 16. Способ по п. 15, отличающийся тем, что дополнительно включает этап осуществления решающего правила для формирования декодированных выходных битов исходя из вероятности того, что бит данных, введенный в кодер в момент времени t, равен нулю. 17. Способ по п. 15, отличающийся тем, что упомянутый решетчатый код с конечной последовательностью битов представляет собой сверточный код. 18. Способ декодирования решетчатого кода с конечной последовательностью битов, генерируемого кодером, путем определения совместной вероятности того, что состояние S_t кодера в момент t есть m и что принята последовательность из L выходных сигналов каналов, имеющих значения Y₁ ^L= { y₁, . . . , y_L} , что соответствует λ_t(m) = P{S_t = m; YL1}, причем упомянутый решетчатый код имеет М состояний кодера, причем упомянутый способ включает этапы определения L матриц Г_t вероятности, по одной для каждого из L уровней решетчатого кода, причем элементы упомянутых матриц вероятности определяются соотношением
Г_t(i, j) = Р{ состояние j в момент времени t-1; y_t/состояние i в момент времени t-1} ,
определения векторов-строк α_t, имеющих М элементов совместной вероятности, определяемых соотношением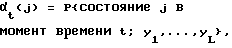

и определения векторов-столбцов β_t, имеющих М элементов условной вероятности, определяемых соотношением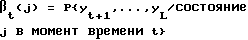
для j = 0, . . . , (M-1),
причем этапы указанного способа включают определение скалярных элементов упомянутых матриц Г_t вероятности из упомянутых выходных сигналов канала, вероятности R(Y_t, X) перехода канала, вероятности p_t(m/m') того, что кодер осуществляет переход из состояния m' в состояние m в момент времени t, и вероятности q_t(X/m', m) того, что выходной символ кодера есть Х при условии, что предыдущее состояние кодера есть m', а текущее состояние кодера есть m, формирование указанных векторов α_t, β_t, λ_t путем (1. а) вычисления, начиная с начального α₀, равного (1/М, . . . , 1/М), рекурсии вперед L раз в виде α_t = α_t-1Г_t, t = 1, . . . , L и нормирования результатов так, чтобы элементы каждого α_t суммировались до единицы, с сохранением всех L векторов α_t, (1. б) вычисления, принимая α₀ равным α_L из этапа (1. а) и начиная с момента t = 1, α_t = α_t-1Г_t, для t = 1, 2, . . . , L_wmin, где L_wmin - предварительно определенное минимальное число каскадов решетчатого кода, и нормирования результатов так, чтобы элементы каждого α_t суммировались до единицы, с сохранением только самого последнего множества из L α_t, найденных путем рекурсивного вычисления согласно этапам (1. а) и (1. б), и α_LWmin, полученного на этапе (1. а), (1. в) сравнения α_LWmin из этапа (1. б), с α_LWmin, полученным на этапе (1. а), и перехода, при нахождении в пределах поля допуска, к этапу (2), или продолжения обработки, в противном случае, на этапе (1. г), (1. г) вычисления, при t = t+1, α_t = α_t-1Г_t, нормирования результатов итерации так, чтобы элементы каждого α_t суммировались до единицы, с сохранением только самого последнего множества из L вычисленных векторов α_t и α_t, найденного ранее на этапе (1. а), (1. д) сравнения значений α_t с самыми последними α_t, ранее вычисленными на этапах (1. а), (1. б), (1в), и перехода, при нахождении в пределах поля допуска, к этапу (2), или продолжения обработки на этапе (1. г), если два самых последних вектора не совпадают в пределах поля допуска и если число рекурсий не превысило определенный максимум, и перехода к этапу (2) в противном случае, (2) инициализации β_L = (1, 1,1, ...,1)^T и формирования предыдущего β_t путем обратной рекурсии в соответствии с соотношением β_t = Г_t+1β_t+1, t = L-1, . . . , 1, и нормирования результатов рекурсии так, чтобы элементы каждого β_t суммировались до единицы, с сохранением всех L векторов β_t;
(3) формирования векторов совместной вероятности λ_t, элементы которой являются упомянутыми совместными вероятностями λ_t(i,j), путем умножения элементов векторов-строк на элементы векторов-столбцов согласно соотношению λ_t(i) = α_t(i)β_t(i) для всех i, t = 1, . . . , L, и определение из λ_t вероятности того, что заданный бит данных, введенный в кодер в момент времени t, равен нулю, причем бит данных является m-м битом из k битов данных, и формирование программируемого выходного результата в качестве функции указанной вероятности. 19. Способ по п. 18, отличающийся тем, что дополнительно включает этап осуществления решающего правила для формирования декодированных выходных битов, исходя из вероятности того, что бит данных, введенный в кодер в момент времени t, равен нулю. 20. Способ по п. 18, отличающийся тем, что упомянутый решетчатый код с конечной последовательностью битов представляет собой сверточный код. 21. Способ по п. 18, отличающийся тем, что кодер обеспечивает кодирование блока битов данных, биты данных группируются в k-битовые символы для кодирования, причем предварительно определенное максимальное число рекурсий содержит двукратное число k-битовых входных символов в блоке битов данных. 22. Способ декодирования решетчатого кода с конечной последовательностью битов, генерируемого кодером, путем определения совместной вероятности того, что состояние S_t кодера в момент t есть m, и что принята последовательность из L выходных сигналов каналов, имеющих значения Y₁ ^L= { y₁, . . . , y_L} , что соответствует λ_t(m) = P{S_t = m;YL1}, причем упомянутый решетчатый код имеет М состояний кодера, при этом упомянутый способ включает этапы определения L матриц Г_t условной вероятности, по одной для каждого из L уровней решетчатого кода, причем элементы упомянутых матриц вероятности определяются соотношением
Г_t(i, j) = Р{ состояние j в момент времени t; y_t/состояние i в момент времени t-1} ,
определения векторов-строк α_t, имеющих М элементов совместной вероятности, определяемых соотношением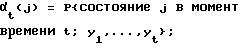

и определения векторов-столбцов β_t, имеющих М элементов условной вероятности, определяемых соотношением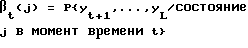
для j = 0,1, . . . , (M-1),
причем этапы указанного способа включают определение скалярных элементов упомянутых матриц Г_t вероятности из упомянутых выходных сигналов канала, вероятности R(Y_t, X) перехода канала, вероятности p_t(m/m') того, что кодер осуществляет переход из состояния m' в состояние m в момент времени t, и вероятности q_t(X/m', m) того, что выходной символ кодера есть Х при условии, что предыдущее состояние кодера есть m', а текущее состояние кодера есть m, формирование указанных векторов α_t, β_t, λ_t путем (1. а) вычисления, начиная с начального α₀, равного (1/М, . . . , 1/М), рекурсии вперед L раз в виде α_t = α_t-1Г_t, t = 1, . . . , L и нормирования результатов так, чтобы элементы каждого α_t суммировались до единицы, с сохранением всех L векторов α_t, (1. б) вычисления, принимая α₀ равным α_L из этапа (1. а) и начиная с момента t = 1, α_t = α_t-1Г_t, для t= 1, 2, . . . , L_w, где глубина цикла L_w представляет собой предварительно определенное число каскадов решетчатого кода, и нормирования результатов так, чтобы элементы каждого α_t суммировались до единицы, заменяя α_t, вычисленные на этапе (1. а), на α_t, вычисленные на этапе (1. б), для t = 1, 2, . . . , L_w, (2. а) инициализации β_L = (1, 1,1,...,1)^T и формирования предыдущего β_t путем обратной рекурсии в соответствии с соотношением β_t = Г_t+1β_t+1, t = L-1, . . . , 1, и нормирования результатов рекурсии так, чтобы элементы каждого β_t суммировались до единицы, с сохранением всех L векторов β_t, (2. б) вычисления, при β_L+1, равном β₁ из этапа (2. a), и при Г_L+1, равном Г₁ начиная с t = L, β_t = Г_t+1β_t+1, t = L, L-1, . . . , L-(L_w+1), где глубина цикла L_w представляет собой предварительно определенное число каскадов решетчатого кода, и нормирования результатов рекурсии так, чтобы элементы каждого β_t суммировались до единицы, с заменой векторов β_t, вычисленных на этапе (2. а), значениями β_t, вычисленными на этапе (2. б), для t = L, L-1, . . . , L-(L_w+1); (3) формирования векторов совместной вероятности λ_t, элементы которой являются упомянутыми совместными вероятностями λ_t(i,j), путем умножения элементов векторов-строк на элементы векторов-столбцов согласно соотношению λ_t(i) = α_t(i)β_t(i) для всех i, t = 1, . . . , L, и определение из λ_t вероятности того, что заданный бит данных, введенный в кодер в момент времени t, равен нулю, причем бит данных является m-м битом из k битов данных, и для формирования программируемого выходного результата в качестве функции указанной вероятности. 23. Способ по п. 22, отличающийся тем, что дополнительно включает этап осуществления решающего правила для формирования декодированных выходных битов, исходя из вероятности того, что бит данных, введенный в кодер в момент времени t, равен нулю. 24. Способ по п. 22, отличающийся тем, что упомянутый решетчатый код с конечной последовательностью битов представляет собой сверточный код. 25. Способ по п. 22, отличающийся тем, что кодер обеспечивает кодирование блока битов данных, биты данных сгруппированы в k-битовые символы для кодирования, а предварительно определенное максимальное число рекурсий содержит двукратное число k-битовых входных символов в блоке битов данных.