Изобретение относится к области машиностроения и может быть использовано при конструировании и эксплуатации динамически уравновешенных жестких роторов, содержащих моментно-неуравновешенные функциональные элементы типа наклонных к плоскости, перпендикулярной оси вращения, дисков или цилиндров с косыми торцами, в частности, находящих применение в шлифовальных блоках с наклонным кругом или в механизмах для преобразования вращательного движения в поступательное (механизмы с наклонной шайбой).
В известных способах уравновешивания валов и роторов конструктивная моментная неуравновешенность устраняется с помощью двух корректирующих грузов, располагаемых в двух плоскостях коррекции [1].
Однако эти способы не всегда применимы по конструктивно-технологическим соображениям, из-за отсутствия или ограниченности пространства, требующегося для размещения корректирующих грузов, особенно при значительной моментной неуравновешенности, характерной, например, для ротора с наклонным к плоскости вращения диском.
Кроме того, в некоторых случаях при проектировании ротора его геометрические параметры целесообразно определять из условия равенства между собой всех центральных осевых моментов инерции распределенных масс, т.е. центральный эллипсоид инерции должен быть сферой. При этом любая центральная ось жесткого ротора становится главной центральной, а динамические реакции опор отсутствуют при любом его повороте вокруг центра тяжести, лежащем на оси вращения. Это обстоятельство положительно сказывается, например, на качестве поверхности обрабатываемой заготовки при шлифовании наклонным шлифовальным кругом.
Применение же в этих целях способа уравновешивания ротора с помощью корректирующих грузов, располагаемых в двух плоскостях коррекции, нерационально, т.к. превращение эллипсоида инерции в сферу оказывается затруднительным.
Известно балансирующее устройство наклонного шлифовального круга [2], в котором предварительное уравновешивание выполняют перемещением корректирующих масс, а точное уравновешивание достигается на рабочих оборотах шлифовального круга путем подачи жидкости в камеры, охватывающие два соосных цилиндрических корпуса для зажима шлифовального круга.
Используемый в этом устройстве способ уравновешивания имеет отмеченные выше недостатки, характерные для способов с применением корректирующих грузов. Он приводит также к усложнению конструкции всего шлифовального блока, включая элементы крепления наклонного круга, а сложность конструктивных форм элементов делает практически невозможным аналитическое решение задачи компенсации моментной неуравновешенности круга на стадии проектирования ротора.
Наиболее близким к предлагаемому является способ уравновешивания жесткого ротора [3], в котором моментная неуравновешенность наклонного диска компенсируется моментной неуравновешенностью уравновешивающего элемента - пары косых шайб, располагаемых по обеим сторонам диска и используемых для его крепления.
Этот способ благодаря простоте конструктивных форм элементов ротора и соответствующим аналитическим зависимостям позволяет решить задачу уравновешивания еще при разработке конструкции ротора, а окончательная его динамическая балансировка, в случае необходимости, осуществляется известными способами на балансировочных станках.
Однако в этом способе, вследствие того что наружные торцы уравновешивающего элемента (пары косых шайб) выполнены прямыми (перпендикулярными оси вращения), компенсация моментной неуравновешенности наклонного диска достигается, как показывают вычисления, при относительно больших размерах уравновешивающего элемента, что приводит к увеличению материалоемкости конструкции, а используемые аналитические зависимости справедливы только для этого частного случая.
Заявляемое изобретение решает задачу расширения возможностей, повышения эффективности и удешевления способа уравновешивания роторов, содержащих моментно-неуравновешенные функциональные элементы типа дисков или цилиндров с косыми торцами.
Это достигается тем, что наружные торцы уравновешивающего элемента (пары косых шайб) выполнены косыми и расположены в параллельных плоскостях, отклоненных от плоскости, перпендикулярной оси вращения, на угол, противоположный по знаку углу наклона торцевых плоскостей моментно-неуравновешенного функционального элемента (наклонного диска или цилиндра с косыми торцами), а компенсация моментной неуравновешенности последнего достигается при условии:
J
где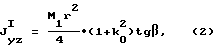
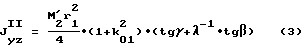
соответственно центробежные моменты инерции моментно-неуравновешенного функционального элемента и уравновешивающего элемента относительно центральных взаимно перпендикулярных осей, из которых ось z есть ось вращения,
M1 = ρ1•π•r2•(1-k
масса моментно-неуравновешенного функционального элемента,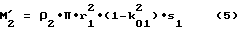
масса цилиндра, соответствующего уравновешивающему элементу,
r, r1 и s, s1 - соответственно радиусы наружных поверхностей вращения и осевые размеры (геометрические параметры) моментно-неуравновешенного функционального и уравновешивающего элементов,
β,γ- углы отклонения торцевых плоскостей моментно-неуравновешенного функционального и уравновешивающего элементов от плоскости, перпендикулярной оси вращения, соответственно,
k0=r0/r, k01=r0/r1, λ = s1/s- (6)
безразмерные параметры,
r0 - радиус посадочной поверхности,
ρ1, ρ2- плотности материалов моментно-неуравновешенного функционального и уравновешивающего элементов.
При этом значения геометрических параметров ротора выбирают так, чтобы соблюдалось условие: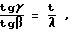 (7)
(7)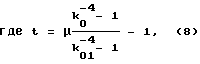
μ = ρ1/ρ2, (9)
и, кроме того, их подчиняют условию получения центральной сферы инерции:
J
где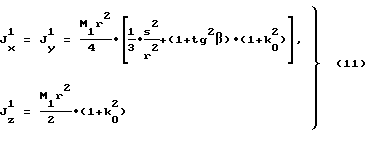
осевые моменты инерции моментно-неуравновешенного функционального элемента,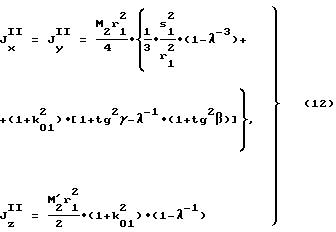
осевые моменты инерции уравновешивающего элемента,
в связи с чем при выборе значений геометрических параметров ротора пользуются зависимостями: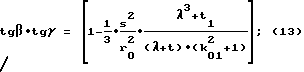
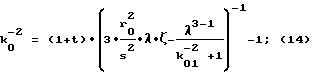
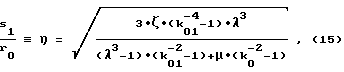
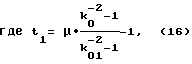
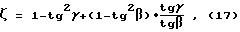
при соблюдении соотношений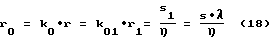
и условия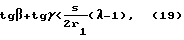
а осевые размеры уравновешивающего элемента находят по формулам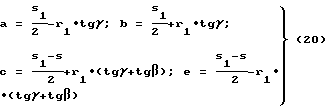
Корректировку моментной уравновешенности ротора в случае уменьшения радиуса наружной поверхности моментно-неуравновешенного функционального элемента, например, за счет износа выполняют дискретно - путем замены начального уравновешивающего элемента на новый, размеры которого определяют по формулам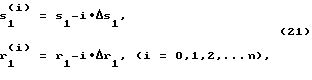
где i - номер наладки, соответствующий радиусу r(i) наружной поверхности моментно-неуравновешенного функционального элемента, определяемому по формуле
r(i) = r-i•Δr, (22)
в которой Δr - величина допустимого уменьшения радиуса r для одной ступени корректировки;
Δr1 и Δs1- значения поправок на геометрические параметры уравновешивающего элемента: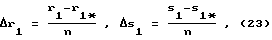
где r1, s1 - начальные значения параметров уравновешивающего элемента, а
r1*, s1* - минимально допустимые их значения,
n - число ступеней корректировки: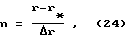
где r, r* - соответственно начальное и минимально допустимое значения радиуса наружной поверхности моментно-неуравновешенного функционального элемента.
При этом значение s1* назначают по конструктивным соображениям, а значения r* и r1* вычисляют:
r*= r0/k
где значение параметра k
y3+py+q=0, (26)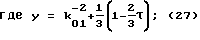
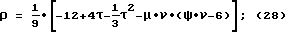
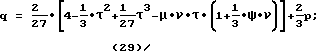
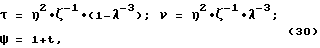
причем k01= k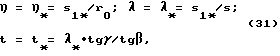
а значение k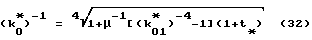
с проверкой результата вычислений согласно зависимости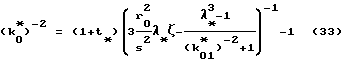
Сущность изобретения поясняется чертежами.
На фиг. 1 приведена схема конструкции жесткого ротора с наклонным к плоскости, перпендикулярной оси вращения, диском, включающая: моментно-неуравновешенный функциональный элемент (наклонный диск) 1 и прилегающий к нему уравновешивающий элемент, состоящий из двух косых шайб 2 и 3, совместно посаженные на втулку 4 и стянутые между собой резьбовым соединением.
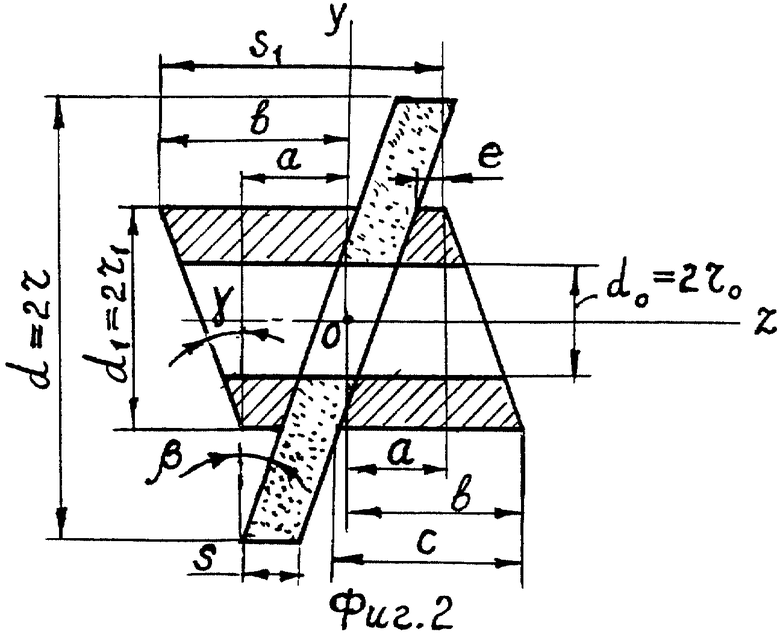
На фиг. 2 - схема к расчету значений геометрических параметров взаимно уравновешенных элементов 1, 2, 3.
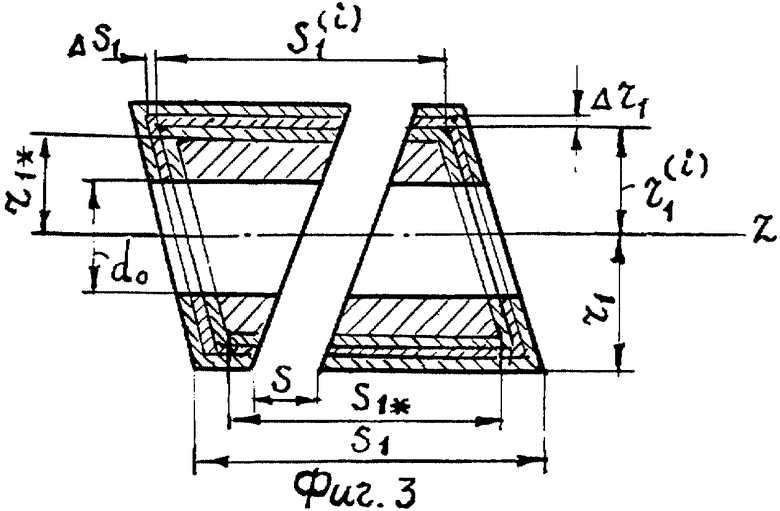
На фиг.3 - схема к расчету параметров уравновешивающего элемента для дискретной корректировки уравновешенности ротора при уменьшении наружного диаметра наклонного диска 1, например, за счет износа и сохранении значений углов наклона β и γ.
Способ осуществляют в следующей последовательности. На стадии проектирования ротора по конструктивно-технологическим соображениям выбирают ориентировочные значения параметров r0, r, r1, s, λ, μ.
По формулам (7), (13) вычисляют значения углов наклона β и γ с проверкой условия (19).
При необходимости изменяют принятые значения параметров и повторяют расчет.
Результаты вычислений проверяют по формуле (15).
Недостающие значения геометрических параметров ротора определяют по формулам (18) и (20).
Для осуществления приближенной дискретной корректировки уравновешенности ротора при уменьшении диаметра 2r наклонного диска, например, за расчет износа назначают минимально допустимое по конструктивным соображениям значение осевого размера s1=s1* уравновешивающего элемента (фиг.2).
При сохранении значений параметров r0, s, β, γ, согласно (31) определяют значения η*, λ*, t*..
Вычисляют значения обобщенных параметров τ, ν, ψ, а также р, q - по (30), (28), (29).
Решают уравнение (26) и согласно (27) определяют необходимое значение k01=k
Определяют соответствующее значение k0= k
Проверяют результаты расчета по формуле (33).
Вычисляют значения минимально допустимых радиусов r* и r1*, соответствующих принятому значению s1*, - по (25).
Назначают приемлемое по соображениям уравновешенности ротора значение Δr - уменьшения наружного радиуса диска и определяют согласно (24) число ступеней корректировки (n) и необходимое число уравновешивающих элементов (пар косых шайб) - m: m=n+1.
Определяют соответствующие величине Δr значения поправок на геометрические параметры уравновешивающего элемента - по (23).
Согласно (21) определяют размеры уравновешивающих элементов для каждой наладки, соответствующей значению радиуса r(i), определяемому по формуле (22).
При значениях r, r1, s1 и r*, r1*, s1*, т.е. при i=0 и i=n, обеспечивается полная уравновешенность ротора. При промежуточных значениях параметров, т.е. при 1≤i≤n-1, имеет место приближенная уравновешенность, приемлемая по условиям эксплуатации ротора.
Последовательность расчетов значений параметров ротора поясним примером.
Пусть требуется определить значения геометрических параметров динамически уравновешенного ротора с наклонным диском при следующих ориентировочных данных:
μ = 0,2; r0=16 мм; r=62,5 мм; r1≅30 мм; s=25 мм; λ ≅ 3.
Согласно (6), (8), (16), (7), (13) имеем:
k0=0,256; k01=0,5333; t=3,08166; t1=0,13362,
tgγ/tgβ = 1,02722, (a)
tgγ•tgβ = 0,196022. (б)
Из системы (а) и (б) находим: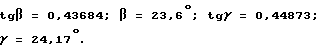
При этом условие (19) не выполнено.
Изменим значения r1 и λ, приняв r1=28 мм и λ = 3,2.
Тогда k0=0,256; k01=0,571429; t=4,53369; t1=0,38267;
tgγ/tgβ = 1,41678; tgγ•tgβ = 0,14132,
откуда 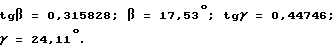
Условие (19) выполнено.
Из (17) и (18) находим:
ζ = 2,07524; η = sλ/r0 = 5,0000; s1=80 мм.
Проверка вычислений по формуле (15) подтверждает справедливость найденных значений. При необходимости их корректировки последовательность указанных действий сохраняется.
Согласно (20) получаем:
а=27,47 мм; в=52,53 мм; с=48,87 мм; e=6,13 мм.
По результатам расчета принимаем:
μ = 0,2; r0=16 мм; r=62,5 мм; r1=28 мм; s=25 мм; s1=80 мм;
β = 17,5°; γ =24,1°; а=27,5 мм; в=52,5 мм; с=48,9 мм; e=6,1 мм.
Предположим, что наружный радиус диска уменьшается в результате износа (шлифовальный круг).
Определим размеры уравновешивающих элементов для каждого комплекта, используемого при ступенчатой корректировке уравновешенности ротора.
Принимаем s1*=72 мм.
Тогда согласно (31)
η* = 4,5; λ* = 2,88; t*=4,0803.
По (30), (28), (29) находим:
τ = 9,3494; ν = 0,408488; ψ = 5,0803; p=-0,379872; q=0,03112.
Решаем кубическое уравнение (26) [4].
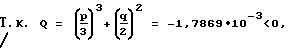
получаем 3 различных действительных корня:
y1=0,57036; y2=0,08345; y3=0,653812,
которым согласно (27) соответствуют 3 значения k
Этим значениям согласно (32) соответствуют 3 значения k
k
Тогда по (25) находим:
r1*=24,3 мм; r*=52 мм.
Следовательно, r-r*=10,5 мм.
Приняв Δr = 3,5 мм, согласно (24) имеем:
n=3(m=4).
Значения поправок на параметры r1 и s1 в соответствии с (23) будут:
Δr1 = 1,233 мм; Δs1 = 2,667 мм.
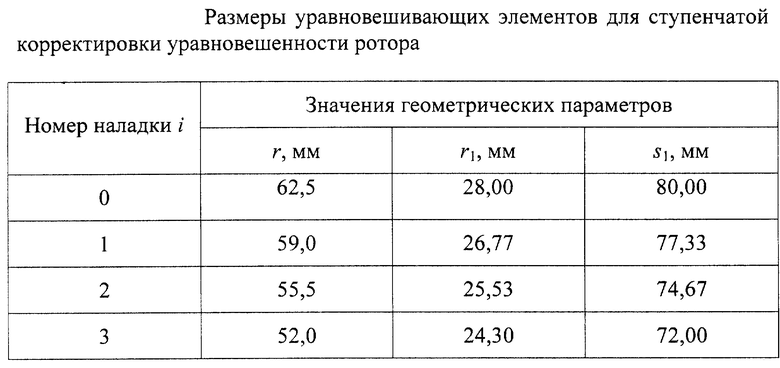
Пользуясь зависимостями (21), находим размеры уравновешивающих элементов для каждой из наладок, характеризуемых зависимостью (22), приведенные в таблице .
Причем при наладках 0 и 3 достигается полная компенсация моментной неуравновешенности наклонного диска, а при наладках 1 и 2 - приближенная. Однако, как показывают вычисления, благодаря тому, что приближенные значения геометрических параметров уравновешивающего элемента, соответствующие наладкам 1 и 2, заключены в "вилку" между точными значениями, найденными для наладок 0 и 3, отклонения приближенных значений параметров от точных малы.
Предложенный способ уравновешивания жестких роторов указанного типа достаточно прост и будет весьма полезен в практике машиностроения.
Источники информации
1. Современные методы и средства балансировки машин и приборов. М.В.Баркан, Т.Т.Гаппоев, А.А.Геркус и др. /Под общ. ред. В.А.Щепетильникова. - М.: Машиностроение, 1985, - с. 198-236.
2. Патент RU 2006804 С1, кл. G 01 M 1/30, 1994, Бюл. 2.
3. Патент RU 2153154 C1, кл. G 01 M 1/38, 20.07.2000, Бюл. 20 (прототип).
4. Г. Корн, Т.Корн. Справочник по математике (для научных работников и инженеров). Перевод со второго американского переработанного изделия И.Г.Арамановича, А. М.Березмана, И.А.Вайнштейна, Л.З.Румшинского, Л.Я.Цлафа. /Под общ.ред. И.Г.Арамановича. - М.: Наука, 1973, - с.43-44.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УРАВНОВЕШИВАНИЯ СБОРНЫХ РОТОРОВ С НАКЛОННЫМИ ДИСКАМИ (ВАРИАНТЫ) | 2002 |
|
RU2217719C1 |
| СПОСОБ УРАВНОВЕШИВАНИЯ СТРУКТУРНО-НЕОДНОРОДНОГО ЖЕСТКОГО РОТОРА С НАКЛОННЫМ ДИСКОМ | 1999 |
|
RU2153154C1 |
| УСТРОЙСТВО УСТАНОВКИ И КОМПЕНСАЦИИ МОМЕНТНОЙ НЕУРАВНОВЕШЕННОСТИ НАКЛОННОГО К ПЛОСКОСТИ ВРАЩЕНИЯ ДИСКА | 2007 |
|
RU2345342C1 |
| СПОСОБ КРЕПЛЕНИЯ И УРАВНОВЕШИВАНИЯ НАКЛОННОГО К ПЛОСКОСТИ ВРАЩЕНИЯ ДИСКА | 2005 |
|
RU2288455C1 |
| СПОСОБ КРЕПЛЕНИЯ И УРАВНОВЕШИВАНИЯ ДИСКА, НАКЛОННОГО К ПЛОСКОСТИ ВРАЩЕНИЯ | 2006 |
|
RU2325266C2 |
| СПОСОБ УСТАНОВКИ, ВЗАИМНОЙ ФИКСАЦИИ И УРАВНОВЕШИВАНИЯ ЭЛЕМЕНТОВ УЗЛА КРЕПЛЕНИЯ НАКЛОННОГО К ПЛОСКОСТИ ВРАЩЕНИЯ ДИСКА | 2007 |
|
RU2330253C1 |
| СПОСОБ БАЛАНСИРОВКИ РОТОРОВ | 2013 |
|
RU2548373C2 |
| ОППОЗИТНЫЙ КРИВОШИПНО-ПОЛЗУННЫЙ МЕХАНИЗМ | 1998 |
|
RU2148744C1 |
| ПРОДОЛЬНО-ПРЕРЫВИСТЫЙ СБОРНЫЙ ШЛИФОВАЛЬНЫЙ КРУГ | 2001 |
|
RU2192344C1 |
| ПЛАНЕТАРНЫЙ ТОРЦОВЫЙ МОТОР-РЕДУКТОР | 1998 |
|
RU2150623C1 |
Способ может быть использован при проектировании и эксплуатации динамически уравновешенных жестких роторов, содержащих моментно-неуравновешенные функциональные элементы. Технический результат - расширение возможностей, повышение эффективности и удешевление. Для этого используется уравновешивающий элемент, наружные торцы которого выполнены косыми и лежат в параллельных плоскостях, отклоненных от плоскости, перпендикулярной оси вращения, на угол, противоположный по знаку углу наклона торцевых плоскостей моментно-неуравновешенного элемента. Значения геометрических параметров ротора определяют на стадии проектирования с использованием предложенных расчетных зависимостей, позволяющих обеспечить моментную уравновешенность ротора и получить центральную сферу инерции его распределенных масс. Для случая уменьшения радиуса наружной поверхности моментно-неуравновешенного элемента, например, за счет износа предложена дискретная корректировка моментной уравновешенности ротора путем замены начального уравновешивающего элемента на новый, размеры которого определяют на основе полученных расчетных зависимостей. 5 з.п. ф-лы, 3 ил., 1 табл.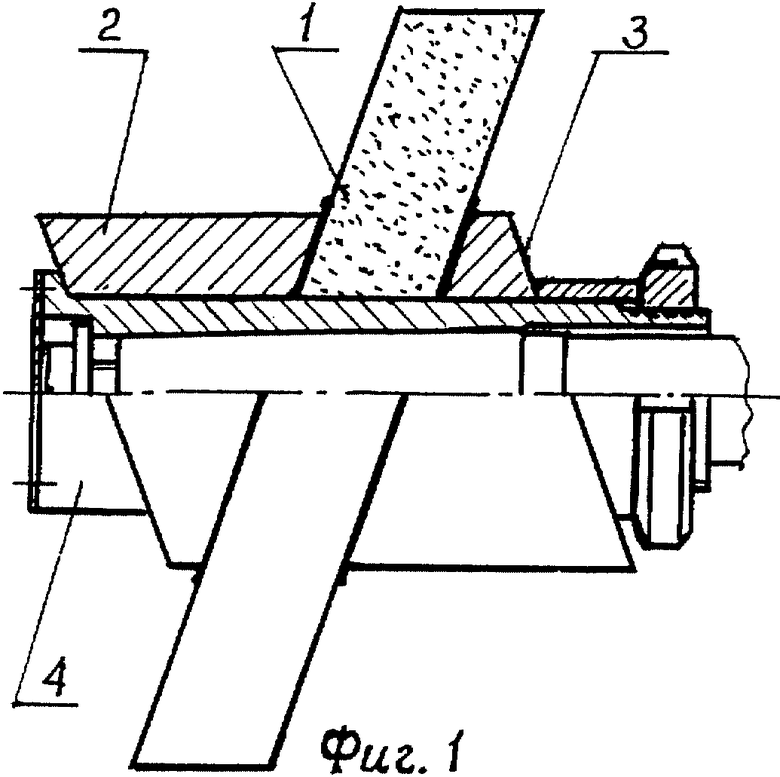
Jyz I= -Jyz II,
где 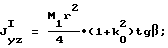
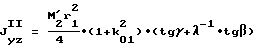
- соответственно центробежные моменты инерции моментно-неуравновешенного функционального элемента и уравновешивающего элемента относительно центральных взаимно перпендикулярных осей, из которых ось z есть ось вращения;
M1 = ρ1•π•r2•(1-k
- масса моментно-неуравновешенного функционального элемента;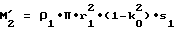
- масса цилиндра, соответствующего уравновешивающему элементу;
r, r1 и s, s1 - соответственно радиусы наружных поверхностей вращения и осевые размеры моментно-неуравновешенного функционального и уравновешивающего элементов;
β, γ - углы отклонения торцевых плоскостей моментно-неуравновешенного функционального и уравновешивающего элементов от плоскости, перпендикулярной оси вращения, соответственно;
k0= r0/r, k01= r0/r1, λ= s1/s - безразмерные параметры;
r0 - радиус посадочной поверхности;
ρ1, ρ2 - плотности материалов моментно-неуравновешенного функционального и уравновешивающего элементов.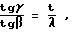
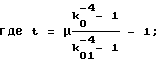
μ = ρ1/ρ2.
3. Способ по п. 1 или 2, отличающийся тем, что значения геометрических параметров ротора подчиняют условию получения центральной сферы инерции:
Jx I+Jx II= Jz I+Jz II,
где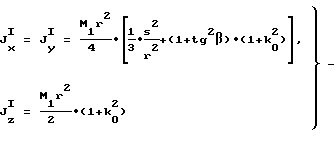
осевые моменты инерции моментно-неуравновешенного функционального элемента;
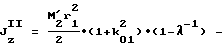
осевые моменты инерции уравновешивающего элемента.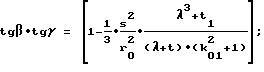
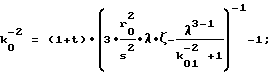
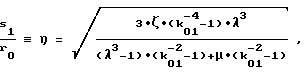
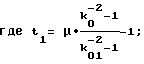
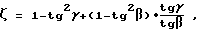
при соблюдении соотношений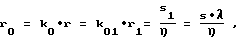
и условия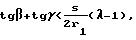
а осевые размеры уравновешивающего элемента находят по формулам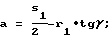
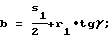
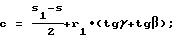
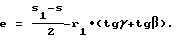
5. Способ по п. 1, отличающийся тем, что корректировку моментной уравновешенности ротора в случае уменьшения радиуса наружной поверхности моментно-неуравновешенного функционального элемента, например, за счет износа выполняют дискретно путем замены начального уравновешивающего элемента на новый, размеры которого определяют по формулам
s
r
где i - номер наладки, соответствующий радиусу r(i) наружной поверхности моментно-неуравновешенного функционального элемента, определяемому по формуле r(i) = r-i•Δr, в которой Δr - величина допустимого уменьшения радиуса r для одной ступени корректировки, Δr1 и Δs1- значения поправок на геометрические параметры уравновешивающего элемента: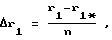
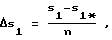
где r1, s1 - начальные значения параметров уравновешивающего элемента;
r1*, s1* - минимально допустимые их значения;
n - число ступеней корректировки: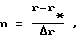
где r, r* - соответственно начальное и минимально допустимое значения радиуса наружной поверхности моментно-неуравновешенного функционального элемента.
r*= r0/k*0; r1*= r0/k*01,
где значение параметра k*01 находят в результате решения уравнения относительно переменной y:
y3+py+q= 0,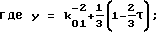
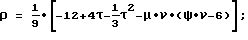
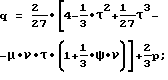
τ = η2•ζ-1•(1-λ-3);
ν = η2•ζ-1•λ-3;
ψ = 1+t,
причем k01= k*01; η = η*= s1*/r0; λ = λ*= s1*/s; t = t*= λ*•tgγ/tgβ,
а значение k*0 находят по формуле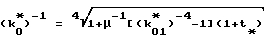
с проверкой результата вычислений согласно зависимости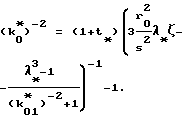
| СПОСОБ УРАВНОВЕШИВАНИЯ СТРУКТУРНО-НЕОДНОРОДНОГО ЖЕСТКОГО РОТОРА С НАКЛОННЫМ ДИСКОМ | 1999 |
|
RU2153154C1 |
| БАЛАНСИРУЮЩЕЕ УСТРОЙСТВО ШЛИФОВАЛЬНОГО КРУГА | 1991 |
|
RU2006804C1 |
| УСТРОЙСТВО ДЛЯ АВТОМАТИЧЕСКОЙ БАЛАНСИРОВКИ ВРАЩАЮЩИХСЯ ТЕЛ | 1998 |
|
RU2148806C1 |
| DE 1573764 А, 02.05.1974. | |||
Авторы
Даты
2002-06-20—Публикация
2001-04-04—Подача