Изобретение относится к автоматической оптимизации многопараметрических объектов управления, обладающих одноэкстремальной функцией качества, основанной на каком-либо критерии оптимальности.
Известны способы случайного поиска экстремума функции качества одноэкстремальных многопараметрических объектов, заключающиеся в формировании случайных входных шаговых воздействий на объект управления [1].
Недостатком таких способов является отсутствие адаптации величины случайных входных шаговых воздействий в процессе поиска, что приводит к значительному снижению их эффективности и быстродействия.
Наиболее близким к изобретению по технической сущности является способ, основанный на формировании случайных равномерно распределенных входных шаговых воздействий на объект управления и адаптации их распределения и величины [2].
Недостатком этого способа является невысокое быстродействие поиска и отсутствие универсальности применения, так как алгоритм адаптации величины входных шаговых воздействий в этом способе был получен для частного случая объекта оптимизации.
Предлагаемый способ заключается в том, что создается режим адаптивного случайного поиска в пространстве оптимизируемых параметров, основанный на формировании случайных входных шаговых воздействий на объект управления, распределенных по равномерному закону, математическое ожидание которых автоматически адаптируется в зависимости от сигнала, поступающего с выхода объекта по каналу обратной связи, а адаптация величины случайных входных шаговых воздействий осуществляется на основе соотношения удачных и неудачных проб в процессе настройки.
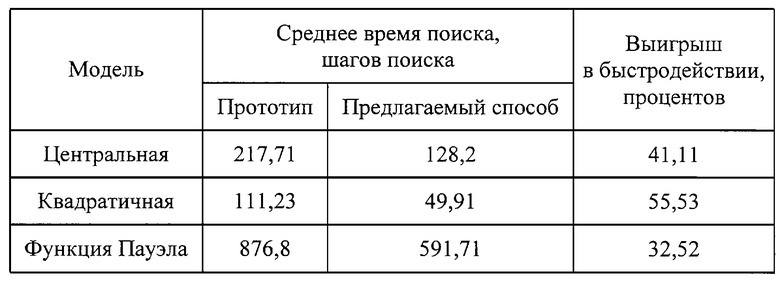
На чертеже представлена блок-схема алгоритма, реализующего предлагаемый способ автоматической настройки многопараметрических систем автоматического управления на оптимальные условия (вариант алгоритма с пересчетом, для определенности представлен случай минимизации функции качества).
Способ реализуется с помощью алгоритма, блок-схема которого включает в себя:
1 - блок формирования шага в случайном направлении в пространстве оптимизируемых параметров в соответствии с равномерным законом распределения, 2 - блок запоминания сформированного шага, 3 - блок определения значения функции качества в новой точке пространства оптимизируемых параметров, 4 - блок определения знака приращения функции качества, 7 - блок запоминания значения функции качества при удачном шаге, 5 и 8 - блоки адаптации распределения направления и величины случайных шагов в пространстве оптимизируемых параметров, 6 - блок формирования шага в обратном направлении при неудачном шаге.
Предлагаемый способ реализуется следующим образом.
В пространстве оптимизируемых параметров из исходного состояния Xi делается шаг в случайном направлении в соответствии с равномерным законом распределения. Если значение функции качества в новом состоянии Q(Xi+1) больше или равно значению функции качества в исходной точке Q(Xi), то есть случайная проба оказалась неудачной (задача минимизации), то система возвращается в первоначальное состояние Хi, после чего снова формируется случайный шаг, отсчитанный из старого состояния.
Рекуррентная формула для смещения в пространстве оптимизируемых параметров по этому алгоритму имеет следующий вид: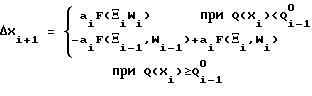
где Qi 0=min Q(Xj), j=1,..., i - наименьшее значение функции качества за i предыдущих шагов поиска;
F(Ξ,W) - единичный вектор, определяющий направление случайного шага: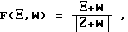
где Ξ- единичный случайный вектор, равномерно распределенный по всем направлениям пространства оптимизируемых параметров с нулевым математическим ожиданием;
W - вектор памяти (математическое ожидание направления случайных шагов), реализующий адаптацию распределения направления шагов,
ai - величина рабочего шага на i-м шаге поиска.
Адаптация распределения направления случайных шагов заключается в изменении их математического ожидания на основе знака приращения функции качества (блоки 5 и 8 на чертеже). Алгоритм непрерывной адаптации математического ожидания случайных шагов можно представить в виде следующего векторного рекуррентного соотношения:
Wi+1 = kWi-δΔQiΔXi,
где W - математическое ожидание равномерно распределенных случайных шагов;
k - коэффициент запоминания (0≤k≤1);
δ - параметр скорости обучения (0≤δ≤1).
При работе по этому алгоритму адаптации вектор W стремится перестроиться в направлении, обратном градиенту функции качества оптимизируемого объекта, то есть шаги поиска будут в среднем направлены в сторону быстрейшего уменьшения функции качества. Алгоритм адаптации величины случайных шагов можно представить в виде следующего выражения: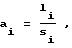
где li и si - соответственно число удачных и неудачных проб, совершенных до i -го шага оптимизации.
Смысл этого алгоритма заключается в следующем. Если в процессе поиска имеется значительное число удачных проб, то величина шага увеличивается. Однако, если начинают преобладать неудачные поисковые шаги, то, очевидно, система приблизилась к экстремуму функции качества, и величина входных шаговых воздействий уменьшается.
Если имеются определенные априорные данные о виде функции качества объекта оптимизации, то необязательно использовать всю информацию о неудачных и удачных пробах, можно ограничиться данными за последние N шагов оптимизации. Однако N не должно быть слишком малым, иначе точность отыскания экстремума будет недостаточно высокой. Как показали эксперименты на модельных функциях, для большинства случаев оптимальным числом является N=100, что достаточно для высокой мобильности алгоритма адаптации величины шага и для отыскания экстремума с высокой точностью.
Достигаемый технический эффект от применения предлагаемого способа позволяет уменьшить потери на поиск и повысить быстродействие отыскания экстремума: экспериментальные исследования, проведенные на модельных функциях, показали, что выигрыш в быстродействии предлагаемого способа по сравнению с прототипом составил от 32 до 55 % в зависимости от вида модельной функции (см. таблицу). Помимо алгоритмической простоты предлагаемого способа, он обладает также универсальностью применения, что позволяет использовать его независимо от конкретного вида функции качества.
Центральная модель: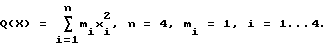
Центральная модель является моделью сепарабельного объекта управления, у которого отсутствует перекрестное влияние входных параметров.
Квадратичная модель: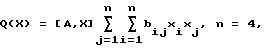
где [A, X] - скалярное произведение вектора параметрических коэффициентов А=(а1, а2, а3, а4)T и вектора входных координат Х = (x1, x2, x3, x4)T, аi=1, i=1...4, bij - элементы матрицы: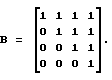
Квадратичная модель имеет более сложную структуру по сравнению с центральной и моделирует несепарабельный объект с перекрестным влиянием параметров.
Функция Пауэла:
Q(X)=(х1+10х2)2+5(х3-х4)4+(х2-2х3)4+10(х1-х4)4
Функция Пауэла моделирует объект оптимизации с ярко выраженной овражностью функции качества.
Все модельные функции имеют один минимум при хi=0, i=1...4.
При проведении сравнительного тестирования использовался одинаковый для всех моделей набор из ста начальных точек поиска, координаты которых представляли собой случайные равномерно распределенные числа в пределах от минус 10 до плюс 10. Цикл поиска экстремума для каждой начальной точки повторялся 1000 раз. Для всех трех моделей параметры поиска были одинаковыми: коэффициент запоминания k=0,7; параметр скорости обучения δ=0,1. Поиск экстремума производился с точностью до 0, 01.
ЛИТЕРАТУРА
1. Растригин Л.А. Системы экстремального управления. М.: Наука, 1974, с. 422-432.
2. Растригин Л.А. Адаптация сложных систем. Рига: Зинатие, 1981, с.88-91, с.106-107 (прототип).
Изобретение относится к автоматической оптимизации многопараметрических объектов управления, обладающих одноэкстремальной функцией качества, основанной на каком-либо критерии оптимальности. Технический результат заключается в повышении быстродействия самонастройки. Способ реализуется следующим образом. В пространстве оптимизируемых параметров из исходного состояния делается шаг в случайном направлении в соответствии с равномерным законом распределения. Если значение функции качества в новом состоянии больше или равно значению функции качества в исходной точке (то есть случайная проба оказалась неудачной), то система возвращается в первоначальное состояние, после чего снова формируется случайный шаг, отсчитанный из старого состояния. Адаптация распределения направления случайных шагов заключается в изменении их математического ожидания на основе знака приращения функции качества, а адаптация величины случайных шагов - на основе соотношения удачных и неудачных проб в процессе настройки. 1 табл.,1 ил.
Способ адаптивной автоматической настройки многопараметрических систем автоматического управления на оптимальные условия путем создания режима адаптивного случайного поиска в пространстве оптимизируемых параметров, основанный на формировании случайных входных шаговых воздействий на объект управления, математическое ожидание которых автоматически адаптируют в зависимости от сигнала, поступающего с выхода объекта по каналу обратной связи в соответствии с соотношением
Wi+1 = kWi-δΔQiΔXi,
где W - математическое ожидание равномерно распределенных случайных шагов;
k - коэффициент запоминания;
δ - параметр скорости обучения;
Q - функция качества;
Х - состояние объекта в пространстве оптимизируемых параметров,
отличающийся тем, что величину случайных входных шаговых воздействий в процессе настройки на оптимальные условия автоматически адаптируют на основе соотношения удачных и неудачных проб в соответствии с выражением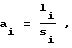
где а - величина шага случайного входного шагового воздействия;
li - число удачных случайных проб, совершенных до i-го шага поиска;
si - число неудачных случайных проб, совершенных до i-го шага поиска.
| РАСТРИГИН Л.А | |||
| Адаптация сложных систем | |||
| - Рига, Зинатне, 1981, с.88-91, с.106-107 | |||
| САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА КОМБИНИРОВАННОГО РЕГУЛИРОВАНИЯ | 1989 |
|
RU2022313C1 |
| Способ размножения копий рисунков, текста и т.п. | 1921 |
|
SU89A1 |
| Справочник по теории автоматического управления/Под ред | |||
| КРАСОВСКОГО А.А | |||
| - М.: Наука, 1987, с.637-639, 643-645 | |||
| РАСТРИГИН Л.А | |||
| Системы экстремального управления | |||
| - М.: Наука, 1974, с 422-432. | |||
Авторы
Даты
2002-09-10—Публикация
2000-08-07—Подача