Предлагаемое изобретение относится к области управления сложными стохастическими системами автоматического управления.
Известен «Способ синтеза многопараметровых автоматизированных измерительных систем» (патент РФ №2220435 на изобретение от 29.02.2002 г.), сущность которого состоит в формировании требований к выбору аппаратуры, каналов по совокупности тестовых воздействий, управляемых и неуправляемых внешних воздействий, совокупности выходных информативных параметров на основе соотношений между показателем качества объекта контроля W и проектировании каналов системы. По приведенным соотношениям определяют состав аппаратуры каналов, требования к динамическому диапазону возможных изменений внешних воздействий на объект контроля, требования к динамическим диапазонам измерений параметров, уточняют состав аппаратуры каналов, получают частные критерии точности каналов измерительной системы и уточняют варианты типов переходных характеристик каналов.
Недостатком рассматриваемого способа является использование размерных весовых коэффициентов для формирования показателя качества многопараметрового объекта, выбор которых достаточно проблематичен, что обуславливает снижение точности и быстродействия способа.
В качестве прототипа принят «Способ адаптивной автоматической самонастройки многопараметрических систем автоматического управления на оптимальные условия» (патент РФ №2251134 на изобретение от 02.04.2003 г.). В соответствии со способом в пространстве оптимизируемых параметров из исходного состояния делают шаг в случайном направлении в соответствии с нормальным законом распределения в нескольких независимых параллельных каналах, производят выбор наилучшего канала на основании значения функции качества. Если значение функции качества в новом состоянии больше или равно значению функции качества в исходной точке, то система возвращается в первоначальное состояние, после чего снова формируют случайный шаг, отсчитанный из старого состояния, в каждом параллельном канале. Если значение функции качества в новом состоянии меньше значения функции качества в исходной точке, то за исходное состояние берут новое, после чего снова формируют случайный шаг, отсчитанный из нового исходного состояния, в каждом параллельном канале.
Недостатком рассматриваемого в качестве прототипа способа является применимость его только для объектов, характеризуемых одноэкстремальной функцией качества, основанной на каком-либо критерии оптимальности, обладающим свойством монотонности, использование метода случайного поиска является ненадежным, особенно в случае отсутствия монотонности критерия качества.
Техническая задача заявленного изобретения заключается в нахождении оптимального многомерного вектора параметров управления сложными стохастическими системами автоматического управления, обеспечивающего максимальную вероятность выполнения предъявляемых к системе требований.
Технические результаты заявленного изобретения заключаются в повышении точности и надежности поиска оптимальных параметров управления системой, в повышении быстродействия поиска оптимальных параметров управления системой, а также в расширении области применения способа.
Данные технические результаты достигаются за счет того, что способ оптимизации многомерного вектора параметров управления сложными стохастическими системами автоматического управления для многомерного вектора выходных показателей качества работы системы заключается в поиске экстремума функции качества. Статистическим методом Монте-Карло моделируют и рассчитывают заданное количество случайных реализаций, для каждого выходного показателя качества работы системы определяют показатель эффективности работы системы - «запас работоспособности», а из всех рассчитанных случайных реализаций выделяют те, в которых для каждого выходного показателя качества работы системы «запас работоспособности» наименьший. Для выделенных случайных реализаций запоминают имеющие место случайные возмущения и параметры системы. Задают многомерную сетку узлов параметров управления системой, для каждого узла которой при повторении запомненных значений случайных возмущений и параметров системы рассчитывают выделенные реализации. По всем выходным показателям качества работы системы которых определяют «запасы работоспособности», среди которых находят наименьший запас и запоминают его значение, а из всех наименьших «запасов работоспособности», соответствующих всем узлам сетки параметров управления, находят наибольший и запоминают параметры управления системой, соответствующие узлу сетки с наибольшим значением «запаса работоспособности», которые составляют оптимальный многомерный вектор параметров управления.
Согласно способу оптимизации многомерного вектора параметров управления сложными стохастическими системами автоматического управления для многомерного вектора выходных показателей качества работы системы процесс оптимизации разбивается на два этапа, обеспечивающих преобразование статистической оптимизации в детерминированную. А оценка выходных показателей качества работы системы проводится с использованием предлагаемого универсального безразмерного комплексного показателя эффективности работы системы, называемого «запас работоспособности», характеризующего выполнение предъявляемых к системе технических требований и позволяющего сравнивать показатели качества работы систем разной размерности. Предлагаемый показатель не использует весовые коэффициенты функции качества работы системы и не требует ее монотонности, что позволяет корректно проводить сравнение выходных переменных разной размерности.
Способ основан на моделировании случайных реализаций, описывающих движение объекта, с использованием статистического метода Монте-Карло с учетом случайных возмущений, действующих на систему, случайных параметров системы и законов распределения случайных величин. Под случайными реализациями подразумевается результат моделирования процесса в системе управления с помощью электронно-вычислительной машины под воздействием случайных возмущений.
По выходным показателям качества работы системы статистическим методом Монте-Карло моделируют и рассчитывают заданное количество случайных реализаций. Расчет случайных реализаций заключается в регистрации числовых характеристик, полученных при моделировании каждой случайной реализации.
Для каждого выходного показателя качества работы системы рассчитывают показатель эффективности работы системы - «запас работоспособности».
Из всех рассчитанных случайных реализаций, выделяют те, которые имеют наименьшее значение «запаса работоспособности» каждого выходного показателя качества работы системы. Для каждой выбранной реализации запоминают имеющие место случайные возмущения и параметры системы. Запоминание происходит путем занесения результатов в оперативное или постоянное запоминающее устройство электронно-вычислительной машины.
Затем для поиска оптимального многомерного вектора параметров управления системой используют способ, основанный на простом надежном методе перебора узлов многомерной сетки. Число узлов и размер шага каждой многомерной сетки могут быть изменены в процессе оптимизации.
Задают многомерную сетку узлов параметров управления системой. Многомерная сетка параметров управления определяется значением выбираемых в процессе оптимизации параметров управления. Узлы многомерной сетки параметров управления рассчитываются по параметрам заданным в качестве начального приближения и заданного шага дискрета перебора параметров и диапазона перебора, то есть из точки начального приближения параметров управления в пространстве параметров диапазон изменения каждого параметра разбивается на равные отрезки, соответствующие шагу, создавая сетку.
При повторении запомненных случайных возмущений и случайных параметров системы для каждого узла многомерной сетки параметров управления системой рассчитывают выделенные реализации, по всем выходным показателям качества работы системы определяют «запасы работоспособности». Среди них находят и запоминают наименьший.
При переборе параметров управления системой по всем узлам многомерной сетки параметров управления по запомненным для каждого узла наименьшим «запасам работоспособности», выбирается тот узел, для которого значение «запаса работоспособности» является наибольшим. Значения параметров управления системой, соответствующие этому узлу многомерной сетки, являются оптимальными параметрами управления системой.
Рассмотрим, как реализуется предлагаемый способ.
Имеет место стохастическая система автоматического управления, характеризующаяся выходными показателями качества работы системы, по каждому из которых заданы технические требования. Имеют место параметры управления стохастической системой автоматического управления. Необходимо обеспечить максимальную вероятность выполнения предъявляемых к системе технических требований за счет нахождения оптимального вектора параметров управления стохастической системой автоматического управления.
Условие выполнения каждого технического требования к качеству работы стохастической системы автоматического управления имеет вид:
 , где:
, где:
Xl - оптимизируемый вектор параметров управления стохастической системой автоматического управления размерности 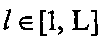 ;
;
m - число рассматриваемых показателей качества работы системы, 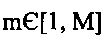 ;
;
TSm - техническое требование номера m;
 - модуль m-го показателя качества работы системы, полученного в результате моделирования и расчета случайных реализаций;
- модуль m-го показателя качества работы системы, полученного в результате моделирования и расчета случайных реализаций;
 - вероятность выполнения технического требования по m-му показателю качества работы системы по результатам статистического моделирования;
- вероятность выполнения технического требования по m-му показателю качества работы системы по результатам статистического моделирования;
Pz - вероятность выполнения технических требований, предъявляемых к стохастической системе автоматического управления.
Учитывая большое число случайных возмущений и случайных параметров системы (более 1000 факторов), большую размерность вектора оптимизируемых параметров управления системой, высокий уровень требуемой вероятности выполнения предъявляемых к системе требований, стандартное применение статистического метода Монте-Карло для выбора параметров управления системой невозможно вследствие необходимости расчета недопустимо большого числа реализаций и, следовательно, недопустимо большого времени моделирования. Для повышения быстродействия предлагаемого способа поиск оптимальных параметров управления системой проводится в два этапа.
На первом этапе по выходным показателям качества работы системы статистическим методом Монте-Карло моделируют и рассчитывают случайные реализации системы, что обеспечивает моделирование большого количества реализаций при вариациях всего набора случайных возмущений и параметров системы в точке начального приближения параметров управления системой, которое задается на основании предварительных теоретических расчетов или из опыта разработки.
Вторым этапом в дополнение к стандартному применению статистического метода Монте-Карло для каждой случайной реализации рассчитывают универсальный безразмерный комплексный показатель эффективности управления системой - «запас работоспособности», характеризующий выполнение предъявляемых к системе технических требований, в котором отсутствуют какие-либо весовые коэффициенты.
Формула «запаса работоспособности» имеет вид:
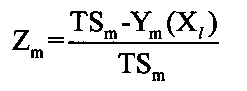
«Запас работоспособности» - непрерывная величина, изменяющаяся в диапазоне от 1 до - ∞. Положительные значения «запаса работоспособности» показывают, какую долю от предъявляемого технического требования составляет расчетное значение выходного показателя качества работы системы. Значение «запаса работоспособности», равного 1, соответствует нулевому значению показателя качества работы системы. При нулевом значении «запаса работоспособности» показатель качества работы системы равен предъявляемому техническому требованию. Отрицательные значения «запаса работоспособности» показывают долю превышения технического требования расчетным значением показателя качества работы системы.
Из всех рассчитанных случайных реализаций выбираются те, которые имеют наименьшее значение «запаса работоспособности» minZm по каждому рассматриваемому показателю качества работы системы. Для этих реализаций запоминают случайные возмущения и параметры системы.
На втором этапе оптимизации для выбранных реализаций для параметров управления системой, соответствующих каждому узлу многомерной сетки параметров управления системой, при повторении запомненных случайных возмущений и параметров системы рассчитывают выделенные реализации, по всем выходным показателям качества работы системы рассчитывают «запасы работоспособности» и запоминают наименьшее значение min[min(Zm)].
При моделировании и расчете выбранных реализаций с перебором параметров управления, соответствующих всем узлам сетки, из запомненных для каждого узла минимальных значений запасов, выбирается узел параметров управления сетки с наибольшим значением запаса max{min[min(Zm)]}.
Значения параметров управления системой, соответствующие этому узлу многомерной сетки параметров управления системой, и являются вектором оптимальных параметров управления системой.
Для обеспечения надежного поиска экстремума функции качества с использованием метода многомерных сеток диапазоны изменения параметров управления системой задаются в окрестности точки начального приближения параметров управления не превышающей ~30%, размер шага многомерной сетки параметров управления системой выбирается на уровне порядка 5% и может подстраиваться в процессе оптимизации. При попадании значений оптимального вектора параметров управления системой на край заданного диапазона повторяется процедура оптимизации, но в качестве начального приближения параметров управления системой используются оптимальные параметры, полученные при процедуре предшествующего поиска оптимального вектора параметров управления системой.
Общее число случайных реализаций, рассчитываемых методом Монте-Карло и число случайных реализаций, в которых рассматриваемый показатель качества работы системы превысил задаваемое техническое требование, определяют вероятность выполнения данного предъявляемого к системе технического требования.
Таким образом, технические результаты от использования изобретения заключается в том, что полученное в результате поиска оптимальное значение параметров управления системой обеспечивает повышение точности и надежности работы системы, за счет использования универсального безразмерного комплексного показателя «запаса работоспособности». Повышение быстродействия способа обеспечивается за счет перехода от статистического метода Монте-Карло с расчетом большого числа реализаций к расчету для каждого узла многомерной сетки параметров управления системой ограниченного числа выбранных реализаций с детерминированным набором возмущений. Расширение области применения способа обеспечивается за счет отсутствия требования монотонности функции качества при расчете показателя эффективности работы системы.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИДЕНТИФИКАЦИИ ХАРАКТЕРИСТИК И ВОЗМУЩЕНИЙ ДИНАМИЧЕСКИХ ОБЪЕКТОВ В СТОХАСТИЧЕСКИХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ | 2015 |
|
RU2623464C2 |
| СПОСОБ ПРОГНОЗА УРОЖАЙНОСТИ СЕЛЬСКОХОЗЯЙСТВЕННЫХ КУЛЬТУР ПОСРЕДСТВОМ ОПРЕДЕЛЕНИЯ КОМПЛЕКСА МЕТЕОРОЛОГИЧЕСКИХ ПАРАМЕТРОВ В СУТОЧНОМ РАЗРЕШЕНИИ | 2020 |
|
RU2770821C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЭЛЕМЕНТОВ СЛОЖНОЙ СИСТЕМЫ В ПЕРЕМЕННЫХ УСЛОВИЯХ | 2020 |
|
RU2726027C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО КОНТРОЛЯ И АДАПТИВНОГО УПРАВЛЕНИЯ РАСПРЕДЕЛЕННОЙ СИСТЕМОЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2006 |
|
RU2312389C1 |
| СПОСОБ РЕГУЛИРОВАНИЯ ДИНАМИЧЕСКИХ ОБЪЕКТОВ | 1995 |
|
RU2116663C1 |
| СПОСОБ ИСПЫТАНИЯ ЭЛЕКТРОННЫХ РЕГУЛЯТОРОВ ГАЗОТУРБИННЫХ ДВИГАТЕЛЕЙ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 1995 |
|
RU2098790C1 |
| СПОСОБ РАСПРЕДЕЛЕННОГО КОНТРОЛЯ И АДАПТИВНОГО УПРАВЛЕНИЯ МНОГОУРОВНЕВОЙ СИСТЕМОЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2011 |
|
RU2450335C1 |
| Способ адаптивного управления система-Ми B уСлОВияХ НЕОпРЕдЕлЕННОСТи | 1979 |
|
SU802922A1 |
| СПОСОБ И УСТРОЙСТВО ОПТИМИЗАЦИИ ПАРАМЕТРОВ СТРАТЕГИИ ДОЛГОСРОЧНОГО ПЛАНИРОВАНИЯ МЕРОПРИЯТИЙ ПО ОБЕСПЕЧЕНИЮ ТРЕБУЕМОГО СОСТОЯНИЯ СЛОЖНОЙ ОРГАНИЗАЦИОННО-ТЕХНИЧЕСКОЙ СИСТЕМЫ | 2019 |
|
RU2706458C1 |
| СПОСОБ КОНТРОЛЯ СОСТОЯНИЯ СТОХАСТИЧЕСКОЙ СИСТЕМЫ | 2020 |
|
RU2743897C1 |
Изобретение относится к области управления сложными стохастическими системами автоматического управления. Технический результат - повышение быстродействия поиска оптимальных параметров управления, в том числе, системами, в которых отсутствует монотонность критерия качества. Изобретение основано на моделировании случайных реализаций, описывающих движение объекта, с использованием статистического метода Монте-Карло с учетом случайных возмущений, действующих на систему, случайных параметров системы и законов распределения случайных величин. Процесс оптимизации разбивается на два этапа, обеспечивающих преобразование статистической оптимизации в детерминированную. Оценка выходных показателей качества работы системы проводится с использованием универсального безразмерного комплексного показателя эффективности работы системы, характеризующего выполнение предъявляемых к системе технических требований и позволяющего сравнивать показатели качества работы систем разной размерности.
Способ оптимизации многомерного вектора параметров управления сложных стохастических систем автоматического управления для многомерного вектора выходных показателей качества работы системы, заключающийся в поиске экстремума функции качества, отличающийся тем, что статистическим методом Монте-Карло моделируют и рассчитывают заданное количество случайных реализаций, для каждого выходного показателя качества работы системы определяют показатель эффективности работы системы - «запас работоспособности», определяемый по формуле:
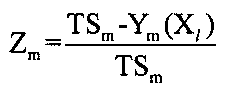 , где
, где
Xl - оптимизируемый вектор параметров управления стохастической системой автоматического управления размерности l ∈ [1, L];
m - число рассматриваемых показателей качества работы системы;
TSm - техническое требование номера m;
Ym (Xl) - модуль m-го показателя качества работы системы, полученного в результате моделирования и расчета случайных реализаций,
а из всех рассчитанных случайных реализаций выделяют те, в которых для каждого выходного показателя качества работы системы «запас работоспособности» наименьший, для выделенных случайных реализаций запоминают имеющие место случайные возмущения и параметры системы, задают многомерную сетку узлов параметров управления системой, для каждого узла которой при повторении запомненных значений случайных возмущений и параметров системы рассчитывают выделенные реализации, по всем выходным показателям качества работы системы которых определяют «запасы работоспособности», среди которых находят наименьший запас и запоминают его значение, а из всех наименьших «запасов работоспособности», соответствующих всем узлам сетки параметров управления, находят наибольший и запоминают параметры управления системой, соответствующие узлу сетки с наибольшим значением «запаса работоспособности», которые составляют оптимальный многомерный вектор параметров управления.
Авторы
Даты
2016-04-10—Публикация
2015-03-30—Подача