УСТРОЙСТВО ДЛЯ УСПОКОЕНИЯ КОЛЕБАНИЙ УПРУГОГО ЭЛЕМЕНТА ПЕРЕМЕННОЙ ЖЕСТКОСТИ Российский патент 2002 года по МПК G05D19/02 F16F15/00 

Изобретение относится к области демпфирования колебаний упругих элементов конструкции объектов и может быть преимущественно использовано при проектировании и создании перспективных систем управления объектами нежесткой конструкции.

Известно устройство [1] (прототип), предназначенное для гашения колебаний упругого элемента, когда пассивным демпфированием в системе возможно пренебречь. На фиг.1 представлена функциональная схема устройства [1], которое содержит объект 1 управления (упругий элемент), датчик 2 отклонения упругого элемента, дифференцирующий блок 3, инвертор 4, два делителя напряжения 5 и 6, сумматор 7, два релейных элемента 8 и 9, схему сравнения знаков 10, регулятор 11 жесткости.

Данное устройство реализует оптимальное управление частотой упругого элемента, успокаивающее его за минимальное время и имеющее следующую структуру [1-4]:

где ω_max,ω_min - максимальная и минимальная частоты колебаний упругого элемента из диапазона возможных изменений; - уравнение линии переключения на минимальную жесткость; q, - фазовые координата и скорость упругого элемента; ϕ∈(-π/2,0] - постоянный при фиксированном значении параметра x = (ω_min/ω_max)² угол логики.

На фиг. 2 показана фазовая траектория упругого элемента на фазовой плоскости (q, ) при осуществлении управления по логике (1), а на фиг.3 - соответствующие зависимости от времени фазовых координат, нормированной на квадрат частоты перегрузки и управляющего параметра.

При построении фиг.2, 3 учтено, что решение дифференциального уравнения

описывающего динамику свободного упругого элемента, при кусочно-постоянном управлении (1) на каждом из участков постоянства управляющего параметра имеет вид:
q_i = A_icos(ω_iΔT_i+β_i),
где ΔT_i = t_i-t_ki, t_i∈[0,t_ki],t_ki>0 - интервал постоянства; L - число интервалов; A_i>0, β_i - постоянные на интервале амплитуда и фаза колебаний, причем
cosβ_i = q_i(t_ki)/A_i;
Первое уравнение в (4) есть уравнение i-го участка траектории осциллятора (2) на фазовой плоскости (q, ). Отсюда непосредственно следует, что при ω_i = ω_max фазовая траектория упругого элемента представляет собой дугу окружности с центром в начале координат и радиусом, равным амплитуде A_i, а при ω_i = ω_min - дугу эллипса, получаемого сжатием дуги соответствующей окружности по оси ординат с коэффициентом Фазовая точка по указанным траекториям движется по часовой стрелке (фиг.2).

Соотношения (3) совместно с условиями непрерывности фазовых координат использованы при построении фиг.3.

Анализ фазовой траектории упругой системы позволяет сделать вывод о том, что переключения режимов движения носят регулярный характер. Это обусловлено свойством симметрии логики управления жесткостью на фазовой плоскости. Нетрудно определить характерные временные параметры управляемого процесса.

В силу симметрии логики управления (1) относительно начала координат в дальнейшем достаточно ограничиться рассмотрением управляемых процессов с начальными состояниями, например, в правой полуплоскости фазовой плоскости (q, ): q≥0. Тогда всякому начальному состоянию {q₀, 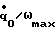} отвечает свой фазовый угол (фиг.2)
γ₀∈(-π/2,π/2].
Пусть для определенности γ₀≥ϕ. Как станет ясно из дальнейшего, такой выбор начального состояния упругого элемента не является принципиальным.

Рассмотрим несколько первых характерных участков фазовой траектории, последовательно определяя длительности каждого из них.

Движение из начального положения осциллятора, отвечающего, согласно логике (1), максимальной жесткости упругой системы, до первого переключения на минимальную жесткость (фиг.2, участок FE) совершается по дуге окружности с постоянной угловой скоростью ω_max. Время движения в данном случае определяется через приращение фазового угла в виде: T₁ = (γ₀-ϕ)/ω_max.
Для нахождения временных затрат на движение по второму эллиптическому участку (ED) целесообразно осуществить переход на фазовую плоскость (q, ). На этой плоскости рассматриваемый участок траектории представляется дугой окружности, движение по которой (см.(3), (4)) осуществляется с постоянной угловой скоростью, равной ω_min, вплоть до достижения оси ординат. Вычислим угол ϕ′, соответствующий углу на новой плоскости. Имеем где - фазовые координата и скорость упругой системы в момент переключения на минимальную жесткость. Следовательно, Время движения по эллиптическому участку (ED) составит

Движение по третьему участку (DC) осуществляется равномерно по дуге окружности с угловой скоростью ω_max, начиная от оси ординат. Время движения в данном случае определяется через приращение фазового угла в виде:
T₃ = (π/2-ϕ)/ω_max. (6)
В силу постоянства угла логики ϕ в течение всего процесса четвертый (СВ) и пятый (ВА₀) участки траектории с точки зрения временных затрат эквивалентны соответственно второму (ED) и третьему (DC) участкам. И так далее.

Как следует из (5), (6), параметры T₂ и T₃ при ϕ = const являются постоянными величинами, не зависящими от начальных условий. Это обстоятельство позволяет использовать их при организации управления в координатно-временной форме.

Анализ зависимостей, представленных на фиг.3, показывает, что возможен отличный от реализованного в устройстве [1] подход к организации оптимального управления жесткостью упругой системы (в координатно-временной форме) следующим образом:

либо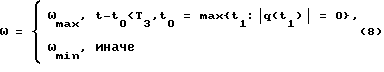

Здесь t - текущее время; t₀ - наиболее поздний момент времени, в который абсолютное значение линейной перегрузки (соответственно, отклонения) обращалось в нуль, T₃ определяется по формуле (6).

Законы управления (7) и (8) эквивалентны в силу связи (2).

Единственное отличие закона (7) от закона (8) состоит в природе используемого информационного сигнала: в первом случае система управления может функционировать по первичной информации с датчика перегрузки, а во втором с датчика отклонений упругого элемента.

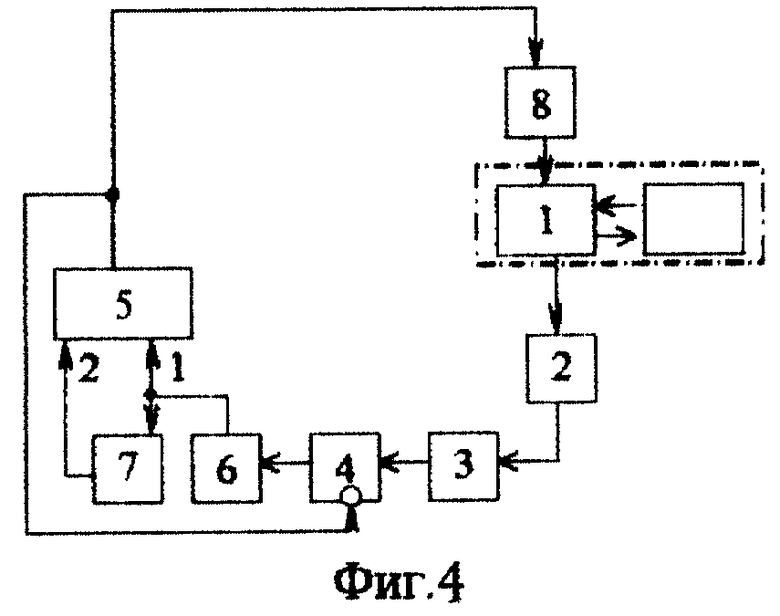
На фиг.4 представлена функциональная схема устройства для успокоения колебаний упругого элемента переменной жесткости, в котором реализуется закон управления (7) либо (8).

Устройство содержит объект 1 управления (упругий элемент), датчик 2 перегрузки (если реализуется закон (7)) или отклонения (если реализуется закон (8)), индикатор нуля 3, ключ 4, триггер 5, первый и второй элементы задержки 6 и 7, регулятор 8 жесткости.

Устройство работает следующим образом.

После воздействия внешнего возмущающего момента упругий элемент начинает колебаться с максимальной частотой ω_max, поскольку в состоянии покоя жесткость упругого элемента максимальна (из условия снижения амплитуды колебаний, возникающих от действия внешнего возмущающего импульса). Датчик 2 первичной информации начинает выдавать текущее значение перегрузки, если реализуется закон (7), или величины обобщенной координаты отклонения упругого элемента, если реализуется закон управления (8), которое поступает на вход индикатора нуля 3. При этом на выходе триггера 5 сформирован сигнал u=0. При первой же смене знака информационного сигнала (например, m.D на фиг.2 и 3) индикатор нуля 3 выдает импульс, который через открытый ключ 4 поступает на вход первого элемента задержки 6, в котором обеспечивается задержка сигнала на период T₃ (см.(6)). В течение интервала времени длительностью T₃ на выходе триггера 5 гарантирован сигнал u=0, что отвечает установлению максимальной жесткости упругого элемента. По окончании этого интервала (т.С на фиг. 2 и 3) импульс с выхода первого элемента задержки 6 переключает триггер 5 в единичное состояние, благодаря чему устанавливается минимальная жесткость системы. При этом ключ 4 закрывается и блокирует входной информационный канал. Этот же импульс, проходя через второй элемент задержки 7, по истечении интервала времени T₂ (см.(5)) переводит триггер 5 в нулевое состояние, благодаря чему в системе устанавливается максимальная жесткость (т. В на фиг.2 и 3), ключ 4 открывается. Система вновь готова реагировать на смену знака информационного сигнала аналогично описанному выше. Необходимо, однако, отметить, что для повышения устойчивости и регулярности переключении на максимальную жесткость, целесообразно обеспечивать задержку сигнала во втором элементе задержки 7 несколько меньше, чем Т₂, с таким расчетом, чтобы импульс с индикатора нуля 3 успевал пройти через ключ 4, вновь открывающийся сигналом с триггера 5.

Источники информации, использованные при составлении описания изобретения
1. Авторское свидетельство СССР 1129585, кл. ⁴ G 05 B 11/01, 1987 (прототип).

2. Мануйлов Ю.С. Синтез оптимального управления жесткостью упругих динамических объектов //Изв. вузов. Приборостроение, 1986. T.XXIX, 11. -С. 27-31.

3. Шалымов С.В., Мануйлов Ю.С. Оптимальное повышение диссипации в упругой системе за счет управления ее жесткостными свойствами // Методы и алгоритмы исследования автоматических систем управления. Вып. 6. Л.: МО СССР. 1988. -С. 26-31.

4. Шалымов С.В. Оптимальное гашение колебаний простых упругих систем с управляемой жесткостью. Л.: МО РФ. 2001, 101 с.

Изобретение относится к демпфированию колебаний упругих элементов конструкции объектов и может быть преимущественно использовано при проектировании и создании перспективных систем управления объектами нежесткой конструкции. Технический результат изобретения заключается в упрощении устройства. Устройство содержит объект управления (упругий элемент), датчик первичной информации (перегрузки либо отклонения упругого элемента), индикатор нуля, ключ, триггер, первый и второй элементы задержки и регулятор жесткости. 2 с. п. ф-лы, 4 ил.

1. Устройство для успокоения колебаний упругого элемента переменной жесткости, содержащее подключенный к выходу упругого элемента датчик отклонения упругого элемента, а к входу - регулятор жесткости упругого элемента, отличающееся тем, что оно дополнительно снабжено индикатором нуля, ключом, первым и вторым элементами задержки и триггером, причем выход датчика отклонения упругого элемента через последовательно соединенные индикатор нуля, ключ и первый элемент задержки соединен с первым входом триггера, выход которого подключен к управляющему входу ключа и к входу регулятора жесткости, выход первого элемента задержки через второй элемент задержки связан со вторым входом триггера. 2. Устройство для успокоения колебаний упругого элемента переменной жесткости, содержащее подключенный к входу упругого элемента регулятор жесткости упругого элемента, отличающееся тем, что оно дополнительно снабжено датчиком перегрузки, индикатором нуля, ключом, первым и вторым элементами задержки и триггером, причем выход упругого элемента через последовательно соединенные датчик перегрузок, индикатор нуля, ключ и первый элемент задержки соединен с первым входом триггера, выход которого подключен к управляющему входу ключа и к входу регулятора жесткости упругого элемента, выход первого элемента задержки через второй элемент задержки связан со вторым входом триггера.