Изобретение относится к области выращивания оптических монокристаллов методом Чохральского.
Известно устройство для выращивания кристаллов методом Чохральского, которое содержит нагреватель, охватывающий тигель с окном, расположенным над расплавом, через которое излучение от нагревателя попадает на кристалл (US, 5429067, С 30 В 15/10, опубл. 04.07.95). В данном устройстве реализуется низкоградиентный метод Чохральского, направленный на выращивание кристаллов с полностью ограненным фронтом кристаллизации.
Недостатком этого устройства является то, что он не обладает достаточной устойчивостью вследствие уменьшения аксиального градиента температуры в кристалле на фронте кристаллизации, что приводит к увеличению времени релаксации фронта кристаллизации к стационарному положению и, следовательно, к снижению однородности полученного кристалла.
Известно устройство для выращивания кристаллов методом Чохральского, которое содержит тигель, затравкодержатель, верхний и нижний керамические экраны (SU, 1228526, С 30 В 15/14, 29/22, опубл. 15.02.93).
Это устройство не позволяет выращивать крупные оптические кристаллы достаточно высокой однородности.
Задачей изобретения является создание устройства для выращивания монокристаллов по методу Чохральского, в котором за счет создания и сохранения большого аксиального градиента температур в зоне фронта кристаллизации даже при изменении уровня расплава, с помощью диафрагмы, расположенной над фронтом кристаллизации, и за счет обеспечения отвода излучения с помощью окна между верхним и нижним керамическими экранами, расположенного на уровне диафрагмы, добиваются высокого уровня динамической устойчивости системы кристалл-расплав в условиях заметного падения уровня расплава при отсутствии подвижных частей в системе выращивания, что позволяет получать оптические кристаллы большого размера и высокой однородности, при этом одновременно позволяет повысить показатель выхода годных кристаллов при их выращивании и тем самым улучшить эффективность использования устройства для выращивания кристаллов.
Вышеуказанный технический результат достигается за счет того, что в устройстве для выращивания кристаллов методом Чохральского, включающем тигель, затравкодержатель, верхний и нижний керамические экраны, включена диафрагма, расположенная над расплавом, между керамическими экранами установлена цилиндрическая вставка из прозрачного для теплового излучения расплава материала (например, плавленого кварца или лейкосапфира), нижняя кромка которой выполнена совпадающей по высоте с верхней поверхностью диафрагмы, а высота вставки s<ΔL, где ΔL = R/√2Bi, R - радиус кристалла, a Bi - число Био, при этом Δh+ΔH≥sd/L, где Δh - расстояние от нижней кромки диафрагмы до начального уровня расплава, ΔН - падение уровня расплава за процесс, d - расстояние между диафрагмой и кристаллом, L - длина верхней обкладки вставки. Диаметр верхнего экрана меньше диаметра нижнего экрана и расстояние от кристалла до верхнего экрана выбрано равным d.
Использование неподвижной диафрагмы обеспечивает увеличение устойчивости при выращивании кристаллов диаметром меньше 1/2 диаметра тигля и падении уровня расплава не более чем на R/(2Bi)1/2, гдe Bi=Rμ/λ, μ - изменение излучательной способности поверхности кристалла при изменении температуры на 1 К, λ - теплопроводность кристалла.
Использование вставки приводит к увеличению устойчивости при большем размере кристалла по сравнению с системой, использующей только диафрагму, за счет уменьшения локальности теплового воздействия излучения системы и обеспечивает независимость условий отжига выращенного кристалла от режима устойчивости за счет того, что наличие вставки обеспечивает дополнительный теплоотвод с поверхности кристалла, который не зависит от плотности излучения в верхней части системы.
Использование верхнего керамического экрана с внутренним диаметром, равным d= Rr, позволяет увеличить теплоотвод от кристалла по сравнению со случаем отсутствия вставки за счет увеличения телесного угла Ω, с которого поступает излучение системы на элементарную площадку поверхности кристалла. Из этого телесного угла поверхность кристалла недополучает излучение системы по сравнению со случаем отсутствия вставки.
При совместном использовании диафрагмы и вставки становится возможным сузить диаметр верхнего экрана, приблизив, тем самым, диаметр экрана к диаметру кристалла, за счет чего увеличить долю телесного угла вставки в телесном угле 2π, с которого излучение системы поступает на элементарный участок поверхности кристалла. Это позволяет добиться значительно большего теплоотвода с зоны кристалла, прилегающей к фронту кристаллизации, по сравнению с использованием одной только вставки, что приводит к увеличению тепловой устойчивости процесса выращивания кристалла при прочих равных условиях (одинаковой высоте вставки s). Это означает, что добиться того же уровня устойчивости, что и при наличии одной только вставки (без диафрагмы), можно при меньшей высоте вставки, и влияние вставки на плотность излучения на поверхности кристалла будет более локальным, то есть высоту, начиная с которой начинается безградиентная зона, можно уменьшить по сравнению с системой с одной только вставкой, что приводит к улучшению температурных условий в верхней части системы, где требуется минимальный градиент температуры при том же уровне устойчивости системы кристалл-расплав.
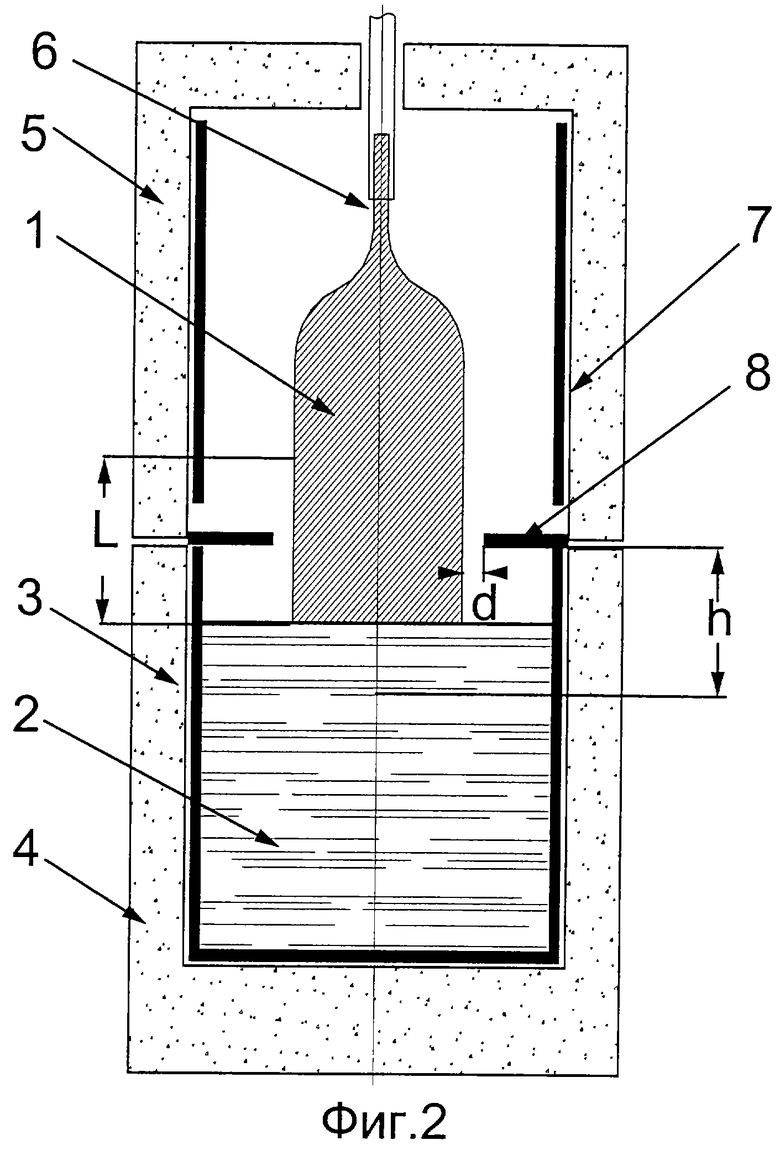
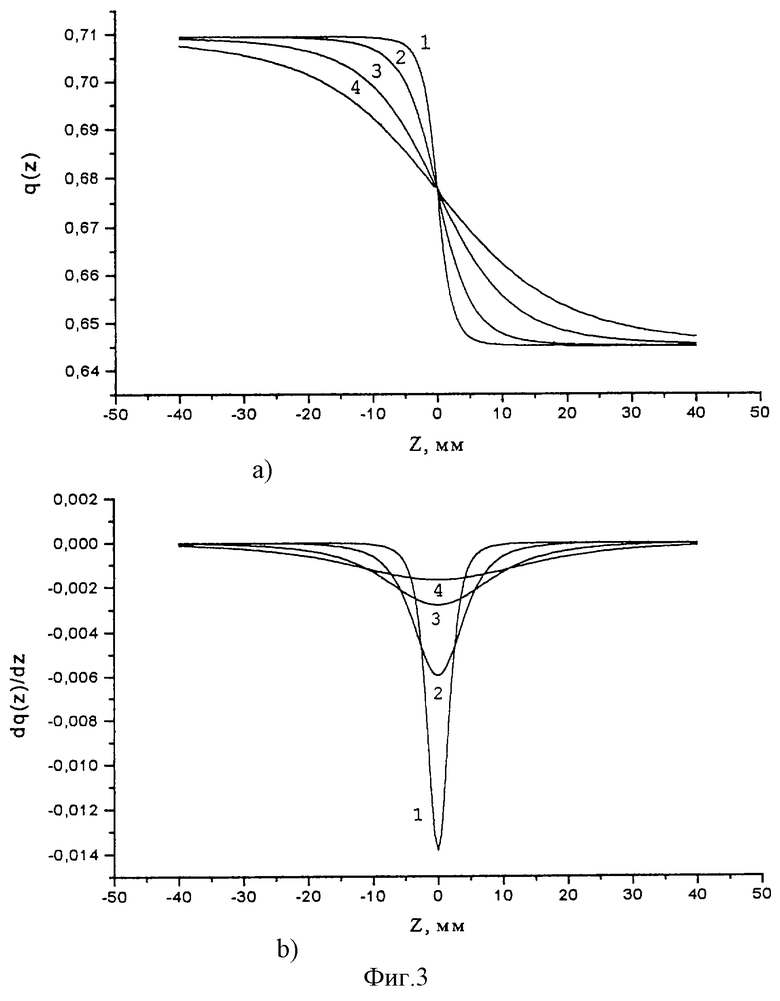
Изобретение поясняется фиг.1-9. На фиг.1 показано устройство для выращивания кристаллов по методу Чохральского, которое содержит кристалл 1, расплав 2, тигель 3, нижний экран 4, верхний экран 5, кристаллодержатель 6, верхний нагреватель 7. На фиг.2 показано устройство для выращивания кристаллов с отражательной диафрагмой 8. На фиг.3(а, b) показаны семейства кривых зависимости прошедшего в кристалл потока излучения от высоты z и производной от этой величины при различных значениях зазора d.
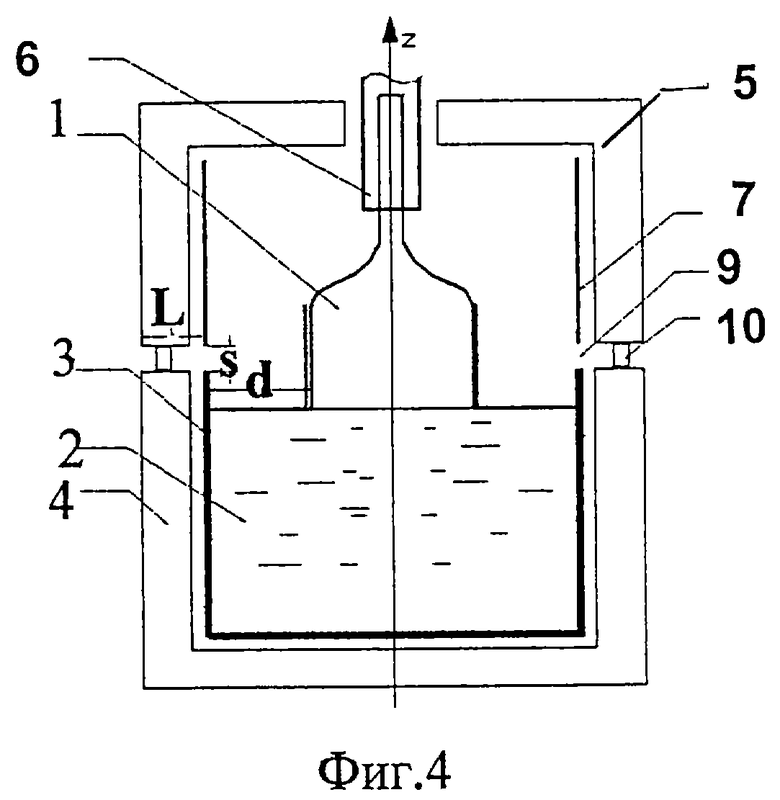
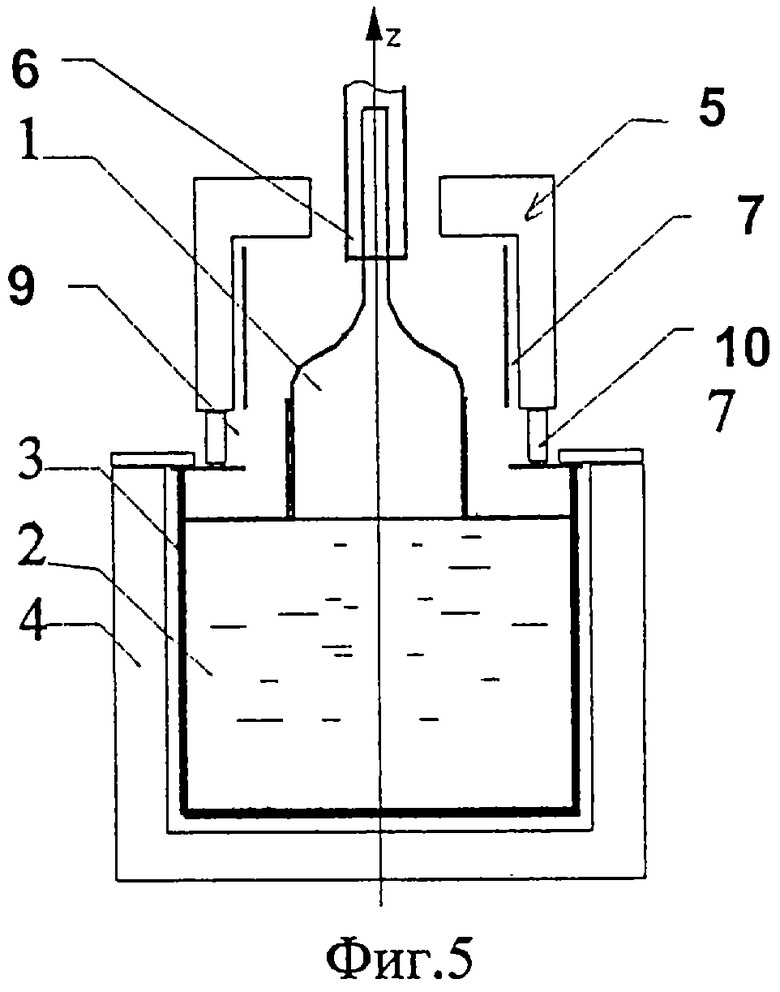
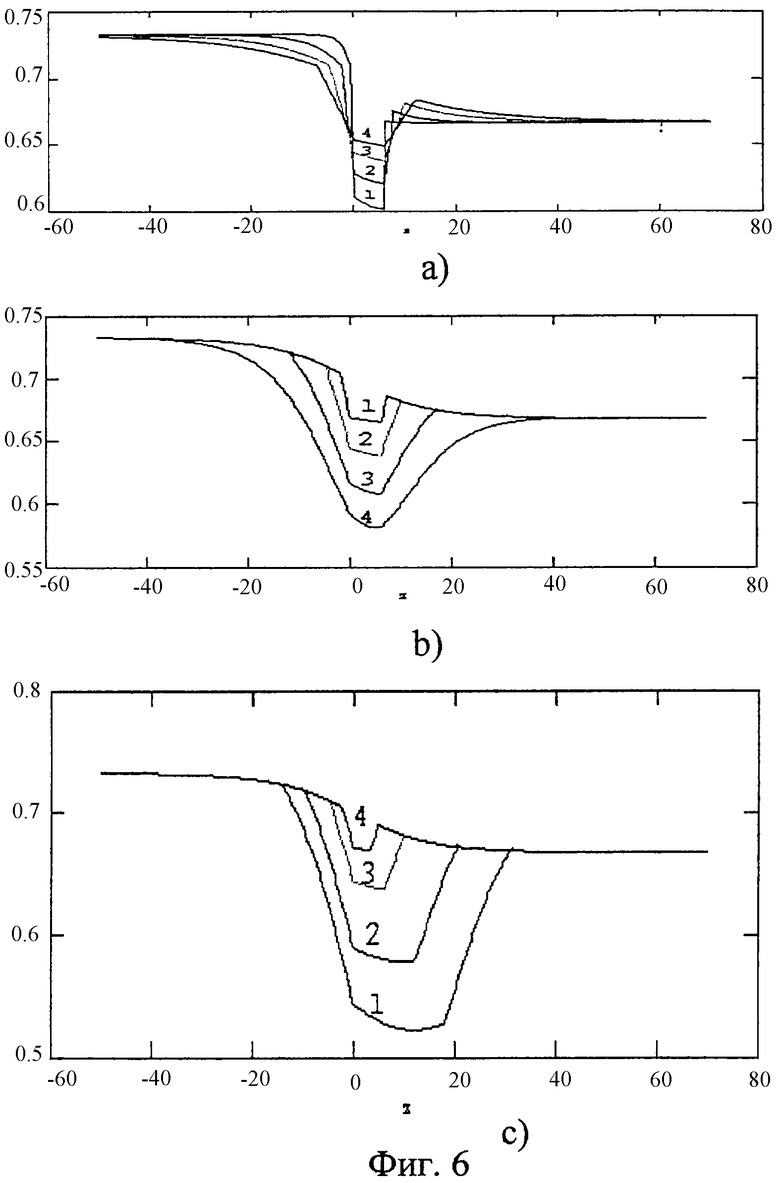
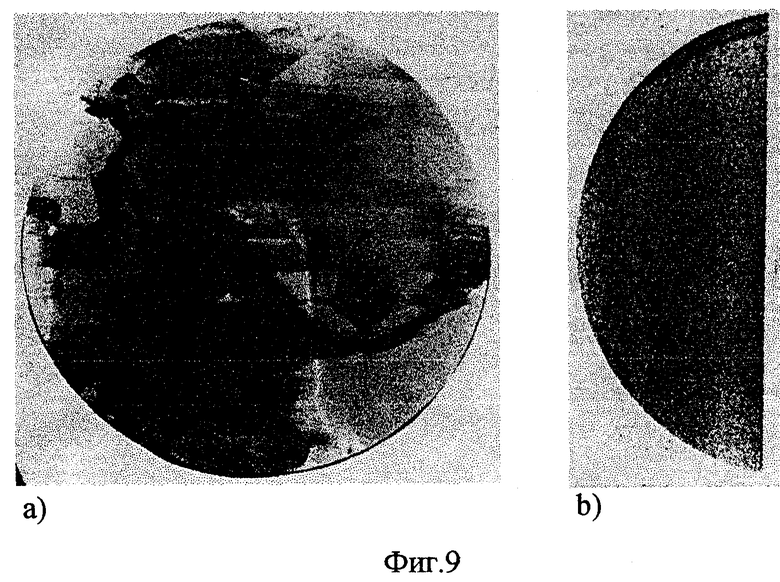
На фиг.4 изображено устройство для выращивания кристаллов с щелью 9 между верхним 5 и нижним экранами 4, в которую установлена вставка 10 из прозрачного для теплового излучения материала. На фиг.5 изображен оптимизированный для заданных размеров кристалла тепловой узел с сочетанием диафрагмы 8 и щели 9 с вставкой 10. На фиг.6(а, b, с) приведены семейства численно рассчитанных зависимостей плотности потока излучения в кристалл от z при изменении одного из параметров теплового узла с щелью между экранами и теплового узла с диафрагмой и щелью. На фиг.7 изображен кристалл LiNbO3, который после выращивания в тепловом узле с диафрагмой был отожжен непосредственно в ростовом узле при его расположении частично над диафрагмой и частично под ней. При постростовом отжиге кристаллов выше среза диафрагмы были получены целые, без трещин, кристаллы LiNbO3. Фотографии кристаллов приведены на фиг.8. Однородность выращенных кристаллов ниобата лития, выращенных с диафрагмой и без нее, можно сравнить по рентген-топограммам кристаллов (фиг.9 a, b), выращенных на одной и той же установке при прочих равных условиях.
Работу устройства можно пояснить следующим образом. Так как работа устройства прежде всего зависит от устойчивости системы кристалл-расплав в процессе выращивания кристалла, обратимся к рассмотрению физических механизмов обеспечения устойчивости системы кристалл-расплав и параметров устройства, влияющих на устойчивость. Устойчивость системы кристалл-расплав или самостабилизация ее параметров - это наличие в ней внутренних механизмов, за счет которых возникающие отклонения ее параметров от заданных со временем затухают. Невозмущенное движение системы кристалл-расплав, характеризуемое постоянным (стационарным) радиусом кристалла и постоянной высотой мениска в процессе роста, асимптотически устойчиво, если при выборе начальных условий (радиуса кристалла и высоты фронта кристаллизации относительно свободной поверхности расплава), мало отличающихся от заданных стационарных, последующее движение системы в отсутствие возмущающих воздействий будет неограниченно приближаться к невозмущенному. Устойчивость системы тем выше, чем быстрее затухают отклонения движения системы от невозмущенного движения. Скорость изменения радиуса кристалла определяется капиллярными условиями, поэтому при наличии в системе самостабилизации радиуса говорят о ее капиллярной устойчивости. Положение фронта кристаллизации относительно расплава определяется тепловыми условиями, поэтому наличии в системе самостабилизации положения фронта кристаллизации относительно уровня расплава говорят о наличии в системе тепловой устойчивости. Анализ тепловых и капиллярных явлений в системе кристалл-расплав при выращивании кристаллов по Чохральскому показал, что в системе отсутствует капиллярная устойчивость и присутствует тепловая устойчивость, а также, что имеет место взаимное влияние параметров системы друг на друга.
Несмотря на наличие капиллярной неустойчивости, устойчивость системы кристалл-расплав достижима за счет тепловой устойчивости и наличия взаимной стабилизации параметров. В нашем рассмотрении фронт кристаллизации считается плоским, и полученные результаты не применимы к процессам выращивания кристаллов с глубоким погружением фазовой границы в расплав. Считается, что преобладающим механизмом теплопереноса в расплаве является теплопроводность, а не конвекция. В этом случае оправдано приближение тепловой задачи в виде одномерного уравнения теплопроводности и для кристалла, и для расплава. При этом считается, что наличие кристалла не влияет на распределение температуры в тепловом узле. Такое предположение допустимо для оценочного расчета, если площадь поверхности и масса кристалла много меньше площади поверхности и массы окружающих его нагретых тел теплового узла. В данном приближении получено следующее основное выражение для коэффициента тепловой устойчивости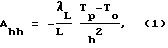
где L - скрытая теплота кристаллизации, Тр - температура расплава под кристаллом на уровне свободной поверхности расплава, То - температура на фронте кристаллизации. Этот коэффициент определяет скорость возвращения фронта кристаллизации к стационарной высоте ho относительно свободной поверхности расплава при условии малого отклонения от него δh=h-ho. Высота фронта кристаллизации обычно мала (около 1 мм), поэтому градиент температуры на фронте кристаллизации в расплаве GL можно считать равным 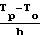 . При малых отклонениях высоты мениска δh от стационарного положения и малых скоростях изменения высоты мениска
. При малых отклонениях высоты мениска δh от стационарного положения и малых скоростях изменения высоты мениска 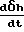 (что обычно подразумевается при рассмотрении устойчивости по Ляпунову) можно считать, что скорость кристаллизации Vc равна скорости вытягивания V, взятой с обратным знаком (здесь, для простоты, будем считать, что уровень расплава постоянен). Тогда условие Стефана на фазовой границе запишется в виде
(что обычно подразумевается при рассмотрении устойчивости по Ляпунову) можно считать, что скорость кристаллизации Vc равна скорости вытягивания V, взятой с обратным знаком (здесь, для простоты, будем считать, что уровень расплава постоянен). Тогда условие Стефана на фазовой границе запишется в виде
-λSGS+λLGL = LV
где Gs, GL - градиенты температуры на фазовой границе, соответственно в кристалле и в расплаве. Откуда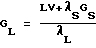
С учетом (1), имеем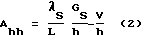
Таким образом, при фиксированной скорости вытягивания тепловая устойчивость процесса по Чохральскому определяется аксиальным градиентом температуры Gs в кристалле на фазовой границе.
При наличии отрицательного аксиального градиента температуры среды dTe/dz<0 в коэффициенте тепловой устойчивости возникает отрицательная добавка, что свидетельствует о повышении устойчивости системы. Температура среды - это граничное условие на поверхности кристалла, входящее в одномерном случае в само уравнение теплопроводности. При выращивании высокотемпературных оксидов основным механизмом теплопереноса является излучение, поэтому аналогом температуры среды для них является плотность потока излучения в кристалл.
При удлинении кристалла оказывается, что условия теплоотвода на удаленных от фронта кристаллизации частях кристалла слабо сказываются на формировании высокого градиента температуры на фронте кристаллизации Gax. Поэтому для создания высокого градиента температуры на фронте кристаллизации Gax достаточно обеспечить сильный теплоотвод в области, прилегающей к фронту кристаллизации. Анализируя вышеуказанную тепловую задачу, можно показать, что при изменении длины кристалла от L=R/(2Bi)1/2 (где Bi=μR/λ - число Био, R - радиус кристалла) до бесконечной Gax изменяется не более чем на 1/3. Поэтому Gax определяется, в основном, потерями тепла с поверхности кристалла, лежащей в высотном диапазоне ΔL=R/(2Bi)1/2 от фронта кристаллизации. Оценка величины ΔL для ниобата лития дала значение 25 мм.
На фиг. 1 показано устройство для выращивания кристаллов, содержащее тигель 3, расплав 2, кристалл 1, нижний керамический экран 4, верхний керамический экран 5, кристаллодержатель 6, верхний нагреватель 7. С учетом имеющихся в тепловом узле лучистых потоков было предложено поместить над поверхностью расплава отражательную диафрагму 8, отсекающую подогрев вследствие излучения расплава и стенок тигля части поверхности кристалла, прилегающей к фронту кристаллизации, что показано на фиг.2.
Для расчета оптимальных параметров диафрагмы, обеспечивающих наибольший уровень устойчивости, была использована модель, основанная на следующих допущениях. Считается, что поверхность деталей теплового узла состоит из ламбертовских источников излучения и что индикатриса отражения кристалла является направленной, а деталей теплового узла - идеально рассеивающей. Для рассмотрения влияния диафрагмы тепловой узел разбивается на две части: его нижняя (индекс 1) состоит из свободной поверхности расплава, оголенной от расплава части стенки тигля и нижней поверхности диафрагмы, а верхняя его часть (индекс 2) состоит из верхней поверхности диафрагмы и внутренней поверхности верхних керамических экранов. Для простоты будем считать, что поверхность каждой из двух частей теплового узла состоит из ламбертовских источников одинаковой эффективной яркости излучения (l1, l2), которая скачком изменяется при переходе из одной части теплового узла (l1) в другую (l2). Такое приближение оправдано для оценочного рассмотрения, так как в эффективную яркость излучения поверхности нагретых тел теплового узла входит как яркость собственного излучения нагретых тел теплового узла, так и яркость отраженного излучения. Поэтому, несмотря на одинаковость температур верхней и нижней поверхностей металлической диафрагмы, эффективные яркости излучения этих поверхностей будут сильно различаться за счет отраженного излучения, так как ее коэффициент отражения составляет около 95%. Хорошей оценкой для эффективной яркости излучения обеих частей теплового узла является равновесная яркость излучения при средней температуре соответствующих частей теплового узла. Абсолютные значения эффективных яркостей излучения верхней и нижней частей теплового узла в наших расчетах не используются, так как для оценки оптимальности параметров теплового узла достаточно знать их отношение, которое нетрудно получить через отношение четвертых степеней температуры. В модели считается, что влияние самого кристалла на распределение температуры в тепловом узле пренебрежимо мало. Это приближение допустимо в случае, если площадь поверхности и масса кристалла много меньше площади поверхности и массы окружающих его нагретых тел теплового узла. При расчете считается, что каждая элементарная площадка кристалла лежит на оси симметрии теплового узла, что на самом деле является приближением, причем расхождение будет в плотности телесного угла Ω(i), приходящейся на определенный интервал углов падения излучения нагретых тел теплового узла на рассматриваемую площадку кристалла [i,i+di]. Однако вводя определенную поправку в расстояние от кристалла до нагретых тел теплового узла, можно добиться почти полного совпадения зависимости Ω(i) с той, которая наблюдается при рассмотрении площадки кристалла, находящейся не на оси симметрии теплового узла. И последним упрощением, позволяющим в выражении для плотности излучения перейти от двукратного к однократному интегралу - это замена угла падения излучения нагретых тел теплового узла на кристалл на угол, лежащий в осевом сечении теплового узла и находящийся под тем же углом к образующей цилиндрической поверхности кристалла (проходящей через рассматриваемую элементарную площадку кристалла), что и рассматриваемый луч. Вычисленное в таком приближении значение плотности излучения даст завышенное значение прошедшего в кристалл потока излучения, так как луч, лежащий в осевом сечении теплового узла, имеет наименьший угол падения из лучей, которые образуют с заданной образующей кристалла определенный угол, поэтому коэффициент отражения будет заниженным. Оправданием этого приближения является то, что лучи нагретых тел теплового узла, падающие под большими углами на поверхность кристалла, будут иметь большой коэффициент отражения и, следовательно, будут оказывать меньшее тепловое влияние на кристалл по сравнению с лучами, лежащими в осевом сечении и падающими на кристалл под наименьшими углами.
На фиг. 3 (a, b) показаны рассчитанные на основе этой модели семейства кривых зависимости прошедшего в кристалл потока излучения от высоты z и производной от этой величины при различных значениях зазора d между кристаллом и диафрагмой. Самый высокий градиент плотности потока излучения в кристалл на высоте диафрагмы обеспечивается минимальным зазором d между кристаллом и диафрагмой. Так как именно градиент плотности потока излучения в кристалл обеспечивает градиент температуры в кристалле на фронте кристаллизации, то максимум этого градиента (который совпадает с уровнем диафрагмы) должен располагаться как можно ближе к фронту кристаллизации. Очевидно, что чем дальше расположен максимум градиента потока излучения в кристалл от фронта кристаллизации, тем меньше его влияние на аксиальный градиент в кристалле на фронте кристаллизации.
Таким образом, оптимальными параметрами диафрагмы, обеспечивающими наибольший вклад в устойчивость системы кристалл-расплав при условии постоянного уровня расплава относительно уровня диафрагмы, будут
1) минимально возможный зазор между кристаллом и диафрагмой;
2) минимально возможная высота диафрагмы над расплавом.
Падение уровня расплава приводит к изменению положения диафрагмы относительно фронта кристаллизации. Поэтому с течением процесса уменьшается градиент плотности потока излучения в кристалл в окрестности фронта кристаллизации и, соответственно, изменяется градиент температуры в кристалле. Скорость этого уменьшения для разных зазоров d различна.
Другим способом получения резкого градиента потока излучения в кристалл в зоне фронта кристаллизации является наличие щели 9 между нижним 4 и верхним 5 керамическими экранами, которые обычно устанавливаются над тиглем при выращивании оптических кристаллов для соблюдения режима постростового отжига, как показано на фиг. 4. Для уменьшения конвективных потоков газа через щель в нее устанавливается прозрачная для излучения расплава термостойкая вставка. Высота вставки равна высоте щели, то есть вставка полностью закрывает собой щель и дополнительного отверстия в экранах за счет щели не образуется. Одновременно вставка может выполнять роль элемента конструкции, на который устанавливается верхний экран. В отличие от диафрагмы, которая лишь локализует имеющийся в тепловом узле вертикальный перепад плотности потока излучения в кристалл вблизи фронта кристаллизации, щель увеличивает градиент плотности потока излучения в кристалл за счет дополнительных теплопотерь, которые возникают вследствие излучения через нее. Поскольку в этом случае величина градиента температуры на фронте кристаллизации не будет так сильно зависеть от разности потока излучения в кристалл в верхней и нижней частях теплового узла, то эта разность может быть сведена к минимуму (за счет введения дополнительного верхнего независимого нагревателя 7), что позволит проводить постростовой отжиг в наиболее благоприятном режиме предплавления. В смысле независимости условий кристаллизации от условий отжига щель еще ближе, чем диафрагма, приближается к идее газового обдува поверхности кристалла в локальной зоне вблизи фронта кристаллизации.
В отличие от диафрагмы щель, как оптическое устройство, имеет не 1, а 3 параметра, включающих толщину верхнего керамического экрана L, ширину s (расстояние между верхним 5 и нижним 4 экранами) и зазор между верхним экраном и кристаллом d. Изменение этих параметров влияет как на условия кристаллизации, так и на условия отжига. Поэтому выбор параметров щели должен обеспечивать
1) максимальный градиент плотности потока излучения в кристалл в диапазоне не более ΔL= R/(2Bi)1/2, прилегающем к фронту кристаллизации с учетом падения уровня расплава;
2) безградиентную высокотемпературную зону в остальной части теплового узла.
Для правильного выбора параметров щели необходимо знать высотную зависимость плотности потока излучения нагретых тел теплового узла через поверхность кристалла при любых значениях ее параметров.
Математическое описание щели является развитием описания диафрагмы.
Поверхность нагретых тел теплового узла разбивается на три части: нижнюю, состоящую из свободной поверхности расплава, оголенной части стенки тигля и верхней торцевой поверхности нижнего керамического экрана; верхнюю, состоящую из внутренней поверхности верхнего керамического экрана и нижней его торцевой поверхности; и саму щель, которую удобно считать состоящей из одной поверхности, имеющей нулевую яркость излучения. Считается, что верхняя часть теплового узла имеет яркость l1, а нижняя - l2.
На фиг.6(а, b, с) приведены семейства численно рассчитанных зависимостей плотности потока излучения в кристалл от z при изменении каждого из параметров при условии постоянства остальных двух. За коэффициент преломления взят коэффициент преломления обыкновенного луча кристалла ниобата лития. Графики приведены в относительных единицах потока излучения. За единицу считается такой поток со стороны нагретых тел теплового узла на кристалл, который создается в кристалле с коэффициентом отражения равным нулю при равномерной по тепловому узлу яркости излучения равной I1. На графике 6, а показано семейство кривых q(z) при различных толщинах верхнего экрана L, на графике 6, b - при различных ширинах щели s, на графике 6, с - при различных расстояниях от кристалла до верхнего экрана d при фиксированных остальных параметрах щели.
Ширина щели s, равная длине кристалла ΔL, начиная с которой излучательный теплоотвод доминирует над теплопроводным во влиянии на градиент температуры на фронте кристаллизации, может оказаться слишком большой, нарушающей условия отжига. Уменьшение зазора d приводит к увеличению плотности потока излучения в кристалл в области, прилегающей к фронту кристаллизации. Это означает повышение устойчивости. Однако в устройстве с одной только щелью зазор d не может быть меньше разности радиусов тигля и кристалла, поэтому следует выбрать наименьший возможный зазор между кристаллом и верхним экраном d=Rтигля-R.
В связи с вышеизложенным предлагается следующая схема оптимизации параметров щели.
1. Чтобы наличие щели в течение всего процесса заведомо приводило к увеличению градиента плотности потока излучения в кристалл на уровне фронта кристаллизации с учетом падения уровня расплава за процесс ΔН необходимо соблюдение следующего соотношения:
Δh+ΔH≤sd/L,
где Δh - высота кромки щели относительно начального уровня расплава, ΔН - величина падения уровня расплава за процесс.
2. Чтобы в течение всего процесса влияние щели обеспечивало коэффициент тепловой устойчивости, сравнимый с максимально достижимым (который достигается при отсутствии экранов), необходимо соблюдение соотношений
ΔL~s,
qмин/qmax<1/2,
где qмин - минимальный поток излучения нагретых тел теплового узла в высотном диапазоне ΔL от фронта кристаллизации, qmax - излучение кристалла, равновесное с излучением нагретых тел теплового узла равномерной яркости равной I1.
3. В случае, если ширина щели ΔSразруш, начиная с которой условия отжига становятся неудовлетворительными, отказывается меньше ΔL, то фактическим ограничителем уровня устойчивости процесса выращивания являются условия отжига выращенной части кристалла во время выращивания (величина максимального градиента плотности потока излучения в кристалл в верхней его части).
При выращивании крупногабаритных кристаллов с падением уровня расплава более чем d щель, то есть участок, откуда кристалл недополучает излучение, оказывается расположена под углом к кристаллу более 45o, поэтому ее температура слабо сказывается на температуре кристалла вследствие сильного отражения излучения, падающего под большими углами. В то же время с увеличением sd/L возникает вредный побочный эффект теплоотвода с поверхности расплава, вызывающий усиление его свободной конвекции, ведущее к увеличению амплитуды флуктуации его температуры, поэтому неравенство Δh+ΔH≤sd/L можно заменить равенством, а при наличии развитой свободной конвекции расплава даже заменить неравенством Δh+ΔH≥sd/L, так как однородность выращиваемого кристалла определяется как скоростью затухания отклонений скорости кристаллизации, вызванных флуктуациями температуры, так и амплитудой самих температурных флуктуаций.
Как следует из вышеизложенного, уменьшение расстояния d от кристалла до верхнего экрана, при прочих равных параметрах, приводит к увеличению устойчивости системы кристалл-расплав за счет увеличения теплоотвода с поверхности кристалла. Одновременное использование щели 9 и диафрагмы 8, показанное на фиг. 5, соответствующее варианту их применения в отсутствие падения уровня расплава, позволяет уменьшить зазор d между верхним экраном 5 и кристаллом, а также уменьшить теплоотвод с поверхности расплава, являющийся основной причиной флуктуаций его температуры. При этом, в отличие от теплового узла с диафрагмой, имеется возможность создать низкую плотность потока излучения в кристалл в окрестности фронта кристаллизации при высоких температурах в верхней части теплового узла.
Математическое описание теплового узла с щелью и диафрагмой в точности совпадает с описанием теплового узла с одной только щелью. Используя вышеизложенное описание щели, идеальными условиями для обеспечения устойчивости при отсутствии падения уровня расплава можно считать следующие параметры теплового узла, включающего диафрагму и имеющего щель между верхним и нижним экранами:
1) d=0 (минимально возможное, что подразумевает наличие диафрагмы);
2) s>L>d;
3) s≈ΔL.
С учетом падения уровня расплава для теплового узла с щелью и диафрагмой проходит точно такая же схема оптимизации, как с тепловым узлом, включающим только щель, с той лишь разницей, что параметр d может принимать значения, меньшие разности радиусов тигля и кристалла, то есть щель 9 может приближаться к кристаллу.
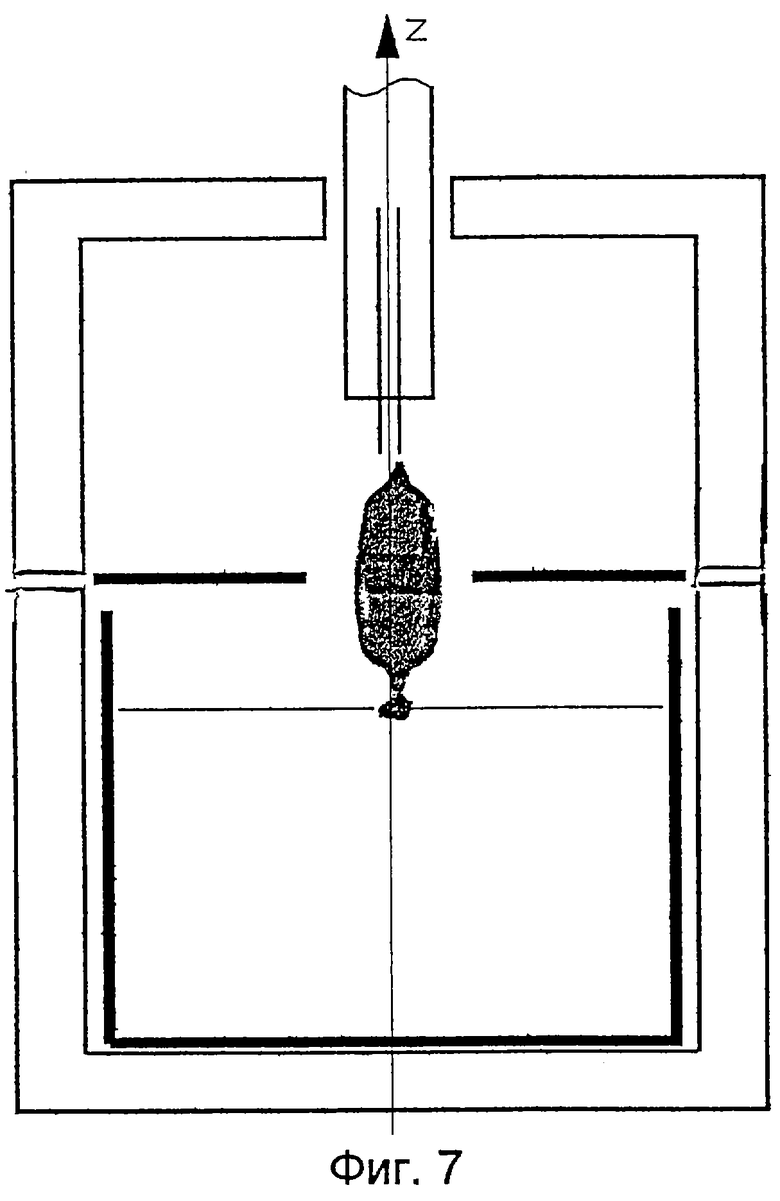
Тот факт, что и диафрагма, и щель могут сильно влиять на условия отжига, хорошо видно из фиг.7. На нем изображен кристалл LiNbO3, который после выращивания в системе с диафрагмой был отожжен в ростовой печи, находясь частично над диафрагмой и частично под ней. На уровне диафрагмы появились трещины, несмотря на то, что в своей верхней части кристалл целый. Эти трещины являются следствием резкого градиента плотности потока излучения в кристалл на уровне диафрагмы во время постростового отжига.
При постростовом отжиге кристаллов выше среза диафрагмы были получены целые, без трещин, кристаллы LiNbO3. Фотографии кристаллов приведены на фиг. 8. Оба эти кристалла были получены на установке без автоматического регулирования. Из формы кристаллов видно, что в системе кристалл-расплав в процессе выращивания кристалла имела место самостабилизация диаметра кристалла. Во время выращивания вручную отслеживался только систематический дрейф режима выращивания. Однородность выращенных кристаллов ниобата лития, выращенных с диафрагмой и без нее, можно сравнить по рентген-топограммам кристаллов (фиг. 9 a, b), выращенных на одной и той же установке при прочих равных условиях. Из рентген-топограмм видно, что кристалл, выращенный в системе с диафрагмой, гораздо однороднее, чем в системе без диафрагмы.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ВЫРАЩИВАНИЯ КРИСТАЛЛОВ | 1999 |
|
RU2177514C2 |
| УСТРОЙСТВО ДЛЯ ВЫРАЩИВАНИЯ КРИСТАЛЛОВ | 2000 |
|
RU2191853C2 |
| АВТОКОРРЕЛЯТОР СВЕТОВЫХ ИМПУЛЬСОВ | 2001 |
|
RU2194256C1 |
| СПОСОБ ИЗМЕРЕНИЯ ОПТИЧЕСКОЙ ТОЛЩИНЫ ПЛОСКОПАРАЛЛЕЛЬНЫХ ПРОЗРАЧНЫХ ОБЪЕКТОВ | 1998 |
|
RU2152588C1 |
| ОПТИЧЕСКОЕ ВОЛОКНО | 1995 |
|
RU2091827C1 |
| СПОСОБ ИНТЕГРИРОВАНИЯ ОПТИЧЕСКИХ СИГНАЛОВ ПО ВРЕМЕНИ И УСТРОЙСТВА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2000 |
|
RU2194300C2 |
| СПОСОБ ЛЕЧЕНИЯ ЛИМФОМ КОЖИ | 1996 |
|
RU2128533C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИИ МНОГОКОМПОНЕНТНЫХ РАСТВОРОВ | 2001 |
|
RU2192632C1 |
| СПОСОБ ВЫРАЩИВАНИЯ КРИСТАЛЛОВ | 2003 |
|
RU2248418C1 |
| СПОСОБ ЛЕЧЕНИЯ ГЕМАНГИОМ КОЖИ | 1995 |
|
RU2121387C1 |

Изобретение относится к области выращивания оптических монокристаллов методом Чохральского. Сущность изобретения: устройство, содержащее тигель, затравкодержатель, верхний и нижний керамические экраны, включает диафрагму, расположенную над расплавом, между керамическими экранами установлена цилиндрическая вставка из прозрачного для теплового излучения материала (например, плавленого кварца или лейкосапфира), нижняя кромка которой выполнена совпадающей по высоте с верхней поверхностью диафрагмы. Высота вставки s<ΔL, где 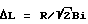 , R - радиус кристалла, Bi - число Био, при этом Δh+ΔH ≥sd/L, где Δh - расстояние от нижней кромки диафрагмы до начального уровня расплава, ΔН - падение уровня расплава за процесс, d - расстояние между диафрагмой и кристаллом, L - длина верхней обкладки вставки. Диаметр верхнего экрана меньше диаметра нижнего экрана и расстояние от кристалла до верхнего экрана выбрано равным d. Изобретение позволяет получать оптические кристаллы большого размера и высокой однородности и повысить показатель выхода годных кристаллов при их выращивании. 1 з.п. ф-лы, 9 ил.
, R - радиус кристалла, Bi - число Био, при этом Δh+ΔH ≥sd/L, где Δh - расстояние от нижней кромки диафрагмы до начального уровня расплава, ΔН - падение уровня расплава за процесс, d - расстояние между диафрагмой и кристаллом, L - длина верхней обкладки вставки. Диаметр верхнего экрана меньше диаметра нижнего экрана и расстояние от кристалла до верхнего экрана выбрано равным d. Изобретение позволяет получать оптические кристаллы большого размера и высокой однородности и повысить показатель выхода годных кристаллов при их выращивании. 1 з.п. ф-лы, 9 ил.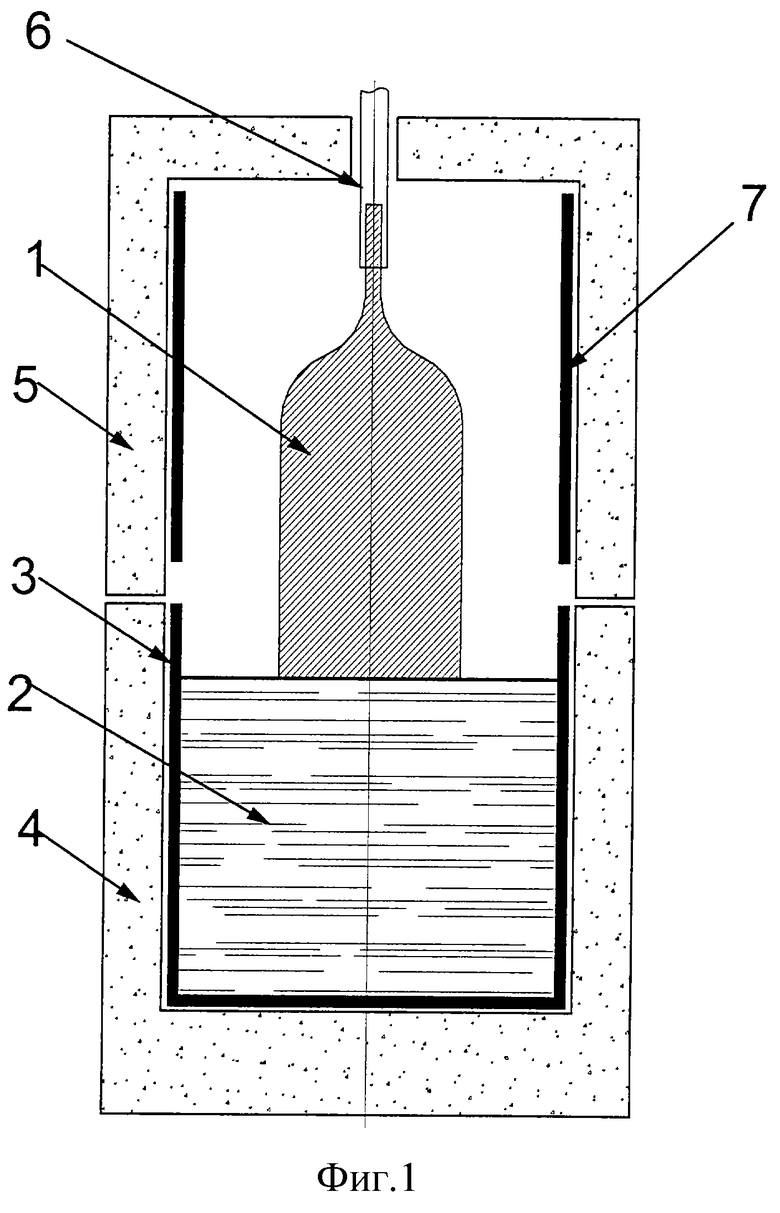
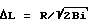 , R - радиус кристалла, а Bi - число Био, при этом Δh+ΔH ≥sd/L, где Δh - расстояние от нижней кромки диафрагмы до начального уровня расплава, ΔН - падение уровня расплава за процесс, d - расстояние между диафрагмой и кристаллом, L - длина верхней обкладки вставки.
, R - радиус кристалла, а Bi - число Био, при этом Δh+ΔH ≥sd/L, где Δh - расстояние от нижней кромки диафрагмы до начального уровня расплава, ΔН - падение уровня расплава за процесс, d - расстояние между диафрагмой и кристаллом, L - длина верхней обкладки вставки.
| Способ выращивания монокристаллов сложных оксидов из расплава и устройство для его осуществления | 1984 |
|
SU1228526A1 |
| US 5450814 А, 19.09.1995 | |||
| Запоминающее устройство с обнаружением ошибок | 1984 |
|
SU1164791A1 |
| JP 57183393 А, 11.11.1982. | |||
Авторы
Даты
2003-04-10—Публикация
2000-12-20—Подача