Область техники, к которой относится изобретение
Изобретение относится к способу и устройству для определения магнитного поля внутри замкнутого объема, не содержащего источников поля и ферромагнитных материалов, и может быть применено для картографирования поля в электрофизических установках, например ускорителях частиц, магнитных детекторах, в области энергетики, например при проектирование электрических силовых установок, медицины, например в томографии, а также в следящих системах на основе магнитного поля, используемых в авиационной технике, охранных системах, в системах слежения, средствах мультимедийной компьютерной технологии.
Уровень техники
Существующие способы определения параметров магнитного поля в замкнутом объеме, также известные как картографирование или построение карты магнитного поля, подразделяются на два типа. К первому типу относятся способы, в которых компоненты магнитного поля измеряют в достаточно часто расположенных точках внутри объема, так называемых узлах пространственной сетки, с последующим вычислением компонент поля в промежуточных точках, см., например, D.Newton, "Картографирование магнитного поля детекторов на основе магнитов", CERN Accelerator School, Magnetic Measurement and Alignment, Proc. CERN 92-05, 15 сентября 1992 г., стр.283-295. Ко второму типу относятся способы, в которых компоненты магнитного поля измеряют в некоторых точках на границе замкнутого объема, то есть в узлах сетки на поверхности объема, с последующим определением параметров поля во внутренних точках объема, в основе которого лежит одно из фундаментальных свойств магнитного поля: dvB=0, rotB=0 и которое осуществляется путем решения задачи Дирихле, Неймана или смешанной краевой задачи для трехмерного уравнения Лапласа. При этом измеренные значения компонент магнитного поля на границе объема используют как граничные условия, а карта поля является результатом решения данного уравнения, Н.Wind, "Оценка компонент магнитного поля только на основании результатов измерений на границе", Nuclear Instruments and Methods, выпуск 84, №1, июль 1970, стр.117-128.
К системам для определения магнитного поля (картографирования) предъявляются достаточно жесткие требования, в особенности применительно к ускорителям заряженных частиц, а также используемым в авиационных следящих системах.
Система картографирования магнитного поля в ускорителе заряженных частиц должна удовлетворять следующим требованиям.
1) Высокая относительная точность определения компонент вектора магнитного поля В, обычно не хуже 10-4, т.е. 0,01%, определяющая соответствующие требования к точности показаний и калибровке датчиков магнитного поля, точности установки датчиков в пространстве и ориентации датчиков, а также количество точек измерения компонент магнитного поля в пространстве.
2) Устойчивость к ошибкам измерения.
3) Погрешность, вносимая вычислительным алгоритмом, должна быть меньше ошибок измерения поля.
Способам первого упомянутого типа присуща относительная простота математической обработки результатов измерений. К преимуществам можно также отнести сравнительно низкие требования к точности установки датчиков в заданных точках и ориентации датчиков, а высокая точность обычно требуется только при измерении координат и ориентации уже установленных датчиков, что технически проще сделать. Однако эти преимущества часто нивелируются главным недостатком способа - очень большим числом точек измерения, что приводит к значительным финансовым затратам, затратам труда и времени проведения измерений. Другой недостаток способа заключается в большом влиянии ошибок измерения, которое может быть несколько снижено применением методов статистической обработки.
В способах второго типа значительно снижено количество измерительных точек, и, как следствие, достигнуто уменьшение затрат, связанных с калибровкой и установкой датчиков, и время проведения измерений. Большим достоинством этого способа является устойчивость к ошибкам измерений, обусловленная тем, что при удалении от границы вглубь объема случайная ошибка вычисления компонент магнитного поля быстро затухает. Действительно, известно, что гармонические функции достигают своего наибольшего и наименьшего значения на границе области. Поскольку как реальное магнитное поле в объеме, так и вычисленное магнитное поле являются гармоническими функциями, то и их разность, представляющая собой ошибку определения поля, также является гармонической функцией (А.Н.Тихонов, А.А.Самарский. "Уравнения математической физики", М. Наука, 1972). Применение способов второго типа предполагает наличие в составе измерительного комплекса сложных компьютерных программ для обработки результатов измерений. Но затраты, связанные с разработкой или приобретением необходимого программного обеспечения, являются, в известной мере, одноразовыми, т.к. разумно организованная программа обычно может быть легко адаптирована к разным условиям эксперимента и разным начальным данным. Главным недостатком этих способов являются жесткие требования к установке датчиков в заранее указанные положения, то есть в заданные точки границы объема, и ориентирование датчиков вдоль заданных направлений или нормали к границе. Для областей с геометрически сложной границей это сделать, как правило, весьма затруднительно, кроме того, некоторые участки границы могут быть просто недоступны в силу, например, конструктивных особенностей ускорителя.
Наиболее близким к заявленному способу является техническое решение, описанное в патенте США №6377041. Известный способ определения параметров магнитного поля внутри объема, имеющего непрерывную границу, включает определение компонент магнитного поля в множестве точек указанной границы и решение краевой задачи с использованием этих компонент в качестве граничных условий. В известном способе предложена возможность увеличения количества точек границы, в которых определяются компоненты поля, за счет использования интерполяции значений, измеренных в относительно небольшом количестве точек границы.
Ближайшим к заявленному устройству является техническое решение, описанное в каталоге продукции фирмы METROLAB's, Швейцария (METROLAB's Product List, 110 Ch. Du Pont-du-Centenarie, CA-1228, Geneva, Planles-Ouates, Switzeland). Известное устройство для определения параметров магнитного поля внутри объема, имеющего непрерывную границу, включает датчики для измерения значений компонент магнитного поля, которые связаны со средствами обработки данных, использующими показания датчиков для решения краевой задачи. Датчики установлены точно на границе объема и в зависимости от решаемой задачи ориентированы либо точно вдоль нормали к границе, либо точно вдоль координатных осей. В первом случае показания датчиков, а также их заданные координаты и ориентацию используют в качестве граничных условий для решения задачи Неймана для уравнения Лапласа, а во втором случае - задачи Дирихле. Результатом вычислений является информация о распределении магнитного поля в объеме, или так называемая карта поля.
Недостатки известного способа и устройства заключаются в следующем.
Для решения уравнения Лапласа с требуемой точностью необходимо, чтобы датчики располагались точно на границе объема, то есть имели заданные координаты, и были ориентированы либо точно по нормали к границе объема, либо по координатным осям, то есть имели заданную ориентацию. Для прецизионных измерений и в случае границы сложной геометрии этому требованию удовлетворить очень тяжело. Положение нельзя исправить более точным измерением уже установленных датчиков и введением поправок. Если даже такие поправки известны, их нельзя ввести в решаемое уравнение, поэтому приходится прибегать к нескольким итерациям типа установка - измерение - новая установка - новое измерение и т.д. вплоть до достижения требуемой точности. Поэтому процесс установки одного датчика весьма трудоемкий.
В описанном известном устройстве также используется установка датчиков на подвижную рамку, перемещаемую по границе объема, что существенно сокращает число требуемых датчиков. Однако это допустимо лишь для границы, близкой к идеально симметричной поверхности, поскольку в случае даже небольших отклонений от идеальной симметрии (вращательной, трансляционной), которая практически возможна лишь тогда, когда выбор границы объема произволен, перемещаемые с рамкой датчики уходят с границы. Для объемов, размеры которых заданы конструкционными особенностями электрофизического оборудования, идеально симметричных границ практически не бывает.
Раскрытие изобретения
Задачей изобретения является повышение точности определения параметров магнитного поля внутри замкнутого объема при использовании преимуществ, свойственных описанным выше способам картографирования первого и второго типа. А именно, настоящее изобретение сочетает в себе низкие требования к точности установки и ориентации датчиков магнитного поля и минимальное количество используемых датчиков.
Сущность изобретения заключается в относительно произвольном размещении датчиков в окрестности границы объема, что позволяет устранить основной недостаток известного решения, то есть прецизионную установку датчиков на заданной поверхности с заданной ориентацией, и в последующем прецизионном измерении координат и ориентации уже установленных датчиков. Для специалиста такой переход от прецизионной установки к прецизионному измерению означает существенное упрощение измерительной процедуры и повышение точности измерений.
В этой части заявленное изобретение аналогично вышеописанному способу первого типа, где также отсутствует необходимость в очень точной установке датчиков. Однако размещение датчиков в предлагаемом решении ограничено окрестностью границы объема, поэтому приводит обычно не более чем к двукратному увеличению количества точек измерения, тогда как в способе первого типа количество точек объема, в которых измеряют компоненты магнитного поля, обычно на порядки больше.
Поставленная задача решена в способе определения компонент магнитного поля внутри объема, имеющего непрерывную границу, в котором определяют компоненты магнитного поля в множестве точек указанной границы и решают краевую задачу с использованием этих компонент в качестве граничных условий. Характерной особенностью способа является размещение датчиков магнитного поля в окрестности непрерывной границы, измерение координат и ориентации датчиков, а также значений компонент магнитного поля в точках расположения датчиков, и определение компонент магнитного поля в множестве точек непрерывной границы на основании значений измеренных компонент, координат и ориентации датчиков.
Размеры окрестности выбирают эмпирическим путем, исходя из заданной точности определения компонент магнитного поля на границе объема. На практике это означает проведение предварительного компьютерного моделирования, заключающегося в вычислении компонент магнитного поля на непрерывной границе при размещения датчиков на различных расстояниях, определяющих размер окрестности, от указанной границы. Окрестность считается выбранной в случае достижения требуемой точности вычисления компонент.
Наиболее естественным и простым решением для вычисления компонент магнитного поля в множестве точек непрерывной границы является применение полиномиальной интерполяции или экстраполяции значений компонент магнитного поля, измеренных в точках расположения датчиков.
Интерполяция является более предпочтительным математическим инструментом и используется при доступности области границы с обеих сторон. В этом случае датчики размещают по обе стороны непрерывной границы, а через точки расположения датчиков проводят по меньшей мере две вспомогательные поверхности.
Экстраполяция измеренных значений компонент магнитного поля целесообразна в случае доступности границы только с одной стороны. Соответственно, в этом случае датчики размещают по одну из сторон непрерывной границы, а через точки расположения датчиков проводят по меньшей мере две вспомогательные поверхности.
В случае использования двух поверхностей обычно применяют линейную интерполяцию или экстраполяцию, требующую по меньшей мере четыре точки измерения компонент магнитного поля. Для повышения точности возможна интерполяция или экстраполяция значений, порядок которой выше линейной.
Непрерывная граница может представлять собой кусочно-гладкую поверхность с линиями излома, а значения компонент магнитного поля измеряют в том числе в множестве точек, окружающих указанные линии излома. В этом случае можно применить интерполяцию значений на границу объема, включающую линии излома.
Кроме того, компоненты магнитного поля в множестве точек непрерывной границы могут быть вычислены посредством решения задач Дирихле, Неймана или смешанной краевой задачи для уравнения Лапласа с использованием в качестве граничных условий значений компонент магнитного поля, измеренных в точках расположения датчиков. Для этого датчики размещают с заданием одной поверхности, охватывающей снаружи непрерывную границу объема, или двух поверхностей, заключающих между собой указанную границу объема, проходящих через точки расположения датчиков.
Вычисленные в результате интерполяции или экстраполяции компоненты магнитного поля используют в качестве граничных условий при решении задачи Дирихле для уравнения Лапласа. Решение уравнения Лапласа может быть осуществлено любым известным способом, в общем случае численным, а для некоторых специальных случаев с помощью разложения в ряды.
В случае размещения датчиков с возможностью измерения значений нормальных компонент магнитного поля компоненты магнитного поля, определенные в множестве точек непрерывной границы, используют в качестве граничных условий при решении задачи Неймана для уравнения Лапласа.
В случае размещения датчиков с возможностью измерения значений тангенциальных компонент магнитного поля в множестве точек непрерывной границы определяют тангенциальные компоненты магнитного поля и используют эти компоненты для вычисления скалярного магнитного потенциала, представляющего собой граничные условия при решении краевой задачи Дирихле для уравнения Лапласа.
Также возможна ситуация, когда на первом участке непрерывной границы определяют тангенциальные компоненты, в на втором участке - нормальные компоненты магнитного поля. На основании тангенциальных компонент вычисляют скалярный потенциал магнитного поля и используют этот потенциал, а также нормальные компоненты в качестве граничных условий при решении смешанной краевой задачи для уравнения Лапласа. В этом случае датчики размещают с возможностью измерения значений тангенциальных и нормальных компонент магнитного поля в точках расположения датчиков.
Значения компонент магнитного поля в множестве точек непрерывной границы могут быть использованы для построения карты магнитного поля внутри объема. Для проверки правильности построения такой карты внутри объема может быть установлен дополнительный датчик магнитного поля, показания которого сравнивают с вычисленными значениями компонент магнитного поля.
С целью практической реализации заявленного способа изобретение предлагает устройство для определения компонент магнитного поля внутри объема, имеющего непрерывную границу. Устройство включает датчики для измерения значений компонент магнитного поля, которые связаны со средствами обработки данных, использующими показания датчиков для решения краевой задачи. Особенностью устройства является то, что датчики установлены в окрестности непрерывной границы объема. Устройство также содержит средства определения координат и ориентации датчиков. При этом средства обработки данных выполнены с возможностью вычисления компонент магнитного поля в множестве точек непрерывной границы, используемых в качестве граничных условий для решения краевой задачи, на основании измеренных датчиками значений компонент магнитного поля, а также координат и ориентации датчиков.
В предпочтительном варианте датчики установлены на рамке с разделением по меньшей мере на две группы, определяющие поверхности, которые проходят либо по одну из сторон, либо по обе стороны непрерывной границы. В этом случае устройство снабжено средствами приведения рамки в движение с перемещением каждой группы датчиков по соответствующей поверхности.
Использование подобных подвижных рамок с датчиками позволяет существенно уменьшить количество датчиков без уменьшения числа точек измерения. Например, в случае цилиндрической границы возможно вращение прямоугольной рамки вокруг оси цилиндра. Предлагаемое устройство, в отличие от известного, не требует идеально симметричной границы объема, поскольку вполне достаточно, чтобы точки измерения компонент магнитного поля были расположены вблизи границы и допускали интерполяцию или экстраполяцию измеренных значений на эту границу.
Заявленный способ также применим для объемов, ограниченных жесткими непроницаемыми конструкциями или выступами. В этом случае часть датчиков закрепляют на конструкционных элементах вне границы объема, а их точные координаты и ориентацию измеряют после установки. Точки расположения этих датчиков будут определять поверхность на внешней стороне границы объема. С внутренней стороны границы поверхность определяется перемещением подвижной рамки с другой частью датчиков. Показания всех датчиков объединяют, в результате чего имеют границу объема, окруженную двумя поверхностями, в множестве точек которых измерены значения компонент магнитного поля.
Краткое описание чертежей
Далее изобретение будет подробно пояснено со ссылками на прилагаемые чертежи, где
на фиг.1 изображена структурная схема системы картографирования магнитного поля;
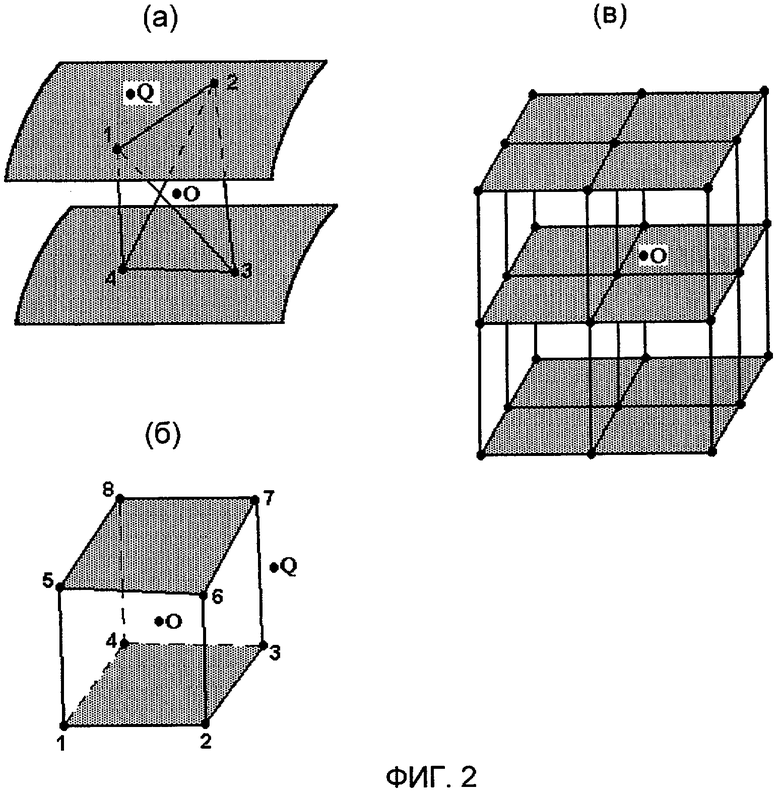
на фиг.2а-в проиллюстрированы, соответственно, примеры линейной, квадратичной и кубической интерполяции;
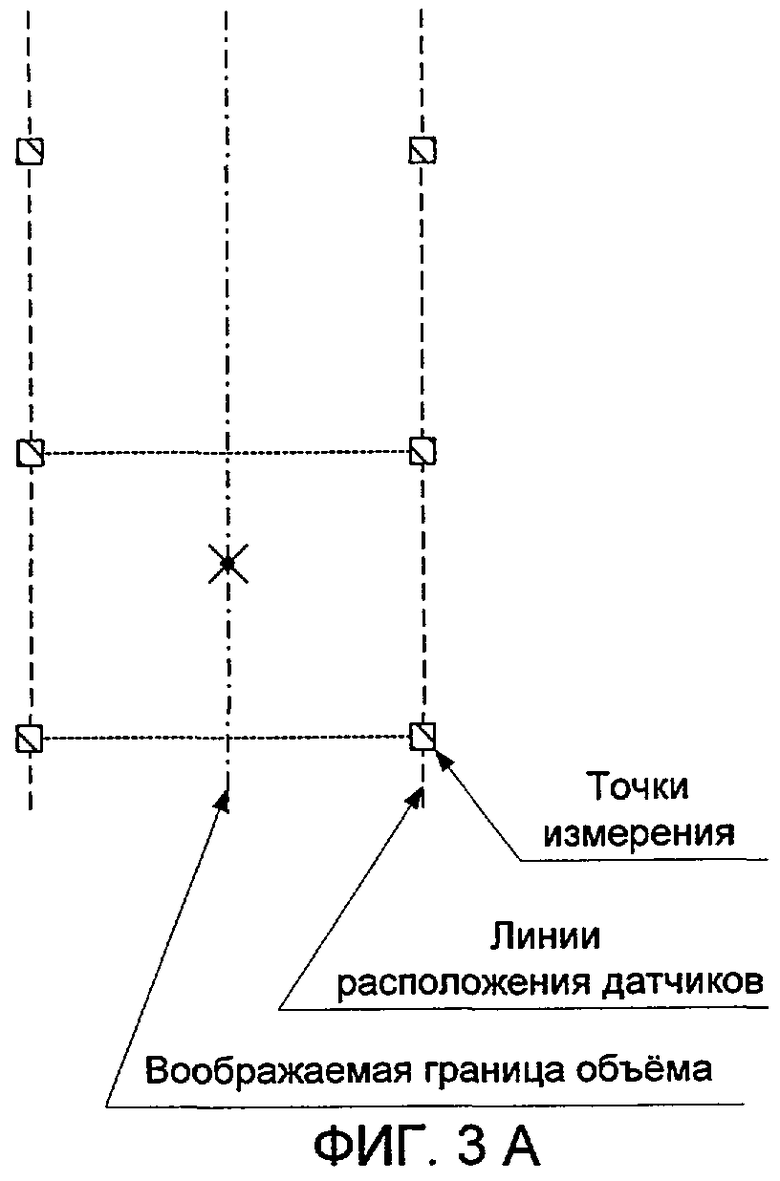
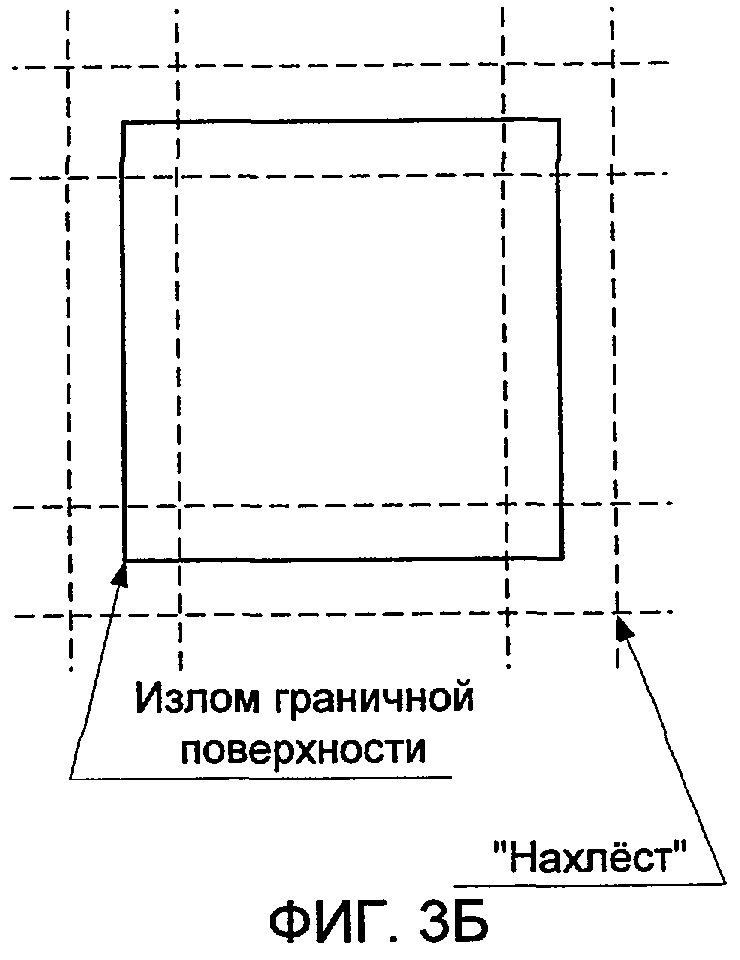
на фиг.3а и 3б приведены примеры гладкой и кусочно-гладкой границы с линиями излома, окруженной двумя поверхностями;
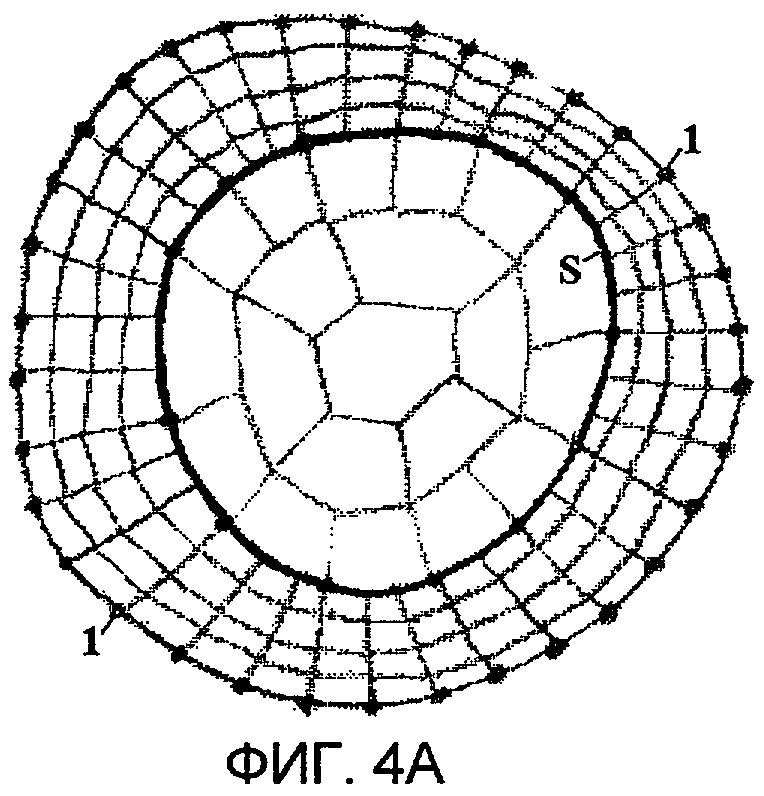
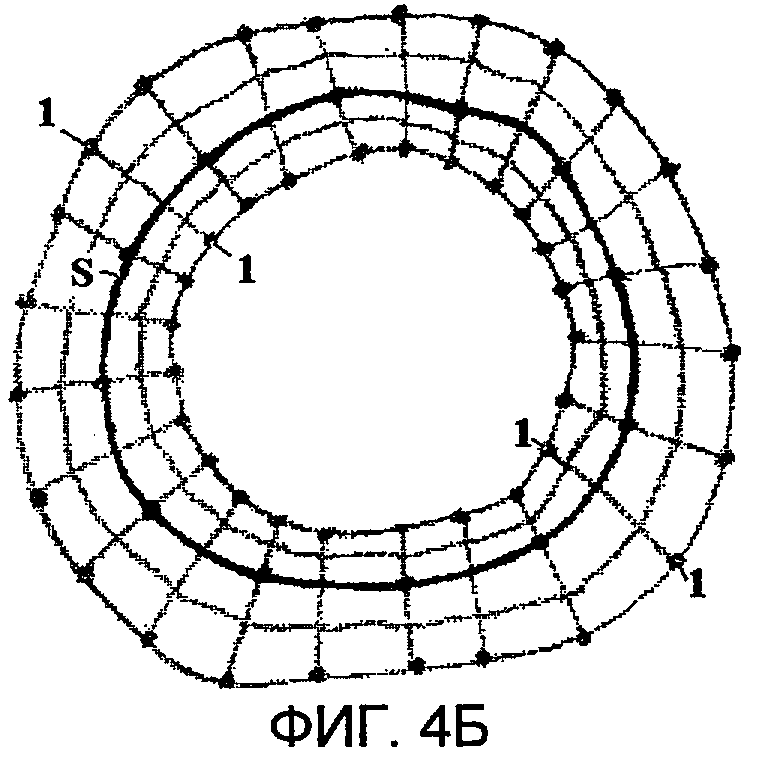
на фиг.4а и 4б приведены примеры способа интерполяции путем промежуточного решения уравнения Лапласа в окрестности непрерывной границы.
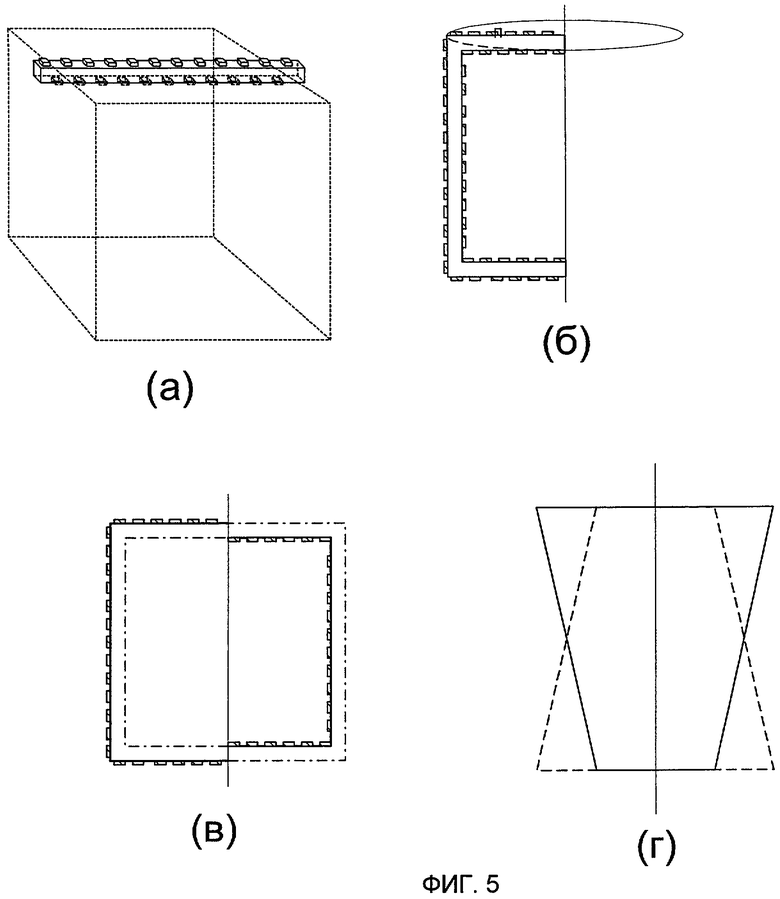
на фиг.5а-г продемонстрировано использование подвижной рамки для некоторых видов границ.
Осуществление изобретения
Устройство для определения компонент магнитного поля, называемое в примере реализации изобретения по фиг.1 системой картографирования, включает датчики 1 для измерений компонент магнитного поля, связанные по шине передачи данных с устройством сбора информации 2, которое в свою очередь связано с компьютером 3, расположенном на измерительном стенде. Устройство сбора информации 2 представляет собой измерительную плату, содержащую мультиплексор и аналого-цифровой преобразователь (АЦП). Датчики 1 установлены на немагнитной рамке 4, перемещаемой поворотным устройством 5 под управлением компьютера 3. Компьютер генерирует сигналы, передаваемые на поворотное устройство 5, и пересчитывает эти сигналы в углы поворота, а затем в декартовы координаты датчиков, а также в направляющие косинусы магнитных осей датчиков, определяющие ориентацию датчиков. Полученный набор данных, включающий показания, координаты и ориентацию датчиков, представляется в стандартизованном виде в вычислительную программу, выполняемую процессорным блоком 6, связанным с компьютером 3. Устройство сбора информации 2, компьютер 3 и процессорный блок 6 составляют средства обработки данных.
В рассматриваемом примере определяют компоненты магнитного поля с последующим построением карты поля внутри цилиндрического объема, имеющего непрерывную границу, фиг.5б, под которой понимается условная замкнутая поверхность, то есть поверхность без разрывов.
В способе согласно изобретению для построения карты поля, иными словами, нахождения его распределения внутри объема, решают краевую задачу для уравнения Лапласа с граничными условиями, определяемыми на непрерывной границе.
Для уравнения Лапласа существует три типа краевых задач, когда на границе задается либо сама искомая функция (задача Дирихле), либо ее нормальная производная (задача Неймана), либо смешанная задача, в которой на первом участке границы задается сама функция, а на втором участке - нормальная производная. Функции, удовлетворяющие уравнению Лапласа, принято называть гармоническими.
Возможны два способа определения компонент магнитного поля внутри объема по значениям компонент на непрерывной границе.
В первом способе решается задача Дирихле, записанная для каждой компоненты магнитного поля:
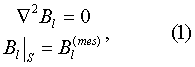
где I=x, y, z - компоненты магнитного поля.
Найденные в результате решения задачи функции 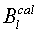 являются гармоническими, как и истинное решение Вl. Из-за присутствия ошибок, а именно ошибок измерения поля, ошибок установки датчиков, конечности числа измерительных точек, вычислительных ошибок, эти функции не равны. Однако их разность
являются гармоническими, как и истинное решение Вl. Из-за присутствия ошибок, а именно ошибок измерения поля, ошибок установки датчиков, конечности числа измерительных точек, вычислительных ошибок, эти функции не равны. Однако их разность 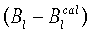 является гармонической функцией. В силу принципа максимального значения эта функция достигает своего максимума и минимума на границе S. Поэтому, если решение краевой задачи найдено точно, разность
является гармонической функцией. В силу принципа максимального значения эта функция достигает своего максимума и минимума на границе S. Поэтому, если решение краевой задачи найдено точно, разность 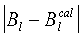 не превосходит ошибки магнитных измерений во всех точках объема Ω:
не превосходит ошибки магнитных измерений во всех точках объема Ω:
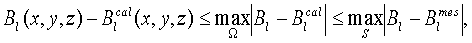
при этом на практике наблюдается быстрое затухание высокочастотной составляющей ошибки, обусловленной случайными ошибками измерений компонент магнитного поля, при перемещении внутрь области, так что интегральная точность определения поля внутри объема, как правило, существенно выше точности измерений компонент на его границе.
Главный недостаток способа первого типа заключается в необходимости измерения всех трех компонент вектора магнитного поля на границе.
В способе второго типа используется возможность представления магнитного поля в виде
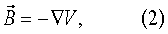
где V - скалярный магнитный потенциал. В терминах функции V могут быть рассмотрены все три краевых задачи.
1) Задача Неймана:
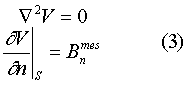
2) Задача Дирихле:
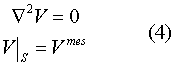
3) Смешанная задача:
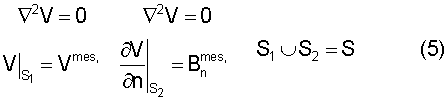
S1 - первый участок границы, на котором задан скалярный магнитный потенциал, S2 - второй участок границы, на котором задана нормальная компонента магнитного поля.
Задача (3) выглядит наиболее привлекательной, т.к. требуется измерить только одну компоненту Bn, нормальную к непрерывной границе S, а не три компоненты вектора 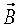 , как в задаче (1). Это приводит к трехкратному уменьшению затрат на проведение измерений.
, как в задаче (1). Это приводит к трехкратному уменьшению затрат на проведение измерений.
Граничные значения скалярного магнитного потенциала (2) в уравнениях (4) и (5) непосредственно не измеряются, но могут быть получены численным интегрированием тангенциальной компоненты магнитного поля Вt по произвольному контуру L, целиком принадлежащему непрерывной границе S и оканчивающемуся в данной точке поверхности:
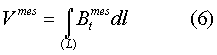
(см. Владимиров B.C. Уравнения математической физики. М.: Наука, 1981). Тем самым граничные условия задач (4) и (5) также связаны с компонентами магнитного поля на границе объема.
Индексом "mes" в уравнениях (1), (3)-(6) указаны значения этих компонент на поверхности S. Обычно это непосредственно измеряемые величины, но они также могут быть получены опосредственно из других измерений, например, интерполяцией, как описано ниже.
Для определения граничных условий, требуемых для решения одной из описанных краевых задач, в способе согласно изобретению вычисляют компоненты магнитного поля в множестве точек непрерывной границы на основании значений компонент, измеренных датчиками в окрестности этой границы, а также координат и ориентации датчиков, используя интерполяцию указанных значений.
Размер окрестности, иными словами, расстояние датчиков от непрерывной границы, определяют эмпирическим путем, исходя из заданной точности определения компонент магнитного поля внутри объема, как проиллюстрировано нижеследующим примером.
Для создания магнитного поля использовали соленоид длиной 1 м, диаметром 30 см с током 1 кА. На расстоянии 2 м от соленоида определили рабочий объем Ω в виде куба с ребром 1 м, границей которого является поверхность, состоящая из шести квадратных граней. Заданная точность измерения компонент магнитного поля на границе была принятой равной 0,01%. Для достижения этой точности необходимо, чтобы датчик, в случае его расположения непосредственно на границе объема, измерял поле с ошибкой 0,01%, или координаты датчика были определены с точностью до 0,1 мм, или датчик был отклонен от нормали на угол, не превышающий 6 минут. В силу принципа максимального значения, упомянутого в дальнейшем, ошибка вычисления поля внутри объема не превосходит ошибку измерения поля на границе, обусловленную совокупностью ошибок установки датчиков, ошибок ориентирования датчиков перпендикулярно грани куба и ошибок измерения поля самими датчиками.
С целью снижения указанных строгих требований при сохранении заданной точности датчики магнитного поля разместили на вспомогательной поверхности, отстоящей от непрерывной поверхности объема на 3 см. При этом ошибка определения координат датчиков составила не более 0,5 мм, отклонение от нормали - не более 30 минут, ошибка измерения поля датчиком - 0,05%, то есть требования были снижены в пять раз.
Точность вычисления компонент магнитного поля в точках непрерывной границы путем решения задачи Неймана для уравнения Лапласа оказалась приблизительно равной заданному значению, то есть 0,01%. В дальнейшем подробно описывается вычисление компонент магнитного поля на непрерывной границе S.
Сначала в окрестности границы S измерили компоненты Вl, Bn или Вt. Далее эти компоненты поля интерполировали любым указанным ниже способом на границу S. Полученные для точек границы S величины 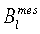 входят в уравнение (1) в качестве граничных значений, величины
входят в уравнение (1) в качестве граничных значений, величины 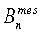 в уравнения (3) или (5), а величины
в уравнения (3) или (5), а величины 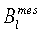 (через интеграл (6)) в уравнения (4) или (5). Измеренные компоненты поля, а также координаты и ориентации датчиков используются исключительно при проведении процедуры интерполяции на границу S, т.е. для получения граничных значений одной из рассмотренных краевых задач.
(через интеграл (6)) в уравнения (4) или (5). Измеренные компоненты поля, а также координаты и ориентации датчиков используются исключительно при проведении процедуры интерполяции на границу S, т.е. для получения граничных значений одной из рассмотренных краевых задач.
На фиг.2а приведен пример линейной интерполяции, в котором используют показания четырех датчиков, установленных по два на вспомогательных поверхностях с образованием тетраэдра. Значения интерполируют в точку О непрерывной границы, расположенную внутри тетраэдра, или экстраполируют в точку Q границы, расположенную вне тетраэдра. Понятно, что линейная интерполяция требует по меньшей мере четыре точки, не лежащие в одной плоскости, в которых производят измерения компонент магнитного поля.
На фиг.2б и 2в приведены примеры квадратичной и кубической интерполяции, где использованы значения компонент, полученные в восьми точках двух поверхностей и двадцати семи точках трех поверхностей. Интерполяционные формулы для разных конечных элементов хорошо известны из литературы (Л.Сагерлинд. Применение метода конечных элементов, М.: Мир, 1979; Р.Галахер. Метод конечных элементов: Основы, М.: Мир, 1984).
Далее на примере линейной интерполяции (фиг.2а) показано вычисление компонент магнитного поля в точке непрерывной границы замкнутого объема на основании значений компонент магнитного поля, измеренных в четырех точках двух вспомогательных поверхностей.
Для произвольной скалярной функции f(x, y, z) можно написать линейное выражение:
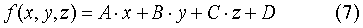
коэффициенты которого определяются по известным значениям функции в четырех точках fi=f(xi, yi, zi), i=1, 2, 3, 4, не лежащих в одной плоскости. Пусть известны координаты точки интерполяции (x0,y0,z0), лежащей внутри образованного этими точками тетраэдра. Тогда значение f0 функции в этой точке может быть найдено подстановкой координат в формулу (7).
Если вместо функции f последовательно подставить компоненты магнитного поля Вx,Вy,Вz, или нормальную компоненту Bn, то данный алгоритм позволяет вычислить компоненты поля в точке интерполяции.
Этот же алгоритм применяется для задачи экстраполяции, но здесь точка находится вне объема, поэтому ошибка обычно больше. Поэтому использование интерполяции всегда более предпочтительно, чем использование экстраполяции, иначе называемой внешней интерполяцией.
Интерполяции более высокого порядка соответствуют различные выражения, отличающиеся от (7) присутствием производных более высокого порядка. При этом количество вспомогательных поверхностей, по которым проводится интерполяция (экстраполяция), может быть как две, так и более (Р.Галахер. "Метод конечных элементов: Основы", М.: Мир, 1984).
На фиг.3а и 3б приведены примеры гладкой и кусочно-гладкой границы замкнутого объема и две вспомогательные поверхности, одна из которых находится внутри объема, а другая - снаружи границы. Граница по фиг.3б содержит линию излома, показано, как должны располагаться датчики около такой линии, чтобы можно было применять интерполяцию данных и избежать экстраполяции.
Интерполяция посредством решения уравнения Лапласа проиллюстрирована на фиг.4а и 4б. В этом альтернативном варианте компоненты магнитного поля в множестве точек непрерывной границы вычисляют, решая задачу Дирихле или Неймана для уравнения Лапласа с использованием в качестве граничных условий значений компонент магнитного поля, измеренных датчиками 1, расположенными на одной наружной вспомогательной поверхности (фиг.4а) или двух вспомогательных поверхностях (фиг.4б), охватывающих непрерывную границу S. Показано разбиение области, ограниченной вспомогательной поверхностью и непрерывной границей или двумя вспомогательными поверхностями, на конечные элементы, более детально представленные на фиг.2а и 2б.
Вычисленные компоненты далее используют в качестве граничных условий при решении уравнения Лапласа для всего замкнутого объема. При этом, в силу принципа максимального значения (см., например, А.Н.Тихонов, А.А.Самарский. "Уравнения математической физики", М. Наука, 1972), ошибки вычисления компонент магнитного поля на непрерывной границе будут меньше ошибок измерения компонент поля на вспомогательных поверхностях.
Возможно исключение внутренней вспомогательной поверхности, тогда решение уравнения Лапласа при разбиении области на более мелкие элементы также приводит к уменьшению ошибок вычисления поля на непрерывной границе. В этом случае фактически решается одно уравнение Лапласа, но с нерегулярным разбиением области на конечные элементы.
При наличии симметрии границы объема, например вращательной или трансляционной, датчики могут быть установлены на подвижной рамке с разделением на две группы. Рамку приводят в движение таким образом, что каждая группа датчиков перемещается через множество точек соответствующей поверхности для измерения компонент магнитного поля, охватывая при этом границу объема. В результате значительно уменьшается требуемое количество датчиков. При этом интерполяция может производиться любым из двух указанных выше способов, т.е. полиномами разной степени или решением уравнения Лапласа, в результате которого получают более точные граничные значения.
На фиг.5а-5г показаны примеры замкнутых объемов и их границ, которые могут быть охвачены датчиками при перемещении подвижной рамки: прямоугольный параллелепипед и перемещаемая по его ребрам рамка в виде бруска с двумя рядами датчиков; цилиндр или конус и вращаемая вокруг его оси П-образная рамка; цилиндр или конус и вращаемая рамка в виде смещенного прямоугольника; цилиндр или конус и вращаемая трапециевидная рамка.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ДЕФЕКТОВ ИЗГОТОВЛЕНИЯ, СБОРКИ И УСТАНОВКИ МАГНИТНЫХ СИСТЕМ | 2009 |
|
RU2431859C2 |
| СПОСОБ НЕИНВАЗИВНОГО ЭЛЕКТРОФИЗИОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ СЕРДЦА | 2008 |
|
RU2409313C2 |
| СПОСОБ НЕИНВАЗИВНОГО ЭЛЕКТРОФИЗИОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ СЕРДЦА | 2008 |
|
RU2435518C2 |
| УСТРОЙСТВО ВЫДЕЛЕНИЯ КОНТУРОВ ОБЪЕКТОВ НА ТЕКСТУРИРОВАННОМ ФОНЕ ПРИ ОБРАБОТКЕ ЦИФРОВЫХ ИЗОБРАЖЕНИЙ | 2013 |
|
RU2522044C1 |
| СПОСОБ СЖАТИЯ ИЗОБРАЖЕНИЯ | 2012 |
|
RU2500067C2 |
| СПОСОБ ВОССТАНОВЛЕНИЯ РЕЛЬЕФА МОРСКОГО ДНА ПРИ ИЗМЕРЕНИИ ГЛУБИН ПОСРЕДСТВОМ ГИДРОАКУСТИЧЕСКИХ СРЕДСТВ | 2011 |
|
RU2466426C1 |
| УСТРОЙСТВО для МОДЕЛИРОВАНИЯ ГИДРОФИЗИЧЕСКИХ | 1973 |
|
SU369580A1 |
| СПОСОБ ДЕТЕКТИРОВАНИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ТЕРАГЕРЦОВОМ ДИАПАЗОНЕ | 2015 |
|
RU2599332C1 |
| УСТРОЙСТВО для РЕШЕНИЯ УРАВНЕНИЯ ЛАПЛАСА | 1973 |
|
SU370615A1 |
| ОСНОВАННЫЕ НА ПРИМЕНЕНИИ КОМПЬЮТЕРА ФОРМИРОВАНИЕ И ПРОВЕРКА ТРЕНИРОВОЧНЫХ ОБРАЗОВ, ПРЕДНАЗНАЧЕННЫХ ДЛЯ МНОГОТОЧЕЧНОГО ГЕОСТАТИСТИЧЕСКОГО АНАЛИЗА | 2006 |
|
RU2391686C2 |
Изобретение относится к картографированию магнитного поля в объеме, не содержащем источников магнитного поля и ферромагнитных материалов. Согласно способу, для определения компонент магнитного поля внутри замкнутого объема, размещают датчики магнитного поля в окрестности, но вне границы объема, измеряют координаты и ориентацию датчиков, а также значения компонент магнитного поля в точках расположения датчиков, и вычисляют компоненты магнитного поля в множестве точек границы объема на основании измеренных значений компонент, координат и ориентации датчиков. Размеры окрестности выбирают, исходя из заданной точности определения компонент магнитного поля внутри замкнутого объема. Краевую задачу решают с использованием вычисленных компонент в качестве граничных условий. Благодаря переходу от прецизионной установки датчиков к прецизионному измерению, снижаются требования к точности установки и ориентации датчиков, упрощается измерительная процедура. 2 н. и 15 з.п. ф-лы, 12 ил.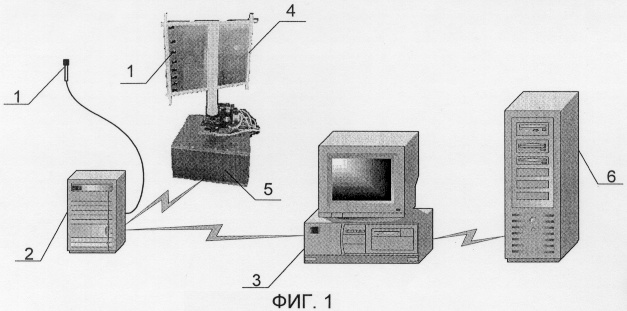
| US 6377041 А, 23.04.2002 | |||
| US 5644229 А, 01.07.1997 | |||
| US 5453686 А, 26.09.1995 | |||
| JP 2002039997 А, 06.02.2002 | |||
| JP 2000003354 А, 07.01.2000 | |||
| Матричный преобразователь магнитных полей к структуроскопу | 1979 |
|
SU859904A1 |
Авторы
Даты
2006-03-10—Публикация
2004-04-08—Подача