Изобретение относится к вычислительной техники и, в частности, к модулярным нейрокомпьютерным средствам и предназначено для выполнения операций округления и масштабирования над числами, представленными в системе остаточных классах (СОК).
Известно устройство для округления чисел в системе остаточных классов (А.С. СССР №398949, М. кл.3 G 06 F 7/52, 1973 г.), содержащее входной регистр, блоки хранения констант, сумматоры констант по основаниям рабочего и дополнительного диапазона, блоки вычисления неточных рангов, блок коррекции округления.
Недостатком данного устройства является большой объем оборудования и низкая скорость округления числа.
Наиболее близким к данному изобретению техническим решением является устройство для округления чисел в системе остаточных классов (А.С. СССР №651305, М. кл.3 G 06 F 7/52 1982 г.), содержащее входной регистр, первую и вторую группу из n-шифраторов (n - количество оснований системы остаточных классов), первый и второй накапливающие сумматоры, группу из n-сумматоров по модулю pi (pi - основания системы остаточных классов), выходы которых являются выходами устройства, входы входного регистра являются информационными входами устройства.
Недостатком устройства является большой объем оборудования, низкая скорость округления числа и суженное функциональное назначение.
Целью изобретения является уменьшение объема оборудования, повышение скорости округления и масштабирования чисел, расширение функциональных возможностей.
Поставленная цель достигается тем, что нейронная сеть для округления и масштабирования чисел, представленных в системе остаточных классов, содержащая входной слой 3 с нейронами 2, НСКК 4, состоящей из нейронной сети конечного кольца по наибольшему модулю 13 и нейронной сети конечного кольца по коэффициенту масштабирования 14, нейронных сетей конечного кольца по модулям СОК 5, нейронной сети конечного кольца по модулям СОК 6, коэффициента масштабирования К 7. В основе изобретения лежит формируемая нейронная сеть прямого распространения. Структура нейронной сети зависит от внешних параметров, которые определяются модулями СОК и коэффициентами масштабирования. Посредствам весовых коэффициентов, коэффициента масштабирования и НСКК нейронная сеть осуществляет округление и масштабирование числа. Функционирование нейронной сети зависит от весовых коэффициентов между слоями нейронов, коэффициента масштабирования, которые являются константами и определяются заранее. Так как сеть формируемая, весовые коэффициенты сети постоянны, поэтому режим обучения сети не используется.
Введем следующие обозначения: p1, р2, ..., pn-основания СОК, 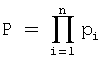 - диапазон системы, при этом число А записывается в СОК в следующей форме: А=(α1, α2, ..., αn), где
- диапазон системы, при этом число А записывается в СОК в следующей форме: А=(α1, α2, ..., αn), где 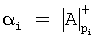 - наименьший неотрицательный остаток от деления целого числа А на основание pi.
- наименьший неотрицательный остаток от деления целого числа А на основание pi.
Как известно, замена позиционной системы на СОК позволяет существенно (порой в десятки раз) повысить выполнение таких операций, как умножение, сложение и вычитание. Однако реализация операции масштабирования в СОК (она связана с делением) вызывает существенные затруднения.
Масштабирование предполагает операцию деления, поэтому можно выбрать такой делитель, который позволяет осуществить легкую реализацию. Например, в двоичной системе счисления выбираются коэффициенты масштабирования, являющиеся степенями двойки. Масштабирование в СОК реализуется наиболее легко, когда коэффициент масштабирования есть один из модулей системы или является произведением нескольких модулей. Известны методы деления, но все они основаны на выполнении ряда последовательных операций. В данном изобретении предлагается распараллеливание операций при реализации округления и масштабирования.
Фундаментальной проблемой, возникающей при реализации масштабирования, является то, что в отличие от сложения и умножения СОК не является замкнутой относительно операции масштабирования. Предположим, что процедура масштабирования осуществляется с округлением путем отбрасывания некоторой части числа. Пусть Х является входной величиной, У- выходной, а К - коэффициент масштабирования, тогда
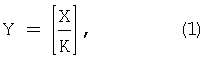
где [•] означает целочисленное значение. Это можно переписать в виде
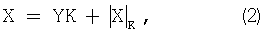
или
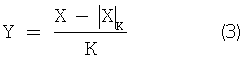
Однако для быстрого определения 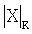 требуется, чтобы К являлось произведением некоторых модулей. Таким образом, алгоритм высокоскоростного масштабирования должен выводить коэффициент масштабирования из одного или произведения нескольких модулей.
требуется, чтобы К являлось произведением некоторых модулей. Таким образом, алгоритм высокоскоростного масштабирования должен выводить коэффициент масштабирования из одного или произведения нескольких модулей.
Если К=р1, тогда 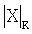 можно получить непосредственно из первого остатка; если
можно получить непосредственно из первого остатка; если 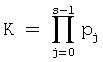 при s>1, то для определения
при s>1, то для определения 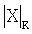 используется итеративный процесс масштабирования.
используется итеративный процесс масштабирования.
Рассмотрим метод масштабирования числа Х на число К с отбрасыванием остатка в предположении, что К - целое положительное число, попарно простое с р1,р2,...,рn. Если Х делится на К без остатка, то операция масштабирования является модульной операцией и сравнительно просто реализуется в табличном варианте. Поэтому перед масштабированием в качестве вспомогательной операции выполняют операцию нахождения числа 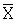 , которое делится на К без остатка. Операция нахождения
, которое делится на К без остатка. Операция нахождения 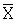 заменяет операцию отбрасывания остатка от деления.
заменяет операцию отбрасывания остатка от деления.
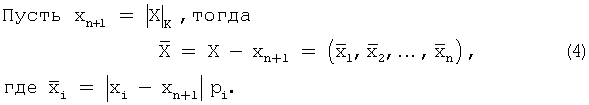
Из (4) видно, что 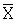 делится без остатка на К. На основании того, что
делится без остатка на К. На основании того, что
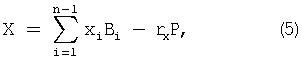
где rx - ранг числа; 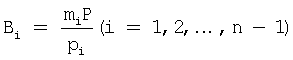 - ортогональные базисы;
- ортогональные базисы;
mi - целое положительно число, удовлетворяющее сравнению
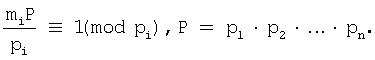
На основе выражения (5) можно записать выражения для xn+1 и rх:
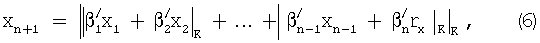
где 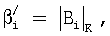 для i=1,2,...,n-1;
для i=1,2,...,n-1; 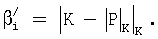
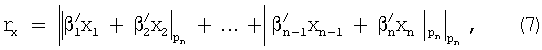
где 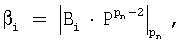 для i=1,2,...,n-1;
для i=1,2,...,n-1; 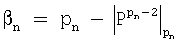
Итак, метод масштабирования числа Х на число K с отбрасыванием остатка можно представить как последовательность следующих операций:
1. Определение ранга числа rх, выражение (7).
2. Определение xn+1, выражение (6).
3. Вычисление 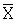 , выражение (4).
, выражение (4).
4. Нахождение масштабированного числа 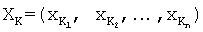 от деления
от деления 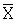 на К.
на К.
При этом нахождение 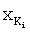 осуществляется с помощью совокупности модульных операций:
осуществляется с помощью совокупности модульных операций:
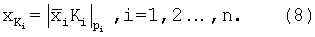
В случае если pi - простое число
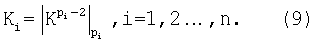
Пример. Пусть задана система оснований р1=2, р2=3, р3=5, р4=7. Требуется число X=(1,2,3,2) промасштабировать числом K=11. В соответствии с выражением (5) и (7) определяем B1=15, В2=10, В3=6, Р=30, а также β1=4, β2=5, β3=3, β4=3. Следовательно, выражение (7) в условиях примера примет вид
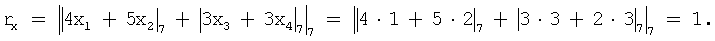
Далее находим  и затем остаток от деления Х на константу К - величину xn+1 по формуле (6):
и затем остаток от деления Х на константу К - величину xn+1 по формуле (6):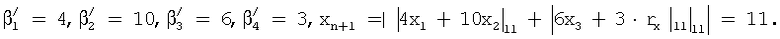
По формуле (4) находим  =(1,2,3,2)-(1,1,1,1)=(0,1,2,1). На основе формулы (9) определяем К1=1, К2=2, К3=1 и К4=2 и далее определяем
=(1,2,3,2)-(1,1,1,1)=(0,1,2,1). На основе формулы (9) определяем К1=1, К2=2, К3=1 и К4=2 и далее определяем 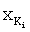 по формуле (8):
по формуле (8):
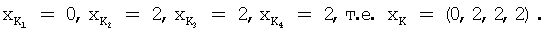
Полученное масштабированное число можно представить в сокращенной либо в расширенной системе оснований.
Предложенный метод округления и масштабирования чисел отличается от известных тем, что его реализация полностью состоит из модульных операций и его можно легко реализовать нейронными сетями конечного кольца, которые выполняют вычисления по модулю pi, где 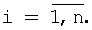
На чертеже представлена структура нейронной сети для реализации округления и масштабирования чисел, представленных в СОК.
Принцип работы данного изобретения излагается ниже. Изобретением является формируемая нейронная сеть прямого распространения, состоящая из совокупности нейронных сетей конечного кольца. Информация в виде остатков (х1, х2,..., хn) 1 поступает на вход нейронов 2 нейронной сети (нейроны 2 входного слоя 3), масштабированное число 8, выходы 17, (xK1, xK2,..., хKn) появляется в выходном слое нейронов 16 НСКК 6.
Входной слой 3 используется для сбора входов числа (х1, х2,..., хn) 1 (нейроны 2), которые масштабируются. Нейронная сеть конечного кольца определения ранга числа (НСКК 4), нейрон 13, определяет ранг числа, реализует вычислительную модель (7). Нейронная сеть конечного кольца вычисления остатка по основанию n+1 (НСКК 4), нейрон 14, реализует вычислительную модель (6). Между входным слоем 3 и входом НСКК 4 (нейрон 13) весовые коэффициенты win 18 определяются значениями βi выражением (7), а входом НСКК 4, нейрон 14, весовые коэффициенты wiK 9 определяются значениями βi' выражения (6), a wnK 10 определяется выражением (7). НСКК 4 (нейрон 13) реализует вычислительную модель (7), а НСКК 4 (нейрон 14) реализует вычислительную модель (6). Значения 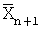 в дополнительном коде
в дополнительном коде 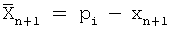 с выхода НСКК 4 (нейрон 14) поступают на вход нейронной сети конечного кольца вычисления разности чисел между входными остатками и остатком по основанию n+1 (НСКК 5), нейроны 15, весовые коэффициенты wi 19 между входным слоем 3 (нейроны 2) равны 1. НСКК 5 (нейроны 15) выполняет вспомогательную операцию нахождения числа
с выхода НСКК 4 (нейрон 14) поступают на вход нейронной сети конечного кольца вычисления разности чисел между входными остатками и остатком по основанию n+1 (НСКК 5), нейроны 15, весовые коэффициенты wi 19 между входным слоем 3 (нейроны 2) равны 1. НСКК 5 (нейроны 15) выполняет вспомогательную операцию нахождения числа 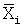 , реализуют вычислительную модель (4), при этом операция вычитания заменяется операцией сложения в дополнительном коде. Значения
, реализуют вычислительную модель (4), при этом операция вычитания заменяется операцией сложения в дополнительном коде. Значения 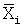 с выхода НСКК 5 (нейроны 15) и значения К (вход 7) поступают на вход нейронной сети конечного кольца вычисления масштабированных остатков (НСКК 6), нейроны 16. Весовые коэффициенты
с выхода НСКК 5 (нейроны 15) и значения К (вход 7) поступают на вход нейронной сети конечного кольца вычисления масштабированных остатков (НСКК 6), нейроны 16. Весовые коэффициенты 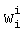 12 и wK 20 равны единице. Масштабированное число 8 появляется на выходе НСКК 6 (выходы 17). Операция масштабирования выполняется за 4 цикла синхронизации и не зависит от количества модулей, что и отличает это изобретение от известного, где операция округления зависит от количества модулей СОК. Изобретение предназначено для быстрого округления и масштабирования чисел в модулярных нейрокомпьютерных системах.
12 и wK 20 равны единице. Масштабированное число 8 появляется на выходе НСКК 6 (выходы 17). Операция масштабирования выполняется за 4 цикла синхронизации и не зависит от количества модулей, что и отличает это изобретение от известного, где операция округления зависит от количества модулей СОК. Изобретение предназначено для быстрого округления и масштабирования чисел в модулярных нейрокомпьютерных системах.
| название | год | авторы | номер документа |
|---|---|---|---|
| НЕЙРОННАЯ СЕТЬ УСКОРЕННОГО МАСШТАБИРОВАНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2007 |
|
RU2359325C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2006 |
|
RU2318239C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННОЙ ХАРАКТЕРИСТИКИ РАНГА ЧИСЛА, ПРЕДСТАВЛЕННОГО В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2271569C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ, ЛОКАЛИЗАЦИИ И ИСПРАВЛЕНИЯ ОШИБОК В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2301442C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ПОЛИАДИЧЕСКОГО КОДА В КОД СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2258257C2 |
| НЕЙРОННАЯ СЕТЬ С ПОРОГОВОЙ (k, t) СТРУКТУРОЙ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2380751C1 |
| НЕЙРОННАЯ СЕТЬ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2008 |
|
RU2400813C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
Заявленное изобретение относится к вычислительной техники и, в частности, к модулярным нейрокомпьютерным средствам. Техническим результатом является уменьшение объема оборудования, повышение скорости округления чисел и расширения функциональных возможностей. Для этого заявленная сеть содержит входной слой нейронов, нейронную сеть конечного кольца определения ранга числа, нейронную сеть конечного кольца вычисления остатка по основанию n+1, n-нейронные сети конечного кольца вычисления масштабированного числа, нейронную сеть вычисления разности чисел между входными остатками и остатком по основанию. 1 ил.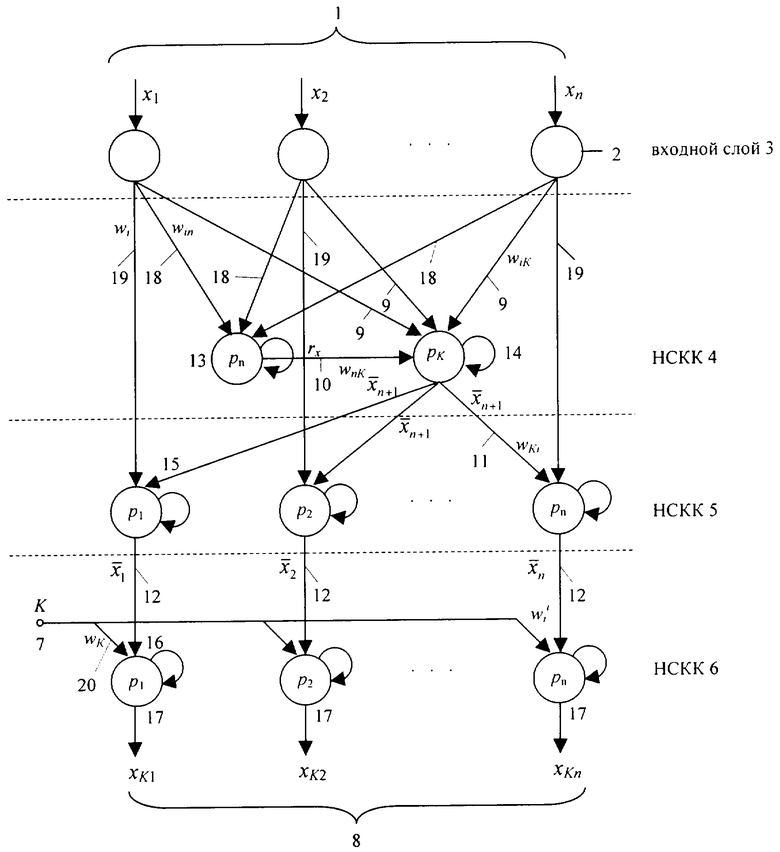
Нейронная сеть для округления и масштабирования чисел, представленных в системе остаточных классов, содержащая входной слой нейронов, нейронную сеть конечного кольца определения ранга числа, нейронную сеть конечного кольца вычисления остатка по основанию n+1, нейронную сеть конечного кольца вычисления разности чисел между входными остатками и остатком по основанию n+1, n-нейронные сети конечного кольца вычисления масштабированного числа, отличающаяся тем, что выходы нейронов входного слоя соединены с нейронами нейронных сетей конечного кольца вычисления ранга числа и остатка по основанию n+1, выход нейронов нейронной сети конечного кольца вычисления ранга числа соединен со входом нейронов нейронной сети вычисления остатка по основанию n+1, выход нейронов нейронной сети конечного кольца вычисления остатка по основанию n+1 соединен с первой группой входов нейронов нейронных сетей конечного кольца вычисления разности чисел между входными остатками и остатком по основанию n+1, вторая группа входов нейронов нейронной сети конечного кольца вычисления разности остатков соединена с выходами нейронов входного слоя, выходы нейронов нейронных сетей конечного кольца вычисления разности остатков соединены с первой группой входов нейронов нейронных сетей конечного кольца вычисления масштабированных остатков, а вторая группа входов нейронов нейронных сетей конечного кольца вычисления масштабированных остатков соединена с входом К-масштабированного коэффициента, масштабируемое число появляется на выходе нейронов нейронных сетей конечного кольца вычисления масштабированных остатков.
| Устройство для округления числа в системе остаточных классов | 1980 |
|
SU951305A1 |
Авторы
Даты
2006-03-10—Публикация
2003-05-26—Подача