Изобретение относится к вычислительной технике и может быть использовано в модулярных нейрокомпьютерах при вычислении позиционных характеристик, необходимых для перевода чисел системы остаточных классов (СОК) в позиционную систему, округления, масштабирования, коррекции ошибок и в других случаях.
Известно устройство для определения ранга числа (А.С. СССР №808950, G 06 F 5/02, 1980 г.), содержащее сумматор по наибольшему модулю, счетчик, блоки умножения на константу, узел сравнения.
Недостатком данного устройства является сложная конструкция и низкое быстродействие.
Наиболее близким к изобретению по технической сущности является устройство для определения ранга числа (А.С. СССР №1125619, G 06 F 5/00, 1984 г.), содержащее блоки умножения на константу, сумматор по наибольшему модулю, элементы ИЛИ.
Недостатками известного устройства являются значительные аппаратные средства и низкое быстродействие.
Целью изобретения является сокращение оборудования и повышение скорости определения ранга числа.
Поставленная цель достигается тем, что устройство для определения ранга числа содержит входной слой нейронной сети 1 с нейронами 4, нейронную сеть конечного кольца (НСКК) 2 с нейронами 5, весовые коэффициенты 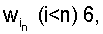 весовые коэффициенты
весовые коэффициенты 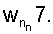 Нейроны 4 входного слоя 1 связаны с нейронами нейронной сети конечного кольца 2 нейронами 5. В основе данного изобретения лежит нейронная сеть прямого распространения для вычисления ранга числа. Структура нейронной сети (см. чертеж) зависит от внешних параметров, которые определяются набором модулей СОК и адаптируются к ним посредствам загрузки весовых коэффициентов и организацией нейронной сети конечного кольца.
Нейроны 4 входного слоя 1 связаны с нейронами нейронной сети конечного кольца 2 нейронами 5. В основе данного изобретения лежит нейронная сеть прямого распространения для вычисления ранга числа. Структура нейронной сети (см. чертеж) зависит от внешних параметров, которые определяются набором модулей СОК и адаптируются к ним посредствам загрузки весовых коэффициентов и организацией нейронной сети конечного кольца.
Посредством весовых коэффициентов и НСКК 2 нейронная сеть осуществляет вычисление ранга числа. Функционирование нейронной сети зависит от весовых коэффициентов между слоями нейронов, являющиеся константами, и определяются заранее перед ее разработкой. В данном изобретении обучение сети не требуется, так как используется формируемая сеть с постоянными весовыми коэффициентами при выбранных модулях системы и в процессе вычисления ранга числа их изменение не происходит.
Число А представляется в СОК набором наименьших неотрицательных остатков (вычетов) α1, α2, ..., αn от деления А на попарно простые числа p1, р2, рn, называемые основаниями (модулями).
При этом число записывается в СОК в следующей форме
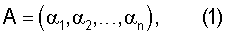
где 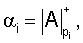 что эквивалентно αi ≡ A mod pi.
что эквивалентно αi ≡ A mod pi.
При этом -Р <А <Р, где Р=p1, p2, ..., pn-1. При выполнении этого условия представление (1) взаимно однозначно с представлением А в позиционной системе счисления, т.е. по (α1, α2, ..., αn) можно определить А. Число А, представленное в СОК, можно восстановить в позиционной системе счисления с помощью выражения
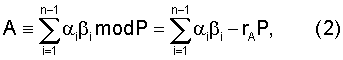
где rA - ранг числа, целое положительное число, показывающее сколько раз диапазон системы был превзойден при переходе от представления числа в системе остаточных классов к его представлению через систему ортогональных базисов;
βi - ортогональные базисы
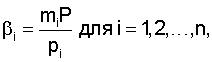
где mi - целое положительное число, называемое весом ортогонального базиса, причем mi должно выбираться таким образом, чтобы имело место следующее сравнение:
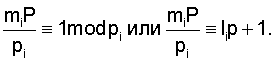
Ввиду малости величины оснований для набора рi можно составить таблицы решений сравнений или решить их методом подбора.
Как видно из выражения (2), для перевода числа А из СОК в позиционную систему счисления необходимо предварительно найти гА. Кроме того, значения rA необходимы и в других случаях, например при масштабировании, округлении и коррекции ошибок в СОК.
Ранг число можно найти следующим образом.
Согласно (1) αn ≡ A mod pn и учитывая (2)
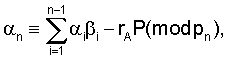
следовательно,
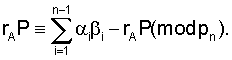
В случае простого рn решения сравнения с помощью теоремы Ферма получим
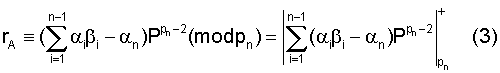
Учитывая, что βi и 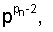 являются константами и не зависят от А,
являются константами и не зависят от А,
выражение (3) можно переписать в более удобной форме, которая облегчает практическую реализацию
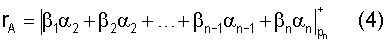
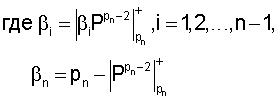
Пример. Пусть задана система оснований p1=2, р2=3, р3=5, рn=7. Требуется найти алгоритм вычисления rA. Согласно (2) и (4)
В1=15, В2=10, В3=6, P=30,
β1,=4, β2=5, β3=6, β4=3.
Следовательно, конкретный алгоритм (4) в условиях примера имеет вид
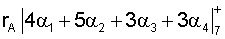
Допустим, что A=17, тогда АСОК (1,2,2,3).
Ранг числа 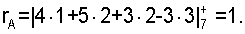
Проведем проверку с использованием выражения (2)
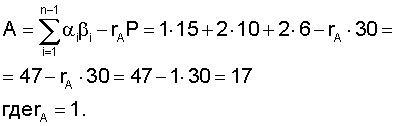
Действительно, при переходе от СОК к позиционной форме диапазон числа был превзойден только один раз, т.к. 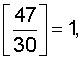
где [·] - целая часть.
Принцип работы данного изобретения излагается ниже. Изобретением является формируемая нейронная сеть прямого распространения. Информация в виде остаточного представления (системы вычетов), выражение (1) поступает на вход 3 нейроны 4, расположенные во входном слое 1, ранг числа появляется в выходном слое нейрона 5 нейронной сети конечного кольца 2.
Между входным слоем 1, нейроны 4 и входом НСКК 2 весовые коэффициенты обозначены  и весовые коэффициенты
и весовые коэффициенты 
Весовые коэффициенты  определяются выражением
определяются выражением 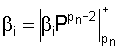 и
и 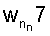 определяется выражением
определяется выражением 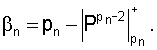
Нейронная сеть конечного кольца 2 реализует вычислительную модель (4). Время определения ранга числа определяется одним тактом синхронизации, чем и достигается цель изобретения.
Определенные внешние параметры заданы в весовых коэффициентах и нейронной сети конечного кольца и хранятся в памяти. Из памяти по требованию в зависимости от изменения системы набора модулей СОК загружает новые весовые коэффициенты, соответственно определяя структуру нейронной сети (см. чертеж).
Изобретение предназначено для определения ранга числа в случаях определения позиционного представления числа, округления, масштабирования, коррекции ошибок и других случаях.
Время вычисления ранга числа определяется одним циклом синхронизации, а в известных устройствах n - циклом синхронизации.
| название | год | авторы | номер документа |
|---|---|---|---|
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ, ЛОКАЛИЗАЦИИ И ИСПРАВЛЕНИЯ ОШИБОК В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2301442C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ПОЛИАДИЧЕСКОГО КОДА В КОД СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2258257C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОКРУГЛЕНИЯ И МАСШТАБИРОВАНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2003 |
|
RU2271570C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
| АДАПТИВНАЯ ПАРАЛЛЕЛЬНО-КОНВЕЙЕРНАЯ НЕЙРОННАЯ СЕТЬ ДЛЯ КОРРЕКЦИИ ОШИБОК | 2003 |
|
RU2279131C2 |
| НЕЙРОННАЯ СЕТЬ С ПОРОГОВОЙ (k, t) СТРУКТУРОЙ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2380751C1 |
| НЕЙРОННАЯ СЕТЬ УСКОРЕННОГО МАСШТАБИРОВАНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2007 |
|
RU2359325C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК НЕПОЗИЦИОННОГО КОДА | 2003 |
|
RU2257615C2 |
Изобретение относится к вычислительной технике и может быть использовано в модулярных нейрокомпьютерах. Техническим результатом является сокращение количества оборудования и повышение скорости определения ранга числа. Для этого нейронная сеть содержит взаимосвязанные между собой входной слой нейронов и нейронную сеть конечного кольца. 1 ил.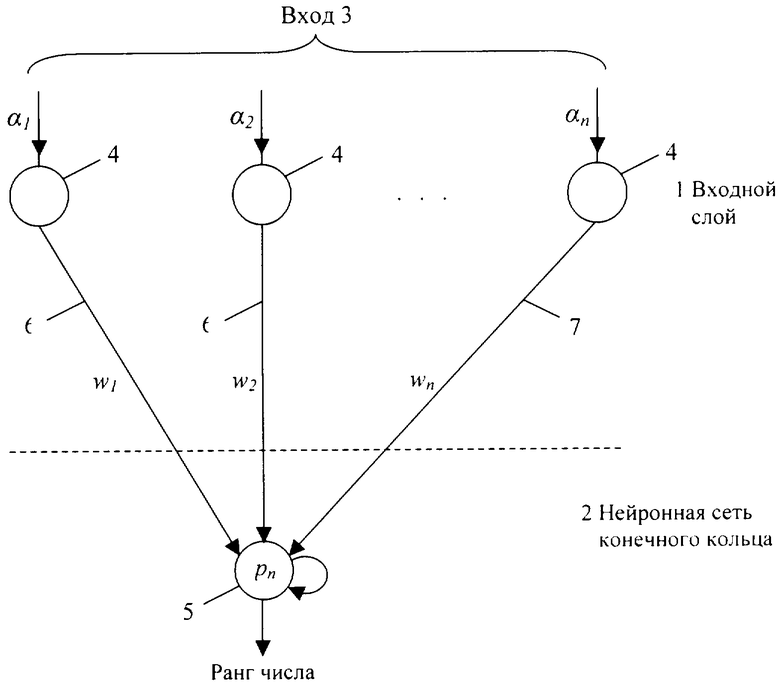
Нейронная сеть для вычисления позиционной характеристики ранга числа, представленного в системе остаточных классов, содержит входной слой нейронов, предназначенный для приема чисел системы остаточных классов, нейронную сеть конечного кольца, отличающаяся тем, что выходы нейронов входного слоя с весовыми коэффициентами 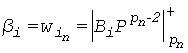 для i<n и
для i<n и 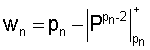 для i=n соединены с входами нейронной сети конечного кольца, реализующей вычислительную модель rA = |β1α1 + β2α2 + ... + βn-1 αn-1 + βn αn|
для i=n соединены с входами нейронной сети конечного кольца, реализующей вычислительную модель rA = |β1α1 + β2α2 + ... + βn-1 αn-1 + βn αn|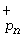 , выходы которой являются рангом числа, где Bi - величина ортогональных базисов, αi - остаток числа, pn - основание системы счисления, P - диапазон представления чисел, rA - ранг числа.
, выходы которой являются рангом числа, где Bi - величина ортогональных базисов, αi - остаток числа, pn - основание системы счисления, P - диапазон представления чисел, rA - ранг числа.
| Устройство для определения ранга числа | 1983 |
|
SU1125619A1 |
Авторы
Даты
2006-03-10—Публикация
2003-05-26—Подача