Изобретение относится к градиентной оптике и может быть использовано в волоконной оптике и оптическом приборостроении для создания коллиматоров, объективов, биноклей, эндоскопов, устройств согласования волоконных световодов с полупроводниковыми лазерами и т.д.
Известна телескопическая градиентная линза, выполненная из материала с радиальным градиентом показателя преломления /ПП/ n(y), ограниченная первой и второй плоскими преломляющими поверхностями, перпендикулярными оптической оси, характеризующаяся зависимостью траектории хода лучей y1(z) в материале линзы (при нормальном падении на первую плоскую поверхность параллельного пучка лучей), имеющая длину периодичности хода лучей L и толщину, кратную L/2 /1/.
В известной линзе входной параллельный пучок, проходя через линзу, периодически самофокусируется в точках на оптической оси линзы и на выходе вновь становится параллельным.
Однако получающийся на выходе параллельный пучок имеет такое же сечение, как и входной, и, таким образом, увеличение известной линзы (в зависимости от ее толщины, кратной L/2) может быть либо +1, либо -1. В результате известная линза практически может лишь передавать изображение без его увеличения, что и является ее основным недостатком. Кроме того, минимальная длина известной линзы не может быть меньше L/2, учитывая свойство внутренней самофокусировки пучка, что также является недостатком, ограничивающим применение известной линзы.
Задача изобретения - создание телескопической градиентной линзы с увеличением, отличным от ±1, и, кроме того, со сниженной минимально толщиной линзы.
Решение поставленной задачи достигается тем, что первая и/или вторая преломляющие поверхности выполняются в виде поверхностей вращения с образующей функцией (далее - образующей) определенного вида и с учетом ограничений на минимально необходимую толщину линзы.
Для этого в телескопической градиентной линзе, выполненной из материала с радиальным градиентом ПП n(y), ограниченной первой и второй преломляющими поверхностями вращения, причем первая поверхность выполнена плоской, характеризующейся зависимостью траектории хода лучей y1(z) в материале линзы, имеющей длину периодичности хода лучей L, вторая преломляющая поверхность выполнена выпуклой с образующей, определяемой из уравнения
где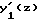 - первая производная от y1(z);
- первая производная от y1(z);
z -оптическая ось линзы;
а толщина линзы с выбирается в зависимости от требуемого увеличения из соотношения ,
,
где
k = 0, 1, 2, ...
На фиг. 1 показана оптическая схема плоско-выпуклой телескопической градиентной линзы и условные обозначения для расчета хода лучей.
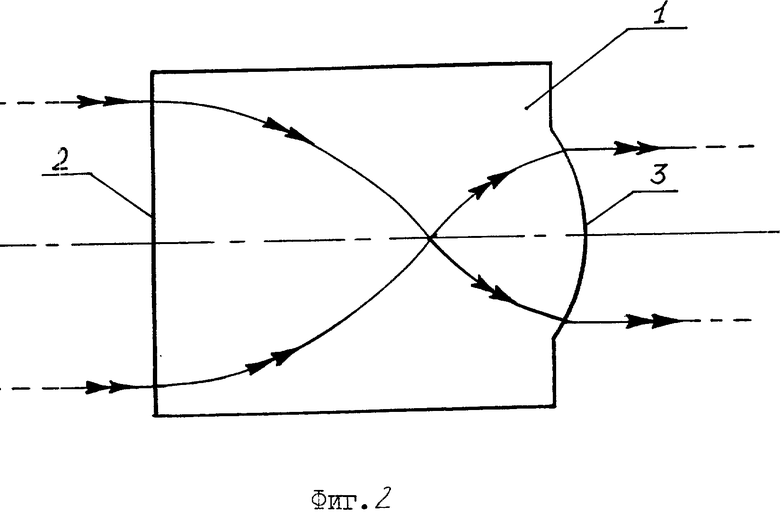
На фиг. 2 показана оптическая схема плоско-выпуклой телескопической градиентной линзы.
На фиг. 1 оптический элемент из материала с радиальным градиентом ПП n(y) находится в однородной среде с ПП n1 = 1 (например, воздух) и ограничен входной плоской (z = 0) (не показана) и выходной поверхностью вращения с образующей y2(z), причем толщина элемента вдоль оси равна c.
При падении на входную плоскость элемента из однородной среды параллельного пучка излучения, направление которого совпадает с оптической осью z элемента, внутри элемента пучок периодически самофокусируется в точках на оси с координатами:
где
L - длина периодичности;
m = 0, ±1, ±2, ...,
а траектория хода каждого луча в пучке в меридиональной плоскости описывается зависимостью y1(z).
Луч с траекторией хода y1(z) преломляется на выходной поверхности в точке A и далее идет параллельно оси z. Нормаль N к поверхности в точке A образует с касательной к траектории луча y1(z) угол падения ε .
Угол ϕ является углом наклона касательной к образующей y2(z) в точке A. Угол ε′ является углом преломления, а β - это угол наклона касательной к траектории хода луча y1(z) в точке преломления. Отрезок h - это высота луча после преломления на выходной поверхности.
Рассмотрение хода лучей в соответствии со случаем преломления, показанным на фиг. 1, дает в результате уравнение вида .
.
Поскольку полученное уравнение зависит от строго взаимосвязанных функций n(y) и y1(z), общее решение его определить не представляется возможным. Однако можно найти его решение для известных зависимостей n(y) и y1(z) аналитически или численно. Для y2(z) должно быть справедливо
y2(c) = 0, (2)
а также желательно, чтобы выполнялось .
.
Причем для выполнения условий (2) и (3) величины z и c должны быть отрицательными.
Таким образом, подавая на входную плоскую поверхность оптического элемента падающий нормально параллельный пучок и применяя на выходе преломляющую поверхность с образующей (1) при выполнении начального условия (2), можно получить на выходе также параллельный пучок, но другого сечения, и образовывать телескопическую систему (линзу). Увеличение такой линзы будет зависеть, очевидно, от выбранной величины c.
Рассмотрим для иллюстрации известные распределения ПП и связанные с ними траектории хода лучей y1(z).
Так называемое "идеально фокусирующее" или гиперсекансное распределение ПП имеет вид
n(y) = n0 • schay,
где
n0 - значение ПП на оси;
a - постоянная.
Ход лучей внутри такого элемента со входным плоским торцем, перпендикулярным оптической оси z, при нормальном падении на входную плоскость параллельного пучка излучения, описывается уравнением .
.
где
b - высота входа луча над осью z.
Тогда производная будет равна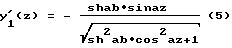 .
.
Зависимость ПП n*(z) в каждой точке траектории y1(z) можно определить в виде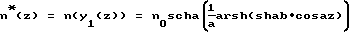 ,
,
или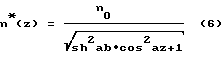 .
.
Подставляя (5) и (6) в уравнение (1), получим после преобразований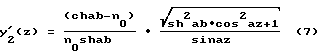
а интегрирование дает следующий вид образующей ,
,
где .
.
При этом значения z и c отрицательны и ограничены соотношением
Аналогично для параболического распределения ПП, при котором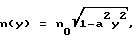 ,
,
производная будет равна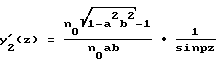 .
.
Интегрирование дает образующую .
.
Значения z и c отрицательны и лежат в пределах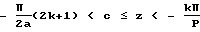 ,
,
а высота входа лучей ограничена .
.
Таким образом, для обоих рассмотренных выше известных распределений ПП и траекторий хода лучей в них принципиально возможно получить телескопические системы (линзы) с заданным увеличением, отличным от ±1. В таких телескопических линзах, однако, присутствует сферическая аберрация, которая может быть строго исправлена (так же, как и у телескопических линз из однородного материала) в общем случае лишь для одной заданной высоты входного луча.
При использовании преломляющих поверхностей можно получить телескопические градиентные линзы с различным увеличением.
Для реализации телескопической градиентной линзы с требуемой величиной увеличения из материала с известным распределением ПП n(y) вначале рассчитывают образующие y
Однако затруднение может вызвать формообразование поверхности вращения с образующими сложного вида. Поэтому для целей изготовления целесообразно сначала аппроксимировать y
Возможно также применение известной технологии алмазного точения на станке с ЧПУ и воздушной или гидравлической подвеской вала с заготовкой для вытачивания сложного профиля образующих y
При изготовлении преломляющих поверхностей, образующие которых задаются в аппроксимированном виде, увеличиваются различные аберрации телескопической линзы, которые будут тем больше, чем больше отклонения реально изготовленных поверхностей от идеальных теоретически рассчитанных профилей, что следует иметь в виду при дальнейшем применении линзы.
Используется предлагаемая телескопическая градиентная линза обычным образом. На первую (входную) поверхность 2 линзы 1 (фиг. 2) подается параллельный пучок излучения (ход лучей показан двойными стрелками), причем оптическая ось линзы должна быть параллельна направлению распространения пучка излучения. После преломления на первой поверхности и прохождения внутри пучок излучения, преломляясь на второй, выходной поверхности 3 линзы, выходит из нее, оставаясь параллельным, но имея меньшее сечение.
Применение телескопических градиентных линз может упростить решение ряда задач. Так, например, использование телескопической линзы в виде волоконного световода в эндоскопе на выходе позволит получить уже увеличенное изображение исследуемого участка. Применение телескопической градиентной линзы с заданным увеличением совместно с полупроводниковым лазером позволит получить на выходе коллимированный пучок излучения с требуемыми характеристиками расходимости, причем длина телескопической линзы при этом будет принципиально меньше, чем у обычно применяемого для этой цели градана длиной L/4, что может уменьшить габариты оптической системы в целом.
| название | год | авторы | номер документа |
|---|---|---|---|
| АПЛАНАТИЧЕСКАЯ ГРАДИЕНТНАЯ ЛИНЗА | 2005 |
|
RU2288490C1 |
| ГРАДИЕНТНАЯ ЛИНЗА | 2005 |
|
RU2289830C1 |
| ГРАДИЕНТНАЯ ЛИНЗА С АПЛАНАТИЧЕСКИМИ И ТЕЛЕСКОПИЧЕСКИМИ СВОЙСТВАМИ | 2013 |
|
RU2529775C1 |
| ГРАДИЕНТНАЯ ЛИНЗА (ВАРИАНТЫ) | 2002 |
|
RU2222819C2 |
| Апланатическая градиентная линза | 1988 |
|
SU1569764A1 |
| Градиентная линза | 1987 |
|
SU1500964A1 |
| Градиентная линза | 1985 |
|
SU1337861A1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ТРЕХМЕРНЫХ ОПТИЧЕСКИХ МИКРОСТРУКТУР С ГРАДИЕНТОМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ ДВУХФОТОННОЙ ЛИТОГРАФИИ | 2023 |
|
RU2826645C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ГЕНЕРИРОВАНИЯ ДАННЫХ, ХАРАКТЕРИЗУЮЩИХ ПИКСЕЛЬНЫЙ ПУЧОК | 2016 |
|
RU2734115C2 |
| УСТРОЙСТВО С ЛАЗЕРОМ ДЛЯ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ | 1997 |
|
RU2162617C2 |
Использование: в оптическом приборостроении. Телескопическая градиентная линза выполнена из материала с радиальным градиентом показателя преломления n(y), имеет длину периодичности хода лучей L. Линза характеризуется уравнением хода лучей в материале линзы y1(z). Первая входная поверхность выполнена плоской. Вторая поверхность выполнена выпуклой с образующей, определяемой из приведенного уравнения. Технический результат - создание телескопической градиентной линзы с увеличением, отличным от ± 1, и, кроме того, со сниженной минимально толщиной линзы. 2 ил.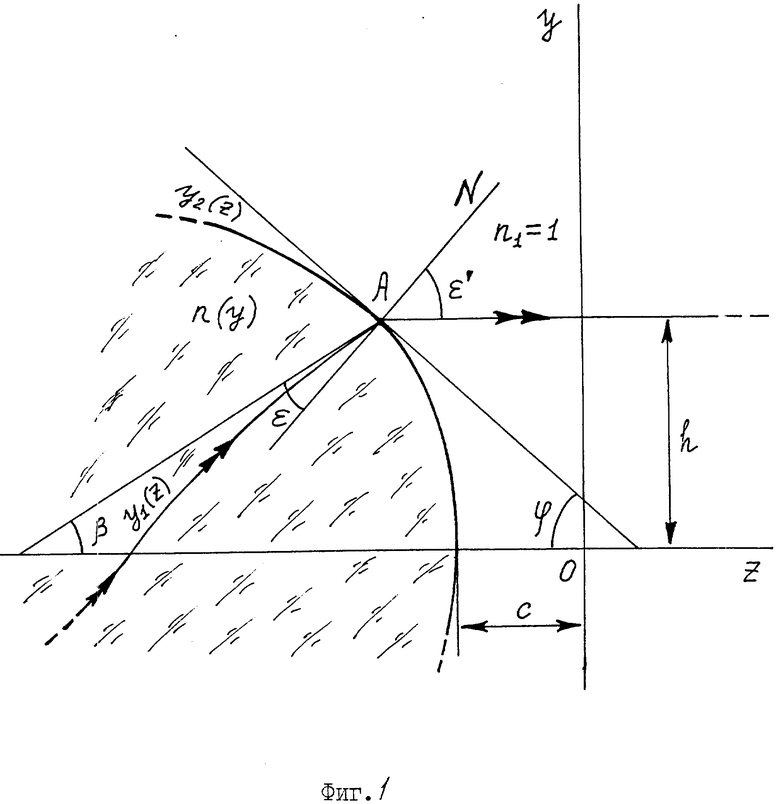
Телескопическая градиентная линза, выполненная из материала с радиальным градиентом показателя преломления n(y), ограниченная первой и второй преломляющими поверхностями, причем первая поверхность выполнена плоской, характеризующаяся зависимостью траектории хода лучей y1(z) в материале линзы, имеющая длину периодичности хода лучей L, отличающаяся тем, что вторая преломляющая поверхность выполнена в виде выпуклой поверхности вращения с образующей y2(z), определяемой из уравнения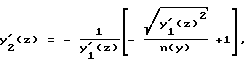
где 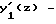 первая производная от y1(z);
первая производная от y1(z);
z - оптическая ось линзы,
а толщина c линзы выбирается в зависимости от требуемого увеличения из соотношения
где k = 0, 1, 2 ....
| Вычислительная оптика | |||
| Справочник / Под ред | |||
| М.М.Русинова | |||
| - М.: Машиност роение, 1984, с | |||
| Паровозный золотник (байпас) | 1921 |
|
SU153A1 |
Авторы
Даты
1998-06-27—Публикация
1996-11-25—Подача