1. Область техники, к которой относится изобретение
Предлагаемое изобретение относится к градиентной оптике и может быть использовано в волоконной оптике и оптическом приборостроении для создания объективов, конденсоров, эндоскопов, устройств согласования волоконно-оптических линий связи с источниками излучения и фотоприемниками и т.д.
2. Уровень техники
Известна апланатическая градиентная линза [1], ограниченная первой и второй преломляющими поверхностями вращения, имеющая по оптической оси z толщину d, кратную удвоенному номинальному фокусному расстоянию, выполненная из материала с радиальным распределением показателя преломления n(y), определяемым из уравнения
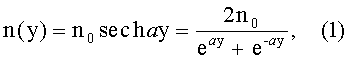
где n0 - значение показателя преломления на оси;
а - постоянная;
имеющая образующую y1(z) первой выпуклой поверхности, определяемую уравнением
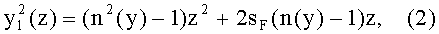
где sF - передний отрезок;
и имеющая образующую y2(z) второй вогнутой поверхности, определяемую уравнением
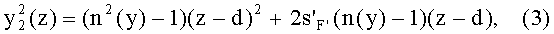
где
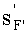 - задний отрезок;
- задний отрезок;
причем
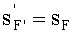 .
.
Заметим, величины sF и
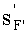 , положительны и указаны здесь и далее без применения правил знаков для отрезков, принятых в геометрической оптике [2].
, положительны и указаны здесь и далее без применения правил знаков для отрезков, принятых в геометрической оптике [2].
Форма обеих преломляющих поверхностей в известной линзе одинакова. Образующие (2) и (3) могут быть условно названы гиперболами высшего порядка.
Известно, что длина периодичности L для распределения показателя преломления (ПП), определяемого уравнением (1) и называемого также гиперсекансным, равна [2]
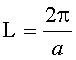 ,
,
соответственно, половина длины периодичности
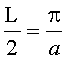
Номинальное фокусное расстояние линзы с гиперсекансным распределением ПП
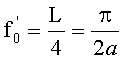 ,
,
удвоенное номинальное фокусное расстояние будет равно половине длины периодичности
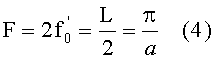
При выборе определенной толщины линзы с распределением ПП вида (1) и плоскими 1-й и 2-й поверхностями, перпендикулярными оптической оси, может быть получена фокусирующая, рассеивающая или телескопическая линза [2]. При этом вполне очевидно, что телескопическая линза получается в случае выбора толщины линзы, равной удвоенному номинальному фокусному расстоянию, в результате чего входной параллельный пучок лучей, также параллельный оптической оси, на выходе линзы останется параллельным.
Известно также уравнение траектории хода луча в среде с распределением ПП (1), так, если начальная высота точки, из которой начинает распространяться луч, равна bT, начальная координата zT и начальный коэффициент наклона (тангенс начального угла наклона луча) φ1, то уравнение траектории хода луча принимает следующий вид [3]
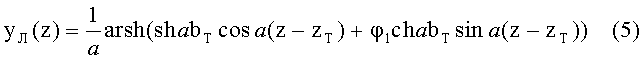
Соответственно, учитывая, что
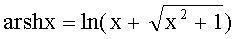
и
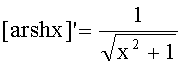
можно записать
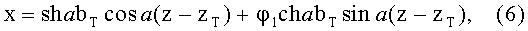
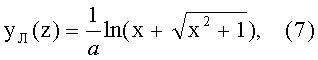
а производная определяется из выражения
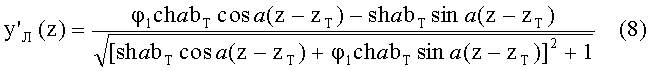
Отметим, что, если длина отрезка между координатами точки выхода луча из линзы zВЫХ и точки входа луча в линзу zВХ
d=zВЫХ-zВХ
равна длине периодичности
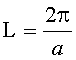 ,
,
то высота точки выхода луча из линзы yВЫХ, согласно (5), будет равна высоте точки входа луча в линзу yВХ, или
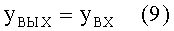
В результате, значение ПП в точке входа луча в линзу будет равно значению ПП в точке выхода луча из линзы
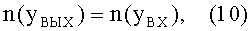
При этом, согласно (8), тангенс угла наклона луча φ2, попадающего в точку выхода луча из линзы перед преломлением, будет равен начальному тангенсу угла наклона φ1
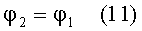
а значение производной будет соответствовать исходному
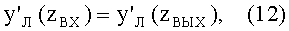
Если же длина отрезка d между координатами точки выхода луча из линзы zВЫХ и точки входа луча в линзу zВХ равна половине длины периодичности
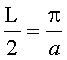
то высота точки выхода луча из линзы yВЫХ, согласно (5), будет равна высоте точки входа луча в линзу yВЫХ, взятой с обратным знаком
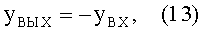
значение ПП в точке входа луча в линзу будет равно значению ПП в точке выхода луча из линзы
n(yВЫX)=n(yВX),
тангенс угла наклона луча φ2, попадающего в точку выхода луча из линзы перед преломлением, будет равен начальному тангенсу угла наклона φ1, взятому с обратным знаком
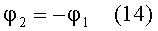
а значение производной будет равно по абсолютной величине исходному, но взятому с обратным знаком
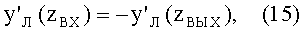
В известной линзе, согласно замыслу, каждый луч гомоцентрического пучка излучения, выходящий из точки на оптической оси, после преломления на первой поверхности приобретает направление, параллельное оптической оси. Затем, распространяясь внутри линзы в градиентной среде по криволинейной симметричной траектории, каждый луч достигает второй преломляющей поверхности. В точке пересечения со второй преломляющей поверхностью луч имеет направление, также параллельное оптической оси.
После преломления на второй поверхности каждый луч приобретает исходное направление, позволяющее вновь образовать гомоцентрический расходящийся пучок, центр которого также располагается на оптической оси на расстоянии
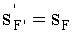 от центра второй поверхности. При этом
от центра второй поверхности. При этом
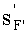 является задним отрезком линзы (фиг.1).
является задним отрезком линзы (фиг.1).
В зависимости от выбираемой толщины линзы d, кратной удвоенному номинальному фокусному расстоянию, преломление на второй поверхности может происходить как выше оптической оси, так и ниже оси (если условно считать начальное преломление на первой поверхности происходящим выше оптической оси), что, однако, не влияет на способность линзы формировать на выходе гомоцентрический расходящийся пучок (фиг.2).
Известная линза выбирается за прототип предполагаемого изобретения.
Известная линза позволяет формировать на выходе расходящийся гомоцентрический пучок излучения только с помощью двух преломляющих поверхностей вращения одинаковой формы, имеющих образующую функцию довольно сложного вида, что усложняет ее изготовление.
Таким образом, невозможность применения в качестве преломляющих поверхностей других поверхностей, в том числе более простой формы, является недостатком известной линзы, ограничивающим возможности ее изготовления.
Кроме того, известная линза является апланатической, но наличие у нее одновременно и телескопических свойств неизвестно.
3. Раскрытие изобретения
Предлагаемое техническое решение призвано устранить указанный недостаток известной линзы.
Техническим результатом, достигаемым при использовании предполагаемого изобретения, является
1) расширение возможностей изготовления за счет возможности выбора разных форм преломляющих поверхностей,
2) упрощение конструкции линзы за счет возможности выбора более простой формы преломляющих поверхностей;
3) расширение функциональных возможностей линзы за счет наличия, наряду с апланатическими, также одновременно телескопических свойств.
Для достижения указанного технического результата предлагается градиентная линза,
ограниченная первой и второй преломляющими поверхностями,
выполненная из материала с радиальным распределением показателя преломления n(y), определяемым из уравнения
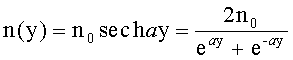 ,
,
где n0 - значение показателя преломления на оси;
а - постоянная;
имеющая по оптической оси z толщину d, кратную удвоенному номинальному фокусному расстоянию F, равному
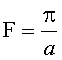 ,
,
имеющая равные величины переднего sF и заднего
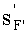 , отрезков.
, отрезков.
причем при толщине, кратной F, проекция толщины линзы на оптическую ось в любой плоскости, содержащую оптическую ось, для любых двух точек 1-й и 2-й поверхностей, имеющих одинаковую по абсолютной величине высоту относительно оптической оси, но расположенных по разные стороны от оптической оси, равна F,
а при толщине, кратной 2F, проекция толщины линзы на оптическую ось в любой плоскости, содержащую оптическую ось, для любых двух точек 1-й и 2-й поверхностей, имеющих одинаковую по величине высоту относительно оптической оси и расположенных по одну сторону от оптической оси, равна 2F.
В отдельных случаях выполнения в предлагаемой линзе 1-я и 2-я преломляющие поверхности являются поверхностями вращения одинаковой формы, в частности, сферическими.
Кроме этого, в предлагаемой линзе образующие 1-й и 2-й преломляющих поверхностей могут быть прямыми, а сами поверхности представлять собой наклонные плоскости и, в частности, плоскости, перпендикулярные оптической оси линзы.
Помимо этого, в предлагаемой линзе 1-я и 2-я преломляющие поверхности могут быть образованы двумя пересекающимися плоскостями, причем образующие каждой плоскости являются прямыми с разными коэффициентами наклона.
Указанный технический результат можно достичь, если принять во внимание замечательное свойство исходной линзы, имеющей толщину кратную длине периодичности, сохранять на выходе исходное направление луча, попадающего на 1-ю поверхность, вне зависимости от выбранной формы для 1-й и 2-й поверхности, а также от величины переднего отрезка и. соответственно, положения источника излучения.
Линза, имеющей толщину, кратную половине длины периодичности, обладает сходным свойством - сохранять на выходе абсолютное значение коэффициента наклона входного луча, попадающего на 1-ю поверхность, вне зависимости от выбранной формы для 1-й и 2-й поверхности, а также от величины переднего отрезка и, соответственно, положения источника излучения, но при этом на выходе знак коэффициента наклона преломленного луча меняется на противоположный.
Покажем действие этих свойств сначала для линз с минимальной толщиной и выберем для рассмотрения линзы с толщиной, равной длине периодичности L и половине длины периодичности L/2.
Для линз с большей толщиной, кратной половине длины периодичности, действие этих свойств также сохраняется.
Линза толщиной d на оптической оси, равной длине периодичности L, выполнена из материала с радиальным распределением ПП n(y), соответствующим уравнению (1) и известным для заданной длины волны, ограничена 1-й и 2-й преломляющими поверхностями одинаковой формы с образующими y1(z) и y2(z) и расположена в однородной среде (примем ПП однородной среды n1=1 (воздух)).
Одинаковая форма преломляющих поверхностей в рассматриваемом случае линзы с толщиной d, равной длине периодичности L, означает, что 2-я поверхность фактически представляет собой 1-ю поверхность после параллельного переноса вдоль оптической оси z на расстояние d.
В результате, расстояние вдоль оси z между любой отдельно взятой исходной точкой на 1-й поверхности, имеющей определенную высоту над осью z, и точкой на 2-й поверхности, имеющей такую же высоту над осью z и находящейся на одной прямой, параллельной оси z, с исходной точкой на 1-й поверхности, будет одинаковым и равным толщине d=L.
В самом простом случае, 1-я и 2-я преломляющие поверхности могут быть поверхностями вращения, но, в более общем случае, это необязательно.
Вершина 1-й поверхности расположена в начале координат. Ось z представляет собой оптическую ось линзы. Принимая, что линза обладает осевой симметрией, рассмотрение проводится в меридиональной плоскости.
Луч падающего на 1-ю поверхность пучка, выходящего из точки М, на оптической оси, имеет направляющий коэффициент и uK1=φ1, преломляется в точке А с координатами zП1, yП1. Угол падения луча на 1-ю поверхность обозначим как ε1, угол преломления на 1-й поверхности -
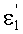 , нормаль к 1-й поверхности в точке А - N1, угол падения луча на 2-ю поверхность - ε2, угол преломления на 2-й поверхности -
, нормаль к 1-й поверхности в точке А - N1, угол падения луча на 2-ю поверхность - ε2, угол преломления на 2-й поверхности -
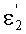 , а нормаль ко 2-й поверхности в точке преломления В - N2.
, а нормаль ко 2-й поверхности в точке преломления В - N2.
Направляющий коэффициент входного луча, преломляющегося на 1-й поверхности в точке А обозначим как и uK1, направляющий коэффициент луча, преломленного на 1-й поверхности в точке А, - uB1, направляющий коэффициент луча, преломляющегося на 2-й поверхности в точке В, - uK2, направляющий коэффициент луча, преломленного на 2-й поверхности в точке В, - uB2.
Направляющий коэффициент uH1 нормали N1 к 1-й поверхности в точке А можно выразить в виде
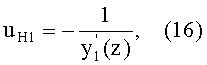
где
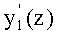 - первая производная от y1(z).
- первая производная от y1(z).
Направляющий коэффициент uH2 нормали N2 ко 2-й поверхности в точке В можно выразить в виде
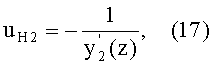
где
 - первая производная от y2(z).
- первая производная от y2(z).
Случай 1-й выпуклой поверхности для линзы с толщиной, кратной L
Рассмотрим случай 1-й выпуклой поверхности для линзы с толщиной, кратной L.
Случаи преломления на 1-й выпуклой и 2-й вогнутой поверхностях показаны на фиг.3 и 5.
Схемы преломления на фиг.3 и 5 относятся к случаям, когда после преломления направляющий коэффициент и g, преломленного на 1-й поверхности (выходного) луча имеет отрицательное значение (фиг.3) и положительное значение (фиг.5).
Соответственно, общая схема хода лучей в линзе показана для uB1<0 на фиг.4, а для uB1>0 - на фиг.6.
Для обеих возможных схем преломления, представленных на фиг.3 и 5, в точке А на 1-й поверхности угол падения ε1 можно определить из выражения
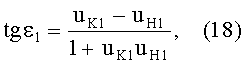
а угол преломления
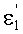 - из выражения
- из выражения
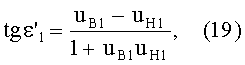
Кроме того, по закону преломления,
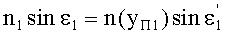 ,
,
где n(yП1) - ПП в точке преломления А.
Тогда, с учетом того, что n1=1, угол преломления выразится в виде
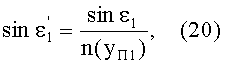
Поскольку преломленный в точке А на 1-й поверхности луч. имея начальное направление uB1, после преломления распространяется по криволинейной траектории с периодом, равным длине периодичности L, то в точке В, после прохождения полного периода,
1) высота yП2 точки преломления В будет равна высоте yП1 точки преломления А, согласно условию (9);
2) направляющий коэффициент uK2=φ2 падающего на 2-ю поверхность луча будет равен uB1=φ1, согласно условию (11), и соответственно,
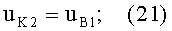
3) направляющий коэффициент uH2 нормали N2 ко 2-й поверхности в точке В будет равен направляющему коэффициенту uH1 нормали N1 к 1-й поверхности в точке А, по условию (11) и соотношениям (12), (16) и (17), поскольку форма 1-й и 2-й поверхностей одинакова, и, таким образом,
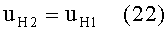
Угол падения ε2 в точке В будет равен
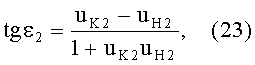
Учитывая (21) и (22) и подставляя в (23), получим
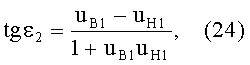
Сравнивая (19) и (24), получаем, что
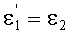
на основе чего можно также записать
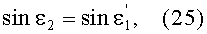
Для точки В на 2-й поверхности, по закону преломления
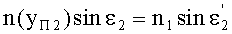 ,
,
где n(yП2) - ПП в точке преломления В.
С учетом того, что n1=1, угол преломления выразится в виде
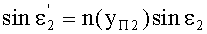
Принимая во внимание соотношения (20) и (25), получим
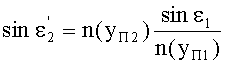
Поскольку в точке В, как указано выше, yП2=yП1, и, соответственно, согласно условию (10), выполняется соотношение n(yП2)=n(yП1), то получим, что
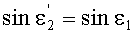
и тогда, как следствие,
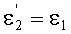
и
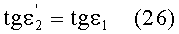
Угол преломления
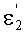 в точке В можно также выразить в виде
в точке В можно также выразить в виде
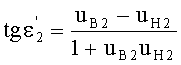
Если использовать в этом выражении соотношение (22), то получим
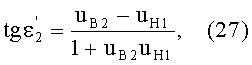
Приравняв, на основе (26), выражения (18) и (27) и проведя простые преобразования, получим
uB2=uK1
Таким образом, направление выходного луча, преломленного в точке В, будет совпадать с направлением входного луча в точке А.
Случай 1-й выпуклой поверхности для линзы толщиной L/2
Рассмотрим случай 1-й выпуклой поверхности для линзы с толщиной, кратной L/2.
Случаи преломления на 1-й выпуклой и 2-й вогнутой поверхностях показаны на фиг.7 и 9.
Схемы преломления, показанные на фиг.7 и 9, относятся к случаям, когда после преломления направляющий коэффициент uB1 преломленного на 1-й поверхности луча имеет отрицательное значение (фиг.7) и положительное значение (фиг.9).
Соответственно, общая схема хода лучей в линзе показана для и uB1<0 на фиг.8, а для uB1>0 - на фиг.10.
Для обеих возможных схем преломления, представленных на фиг.7 и 9, в точке А на 1-й поверхности угол падения ε1 можно определить из выражения
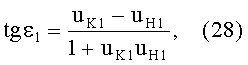
а угол преломления
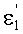 - из выражения
- из выражения
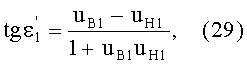
Кроме того, по закону преломления,
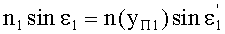
Тогда, с учетом того, что n1=1, угол преломления выразится в виде
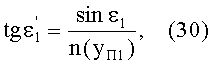
Для линзы с длиной периодичности L/2 преломленный в точке А на 1-й поверхности луч, имея начальное направление uB1, после преломления распространяется по периодической криволинейной траектории, и в точке В, после прохождения половины периода,
1) высота yП2 точки преломления В будет равна по абсолютной величине высоте yП1 точки преломления А, но будет иметь отрицательное значение, согласно условию (13);
2) направляющий коэффициент uK2=φ2 падающего на 2-ю поверхность луча будет равен uB1=φ1 по абсолютной величине, но будет иметь отрицательное значение, согласно условию (14), и, таким образом,
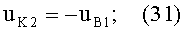
3) направляющий коэффициент uH2 нормали N2 к 1-й поверхности в точке В будет равен направляющему коэффициенту uH1 нормали N1 к 1-й поверхности в точке А по абсолютной величине, но будет иметь отрицательное значение, согласно условию (15)
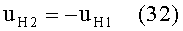
Угол падения ε2 в точке В будет равен
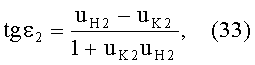
Учитывая (31) и (32) и подставляя в (33), получим
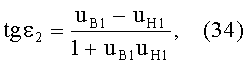
Сравнивая (29) и (34), получаем, что
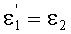 ,
,
на основе чего можно также записать

Для точки В на 2-й поверхности, по закону преломления
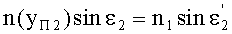 ,
,
где n(yП2) - ПП в точке преломления В.
Соответственно, с учетом того, что n1=1, угол преломления выразится в виде
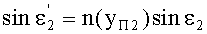
Принимая во внимание соотношение (30) и (35), получим
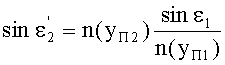
Поскольку в точке В, как указано выше, yП2=-yП1, но при этом n(yП2)=n(-yП1), то получим, что
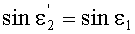
и тогда, как следствие,
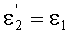 ,
,
и
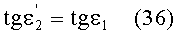
Угол преломления
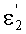 в точке В можно также выразить в виде
в точке В можно также выразить в виде
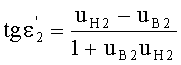
Если использовать в этом выражении соотношение (32), то получим
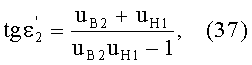
Приравняв, на основе (36), выражения (28) и (37) и проведя простые преобразования, получим
uB2=-uK1
В результате, направляющий коэффициент uB2 выходного луча, преломленного в точке В, будет по абсолютной величине равен направляющему коэффициенту uK1 входного луча в точке А, но будет иметь отрицательное значение.
Случай 1-й вогнутой поверхности для линзы толщиной L
Рассмотрим случай 1-й вогнутой поверхности для линзы с толщиной, кратной L.
Случаи преломления на 1-й вогнутой и 2-й выпуклой поверхностях показаны на фиг.11 и 13.
Схемы преломления, показанные на фиг.11 и 13, относятся к случаям, когда направляющий коэффициент uK1 входного луча больше направляющего коэффициента нормали uH1 в точке преломления (фиг.11) и когда направляющий коэффициент uK1 входного луча меньше направляющего коэффициента нормали uH1 в точке преломления (фиг.13).
Соответственно, общая схема хода лучей в линзе показана для случая uK1>uH1 на фиг.12, а для случая uK1<uH1 - на фиг.14.
Для схемы преломления, представленных на фиг.11, в точке А на 1-й поверхности угол падения ε1 можно определить из выражения
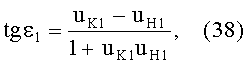
а угол преломления
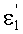 - из выражения
- из выражения
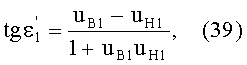
Для схемы преломления, представленных на фиг.13, в точке А на 1-й поверхности угол падения ε1 можно определить из выражения (40)
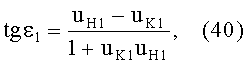
а угол преломления
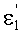 - из выражения
- из выражения
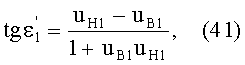
Для обеих схем преломления, представленных на фиг.11 и 13, в точке А на 1-й поверхности, по закону преломления,
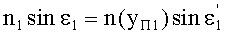
Тогда, с учетом того, что n1=1, угол преломления выразится в виде
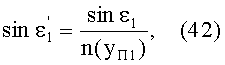
Поскольку преломленный в точке А на 1-й поверхности луч, имея начальное направление uB1, после преломления распространяется по криволинейной траектории с периодом, равным длине периодичности, то в точке В, после прохождения полного периода,
1) высота yП2 точки преломления В будет равна высоте yП1 точки преломления А, согласно условию (9);
2) направляющий коэффициент uK2=φ2 падающего на 2-ю поверхность луча будет равен uB1=φ1, согласно условию (11), и соответственно,
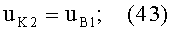
3) направляющий коэффициент uH2 нормали N2 ко 2-й поверхности в точке В будет равен направляющему коэффициенту uH1 нормали N1 к 1-й поверхности в точке А, по условию (11) и соотношениям (12), (16) и (17), поскольку форма 1-й и 2-й поверхностей одинакова, и, таким образом,
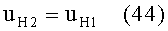
Угол падения ε2 в точке В для схемы фиг.11 будет равен
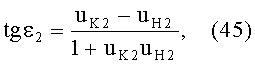
Учитывая (43) и (44) и подставляя в (45), получим
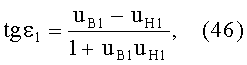
Сравнивая (39) и (46), получаем, что
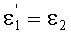 ,
,
на основе чего можно также записать
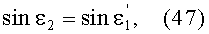
Угол падения ε2 в точке В для схемы фиг.13 будет равен
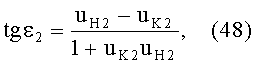
Учитывая (43) и (44) и подставляя в (48), получим
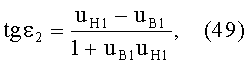
Сравнивая (41) и (49), получаем, что
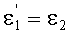 ,
,
на основе чего можно также записать
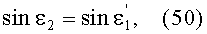
Для точки В на 2-й поверхности для обеих схем преломления на фиг.11 и 13, по закону преломления
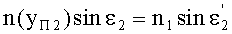 ,
,
где n(yП2) - ПП в точке преломления В.
С учетом того, что n1=1, угол преломления выразится в виде
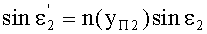
Принимая во внимание соотношения (47), (50) и (42), получим
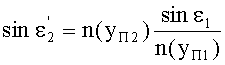
Поскольку в точке В, как указано выше, yП2=yП1, и, соответственно, согласно условию (10), выполняется соотношение n(yП2)=n(yП1), то получим, что
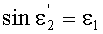
и тогда, как следствие,
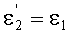
и
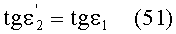
Угол преломления
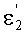 в точке В для схемы фиг.11 можно также выразить в виде
в точке В для схемы фиг.11 можно также выразить в виде
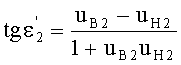
Если использовать в этом выражении соотношение (44), то получим
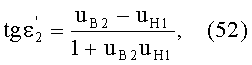
Приравняв, на основе (51), выражения (38) и (52) и проведя простые преобразования, получим
uB2=uK1
Угол преломления
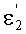 в точке В для схемы фиг.13 можно также выразить в виде
в точке В для схемы фиг.13 можно также выразить в виде
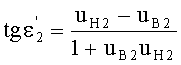
Если использовать в этом выражении соотношение (44), то получим
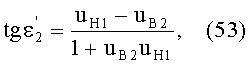
Приравняв, на основе (51), выражения (40) и (53) и проведя простые преобразования, также получим
uB2=uK1
Таким образом, направление выходного луча, преломленного в точке В, будет совпадать, для обеих возможных схем преломления на фиг.11 и 13, с направлением входного луча в точке А.
Случаи 1-й вогнутой поверхности для линзы толщиной L/2
Рассмотрим случай 1-й вогнутой поверхности для линзы толщиной L/2. Случаи преломления на 1-й вогнутой и 2-й выпуклой поверхностях показаны на фиг.15 и 17.
Схемы преломления, показанные на фиг.15 и 17, относятся к случаям, когда направляющий коэффициент uK1 входного луча больше направляющего коэффициента нормали uH1 в точке преломления (фиг.15) и когда направляющий коэффициент uK1 входного луча меньше направляющего коэффициента нормали uH1 в точке преломления (фиг.17).
Соответственно, общая схема хода лучей в линзе показана для случая uK1>uH1 на фиг.16, а для случая uK1<uH1 - на фиг.18.
Для схемы преломления, представленных на фиг.15, в точке А на 1-й поверхности угол падения ε1 можно определить из выражения
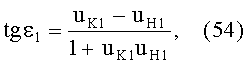
а угол преломления
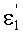 - из выражения
- из выражения
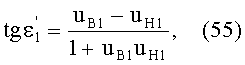
Для схемы преломления, представленных на фиг.17, в точке А на 1-й поверхности угол падения ε1 можно определить из выражения
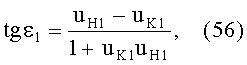
а угол преломления
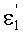 - из выражения
- из выражения
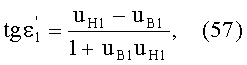
Для обеих возможных схем преломления, представленных на фиг.15 и 17. в точке А на 1-й поверхности, по закону преломления,
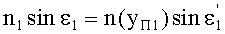 ,
,
где n(yП1) - ПП в точке преломления А.
Тогда, с учетом того, что n1=1, угол преломления выразится в виде
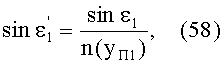
Для линзы с длиной периодичности L/2 преломленный в точке А на 1-й поверхности луч, имея начальное направление uB1, после преломления распространяется по периодической криволинейной траектории, и в точке В, после прохождения половины периода,
1) высота yП2 точки преломления В будет равна по абсолютной величине высоте yП1 точки преломления А, но будет иметь отрицательное значение, согласно условию (13);
2) направляющий коэффициент uK2=φ2 падающего на 2-ю поверхность луча будет равен uB1=φ1 по абсолютной величине, но будет иметь отрицательное значение, согласно условию (14), и, таким образом,
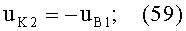
3) направляющий коэффициент uH2 нормали N2 к 1-й поверхности в точке В будет равен направляющему коэффициенту uH1 нормали N1 к 1-й поверхности в точке А по абсолютной величине, но будет иметь отрицательное значение, согласно условию (15)
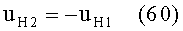
Угол падения ε2 в точке В для схемы фиг.15 будет равен
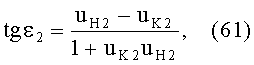
Учитывая (59) и (60) и подставляя в (61), получим
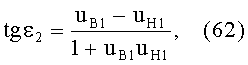
Сравнивая (55) и (62), получаем, что
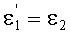 ,
,
на основе чего можно также записать
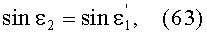
Угол падения ε2 в точке В для схемы фиг.17 будет равен
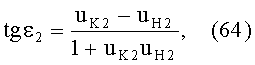
Учитывая (59) и (60) и подставляя в (64), получим
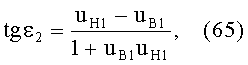
Сравнивая (57) и (65), получаем, что
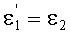 ,
,
на основе чего можно также записать
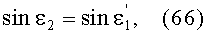
Для точки В на 2-й поверхности для обеих схем преломления на фиг.15 и 17, по закону преломления
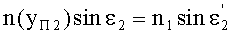
Соответственно, с учетом того, что n1=1, угол преломления выразится в виде
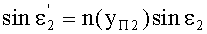
Принимая во внимание соотношения (63), (66) и (58), получим
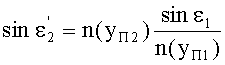
Поскольку в точке В, как указано выше, yП2=-yП1, но при этом
n(yП2)=n(yП1), то получим, что
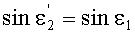 ,
,
и тогда, как следствие,
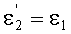
и
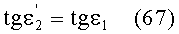
Угол преломления
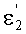 в точке В для схемы фиг.15 можно также выразить в виде
в точке В для схемы фиг.15 можно также выразить в виде
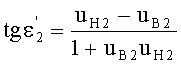
Если использовать в этом выражении соотношение (60), то получим
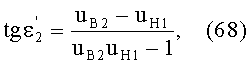
Приравняв, на основе (67), выражения (54) и (68) и проведя простые преобразования, получим
uB2=-uK1
Угол преломления
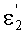 в точке В для схемы фиг.17 можно также выразить в виде
в точке В для схемы фиг.17 можно также выразить в виде
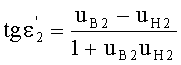
Если использовать в этом выражении соотношение (60), то получим
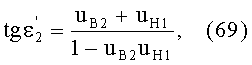
Приравняв, на основе (67), выражения (56)и (69) и проведя простые преобразования, получим
uB2=-uK1
В результате, направляющий коэффициент uB2 выходного луча, преломленного в точке В, для обеих возможных схем преломления на фиг.15 и 17, по абсолютной величине равен направляющему коэффициенту uK1 входного луча в точке А, но будет иметь отрицательное значение.
Случай плоских поверхностей для линзы толщиной L
Рассмотрим также случай 1-й и 2-й плоских преломляющих поверхностей, перпендикулярных оптической оси, для линзы толщиной L.
Схема преломления показана на фиг.19.
Общая схема хода лучей в линзе показана на фиг.20. Для схемы преломления, представленной на фиг.19, в точке А на 1-й поверхности, учитывая, что uH1=uH2=0, угол падения ε1 можно определить из выражения
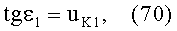
а угол преломления
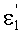 - из выражения
- из выражения
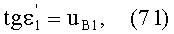
Кроме того, по закону преломления,
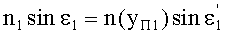
Тогда, с учетом того, что n1=1, угол преломления выразится в виде
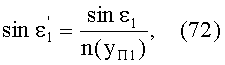
Поскольку преломленный в точке А на 1-й поверхности луч, имея начальное направление uB1 после преломления распространяется по криволинейной траектории с периодом, равным длине периодичности L, то в точке В, после прохождения полного периода,
1) высота yП2 точки преломления В будет равна высоте yП1 точки преломления А, согласно условию (9);
2) направляющий коэффициент uK2=φ2 падающего на 2-ю поверхность луча будет равен uB1=φ1, согласно условию (11), и соответственно,
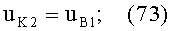
3) направляющий коэффициент uH2 нормали N2 ко 2-й поверхности в точке В будет равен направляющему коэффициенту uH1 нормали N1 к 1-й поверхности в точке А, по условию (11) и соотношениям (12), (16) и (17), поскольку форма 1-й и 2-й поверхностей одинакова, и, таким образом,
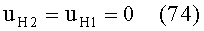
Угол падения ε2 в точке В будет равен
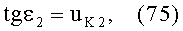
Учитывая (73) и подставляя в (75), получим
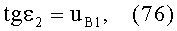
Сравнивая (71) и (76), получаем, что
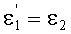 ,
,
на основе чего можно также записать
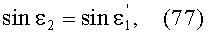
Для точки В на 2-й поверхности, по закону преломления
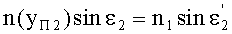 ,
,
где n(yП2) - ПП в точке преломления В.
С учетом того, что n1=1, угол преломления выразится в виде
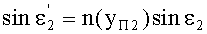
Принимая во внимание соотношения (72) и (77), получим
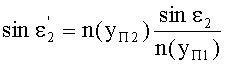
Поскольку в точке В, как указано выше, yП2=yП1, и, соответственно, согласно условию (10), выполняется соотношение n(yП2)=n(yП1), то получим, что
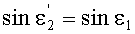 ,
,
и тогда, как следствие,
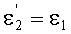
и
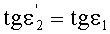
Угол преломления
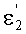 в точке В можно также выразить в виде
в точке В можно также выразить в виде
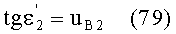
Приравняв, на основе (78), выражения (70) и (79), получим
uB2=uK1
Таким образом, направление выходного луча, преломленного в точке В, будет совпадать с направлением входного луча в точке А.
Случай плоских поверхностей для линзы толщиной L/2
Рассмотрим также случай 1-й и 2-й плоских преломляющих поверхностей, перпендикулярных оптической оси, для линзы толщиной L/2.
Схема преломления показана на фиг.21.
Общая схема хода лучей в линзе показана на фиг.22.
Для схемы преломления, представленной на фиг.21, в точке А на 1-й поверхности, учитывая, что uH1=uH2=0, угол падения ε1 можно определить из выражения
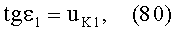
а угол преломления
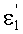 - из выражения
- из выражения
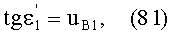
Кроме того, по закону преломления,
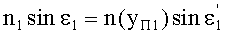
Тогда, с учетом того, что n1=1, угол преломления выразится в виде
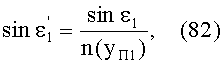
Для линзы с длиной периодичности L/2 преломленный в точке А на 1-й поверхности луч, имея начальное направление uB1, после преломления распространяется по периодической криволинейной траектории, и в точке В, после прохождения половины периода,
1) высота yП2 точки преломления В будет равна по абсолютной величине высоте yП1 точки преломления А, но будет иметь отрицательное значение, согласно условию (13);
2) направляющий коэффициент uK2=φ2 падающего на 2-ю поверхность луча будет равен uB1=φ1 по абсолютной величине, но будет иметь отрицательное значение, согласно условию (14), и, таким образом,
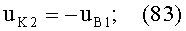
3) направляющий коэффициент uH2 нормали N2 к 1-й поверхности в точке В будет равен направляющему коэффициенту uH1 нормали N, к 1-й поверхности в точке А по абсолютной величине, но будет иметь отрицательное значение, согласно условию (15), в результате чего
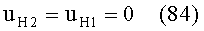
Угол падения ε2 в точке В будет равен
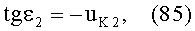
Учитывая (83) и (84) и подставляя в (85), получим
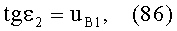
Сравнивая (81) и (86), получаем, что
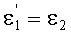
на основе чего можно также записать
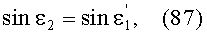
Для точки В на 2-й поверхности, по закону преломления
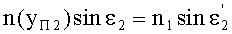
Соответственно, с учетом того, что n1=1, угол преломления выразится в виде
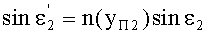
Принимая во внимание соотношение (82) и (87), получим
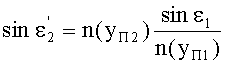
Поскольку в точке В, как указано выше, yП2=yП1, ко при этом n(yП2)=n(-yП1), то получим, что
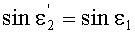
и тогда, как следствие,
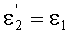
и
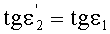
Угол преломления
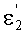 в точке В можно также выразить в виде
в точке В можно также выразить в виде
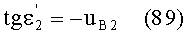
Приравняв, на основе (88), выражения (80) и (89), получим
uB2=-uК1
В результате, направляющий коэффициент uB2 выходного луча, преломленного в точке В, будет по абсолютной величине равен направляющему коэффициенту uK1 входного луча в точке А, но будет иметь отрицательное значение.
Показанное свойство предложенных линз сохранять на выходе направление входящего луча (или сохранять абсолютное значение направляющего коэффициента луча с изменением знака коэффициента на противоположный) приводит, как следствие, к тому, что входной расходящийся гомоцентрический пучок лучей (с центром, расположенным как на оптической оси. так и вне оптической оси) сохранит гомоцентричность на выходе линзы, а мнимые продолжения лучей на выходе пересекутся в одной точке, образуя мнимое изображение предметной точки.
Интересно отметить, что при этом будет отсутствовать необходимость фиксированного положения предметной точки на оптической оси. Это означает, что предметная точка может располагаться на оптической оси на любом удалении от линзы, и гомоцентричность пучка на выходе линзы не нарушится.
Дополнительным следствием отмеченного свойства будет наличие у предложенных линз одновременно и телескопических свойств, поскольку входной параллельный пучок лучей на выходе линзы сохранит свое направление, и все лучи выходного пучка останутся параллельными, причем входной параллельный пучок лучей не обязательно должен быть параллельным оптической оси предложенной линзы.
В результате, предложенные линзы будут обладать одновременно апланатическими и телескопическими свойствами, что ранее не было известно.
Так, для известной линзы, принятой за прототип, ранее было доказано наличие апланатических свойств, но одновременно с этим телескопические свойства не были известны.
Для другой известной линзы с 1-й и 2-й плоскими преломляющими поверхностями, перпендикулярными оптической оси [2], было указано наличие телескопических свойств, но одновременно с этим наличие апланатических свойств не было известно.
Показанное свойство предложенных линз с толщиной, кратной L и L/2, можно использовать для формирования градиентных линз, имеющих одновременно апланатические и телескопические свойства и различные преломляющие поверхности.
Вполне естественным путем является использование поверхностей вращения с различными образующими более простого вида, чем образующая вида (2), - прямая, окружность и др. В этом случае преломляющие поверхности будут симметричны относительно оптической оси.
Однако, это необязательно.
В общем случае, преломляющие поверхности могут быть несимметричны относительно оптической оси. Возникает возможность использовать преломляющие поверхности, например, в виде наклонных плоскостей, а также комбинации из наклонной плоскости и плоскости, перпендикулярной оптической оси, двух наклонных плоскостей с разным углом наклона и т.д.
Отметим, что в случае использования наклонных 1-й и 2-й плоскостей доказать апланатические и телескопические свойства линзы можно, используя приведенный выше подход, если рассматривать ход каждого луча входного гомоцентрического или параллельного пучка в плоскости, содержащей этот луч и оптическую ось линзы. Тогда рассмотрение можно свести к одному из рассмотренных выше случаев (здесь не приводится).
Рассмотрим возможные варианты выполнения предложенных линз.
Телескопические линзы
На основе доказанного выше свойства можно предложить разные варианты выполнения телескопических линз.
Телескопическикие линзы толщиной, кратной L и L/2, могут иметь преломляющие поверхности в виде поверхностей вращения любого вида, в том числе с более простыми в изготовлении, чем у прототипа, например, сферическими (фиг.23, 24), коническими (фиг.25, 26).
Отметим, что, согласно принципу обратимости хода лучей, показанные на фиг.23-26 линзы одновременно иллюстрируют ход лучей для случаев, когда 1-я преломляющая поверхность является вогнутой, а 2-я поверхность - выпуклой.
Предложенные телескопические линзы длиной L и L/2 могут иметь также, как частный случай, плоские преломляющие поверхности (фиг.27, 28). Заметим, что такие линзы были известны и ранее описаны [2].
Вместо сферических поверхностей могут быть использованы поверхности вращения с образующими и другого вида (парабола, эллипс и др.), в том числе с известными образующими вида (2) и (3).
Могут быть также использованы поверхности вращения с образующими, имеющими точки перегиба. Доказать апланатические и телескопические свойства линзы с такими преломляющими поверхностями можно, используя приведенный выше подход, если рассматривать ход каждого луча входного гомоцентрического или параллельного пучка отдельно для участков образующей с разными знаками кривизны. Соответственно, рассмотрение для каждого участка можно свести к одному из рассмотренных выше случаев (здесь не приводится).
Преломляющие поверхности могут и не являться поверхностями вращения, например, поверхности могут быть наклонными плоскими (фиг.29, 30), выполнены в виде комбинации из плоскости и наклонной плоскости (фиг.31, 32), комбинации двух наклонных плоскостей с разным углом наклона (фиг.33, 34) и т.д.
Следует отметить, что если входной параллельный пучок входит в линзу под углом к оси, то выходит он из линзы с тем же самым углом, оставаясь строго параллельным, что следует из показанного выше свойства линзы сохранять направление входного луча.
Полезным свойством предлагаемой линзы является также сохранение неизменным положения выходного пятна излучения при изменении угла наклона входного параллельного пучка излучения.
Апланатические линзы
Как известно, две сопряженные точки в пространстве предметов и изображений называются апланатическими, если в изображении отсутствует сферическая аберрация и выполняется условие синусов (или закон синусов Аббе) [4].
Доказанное выше свойство рассмотренных линз с толщиной, кратной половине длины периодичности, сохранять на выходе исходное направление луча, попадающего на первую поверхность, вне зависимости от выбранной формы 1-й и 2-й поверхности, обеспечивает отсутствие сферической аберрации для точки на оптической оси на конечном расстоянии от линзы и для бесконечно удаленной точки.
Покажем теперь, что для пары сопряженных точек М1 и
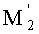 на оптической оси выполняется закон синусов Аббе.
на оптической оси выполняется закон синусов Аббе.
Закон синусов Аббе в общем случае имеет вид
nsinσ=βn'sinσ'
или
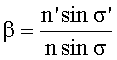 ,
,
где n - показатель преломления среды, в которой расположен предмет;
n' - показатель преломления среды, в которой формируется изображение;
σ - угол между оптической осью и лучом, выходящим из осевой точки предмета;
σ' - угол между оптической осью и лучом, выходящим из оптической системы и проходящим через осевую точку изображения;
β - линейное увеличение оптической системы.
Для всех рассмотренных вариантов предложенной линзы соотношение примет вид
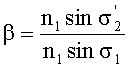 ,
,
или
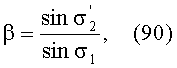
σ1 - угол между оптической осью и лучом, выходящим из осевой (предметной) точки М1;
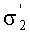 - угол между оптической осью и лучом, выходящим из линзы и проходящим через осевую точку изображения
- угол между оптической осью и лучом, выходящим из линзы и проходящим через осевую точку изображения
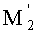 (мнимое изображение).
(мнимое изображение).
Рассмотрим линзы с 1-й выпуклой и 2-й вогнутой поверхностями.
Для линзы толщиной L с 1-й выпуклой поверхностью и 2-й вогнутой поверхностью схема преломления на 1-й выпуклой поверхности для случая uB1<0 приведена на фиг.35, а для 2-й поверхности - на фиг.36.
Для линзы толщиной L с 1-й выпуклой поверхностью и 2-й вогнутой поверхностью схема преломления на 1-й выпуклой поверхности для случая uB1>0 приведена на фиг.37, а для 2-й поверхности - на фиг.38.
Для линзы толщиной L/2 с 1-й выпуклой поверхностью и 2-й вогнутой поверхностью схема преломления на 1-й выпуклой поверхности для случая uB1<0 приведена на фиг.35, а для 2-й поверхности - на фиг.39.
Для линзы толщиной L/2 с 1-й выпуклой поверхностью и 2-й вогнутой поверхностью схема преломления на 1-й сферической поверхности для случая uB1>0 приведена на фиг.37, а для 2-й поверхности - на фиг.40.
Для всех рассмотренных случаев на фиг.35-40 соотношение (90) примет вид
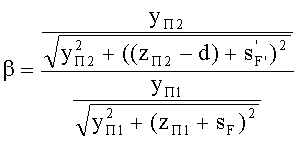
Поскольку, образующие 1-й и 2-й поверхностей имеют одинаковую форму, то стрелки прогиба поверхностей ΔП для одной и той же высоты также равны, соответственно
ΔП=zП1=zП1-d
Кроме того, согласно исходным данным, равны также передний и задний отрезки
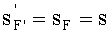
В результате можно записать
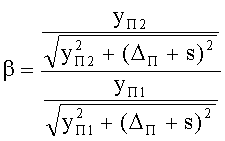
Для линз толщиной L, как указывалось выше,
yП1=yП2,
а для линз толщиной L 1 2
yП1=-yП2
В результате, линейное увеличение линз будет постоянно и равно
для линз с толщиной, кратной L,
β=1,
а для линз с толщиной, кратной L/2,
β=-1
Тогда в рассматриваемой линзе для пары сопряженных точек М1 и
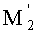 на оси также будет отсутствовать сферическая аберрация, и будет выполняться закон синусов Аббе для любого луча, выходящего из предметной осевой точки. Соответственно, точки М1 и
на оси также будет отсутствовать сферическая аберрация, и будет выполняться закон синусов Аббе для любого луча, выходящего из предметной осевой точки. Соответственно, точки М1 и
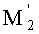 будут являться парой апланатических точек, а саму линзу в рассматриваемом случае также можно назвать апланатической.
будут являться парой апланатических точек, а саму линзу в рассматриваемом случае также можно назвать апланатической.
Рассмотрим линзы с 1-й вогнутой и 2-й выпуклой поверхностями.
Для линзы толщиной L с 1-й вогнутой поверхностью и 2-й выпуклой поверхностью схема преломления на 1-й вогнутой поверхности для случая uB1>uH1 приведена на фиг.41. а для 2-й поверхности - на фиг.42.
Для линзы толщиной L с 1-й вогнутой поверхностью и 2-й выпуклой поверхностью схема преломления на 1-й вогнутой поверхности для случая uB1<uH1 приведена на фиг.43, а для 2-й поверхности - на фиг.44.
Для линзы толщиной L/2 с 1-й вогнутой поверхностью и 2-й выпуклой поверхностью схема преломления на 1-й вогнутой поверхности для случая uB1>uH1 приведена на фиг.41, а для 2-й поверхности - на фиг.45.
Для линзы толщиной L/2 с 1-й вогнутой поверхностью и 2-й выпуклой поверхностью схема преломления на 1-й вогнутой поверхности для случая uB1<uH1 приведена на фиг.43, а для 2-й поверхности - на фиг.46.
Для всех рассмотренных случаев на фиг.41-46 соотношение (90) примет вид
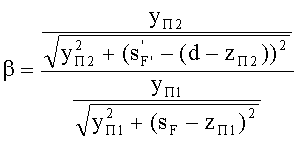
Поскольку, образующие 1-й и 2-й поверхностей имеют одинаковую форму, то стрелки прогиба поверхностей ΔП тоже равны, соответственно
ΔП=zП1=d-zП2
Кроме того, согласно исходным данным, равны также передний и задний отрезки
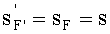
В результате можно записать
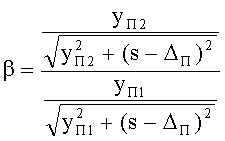
Для линз толщиной L, как указывалось выше,
yП1=yП2,
а для линз толщиной L/2
yП1=-yП2
В результате, линейное увеличение линз также будет постоянно и равно
для линз с толщиной, кратной L,
β=1,
а для линз с толщиной, кратной L/2,
β=-1
Тогда в рассматриваемой линзе для пары сопряженных точек М1 и
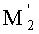 на оси также будет отсутствовать сферическая аберрация, и будет выполняться закон синусов Аббе для любого луча, выходящего из предметной осевой точки. Соответственно, точки М1 и
на оси также будет отсутствовать сферическая аберрация, и будет выполняться закон синусов Аббе для любого луча, выходящего из предметной осевой точки. Соответственно, точки М1 и
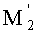 будут являться парой апланатических точек, а саму линзу в рассматриваемом случае также можно назвать апланатической.
будут являться парой апланатических точек, а саму линзу в рассматриваемом случае также можно назвать апланатической.
Рассмотрим линзы с 1-й и 2-й плоскими поверхностями.
Для линзы толщиной L схема преломления для 1-й поверхности приведена на фиг.47, а для 2-й поверхности - на фиг.48.
Для линзы толщиной L/2 схема преломления для 1-й поверхности приведена на фиг.47, а для 2-й поверхности - на фиг.49.
Для всех рассмотренных случаев на фиг.47-49 соотношение (90) примет вид
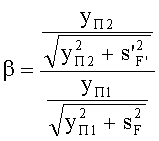
Согласно исходным данным, передний и задний отрезки равны
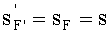
В результате можно записать
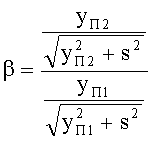
Для линз толщиной L, как указывалось выше,
yП1=yП2,
а для линз толщиной L/2
yП1=-yП2
В результате, линейное увеличение линз также будет постоянно и равно
для линз с толщиной, кратной L,
β=1,
а для линз с толщиной, кратной L/2,
β=-1
Тогда в рассматриваемой линзе для пары сопряженных точек М1 и
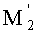 на оси также будет отсутствовать сферическая аберрация, и будет выполняться закон синусов Аббе для любого луча, выходящего из предметной осевой точки.
на оси также будет отсутствовать сферическая аберрация, и будет выполняться закон синусов Аббе для любого луча, выходящего из предметной осевой точки.
Соответственно, точки М1 и
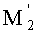 будут являться парой апланатических точек, а саму линзу в рассматриваемом случае также можно назвать апланатической.
будут являться парой апланатических точек, а саму линзу в рассматриваемом случае также можно назвать апланатической.
Таким образом, линзы всех рассмотренных вариантов являются апланатическими.
Предложенные апланатические линзы могут иметь преломляющие поверхности в виде поверхностей вращения любого вида, в том числе с более простыми в изготовлении, чем у прототипа, например, сферическими (фиг.50, 51), плоскими (фиг.52, 53).
Преломляющие поверхности могут и не являться поверхностями вращения, например, поверхности могут быть наклонными плоскими (фиг.54, 55), выполнены в виде комбинации из плоскости и наклонной плоскости (фиг.56, 57), комбинации двух наклонных плоскостей с разным углом наклона (фиг.58, 59) и т.д.
Преломляющие поверхности апланатических линз могут также иметь точки перегиба, при этом апланатические свойства у линз сохраняются.
С точки зрения рассмотренных вариантов выполнения предложенной линзы, известная линза, принятая за прототип, является частным случаем, для которого
1) в качестве преломляющих выбраны поверхности вращения,
2) выбран вариант с 1-й выпуклой и 2-й вогнутой поверхностями,
3) в качестве образующих для поверхностей вращения выбраны специальные функции (2) и (3). применение которых обеспечивает для входного луча, после преломления на 1-й поверхности, приобретение направления, параллельного оптической оси.
Можно также отметить, что максимально достижимая числовая апертура у всех рассмотренных апланатических линз будет принципиально меньше, чем у известной линзы, выбранной за прототип, при одинаковом диаметре линзы, поскольку после преломления на 1-й поверхности лучи идут под углом к оптической оси, а это означает, что затем, при прохождении в материале линзы, максимальная высота луча на траектории превысит высоту входа на определенную величину, зависящую от этого угла. В известной линзе, выбранной за прототип, согласно замыслу, после преломления на 1-й поверхности все лучи параллельны оптической оси, и затем, в ходе прохождения в материале линзы, максимальная высота луча на траектории не превышает высоты входа луча.
Схемы хода лучей в линзах толщиной L и L/2 для входных параллельных и гомоцентрических пучков с разными видами преломляющих поверхностей показаны на фиг.60-63.
Телескопические и апланатические свойства предложенных вариантов выполнения линзы подтверждаются численными расчетами, результаты которых приведены далее в разделе 6 "Последовательность и результаты численных расчетов".
4. Краткое описание чертежей
На фиг.1 показана схема хода лучей в известной апланатической линзе, принятой за прототип, с толщиной L, с 1-й выпуклой поверхностью и 2-й вогнутой поверхностью, в меридиональной плоскости.
На фиг.2 показана схема хода лучей в известной апланатической линзе, принятой за прототип, с толщиной L/2, с 1-й выпуклой поверхностью и 2-й вогнутой поверхностью, в меридиональной плоскости.
На фиг.3 показаны схемы преломления лучей на 1-й выпуклой поверхности линзы в точке А и на 2-й вогнутой поверхности линзы в точке В, в меридиональной плоскости.
На фиг.4 показана схема хода лучей в апланатической линзе, с толщиной L, с 1-й выпуклой поверхностью и 2-й вогнутой поверхностью, в меридиональной плоскости.
На фиг.5 показаны схемы преломления лучей на 1-й выпуклой поверхности линзы в точке А и на 2-й вогнутой поверхности линзы в точке В, в меридиональной плоскости.
На фиг.6 показана схема хода лучей в апланатической линзе, с толщиной L, с 1-й выпуклой поверхностью и 2-й вогнутой поверхностью, в меридиональной плоскости.
На фиг.7 показаны схемы преломления лучей на 1-й выпуклой поверхности линзы в точке А и на 2-й вогнутой поверхности линзы в точке В, в меридиональной плоскости.
На фиг.8 показана схема хода лучей в апланатической линзе, с толщиной L/2, с 1-й выпуклой поверхностью и 2-й вогнутой поверхностью, в меридиональной плоскости.
На фиг.9 показаны схемы преломления лучей на 1-й выпуклой поверхности линзы в точке А и на 2-й вогнутой поверхности линзы в точке В, в меридиональной плоскости.
На фиг.10 показана схема хода лучей в апланатической линзе, с толщиной L/2, с 1-й выпуклой поверхностью и 2-й вогнутой поверхностью, в меридиональной плоскости.
На фиг.11 показаны схемы преломления лучей на 1-й вогнутой поверхности линзы в точке А и на 2-й выпуклой поверхности линзы в точке В, в меридиональной плоскости.
На фиг.12 показана схема хода лучей в апланатической линзе, с толщиной L, с 1-й вогнутой поверхностью и 2-й выпуклой поверхностью, в меридиональной плоскости.
На фиг.13 показаны схемы преломления лучей на 1-й вогнутой поверхности линзы в точке А и на 2-й выпуклой поверхности линзы в точке В, в меридиональной плоскости.
На фиг.14 показана схема хода лучей в апланатической линзе, с толщиной L, с 1-й вогнутой поверхностью и 2-й выпуклой поверхностью, в меридиональной плоскости.
На фиг.15 показаны схемы преломления лучей на 1-й вогнутой поверхности линзы в точке А и на 2-й выпуклой поверхности линзы в точке В, в меридиональной плоскости.
На фиг.16 показана схема хода лучей в апланатической линзе, с толщиной L/2, с 1-й вогнутой поверхностью и 2-й выпуклой поверхностью, в меридиональной плоскости.
На фиг.17 показаны схемы преломления лучей на 1-й вогнутой поверхности линзы в точке А и на 2-й выпуклой поверхности линзы в точке В, в меридиональной плоскости.
На фиг.18 показана схема хода лучей в апланатической линзе, с толщиной L/2, с 1-й вогнутой поверхностью и 2-й выпуклой поверхностью, в меридиональной плоскости.
На фиг.19 показаны схемы преломления лучей на 1-й плоской поверхности линзы в точке А и на 2-й плоской поверхности линзы в точке В, в меридиональной плоскости.
На фиг.20 показана схема хода лучей в апланатической линзе, с толщиной L, с 1-й и 2-й плоскими поверхностями, в меридиональной плоскости.
На фиг.21 показаны схемы преломления лучей на 1-й плоской поверхности линзы в точке А и на 2-й плоской поверхности линзы в точке В, в меридиональной плоскости.
На фиг.22 показана схема хода лучей в апланатической линзе, с толщиной L/2, с 1-й и 2-й плоскими поверхностями, в меридиональной плоскости.
На фиг.23 показана схема хода лучей в телескопической линзе, с толщиной L, с 1-й выпуклой и 2-й вогнутой сферическими поверхностями, в меридиональной плоскости.
На фиг.24 показана схема хода лучей в телескопической линзе, с толщиной L/2, с 1-й выпуклой и 2-й вогнутой сферическими поверхностями, в меридиональной плоскости.
На фиг.25 показана схема хода лучей в телескопической линзе, с толщиной L, с 1-й выпуклой и 2-й вогнутой коническими поверхностями, в меридиональной плоскости.
На фиг.26 показана схема хода лучей в телескопической линзе, с толщиной L/2, с 1-й выпуклой и 2-й вогнутой коническими поверхностями, в меридиональной плоскости.
На фиг.27 показана схема хода лучей в телескопической линзе, с толщиной L, с 1-й и 2-й плоскими поверхностями, в меридиональной плоскости.
На фиг.28 показана схема хода лучей в телескопической линзе, с толщиной L/2, с 1-й и 2-й плоскими поверхностями, в меридиональной плоскости.
На фиг.29 показана схема хода лучей в телескопической линзе, с толщиной L, с 1-й и 2-й наклонными плоскими поверхностями, в меридиональной плоскости.
На фиг.30 показана схема хода лучей в телескопической линзе, с толщиной L/2, с 1-й и 2-й наклонными плоскими поверхностями, в меридиональной плоскости.
На фиг.31 показана схема хода лучей в телескопической линзе, с толщиной L, с 1-й и 2-й комбинированными поверхностями, образованными из наклонной плоскости и плоскости, перпендикулярной оптической оси, в меридиональной плоскости.
На фиг.32 показана схема хода лучей в телескопической линзе, с толщиной L/2, с 1-й и 2-й комбинированными поверхностями, образованными из наклонной плоскости и плоскости, перпендикулярной оптической оси, в меридиональной плоскости.
На фиг.33 показана схема хода лучей в телескопической линзе, с толщиной L, с 1-й и 2-й комбинированными поверхностями, образованными из наклонных плоскостей с разным углом наклона, в меридиональной плоскости.
На фиг.34 показана схема хода лучей в телескопической линзе, с толщиной L/2, с 1-й и 2-й комбинированными поверхностями, образованными из наклонных плоскостей с разным углом наклона, в меридиональной плоскости.
На фиг.35 показана схема преломления лучей на 1-й выпуклой поверхности линзы в точке А для случая отрицательного значения направляющего коэффициента преломленного луча uB1<0, в меридиональной плоскости.
На фиг.36 показана схема преломления лучей в точке В на 2-й вогнутой поверхности линзы с толщиной L для случая отрицательного значения направляющего коэффициента преломленного на 1-й поверхности луча uB1<0, в меридиональной плоскости.
На фиг.37 показана схема преломления лучей на 1-й выпуклой поверхности линзы в точке А для случая положительного значения направляющего коэффициента преломленного луча uB1>0, в меридиональной плоскости.
На фиг.38 показана схема преломления лучей в точке В на 2-й вогнутой поверхности линзы с толщиной L для случая положительного значения направляющего коэффициента преломленного на 1-й поверхности луча uB1>0, в меридиональной плоскости.
На фиг.39 показана схема преломления лучей в точке В на 2-й вогнутой поверхности линзы с толщиной L/2 для случая отрицательного значения направляющего коэффициента преломленного на 1-й поверхности луча uB1<0, в меридиональной плоскости.
На фиг.40 показана схема преломления лучей в точке В на 2-й вогнутой поверхности линзы с толщиной L/2 для случая положительного значения направляющего коэффициента преломленного на 1-й поверхности луча uB1>0, в меридиональной плоскости.
На фиг.41 показана схема преломления лучей на 1-й вогнутой поверхности линзы в точке А для случая превышения значения направляющего коэффициента преломленного луча значения направляющего коэффициента нормали к 1-й поверхности uB1>uH1, в меридиональной плоскости.
На фиг.42 показана схема преломления лучей в точке В на 2-й выпуклой поверхности линзы с толщиной L для случая превышения значения направляющего коэффициента преломленного луча значения направляющего коэффициента нормали к 1-й поверхности uB1>uH1, в меридиональной плоскости.
На фиг.43 показана схема преломления лучей на 1-й вогнутой поверхности линзы в точке А для случая превышения значения направляющего коэффициента нормали к 1-й поверхности значения направляющего коэффициента преломленного луча uB1<uH1, в меридиональной плоскости.
На фиг.44 показана схема преломления лучей в точке В на 2-й выпуклой поверхности линзы с толщиной L для случая превышения значения направляющего коэффициента нормали к 1-й поверхности значения направляющего коэффициента преломленного луча uB1<uH1, в меридиональной плоскости.
На фиг.45 показана схема преломления лучей в точке В на 2-й выпуклой поверхности линзы с толщиной L/2 для случая превышения значения направляющего коэффициента преломленного луча значения направляющего коэффициента нормали к 1-й поверхности uB1>uH1, в меридиональной плоскости.
На фиг.46 показана схема преломления лучей в точке В на 2-й выпуклой поверхности линзы с толщиной L/2 для случая превышения значения направляющего коэффициента нормали к 1-й поверхности значения направляющего коэффициента преломленного луча uB1<uH1, в меридиональной плоскости.
На фиг.47 показана схема преломления лучей на 1-й плоской поверхности линзы в точке А, в меридиональной плоскости.
На фиг.48 показана схема преломления лучей в точке В на 2-й плоской поверхности линзы с толщиной L, в меридиональной плоскости.
На фиг.49 показана схема преломления лучей в точке В на 2-й плоской поверхности линзы с толщиной L/2, в меридиональной плоскости.
На фиг.50 показана схема хода лучей в апланатической линзе с толщиной L, с 1-й выпуклой и 2-й вогнутой сферическими поверхностями, в меридиональной плоскости.
На фиг.51 показана схема хода лучей в апланатической линзе с толщиной L/2, с 1-й выпуклой и 2-й вогнутой сферическими поверхностями, в меридиональной плоскости.
На фиг.52 показана схема хода лучей в апланатической линзе с толщиной L, с 1-й и 2-й плоскими поверхностями, в меридиональной плоскости.
На фиг.53 показана схема хода лучей в апланатической линзе с толщиной L/2, с 1-й и 2-й плоскими поверхностями, в меридиональной плоскости.
На фиг.54 показана схема хода лучей в апланатической линзе, с толщиной L, с 1-й и 2-й наклонными плоскими поверхностями, в меридиональной плоскости.
На фиг.55 показана схема хода лучей в апланатической линзе, с толщиной L/2, с 1-й и 2-й наклонными плоскими поверхностями, в меридиональной плоскости.
На фиг.56 показана схема хода лучей в апланатической линзе, с толщиной L, с 1-й и 2-й комбинированными поверхностями, образованными из наклонной плоскости и плоскости, перпендикулярной оптической оси, в меридиональной плоскости.
На фиг.57 показана схема хода лучей в апланатической линзе, с толщиной L/2, с 1-й и 2-й комбинированными поверхностями, образованными из наклонной плоскости и плоскости, перпендикулярной оптической оси, в меридиональной плоскости.
На фиг.58 показана схема хода лучей в апланатической линзе, с толщиной L, с 1-й и 2-й комбинированными поверхностями, образованными из наклонных плоскостей с разным углом наклона, в меридиональной плоскости.
На фиг.59 показана схема хода лучей в апланатической линзе, с толщиной L/2, с 1-й и 2-й комбинированными поверхностями, образованными из наклонных плоскостей с разным углом наклона, в меридиональной плоскости.
На фиг.60 показана схема хода лучей для входных параллельных и гомоцентрических пучков в линзе с толщиной L, с 1-й выпуклой и 2-й вогнутой сферическими поверхностями, в меридиональной плоскости.
На фиг.61 показана схема хода лучей для входных параллельных и гомоцентрических пучков в линзе с толщиной L/2, с 1-й выпуклой и 2-й вогнутой коническими поверхностями, в меридиональной плоскости.
На фиг.62 показана схема хода лучей для входных параллельных и гомоцентрических пучков в линзе с толщиной L/2, с 1-й и 2-й наклонными плоскими поверхностями, в меридиональной плоскости.
На фиг.63 показана схема хода лучей для входных параллельных и гомоцентрических пучков в линзе с толщиной L/2, с 1-й и 2-й плоскими поверхностями, в меридиональной плоскости.
На фиг.64 показана схема хода лучей в эндоскопе с использованием предложенной апланатической линзы, в меридиональной плоскости.
На фиг.65 показана схема хода лучей в эндоскопе с использованием телескопических и апланатических свойств предложенной линзы, в меридиональной плоскости.
5. Осуществление изобретения
Для реализации предложенной градиентной линзы из материала с гиперсекансным распределением ПП n(y) вида (1) и известными значениями n0 и а вначале, исходя из параметров распределения n(y), определяют номинальное фокусное расстояние, согласно (4).
Затем определяется конструктивно необходимая толщина линзы d (кратная удвоенному номинальному фокусному расстоянию F), например, L или L/2.
Выбирается также назначение линзы - телескопическая или апланатическая. В последнем случае задают, при необходимости, величину переднего отрезка
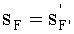 .
.
Определяется также форма используемых преломляющих поверхностей - плоская, наклонная плоская, сферическая, комбинированная (из двух плоскостей) или другая.
Затем берется заготовка для линзы необходимого диаметра из материала с известным распределением ПП n(y) и обрезается до рассчитанной толщины, кратной удвоенному номинальному фокусному расстоянию (с определенным технологическим припуском). Формообразование 1-й и 2-й преломляющих поверхностей на торцах заготовки производится по одной из известных оптических технологий, например, путем последовательной шлифовки и полировки, до достижения заданной формы поверхностей.
Используется предлагаемая градиентная линза обычным образом. В случае использования предлагаемой линзы как телескопической линзы на 1-ю поверхность линзы (см., например, фиг.23-34) подается параллельный пучок излучения. После преломления на 1-й поверхности и прохождения внутри линзы параллельный пучок излучения, преломляясь на 2-й поверхности линзы, выходит из нее, оставаясь параллельным.
В случае апланатической линзы точечный источник излучения 1 помещается в точку М1 на оптической оси перед 1-й преломляющей поверхностью линзы 2 (фиг.64). После преломления на 1-й поверхности и прохождения внутри линзы гомоцентрический пучок излучения, преломляясь на 2-й поверхности линзы, выходит из нее, оставаясь гомоцентрическим (с центром в точке
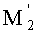 на оптической оси).
на оптической оси).
Использование предложенной апланатической линзы возможно, например, в качестве градана в эндоскопах (фиг.64), как и линзы-прототипа [1, 5]. В этом случае исследуемый объект 1 помещается в передний фокус апланатической линзы 2. Мнимое изображение объекта через окуляр 3 (с использованием компенсатора аберраций 4) попадает в глаз наблюдателя 5. В результате, в эндоскопе можно обойтись без обычно применяемого входного объектива в виде короткофокусной градиентной линзы (обычно она приклеивается к линзе - транслятору изображения), что упрощает и удешевляет конструкцию.
Поскольку апланатические свойства линзы сохраняются при изменении переднего фокуса, то возникает возможность фокусировки на исследуемые объекты, расположенные на некотором интервале вдоль оптической оси, причем без перемещения самого эндоскопа в целом. Для обеспечения просмотра объектов, расположенных на некотором интервале вдоль оси, можно перемещать вдоль оси окуляр с фиксированным фокусным расстоянием или применять неподвижный окуляр с изменяемым фокусным расстоянием.
Возможно также одновременное использование телескопических и апланатических свойств предложенной линзы в эндоскопе. Для этого в схему добавляется объектив 6, который совместно с окуляром образует телескопическую систему с отрицательным увеличением - W (фиг.65). Заметим, что объектив может быть обычного типа, а не в виде дорогостоящей и сложной в производстве градиентной линзы, что упрощает конструкцию эндоскопа.
Тогда предложенная линза используется как телескопическая, предпочтительно с увеличением -1 (соответственно, имеющая толщину k*L/2, где k - нечетное число, равное 1, 3, 5, …), и параллельный пучок на входе линзы преобразуется в параллельный пучок на выходе. Затем этот параллельный пучок поступает на вход объектива 6 телескопической системы, после выхода из которого параллельный пучок попадает в глаз наблюдателя 5. В результате, наблюдатель увидит прямое и увеличенное в W раз изображение исследуемого объекта 1, расположенного в бесконечности (или, реально, на значительном удалении от эндоскопа).
Если исследуемый объект 1 приблизить к эндоскопу, то для получения изображения объекта достаточно изменить положение объектива 6 или, что предпочтительно, окуляра 3, т.е. расфокусировать телескопическую систему. В этом случае предложенная линза будет работать как апланатическая для объекта на конечном расстоянии. Соответственно, исследуемый объект 1 оказывается в переднем фокусе апланатической линзы 2. Мнимое изображение объекта рассматривается через объектив 6, и затем через окуляр 3 попадает в глаз наблюдателя 5.
Эндоскоп с использованием предложенной линзы, схема которого приведена на фиг.65, обладает дополнительным преимуществом по сравнению с известной конструкцией эндоскопа. Для фокусирования на предмет известный эндоскоп необходимо перемещать целиком. Эндоскоп с использованием предложенной линзы можно установить в определенное фиксированное положение, а фокусировку осуществлять с помощью окуляра, что при осмотре в ограниченном пространстве может быть более удобно и позволит снизить возможность нежелательных механических контактов оптических элементов эндоскопа с предметами исследуемой полости.
Другой возможностью использования предложенной линзы является применение ее, как отдельного апланатического и/или телескопического элемента, в составе сложной оптической системы, например, объектива, телескопа, конденсора и т.п.
6. Последовательность и результаты численных расчетов
6.1. Последовательность проведения расчетов
6.1.1. Общие условия и исходные данные
Целью проведения расчетов является подтверждение апланатического и телескопического хода лучей в заявляемой линзе толщиной L и L/2 для следующих вариантов выполнения:
- линза с 1-й выпуклой и 2-й вогнутой поверхностями (п.6.2.1), имеющая о сферические поверхности, линза толщиной L (п.6.2.1.1);
- сферические поверхности, линза толщиной L/2 (п.6.2.1.2);
- конические поверхности, линза толщиной L (п.6.2.1.3);
- конические поверхности, линза толщиной L/2 (п.6.2.1.4);
- гиперболические поверхности высшего порядка, линза толщиной L (п.6.2.1.5);
- гиперболические поверхности высшего порядка, линза толщиной L/2 (п.6.2.1.6);
- линза с 1-й вогнутой и 2-й выпуклой поверхностями (п.6.2.2), имеющая
- сферические поверхности, линза толщиной L (п.6.2.2.1);
- сферические поверхности, линза толщиной L/2 (п.6.2.2.2);
- конические поверхности, линза толщиной L (п.6.2.2.3);
- конические поверхности, линза толщиной L/2 (п.6.2.2.4);
- линза с 1-й и 2-й плоскими поверхностями (п.6.2.3), имеющая о плоские поверхности, линза толщиной L (п.6.2.3.1);
- плоские поверхности, линза толщиной L/2 (п.6.2.3.2).
Расчеты проводились для меридиональной плоскости, численные значения даны в миллиметрах, результаты приведены с точностью до семи значащих цифр.
Вершина 1-й поверхности расположена в начале координат, каждый луч гомоцентрического пучка выходит из предметной точки на оптической оси. Общими исходными данными для расчета являются:
1) закон распределения показателя преломления
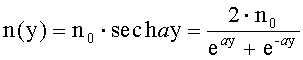 ;
;
2) значения n0=1,60; a=0,5 мм-1 - принимаются как типичные для производимых серийно градиентных микролинз;
3) длина периодичности
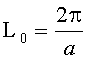 ,
,
и половина длины периодичности
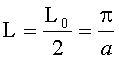 ;
;
4) величины переднего и заднего отрезков
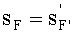 выбираются равными sF1= 2,0 и sF2=7,0 мм;
выбираются равными sF1= 2,0 и sF2=7,0 мм;
5) высоты входных лучей bT=0,1-0,8 мм;
6) уравнение траектории хода для луча с начальной высотой bT, начальной координатой zT и с начальным коэффициентом наклона (тангенсом начального угла наклона) φ1 определяется формулой (5), а производная
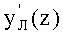 - формулой (8);
- формулой (8);
7) радиусы сферических поверхностей выбираются одинаковыми и равными в расчетах RC1=3,0 и RC2=5,0 мм (в случае сферических поверхностей);
8) точность расчетов по методу Ньютона для системы нелинейных уравнений принимается равной ΔH=1,0×10-12;
9) для известной апланатической линзы, принятой за прототип, в качестве исходных данных для численных расчетов приняты параметры преломляющих поверхностей, указанные в [1], при этом изменены только величины переднего отрезка.
6.1.2. Последовательность расчетов
для случая линзы с 1-й выпуклой и 2-й вогнутой поверхностями 1.
Задается толщина линзы d, кратная половине длины периодичности и выбирается
кратность x1=2 (длина периодичности) для линзы толщиной L
d1=x1,L
кратность x2=1 для линзы толщиной L/2
d2=x2L
2. Уравнение образующей для 1-й выпуклой поверхности
- для сферической поверхности с радиусом R (в случае 1-й и 2-й сферических поверхностей для них устанавливаются радиусы одинаковой величины R=R1=R2) задается в виде
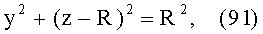
или, для участка образующей окружности с координатами z=0-R, y=0-R
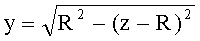 ,
,
- для конической поверхности (образующая представляет собой прямую) и коэффициента наклона р образующей прямой задается в виде
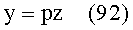
3. Исходя из заданной высоты bT пересечения входного луча с 1-й поверхностью фиксируется координата yП1=bT точки пересечения, а вторая координата zП1 определяется
- для образующей в виде окружности - на основе (91), для участка образующей окружности с координатами z=0-R, y=0-R, по формуле
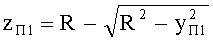 ;
;
- для образующей в виде прямой - на основе (92), по формуле
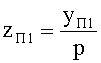
4. Направляющий коэффициент uK1 входного луча для 1-й поверхности определяется
- для апланатической линзы по формуле
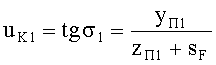 ;
;
- для телескопической линзы
uK1=0
5. Для определения направляющего коэффициента нормали uH1 1-й поверхности определяется производная
- для образующей в виде окружности - на основе (91), для участка образующей окружности с координатами z=0-R, y=0-R, по формуле
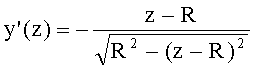 ;
;
- для образующей в виде прямой - на основе (92), по формуле
y'(z)=p
Значение производной находится в точке zП1, zП1.
6. По известной формуле вычисляется направляющий коэффициент нормали к 1-й поверхности в точке пересечения
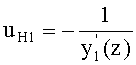
7. Рассчитывается угол падения по формуле
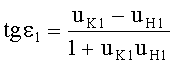 ,
,
8. Затем по известной формуле вычисляется
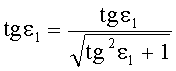
9. Для известного значения yП1 по формуле (1) вычисляется n(yП1) и затем определяется угол преломления
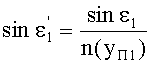
10. Затем по известной формуле вычисляется угол преломления на 1-й поверхности
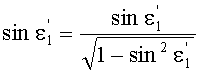
При определении угла преломления принимается во внимание, что, в зависимости от параметров линзы, могут быть два расчетных случая (фиг.35 и 37, случай направления преломленного луча параллельно оптической оси здесь не рассматривается), однако, для обоих случаев расчетные формулы совпадают.
Угол преломления на 1-й поверхности также может быть вычислен в обоих случаях из соотношения
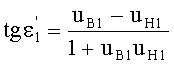 ,
,
откуда коэффициент наклона преломленного луча
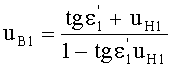
11. Уравнение (5) траектории хода луча после преломления на 1-й поверхности в точке пересечения с координатой zП1 можно представить в форме неявной функции
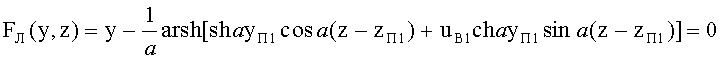 ,
,
где yП1 - начальная высота луча;
uB1 - начальный направляющий коэффициент луча.
С учетом (6) и (7) функцию можно выразить в виде
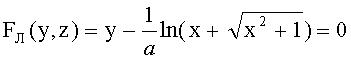 ,
,
где
x=shayП1cosa(z-zП1)+uB1chayП1sina(z-zП1)
Частная производная FЛ(y, z) по z
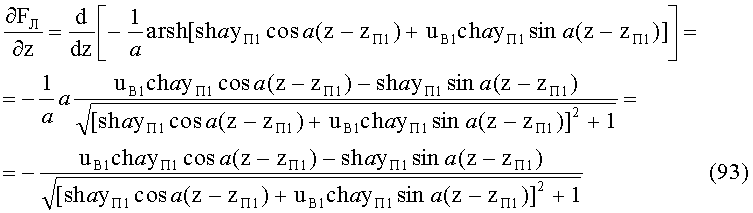
Частная производная FЛ(y, z) по y
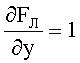
12. Уравнение образующей для 2-й вогнутой поверхности
- для образующей в виде окружности радиусом R и участка образующей окружности с координатами z=d-(d+R), y=0-R (линза толщиной L) уравнение имеет вид
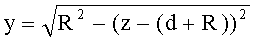
- для участка образующей окружности с координатами z=d-(d+R), у=0-(-R) (линза толщиной L/2) уравнение имеет вид
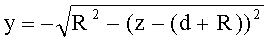
- для образующей в виде прямой (для 2-й вогнутой конической поверхности, линза толщиной L) уравнение задается в виде
y=p(z-d)
- для образующей в виде прямой (для 2-й вогнутой конической поверхности, линза толщиной L/2) уравнение задается в виде
y=-p(z-d)
13. Уравнение образующей для 2-й вогнутой поверхности линзы можно записать в виде неявной функции
Для 2-й вогнутой сферической поверхности неявная функция, с учетом (X), примет вид
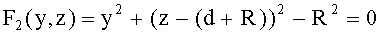
Частная производная этой неявной функции по z
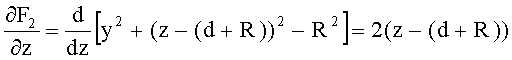
Частная производная этой неявной функции по y
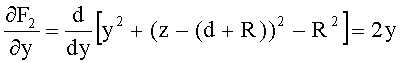
Для образующей в виде прямой (для 2-й вогнутой конической поверхности, линза толщиной L) неявная функция примет вид
F2(y,z)=y-p(z-d)=0
Частная производная этой неявной функции по z
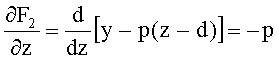
Частная производная этой неявной функции по y
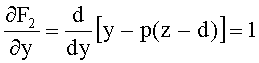
Для образующей в виде прямой (для 2-й вогнутой конической поверхности, линза толщиной L/2) неявная функция примет вид
F2(y,z)=y+p(z-d)=0
Частная производная этой неявной функции по z
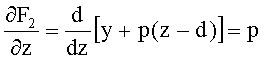
Частная производная этой неявной функции по y
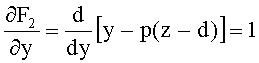
14. Координаты zП2, yП2 точки пересечения траектории хода луча yЛ с соответствующей образующей 2-й поверхности F2(y,z) определяется из численного решения системы нелинейных уравнений
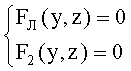
Если имеются две функции
FЛ(y,z)=0
F2(y,z)=0
то для метода Ньютона получаются следующие расчетные итерационные формулы [6]
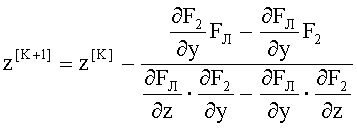
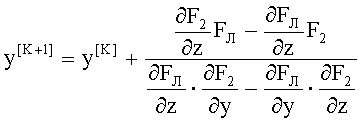
После проведения итерационного процесса определяются с заданной точностью значения координат zП2, yП2 точки пересечения траектории хода луча yЛ с соответствующей образующей F2(y,z) для 2-й поверхности.
15. Направляющий коэффициент uK2 луча в точке пересечения zП1, zП2 траектории хода луча yЛ с образующей 2-й вогнутой поверхности определяется на основе (93) по формуле
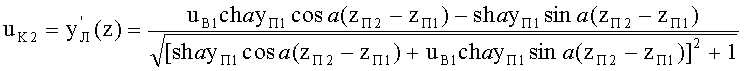
16. Производная образующей для 2-й вогнутой поверхности в точке пересечения zП2, yП2 вычисляется
- для образующей в виде окружности радиусом R и участка образующей окружности с координатами z=d-(d+R), y=0-R (линза толщиной L) с уравнением
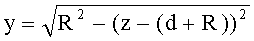
по формуле
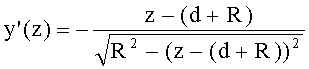
- для образующей в виде окружности радиусом R и участка образующей окружности с координатами z=d-(d+R), y=0-(-R) (линза толщиной L/2) с уравнением
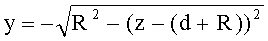
по формула
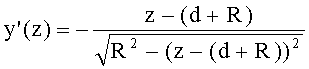
- для образующей в виде прямой (для 2-й вогнутой конической поверхности, линза толщиной L) с уравнением
y=p(z-d)
по формуле
y'(z)=р
- для образующей в виде прямой (для 2-й вогнутой конической поверхности, линза толщиной L/21) с уравнением
y=-p(z-d)
по формуле
y(z)=-p
17. Направляющий коэффициент нормали ко 2-й поверхности в точке пересечения вычисляется для соответствующей образующей по известной формуле
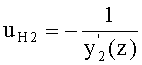
18. Определяется угол падения
Для линзы толщиной L при определении угла падения принимается во внимание, что могут быть два расчетных случая преломления на 2-й поверхности, зависящие от параметров преломления на 1-й поверхности (фиг.36 и 38), однако, для обоих случаев расчетная формула совпадает
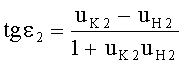
Для линзы толщиной L/2 при определении угла падения принимается во внимание, что могут быть два расчетных случая преломления на 2-й поверхности, зависящие от параметров преломления на 1-й поверхности (фиг.39 и 40), однако, для обоих случаев расчетная формула также совпадает
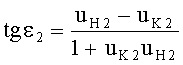
19. Затем вычисляется
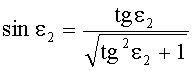
20. Определяется угол преломления
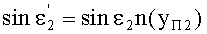
21. Затем вычисляется угол преломления на 2-й поверхности
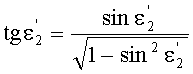
22. Вычисляется направляющий коэффициент uB2 преломленного на 2-й поверхности входного луча
- для линзы толщиной L по формуле
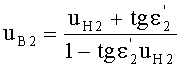
- для линзы толщиной L/2 по формуле
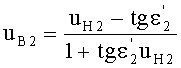
23. Определяется теоретическое значение направляющего коэффициента выходного луча
- для апланатической линзы толщиной L по формуле
uB2T=uK1,
- для апланатической линзы толщиной L/2 по формуле
uВ2Т=-uK1,
- для телескопической линзы
uВ2Т=0
24. Определяется разница ΔuB2 между полученным в результате преломления uB2 и теоретическим значением uB2T направляющего коэффициента выходного луча
ΔuB2=uB2T-uB2,
которая, согласно замыслу, должна быть равна нулю.
6.1.3. Последовательность расчетов
для случая линзы с 1-й вогнутой и 2-й выпуклой поверхностями
1. Задается толщина линзы d, кратная половине длины периодичности и выбирается
кратность x1=2 (длина периодичности) для линзы толщиной L
d1=x1L,
кратность х2=1 для линзы толщиной L/2
d2=x2L
1. Уравнение образующей для 1-й вогнутой поверхности
- для сферической поверхности с радиусом R (в случае 1-й и 2-й сферических поверхностей для них устанавливаются радиусы одинаковой величины R=R1=R2) задается в виде
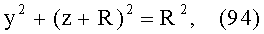
или, для участка образующей окружности с координатами z=0-(-R), y=0-R
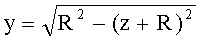 ,
,
- для конической поверхности (образующая представляет собой прямую) и коэффициента наклона - р образующей прямой задается в виде
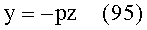
3. Исходя из заданной высоты bT пересечения входного луча с 1-й поверхностью фиксируется координата yП1=bT точки пересечения, а вторая координата zП1 определяется
- для образующей в виде окружности - на основе (94), для участка образующей окружности с координатами z=0-(-R), н=0-R, по формуле
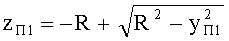 ;
;
- для образующей в виде прямой - на основе (95), по формуле
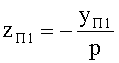
4. Направляющий коэффициент uK1 входного луча для 1-й поверхности определяется
- для апланатической линзы по формуле
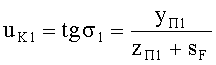 ;
;
- для телескопической линзы
uK1=0
5. Для определения направляющего коэффициента нормали uH1 1-й поверхности определяется производная
- для образующей в виде окружности - на основе (94), для участка образующей окружности с координатами z=0-(-R), y=0-R, по формуле
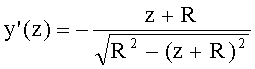 ;
;
- для образующей в виде прямой - на основе (95), по формуле
y'(z)=-p
Значение производной находится в точке zП1, yП1.
6. По известной формуле вычисляется направляющий коэффициент нормали к 1-й поверхности в точке пересечения
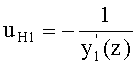
1. Угол падения луча на 1-ю поверхность рассчитывается, принимая во внимание следующие случаи, зависящие от параметров линзы:
- при uK1>uH1 (луч ниже нормали, фиг.41) угол падения определяется по формуле
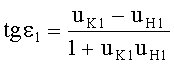 ,
,
- при uK1<uH1 (луч выше нормали, фиг.43) угол падения определяется по формуле
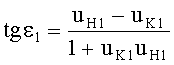 ;
;
8. Затем по известной формуле вычисляется
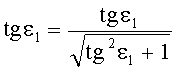
9. Для известного значения yП1 по формуле (1) вычисляется n(yП1) и затем определяется угол преломления
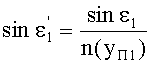
10. Затем по известной формуле вычисляется угол преломления на 1-й поверхности
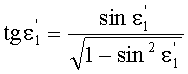
Угол преломления на 1-й поверхности также может быть вычислен
- при uK1>uH1 (фиг.41) по формуле
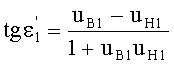 ,
,
- при uK1<uH1 (фиг.43) по формуле
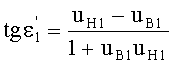 ,
,
Соответственно, направляющий коэффициент uB1 преломленного на 1-й поверхности входного луча рассчитывается
- при uK1>uH1 (фиг.41) по формуле
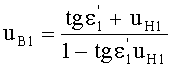
- при uK1<uH1 (фиг.43) по формуле
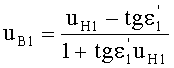
11. Расчет частных производных для уравнения (5) траектории хода луча после преломления на 1-й поверхности проводится аналогично п.11 раздела 6.1.2.
12. Уравнение образующей для 2-й выпуклой поверхности
- для образующей в виде окружности радиусом R и участка образующей окружности с координатами z=d-(d-R), y=0-R (линза толщиной L) уравнение имеет вид
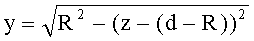 ,
,
- для участка образующей окружности с координатами z=d-(d-R), y=0-(-R) (линза толщиной L/2) уравнение имеет вид
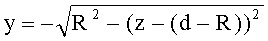 ,
,
- для образующей в виде прямой (для 2-й выпуклой конической поверхности, линза толщиной L) уравнение задается в виде
y=-p(z-d),
- для образующей в виде прямой (для 2-й выпуклой конической поверхности, линза толщиной L 12) уравнение задается в виде
y=p(z-d)
13. Уравнение образующей для 2-й выпуклой поверхности линзы можно записать в виде неявной функции.
Для 2-й выпуклой сферической поверхности неявная функция, с учетом (X), примет вид
F2(y,z)=y2+(z-(d-R))2-R2=0
Частная производная этой неявной функции по z
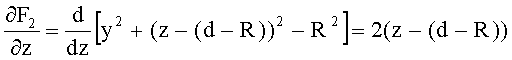
Частная производная этой неявной функции по y
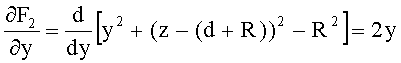
Для образующей в виде прямой (для 2-й выпуклой конической поверхности, линза толщиной L) неявная функция примет вид
F2(y,z)=y+p(z-d)=0
Частная производная этой неявной функции по z
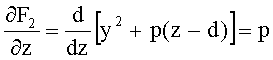
Частная производная этой неявной функции по y
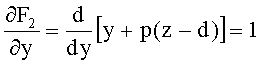
Для образующей в виде прямой (для 2-й выпуклой конической поверхности, линза толщиной L 11) неявная функция примет вид
F2(y,z)=y-p(z-d)=0
Частная производная этой неявной функции по z
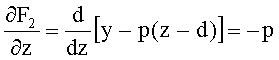
Частная производная этой неявной функции по y
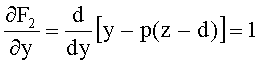
14. Координаты zП2, yП2 точки пересечения траектории хода луча yЛ с соответствующей образующей F2(y,z) для 2-й поверхности определяется из численного решения системы нелинейных уравнений аналогично п.14 раздела 6.1.2.
15. Направляющий коэффициент uK2 луча в точке пересечения zП2, yП2 траектории хода луча yЛ с образующей 2-й выпуклой поверхности определяется на основе (93) по формуле
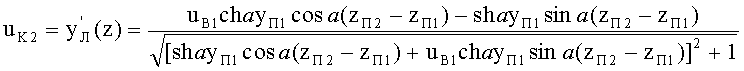
16. Производная образующей для 2-й выпуклой поверхности в точке пересечения с координатами zП2, yП2 вычисляется
- для образующей в виде окружности радиусом R и участка образующей окружности с координатами z=d-(d-R), y=0-R (линза толщиной L) с уравнением
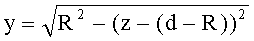 ,
,
по формуле
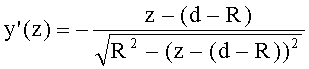
- для образующей в виде окружности радиусом R и участка образующей окружности с координатами z=d-(d+R), y=0-(-R) (линза толщиной L/2) с уравнением
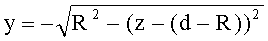
по формуле
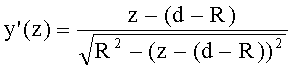
- для образующей в виде прямой (для 2-й выпуклой конической поверхности, линза толщиной L) с уравнением
y=-p(z-d)
по формуле
y'(z)=-p
- для образующей в виде прямой (для 2-й выпуклой конической поверхности, линза толщиной L/2) с уравнением
y=p(z-d)
по формуле
y'(z)=p
17. Направляющий коэффициент нормали ко 2-й поверхности в точке пересечения вычисляется для соответствующей образующей по известной формуле
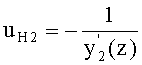
18. Определяется угол падения на 2-ю поверхность
Для линзы толщиной L при определении угла падения принимается во внимание, что могут быть два расчетных случая преломления на 2-й выпуклой поверхности, зависящие от параметров преломления на 1-й вогнутой поверхности (фиг.42 и 44).
Угол падения на 2-ю выпуклую поверхность
- при uK2>uH2 (фиг.42) определяется по формуле
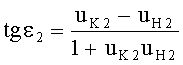 ,
,
- при uK2<uH2 (фиг.44) определяется по формуле
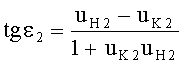
Для линзы толщиной L/2 при определении угла падения также принимается во внимание, что могут быть два расчетных случая преломления на 2-й выпуклой поверхности, зависящие от параметров преломления на 1-й вогнутой поверхности (фиг.45 и 46)
Соответственно, угол падения на 2-ю выпуклую поверхность
- при uK2<uH2 (фиг.45) определяется по формуле
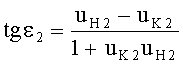 ;
;
- при uK2>uH2 (фиг.46) определяется по формуле
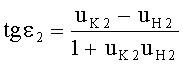
19. Затем вычисляется
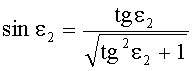
20. Определяется угол преломления
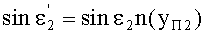
21. Затем вычисляется угол преломления на 2-й поверхности
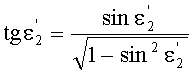
22. Вычисляется направляющий коэффициент uB2 преломленного на 2-й поверхности входного луча
Для линзы толщиной L при определении, угла падения принимается во внимание, что могут быть два расчетных случая преломления на 2-й выпуклой поверхности, зависящие от параметров преломления на 1-й вогнутой поверхности (фиг.42 и 44).
Угол падения на 2-ю выпуклую поверхность
- при uK2>uH2 (фиг.42) определяется по формуле
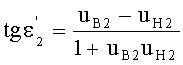 ,
,
откуда направляющий коэффициент uB2 преломленного на 2-й поверхности входного луча
 ;
;
- при uK2<uH2 (фиг.44) определяется по формуле
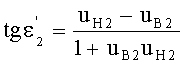
откуда направляющий коэффициент uB2 преломленного на 2-й поверхности входного луча
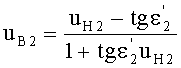
Для линзы толщиной L/2 при определении угла падения также принимается во внимание, что могут быть два расчетных случая преломления на 2-й выпуклой поверхности, зависящие от параметров преломления на 1-й вогнутой поверхности (фиг.45 и 46)
Угол падения на 2-ю выпуклую поверхность
- при uK2<uH2 (фиг.45) определяется по формуле
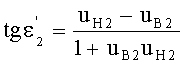
откуда направляющий коэффициент uB2 преломленного на 2-й поверхности входного луча
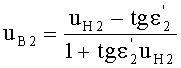
- при uK2>uH2 (фиг.46) определяется по формуле
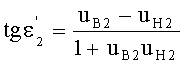
откуда направляющий коэффициент uB2 преломленного на 2-й поверхности входного луча
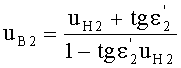 ;
;
23. Определяется теоретическое значение направляющего коэффициента выходного луча
- для апланатической линзы толщиной L по формуле
uB2T=uK1,
- для апланатической линзы толщиной L/2 по формуле
uB2T=-uK1,
- для телескопической линзы
uB2T=0
24. Определяется разница ΔuB2 между полученным в результате преломления uB2 и теоретическим значением uB2T направляющего коэффициента выходного луча
ΔuВ2=uB2T-uB2,
которая, согласно замыслу, должна быть равна нулю.
6.1.4. Последовательность расчетов для случая линзы с 1-й и 2-й плоскими поверхностями, перпендикулярными оптической оси
1. Задается толщина линзы d, кратная половине длины периодичности и выбирается
кратность x1=1 (длина периодичности) для линзы толщиной L
d1=x1L,
кратность x2=1 для линзы толщиной L/2
d2=x2L
2. Уравнение образующей для 1-й плоской поверхности
z=0
3. Исходя из заданной высоты bT пересечения входного луча с 1-й поверхностью фиксируется координата yП1=bT точки пересечения, а вторая координата zП1=0.
4. Направляющий коэффициент uK1 входного луча для 1-й поверхности определяется
- для апланатической линзы по формуле
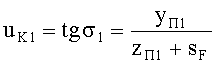 ;
;
- для телескопической линзы
uK1=0
5. Направляющий коэффициент нормали uH1 для 1-й поверхности
uH1=0
6. Рассчитывается угол падения луча на 1-ю поверхность
tgε1=uK1
7. Затем по известной формуле вычисляется
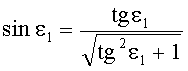
8. Для известного значения yП1 по формуле (1) вычисляется n(yП1) и затем определяется угол преломления
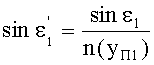
9. Затем по известной формуле вычисляется угол преломления на 1-й поверхности
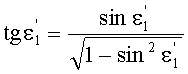
Угол преломления на 1-й плоской поверхности также может быть вычислен из соотношения
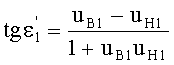 ,
,
откуда коэффициент наклона преломленного на 1-й поверхности луча
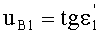
10. Уравнение для 2-й плоской поверхности
- для линзы толщиной L (кратность х1=2)
z=d1,
- для линзы толщиной L/2 (кратность х2=1)
z=d2
11. Координаты zП2, yП2 точки пересечения траектории хода луча yЛ с плоской 2-й поверхностью не вычисляются из-за очевидности и принимаются
- для линзы толщиной L (кратность х1=2)
zП1=d1, yП2=yП1
- для линзы толщиной L/2 (кратность х2=1)
zП2=d2, yП2=-yП1
12. Направляющий коэффициент uK2 луча в точке пересечения zП2, yП1 траектории хода луча yЛ с образующей 2-й вогнутой поверхности определяется на основе (93) по формуле
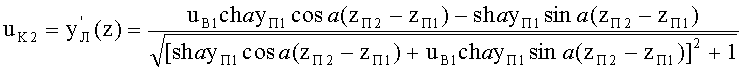
13. Направляющий коэффициент нормали uH2 для 2-й поверхности
uН2=0
14. Определяется угол падения
- для линзы толщиной L (фиг.48) по формуле
tgε2=uK2
- для линзы толщиной L/2 (фиг.49) по формуле
tgε2=-uK2
15. Затем вычисляется
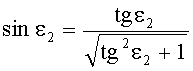
16. Определяется угол преломления
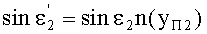
17. Затем вычисляется угол преломления на 2-й поверхности
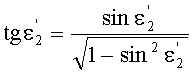
18. Вычисляется направляющий коэффициент uB2 преломленного на 2-й поверхности входного луча
- для линзы толщиной L (фиг.48), исходя из соотношения
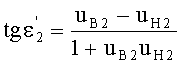
по формуле
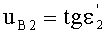
- для линзы толщиной L/2 (фиг.49), исходя из соотношения
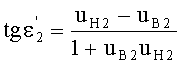
по формуле
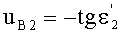
19. Определяется теоретическое значение направляющего коэффициента выходного луча
- для апланатической линзы толщиной L по формуле
uB2T=uK1,
- для апланатической линзы толщиной L/2 по формуле
uВ2Т=-uК1,
- для телескопической линзы
uВ2Т=0
20. Определяется разница ΔuB2 между полученным в результате преломления uB2 и теоретическим значением uB2T направляющего коэффициента выходного луча
ΔuB2=uB2T-uB2,
которая, согласно замыслу, должна быть равна нулю.
6.1.5. Последовательность расчетов для случая линзы с 1-й выпуклой и 2-й вогнутой гиперсекансными поверхностями
1. Задается толщина линзы d, кратная половине длины периодичности и выбирается
кратность х1=2 (длина периодичности) для линзы толщиной L
d1=x1L,
кратность х2=1 для линзы толщиной L/2
d2=x2L
2. Уравнение образующей для 1-й выпуклой поверхности задается в виде (2)
y2(z)=(n2(y)-1)z2+2sF(n(y)-1)z
Известно также [1], что можно представить уравнение образующей 1-й поверхности и как зависимость z(y) в виде
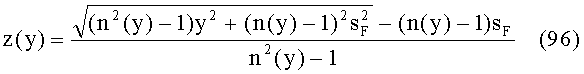
3. Исходя из заданной высоты bT пересечения входного луча с 1-й поверхностью фиксируется координата yП1=bT точки пересечения, а координата zП1 определяется на основе (96) по формуле
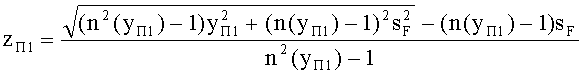 .
.
4. Направляющий коэффициент uK1 входного луча для 1-й поверхности определяется
- для апланатической линзы по формуле
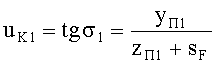 ;
;
- для телескопической линзы
uK1=0
5. Для определения направляющего коэффициента нормали uH1 1-й поверхности определяется производная для образующей 1-й поверхности по известной формуле [1]
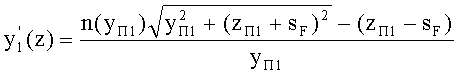
6-11. Расчеты по п.6-11 ведутся аналогично соответствующим пунктам раздела
6.1.2.
12. Уравнение образующей для 2-й вогнутой поверхности задается в виде (3)
y2(z)=(n2(y)-1)(z-d)2+2sF(n(y)-1)(z-d)
Для 2-й вогнутой поверхности неявная функция, с учетом (3), примет вид
F2(y,z)=(n2(y)-1)(z-d)2+2sF(n(y)-1)(z-d)-y2(z)=0,
Частная производная этой неявной функции по z
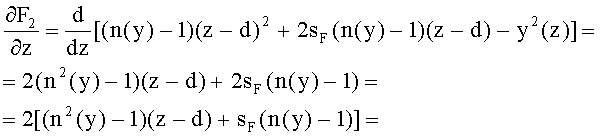
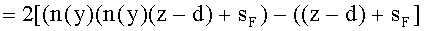
Частная производная этой неявной функции по y
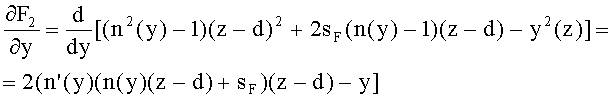 ,
,
где
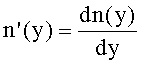
Учитывая закон распределения ПП (1), а также известные соотношения
[chx]'=shx
и
[xa]'=axa-1,
получим
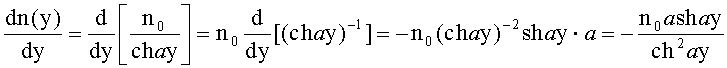
и, соответственно
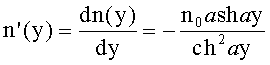
14. Координаты zП2, yП2 точки пересечения траектории хода луча yЛ с соответствующей образующей 2-й поверхности F2(y,z) определяется из численного решения системы нелинейных уравнений аналогично п.14 раздела 6.1.2.
15. Направляющий коэффициент uK2 луча в точке пересечения zП2, yП2 траектории хода луча yЛ с образующей 2-й вогнутой поверхности определяется аналогично п.15 раздела 6.1.2.
16. Производная образующей для 2-й вогнутой поверхности в точке пересечения zП2, yП2 вычисляется по известной формуле [1]
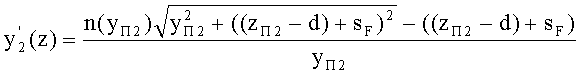
17-24. Расчеты по п.17-24 ведутся аналогично соответствующим пунктам раздела 6.1.2.
6.2. Результаты расчетов
6.2.1. Линза с 1-й выпуклой и 2-й вогнутой поверхностями
6.2.1.1. Сферические поверхности, линза толщиной L
Толщина линзы d=L=12,566370 мм
Апланатический ход лучей
Передний отрезок sF1=2,0 мм
Радиусы сферических поверхностей выбираются равными RC1=3,0 мм
Таблица 1
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0,10
1,667129Е-3
4,995835Е-2
-3,335186Е-2
8,344926Е-2
1,598002
1,872631Е-2
0,20
6,674090Е-3
9,966740Е-2
-6,681531Е-2
1,675988Е-1
1,592033
3,731394Е-2
0,30
1,503768Е-2
1,488805Е-1
-1,005037Е-1
2,531726Е-1
1,582167
5,564100Е-2
0,40
2,678625Е-2
1,973567Е-1
-1,345345Е-1
3,409438Е-1
1,568524
7,361760Е-2
0, 50
4,196010Е-2
2,448627Е-1
-1,690308Е-1
4,317640Е-1
1,551269
9,119813Е-2
0,60
6,061230Е-2
2,911755Е-1
-2,041241Е-1
5,265986Е-1
1,530604
1,083901Е-1
0,70
8,280957Е-2
3,360844Е-1
-2,399569Е-1
6,265717Е-1
1,506764
1,252596Е-1
0,80
1,086335Е-1
3,793926Е-1
-2,766857Е-1
7,330260Е-1
1,480011
1,419344Е-1
Таблица 2
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0,10
0,10
1,256803E+1
1,872631E-2
-3,335186E-2
1,598002
0,20
0,20
1,257304E+1
3,731394E-2
-6,681531E-2
1,592033
0,30
0,30
1,258140E+1
5,564100E-2
-1,005037E-1
1,582167
0,40
0,40
1,259315E+1
7,361760E-2
-1,345345E-1
1,568524
0,50
0,50
1,260833E+1
9,119813E-2
-1,690308E-1
1,551269
0,60
0,60
1,262698E+1
1,083901E-1
-2,041241E-1
1,530604
0,70
0,70
1,264918E+1
1,252596E-1
-2,399569E-1
1,506764
0,80
0,80
1,267500E+1
1,419344E-1
-2,766857E-1
1,480011
Продолжение таблицы 2
bt
tgε2
uB2T
uB2
ΔuB2
0,10
5,211072E-2
4,995835E-2
4,995835E-2
5,377642E-15
0,20
1,043895E-1
9,966740E-2
9,966740E-2
-2,678413E-15
0,30
1,570228E-1
1,488805E-1
1,488805E-1
5,551115E-17
0,40
2,102343E-1
1,973567E-1
1,973567E-1
1,110223E-16
0,50
2,643033E-1
2,448627E-1
2,448627E-1
7,771561E-16
0,60
3,19585aE-l
2,911755E-1
2,911755E-1
1,110223E-16
0,70
3,765340E-1
3,360844E-1
3,360844E-1
2,775557E-16
0,80
4,357319E-1
3,793926E-1
3,793926E-1
2,220446E-16
Передний отрезок sF2=7,0 мм
Радиусы сферических поверхностей выбираются равными RC1=3,0 мм
Таблица 3
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0,10
1,667129Е-3
1,428231E-2
-3,335186E-2
4,765688E-2
1,598002
-3,546135E-3
0,20
6,674090Е-3
2,854421E-2
-6,681531E-2
9,554174E-2
1,592033
-6,940305E-3
0,30
1,503768Е-2
4,276527E-2
-1,005037E-1
1,438874E-1
1,582167
-1,002951E-2
0,40
2,678625Е-2
5,692502E-2
-1,345345E-1
1,929371E-1
1,568524
-1,265861E-2
0,50
4,196010Е-2
7,100295E-2
-1,690308E-1
2,429496E-1
1,551269
-1,466905E-2
0,60
6,061230Е-2
8,497846E-2
-2,041241E-1
2,942059E-1
1,530604
-1,589737E-2
0,70
8,280957Е-2
9,883083E-2
-2,399569E-1
3,470173E-1
1,506764
-1,617326E-2
0,80
1,086335Е-1
1,125392E-1
-2,766857E-1
4,017341E-1
1,480011
-1,531711E-2
Таблица 4
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0,10
0,10
1,256803Е+1
-3,546135E-3
-3,335186E-2
1,598002
0,20
0,20
1,257304Е+1
-6,940305E-3
-6,681531E-2
1,592033
0,30
0,30
1,258140Е+1
-1,002951E-2
-1,005037E-1
1,582167
0,40
0,40
1,259315Е+1
-1,265861E-2
-1,345345E-1
1,568524
0,50
0,50
1,260833Е+1
-1,466905E-2
-1,690308E-1
1,551269
0,60
0,60
1,262698Е+1
-1,589737E-2
-2,041241E-1
1,530604
0,70
0,70
1,264918Е+1
-1,617326E-2
-2,399569E-1
1,506764
0,80
0,80
1,267500Е+1
-1,531711E-2
-2,766857E-1
1,480011
Продолжение таблицы 4
bt
tgε2
uB2T
uB2
ΔuB2
0,10
2,980220E+2
1,428231E-2
1,428231E-2
5,346417E-15
0,20
5,984725E-2
2,854421E-2
2,854421E-2
-2,602085E-15
0,30
9,038316E-2
4,276527E-2
4,276527E-2
1,179611E-16
0,40
1,216687E-1
5,692502E-2
5,692502E-2
6,938893E-17
0,50
1,539799E-1
7,100295E-2
7,100295E-2
6,383782E-16
0,60
1,876179E-1
8,497846E-2
8,497846E-2
1,804112E-16
0,70
2,229185E-1
9,883083E-2
9,883083E-2
4,163336E-17
0,80
2,602656E-1
1,125392E-1
1,125392E-1
1,526556E-16
Передний отрезок sF2=2,0 мм
Радиусы сферических поверхностей выбираются равными RC1=5,0 мм
Таблица 5
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.000100E-3
4.997500E-2
-2.000400E-2
7.004903E-2
1.598002
2.374530E-2
0.20
4.001601E-3
9.980031E-2
-4.003203E-2
1.403932E-1
1.592033
4.746475E-2
0.30
9.008114E-3
1.493274E-1
-6.010829E-2
2.113325E-1
1.582167
7.114365E-2
0.40
1.602568E-2
1.984101E-1
-8.025723E-2
2.831766E-1
1.568524
9.478899E-2
0.50
2.506281E-2
2.469059E-1
-1.005037E-1
3.562500E-1
1.551269
1.184384E-1
0.60
3.613054E-2
2.946765E-1
-1.208734E-1
4.308980E-1
1.530604
1.421677E-1
0.70
4.924248E-2
3.415896E-1
-1.413925E-1
5.074931E-1
1.506764
1.660968E-1
0.80
6.441492E-2
3.875189E-1
-1.620881E-1
5.864429E-1
1.480011
1.903949E-1
Таблица 6
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.256737Е+1
2.374530E-2
-2.000400E-2
1.598002
0.20
0.20
1.257037Е+1
4.746475E-2
-4.003203E-2
1.592033
0.30
0.30
1.257537Е+1
7.114365E-2
-6.010829E-2
1.582167
0.40
0.40
1.258239Е+1
9.478899E-2
-8.025723E-2
1.568524
0.50
0.50
1.259143Е+1
1.184384E-1
-1.005037E-1
1.551269
0.60
0.60
1.260250Е+1
1.421677E-1
-1.208734E-1
1.530604
0.70
0.70
1.261561Е+1
1.660968E-1
-1.413925E-1
1.506764
0.80
0.80
1.263078Е+1
1.90394SE-1
-1.620881E-1
1.480011
Продолжение таблицы 6
bt
tgε2
uB2T
uB2
ΔuB2
0.10
4.377010E-2
4.997500E-2
4.997500E-2
5.287437Е-15
0.20
8.766335E-2
9.980031E-2
9.980031E-2
2.775557Е-17
0.30
1.318156E-1
1.493274E-1
1.493274E-1
2.775557Е-17
0.40
1.763880E-1
1.984101E-1
1.984101E-1
1.526556Е-15
0.50
2.215797E-1
2.469059E-1
2.469059E-1
-1.026956Е-15
0.60
2.676404E-1
2.946765E-1
2.946765E-1
1.054711Е-15
0.70
3.148844E-1
3.415896E-1
3.415896E-1
-8.326672Е-16
0.80
3.637073E-1
3.875189E-1
3.875189E-1
1.665334Е-16
Передний отрезок sF1=7,0 мм
Радиусы сферических поверхностей выбираются равными RC1=5,0 мм
Таблица 7
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.000100Е-3
1.428367Е-2
-2.000400E-2
3.429747E-2
1.598002
1.450422E-3
0.20
4.001601Е-3
2.855510Е-2
-4.003203E-2
6.866563E-2
1.592033
3.032084E-3
0.30
9.008114Е-3
4.280206Е-2
-6.010829E-2
1.031758E-1
1.582167
4.876899E-3
0.40
1.602568Е-2
5.701233Е-2
-8.025723E-2
1.379005E-1
1.568524
7.118171E-3
0.50
2.506281Е-2
7.117374Е-2
-1.005037E-1
1.729144E-1
1.551269
9.891399E-3
0.60
3.613054Е-2
8.527414Е-2
-1.208734E-1
2.082945E-1
1.530604
1.333521E-2
0.70
4.924248Е-2
9.930145Е-2
-1.413925E-1
2.441215E-1
1.506764
1.759251E-2
0.80
6.441492Е-2
1.132436Е-1
-1.620881E-1
2.804801E-1
1.480011
2.281191E-2
Таблица 8
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.256737Е+1
1.450422E-3,
-2.000400E-2
1.598002
0.20
0.20
1.257037Е+1
3.032084E-3
-4.0Q3203E-2
1.592033
0.30
0.30
1.257537Е+1
4.876899E-3
-6.010829E-2
1.582167
0.40
0.40
1.258239Е+1
7.118171E-3
-8.025723E-2
1.568524
0.50
0.50
1.259143Е+1
9.891399E-3
-1.005037E-1
1.551269
0.60
0.60
1.260250Е+1
1.333521E-2
-1.208734E-1
1.530604
0.70
0.70
1.261561Е+1
1.759251E-2
-1.413925E-1
1.506764
0.80
0.80
1.263078Е+1
2.281191E-2
-1.620881E-1
1.480011
Продолжение таблицы 8
bt
tgε2
uB2T
uB2
ΔuB2
0.10
2.145504E-2
1.428367Е-2
1.428367Е-2
5.263151Е-15
0.20
4.306935E-2
2.855510Е-2
2.855510Е-2
3.816391Е-17
0.30
6.500424E-2
4.280206Е-2
4.280206Е-2
6.245004Е-17
0.40
8.742535E-2
5.701233Е-2
5.701233Е-2
1.387778Е-15
0.50
1.105050E-1
7.117374Е-2
7.117374Е-2
-9.020562Е-16
0.60
1.344253E-1
8.527414Е-2
8.527414Е-2
9.436895Е-16
0.70
1.593814E-1
9.930145Е-2
9.930145Е-2
-5.828670Е-16
0.80
1.855863E-1
1.132436Е-1
1.132436Е-1
1.249000Е-16
Телескопический ход лучей
Направляющий коэффициент для любого входного луча uK1=0
Радиусы сферических поверхностей выбираются равными RC1=3,0 мм
Таблица 9
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.667129Е-3
0.0
-3.335186E-2
3.335186Е-2
1.598002
-1.247926E-2
0.20
6.674090Е-3
0.0
-6.681531E-2
6.681531Е-2
1.592033
-2.483383E-2
0.30
1.503768Е-2
0.0
-1.005037E-1
1.005037Е-1
1.582167
-3.693760E-2
0.40
2.678625Е-2
0.0
-1.345345E-1
1.345345Е-1
1.568524
-4.866167E-2
0.50
4.196010Е-2
0.0
-1.690308E-1
1.690308Е-1
1.551269
-5.987282E-2
0.60
6.061230Е-2
0.0
-2.041241E-1
2.041241Е-1
1.530604
-7.043200E-2
0.70
8.280957Е-2
0.0
-2.399569E-1
2.399569Е-1
1.506764
-8.019258E-2
0.80
1.086335Е-1
0.0
-2.766857E-1
2.766857Е-1
1.480011
-8.899851E-2
Таблица 10
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.256803Е+1
-1.247926E-2
-3.335186E-2
1.598002
0.20
0.20
, 1.257304Е+1
-2.483383E-2
-6.681531E-2
1.592033
0.30
0.30
1.258140Е+1
-3.693760E-2
-1.005037E-1
1.582167
0.40
0.40
1.259315Е+1
-4.866167E-2
-1.345345E-1
1.568524
0.50
0.50
1.260833Е+1
-5.987282E-2
-1.690308E-1
1.551269
0.60
0.60
1.262698Е+1
-7.043200E-2
-2.041241E-1
1.530604
0.70
0.70
1.264918Е+1
-8.019258E-2
-2.399569E-1
1.506764
0.80
0.80
1.267500Е+1
-8.899851E-2
-2.766857E-1
1.480011
Продолжение таблицы 10
bt
tgε2
uB2T
uB2
ΔuB2
0.10
2.086392E-2
0.0
5.337011E-15
5.337011E-15
0.20
4.191193E-2
0.0
-2.597428E-15
-2.597428E-15
0.30
6.333106E-2
0.0
6.869504E-17
6.869504E-17
0.40
8.531436E-2
0.0
5.452428E-17
5.452428E-17
0.50
1.080643E-1
0.0
5.936609E.-16
5.936609E-16
0.60
1.317973E-1,,
0.0
1.332267E-16
1.332267E-16
0.70
1.567480E-1
0.0
7.873331E-17
7.873331E-17
0.80
1.831766E-1
0.0
1.546910E-16
1.546910E-16
Радиусы сферических поверхностей выбираются равными RС1=5,0 мм
Таблица 11
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.000100Е-3
0.0
-2.000400E-2
2.000400E-2
1.598002
-7.485518Е-3
0.20
4.001601Е-3
0.0
-4.003203E-2
4.003203E-2
1.592033
-1.488402Е-2
0.30
9.008114Е-3
0.0
-6.010829E-2
6.010829E-2
1.582167
-2.210789Е-2
0.40
1.602568Е-2
0.0
-8.025723E-2
8.025723E-2
1.568524
-2.906828Е-2
0.50
2.506281Е-2
0.0
-1.005037E-1
1.005037E-1
1.551269
-3.567449Е-2
0.60
3.613054Е-2
0.0
-1.208734E-1
1.208734E-1
1.530604
-4.183333Е-2
0.70
4.924248Е-2
0.0
-1.413925E-1
1.413925E-1
1.506764
-4.744845Е-2
0.80
6.441492Е-2
0.0
-1.620881E-1
1.620881E-1
1.480011
-5.241965Е-2
Таблица 12
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.256737Е+1
-7.485518Е-3
-2.000400E-2
1.598002
0.20
0.20
1.257037Е+1
-1.488402Е-2
-4.003203E-2
1.592033
0.30
0.30
1.257537Е+1
-2.210789Е-2
-6.010829E-2
1.582167
0.40
0.40
1.258239Е+1
-2.906828Е-2
-8.025723E-2
1.568524
0.50
0.50
1.259143Е+1
-3.567449E-2
-1.005037E-1
1.551269
0.60
0.60
1.260250Е+1
-4.183333Е-2
-1.208734E-1
1.530604
0.70
0.70
1.261561Е+1
-4.744845Е-2
-1.413925E-1
1.506764
0.80
0.80
1.263078Е+1
-5.241965Е-2
-1.620881E-1
1.480011
Продолжение таблицы 12
bt
tgε2
uB2T
uB2
ΔuB2
0.10
1.251660E-2
0.0
5.257577Е-15
5.257577Е-15
0.20
2.513303E-2
0.0
4.156675Е-17
4.156675Е-17
0.30
3.794996E-2
0.0
6.913913Е-17
6.913913Е-17
0.40
5.106980E-2
0.0
1.337530Е-15
1.337530Е-15
0.50
6.459767E-2
0.0
-9.067746Е-16
-9.067746Е-16
0.60
7.864245E-2
0.0
9.301004Е-16
9.301004Е-16
0.70
9.331799E-2
0.0
-5.442313Е-16
-5.442313Е-16
0.80
1.087445E-1
0.0
1.352251Е-16
1.352251Е-16
6.2.1.2. Сферические поверхности, линза толщиной L/2
Толщина линзы d=L/2=6,283185 мм
Апланатический ход лучей
Передний отрезок sF1=2,0 мм
Радиусы сферических поверхностей выбираются равными RC1=3,0 мм
Таблица 13
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.667129Е-3
4.995835Е-2
-3.335186E-2
8.344926E-2
1.598002
1.872631E-2
0.20
6.674090Е-3
9.966740Е-2
-6.681531E-2
1.675.988E-1
1.592033
3.731394E-2
0.30
1.503768Е-2
1.4888Q5E-1
-1.005037E-1
2.531726E-1
1.582167
5.564100E-2
0.40
2.678625Е-2
1.973567Е-1
-1.345345E-1
3.409438E-1
1.568524
7.361760E-2
0.50
4.196010Е-2
2.448627Е-1
-1.690308E-1
4.317640E-1
1.551269
9.119813E-2
0.60
6.061230Е-2
2.911755Е-1
-2.041241E-1
5.265986E-1
1.530604
1.083901E-1
0.70
8.280957Е-2
3.360844Е-1
-2.399569E-1
6.265717E-1
1.506764
1.252596E-1
0.80
1.086335Е-1
3.793926Е-1
-2.766857E-1
7.330260E-1
1.480011
1.419344E-1
Таблица 14
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
-0.10
6.284852
-1.872631E-2
3.335186E-2
1.598002
0.20
-0.20
6.289859
-3.731394E-2
6.681531E-2
1.592033
0.30
-0.30
6.298222
-5.564100E-2
1.005037E-1
1.582167
0.40
-0.40
6.309971
-7.361760E-2
1.345345E-1
1.568524
0.50
-0.50
6.325145
-9.119813E-2
1.690308E-1
1.551269
0.60
-0.60
6.343797
-1.083901E-1
2.041241E-1
1.530604
0.70
-0.70
6.365994
-1.252596E-1
2.399569E-1
1.506764
0.80
-0.80
6.391818
-1.419344E-1
2.766857E-1
1.480011
Продолжение таблицы 14
bt
tgε2
uB2T
uB2
ΔuB2
0.10
5.211072E-2
-4.995835Е-2
-4.995835Е-2
-2.081668Е-17
0.20
1.043895E-1
-9.966740Е-2
-9.966740Е-2
-1.387778Е-17
0.30
1.570228E-1
-1.488805E-1
-1.488805E-1
0.0
0.40
2.102343E-1
-1.973567Е-1
-1.973567Е-1
-5.551115Е-17
0.50
2.643033E-1
-2.448627Е-1
-2.448627Е-1
-7.771561Е-16
0.60
3.195851E-1
-2.911755Е-1
-2.911755Е-1
-1.110223Е-16
0.70
3.765340E-1
-3.360844Е-1
-3.360844Е-1
0.0
0.80
4.357319E-1
-3.793926Е-1
-3.793926Е-1
-5.551115Е-17
Передний отрезок sF2=7,0 мм
Радиусы сферических поверхностей выбираются равными RC1=3,0 мм
Таблица 15
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0,10
1.667129E-3
1.428231E-2
-3.335186E-2
4,765688E-2
1,598002
-3.546135E-3
0,20
6.674090E-3
2.854421E-2
-6,681531E-2
9,554174E-2
1,592033
-6.940305E-3
0,30
1,503768E-2
4,276527E-2
-1,005037E-1
1,438874E-1
1,582167
-1.002951E-2
0,40
2,678625E-2
5,692502E-2
-1.345345E-1
1,929371E-1
1,568524
-1.265861E-2
0,50
4,196010E-2
7,100295E-2
-1,690308E-1
2,429496E-1
1,551269
-1,4бб905Е-2
0,60
6,061230E-2
8,497846E-2
-2,041241E-1
2,942059E-1
1,530604
-1.589737Е-2
0,70
8,280957E-2
9,883083E-2
-2.399569E-1
3.470173E-1
1,506764
-1,617326Е-2
0,80
1,086335E-1
1,125392E-1
-2.766857E-1
4.017341E-1
1,480011
-1.531711Е-2
Таблица 16
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0,10
-0.10
6,284852
3,546135Е-3
3,335186Е-2
1,598002
0,20
-0.20
6,289859
6.940305Е-3
б,681531Е-2
1,592033
0,30
-0.30
6,298222
1,002951Е-2
1.005037Е-1
1,582167
0,40
-0.40
6,309971
1.265861Е-2
1.345345Е-1
1,568524
0,50
-0.50
6,325145
1.466905Е-2
1,690308Е-1
1,551269
0,60
-0.60
6,343797
1,589737Е-2
2.041241Е-1
1,530604
0,70
-0.70
6,365994
1.617326Е-2
2.399569Е-1
1,506764
0,80
-0.80
6,391818
1,531711Е-2
2,766857Е-1
1,480011
Продолжение таблицы 16
bt
tgε2
uB2T
uB2
ΔuB2
0,10
2.980220E-2
-1.428231E-2
-1.428231Е-2
-1.734723Е-17
0,20
5.984725E-2
-2.854421E-2
-2.854421Е-2
-3.469446Е-17
0,30
9,038316E-2
-4,27б527Е-2
-4.276527Е-2
-3,469446Е-17
0,40
1,216687E-1
-5.692502Е-2
-5.692502Е-2
-4.163336Е-17
0,50
1.539799E-1
-7,100295Е-2
-7.100295Е-2
-5,828670Е-16
0,60
1.876179E-1
-8.497846Е-2
-8,497846Е-2
-6.938893Е-17
0,70
2.229185E-1
-9.883083Е-2
-9,883083Е-2
-4.163336Е-17
0,80
2,602656E-1
-1,125392E-1
-1,125392E-1
-1.526556Е-16
Передний отрезок sF1=2,0 мм
Радиусы сферических поверхностей выбираются равными RC2=5,0 мм
Таблица 17
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.000100E-3
4.997500E-2
-2.000400E-2
7.004903E-2
1.598002
2.374530E-2
0.20
4.001601E-3
9.980031E-2
-4.003203E-2
1.403932E-1
1.592033
4.746475E-2
0.30
9.008114E-3
1.493274E-1
-6.010829E-2
2.113325E-1
1.582167
7.114365E-2
0.40
1.602568E-2
1.984101E-1
-8.025723E-2
2.831766E-1
1.568524
9.478899E-2
0.50
2.506281E-2
2.469059E-1
-1.005037E-1
3.562500E-1
1.551269
1.184384E-1
0.60
3.613054E-2
2.946765E-1
-1.208734E-1
4.308980E-1
1.530604
1.421677E-1
0.70
4.924248E-2
3.415896E-1
-1.413925E-1
5.074931E-1
1.506764
1.660968E-1
0.80
6.441492E-2
3.875189E-1
-1.620881E-1
5.864429E-1
1.480011
1.903949E-1
Таблица 18
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
-0.10 1
6.284185
-2.374530E-2
2.000400Е-2
1.598002
0.20
-0.20
6.287186
-4.746475E-2
4.003203Е-2
1.592033
0.30
-0.30
6.292193
-7.114365E-2
6.010829Е-2
1.582167
0.40
-0.40
6.299210
-9.478899E-2
8.025723Е-2
1.568524
0.50
-0.50
6.308248
-1.184384E-1
1.005037Е-1
1.551269
0.60
-0.60
6.319315
-1.421677E-1
1.208734Е-1
1.530604
0.70
-0.70
6.332427
-1.660968E-1
1.413925Е-1
1.506764
0.80
-0.80
6.347600
-1.903949E-1
1.620881Е-1
1.480011
Продолжение таблицы 18
bt
tgε2
uB2T
uB2
ΔuB2
0.10
4.377010Е-2
-4.997500E-2
-4.997500E-2
0.0
0.20
8.766335Е-2
-9.980031E-2
-9.980031E-2
0.0
0.30
1.318156Е-1
-1.493274E-1
-1.493274E-1
-2.775557Е-17
0.40
1.763880Е-1
-1.984101Е-1
-1.984101Е-1
-2.775557Е-17
0.50
2.215797Е-1
-2.469059E-1
-2.469059E-1
-1.110223Е-16
0.60
2.676404Е-1
-2.946765E-1
-2.946765E-1
-5.551115Е-17
0.70
3.148844Е-1
-3.415896E-1
-3.415896E-1
0.0
0.80
3.637073Е-1
-3.875189E-1
-3.875189E-1
3.885780Е-16
Передний отрезок sF2=7,0 мм
Радиусы сферических поверхностей выбираются равными RC2=5,0 мм
Таблица 19
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.000100Е-3
,1.428367Е-2
-2.000400E-2
3.429747E-2
1.598002
1.450422E-3
0.20
4.001601Е-3
2.855510Е-2
-4.003203E-2
6.866563E-2
1.592033
3.032084E-3
0.30
9.008114Е-3
4.280206Е-2
-6.010829E-2
1.031758E-1
1.582167
4.876899E-3
0.40
1.602568Е-2
5.701233Е-2
-8.025723E-2
1.379005E-1
1.568524
7.118171E-3
0.50
2.506281Е-2
7.117374Е-2
-1.005037E-1
1.729144E-1
1.551269
9.891399E-3
0.60
3.613054Е-2
8.527414Е-2
-1.208734E-1
2.082945E-1
1.530604
1.333521E-2
0.70
4.924248Е-2
9.930145Е-2
-1.413925E-1
2.441215E-1
1.506764
1.759251E-2
0.80
6.441492Е-2
1.132436Е-1
-1.620881E-1
2.804801E-1
1.480011
2.281191E-2
Таблица 20
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
-0.10
6.284185
-1.450422E-3
2.000400E-2
1.598002
0.20
-0.20
6.287186
-3.032084E-3
4.003203E-2
1.592033
0.30
-0.30
6.292193
-4.876899E-3
6.010829E-2
1.582167
0.40
-0.40
6.299210
-7.118171E-3
8.025723E-2
1.568524
0.50
-0.50
6.308248
-9.891399E-3
1.005037E-1
1.551269
0.60
-0.60
6.319315
-1.333521E-2
1.208734E-1
1.530604
0.70
-0.70
6.332427
-1.759251E-2
1.413925E-1
1.506764
0.80
-0.80
6.347600
-2.281191E-2
1.620881E-1
1.480011
Продолжение таблицы 20
bt
tgε2
uB2T
uB2
ΔuB2
0.10
2.145504E-2
-1.428367E-2
-1.428367E-2
-5.204170Е-18
0.20
4.306935E-2
-2.855510Е-2
-2.855510Е-2
-2.428612Е-17
0.30
6.500424E-2
-4.280206Е-2
-4.280206Е-2
-2.081668Е-17
0.40
8.742535E-2
-5.701233Е-2
-5.701233Е-2
-3.469446Е-17
0.50
1.105050E-1
-7.117374Е-2
-7.117374Е-2
-5.551115Е-17
0.60
1.344253E-1
-8.527414Е-2
-8.527414Е-2
-2.775557Е-17
0.70
1.593814E-1
-9.930145Е-2
-9'.930145Е-2
-8.326672Е-17
0.80
1.855863E-0
-1.132436Е-1
-1.132436Е-1
2.498001Е-16
Телескопический ход лучей
Направляющий коэффициент для любого входного луча uK1=0
Радиусы сферических поверхностей выбираются равными RC1=3,0 мм
Таблица 21
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.667129Е-3
0.0
-3.335186E-2
3.335186E-2
1.598002
-1.247926E-2
0.20
6.674090Е-3
0.0
-6.681531E-2
6.681531E-2
1.592033
-2.483383E-2
0.30
1.503768Е-2
0.0
-1.005037E-1
1.005037E-1
1.582167
-3.693760E-2
0.40
2.678625Е-2
0.0
-1.345345E-1
1.345345E-1
1.568524
-4.866167E-2
0.50
4.196010Е-2
0.0
-1.690308E-1
1.690308E-1
1.551269
-5.987282E-2
0.60
6.061230Е-2
0.0
-2.041241E-1
2.041241E-1
1.530604
-7.043200E-2
0.70
8.280957Е-2
0.0
-2.399569E-1
2.399569E-1
1.506764
-8.019258E-2
0.80
1.086335Е-1
0.0
-2.766857E-1
2.766857E-1
1.480011
-8.899851E-2
Таблица 22
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
-0.10
6.284852
1.247926Е-2
3.335186E-2
1.598002
0.20
-0.20
6.289859
2.483383Е-2
6.681531E-2
1.592033
0.30
-0.30
6.298222
3.693760Е-2
1.005037E-1
1.582167
0.40
-0.40
6.309971
4.866167Е-2
1.345345E-1
1.568524
0.50
-0.50
6.325145
5.987282Е-2
1.690308E-1
1.551269
0.60
-0.60
6.343797
7.043200Е-2
2.041241E-1
1.530604
0.70
-0.70
6.365994
8.019258Е-2
2.399569E-1
1.506764
0.80
-0.80
6.391818
8.899851Е-2
2.766857E-1
1.480011
Продолжение таблицы 22
bt
tgε2
uB2T
uB2
ΔuB2
0.10
2.086392E-2
0.0
-1.386236Е-17
-1.386236Е-17
0.20
4.191193E-2
0.0
-2.763221Е-17
-2.763221Е-17
0.30
6.333106E-2
0.0
-2.747801Е-17
-2.747801Е-17
0.40
8.531436E-2
0.0
-2.726214Е-17
-2.726214Е-17
0.50
1.080643E-1
0.0
-5.396917Е-16
-5.396917Е-16
0.60
1.317973E-1
0.0
-7.9936Q5E-17
-7.993605Е-17
0.70
1.567480E-1
0.0
-5.248887Е-17
-5.248887Е-17
0.80
1.831766E-1
0.0
-1.031273Е-16
-1.031273Е-16
Радиусы сферических поверхностей выбираются равными RC2=5,0 мм
Таблица 23
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.000100Е-3
0.0
-2.000400E-2
2.000400E-2
1.598002
-7.485518Е-3
0.20
4.001601Е-3
0.0
-4.003203E-2
4.003203E-2
1.592033
-1.488402Е-2
0.30
9.008114Е-3
0.0
-6.010829E-2
6.010829E-2
1.582167
-2.210789Е-2
0.40
1.602568Е-2
0.0
-8.025723E-2
8.025723E-2
1.568524
-2.906828Е-2
0.50
2.506281Е-2
0.0
-1.005037E-1
1.005037E-1
1.551269
-3.567449Е-2
0.60
3.613054Е-2
0.0
-1.208734E-1
1.208734E-1
1.530604
-4.183333Е-2
0.70
4.924248Е-2
0.0
-1.413925E-1
1.413925E-1
1.506764
-4.744845Е-2
0.80
6.441492Е-2
0.0
-1.620881E-1
1.62088LE-1
1.480011
-5.241965Е-2
Таблица 24
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
-0.10
6.284185
7.485518Е-3
2.000400E-2
1.598002
0.20
-0.20
6.287186
1.488402Е-2
4.003203E-2
1.592033
0.30
-0.30
6.292193
2.210789Е-2
6.010829E-2
1.582167
0.40
-0.40
6.299210
2.906828Е-2
8.025723E-2
1.568524
0.50
-0.50
6.308248
3.567449Е-2
1.005037E-1
1.551269
0.60
-0.60
6.319315
4.183333Е-2
1.208734E-1
1.530604
0.70
-0.70
6.332427
4.744845Е-2
1.413925E-1
1.506764
0.80
-0.80
6.347600
5.241965Е-2
1.620881Е-1
1.480011
Продолжение таблицы 24
bt
tgε2
uB2T
uB2
ΔuB2
0.10
1.251660Е-2
0.0
-1.040417Е-17
-1.040417Е-17
0.20
2.513303Е-2
0.0
-2.078337Е-17
-2.078337Е-17
0.30
3.794996Е-2
0.0
-3.456956Е-17
-3.456956Е-17
0.40
5.106980Е-2
0.0
-4.136690Е-17
-4.136690Е-17
0.50
6.459767Е-2
0.0
-4.121702Е-17
-4.121702Е-17
0.60
7.864245Е-2
0.0
-5.471179Е-17
-5.471179Е-17
0.70
9.331799Е-2
0.0
-8.163469Е-17
-8.163469Е-17
0.80
1.087445Е-1
0.0
2.434052Е-16
2.434052Е-16
6.2.1.3. Конические поверхности, линза толщиной L
Толщина линзы d=L=12,566370 мм
Апланатический ход лучей
Передний отрезок sF1=2,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p1=1,3
Таблица 25
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
7.692307Е-2
4.814814E-2
-7.692307E-1
8.488165E-1
1.598002
-2.434051E-1
0.20
1.538461Е-1
9.285714E-2
-7.692307E-1
9.284023E-1
1.592033
-2.174489E-1
0.30
2.307692Е-1
1.344827Е-1
-7.692307E-1
1.007988E+0
1.582167
-1.927227E-1
0.40
3.076923Е-1
1.733333E-1
-7.692307E-1
1.087573E+0
1.568524
-1.687630E-1
0.50
3.846153Е-1
2.096774E-1
-7.692307E-1
1.167159E+0
1.551269
-1.451521E-1
0.60
4.615384Е-1
2.437500E-1
-7.692307E-1
1.246745E+0
1.530604
-1.215097E-1
0.70
5.384615Е-1
2.757575E-1
-7.692307E-1
1.326331E+0
1.506764
-9.748457E-2
0.80
6.153846Е-1
3.058823E-1
-7.692307E-1
1.405917E+0
1.480011
-7.274397E-2
Таблица 26
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.264329Е+1
-2.434051E-1
-7.692307Е-1
1.598002
0.20
0.20
1.272021Е+1
-2.174489E-1
-7.692307Е-1
1.592033
0.30
0.30
1.279713Е+1
-1.927227E-1
-7.692307E-1
1.582167
0.40
0.40
1.287406Е+1
-1.687630E-1
-7.692307E-1
1.568524
0.50
0.50
1.295098Е+1
-1.451521E-1
-7.692307E-1
1.551269
0.60
0.60
1.302790Е+1
-1.215097E-1
-7.692307E-1
1.530604
0.70
0.70
1.310483Е+1
-9.748457E-2
-7.692307E-1
1.506764
0.80
0.80
1.318175Е+1
-7.274397E-2
-7.692307E-1
1.480011
Продолжение таблицы 26
bt
tgε2
uB2T
uB2
ΔuB2
0.10
4.428994E-1
4.814814E-2
4.814814E-2
-1.387778Е-17
0.20
4.727119E-1
9.285714E-2
9.285714E-2
1.526556Е-16
0.30
5.020761E-1
1.344827Е-1
1.344827Е-1
8.326672Е-17
0.40
5.314730E-1
1.733333E-1
1.733333E-1
-5.551115Е-17
0.50
5.613957E-1
2.096774E-1
2.096774E-1
5.551115Е-17
0.60
5.923541E-1
2.437500E-1
2.437500E-1
-1.387778Е-16
0.70
6.248870E-1
2.757575E-1
2.757575E-1
2.220446Е-16
0.80
6.595788E-1
3.058823E-1
3.058823E-1
4.996003Е-16
Передний отрезок sF2=7,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p1=1,3
Таблица 27
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
7.692307Е-2
1.413043Е-2
-7.692307E-1
7.919695E-1
1.598002
-2.624648E-1
0.20
1.538461Е-1
2.795698Е-2
-7.692307E-1
8.147083E-1
1.592033
-2.529284E-1
0.30
2.307692Е-1
4.148936Е-2
-7.692307E-1
8.374471E-1
1.582167
-2.424300E-1
0.40
3.076923Е-1
5.473684Е-2
-7.692307E-1
6.601859E-1
1.568524
-2.309010E-1
0.50
3.846153Е-1
6.770833Е-2
-7.692307E-1
8.829247E-1
1.551269
-2.182711E-1
0.60
4.615384Е-1
8.041237Е-2
-7.692307E-1
9.056635E-1
1.530604
-2.044661E-1
0.70
5.384615Е-1
9.285714Е-2
-7.692307E-1
9.284023E-1
1.506764
-1.894076E-1
0.80
6.153846Е-1
1.050505Е-1
-7.692307E-1
9.511411E-1
1.480011
-1.730099E-1
Таблица 28
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.264329Е+1
-2.624648E-1
-7.692307E-1
1.598002
0.20
0.20
1.272021Е+1
-2.529284E-1
-7.692307E-1
1.592033
0.30
0.30
1.279713Е+1
-2.424300E-1
-7.692307E-1
1.582167
0.40
0.40
1.287406Е+1
-2.309010E-1
-7.692307E-1
1.568524
0.50
0.50
1.295098Е+1
-2.182711E-1
-7.692307E-1
1.551269
0.60
0.60
1.302790Е+1
-2.044661E-1
-7.692307E-1
1.530604
0.70
0.70
1.310483Е+1
-1.894076E-1
-7.692307E-1
1.506764
0.80
0.80
1.318175Е+1
-1.730099E-1
-7.692307E-1
1.480011
Продолжение таблицы 28
bt
tgε2
uB2T
uB2
ΔuB2
0.10
4.216387E-1
1.413043Е-2
1.413043Е-2
-3.295974Е-17
0.20
4.322112E-1
2.795698Е-2
2.795698Е-2
2.012279Е-16
0.30
4.440013E-1
4.148936Е-2
4.148936Е-2
1.040834Е-16
0.40
4.571350E-1
5.473684Е-2
5.473684Е-2
1.318389Е-16
0.50
4.717520E-1
6.770833Е-2
6.770833Е-2
2.359223Е-16
0.60
4.880096E-1
8.041237Е-2
8.041237Е-2
2.636779Е-16
0.70
5.060871E-1
9.285714Е-2
9.285714Е-2
4.163336Е-17
0.80
5.261926E-1
1.050505Е-1
1.050505Е-1
1.110223Е-16
Передний отрезок sF1=2,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p2=9,0
Таблица 29
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.111111E-2
4.972375E-2
-1.111111E-1
1.617283E-1
1.598002
-1.058220E-2
0.20
2.222222E-2
9.890109E-2
-1.111111E-1
2.123456E-1
1.592033
2.018964E-2
0.30
3.333333E-2
1.475409E-1
-1.111111E-1
2.629629E-1
1.582167
5.082646E-2
0.40
4.444444E-2
1.956521E-1
-1.111111E-1
3.135802E-1
1.568524
8.145992E-2
0.50
5.555555E-2
2.432432E-1
-1.111111E-1
3.641975E-1
1.551269
1.122392E-1
0.60
6.666666E-2
2.903225E-1
-1.111111E-1
4.148148E-1
1.530604
1.433343E-1
0.70
7.777777E-2
3.368983E-1
-1.111111E-1
1.654320E-1
1.506764
1.749392E-1
0.80
8.888888E-2
3.829787E-1
-1.111111E-1
5.160493E-1
1.480011
2.072760E-1
Таблица 30
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.257748Е+1
-1.058220E-2
-1.111111E-1
1.598002
0.20
0.20
1.258859Е+1
2.018964E-2
-1.111111E-1
1.592033
0.30
0.30
1.259970Е+1
5.082646E-2
-1.111111E-1
1.582167
0.40
0.40
1.261081Е+1
8.145992E-2
-1.111111E-1
1.568524
0.50
0.50
1.262192Е+1
1.122392E-1
-1.111111E-1
1.551269
0.60
0.60
1.263303Е+1
1.433343E-1
-1.111111E-1
1.530604
0.70
0.70
1.264414Е+1
1.749392E-1
-1.111111E-1
1.506764
0.80
0.80
1.265525Е+1
2.072760E-1
-1.111111E-1
1.480011
Продолжение таблицы 30
bt
tgε2
uB2T
uB2
ΔuB2
0.10
1.004108E-1
4.972375E-2
4.972375E-2
2.775557Е-17
0.20
1.315959E-1
9.890109E-2
9.890109E-2
2.775557Е-17
0.30
1.628572E-1
1.475409E-1
1.475409E-1
5.551115Е-17
0.40
1.943299E-1
1.956521E-1
1.956521Е-1
1.942890Е-16
0.50
2.261709Ет1
2.432432E-1
2.432432E-1
5.551115Е-17
0.60
2.585633Е-1
2.903225E-1
2.903225E-1
1.110223Е-16
0.70
2.917206Е-1
3.368983E-1
3.368983E-1
5.551115Е-17
0.80
3.258926Е-1
3.829787E-1
3.829787E-1
2.220446Е-16
Передний отрезок sF2=7,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p2=9,0
Таблица 31
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.111111E-2
1.426307E-2
-1.111111E-1
1.255731E-1
1.598002
-3.262052E-2
0.20
2.222222E-2
2.848101E-2
-1.111111E-1
1.400352E-1
1.592033
-2.344090E-2
0.30
3.333333E-2
4.265402E-2
-1.111111E-1
1.544973E-1
1.582167
-1.400347E-2
0.40
4.444444E-2
5.678233E-2
-1.111111E-1
1.689594E-1
1.568524
-4.243215E-3
0.50
5.555555E-2
7.086614E-2
-1.111111E-1
1.834215E-1
1.551269
5.906048E-3
0.60
6.666666E-2
8.490566E-2
-1.111111E-1
1.978835E-1
1.530604
1.651208E-2
0.70
7.777777E-2
9.890109E-2
-1.111111E-1
2.123456E-1
1.506764
2.764474E-2
0.80
8.888888E-2
1.128526E-1
-1.111111E-1
2.268077E-1
1.480011
3.937656E-2
Таблица 32
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.257748Е+1
-3.262052E-2
-1.111111E-1
1.598002
0.20
0.20
1.258859Е+1
-2.344090E-2
-1.111111E-1
1.592033
0.30
0.30
1.259970Е+1
-1.400347E-2
-1.111111E-1
1.582167
0.40
0.40
1.1261081Е+1
-4.243215E-3
-1.111111E-1
1.568524
0.50
0.50
1.262192Е+1
5.906048E-3
-1.111111E-1
1.551269
0.60
0.60
1.263303Е+1
1.651208E-2
-1.111111E-1
1.530604
0.70
0.70
1.264414Е+1
2.764474E-2
-1.111111E-1
1.506764
0.80
0.80
1.265525Е+1
3.937656E-2
-1.111111E-1
1.480011
Продолжение таблицы 32
bt
tgε2
uB2T
uB2
ΔuB2
0.10
7.820712E-2
1.426307E-2
1.426307E-2
3.642919Е-17
0.20
8.744245E-2
2.848101E-2
2.848101E-2
1.734723Е-17
0.30
9.695677E-2
4.265402E-2
4.265402E-2
9.020562Е-17
0.40
1.068175E-1
5.678233E-2
5.678233E-2
9.020562Е-17
0.50
1.170940E-1
7.086614E-2
7.086614E-2
8.326672Е-17
0.60
1.278577E-1
8.490566E-2
8.490566E-2
1.526556Е-16
0.70
1.391833E-1
9.890109E-2
9.890109E-2
9.714451Е-17
0.80
1.511489Е-1
1.128526E-1
1.128526E-1
9.714451Е-17
Телескопический ход лучей
Направляющий коэффициент для любого входного луча uK1=0
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p1=1,3
Таблица 33
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
7.692307E-2
0.0
-7.692307E-1
7.692307E-1
1.598002
-2.705535E-1
0.20
1.538461E-1
0.0
-7.692307E-1
7.692307E-1
1.592033
-2.688929E-1
0.30
2.307692E-1
0.0
-7.692307E-1
7.692307E-1
1.582167
-2.661211E-1
0.40
3.076923E-1
0.0
-7.692307E-1
7.692307E-1
1.568524
-2.622324E-1
0.50
3.846153E-1
0.0
-7.692307E-1
7.692307E-1
1.551269
-2.572180E-1
0.60
4.615384E-1
0.0
-7.692307E-1
7.692307E-1
1.530604
-2.510667E-1
0.70
5.384615E-1
0.0
-7.692307E-1
7.692307E-1
1.506764
-2.437637E-1
0.80
6.153846E-1
0.0
-7.692307E-1
7.692307E-1
1.480011
-2.352911E-1
Таблица 34
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.264329Е+1
-2.705535E-1
-7.692307E-1
1.598002
0.20
0.20
1.272021Е+1
-2.688929E-1
-7.692307E-1
1.592033
0.30
0.30
1.279713Е+1
-2.661211E-1
-7.692307E-1
1.582167
0.40
0.40
1.287406Е+1
-2.622324E-1
-7.692307E-1
1.568524
0.50
0.50
1.295098Е+1
-2.572180E-1
-7.692307E-1
1.551269
0.60
0.60
1.302790Е+1
-2.510667E-1
-7.692307E-1
1.530604
0.70
0.70
1.310483Е+1
-2.437637E-1
-7.692307E-1
1.506764
0.80
0.80
1.318175Е+1
-2.352911E-1
-7.692307E-1
1.480011
Продолжение таблицы 34
bt
tgε2
uB2T
uB2
ΔuB2
0.10
4.127718E-1
0.0
0.0
0.0
0.20
4.145848E-1
0.0
1.395001Е-16
1.395001Е-16
0.30
4.176193E-1
0.0
1.395001Е-16
1.395001Е-16
0.40
4.218948E-1
0.0
1.395001Е-16
1.395001Е-16
0.50
4.274394E-1
0.0
1.395001Е-16
1.395001Е-16
0.60
4.342903E-1
0.0
2.790002Е-16
2.790002Е-16
0.70
4.424945E-1
0.0
1.395001Е-16
1.395001Е-16
0.80
4.521106Е-1
0.0
2.790002Е-16
2.790002Е-16
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p2=9,0
Таблица 35
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.111111Е-2
0.0
-1.111111E-1
1.111111E-1
1.598002
-4.151993Е-2
0.20
2.222222Е-2
0.0
-1.111111E-1
1.111111E-1
1.592033
-4.125977Е-2
0.30
З.ЗЗЗЗЗЗЕ-2
0.0
-1.111111E-1
1.111111E-1
1.582167
-4.082545Е-2
0.40
4.444444Е-2
0.0
-1.111111E-1
1.111111E-1
1.568524
-4.021588Е-2
0.50
5.555555Е-2
0.0
-1.111111E-1
1.111111E-1
1.551269
-3.942954Е-2
0.60
6.666666Е-2
0.0
-1.111111E-1
1.111111E-1
1.530604
-3.846447Е-2
0.70
7.777777Е-2
0.0
-1.111111E-1
1.111111E-1
1.506764
-3.731826Е-2
0.80
8.888888Е-2
0.0
-1.111111E-1
1.111111E-1
1.480011
-3.598804Е-2
Таблица 36
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.257748Е+1
-4.151993Е-2
-1.111111E-1
1.598002
0.20
0.20
1.258859Е+1
-4.125977Е-2
-1.111111E-1
1.592033
0.30
0.30
1.259970Е+1
-4.082545Е-2
-1.111111E-1
1.582167
0.40
0.40
1.261081Е+1
-4.021588Е-2
-1.111111E-1
1.568524
0.50
0.50
1.262192Е+1
-3.942954Е-2
-1.111111E-1
1.551269
0.60
0.60
1.263303Е+1
-3.846447Е-2
-1.111111E-1
1.530604
0.70
0.70
1.264414Е+1
-3.731826Е-2
-1.111111E-1
1.506764
0.80
0.80
1.265525Е+1
-3.598804Е-2
-1.111111E-1
1.480011
Продолжение таблицы 36
bt
tgε2
uB2T
uB2
ΔuB2
0.10
6.927160E-2
0.0
2.741709E-17
2.741709E-17
0.20
6.953257E-2
0.0
5.483418E-17
5.483418E-17
0.30
6.996827E-2
0.0
6.854273E-17
6.854273E-17
0.40
7.057984E-2
0.0
5.483418E-17
5.483418E-17
0.50
7.136889E-2
0.0
8.225127E-17
8.225127E-17
0.60
7.233747E-2
0.0
9.595982E-17
9.595982E-17
0.70
7.348812E-2
0.0
1.233769E-16
1.233769E-16
0.80
7.482387E-2
0.0
1.370854E-16
1.370854E-16
6.2.1.4. Конические поверхности, линза толщиной L/2
Толщина линзы d=L/ 2=6,283185 мм
Апланатический ход лучей
(Передний отрезок sF1=2,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p1=1,3
Таблица 37
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
7.692307E-2
4.814814E-2
-7.692307E-1
8.488165E-1
1.598002
-2.434051E-1
0.20
1.538461E-1
9.285714E-2
-7.692307E-1
9.284023E-1
1.592033
-2.174489E-1
0.30
2.307692E-1
1.344827E-1
-7.692307E-1
1.007988
1.582167
-1.927227E-1
0.40
3.076923E-1
1.733333E-1
-7.692307E-1
1.087573
1.568524
-1.687630E-1
0.50
3.846153E-1
2.0-96774E-1
-7.692307E-1
1.167159
1.551269
-1.451521E-1
0.60
4.615384E-1
2.437500E-1
-7.692307E-1
1.246745
1.530604
-1.215097E-1
0.70
5.384615E-1
2.757575E-1
-7.692307E-1
1.326331
1.506764
-9.748457E-2
0.80
6.153846E-1
3.058823E-1
-7.692307E-1
1.405917
1.480011
-7.274397E-2
Таблица 38
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
-0.10
6.360108
2.434051Е-1
7.692307Е-1
1.598002
0.20
-0.20
6.437031
2.174489Е-1
7.692307Е-1
1.592033
0.30
-0.30
6.513954
1.927227Е-1
7.692307Е-1
1.582167
0.40
-0.40
6.590877
1.687630Е-1
7.692307Е-1
1.568524
0.50
-0.50
6.667800
1.451521Е-1
7.692307Е-1
1.551269
0.60
-0.60
6.744723
1.215097Е-1
7.692307Е-1
1.530604
0.70
-0.70
6.821646
9.748457Е-2
7.692307Е-1
1.506764
0.80
-0.80
' 6.898569
7.274397Е-2
7.692307Е-1
1.480011
Продолжение таблицы 38
bt
tgε2
uB2T
uB2
ΔuB2
0.10
4.428994E-1
-4.814814E-2
-4.814814E-2
1.387778Е-17
0.20
4.727119E-1
-9.285714E-2
-9.285714E-2
-1.526556Е-16
0.30
5.020761E-1
-1.344827E-1
-1.344827E-1
2.775557Е-17
0.40
5.314730E-1
-1.733333E-1
-1.733333E-1
5.551115Е-17
0.50
5.613957E-1
-2.096774E-1
-2.096774E-1
-5.551115Е-17
0.60
5.923541E-1
-2.437500E-1
-2.437500E-1
1.387778Е-16
0.70
6.248870E-1
-2.757575E-1
-2.757575E-1
-2.220446Е-16
0.80
6.595788E-1
-3.058823E-1
-3.058823E-1
-4.996003Е-16
Передний отрезок sF2=7,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p1=1,3
Таблица 39
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
7.692307Е-2
1.413043Е-2
-7.692307E-1
7.919695E-1
1.598002
-2.624648E-1
0.20
1.538461Е-1
2.795698Е-2
-7.692307E-1
8. 147083E-1
1.592033
-2.529284E-1
0.30
2.307692Е-1
4.148936Е-2
-7.692307E-1
8.374471E-1
1.582167
-2.424300E-1
0.40
3.076923Е-1
5.473684Е-2
-7.692307E-1
8.601859E-1
1.568524
-2.309010E-1
0.50
3.846153Е-1
6.770833Е-2
-7.692307E-1
8.829247E-1
1.551269
-2.182711E-1
0.60
4.615384Е-1
8.041237Е-2
-7.692307E-1
S.056635E-1
1.530S04
-2.044661E-1
0.70
5.384615Е-1
9.285714Е-2
-7.692307E-1
9.284023E-1
1.506764
-1.894076E-1
0.80
6.153846Е-1
1.050505Е-1
-7.692307E-1
9.511411E-1
1.480011
-1.730099E-1
Таблица 40
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
-0.10
6.360108
2.624648Е-1
7.692307Е-1
1.598002
0.20
-0.20
6.437031
2.529284Е-1
7.692307Е-1
1.592033
0.30
-0.30
6.513954
2.424300Е-1
7.692307Е-1
1.582167
0.40
-0.40
6.590877
2.309010Е-1
7.692307Е-1
1.568524
0.50
-0.50
6.667800
2.182711Е-1
7.692307Е-1
1.551269
0.60
-0.60
6.744723
2.044661Е-1
7.692307Е-1
1.530604
0.70
-0.70
6.821646
1.894076Е-1
7.692307Е-1
1.506764
0.80
-0.80
6.898569
1.730099Е-1
7.692307Е-1
1.480011
Продолжение таблицы 40
bt
tgε2
uB2T
uB2
ΔuB2
0.10
4.216387E-1
-1.413043Е-2
-1.413043Е-2
3.295974Е-17
0.20
4.322112E-1
-2.795698Е-2
-2.795698Е-2
-2.012279Е-16
0.30
4.440013E-1
-4.148936Е-2
-4.148936Е-2
-1.040834Е-16
0.40
4.571350E-1
-5.473684Е-2
-5.473684Е-2
-1.318389Е-16
0.50
4.717520E-1
-6.770833Е-2
-6.770833Е-2
-1.110223Е-16
0.60
4.880096E-1
-8.041237Е-2
-8.041237Е-2
4.163336Е-17
0.70
5.060871E-1
-9.285714Е-2
-9.285714Е-2
-1.665334Е-16
0.80
5.261926E-1
-1.050505Е-1
-1.050505Е-1
0.0
Передний отрезок sF1=2,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p2=9,0
Таблица 41
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.111111E-2
4.972375E-2
-1.11111E-1
1.617283E-1
1.598002
-1.058220E-2
0.20
2.222222E-2
9.890109E-2
-1.11111E-1
2.123456E-1
1.592033
2.018964E-2
0.30
3.333333E-2
1.475409E-1
-1.11111E-1
2.629629E-1
1.582167
5.082646E-2
0.40
4.444444E-2
1.956521E-1
-1.11111E-1
3.135802E-1
1.568524
8.145992E-2
0.50
5.555555E-2
2.432432E-1
-1.11111E-1
3.641975E-1
1.551269
1.122392E-1
0.60
6.666666E-2
2.903225E-1
-1.11111E-1
4.148148E-1
1.530604
1.433343E-1
0.70
7.777777E-2
3.368983E-1
-1.11111E-1
4.654320E-1
1.506764
1.749392E-1
0.80
8.888888E-2
3.829787E-1
-1.11111E-1
5.160493E-1
1.480011
2.072760E-1
Таблица 42
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
-0.10
6.294296
1.058220Е-2
1.11111E-1
1.598002
0.20
-0.20
6.305407
-2.018964E-2
1.11111E-1
1.592033
0.30
-0.30
6.316518
-5.082646E-2
1.11111E-1
1.582167
0.40
-0.40
6.327629
-8.145992E-2
1.11111E-1
1.568524
0.50
-0.50
6.338740
-1.122392E-1
1.11111E-1
1.551269
0.60
-0.60
6.349851
-1.433343E-1
1.11111E-1
1.530604
0.70
-0.70
6.360963
-1.749392E-1
1.11111E-1
1.506764
0.80
-0.80
6.372074
-2.072760E-1
1.11111E-1
1.480011
Продолжение таблицы 42
bt
tgε2
uB2T
uB2
ΔuB2
0.10
1.004108E-1
-4.972375E-2
-4.972375E-2
-2.775557Е-17
0.20
1.315959E-1
-9.890109E-2
-9.890109E-2
0.0
0.30
1.628572E-1
-1.475409E-1
-1.475409E-1
-5.551115Е-17
0.40
1.943299E-1
-1.956521E-1
-1.956521E-1
-1.387778Е-16
0.50
2.261709E-1
-2.432432E-1
-2.432432E-1
-5.551115Е-17
0.60
2.585633E-1
-2.903225E-1
-2.903225E-1
-5.551115Е-17
0.70
2.917206E-1
-3.368983E-1
-3.368983E-1
0.0
0.80
3.258926E-1
-3.829787E-1
-3.829787E-1
0.0
Передний отрезок sF2=7,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p2=9,0
Таблица 43
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.111111E-2
1.426307E-2
-1.111111E-1
1.255731E-1
1.598002
-3.262052E-2
0.20
2.222222E-2
2.848101E-2
-1.111111E-1
1.400352E-1
1.592033
-2.344090E-2
0.30
3.333333E-2
Ф.265402Е-2
-1.111111E-1
1.544973E-1
1.582167
-1.400347E-2
0.40
4.444444E-2
5.678233E-2
-1.111111E-1
1.689594E-1
1.568524
-4.243215E-3
0.50
5.555555E-2
7.086614E-2
-1.111111E-1
1.834215E-1
1.551269
5.906048E-3
0.60
6.666666E-2
8.490566E-2
-1.111111E-1
1.978835E-1
1.530604
1.651208E-2
0.70
7.777777E-2
9.890109E-2
-1.111111E-1
2.123456E-1
1.506764
2.764474E-2
0.80
8.888888E-2
1.128526E-1
-1.111111E-1
2.268077E-1
1.480011
3.937656E-2
Таблица 44
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
-0.10
6.294296
3.262052Е-2
1.111111Е-1
1.598002
0.20
-0.20
6.305407
2.344090Е-2
1.111111Е-1
1.592033
0.30
-0.30
6.316518
1.400347Е-2
1.111111Е-1
1.582167
0.40
-0.40
6.327629
4.243215Е-3
1.111111Е-1
1.568524
0.50
-0.50
6.338740
-5.906048E-3
1.111111Е-1
1.551269
0.60
-0.60
6.349851
-1.651208E-2
1.111111Е-1
1.530604
0.70
-0.70
6.360963
-2.764474E-2
1.111111Е-1
1.506764
0.80
-0.80
6.372074
-3.937656E-2
1.111111Е-1
1.480011
Продолжение таблицы 44
bt
tgε2
uB2T
uB2
ΔuB2
0.10
7.820712E-2
-1.426307E-2
-1.426307E-2
-3.642919Е-17
0.20
8.7Д4245Е-?
-2.848101E-2
-2.848imE-?
1.040834Е-17
0.30
9.695677E-2
-4.265402E-2
-4.265402E-2
-3.469446Е-17
0.40
1.068175E-1
-5.678233E-2
-5.678233E-2
-6.938893Е-17
0.50
1.170940E-1
-7.086614E-2
-7.086614E-2
-5.551115Е-17
0.60
1.278577E-1
-8.490566E-2
-8.490566E-2
-6.938893Е-17
0.70
1.391833E-1
-9.890109E-2
-9.890109E-2
-1.387778Е-17
0.80
1.511489E-1
-1.128526E-1
-1.128526E-1
-1.387778Е-17
Телескопический ход лучей
Направляющий коэффициент для любого входного луча uK1=0
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p1=1,3
Таблица 45
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
7.692307E-2
0.0
-7.692307E-1
7.69230.7E-1
1.598002
-2.705535E-1
0.20
1.538461E-1
0.0
-7.692307E-1
7.692307E-1
1.592033
-2.688929E-1
0.30
2.307692E-1
0.0
-7.692307E-1
7.692307E-1
1.582167
-2.661211E-1
0.40
3.076923E-1
0.0
-7.692307E-1
7.692307E-1
1.568524
-2.622324E-1
0.50
3.846153E-1
0.0
-7.692307E-1
7.692307E-1
1.551269
-2.572180E-1
0.60
4.615384E-1
0.0
-7.692307E-1
7.692307E-1
1.530604
-2.510667E-1
0.70
5.384615E-1
0.0
-7.692307E-1
7.692307E-1
1.506764
-2.437637E-1
0.80
6.153846E-1
0.0
-7.692307E-1
7.692307E-1
1.480011
-2.352911E-1
Таблица 46
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0 10
-0.10
6.360108
2.705535Е-1
7.692307E-1
1.598002
0.20
-0.20
6.437031
2.688929Е-1
7.692307E-1
1.592033
0.30
-0.30
6.513954
2.661211Е-1
7.692307E-1
1.582167
0.40
-0.40
6.590877
2.622324Е-1
7.692307E-1
1.568524
0.50
-0.50
16.667800
2.572180Е-1
7.692307E-1
1.551269
0.60
-0.60
6.744723
2.510667Е-1
7.692307E-1
1.530604
0.70
-0.70
6.821646
2.437637Е-1
7.692307E-1
1.506764
0.80
-0.80
6.898569
2.352911Е-1
7.692307E-1
1.480011
Продолжение таблицы 46
bt
tgε2
uB2T
uB2
ΔuB2
0.10
4.127718E-1
0.0
0.0
0.0
0.20
4.145848E-1
0.0
-1.395001Е-16
-1.395001Е-16
0.30
4.176193E-1
0.0
0.0
0.0
0.40
4.218948E-1
0.0
0.0
0.0
0.50
4.274394E-1
0.0
-1.395001Е-16
-1.395001Е-16
0.60
4.342903E-1
0.0
-1.395001Е-16
-1.395001Е-16
0.70
4.424945E-1
0.0
0.0
0.0
0.80
4.521106E-1
0.0
0-.0
0.0
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p2=9,0
Таблица 47
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
1.111111Е-2
0.0
-1.111111E-1
1.11U11E-1
1.598002
-4.151993Е-2
0.20
2.222222Е-2
0.0
-1.111111E-1
1.11U11E-1
1.592033
-4.125977Е-2
0.30
3.ЗЗЗЗЗЗЕ-2
0.0
-1.11U11E-1
1.111111E-1
1.582167
-4.082545Е-2
0.40
4.444444Е-2
0.0
-1.111111E-1
1.11U11E-1
1.568524
-4.021588Е-2
0.50
5.555555Е-2
0.0
-1.111111E-1
1.11U11E-1
1.551269
-3.942954Е-2
0.60
6.666666Е-2
0.0
-1.111111E-1
1.11U11E-1
1.530604
-3.846447Е-2
0.70
7.777777E-2
0.0
-1.111111E-1
1.11U11E-1
1.506764
-3.731826Е-2
0.80
8.888888E-2
0.0
-1.111111E-1
1.11U11E-1
1.480011
-3.598804Е-2
Таблица 48
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
-0.10
6.294296
4.151993Е-2
1.11U11E-1
1.598002
0.20
-0.20
6.305407
4.125977Е-2
1.11U11E-1
1.592033
0.30
-0.30
6.316518
4.082545Е-2
1.11U11E-1
1.582167
0.40
-0.40
6.327629
4.021588Е-2
1.11U11E-1
1.568524
0.50
-0.50
6.338740
3.942954Е-2
1.11U11E-1
1.551269
0.60
-0.60
6.349851
3.846447Е-2
1.11U11E-1
1.530604
0.70
-0.70
6.360963
3.731826Е-2
1.11U11E-1
1.506764
0.80
-0.80
6.372074
3.598804Е-2
1.11U11E-1
1.480011
Продолжение таблицы 48
bt
tgε2
uB2T
uB2
ΔuB2
0.10
6.927160
0.0
-2.741709E-17
-2.741709E-17
0.20
6.953257
0.0
-4.112563E-17
-4.112563E-17
0.30
6.996827
0.0
-4.112563E-17
-4.112563E-17
0.40
7.057984
0.0
-1.370854E-17
-1.370854E-17
0.50
7.136889
0.0
-4.112563E-17
-4.112563E-17
0.60
7.233747
0.0
-5.483418E-17
-5.483418E-17
0.70
7.348812
0.0
-5.483418E-17
-5.483418E-17
0.80
7.482387
0.0
-6.854273E-17
-6.854273E-17
6.2.1.5. Гиперболические поверхности высшего порядка, линза толщиной L
Толщина линзы d=L=12,566370 мм
Апланатический ход лучей
Передний отрезок sF1=1,8 мм Постоянная в уравнениях образующих 1-й и 2-й поверхностей (2) и (3)
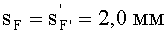
Таблица 49
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
4.169297Е-3
5.542717Е-2
-8.316135E-2
1.392302E-1
1.598002
3.432366E-3
0.20
1.671000Е-2
1.100891Е-1
-1.653290E-1
2.805239E-1
1.592033
6.633603E-3
0.30
3.772973Е-2
1.632448Е-1
-2.456898E-1
4.260214E-1
1.582167
9.409822E-3
0.40
6.743725Е-2
2.141972Е-1
-3.237487E-1
5.780301E-1
1.568524
1.163011E-2
0.50
1.061832Е-1
2.623042Е-1
-3.993993E-1
7.391388E-1
1.551269
1.323488E-2
0.60
1.545136Е-1
3.069817E-1
-4.729315E-1
9.123728E-1
1.530604
1.422819E-2
0.70
2.132345Е-1
3.476991Е-1
-5.449974E-1
1.101408E+0
1.506764
1.466055E-2
0.80
2.834955Е-1
3.839700Е-1
-6.165670E-1
1.310878E+0
1.480011
1.460924E-2
Таблица 50
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.257053Е+1
3.432366E-3
-8.31С135Е-2
1.598002
0.20
0.20
1.258308Е+1
6.633603E-3
-1.653290E-1
1.592033
0.30
0.30
1.260410Е+1
9.409822E-3
-2.456898E-1
1.582167
0.40
0.40
1.263380Е+1
1.163011E-2
-3.237487E-1
1.568524
0.50
0.50
1.267255Е+1
1.323488E-2
-3.993993E-1
1.551269
0.60
0.60
1.272088Е+1
1.422819E-2
-4.729315E-1
1.530604
0.70
0.70
1.277960Е+1
1.466055E-2
-5.449974E-1
1.506764
0.80
0.80
1.284986Е+1
1.460924E-2
-6.165670E-1
1.480011
Продолжение таблицы 50
bt
tgε2
uB2T
uB2
ΔuB2
0.10
8.661844E-2
5.542717Е-2
5.542717Е-2
4.857225Е-17
0.20
1.721514E-1
1.100891Е-1
1.100891Е-1
8.326672Е-17
0.30
2.556907E-1
1.632448Е-1
1.632448Е-1
1.665334Е-16
0.40
3.366463E-1
2.141972Е-1
2.141972Е-1
5.551115Е-17
0.50
4.]48270E-]
2.623042E-3
?.62304?F,-1
5.551115Е-17
0.60
4.904600E-1
3.069817E-1
3.069817E-1
3.885780Е-16
0.70
5.641656E-1
3.476991Е-1
3.476991Е-1
2.775557Е-16
0.80
6.369133E-1
3.839700Е-1
3.839700Е-1
5.551115Е-17
Передний отрезок sF2=7,0 мм
Постоянная в уравнениях образующих 1-й и 2-й поверхностей (2) и (3)
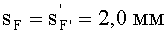
Таблица 51
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
4.169297E-3
1.427721E-2
-8.316135E-2
9.755439E-2
1.598002
-2.217733E-2
0.20
1.671000E-2
2.850338E-2
-1.653290E-1
1.947501E-1
1.592033
-4.351180E-2
0.30
3.772973E-2
4.262738E-2
-2.456898E-1
2.913687E-1
1.582167
-6.326192E-2
0.40
6.743725E-2
5.659760E-2
-3.237487E-1
3.874456E-1
1.568524
-8.085934E-2
0.50
1.061832E-1
7.036125E-2
-3.993993E-1
4.833436E-1
1.551269
-9.593596E-2
0.60
1.545136E-1
8.386314E-2
-4.729315E-1
5.797900E-1
1.530604
-1.083096E-1
0.70
2.132345E-1
9.704384E-2
-5.449974E-1
6.77S941E-1
1. 506764
-1.179442E-1
0.80
2.834955E-1
1.098373E-1
-6.165670E-1
7.791715E-1
1.480011
-1.249005E-1
Таблица 52
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
Г.257053Е+1
-2.217733E-2
-8.316135Е-2
1.598002
0.20
0.20
1.258308Е+1
-4.351180E-2
-1.653290E-1
1.592033
0.30
0.30
1.260410Е+1
-6.326192E-2
-2.456898E-1
1.582167
0.40
0.40
1.263380Е+1
-8.085934E-2
-3.237487E-1
1.568524
0.50
0.50
1.267255Е+1
-9.593596E-2
-3.993993E-1
1.551269
0.60
0.60
1.272088Е+1
-1.083096E-1
-4.729315E-1
1.530604
0.70
0.70
1.277960Е+1
-1.179442E-1
-5.449974E-1
1.506764
0.80
0.80
1.284986Е+1
-1.249005E-1
-6.165670E-1
1.480011
Продолжение таблицы 52
bt
tgε2
uB2T
uB2
ΔuB2
0.10
6.087175E-2
1.427721E-2
1.427721E-2
5.030698Е-17
0.20
1.209471E-1
2.850338E-2
2.850338E-2
6.938893Е-17
0.30
1.796358E-1
4.262738E-2
4.262738E-2
2.151057Е-16
0.40
2.366931E-1
5.659760E-2
5.659760E-2
4.857225Е-17
0.50
2.92264i7E-l
7.036125E-2
7.036125E-2
5.551115Е-17
0.60
3.468549E-1
8.386314E-2
8.386314E-2
9.714451Е-17
0.70
4.012604E-1
9.704384E-2
9.704384E-2
1.526556Е-16
0.80
4.565107E-1
1.098373E-1
1.098373E-1
2.498001Е-16
Передний отрезок sF1=1,8 мм
Постоянная в уравнениях образующих 1-й и 2-й поверхностей (2) и (3)
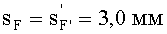
Таблица 53
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
2.783702Е-3
5.546977E-2
-5.560711E-2
1.114205E-1
1.598002
1.380265E-2
0.20
1.120637Е-2
1.104236E-1
-1.115264E-1
2.247175E-1
1.592033
2.709512E-2
0.30
2.548625Е-2
1.643397E-1
-1.680847E-1
3.418679E-1
1.582167
3.940216E-2
0.40
4.599921Е-2
2.166848E-1
-2.256386E-1
4.650615E-1
1.568524
5.031371E-2
0.50
7.329854Е-2
2.669088E-1
-2.845922E-1
5.968370E-1
1.551269
5.950653E-2
0.60
1.081457Е-1
3.144413E-1
-3.454178E-1
7.402617E-1
1.530604
6.675556E-2
0.70
1.515565Е-1
3.586880E-1
-4.086821E-1
8.991805E-1
1.506764
7.193496E-2
0.80
2.048685Е-1
3.990286E-1
-4.750823E-1
1.078578E+0
1.480011
7.501060E-2
Таблица 54
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.256915Е+1
1.380265E-2
-5.560711E-2
1.598002
0.20
0.20
1.257757Е+1
2.709512E-2
-1.115264E-1
1.592033
0.30
0.30
:U.259185E+1
3.940216E-2
-1.680847E-1
1.582167
0.40
0.40
1.261236Е+1
5.031371E-2
-2.256386E-1
1.568524
0.50
0.50
1.263966Е+1
5.950653E-2
-2.845922E-1
1.551269
0.60
0.60
1.267451Е+1
6.675556E-2
-3.454178E-1
1.530604
0.70
0.70
1.271792Е+1
7.193496E-2
-4.086821E-1
1.506764
0.80
0.80
1.277123Е+1
7.501060E-2
-4.750823E-1
1.480011
Продолжение таблицы 54
bt
tgε2
uB2T
uB2
ΔuB2
0.10
6.946308E-2
5.546977E-2
5.546977E-2
6.938893E-18
0.20
1.390417E-1
1.104236E-1
1.104236E-1
1.387778E-17
0.30
2.088702E-1
1.643397E-1
1.643397E-1
-2.775557E-17
0.40
2.791211E-1
2.166848E-1
2.166848E-1
8.326672E-17
0.50
3.500265E-1
2.669088E-1
2.669088E-1
1.665334E-16
0.60
4.219018E-1
3.144413E-1
3.144413E-1
1.110223E-16
0.70
4.951745E-1
3.586880E-1
3.586880E-1
-1.110223E-16
0.80
5.704206E-1
3.990286E-1
3.990286E-1
2.220446E-16
Передний отрезок sF2=7,0 мм
Постоянная в уравнениях образующих 1-й и 2-й поверхностей (2) и (3)
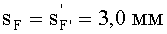
Таблица 55
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
2.783702Е-3
1.428003Е-2
-5.560711E-2
6.994268E-2
1.598002
-1.187441E-2
0.20
1.120637Е-2
2.852576Е-2
-1.115264E-1
1.404991E-1
1.592033
-2.356714E-2
0.30
2.548625Е-2
4.270167Е-2
-1.680847E-1
2.123102E-1
1.582167
-3.489863E-2
0.40
4.599921Е-2
5.676980Е-2
-2.256386E-1
2.860729E-1
1.568524
-4.569336E-2
0.50
7.329854Е-2
7.068837Е-2
-2.845922E-1
3.625747E-1
1.551269
-5.578149E-2
0.60
1.081457Е-1
8.441019Е-2
-3.454178E-1
4.427368E-1
1.530604
-6.500006E-2
0.70
1.515565Е-1
9.788078Е-2
-4.086821E-1
5.276709E-1
1.506764
-7.319362E-2
0.80
2.048685Е-1
1.110360Е-1
-4.750823E-1
6.187586E-1
1.480011
-8.021429E-2
Таблица 56
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.256915Е+1
-1.187441E-2
-5.560711E-2
1.598002
0.20
0.20
1.257757Е+1
-2.356714E-2
-1.115264E-1
1.592033
0.30
0.30
1.259185Е+1
-3.489863E-2
-1.680847E-1
1.582167
0.40
0.40
1.261236Е+1
-4.569336E-2
-2.256386E-1
1.568524
0.50
0.50
1.263966Е+1
-5.578149E-2
-2.845922E-1
1.551269
0.60
0.60
1.267451Е+1
-6.500006E-2
-3.454178E-1
1.530604
0.70
0.70
1.271792Е+1
-7.319362E-2
-4.086821E-1
1.506764
0.80
0.80
1.277123Е+1
-8.021429E-2
-4.750823E-1
1.480011
Продолжение таблицы 56
bt
tgε2
uB2T
uB2
ΔuB2
0.10
4.370384E-2
1.428003Е-2
1.428003Е-2
2.081668Е-17
0.20
8.772872E-2
2.852576Е-2
2.852576Е-2
1.734723Е-17
0.30
1.324094E-1
4.270167Е-2
4.270167Е-2
-3.469446Е-17
0.40
1.781085E-1
5.676980Е-2
5.676980Е-2
8.32G672E-17
0.50
2.252351E-1
7.068837Е-2
7.068837Е-2
1.110223Е-16
0.60
2.742600E-1
8.441019Е-2
8.441019Е-2
1.526556Е-16
0.70
3.257445E-1
9.788078Е-2
9.788078Е-2
1.249000Е-16
0.80
3.803726E-1
1.110360Е-1
1.110360Е-1
2.636779Е-16
Телескопический ход лучей
Направляющий коэффициент для любого входного луча uK1=0
Постоянная в уравнениях образующих 1-й и 2-й поверхностей (2) и (3)
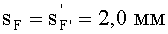
Таблица 57
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uВ1
0.10
4.169297E-3
0.0
-8.316135E-2
8.316135E-2
1.598002
-3.109537E-2
0.20
1.671000E-2
0.0
-1.653290E-1
1.653290E-1
1.592033
-6.128644E-2
0.30
3.772973E-2
0.0
-2.456898E-1
2.456898E-1
1.582167
-8.977837E-2
0.40
6.743725E-2
0.0
-3.237487E-1
3.237487E-1
1.568524
-1.159622E-1
0.50
1.061832E-1
0.0
-3.993993E-1
3.993993E-1
1.551269
-1.394422E-1
0.60
1.545136E-1
0.0
-4.729315E-1
4.729315E-1
1.530604
-1.600172E-1
0.70
2.132345E-1
0.0
-5.449974E-1
5.449974E-1
1.506764
-1.776347E-1
0.80
2.834955E-1
0.0
-6.165670E-1
6.165670E-1
1.480011
-1.923354E-1
Таблица 58
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uH2
n(yП2)
0.10
0.10
1.257053Е+1
-3.109537E-2
-8.316135E-2
1.598002
0.20
0.20
1.258308Е+1
-6.128644E-2
-1.653290E-1
1.592033
0.30
0.30
1.260410Е+1
-8.977837E-2
-2.456898E-1
1.582167
0.40
0.40
1.263380Е+1
-1.159622E-1
-3.237487E-1
1.568524
0.50
0.50
1.267255Е+1
-1.394422E-1
-3.993993E-1
1.551269
0.60
0.60
1.272088Е+1
-1.600172E-1
-4.729315E-1
1.530604
0.70
0.70
il.277960E+l
-1.776347E-1
-5.449974E-1
1.506764
0.80
0.80
1.284986E+1
-1.923354E-1
-6.165670E-1
1.480011
Продолжение таблицы 58
bt
tgε2
uB2T
uB2
ΔuB2
0.10
5.193169E-2
0.0
4.134741Е-17
4.134741Е-17
0.20
1.029989E-1
0.0
5.403419Е-17
5.403419Е-17
0.30
1.525466E-1
0.0
2.094042Е-16
2.094042Е-16
0.40
2.002678E-1
0.0
1.004896Е-16
1.004896Е-16
0.50
2.462430E-1
0.0
9.574851Е-17
9.574851Е-17
0.60
2.908998E-1
0.0
4.536469Е-17
4.536469Е-17
0.70
3.349372E-1
0.0
2.567935Е-16
2.567935Е-16
0.80
3.792564E-1
0.0
8.044191Е-17
8.044191Е-17
Постоянная в уравнениях образующих 1-й и 2-й поверхностей (2) и (3)
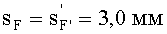
Таблица 59
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
2.783702Е-3
0.0
-5.560711E-2
5.560711E-2
1.598002
-2.080168E-2
0.20
1.120637Е-2
0.0
-1.115264E-1
1.115264E-1
1.592033
-4.141356E-2
0.30
2.548625Е-2
0.0
-1.680847E-1
1.680847E-1
1.582167
-6.164604E-2
0.40
4.599921Е-2
0.0
-2.256386E-1
2.256386E-1
1.568524
-8.130986E-2
0.50
7.329854Е-2
0.0
-2.845922E-1
2.845922E-1
1.551269
-1.002157E-1
0.60
1.081457Е-1
0.0
-3.454178E-1
3.454178E-1
1.530604
-1.181734E-1
0.70
1.515565Е-1
0.0
-4.086821E-1
4.086821E-1
1.506764
-1.349904E-1
0.80
2.048685Е-1
0.0
-4.750823E-1
4.750823E-1
1.480011
-1.504697E-1
Таблица 60
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.256915Е+1
-2.080168E-2
-5.560711E-2
1.598002
0.20
0.20
1.257757Е+1
-4.141356E-2
-1.115264E-1
1.592033
0.30
0.30
1.259185Е+1
-6.164604E-2
-1.680847E-1
1.582167
0.40
0.40
1.261236Е+1
-8.130986E-2
-2.256386E-1
1.568524
0.50
0.50
1.263966Е+1
-1.002157E-1
-2.845922E-1
1.551269
0.60
0.60
1.267451Е+1
-1.181734E-1
-3.454178E-1
1.530604
0.70
0.70
1.271792Е+1
-1.349904E-1
-4.086821E-1
1.506764
0.80
0.80
1.277123Е+1
-1.504697E-1
-4.750923Е-1
1.480011
Продолжение таблицы 60
bT
tgε2
uB2T
uB2
ΔuB2
0.10
3.476521E-2
0.0
1.383500E-17
1.383500E-17
0.20
6.979054E-2
0.0
5.482917E-17
5.482917E-17
0.30
1.053471E-1
0.0
5.398591E-17
5.398591E-17
0.40
1.417285E-1
0.0
7.923276E-17
7.923276E-17
0.50
1.792638E-1
0.0
1.540560E-16
1.540560E-16
0.60
2.183322E-1
0.0
1.983757E-16
1.983757E-16
0.70
2.593820E-1
0.0
1.426996E-16
1.426996E-16
0.80
3.029556E-1
0.0
3.170245E-16
3.170245E-16
6.2.1.6. Гиперболические поверхности высшего порядка, линза толщиной L/2
Толщина линзы d=L/2=6,283185 мм
Апланатический ход лучей
Передний отрезок sF1=1,8 мм
Постоянная в уравнениях образующих 1-й и 2-й поверхностей (2) и (3)
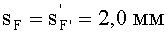
Таблица 61
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
4.169297Е-3
5.542717E-2
-8.316135E-2
1.392302E-1
1.598002
3.432366E-3
0.20
1.671000Е-2
1.100891E-1
-1.653290E-1
2.805239E-1
1.592033
6.633603E-3
0.30
3.772973Е-2
1.632448E-1
-2.456898E-1
4.260214E-1
1.582167
9.409822E-3
0.40
6.743725Е-2
2.141972E-1
-3.237487E-1
5.780301E-1
1.568524
1.163011E-2
0.50
1.061832Е-1
2.623042E-1
-3.993993E-1
7.391388E-1
1.551269
1.323488E-2
0.60
1.545136Е-1
3.069817E-1
-4.729315E-1
9.123728E-1
1.530604
1.422819E-2
Таблица 62
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.287354
-3.432366E-3
8.316135E-2
1.598002
0.20
-0.20
6.299895
-6.633603E-3
1.653290E-1
1.592033
0.30
-0.30
6.320915
-9.409822E-3
2.456898E-1
1.582167
0.40
-0.40
6.350622
-1.163011E-2
3.237487E-1
1.568524
0.50
-0.50
6.389368
-1.323488E-2
3.qQ3993E-l
3.551269
0.60
-0.60
6.437698
-1.422819E-2
4.729315Е-1
1.530604
Продолжение таблицы 62
bT
tgε2
uB2T
uB2
ΔuB2
0.10
8.661844E-2
-5.542717E-2
-5.542717E-2
-2.081668Е-17
0.20
1.721514E-1
-1.100891E-1
-1.100891E-1
-1.387778Е-17
0.30
2.556907E-1
-1.632448E-1
-1.632448E-1
-8.326672Е-17
0.40
3.366463E-1
-2.141972E-1
-2.141972E-1
2.775557Е-17
0.50
4.148270E-1
-2.623042E-1
-2.623042E-1
-3.885780Е-16
0.60
4.904600E-1
-3.069817E-1
-3.069817E-1
-1.665334Е-16
Передний отрезок sF2=7,0 мм
Постоянная в уравнениях образующих 1-й и 2-й поверхностей (2) и (3)
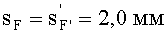
Таблица 63
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
4.169297Е-3
1.427721E-2
-8.316135E-2
9.755439E-2
1.598002
-2.2177333E-2
0.20
1.671000Е-2
2.850338E-2
-1.653290E-1
1.947501E-1
1.592033
-4.3511804E-2
0.30
3.772973Е-2
4.262738E-2
-2.456898E-1
2.913687E-1
1.582167
-6.3261921E-2
0.40
6.743725Е-2
5.659760E-2
-3.237487E-1
3.874456E-1
1.568524
-8.0859349E-2
0.50
1.061832Е-1
7.036125E-2
-3.993993E-1
4.833436E-1
1.551269
-9.5935969E-2
0.60
1.545136Е-1
8.386314E-2
-4.729315E-1
5.797900E-1
1.530604
-1.0830966E-1
Таблица 64
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.287354
2.217733Е-2
8.316135Е-2
1.598002
0.20
-0.20
6.299895
4.351180Е-2
1.653290Е-1
1.592033
0.30
-0.30
6.320915
6.326192Е-2
2.456898Е-1
1.582167
0.40
-0.40
6.350622
8.085934Е-2
3.237487Е-1
1.568524
0.50
-0.50
6.389368
9.593596Е-2
3.993993Е-1
1.551269
0.60
-0.60
6.437698
1.083096Е-1
4.729315Е-1
1.530604
Продолжение таблицы 64
bT
tgε2
uB2T
uB2
ΔuB2
0.10
6.087175Е-2
-1.427721E-2
-1.427721E-2
-2.428612Е-17
0.20
1.209471Е-1
-2.850338E-2
-2.850338E-2
-1.734723Е-17
0.30
1.796358Е-1
-4.262738E-2
-4.262738E-2
-1.665334Е-16
0.40
2.366931Е-1
-5.659760E-2
-5.659760E-2
-6.938893Е-18
0.50
2.922647Е-1
-7.036125E-2
-7.036125E-2
0.0
0.60
3.468549Е-1
-8.386314E-2
-8.386314E-2
-1.387778Е-17
Передний отрезок sF1=1,8 мм
Постоянная в уравнениях образующих 1-й и 2-й поверхностей (2) и (3)
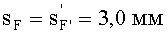
Таблица 65
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
2.783702Е-3
5.546977Е-2
-5.560711E-2
1.114205E-1
1.598002
1.380265E-2
0.20
1.120637Е-2
1.104236Е-1
-1.115264E-1
2.247175E-1
1.592033
2.709512E-2
0.30
2.548625Е-2
1.-643397Е-1
-1.680847E-1
3.418679E-1
1.582167
3.940216E-2
0.40
4.599921Е-2
2.166848Е-1
-2.256386E-1
4.650615E-1
1.568524
5.031371E-2
0.50
7.329854Е-2
2.669088Е-1
-2.845922E-1
5.968370E-1
1.551269
5.950653E-2
0.60
1.081457Е-1
3.144413Е-1
-3.454178E-1
7.402617E-1
1.530604
6.675556E-2
Таблица 66
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.285969
-1.380265E-2
5.560711E-2
1.598002
0.20
-0.20
6.294391
-2.709512E-2
1.115264E-1
1.592033
0.30
-0.30
6.308671
-3.940216E-2
1.680847E-1
1.582167
0.40
-0.40
6.329184
-5.031371E-2
2.256386E-1
1.568524
0.50
-0.50
6.356483
-5.950653E-2
2.845922E-1
1.551269
0.60
-0.60
6.391331
-6.675556E-2
3.454178E-1
1.530604
Продолжение таблицы 66
bT
tgε2
uB2T
uB2
ΔuB2
0.10
6.946308E-2
-5.546977Е-2
-5.546977Е-2
6.938893Е-18
0.20
1.390417E-1
-1.104236Е-1
-1.104236Е-1
1.387778Е-17
0.30
2.088702E-1
-1.643397E-1
-1.643397E-1
2.775557Е-17
0.40
2.791211E-1
-2.166848Е-1
-2.166848Е-1
-8.326672Е-17
0.50
3.500265E-1
-2.669088Е-1
-2.669088Е-1
-1.665334Е-16
0.60
4.219018E-1
-3.144413Е-1
-3.144413Е-1
0.0
Передний отрезок sF2=7,0 мм Постоянная в уравнениях образующих 1-й и 2-й поверхностей (2) и (3)
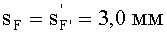
Таблица 67
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
2.783702Е-3
1.428003Е-2
-5.560711E-2
6.994268E-2
1.598002
-1.187441E-2
0.20
1.120637Е-2
2.852576Е-2
-1.115264E-1
1.404991E-1
1.592033
-2.356714E-2
0.30
2.548625Е-2
4.270167Е-2
-1.680847E-1
2.123102E-1
1.582167
-3.489863E-2
0.40
4.599921Е-2
5.676980Е-2
-2.256386E-1
2.860729E-1
1.568524
-4.569336E-2
0.50
7.329854Е-2
7.068837Е-2
-2.845922E-1
3.625747E-1
1.551269
-5.578149E-2
0.60
1.081457Е-1
8.441019Е-2
-3.454178E-1
4.427368E-1
1.530604
-6.500006E-2
Таблица 68
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.285969
1.187441Е-2
5.560711E-2
1.598002
0.20
-0.20
6.294391
2.356714Е-2
1.115264E-1
1.592033
0.30
-0.30
6.308671
3.489863Е-2
1.68П847Е-1
1.582167
0.40
-0.40
6.329184
4.569336Е-2
2.256386E-1
1.568524
0.50
-0.50
6.356483
5.578149Е-2
2.845922E-1
1.551269
0.60
-0.60
6.391331
6.500006Е-2
3.454178E-1
1.530604
Продолжение таблицы 68
bT
tgε2
uB2T
uB2
ΔuB2
0.10
4.370384E-2
-1.428003Е-2
-1.428003Е-2
-6.938893Е-18
0.20
8.772872E-2
-2.852576Е-2
-2.852576Е-2
3.816391Е-17
0.30
1.324094E-1
-4.270167Е-2
-4.270167Е-2
6.938893Е-18
0.40
1.781089E-1
-5.676980Е-2
-5.676980Е-2
-3.469446Е-17
0.50
2.252351E-1
-7.068837Е-2
-7.068837Е-2
-1.526556Е-16
0.60
2.742600E-1
-8.441019E-2
-8.441019E-2
-2.359223Е-16
Телескопический ход лучей
Направляющий коэффициент для любого входного луча uK1=0
Постоянная в уравнениях образующих 1-й и 2-й поверхностей (2) и (3)
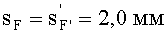
Таблица 69
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
4.169297E-3
0.0
-8.316135E-2
8.316135E-2
1.598002
-3.109537E-2
0.20
1.671000E-2
0.0
-1.653290E-1
1.653290E-1
1.592033
-6.128644E-2
0.30
3.772973E-2
0.0
-2.456898E-1
2.456898E-1
1.582167
-8.977837E-2
0.40
6.743725E-2
0.0
-3.237487E-1
3.237487E-1
1.568524
-1.159622E-1
0.50
1.061832E-1
0.0
-3.993993E-1
3.993993E-1
1.551269
-1.394422E-1
0.60
1.545136E-1
-0.0
-4.729315E-1
4.729315E-1
1.530604
-1.600172E-1
Таблица 70
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.287354
3.109537Е-2
8.316135E-2
1.598002
0.20
-0.20
6.299895
6.128644Е-2
1.653290E-1
1.592033
0.30
-0.30
6.320915
0.977S37E-2
2.456898Е-1
1.582167
0.40
-0.40
6.350622
1.159622Е-1
3.237487E-1
1.568524
0.50
-0.50
6.389368
1.394422Е-1
3.993993E-1
1.551269
0.60
-0.60
6.437698
1.600172Е-1
4.729315E-1
1.530604
Продолжение таблицы 70
bT
tgε2
uB2T
uB2
ΔuB2
0.10
5.193169E-2
0.0
-1.378247E-17
-1.378247E-17
0.20
1.029989E-1
0.0
-2.701709E-17
-2.701709E-17
0.30
1.525466E-1
0.0
-1.832287E-16
-1.832287E-16
0.40
2.002678E-1
0.0
0.0
0.0
0.50
2.462430E-1
0.0
-4.787425E-17
-4.787425E-17
0.60
2.908998E-1
0.0
-4.536469E-17
-4.536469E-17
Постоянная в уравнениях образующих 1-й и 2-й поверхностей (2) и (3)
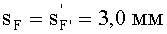
Таблица 71
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
2.783702Е-3
0.0
-5.560711E-2
5.560711E-2
1.598002
-2.080168E-2
0.20
1.120637Е-2
0.0
-1.115264E-1
1.115264E-1
1.592033
-4.141356E-2
0.30
2.548625Е-2
0.0
-1.680847E-1
1.680847E-1
1.582167
-6.164604E-2
0.40
4.599921Е-2
0.0
-2.256386E-1
2.256386E-1
1.568524
-8.130986E-2
0.50
7.329854Е-2
0.0
-2.845922E-1
2.845922E-1
1.551269
-1.002157E-1
0.60
1.081457Е-1
0.0
-3.454178E-1
3.454178E-1
1.530604
-1.181734E-1
Таблица 72
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.285969
2.080168Е-2
5.560711E-2
1.598002
0.20
-0.20
6.294391
4.141356Е-2
1.115264E-1
1.592033
0.30
-0.30
6.308671
6.164604Е-2
1.680847E-1
1.582167
0.40
-0.40
6.329184
8.130986Е-2
2.256386E-1
1.568524
0.50
-0.50
6.356483
1.002157Е-1
2.845922E-1
1.551269
0.60
-0.60
6.391331
1.181734Е-1
3.454178E-1
1.530604
Продолжение таблицы 72
bT
tgε2
uB2T
uB2
ΔuB2
0.10
3.476521E-2
0.0
0.0
0.0
0.20
6.979054E-2
0.0
-1.370729E-17
-1.370729Е-17
0.30
1.053471E-1
0.0
0.0
0.0
0.40
1.417285E-1
0.0
0.0
0.0
0.50
1.792638E-1
0.0
-5.135200Е-17
-5.135200Е-17
0.60
2.183322E-1
0.0
-1.487817Е-16
-1.487817Е-16
6.2.2. Линза с 1-й вогнутой и 2-й выпуклой поверхностями
6.2.2.1. Сферические поверхности, линза толщиной L
Толщина линзы d=L=12,566370 мм
Апланатический ход лучей
Передний отрезок sF1=2,0 мм
Радиусы сферических поверхностей выбираются равными RC1=3,0 мм
Таблица 73
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.667129Е-3
5.004171Е-2
3.335186Е-2
1.666203E-2
1.598002
4.379300E-2
0.20
-6.674090Е-3
1.003348Е-1
6.681531Е-2
3.329629E-2
1.592033
8.784533E-2
0.30
-1.503768Е-2
1.511363Е-1
1.005037Е-1
4.987499E-2
1.582167
1.324227E-1
0.40
-2.678625Е-2
2.027149Е-1
1.345345Е-1
6.637036E-2
1.568524
1.778040E-1
0.50
-4.196010Е-2
2.553574Е-1
1.690308Е-1
8.275460E-2
1.551269
2.242891E-1
0.60
-6.061230Е-2
3.093759Е-1
2.041241Е-1
9.899989E-2
1.530604
2.722073E-1
0.70
-8.280957Е-2
3.651176Е-1
2.399569Е-1
1.150784E-1
1.506764
3.219281E-1
0.80
-1.086335Е-1
4.229746Е-1
2.766857Е-1
1.309621E-1
1.480011
3.738747E-1
Таблица 74
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.256470Е+1
4.379300E-2
3.335186Е-2
1.598002
0.20
0.20
1.255969Е+1
8.784533E-2
6.681531Е-2
1.592033
0.30
0.30
1.255133Е+1
1.324227E-1
1.005037Е-1
1.582167
0.40
0.40
1.253958Е+1
1.778040Е-1
1.345345Е-1
1.568524
0.50
0.50
1.252441Е+1
2.242891E-1
1.690308E-1
1.551269
0.60
0.60
1.250575Е+1
2.722073E-1
2.041241E-1
1.530604
0.70
0.70
1.248356Е+1
3.219281E-1
2.399569Е-1
1.506764
0.80
0.80
1.245773Е+1
3.738747Е-1
2.766857Е-1
1.480011
Продолжение таблицы 74
bT
tgε2
uB2T
uB2
ΔuB2
0.10
1.042591E-2
5.004171Е-2
5.004171Е-2
-5.280498Е-15
0.20
2.090730E-2
1.003348Е-1
1.003348Е-1
2.692290Е-15
0.30
3.149969E-2
1.511363Е-1
1.511363Е-1
2.775557Е-17
0.40
4.225866E-2
2.027149Е-1
2.027149Е-1
8.326672Е-17
0.50
5.323992E-2
2.553574Е-1
2.553574Е-1
-3.885780Е-16
0.60
6.449934E-2
3.093759Е-1
3.093759Е-1
1.110223Е-16
0.70
7.609309E-2
3.651176Е-1
3.651176Е-1
5.551115Е-17
0.80
8.807771E-2
4.229746Е-1
4.229746Е-1
5.551115Е-17
Передний отрезок sF2=7,0 мм
Радиусы сферических поверхностей выбираются равными RC1=3,0 мм
Таблица 75
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.667129Е-3
1.428911E-2
3.335186E-2
1.905366E-2
1.598002
2.142123Е-2
0.20
-6.674090Е-3
2.859869E-2
6.681531E-2
3.814372E-2
1.592033
4.279824Е-2
0.30
-1.503768Е-2
4.294940E-2
1.005037E-1
5.730700E-2
1.582167
6.408581Е-2
0.40
-2.678625Е-2
5.736236E-2
1.345345E-1
7.658120E-2
1.568524
8.523669Е-2
0.50
-4.196010Е-2
7.185931E-2
1.690308E-1
9.600540E-2
1.551269
1.062006Е-1
0.60
-6.061230Е-2
8.646295E-2
2.041241E-1
1.156205E-1
1.530604
1.269231Е-1
0.70
-8.280957Е-2
1.011971E-1
2.399569E-1
1.354701E-1
1.506764
1.473444Е-1
0.80
-1.086335Е-1
1.160872E-1
2.766857E-1
1.556006E-1
1.480011
1.673982Е-1
Таблица 76
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.256470Е+1
2.142123Е-2
3.335186E-2
1.598002
0.20
0.20
1.255969Е+1
4.279824Е-2
6.681531E-2
1.592033
0.30
0.30
1.255133Е+1
6.408581Е-2
1.005037E-1
1.582167
0.40
0.40
1.253958Е+1
8.523669Е-2
1.345345E-1
1.568524
0.50
0.50
1.252441Е+1
1.062006Е-1
1.690308E-1
1.551269
0.60
0.60
1.250575Е+1
1.269231Е-1
2.041241E-1
1.530604
0.70
0.70
1.248356Е+1
1.473444Е-1
2.399569E-1
1.506764
0.80
0.80
1.245773Е+1
1.673982Е-1
2.766857E-1
1.480011
Продолжение таблицы 76
bT
tgε2
uB2T
uB2
ΔuB2
0.10
1.192211Е-2
1.428911E-2
1.428911E-2
-5.285702Е-15
0.20
2.394858Е-2
2.859869E-2
2.859869E-2
2.671474Е-15
0.30
3.618490Е-2
4.294940E-2
4.294S4UE-2
5.551115Е-17
0.40
4.873895Е-2
5.736236E-2
5.736236E-2
7.632783Е-17
0.50
6.172225Е-2
7.185931E-2
7.185931E-2
-4.024558Е-16
0.60
7.525141Е-2
8.646295E-2
8.646295E-2
1.526556Е-16
0.70
8.944986Е-2
1.011971E-1
1.011971E-1
1.804112Е-16
0.80
1.044497Е-1
1.160872E-1
1.160872E-1
1.110223Е-16
Передний отрезок sF1=2,0 мм
Радиусы сферических поверхностей выбираются равными RC2=5,0 мм
Таблица 77
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.000100E-3
5.00250E-2
2.000400E-2
2.999100E-2
1.598002
3.878123Е-2
0.20
-4.001601E-3
1.00200E-1
4.003203E-2
5.992805E-2
1.592033
7.775068Е-2
0.30
-9.008114E-3
1.50678E-1
6.010829E-2
8.975743E-2
1.582167
1.171005Е-1
0.40
-1.602568E-2
2.01615E-1
8.025723E-2
1.194258E-1
1.568524
1.570314Е-1
0.50
-2.506281E-2
2.53172E-1
1.005037E-1
1.488805E-1
1.551269
1.977567Е-1
0.60
-3.613054E-2
3.05519E-1
1.208734E-1
1.780698E-1
1.530604
2.395078Е-1
0.70
-4.924248E-2
3.58834E-1
1.413925E-1
2.069428E-1
1.506764
2.825406Е-1
0.80
-6.441492E-2
4.13311E-1
1.620881E-1
2.354500E-1
1.480011
3.271425Е-1
Таблица 78
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.256537Е+1
3.878123Е-2
2.000400E-2
1.598002
0.20
0.20
1.256236Е+1
7.775068Е-2
4.003203E-2
1.592033
0.30
0.30
1.255736Е+1
1.171005Е-1
6.010829E-2
1.582167
0.40
0.40
1.255034Е+1
1.570314Е-1
8.025723E-2
1.568524
0.50
0.50
1.254130Е+1
1.977567Е-1
1.005037E-1
1.551269
0.60
0.60
1.253024Е+1
2.395078Е-1
1.208734E-1
1.530604
0.70
0.70
1.251712Е+1
2.825406Е-1
1.413925E-1
1.506764
0.80
0.80
1.250195Е+1
3.271425Е-1
1.620881E-1
1.480011
Продолжение таблицы 78
bT
tgε2
uB2T
uB2
ΔuB2
0.10
1.876267Е-2
5.00250E-2
5.00250E-2
-5.238864E-15
0.20
3.760160Е-2
1.00200E-1
1.00200E-1
1.387778E-17
0.30
5.659395Е-2
1.50678E-1
1.50678E-1
2.775557E-17
0.40
7.581871Е-2
2.01615E-1
2.01615E-1
-1.276756E-15
0.50
9.535769Е-2
2.53172E-1
2.53172E-1
1.165734E-15
0.60
1.152965Е-1
3.05519Е-1
3.0S519F-1
-9 Ч?6672Е-36
0.70
1.357260Е-1
3.58834E-1
3.58834Е-1
7.771561Е-16
0.80
1.567429Е-1
4.13311E-1
4.13311E-1
5.551115Е-17
Передний отрезок sF2=7,0 mm
Радиусы сферических поверхностей выбираются равными RC2=5,0 мм
Таблица 79
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.000100Е-3
1.428775Е-2
2.000400E-2
5.714612E-3
1.598002
1.642676Е-2
0.20
-4.001601Е-3
2.858777E-2
4.003203E-2
1.143118E-2
1.5Э2033
3.284263Е-2
0.30
-9.008114Е-3
4.291236E-2
6.010829E-2
1.715168E-2
1.582167
4.923654Е-2
0.40
-1.602568Е-2
5.727397E-2
8.025723E-2
2.287809E-2
1.568524
6.559698Е-2
0.50
-2.506281Е-2
7.168523E-2
1.005037E-1
2.861240E-2
1.551269
8.191187Е-2
0.60
-3.613054Е-2
8.615899E-2
1.208734E-1
3.435664E-2
1.530604
9.816832Е-2
0.70
-4.924248Е-2
1.007084E-1
1.413925E-1
4.011287E-2
1.506764
1.143523Е-1
0.80
-6.441492Е-2
1.153471E-1
1.620881E-1
4.588317E-2
1.480011
1.304488Е-1
Таблица 80
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.256537Е+1
1.642676Е-2
2.000400E-2
1.598002
0.20
0.20
1.256236Е+1
3.284263Е-2
4.003203E-2
1.592033
0.30
0.30
1.255736Е+1
4.923654Е-2
6.010829E-2
1.582167
0.40
0.40
1.255034Е+1
6.559698Е-2
8.025723E-2
1.568524
0.50
0.50
1.254130Е+1
8.191187Е-2
1.005037E-1
1.551269
0.60
0.60
1.253024Е+1
9.816832Е-2
1.208734E-1
1.530604
0.70
0.70
1.251712Е+1
1.143523Е-1
1.413925E-1
1.506764
0.80
0.80
1.250195Е+1
1.304488Е-1
1.620881E-1
1.480011
Продолжение таблицы 80
bT
tgε2
uB2T
uB2
ΔuB2
0.10
3.576062Е-3
1.428775Е-2
1.428775Е-2
-5.216313Е-15
0.20
7.179959Е-3
2.858777E-2
2.858777E-2
3.816391Е-17
0.30
1.083967Е-2
4.291236E-2
4.291236E-2
4.857225Е-17
0.40
1.458347Е-2
5.727397E-2
5.727397E-2
-1.193489Е-15
0.50
1.844009Е-2
7.168523E-2
7.168523E-2
1.068589Е-15
0.60
2.243886Е-2
8.615899E-2
8.615899E-2
-7.077671Е-16
0.70
2.660987Е-2
1.007084E-1
1.007084E-1
7.632783Е-16
0.80
3.098417Е-2
1.153471E-1
1.153471E-1
1.110223Е-16
Телескопический ход лучей
Направляющий коэффициент для любого входного луча uK1=0
Радиусы сферических поверхностей выбираются равными RC1=3,0 мм
Таблица 81
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.667129E-3
0.0
3.335186E-2
3.335186E-2
1.598002
1.247926E-2
0.20
-6.674090E-3
0.0
6.681531E-2
6.681531E-2
1.592033
2.483383E-2
0.30
-1.503768E-2
0.0
1.005037E-1
1.005037E-1
1.582167
3.693760E-2
0.40
-2.678625E-2
0.0
1.345345E-1
1.345345E-1
1.568524
4.866167E-2
0.50
-4.196010E-2
0.0
1.690308E-1
1.690308E-1
1.551269
5.987282E-2
0.60
-6.061230E-2
0.0
2.041241E-1
2.041241E-1
1.530604
7.043200E-2
0.70
-8.280957E-2
0.0
2.399569E-1
2.399569E-1
1.506764
8.019258E-2
0.80
-1.086335E-1
0.0
2.766857E-1
2.766857E-1
1.480011
8.899851E-2
Таблица 82
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.256470Е+1
1.247926E-2
3.335186E-2
1.598002
0.20
0.20
1.255969Е+1
2.483383E-2
6.681531E-2
1.592033
0.30
0.30
1.255133Е+1
3.693760E-2
1.005037E-1
1.582167
0.40
0.40
1.253958Е+1
4.866167E-2
1.345345E-1
1.568524
0.50
0.50
1.252441Е+1
5.987282E-2
1.690308E-1
1.551269
0.60
0.60
1.250575Е+1
7.043200E-2
2.041241E-1
1.530604
0.70
0.70
1.248356Е+1
8.019258E-2
2.399569E-1
1.506764
0.80
0.80
1.245773Е+1
8.899851E-2
2.766857E-1
1.480011
Продолжение таблицы 82
bT
tgε2
uB2T
uB2
ΔuB2
0.10
2.086392У-2
0.0
-5.295424E-15
-5.295424E-15
0.20
4.191193E-2
0.0
2.666508E-15
2.666508E-15
0.30
6.333106E-2
0.0
4.121702E-17
4.121702E-17
0.40
8.531436E-2
0.0
8.178642E-17
8.178642E-17
0.50
1.080643E-1
0.0
-4.317533E-16
-4.317533E-16
0.60
1.317973E-1
0.0
7.993605E-17
7.993605E-17
0.70
1.567480E-1
0.0
1.312221E-16
1.312221E-16
0.80
1.831766E-1
0.0
1.546910E-16
1.546910E-16
Радиусы сферических поверхностей выбираются равными RC2=5,0 мм
Таблица 83
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.000100Е-3
0.0
2.000400E-2
2.000400E-2
1.598002
7.485518E-3
0.20
-4.001601Е-3
0.0
4.003203E-2
4.003203E-2
1.592033
1.488402E-2
0.30
-9.008114Е-3
0.0
6.010829E-2
6.010829E-2
1.582167
2.210789E-2
0.40
-1.602568Е-2
0.0
8.025723E-2
8.025723E-2
1.568524
2.906828E-2
0.50
-2.506281Е-2
0.0
1.005037E-1
1.005037E-1
1.551269
3.567449E-2
0.60
-3.613054Е-2
0.0
1.208734E-1
1.208734E-1
1.530604
4.183333E-2
0.70
-4.924248Е-2
0.0
1.413925E-1
1.413925E-1
1.506764
4.744845E-2
0.80
-6.441492Е-2
0.0
1.620881E-1
1.620881E-1
1.480011
5.241965E-2
Таблица 84
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.256537Е+1
7.485518E-3
2.000400E-2
1.598002
0.20
0.20
1.256236Е+1
1.488402E-2
4.003203E-2
1.592033
0.30
0.30
1.255736Е+1
2.210789E-2
6.010829E-2
1.582167
0.40
0.40
1.255034Е+1
2.906828E-2
8.025723E-2
1.568524
0.50
0.50
1.254130Е+1
3.567449E-2
1.005037E-1
1.551269
0.60
0.60
1.253024Е+1
4.183333E-2
1.208734E-1
1.530604
0.70
0.70
1.251712Е+1
4.744845E-2
1.413925E-1
1.506764
0.80
0.80
1.250195Е+1
5.241965E-2
1.620881E-1
1.480011
Продолжение таблицы 84
bT
tgε2
uB2T
uB2
ΔuB2
0.10
1.251660E-2
0.0
-5.219429E-15
-5.219429E-15
0.20
2.513303E-2
0.0
4.156675E-17
4.156675E-17
0.30
3.794996E-2
0.0
5.531131E-17
5.531131E-17
0.40
5.106980E-2
0.0
-1.199640E-15
-1.199640E-15
0.50
6.459767E-2
0.0
1.099120E-15
1.099120E-15
0.60
7.864245E-2
0.0
-6.838973E-16
-6.838973E-16
0.70
9.331799E-2
0.0
7.619238E-16
7.619238E-16
0.80
1.087445E-1
0.0
1.352251E-16
1.352251E-16
6.2.2.2. Сферические поверхности, линза толщиной L/2
Толщина линзы d=L/2=6,283185 мм
Апланатический ход лучей
Передний отрезок sF1=1=2,0 мм
Радиусы сферических поверхностей выбираются равными RC1=3,0 мм
Таблица 85
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.667129E-3
5.004171E-2
3.335L86E-2
1.666203E-2
1.598002
4.379300E-2
0.20
-6.674090E-3
1.003348E-1
6.681531E-2
3.329629E-2
1.592033
8.784533E-2
0.30
-1.503768E-2
1.511363E-1
1.005037E-1
4.987499E-2
1.582167
1.324227E-1
0.40
-2.678625E-2
2.027149E-1
1.345345E-1
6.637036E-2
1.568524
1.778040E-1
0.50
-4.196010E-2
2.553574E-1
1.690308E-1
8.275460E-2
1.551269
2.242891E-1
0.60
-6.061230E-2
3.093759E-1
2.041241E-1
9.899989E-2
1.530604
2.722073E-1
0.70
-8.280957E-2
3.651176E-1
2.399569E-1
1.150784E-1
1.506764
3.219281E-1
0.80
-1.086335E-1
4.229746E-1
2.766857E-1
1.309621E-l
1.480011
3.738747E-1
Таблица 86
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.281518
-4.379300E-2
-3.335186Е-2
1.598002
0.20
-0.20
6.276511
-8.784533E-2
-6.681531E-2
1.592033
0.30
-0.30
6.268147
-1.324227E-1
-1.005037E-1
1.582167
0.40
-0.40
6.256399
-1.778040E-1
-1.345345Е-1
1.568524
0.50
-0.50
6.241225
-2.242891E-1
-1.690308E-1
1.551269
0.60
-0.60
6.222572
-2.722073E-1
-2.041241E-1
1.530604
0.70
-0.70
6.200375
-3.219281E-1
-2.399569Е-3
1.506764
0.80
-0.80
6.174551
-3.738747E-1
-2.766857E-1
1.480011
Продолжение таблицы 86
bT
tgε2
uB2T
uB2
ΔuB2
0.10
1.042591Е-2
-5.004171E-2
-5.004171E-2
-2.775557Е-17
0.20
2.090730Е-2
-1.003348E-1
-1.003348E-1
-2.775557Е-17
0.30
3.149969Е-2
-1.511363E-1
-1.511363E-1
0.0
0.40
4.225866Е-2
-2.027149E-1
-2.027149E-1
-2.775557Е-17
0.50
5.323992Е-2
-2.553574E-1
-2.553574E-1
4.440892Е-16
0.60
6.449934Е-2
-3.093759E-1
-3.093759E-1
-1.110223Е-16
0.70
7.609309Е-2
-3.651176E-1
-3.651176E-1
0.0
0.80
8.807771Е-2
-4.229746E-1
-4.22271£^-1
0.0
Передний отрезок sF2=7,0 мм
Радиусы сферических поверхностей выбираются равными RC1=3,0 мм
Таблица 87
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.667129E-8
1.428911E-2
3.335186E-2
1.905366E-2
1.598002
2.142123E-2
0.20
-6.674090E-3
2.859869E-2
6.681531E-2
3.814372E-2
1.592033
4.279824E-2
0.30
-1.503768E-2
4.294940E-2
1.005037E-1
5.730700E-2
1.582167
6.408581E-2
0.40
-2.678625E-2
5.736236E-2
1.345345E-1
7.658120E-2
1.568524
8.523669E-2
0.50
-4.196010E-2
7.385931E-2
1.690308E-1
9.600540E-2
1.551269
1.062006E-1
0.60
-6.061230E-2
8.646295E-2
2-04L241E-1
1.156205E-1
1.530604
1.269231E-1
0.70
-8.280957E-2
1.011971E-1
2.399569E-1
1.354701E-1
1.506764
1.473444E-1
0.80
-1.086335E-1
1.160872E-1
2.766857E-1
1.556006E-1
1.480011
1.673982E-1
Таблица 88
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.281518
-2.142123E-2
-3.335186E-2
1.598002
0.20
-0.20
6.276511
-4.279824E-2
-6.681531Е-2
1.592033
0.30
-0.30
6.268147
-6.408581E-2
-1.005037E-1
1.582167
0.40
-0.40
6.256399
-8.523669E-2
-1.345345E-1
1.568524
0.50
-0.50
6.241225
-1.062006E-1
-1.690308Е-1
1.551269
0.60
-0.60
6.222572
-1.269231E-1
-2.041241Е-1
1.530604
0.70
-0.70
6.200375
-1.473444E-1
-2.399569E-1
1.506764
0.80
-0.80
6.174551
-1.673982E-1
-2.766857E-1
1.480011
Продолжение таблицы 88
bT
tgε2
uB2T
uB2
ΔuB2
0.10
1.192211E-2
-1.428911E-2
-1.428911E-2
-1.561251Е-17
0.20
2.394858E-2
-2.859869E-2
-2.859869E-2
-1.387778Е-17
0.30
3.618490E-2
-4.294940E-2
-4.294940E-2
-3.469446Е-17
0.40
4.873895E-2
-5.736236E-2
-5.736236E-2
-6.245004Е-17
0.50
6.172225E-2
-7.185931E-2
-7.185931E-2
4.440892Е-16
0.60
7.525141E-2
-8.646295E-2
-8.646295E-2
-6.938893Е-17
0.70
8.944986E-2
-1.011971E-1
-1.011971E-1
-9.714451Е-17
0.80
1.044497E-1
-1.160872E-1
-1.160872E-1
-8.326672Е-17
Передний отрезок sF1=2,0 мм
Радиусы сферических поверхностей выбираются равными RC2=5,0 мм
Таблица 89
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.000100Е-3
5.00250Е-2
2.000400E-2
2.999100E-2
1.598002
3.878123E-2
0.20
-4.001601Е-3
1.00200Е-1
4.003203E-2
5.992805E-2
1.592033
7.775068E-2
0.30
-9.008114Е-3
1.50678Е-1
6.010829E-2
8.975743E-2
1.582167
1.171005E-1
0.40
-1.602568Е-2
2.01615Е-1
8.025723E-2
1.194258E-1
1.568524
1.570314E-1
0.50
-2.506281Е-2
2.53172Е-1
1.005037E-1
1.488805E-1
1.551269
1.977567E-1
0.60
-3.613054Е-2
3.055L9E-1
1.208734E-1
1.780«98E-1
1.530604
2.395078E-1
0.70
-4.924248Е-2
3.58834Е-1
1.413925E-1
2.069428E-1
1.506764
2.825406E-1
0.80
-6.441492Е-2
4.13311Е-1
1.620881E-1
2 354500E-1
1 480011
3.271425E-1
Таблица 90
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.282185
-3.878123E-2
-2.000400E-2
1.598002
0.20
-0.20
6.279183
-7.775068E-2
-4.003203E-2
1.592033
0.30
-0.30
6.274177
-1.171005E-1
-6.010829E-2
1.582167
0.40
-0.40
6.267159
-1.570314E-1
-8.025723E-2
1.568524
0.50
-0.50
1 6.258122
-1.977567E-1
-1.005037E-1
1.551269
0.60
-0.60
6.247054
-2.395078E-1
-1.208734E-1
1.530604
0.70
-0.70
6.233942
-2.825406E-1
-1.413925E-1
1.506764
0.80
-0.80
6.218770
-3.271425E-1
-1.620881E-1
1.480011
Продолжение таблицы 90
bT
tgε2
uB2T
uB2
ΔuB2
0.10
1.876267E-2
-5.002501E-2
-5.002501E-2
-6.938893Е-18
0.20
J.760160E-2
-1.002004E-1
-1.002004E-1
0.0
0.30
5.659395E-2
-1.506786E-1
-1.506786E-1
-2.775557Е-17
0.40
7.581871E-2
-2.016155E-1
-2.016155E-1
-2.775557Е-17
0.50
9.535769E-2
-2.531726E-1
-2.531726E-1
-5.551115Е-17
0.60
1.152965E-1
-3.055192E-1
-3.055192E-1
-5.551115Е-17
0.70
1.357260E-1
-3.588349E-1
-3.588349E-1
-5.551115Е-17
0.80
1.567429E-1
-4.133117E-1
-4.133117E-1
-5.551115Е-17
Передний отрезок sF2=7,0 мм
Радиусы сферических поверхностей выбираются равными RC2=5,0 мм
Таблица 91
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.000100Е-3
1.428775E-2
2.000400E-2
5.714612E-3
1.598002
1.642676E-2
0.20
-4.001601Е-3
2.858777E-2
4.003203E-2
1.143118E-2
1.592033
3.284263E-2
0.30
-9.008114Е-3
4.291236E-2
6.010829E-2
1.715168E-2
1.582167
4.923654E-2
0.40
-1.602568Е-2
5.727397E-2
8.025723E-2
2.287809E-2
1.568524
6.559698E-2
0.50
-2.506281Е-2
7.168523E-2
1.005037E-1
2.861240E-2
1.551269
8.191187E-2
0.60
-3.613054Е-2
8.615899E-2
1.208734E-L
3.435664E-2
1.530604
9.816832E-2
0.70
-4.924248Е-2
1.007084E-1
1.413925E-1
4.011287E-2
1.506764
1.143523E-1
0.80
-6.441492Е-2
1.153471E-1
1.620881E-1
4.588317E-2
1.480011
1.304488E-1
Таблица 92
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.282185
-1.642676E-2
-2.000400E-2
1.598002
0.20
-0.20
6.279183
-3.284263E-2
-4.003203E-2
1.592033
0.30
-0.30
6.274177
-4.923654E-2
-6.010829E-2
1.582167
0.40
-0.40
6.267159
-6.559698E-2
-8.025723E-2
1.568524
0.50
-0.50
6.258122
-9.19П87Е-?
-1.005037Е-1
1.551269
0.60
-0.60
6.247054
-9.816832E-2
-1.208734Е-1
1.530604
0.70
-0.70
6.233942
-1.143523E-1
-1.413925E-1
1.506764
0.80
-0.80
6.218770
-1.304488E-1
-1.620881E-1
1.480011
Продолжение таблицы 92
bT
tgε2
uB2T
uB2
ΔuB2
0.10
3.576062E-3
-1.428775E-2
-1.428775E-2
-1.214306Е-17
0.20
7.179959E-3
-2.858777E-2
-2.858777E-2
-1.734723Е-17
0.30
1.083967E-2
-4.291236E-2
-4.291236E-2
-2.775557Е-17
0.40
1.45834 7E-2
-5. /27397E-2
-3.72/ЗУ/Ь-2
-j.4b9446E-17
0.50
1.844009E-2
-7.168523E-2
-7.168523E-2
-4.163336E-17
0.60
2.243886E-2
-8.615899E-2
-8.615899E-2
-2.775557Е-17
0.70
2.660987E-2
-1.007084E-1
-1.007084E-1
-4.163336E-17
0.80
3.098417E-2
-1.153471E-1
-1.153471E-1
-3.330669E-16
Телескопический ход лучей
Направляющий коэффициент для любого входного луча uK1=0
Радиусы сферических поверхностей выбираются равными RC1=3,0 мм
Таблица 93
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.667129E-3
0.0
3.335186E-2
3.335186E-2
1.598002
1.247926E-2
0.20
-6.674090E-3
0.0
6.681531E-2
6.681531E-2
1.592033
2.483383E-2
0.30
-1.503768E-2
0.0
1.005037E-1
1.005037E-1
1.582167
3.693760E-2
0.40
-2.678625E-2
0.0
1.345345E-1
1.345345E-1
1.568524
4.866167E-2
0.50
-4.196010E-2
0.0
1.690308E-1
1.690308E-1
1.551269
5.987282E-2
0.60
-6.061230E-2
0.0
2.041241E-1
2.041241E-1
1.530604
7.043200E-2
0.70
-8.280957E-2
0.0
2.399569E-1
2.399569E-1
1.506764
8.019258E-2
0.80
-1.086335E-1
0.0
2.766857E-1
2.766857E-1
1.480011
8.899851E-2
Таблица 94
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.281518
-1.247926E-2
-3.335186E-2
1.598002
0.20
-0.20
6.276511
-2.483383E-2
-6.681531E-2
1.592033
0.30
-0.30
6.268147
-3.693760E-2
-1.005037E-1
1.582167
0.40
-0.40
6.256399
-4.866167E-2
-1.345345E-1
1.568524
0.50
-0.50
6.241225
-5.987282E-2
-1.690308E-1
1.551269
0.60
-0.60
6.222572
-7.043200E-2
-2.041241E-1
1.530604
0.70
-0.70
6.200375
-8.019258E-2
-2.399569E-1
1.506764
0.80
-0.80
6.174551
-8.899851E-2
-2.766857E-1
1.480011
Продолжение таблицы 94
bT
tgε2
uB2T
uB2
ΔuB2
0.10
2.086392E-2
0.0
-1.386236E-17
-1.386236E-17
0.20
4.191193E-2
0.0
-2.763221E-17
-2.763221E-17
0.30
6.333106E-?
0.0
-1.Р73900Е-П
-1.ЭТ?ОППЕ-17
0.40
8.531436E-2
0.0
-5.452428E-17
-5.452428E-17
0.50
1.080643E-1
0.0
4.317533E-16
4.317533E-16
0.60
1.317973E-1
0.0
-2.664535E-17
-2.664535E-17
0.70
1.567480E-1
0.0
-2.624443E-17
-2.624443E-17
0.80
1.831766E-1
0.0
0.0
0.0
Радиусы сферических поверхностей выбираются равными RC2=5,0 мм
Таблица 95
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.000100Е-3
0.0
2.000400Е-2
2.000400Е-2
1.598002
7.485518E-3
0.20
-4.001601Е-3
0.0
4.003203Е-2
4.003203Е-2
1.592033
1.488402E-2
0.30
-9.008114Е-3
0.0
6.010829Е-2
6.010829Е-2
1.582167
2.210789E-2
0.40
-1.602568Е-2
0.0
8.025723Е-2
8.025723Е-2
1.568524
2.906828E-2
0.50
-2.5062S1E-2
0.0
1.G05037E-1
1.005037E-1
1.551269
3.567449E-2
0.60
-3.613054Е-2
0.0
1.208734Е-1
1.208734Е-1
1.530604
4.183333E-2
0.70
-4.924248Е-2
0.0
1.413925Е-1
1.413925Е-1
1.506764
4.744845E-2
0.80
-6.441492Е-2
0.0
1.620881Е-1
1.620881Е-1
1.480011
5.241965E-2
Таблица 96
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.282185
-7.485518E-3
-2.000400Е-2
1.598002
0.20
-0.20
6.279183
-1.488402E-2
-4.003203Е-2
1.592033
0.30
-0.30
6.274177
-2.210789E-2
-6.010829Е-2
1.582167
0.40
-0.40
6.267159
-2.906828E-2
-8.025723Е-2
1.568524
0.50
-0 50
б ?5812?
-3.567449F-2
-1.005037E-1
1.551269
0.60
-0.60
6.247054
-4.183333E-2
-1.208734Е-1
1.530604
0.70
-0.70
6.233942
-4.744845E-2
-1.413925Е-1
1.506764
0.80
-0.80
6.218770
-5.241965E-2
-1.620881Е-1
1.480011
Продолжение таблицы 96
bT
tgε2
uB2T
uB2
ΔuB2
0.10
1.251660E-2
0.0
-1.040417Е-17
-1.040417Е-17
0.20
2.513303E-2
0.0
-1.385558Е-17
-1.385558Е-17
0.30
3.794996E-2
0.0
-2.074174Е-17
-2.074174Е-17
0.40
5.106980E-2
0.0
-4.136690E-L7
-4.136690Е-17
0.50
6.459767E-2
0.0
-5.495603Е-17
-5.495603Е-17
0.60
7.864245E-2
0.0
5.471179Е-16
5.471179Е-16
0.70
9.331799E-2
0.0
-5.442313Е-17
-5.442313Е-17
0.80
1.087445E-1
0.0
-3.515854Е-16
-3.515854Е-16
6.2.2.3. Конические поверхности, линза толщиной L
Толщина линзы d=L=12,566370 мм
Апланатический ход лучей
Передний отрезок sF1=2,0 мм
I Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p1=-1,3
Таблица 97
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-7.692307Е-2
5.200000E-2
7.692307E-1
6.896449E-1
1.598002
3.011258E-1
0.20
-1.538461Е-1
1.083333E-1
7.692307E-1
6.100591E-1
1.592033
3.340935E-1
0.30
-2.307692Е-1
1.695652E-1
7.692307E-1
5.304733E-1
1.582167
3.707003E-1
0.40
-3.076923Е-1
2.363636E-1
7.692307E-1
4.508875E-1
1.568524
4.116934E-1
0.50
-3.846153Е-1
3.095238E-1
7.692307E-1
3.713017E-1
1.551269
4.578750E-1
0.60
-4.615384Е-1
3.900000E-1
7.692307E-1
2,917159E-1
1.530604
5.101018E-1
0.70
-5.384615Е-1
4.789473E-1
7.692307E-1
2.121301E-1
1.506764
5.692944E-1
0.80
-6.153846Е-1
5.777777E-1
7.692307E-1
1.325443E-1
1.480011
6.364613E-1
Таблица 98
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.248944E+1
3.011258E-1
7.692307E-1
1.598002
0.20
0.20
1.241252E+1
3.340935E-1
7.692307E-1
1.592033
0.30
0.30
1.233560E+1
3.707003E-1
7.692307E-1
1.582167
0.40
0.40
1.225867E+1
4.116934E-1
7.692307E-1
1.568524
0.50
0.50
1.218175E+1
4.578750E-1
7.692307E-1
1.551269
0.60
0.60
1.210483E+1
5.101018E-1
7.692307E-1
1.530604
0.70
0.70
1.202790E+1
5.692944E-1
7.692307E-1
1.506764
0.80
0.80
L.195098E+1
6.364613E-1
7.692307E-1
1.480011
Продолжение таблицы 98
bT
tgε2
uB2T
uB2
ΔuB2
0.10
3.800678E-1
5.200000E-2
5.200000E-2
5.551115Е-17
0.20
3.461725E-1
1.083333E-1
1.083333E-1
-1.110223Е-16
0.30
3.101032E-1
1.695652E-1
1.695652E-1
5.551115Е-17
0.40
2.715430E-1
2.363636E-1
2.363636E-1
5.551115E-L7
0.50
2.302566E-1
3.095238E-1
3.095238E-1
1.665334Е-16
0.60
1.861042E-1
3.900000E-1
3.900000E-1
5.551115Е-17
0.70
L.390455E-1
4.789473E-1
4.789473E-1
1.665334Е-16
0.80
8.9L3180E-2
5.777777E-1
5.777777E-1
2.220446Е-16
Передний отрезок sF2=7,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p1=-1,3
Таблица 99
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-7.692307Е-2
1.444444Е-2
7.692307E-1
7.464919E-1
1.598002
2.789216E-1
0.20
-1.538461Е-1
2.921348Е-2
7.692307E-1
7.237531E-1
1.592033
2.859776E-1
0.30
-2.307692Е-1
4.431818Е-2
7.692307E-1
7.010143E-1
1.582167
2.923441E-1
0.40
-3.Q76923E-1
5.977011Е-2
7.692307E-1
6.782755E-1
1.568524
2.980924E-1
0.50
-3.846153Е-1
7.558139Е-2
7.692307E-1
6.555367E-1
1.551269
3.032963E-1
0.60
-4.615384Е-1
9.176470Е-2
7.692307E-1
6.327979E-1
1.530604
3.080324E-1
0.70
-5.384615Е-1
1.083333Е-1
7.692307E-1
6.100591E-1
1.506764
3.123809E-1
0.80
-6.153846Е-1
1.253012Е-1
7.692307E-1
5.873203E-1
1.480011
3.164255E-1
Таблица 100
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.248944Е+1
2.789216E-1
7.692307E-1
1.598002
о.20
0.20
1.241252E+1
2.859776E-1
7.692307E-1
1.592033
0.30
0.30
1.233560E+1
2.923441E-1
7.692307E-1
1.582167
0.40
0.40
1.225867E+1
2.980924E-1
7.692307E-1
1.568524
0.50
0.50
1.218175E+1
3.032963E-1
7.692307E-1
1.551269
0.60
0.60
1.210483E+1
3.080324E-1
7.692307E-1
1.530604
0.70
0.70
1.202790E+1
3.123809E-1
7.692307E-1
1.506764
0.80
0.80
1.195098E+1
3.164255E-1
7.692307E-1
1.480011
Продолжение таблицы 100
bT
tgε2
uB2T
uB2
ΔuB2
0.10
4.036943E-1
1.444444Е-2
1.444444Е-2
3.642919E-17
0.20
3.961146E-1
2.921348Е-2
2.921348Е-2
-7.285838E-17
0.30
3.893332E-1
4.431818Е-2
4.431818Е-2
-3.469446E-17
0.40
3.832567E-1
5.977011Е-2
5.977011Е-2
7.632783E-17
0.50
3.777933E-1
7.558139Е-2
7.558139Е-2
1.249000E-16
0.60
3.728517E-1
9.176470Е-2
9.176470Е-2
1.665334E-16
0.70
3.683402E-1
1.083333Е-1
1.083333Е-1
5.551115E-17
0.80
3.641656E-1
1.253012Е-1
1.253012Е-1
8.326672E-17
Передний отрезок sF1=2,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p2=-9,0
Таблица 101
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.111111Е-2
5.027932Е-2
1.111111E-1
6.049382E-2
1.598002
7.299059E-2
0.20
-2.222222Е-2
1.011235Е-1
1.111111E-1
9.876543E-3
1.592033
1.048353E-1
0.30
-З.ЗЗЗЗЗЗЕ-2
1.525423Е-1
1.111111E-1
4.074074E-2
1.582167
1.372407E-1
0.40
-4.444444Е-2
2.045454Е-1
1.111111E-1
9.135802E-2
1.568524
1.703113E-1
0.50
-5.555555Е-2
2.571428Е-1
1.111111E-1
1.419753E-1
1.551269
2.041627E-1
0.60
-6.666666Е-2
3.103448Е-1
1.111111E-1
1.925925E-1
1.530604
2.389278E-1
0.70
-7.777777Е-2
3.641618Е-1
1.111111E-1
2.432098E-1
1.506764
2.747647E-1
0.80
-8.888888Е-2
4.186046Е-1
1.111111E-1
2.938271E-1
1.480011
3.118650E-1
Таблица 102
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.255525Е+1
7.299059E-2
1.111111E-1
1.598002
0.20
0.20
1.254414Е+1
1.048353E-1
1.111111E-1
1.592033
0.30
0.30
1.253303Е+1
1.372407E-1
1.111111E-1
1.582167
0.40
0.40
1.252192Е+1
1.703113E-1
1.111111E-1
1.568524
0.50
0.50
1.251081Е+1
2.041627Е-1
1.111111E-1
1.551269
0.60
0.60
1.249970Е+1
2.389278E-1
1.111111E-1
1.530604
0.70
0.70
1.248859Е+1
2.747647E-1
1.111111E-1
1.506764
0.80
0.80
1.247748Е+1
3.118650E-1
1.111111E-1
1.480011
Продолжение таблицы 102
bT
tgε2
uB2T
uB2
ΔuB2
0.10
3.781384E-2
5.027932E-2
5.027932E-2
1.3S7778E-17
0.20
6.203546E-3
1.011235Е-1
1.011235Е-1
1.387778Е-17
0.30
2.573713E-2
1.525423Е-1
1.525423Е-1
5.551115Е-17
0.40
5.810081E-2
2.045454Е-1
2.045454Е-1
8.326672Е-17
0.50
9.098761E-2
2.571428Е-1
2.571428Е-1
1.110223Е-16
0.60
1.245112E-1
3.103448Е-1
3.103448Е-1
1.665334Е-16
0.70
1.588053E-1
3.641618Е-1
3.641618Е-1
1.110223Е-16
0.80
1.940304E-1
4.186046Е-1
4.186046Е-1
2.220446Е-16
Передний отрезок sF2=7,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p2=-9,0
Таблица 103
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.111111Е-2
1.430842Е-2
1.111111E-1
9.664902E-2
1.598002
5.046291E-2
0.20
-2.222222Е-2
2.866242Е-2
1.111111E-1
8.218694E-2
1.592033
5.925327E-2
0.30
-3.333333Е-2
4.306220Е-2
1.111111E-1
6.772486E-2
1.582167
6.804164E-2
0.40
-4.444444Е-2
5.750798Е-2
1.111111E-1
5.326278E-2
1.568524
7.689254E-2
0.50
-5.555555Е-2
7.200000Е-2
1.111111E-1
3.880070E-2
1.551269
8.587134E-2
0.60
-6.666666Е-2
8.653846Е-2
1.111111E-1
2.433862E-2
1.530604
9.504459E-2
0.70
-7.777777Е-2
1.011235Е-1
1.111111E-1
9.876543E-3
1.506764
1.044803E-1
0.80
-8.888888Е-2
1.157556Е-1
1.111111E-1
4.585537E-3
1.480011
1.142487E-1
Таблица 104
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.255525Е+1
5.046291E-2
1.111111E-1
1.598002
0-20
0.20
1.254414Е+1
5.925327E-2
1.111111E-1
1.592033
0.30
0.30
1.253303Е+1
6.804164E-2
1.111111E-1
1.582167
0.40
0.40
1.252192Е+1
7.689254E-2
1.111111E-1
1.568524
0.50
0.50
1.251081Е+1
8.587134E-2
1.111111E-1
1.551269
0.60
0.60
1.249970Е+1
9.504459E-2
1.111111E-1
1.530604
0.70
0.70
1.248859Е+1
1.044803E-1
1.111111E-1
1.506764
0.80
0.80
1.247748Е+1
1.142487E-1
1.111111E-1
1.480011
Продолжение таблицы 104
bT
tgε2
uB2T
uB2
ΔuB2
0.10
6.031003E-2
1.430842Е-2
1.430842Е-2
2.255140E-17
0.20
5.151865E-2
2.866242Е-2
2.866242Е-2
3.469446E-17
0.30
4.274629E-2
4.306220Е-2
4.306220Е-2
6.245004E-17
0.40
З.3928С9Е-2
5.750798Е-2
5.750798E-2
3.326672E-17
0.50
2.500122E-2
7.200000Е-2
7.200000Е-2
9.714451E-17
0.60
1.589861E-2
8.653846Е-2
8.653846Е-2
1.110223E-16
0.70
6.554622E-3
1.011235Е-1
1.011235Е-1
1.110223E-16
0.80
3.098293E-3
1.157556Е-1
1.157556Е-1
1.249000E-16
Телескопический ход лучей
Направляющий коэффициент для любого входного луча uK1=0
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p1=-1,3
Таблица 105
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-7.692307Е-2
0.0
7.692307E-1
7.692307E-1
1.598002
2-705535Е-1
0.20
-1.53d461E-l
0.0
7.6У2307Е-1
?.692J07E-1
1.5920J3
2.688929Е-1
0.30
-2.307692E-L
0.0
7.692307E-1
7.692307E-1
1.582167
2.661211Е-1
0.40
-3.076923E-1
0.0
7.692307E-1
7.692307E-1
1.568524
2.622324Е-1
0.50
-3.846153E-1
0.0
7.692307E-1
7.692307E-1
1.551269
2.572180Е-1
0.60
-4.615384E-1
0.0
7.692307E-1
7.692307E-1
1.530604
2.510667Е-1
0.70
-5.384615E-1
0.0
7.692307E-1
7.692307E-1
1.506764
2.437637Е-1
0.80
-6.153846E-1
0.0
7.692307E-1
7.692307E-1
1.480011
2.352911Е-1
Таблица 106
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.248944E+1
2.705535Е-1
7.692307E-1
1.598002
0.20
0.20
1.241252E+1
2.688929Е-1
7.692307E-1
1.592033
0.30
0.30
1.233560E+1
2.661211Е-1
7.692307E-1
1.582167
0.40
0.40
1.225867E+1
2.622324Е-1
7.692307E-1
1.568524
0.50
0.50
1.218175E+1
2.572180Е-1
7.692307E-1
1.551269
0.60
0.60
1.210483E+1
2.510667Е-1
7.692307E-1
1.530604
0.70
0.70
1.202790E+1
2.437637Е-1
7.692307E-1
1.506764
0.80
0.80
1.195098E+1
2.352911Е-1
7.692307E-1
1.480011
Продолжение таблицы 106
bT
tgε2
uB2T
uB2
ΔuB2
0.10
4.127718E-1
0.0
1.395001E-16
1.395001E-16
0.20
4.145848E-1
0.0
0.0
0.0
0.30
4.176193E-1
0.0
0.0
0.0
0.40
4.218948E-1
0.0
0.0
0.0
0.50
4.274394E-1
0.0
0.0
0.0
0.60
4.342903E-1
0.0
0.0
0.0
0.70
4.424945E-1
0.0
1.395001E-16
1.395001E-16
0.80
4.521106E-1
0.0
0.0
0.0
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p2=-9,0
Таблица 107
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.111111E-2
0.0
1.111111E-1
1.111111E-1
1.598002
4.151993E-2
0.20
-2.222222E-2
0.0
1.111111E-1
1.111111E-1
1.592033
4.125977E-2
0.30
-3.333333E-2
0.0
1.111111E-1
1.111111E-1
1.582167
4.082545E-2
0.40
-4.444444E-2
0.0
1.111111E-1
1.111111E-1
1.568524
4.021588E-2
0.50
-5.555555E-2
0.0
1.111111E-1
1.111111E-1
1.551269
3.942954E-2
0.60
-6.666666E-2
0.0
1.111111E-1
1.111111E-1
1.530604
3.846447E-2
0.10
-7.7-77777E-2
0.0
1.111111E-1
1.111111E-1
1.506764
3.731826E-2
0.80
-8.888888E-2
0.0
1.111111E-1
1.111111E-1
1.480011
3.598804E-2
Таблица 108
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.255525Е+1
4.151993E-2
1.111111E-1
1.598002
0.20
0.20
1.254414Е+1
4.125977E-2
1.111111E-1
1.592033
0.30
0.30
1.253303Е+1
4.082545E-2
1.111111E-1
1.582167
0.40
0.40
1.252192Е+1
4.021588E-2
1.111111E-1
1.568524
0.50
0.50
1.251081Е+1
3.942954Е-2
1.111111E-1
1.551269
0.60
0.60
1.249970Е+1
3.846447E-2
1.111111E-1
1.530604
0.70
0.70
1.248859Е+1
3.731826E-2
1.111111E-1
1.506764
0.80
0.80
1.247748Е+1
3.598804E-2
1.111111E-1
1.480011
Продолжение таблицы 108
bT
tgε2
uB2T
uB2
ΔuB2
0.10
6.927160E-2
0.0
1.370854E-17
1.370854E-17
0.20
6.953257E-2
0.0
2.741709E-17
2.741709E-17
0.30
6.996827E-2
0.0
4.112563E-17
4.112563Е-17
0.40
7.057984E-2
0.0
9.595982E-17
9.595982E-17
0.50
7.136889E-2
0.0
1.096683E-16
1.096683E-16
0.60
7.233747E-2
0.0
1.096683E-16
1.096683E-16
0.70
7.348812E-2
0.0
1.233769E-16
1.233769E-16
0.80
7.482387E-2
0.0
1.507940E-16
1.507940E-16
6.2.2.4. Конические поверхности, линза толщиной L/2
Толщина линзы d=L 11=6,283185 мм
Апланатический ход лучей
Передний отрезок sF1=2,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p1=-1,3
Таблица 109
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-7.692307E-2
5.200000E-2
7.692307E-1
6.896449E-1
1.598002
3.011258E-1
0.20
-1.538461E-1
1.083333E-1
7.692307E-1
6.100591E-1
1.592033
3.340935E-1
0.30
-2.307692E-1
1.695652E-1
7.692307E-1
5.304733E-1
1.582167
3.707003E-1
0.40
-3.076923E-1
2.363636E-1
7.692307E-1
4.508875E-1
1.568524
4.116934E-1
0.50
-3.846153E-1
3.095238E-1
7.692307E-1
3.713017E-1
1.551269
4.578750E-1
0.60
-4.615384E-1
3.900000E-1
7.692307E-1
2.917159E-1
1.530604
5.101018E-1
0.70
-5.384615E-1
4.789473E-1
7.692307E-1
2.121301E-1
1.506764
5.692944E-1
0.80
-6.153846E-1
5.777777E-1
7.692307E-1
1.325443E-1
1.480011
6.364613E-1
Таблица 110
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.206262
-3.011258E-1
-7.692307E-1
1.598002
0.20
-0.20
6.129339
-3.340935E-1
-7.692307E-1
1.592033
0.30
-0.30
6.052416
-3.707003E-1
-7.692307E-1
1.582167
0.40
-0.40
5.975492
-4.116934E-1
-7.692307E-1
1.568524
0.50
-0.50
5.898569
-4.578750E-1
-7.692307E-1
1.551269
0.60
-0.60
5.921646
-5.101018E-1
-7.692307E-1
1.530604
0.70
-0.70
5.744723
-5.692944E-1
-7.692307E-1
1.506764
0.80
-0.80
5.667800
-6.364613E-1
-7.692307E-1
1.480011
Продолжение таблицы 110
bT
tgε2
uB2T
uB2
ΔuB2
0.10
3.800678Е-1
-5.200000E-2
-5.200000E-2
-5.551115E-17
0.20
3.461725Е-1
-1.083333E-1
-1.083333Е-1
1.110223E-16
0.30
3.101032Е-1
-1.695652E-1
-1.695652E-1
-5.551115E-17
0.40
2.715430Е-1
-2.363636E-1
-2.363636E-1
-5.551115E-17
0.50
2.302566Е-1
-3.095238E-1
-3.095238E-1
-5.551115E-17
0.60
1.861042Е-1
-3.900000E-1
-3.900000E-1
5.551115E-17
0.70
1.390455Е-1
-4.789473E-1
-4.789473E-1
5.551115E-17
0.80
8.913180Е-2
-5.777777E-1
-5.777777E-1
0.0
Передний отрезок sF2=7,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p1=-1,3
Таблица 111
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-7.692307E-2
1.444444E-2
7.692307E-1
7.464919E-1
1.598002
2.789216E-1
0.20
-1.538461E-1
2.921348E-2
7.692307E-1
7.237531E-1
1.592033
2.859776E-1
0.30
-2.307692E-1
4.431818E-2
7.692307E-1
7.010143E-1
1.582167
2.923441E-1
0.40
-3.076923E-1
5.977011E-2
7.692307E-1
6.782755E-1
1.568524
2.980924E-1
0.50
-3.846153E-1
7.558139E-2
7.692307E-1
6.555367E-1
1.551269
3.032963E-1
0.60
-4.615384E-1
9.176470E-2
7.692307E-1
6.327979E-1
1.530604
3.080324E-1
0.70
-5.384615E-1
1.083333E-1
7.692307E-1
6.100591E-1
1.506764
3.123809E-1
0.80
-6.153846E-1
1.253012E-1
7.692307E-1
5.873203E-1
1.480011
3.164255Е-1
Таблица 112
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.206262
-2.789216E-1
-7.692307E-1
1.598002
0.20
-0.20
6.129339
-2.859776E-1
-7.692307E-1
1.592033
0.30
-0.30
6.052416
-2.923441E-1
-7.692307E-1
1.582167
0.40
-0.40
5.975492
-2.980924Е-1
-7.692307E-1
1.568524
0.50
-0.50
5.898569
-3.032963E-1
-7.692307E-1
1.551269
0.60
-0.60
5.821646
-3.080324E-1
-7.692307E-L
1.530604
0.70
-0.70
5.744723
-3.123809E-1
-7.692307E-1
1.506764
0.80
-0.80
5.667800
-3.164255Е-1
-7.692307E-1
1.480011
Продолжение таблицы 112
bT
tgε2
uB2T
uB2
ΔuB2
0.10
4.036943E-1
-1.444444E-2
-1.444444E-2
-3.642919Е-17
0.20
3.961146E-1
-2.921348E-2
-2.921348E-2
1.457167Е-16
0.30
3.893332E-1
-4.431818E-2
-4.4318L8E-2
3.469446Е-17
0.40
3.832567E-1
-5.977011E-2
-5.977011E-2
7.632783Е-17
0.50
3.777933E-1
-7.558139E-2
-7.558139E-2
-1.249000Е-16
0.60
3.728517E-1
-9.176470E-2
-9.176470E-2
-8.326672Е-17
0.70
3.683402E-1
-1.083333E-1
-1.083333E-1
9.714451Е-17
0.80
3.641656E-1
-1.253012E-1
-1.253012E-1
-8.326672Е-17
Передний отрезок sF1=2,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p2=-9,0
Таблица 113
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.111111Е-2
5.027932Е-2
1.111111E-1
6.049382E-2
1.598002
7.299059E-2
0.20
-2.222222Е-2
1.011235Е-1
1.111111E-1
9.876543E-3
1.592033
1.048353E-1
0.30
-3.333333Е-2
1.525423Е-1
1.111111E-1
4.074074E-2
1.582167
1.372407E-1
0.40
-4.444444Е-2
2.045454Е-1
1.111111E-1
9.135802E-2
1.568524
1.703113E-1
0.50
-5.555555Е-2
2.571428Е-1
1.111111E-1
1.419753E-1
1.551269
2.041627E-1
0.60
-6.666666Е-2
3.103448Е-1
1.111111E-1
1.925925E-1
1.530604
2.389278E-1
0.70
-7.777777Е-2
3.641618Е-1
1.111111E-1
2.432098E-1
1.506764
2.747647E-1
0.80
-8.888888Е-2
4.186046Е-1
1.111111E-1
2.938271E-1
1.480011
3.118650E-1
Таблица 114
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.272074
-7.299059E-2
-1.111111E-1
1.598002
0.20
-0.20
6.260963
-1.048353E-1
-1.111111E-1
1.592033
0.30
-0.30
6.249851
-1.372407E-1
-1.111111E-1
1.582167
0.40
-0.40
6.238740
-1.703113E-1
-1.111111E-1
1.568524
0.50
-0.50
6.227629
-2.041627E-1
-1.111111E-1
1.551269
0.60
-0.60
6.216518
-2.389278E-1
-1.111111E-1
1.530604
0.70
-0.70
6.205407
-2.747647E-1
-1.111111E-1
1.506764
0.80
-0.80
6.194296
-3.118650E-1
-1.111111E-1
1.480011
Продолжение таблицы 114
bT
tgε2
uB2T
uB2
ΔuB2
0.10
3.781384E-2
-5.027932Е-2
-5.027932Е-2
-1.387778Е-17
0.20
6.203546E-3
-1.011235Е-1
-1.011235Е-1
1.387778Е-17
0.30
2.573713E-2
-1.525423Е-1
-1.525423Е-1
0.0
0.40
5.810081E-2
-2.045454Е-1
-2.045454Е-1
-2.775557R-17
0.50
9.098761E-2
-2.571428Е-1
-2.571428Е-1
-5.551115Е-17
0.60
1.245112E-1
-3.103448Е-1
-3.103448Е-1
-5.551115Е-17
0.70
1.588053E-1
-3.641618Е-1
-3.641618Е-1
-5.551115Е-17
0.80
1.940304E-1
-4.186046Е-1
-Й.186046Е-1
-5.551115Е-17
Передний отрезок sF2=7,0 мм
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p2=-9,0
Таблица 115
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.111111E-2
1.430842E-2
1.111111E-1
9.664902E-2
1.598002
5.046291Е-2
0.20
-2.222222E-2
2.866242E-2
1.111111E-1
8.218694E-2
1.592033
5.925327Е-2
0.30
-3.333333E-2
4.306220E-2
1.111111E-1
6.772486E-2
1.582167
6.804164Е-2
0.40
-4.444444E-2
5.750798E-2
1.111111E-1
5.326278E-2
1.568524
7.689254Е-2
0.50
-5.555555E-2
7.200000E-2
1.111111E-1
3.880070E-2
1.551269
8.587134Е-2
0.60
-6.666666E-2
8.653846E-2
1.111111E-1
2.433862E-2
1.530604
9.504459Е-2
0.70
-7.777777E-2
1.011235E-1
1.111111E-1
9.876543E-3
1.506764
1.044803Е-1
0.80
-8.888888E-2
1.157556E-1
1.111111E-1
4.585537E-3
1.480011
1.142487Е-1
Таблица 116
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.272074
-5.046291Е-2
-1.111111E-1
1.598002
0.20
-0.20
6.260963
-5.925327Е-2
-1.111111E-1
1.592033
0.30
-0.30
6.249851
-6.804164Е-2
-1.111111E-1
1.582167
0.40
-0.40
6.238740
-7.689254Е-2
-1.111111E-1
1.568524
0.50
-0.50
6.227629
-8.587134Е-2
-1.111111E-1
1.551269
0.60
-0.60
6.216518
-9.504459Е-2
-1.111111E-1
1.530604
0.70
-0.70
6.205407
-1.044803Е-1
-1.111111E-1
1.506764
0.80
-0.80
6.194296
-1.142487Е-1
-1.111111E-1
1.480011
Продолжение таблицы 116
bT
tgε2
uB2T
uB2
ΔuB2
0.10
6.031003E-2
-1.430842E-2
-1.430842E-2
-8.673617Е-18
0.20
5.151865E-2
-2.866242E-2
-2.866242E-2
-2.081668Е-17
0.30
4.274629E-2
-4.306220E-2
-4.306220E-2
-2.081668Е-17
0.40
3.392869E-2
-5.750798E-2
-5.750798E-2
-4.163336Е-17
0.50
2.500122E-2
-7.200000E-2
-7.200000E-2
-4.163336Е-17
0.60
1.589861E-2
-8.653846E-2
-8.653846E-2
-6.938893Е-17
0.70
6.554622E-3
-1.011235E-1
-1.011235E-1
-4.163336Е-17
0.80
3.098293E-3
-1.157556E-1
-1.157556E-1
-5.551115Е-17
Телескопический ход лучей
Направляющий коэффициент для любого входного луча uK1=0
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p1=-1,3
Таблица 117
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-7.692307E-2
0.0
7.692307E-1
7.692307E-1
1.598002
2.705535E-1
0.20
-1.538461E-1
0.0
7.692307E-1
7.692307E-1
1.592033
2.688929E-1
0.30
-2.307692E-1
0.0
7.692307E-1
7.692307E-1
1.592167
2.661211E-1
0.40
-3.076923E-1
0.0
7.692307E-1
7.692307E-1
1.568524
2.622324E-1
0.50
-3.846153E-1
0.0
7.692307E-1
7.692307E-1
1.551269
2.572180E-1
0.60
-4.615384E-1
0.0
7.692307E-1
7.692307E-1
1.530604
2.510667E-1
0.70
-5.384615E-1
0.0
7.692307E-1
7.692307E-1
1.506764
2.437637E-1
0.80
-6.153846E-1
0.0
7.692307E-1
7.692307E-1
1.480011
2.352911E-1
Таблица 118
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.206262
-2.705535E-1
-7.692307E-1
1.598002
0.20
-0.20
6.129339
-2.688929E-1
-7.692307E-1
1.592033
0.30
-0.30
6.052416
-2.661211E-1
-7.692307E-1
1.582167
0.40
-0.40
5.975492
-2.622324E-1
-7.692307E-1
1.568524
0.50
-0.50
5.898569
-2.572180E-1
-7.692307E-1
1.551269
0.60
-0.60
5.821646
-2.510667E-1
-7.692307E-1
1.530604
0.70
-0.70
5.744723
-2.437637E-1
-7.692307E-1
1.506764
0.80
-0.80
5.667800
-2.352911E-1
-7.692307E-1
1.480011
Продолжение таблицы 118
bT
tgε2
uB2T
uB2
ΔuB2
0.10
4.127718E-1
0.0
0.0
0.0
0.20
4.145848E-1
0.0
0.0
0.0
0.30
4.176193E-1
0.0
0.0
0.0
0.40
4.218948E-1
0.0
0.0
U.D
0.50
4.274394E-1
0.0
0.0
0.0
0.60
4.342903E-1
0.0
0.0
0.0
0.70
4.424945E-1
0.0
-1.395001E-16
-1.395001E-16
0.80
4.521106E-1
0.0
0.0
0.0
Коэффициенты наклона прямой (для образующих 1-й и 2-й поверхностей) выбираются равными p2=-9,0
Таблица 119
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
-1.111111Е-2
0.0
1.111111E-1
1.111111E-1
1.598002
4.151993E-2
0.20
-2.222222Е-2
0.0
1.111111E-1
1.111111E-1
1.592033
4.125977E-2
0.30
-3.333333Е-2
0.0
1.111111E-1
1.111111E-1
1.582167
4.082545E-2
0.40
-4.444444Е-2
0.0
1.111111E-1
1.111111E-1
1.568524
4.021588E-2
0.50
-5.555555Е-2
0.0
1.111111E-1
1.111111Е-1
1. SS1269
3.942954E-2
0.60
-6.666666Е-2
0.0
1.111111E-1
1.111111E-1
1.530604
3.846447E-2
0.70
-7.777777Е-2
0.0
1.111111E-1
1.111111E-1
1.506764
3.731826E-2
0.80
-8.888888Е-2
0.0
1.111111E-1
1.111111E-1
1.480011
3.598804E-2
Таблица 120
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.272074
-4.151993E-2
-1.111111E-1
1.598002
0.20
-0.20
6.260963
-4.125977E-2
-1.111111E-1
1.592033
0.30
-0.30
6.249851
-4.082545E-2
-1.111111Е-1
1.582167
0.40
-0.40
6.238740
-4.021588E-2
-1.111111E-1
1.568524
0.50
-0.50
6.227629
-3.942954E-2
-1.111111E-1
1.551269
0.60
-0.60
6.216518
-3.846447E-2
-1.111111E-1
1.530604
0.70
-0.70
6.205407
-3.731826E-2
-1.111111E-1
1.506764
0.80
-0.80
6.194296
-3.5У8804Е-2
-1.111111E-l
1.480011
Продолжение таблицы 120
bT
tgε2
uB2T
uB2
ΔuB2
0.10
6.927160E-2
0.0
1.370854Е-17
1.370854Е-17
0.20
6.953257E-2
0.0
0.0.
0.0
0.30
6.996827E-2
0.0
-1.370854Е-17
-1.370854Е-17
0.40
7.057984E-2
0.0
-5.483418Е-17
-5.483418Е-17
0.50
7.136889E-2
0.0
-4.112563Е-17
-4.112563Е-17
0.60
7.233747E-2
0.0
-6.854273Е-17
-6.854273Е-17
0.70
7.348812E-2
0.0
-6.854273Е-17
-6.854273Е-17
0.80
7.482387E-2
0.0
-6.854273Е-17
-6.854273Е-17
6.2.3. Линза с 1-й и 2-й плоскими поверхностями
6.2.3.1. Плоские поверхности, линза толщиной L
Толщина линзы d=L=12,566370 мм
Апланатический ход лучей
Передний отрезок sF1=2,0 мм
Таблица 121
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
0.0
5.0E-2
0.0
5.0E-2
1.598002
3.126530E-2
0.20
0.0
1.0E-1
0.0
1.0E-1
1.592033
6.262346E-2
0.30
0.0
1.5E-1
0.0
1.5E-1
1.582167
9.417258E-2
0.40
0.0
2.0E-1
0.0
2.0E-1
1.568524
1.260211E-1
0.50
0.0
2.5E-1
0.0
2.5E-1
1.551269
1.582931E-1
0.60
0.0
3.0E-1
0.0
3.0E-1
1.530604
1.911332E-1
0.70
0.0
3.5E-1
0.0
3.5E-1
1.506764
2.247121E-1
0.80
0.0
4.0E-1
0.0
4.0E-1
1.480011
2.592322E-1
Таблица 122
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.256637Е+1
3.126530E-2
0.0
1.598002
0.20
0.20
1.256637Е+1
6.262346E-2
0.0
1.592033
0.30
0.30
1.256637Е+1
9.417258E-2
0.0
1.582167
0.40
0.40
1.256637Е+1
1.260211E-1
0.0
1.568524
0.50
0.50
1.256637Е+1
1.582931E-1
0.0
1.551269
0.60
0.60
1.256637Е+1
1.911332E-1
0.0
1.530604
0.70
0.70
1.256637Е+1
2.247121E-1
0.0
1.506764
0.80
0.80
1.256637Е+1
2.592322E-1
0.0
1.480011
Продолжение таблицы 122
bT
tgε2
uB2T
uB2
ΔuB2
0.10
3.126530E-2
5.0E-2
5.0E-2
2.775557Е-17
0.20
6.262346E-2
1.0E-1
1.0E-1
2.775557Е-17
0.30
9.417258E-2
1.5E-1
1.5E-1
2.775557Е-17
0.40
1.260211E-1
2.0E-1
2.0E-1
1.110223Е-16
0.50
1.582931E-1
2.5E-1
2.5E-1
1.110223Е-16
0.60
1.911332E-1
3.0E-1
3.0E-1
1.110223Е-16
0.70
2.247121E-1
3.5E-1
3.5E-1
1.665334Е-16
0.80
2.592322E-1
4.0E-1
4.0E-1
1.665334Е-16
Передний отрезок sF2=7,0 мм
Таблица 123
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
0.0
1.428571E-2
0.0
1.4285714E-2
1.598002
8.939179E-3
0.20
0.0
2.857142E-2
0.0
2.8571428E-2
1.592033
1.794206E-2
0.30
0.0
4.285714E-2
0.0
4.2857142E-2
1.582167
2.707269E-2
0.40
0.0
5.714285E-2
0.0
5.7142857E-2
1.568524
3.639570E-2
0.50
0.0
7.142857E-2
0.0
7.1428571E-2
1.551269
4.597673E-2
0.60
0.0
8.571428E-2
0.0
8.5714285E-2
1.530604
5.588274E-2
0.70
0.0
1.000000E-1
0.0
1.0000000E-1
1.506764
6.618246E-2
0.80
0.0
1.142857E-1
0.0
1.1428571E-1
1.480011
7.694683E-2
Таблица 124
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
0.10
1.256637Е+1
8.939179E-3
0.0
1.598002
0.20
0.20
1.256637Е+1
1.794206E-2
0.0
1.592033
0.30
0.30
1.256637Е+1
2.707269E-2
0.0
1.582167
0.40
0.40
1.256637Е+1
3.639570E-2
0.0
1.568524
0.50
0.50
1.256637Е+1
4.597673Е-.2
0.0
1.551269
0.60
0.60
1.256637Е+1
5.588274E-2
0.0
1.530604
0.70
0.70
1.256637Е+1
6.618246E-2
0.0
1.506764
0.80
0.80
1.256637Е+1
7.694683E-2
0.0
1.480011
Продолжение таблицы 124
bT
tgε2
uB2T
uB2
ΔuB2
0.10
8.939179E-3
1.428571E-2
1.428571E-2
1.908195Е-17
0.20
1.794206E-2
2.857142E-2
2.857142E-2
4.163336Е-17
0.30
2.707269E-2
1.285714E-2
4.285714E-2
6.245004E-17
0.40
3.639570E-2
5.714285E-2
5.714285E-2
6.938893Е-17
0.50
4.597673E-2
7.142857E-2
7.142857E-2
8.326672Е-17
0.60
5.588274E-2
8.571428E-2
8.571428E-2
1.110223Е-16
0.70
6.618246E-2
1.000000E-1
1.000000E-1
9.714451Е-17
0.80
7.694683E-2
1.142857E-1
1.142857E-1
1.249000Е-16
6.2.3.2. Плоские поверхности, линза толщиной L/2
Толщина линзы d=L 11=6,283185 мм
Апланатический ход лучей
Передний отрезок sF1=2,0 мм
Таблица 125
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
0.0
5.0E-2
0.0
5.0E-2
1.598002
3.126530Е-2
0.20
0.0
1.0E-1
0.0
1.0E-1
1.592033
6.262346Е-2
0.30
0.0
1.5E-1
0.0
1.5E-1
1.582167
9.417258Е-2
0.40
0.0
2.0E-1
0.0
2.0E-1
1.568524
1.260211Е-1
0.50
0.0
2.5E-1
0.0
2.5E-1
1.551269
1.582931Е-1
0.60
0.0
3.0Е-1
0.0
З.ОЕ-1
1.530604
1.911332Е-1
0.70
0.0
3.5Е-1
0.0
3.5Е-1
1.506764
2.247121Е-1
0.80
0.0
4.0Е-1
0.0
4.0Е-1
1.480011
2.592322Е-1
Таблица 126
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.283185
-3.126530Е-2
0.0
1.598002
0.20
-0.20
6.283185
-6.262346Е-2
0.0
1.592033
0.30
-0.30
6.283185
-9.417258Е-2
0.0
1.582167
0.40
-0.40
6.283185
-1.260211Е-1
0.0
1.568524
0.50
-0.50
6.283185
-1.582931Е-1
0.0
1.551269
0.60
-0.60
6.283185
-1.911332Е-1
0.0
1.530604
0.70
-0.70
6.283185
-2.247121Е-1
0.0
1.506764
0.80
-0.80
6.283185
-2.592322Е-1
0.0
1.480011
Продолжение таблицы 126
bT
tgε2
uB2T
uB2
ΔuB2
0.10
3.126530Е-2
-5.0E-2
-5.0E-2
6.938893Е-18
0.20
6.262346Е-2
-1.0E-1
-1.0E-1
1.387778Е-17
0.30
9.417258Е-2
-1.5E-1
-1.5E-1
5.551115Е-17
0.40
1.260211Е-1
-2.0E-1
-2.0E-1
-2.775557F-17
0.50
1.582931Е-1
-2.5E-1
-2.5E-1
5.551115Е-17
0.60
1.911332Е-1
-З.ОЕ-1
-З.ОЕ-1
1.110223Е-16
0.70
2.247121Е-1
-3.5Е-1
-3.5Е-1
1.110223Е-16
0.80
2.592322E-1
-4.0Е-1
-4.0Е-1
1.110223Е-16
Передний отрезок sА2=7,0 мм
Таблица 127
Преломление лучей на 1-й поверхности
bT
zП1
uK1
uH1
tgε1
n(bT)
uB1
0.10
0.0
1.428571E-2
0.0
1.428571E-2
1.598002
8.939179E-3
0.20
0.0
2.857142E-2
0.0
2.857L42E-2
1.592033
1.794206E-2
0.30
0.0
4.285714E-2
0.0
4.285714E-2
1.582167
2.707269E-2
0.40
0.0
5.714285E-2
0.0
5.714285E-2
1.568524
3.639570E-2
0.50
0.0
7.142857E-2
0.0
7.142857E-2
1.551269
4.597673E-2
0.60
0.0
8.57L428E-2
0.0
8.571428E-2
1.530604
5.588274E-2
0.70
0.0
1.000000E-1
0.0
1.000000E-1
1.506764
6.618246E-2
0.80
0.0
1.142857E-1
0.0
1.142857E-1
1.480011
7.694683E-2
Таблица 128
Преломление лучей на 2-й поверхности
bT
yП2
zП2
uK2
uН2
n(yП2)
0.10
-0.10
6.283185
-8.939179E-3
0.0
1.598002
0.20
-0.20
6.283185
-1.794206E-2
0.0
1.592033
0.30
-0.30
6.283185
-2.707269E-2
0.0
1.582167
0.40
-0.40
6.2G31SS
-3.633570Е-2
-3,639570E-2
1.563524
0.50
-0.50
6.283185
-4.597673E-2
0.0
1.551269
0.60
-0.60
6.283185
-5.588274E-2
0.0
1.530604
0.70
-0.70
6.283185
-6.618246E-2
0.0
1.506764
0.80
-0.80
6.283185
-7.694683E-2
0.0
1.480011
Продолжение таблицы 128
bT
tgε2
uB2T
uB2
ΔuB2
0.10
8.939179E-3
-1.428571E-2
-1.428571E-2
8.673617E-18
0.20
1.794206E-2
-2.857142E-2
-2.857142E-2
2.081668E-17
0.30
2.707269E-2
-4.285714E-2
-4.285714E-2
2.775557E-17
0.40
3.639570E-2
-5.714285E-2
-5.714285E-2
4.163336E-17
0.50
4.597673E-2
-7.142857E-2
-7.142857E-2
4.163336E-17
0.60
5.588274E-2
-8.571428E-2
-8.571428E-2
5.551115E-17
0.70
6.618246E-2
-1.000000E-1
-9.999999E-2
6.938893E-17
0.80
7.694683E-2
-1.142857E-1
-1.142857E-1
5.551115E-17
7. Краткие выводы по результатам численных расчетов
Приведенные результаты численных расчетов хода лучей для различных вариантов заявляемой линзы показывают следующее.
1. Все рассмотренные варианты выполнения линз обладают одновременно апланатическими и телескопическими свойствами (отклонение величины ΔuB2 от нуля в таблицах определяется только погрешностью машинного расчета).
2. Апланатические свойства линз не зависят от положения предметной точки на оптической оси.
3. Апланатические и телескопические свойства линз не зависят от формы преломляющих поверхностей.
4. Известная апланатическая линза, принятая за прототип, также одновременно является и телескопической линзой, причем апланатические свойства известной линзы не зависят от положения предметной точки на оптической оси и параметров ее преломляющих поверхностей.
8. Источники информации
1. Патент РФ №2288490 "Апланатическая градиентная линза", приоритет от 05.04.2005 г., опубл. 27.11.2006 г., бюл. №33.
2. Вычислительная оптика. Справочник / Под ред. М.М. Русинова - М., Машиностроение, 1984, 423 с.
3. Ильин В.Г. и др. Физические основы градиентной оптики / Учебное пособие - Л., Ленингр. политехн. институт, 1990, 55 с.
4. Заказнов Н.П. и др. Теория оптических систем. Учебник для вузов. 3-е изд. М., Машиностроение, 1992.
5. Хацевич Т.Н., Михайлов И.О. Эндоскопы: Учеб. пособие. - Новосибирск: СГГА, 2002.
6. Турчак Л.И. Плотников П.В. Основы численных методов: Учебное пособие. 2-е изд. М.: Физматлит, 2003.
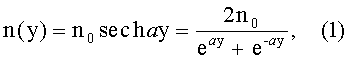
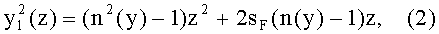
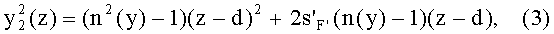
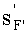
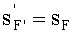
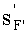
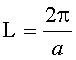
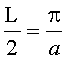
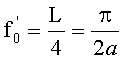
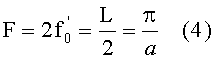
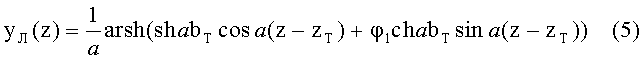
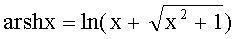
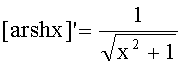
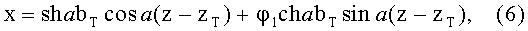
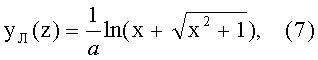
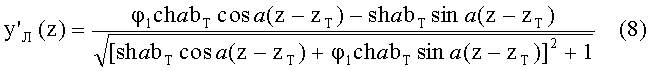
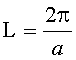
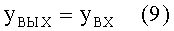
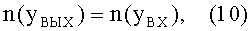
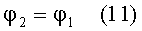
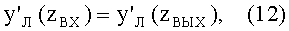
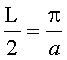
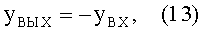
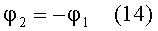
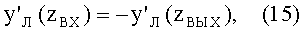
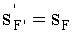
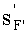
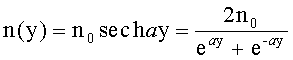
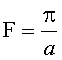
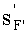
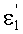
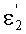
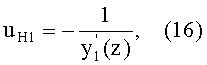
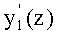
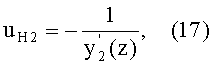

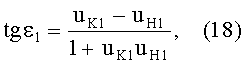
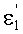
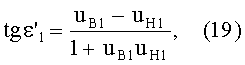
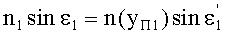
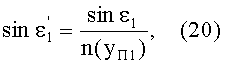
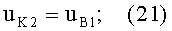
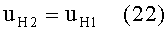
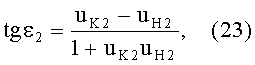
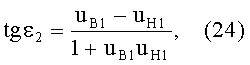
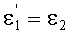
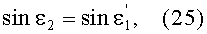
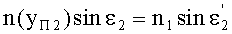
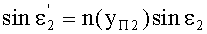
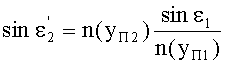
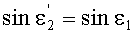
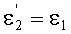
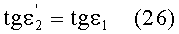
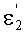
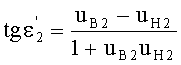
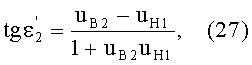
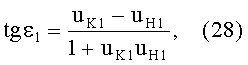
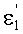
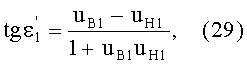
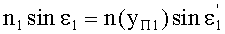
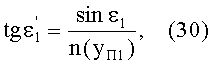
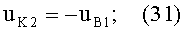
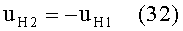
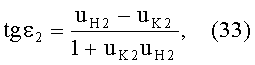
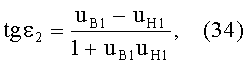
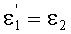

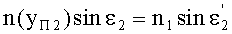
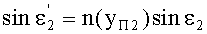
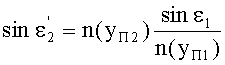
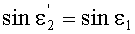
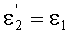
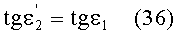
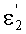
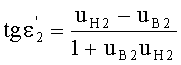
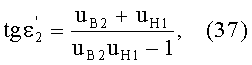
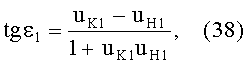
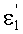
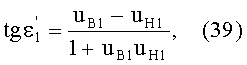
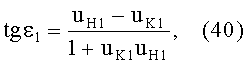
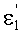
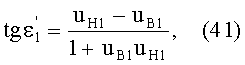
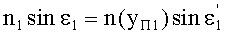
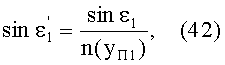
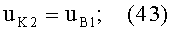
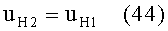
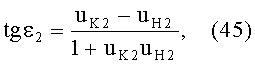
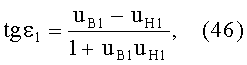
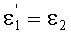
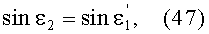
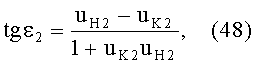
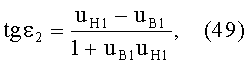
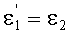
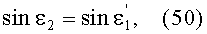
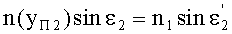
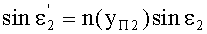
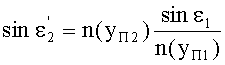
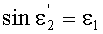
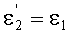
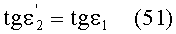
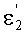
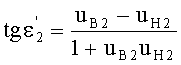
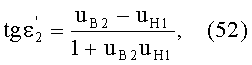
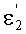
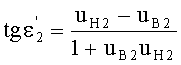
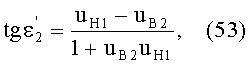
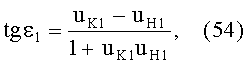
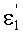
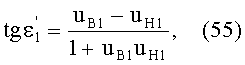
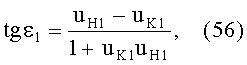
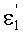
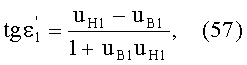
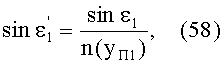
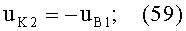
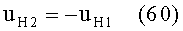
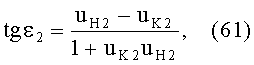
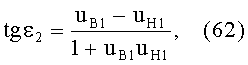
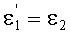
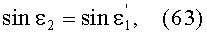
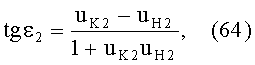
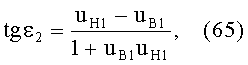
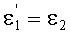
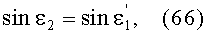
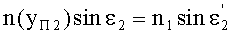
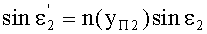
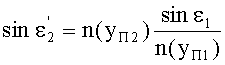
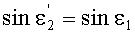
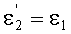
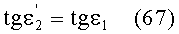
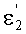
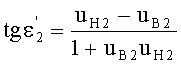
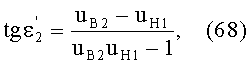
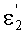
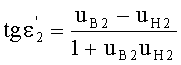
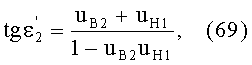
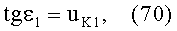
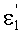
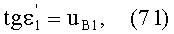
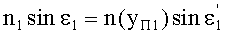
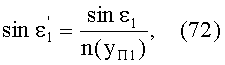
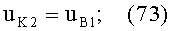
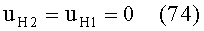
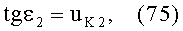
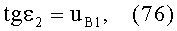
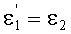
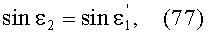
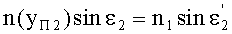
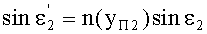
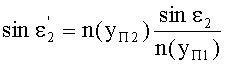
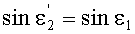
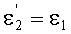
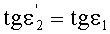
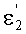
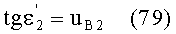
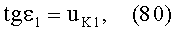
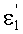
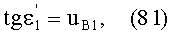
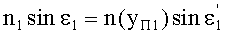
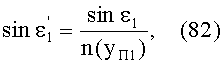
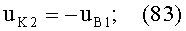
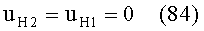
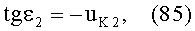
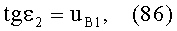
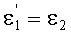
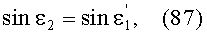
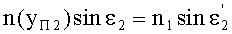
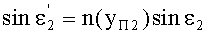
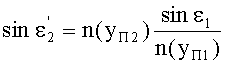
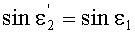
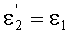
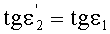
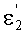
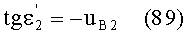
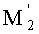
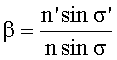
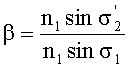
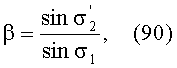
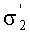
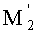
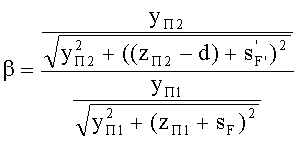
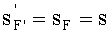
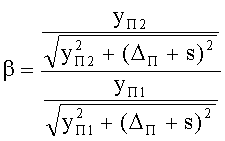
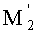
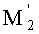
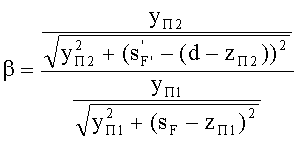
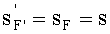
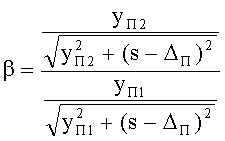
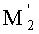
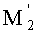
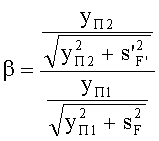
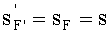
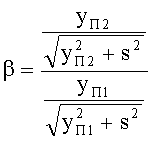
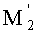
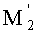
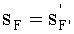
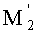
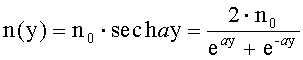
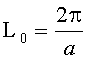
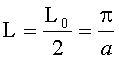
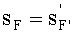
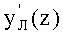
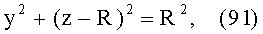
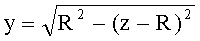
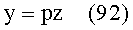
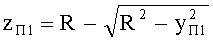
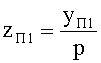
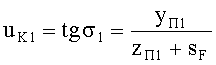
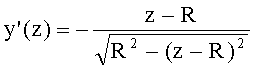
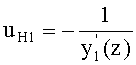
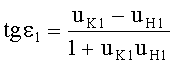
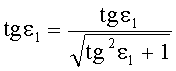
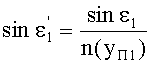
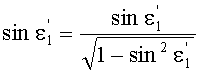
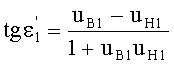
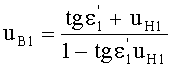
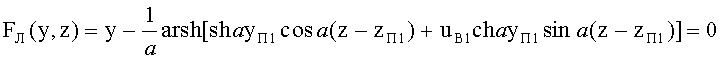
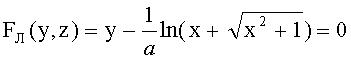
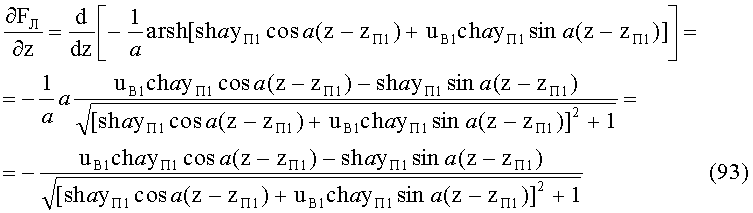
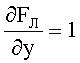
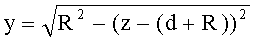
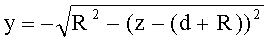
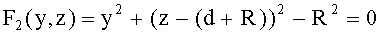
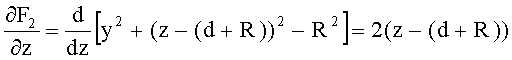
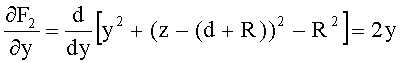
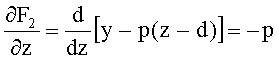
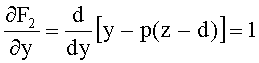
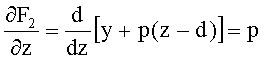
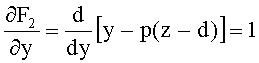
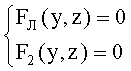
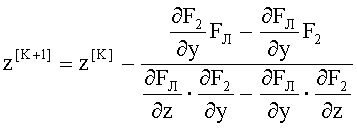
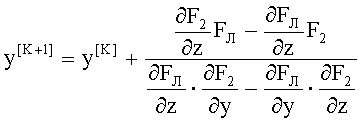
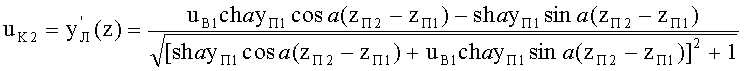
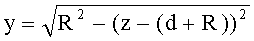
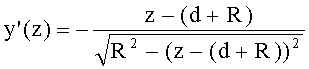
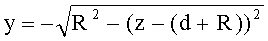
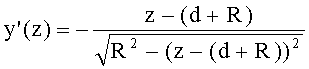
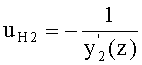
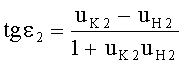
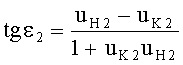
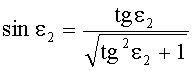
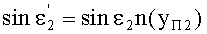
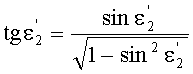
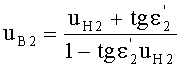
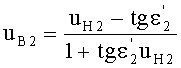
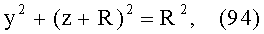
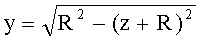
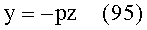
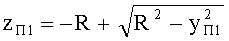
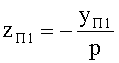
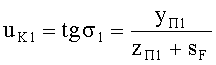
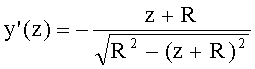
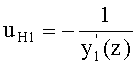
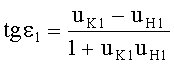
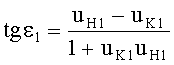
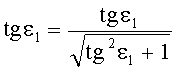
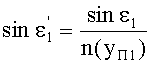
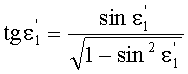
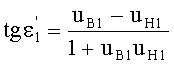
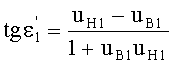
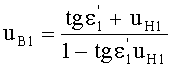
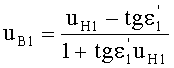
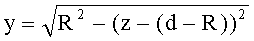
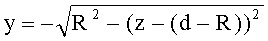
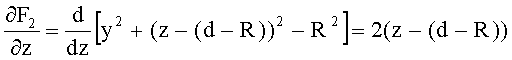
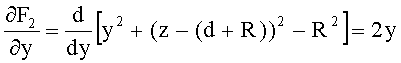
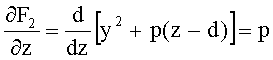
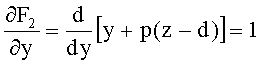
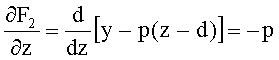
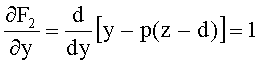
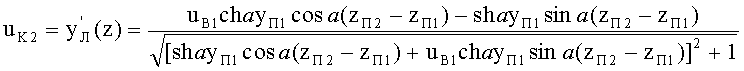
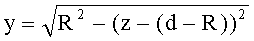
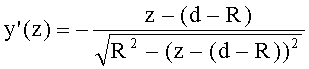
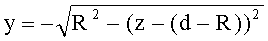
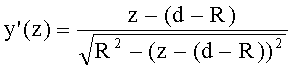
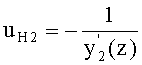
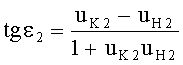
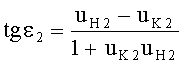
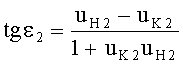
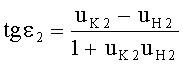
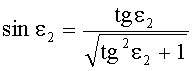
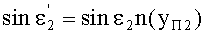
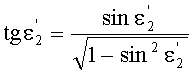
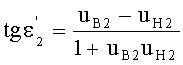

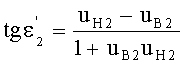
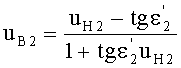
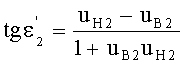
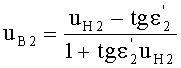
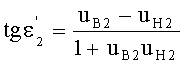
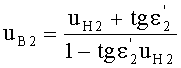
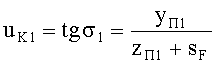
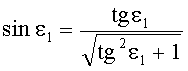
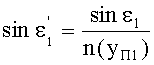
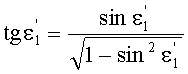
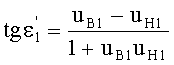
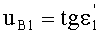
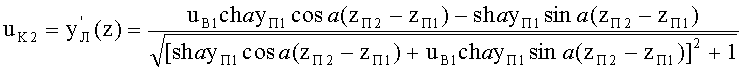
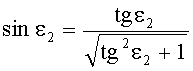
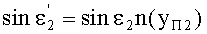
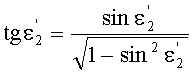
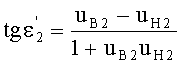
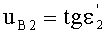
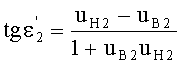
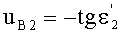
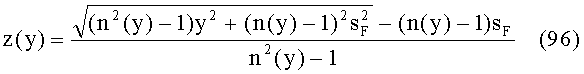
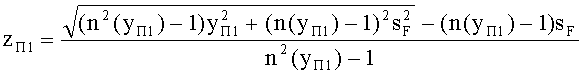
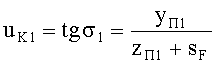
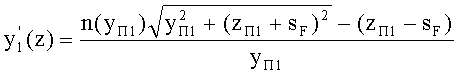
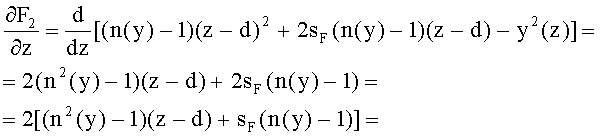
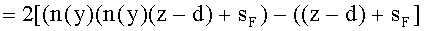
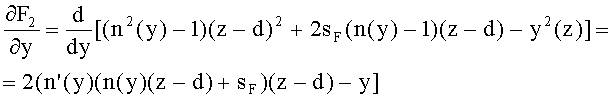
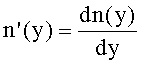
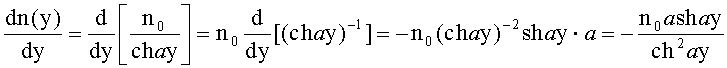
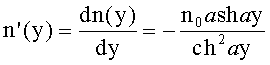
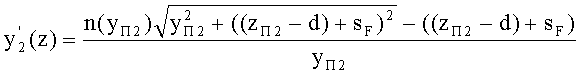
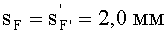
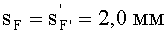
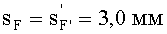
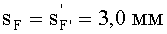
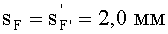
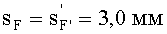
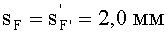
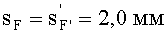
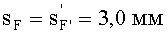
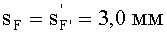
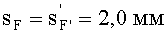
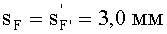

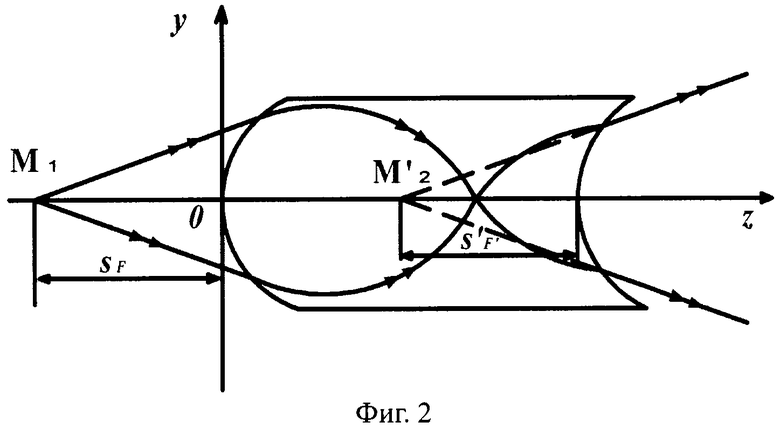
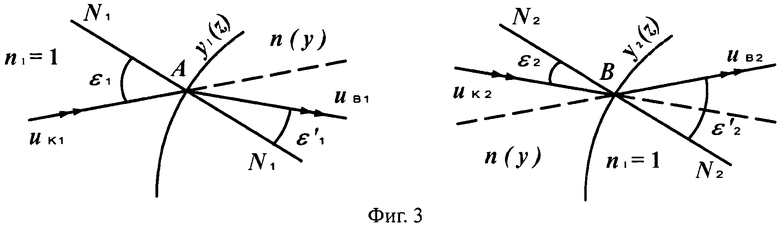
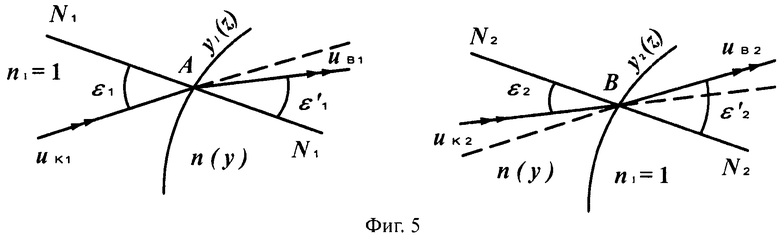
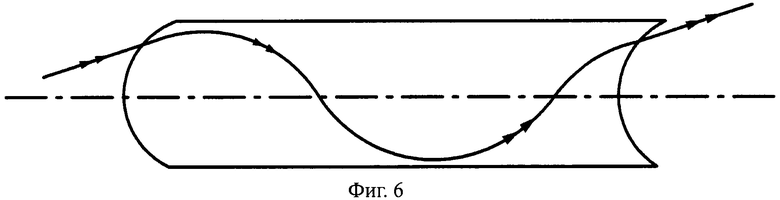
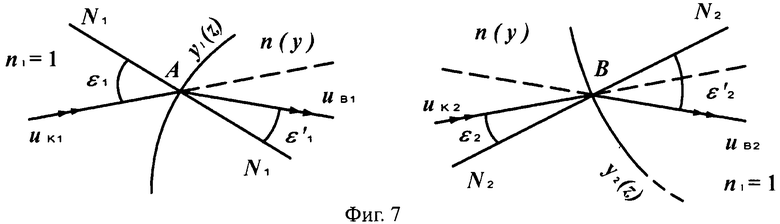
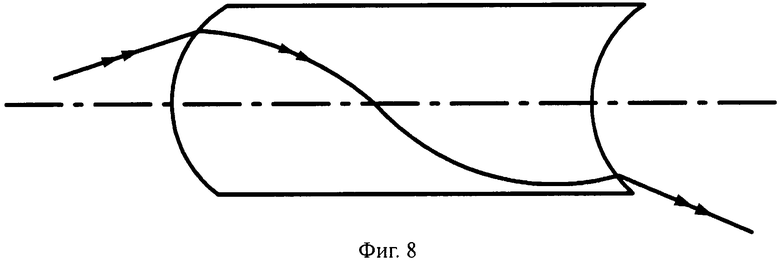
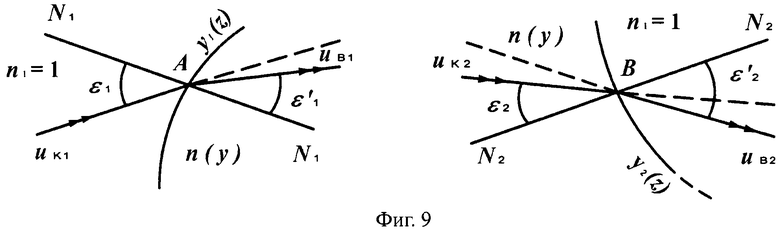
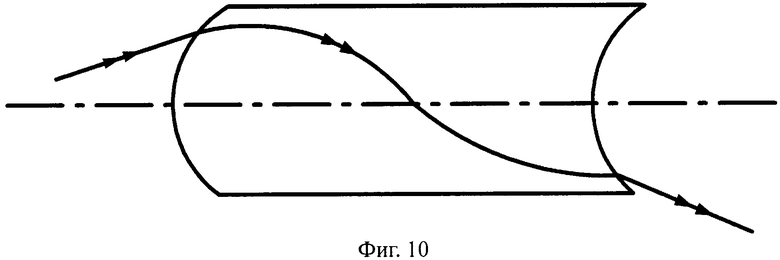
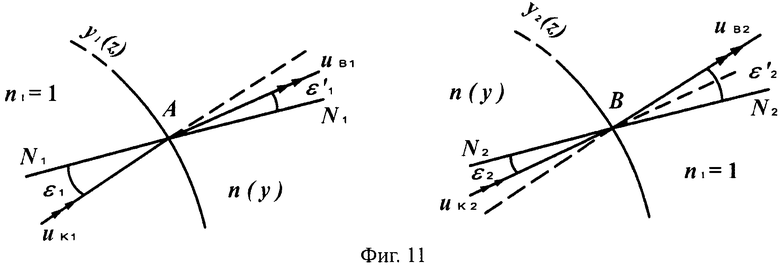
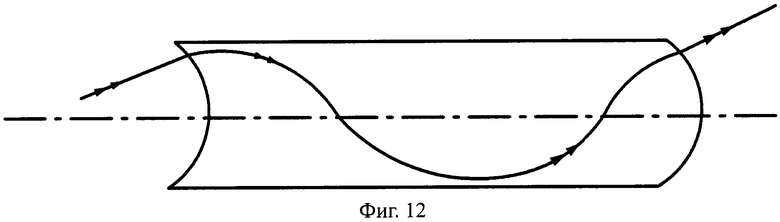
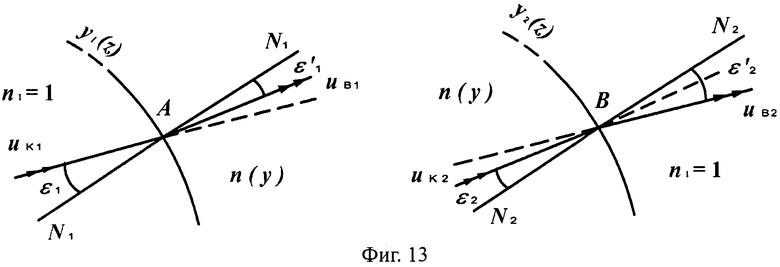
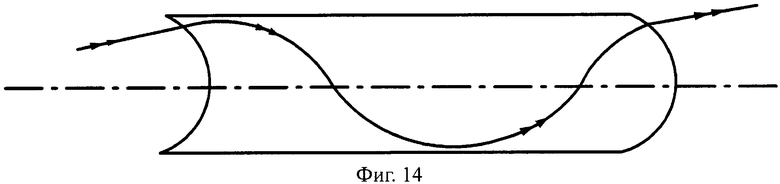
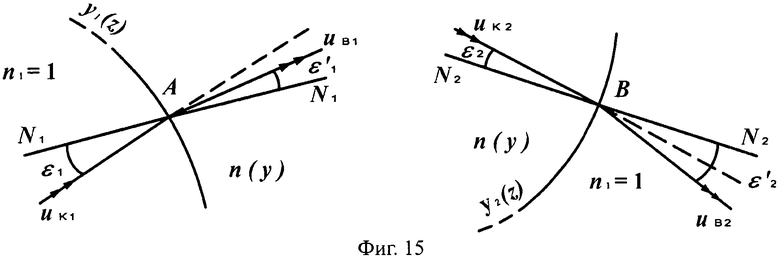
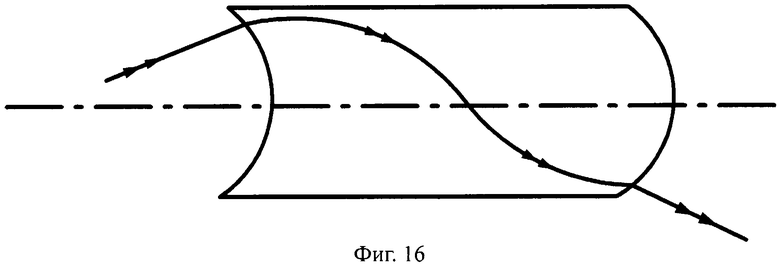
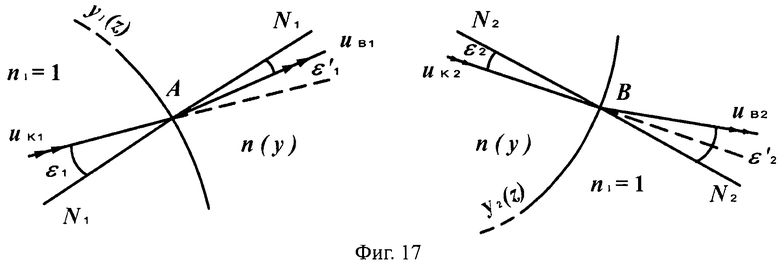
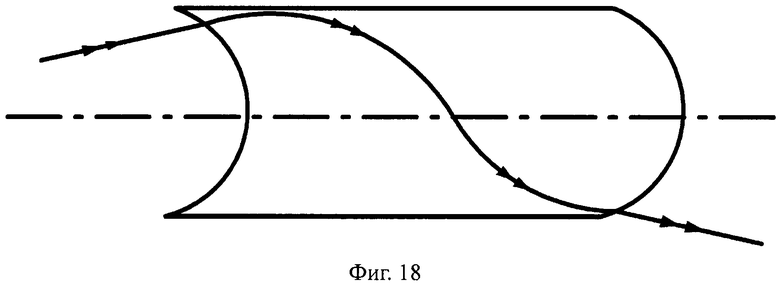
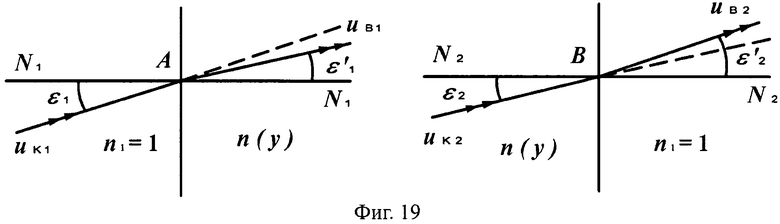
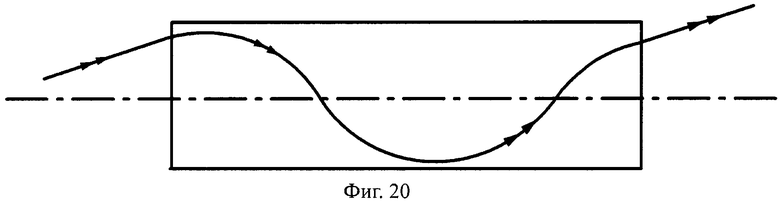
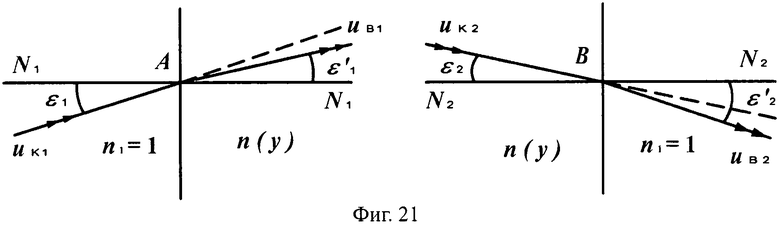
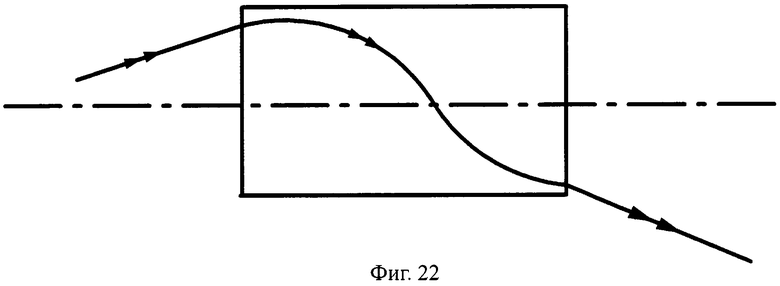
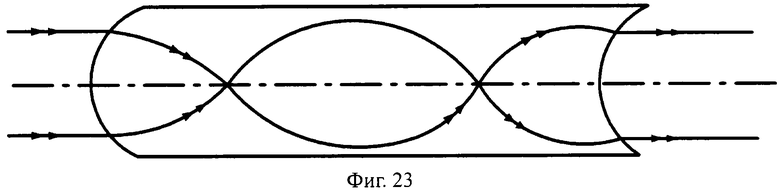
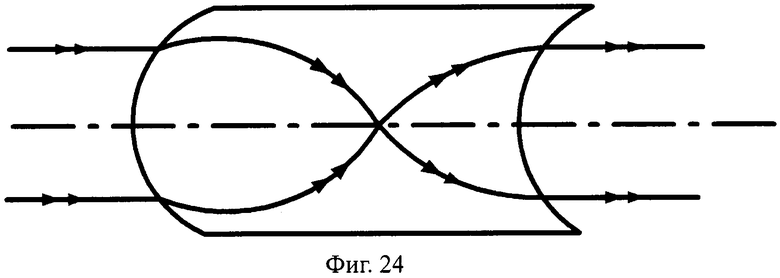
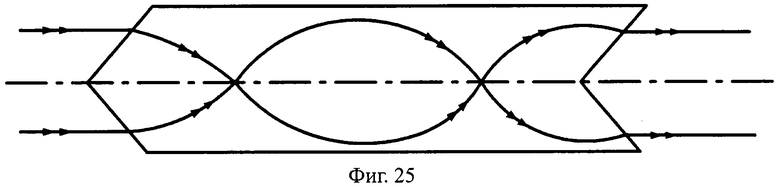
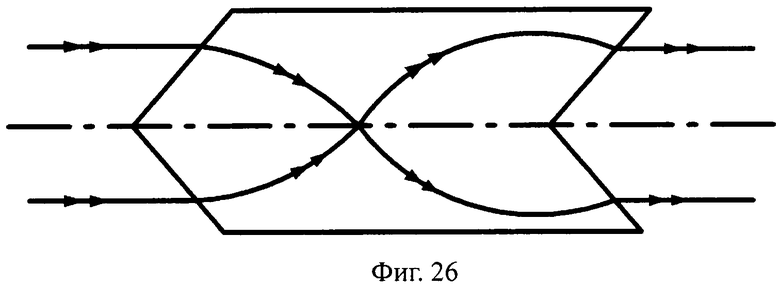
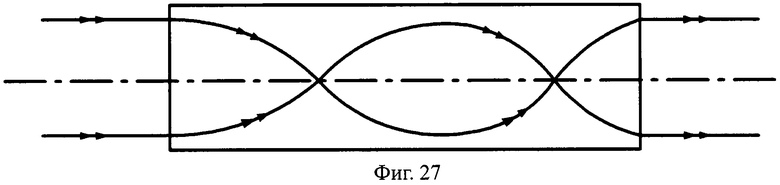
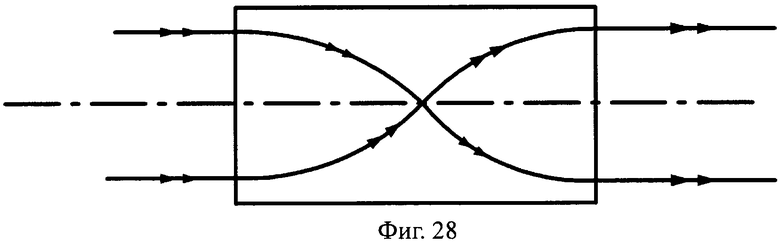
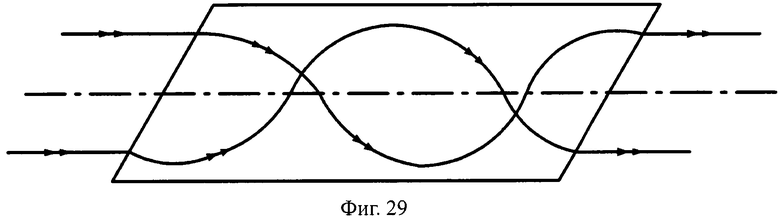
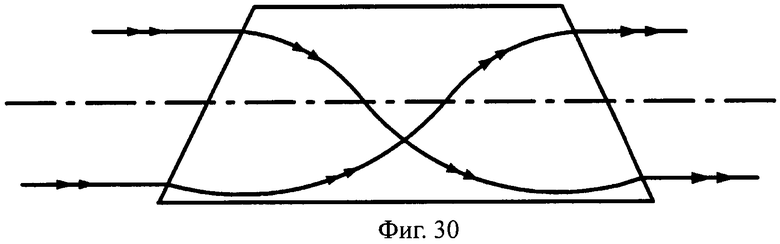
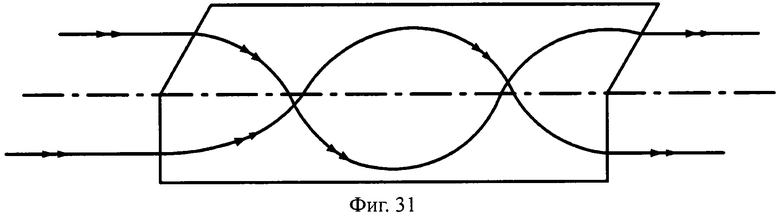
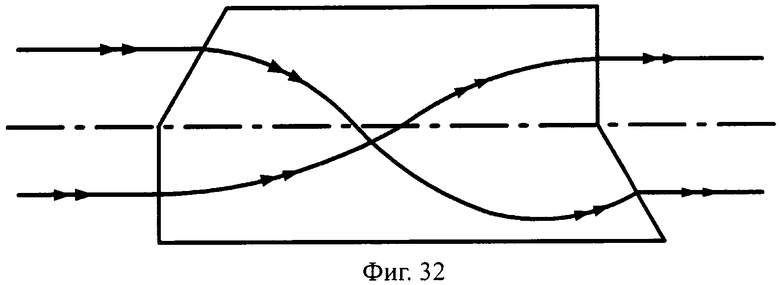
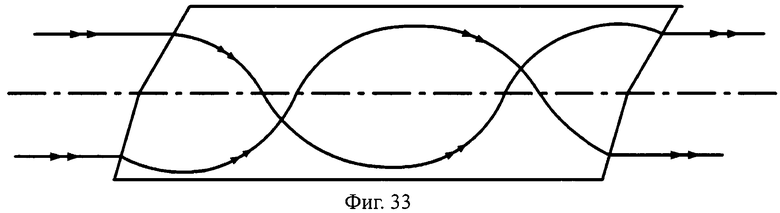
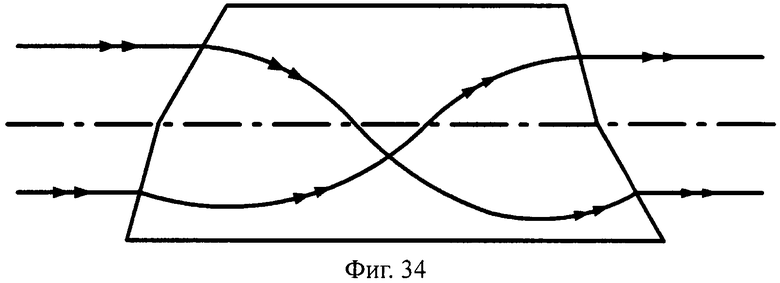
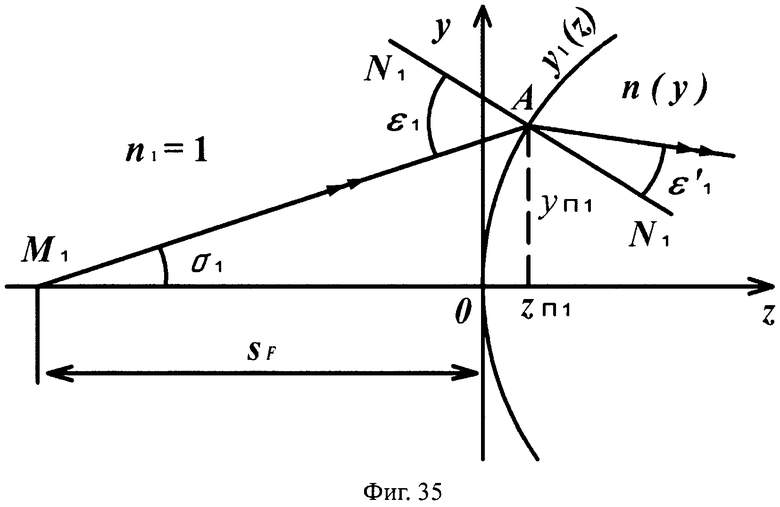
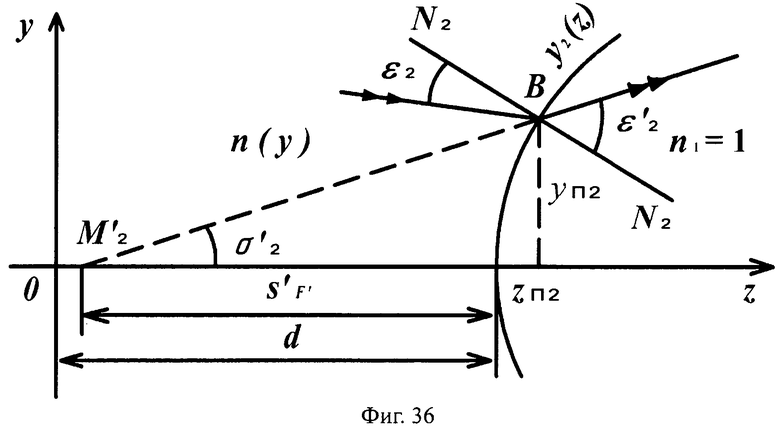
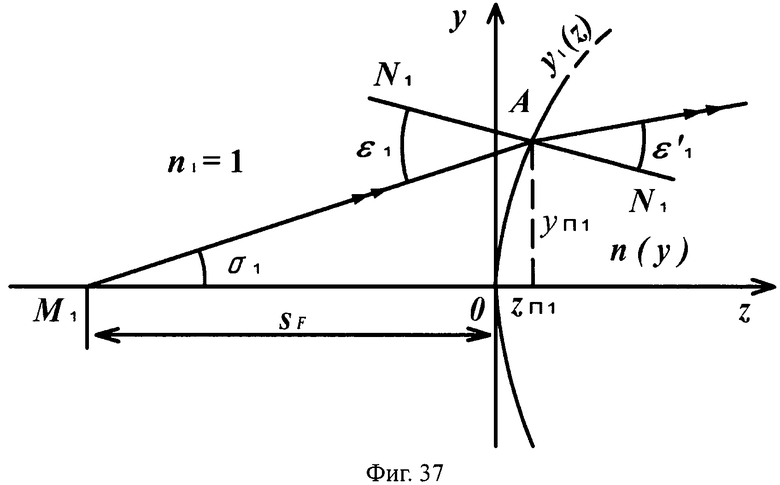
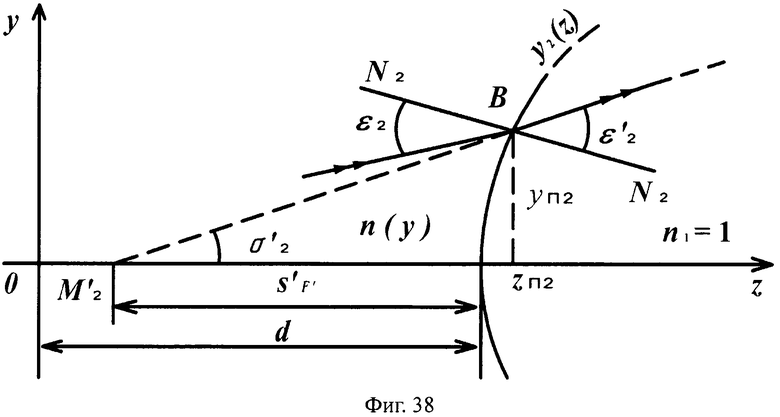
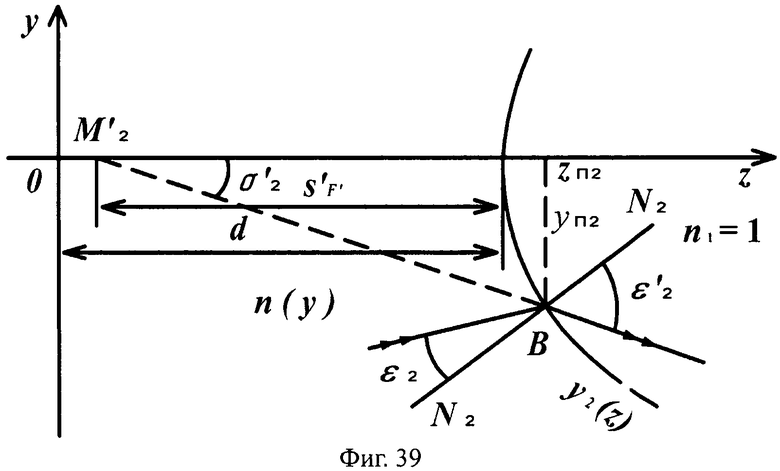
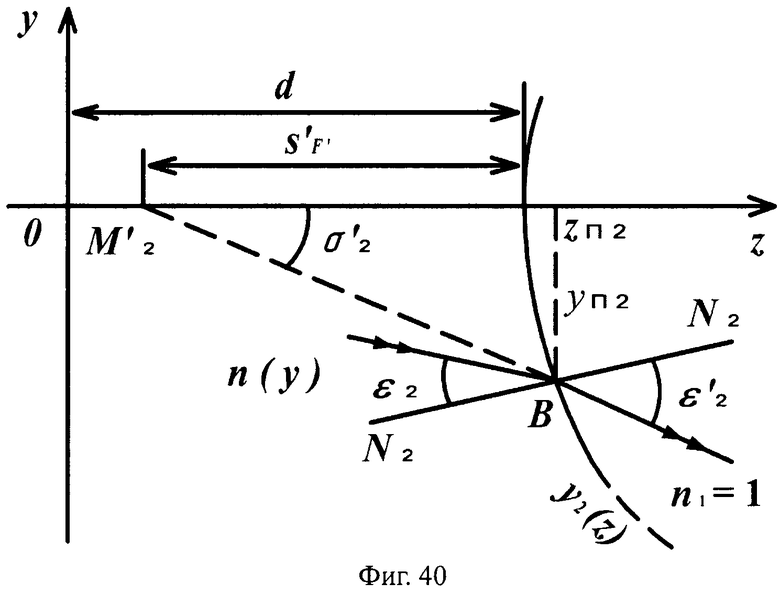
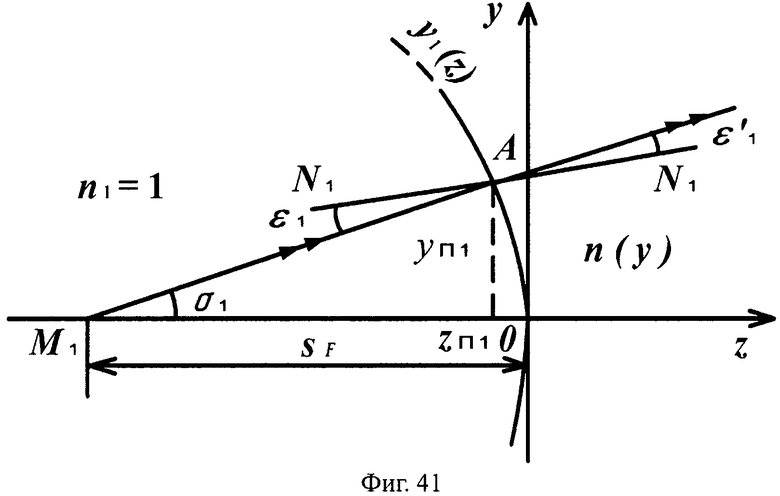
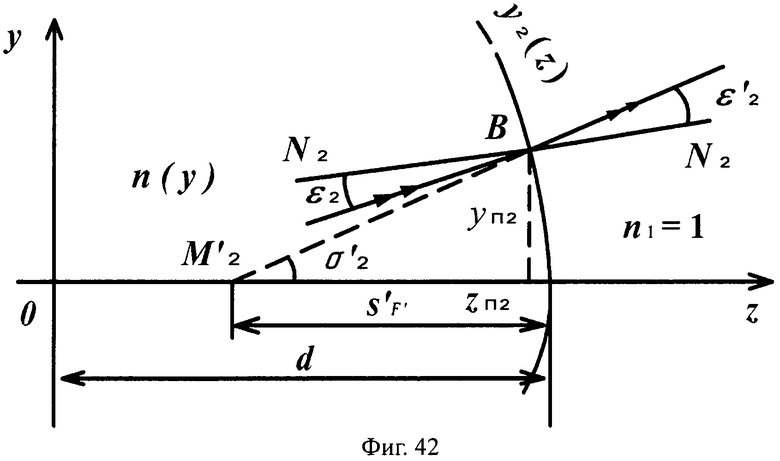
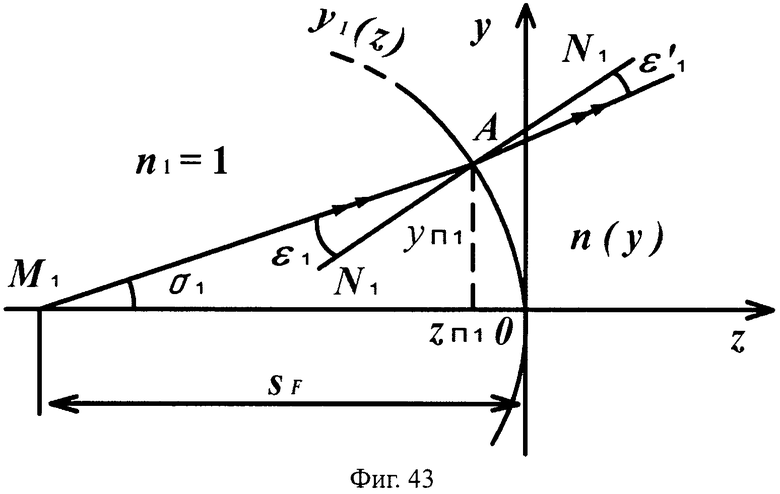
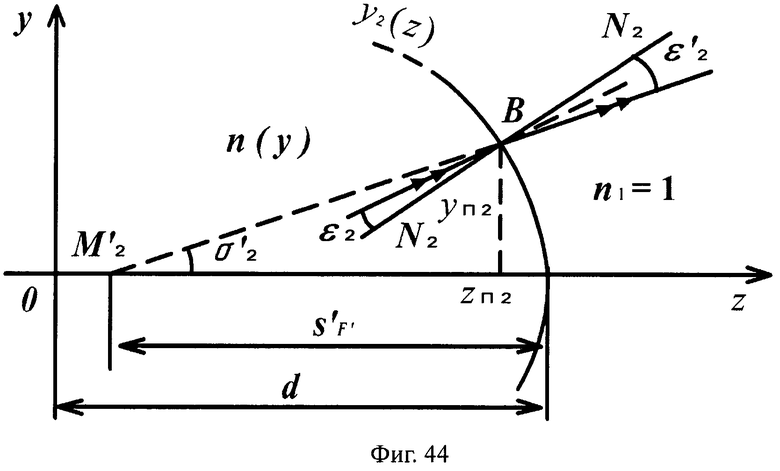
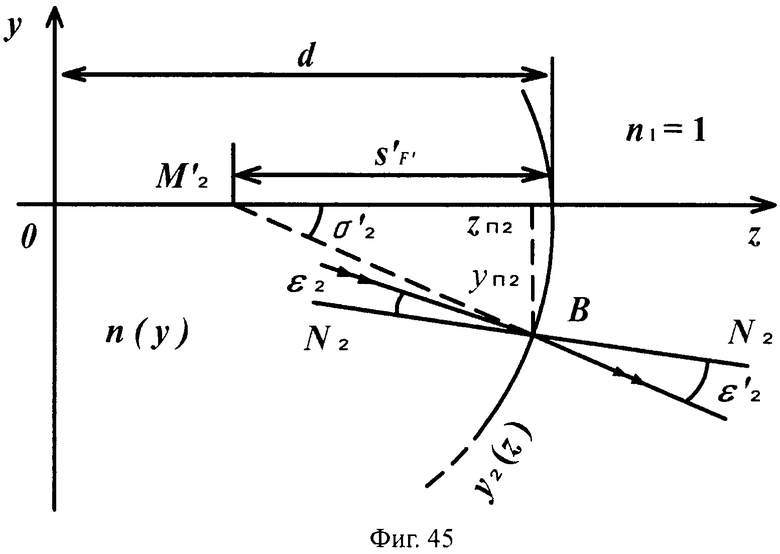
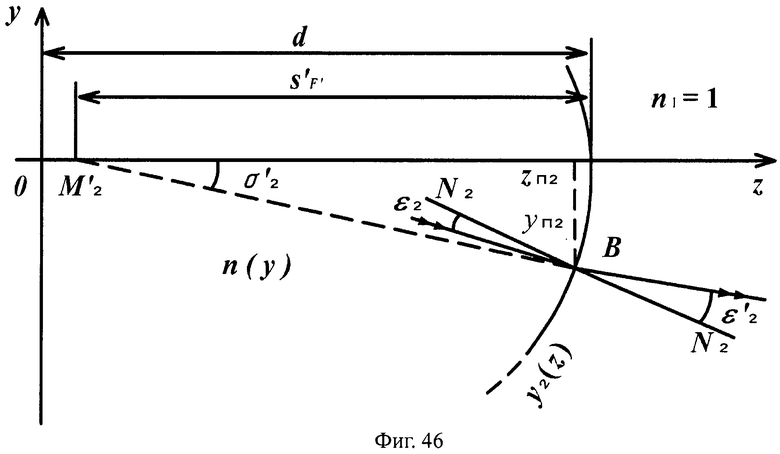
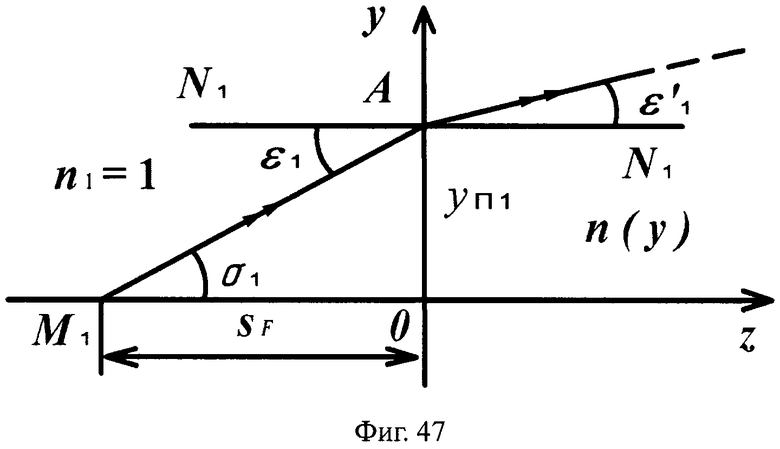
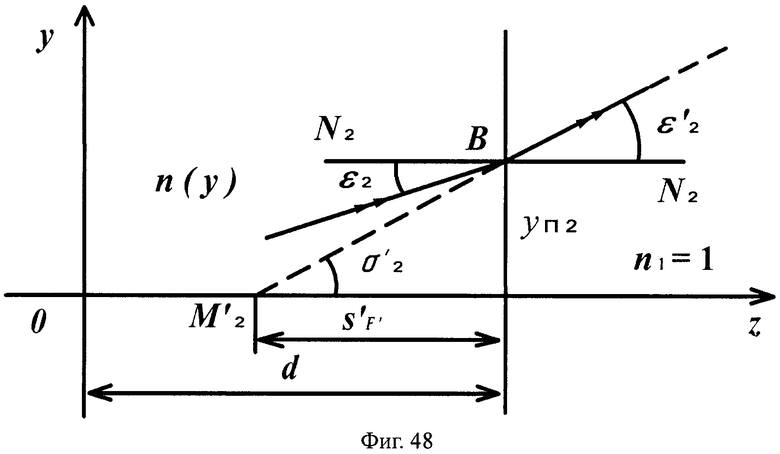
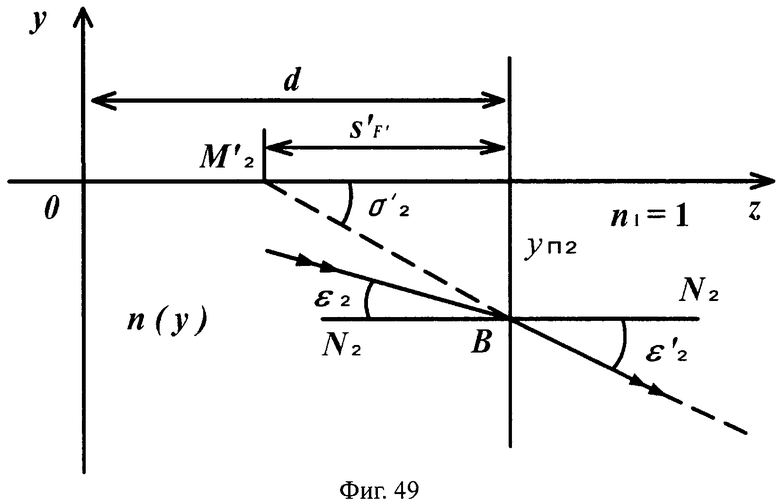
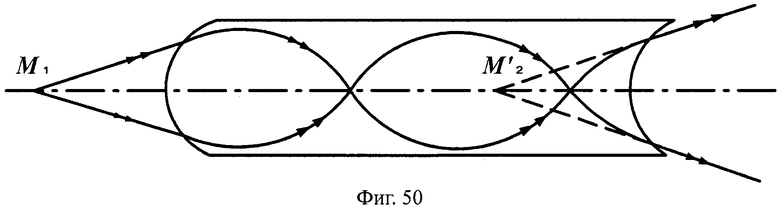
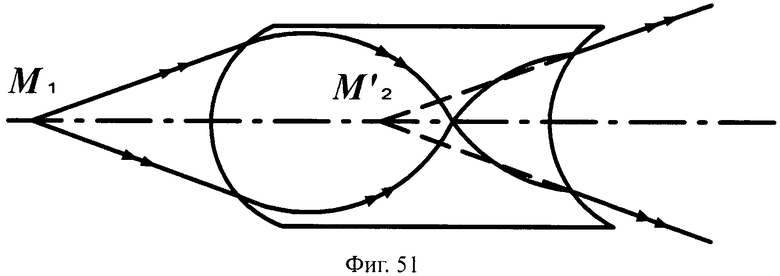
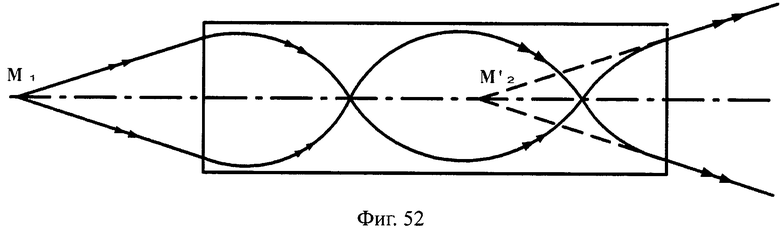
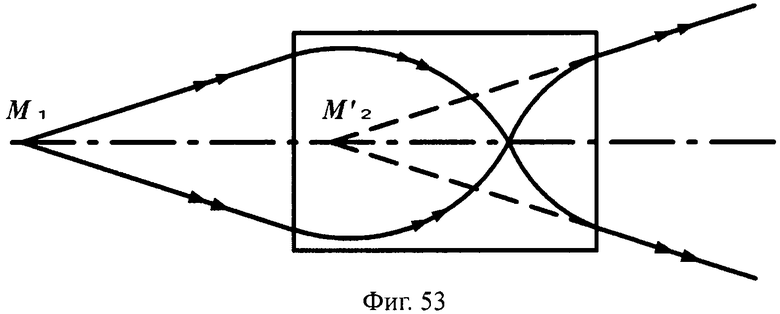
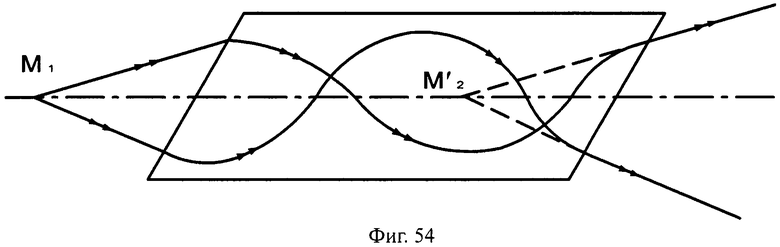
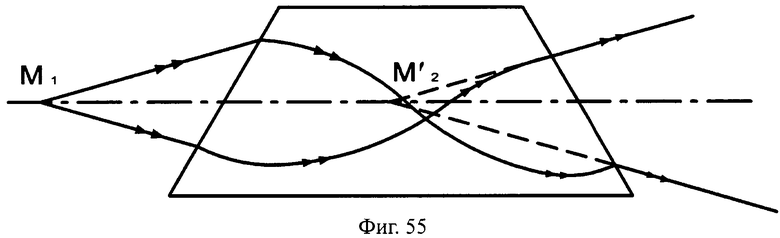
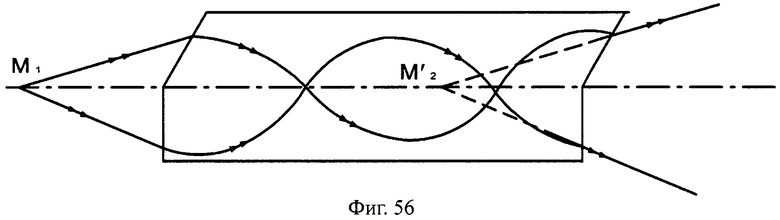
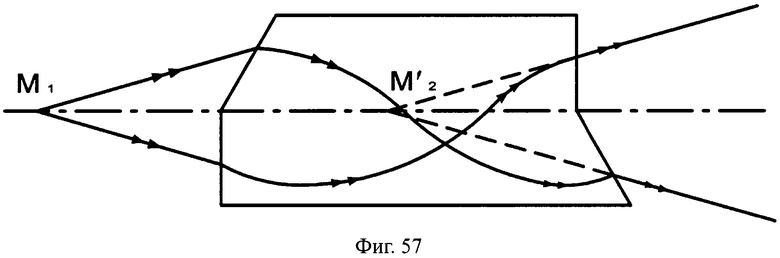
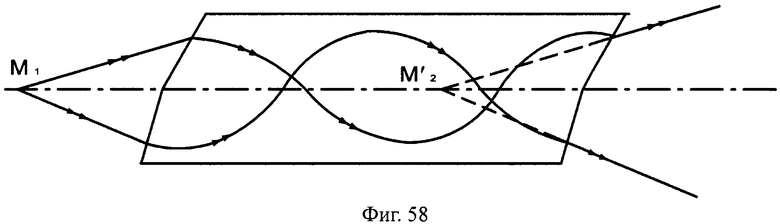
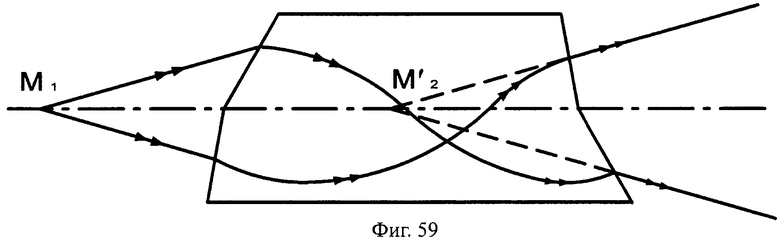
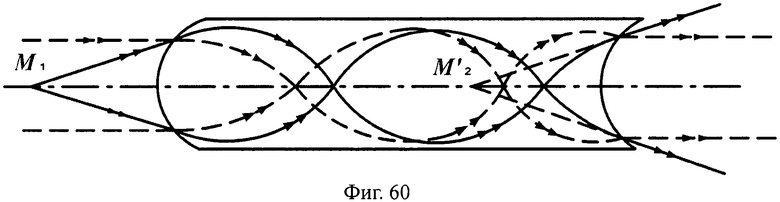
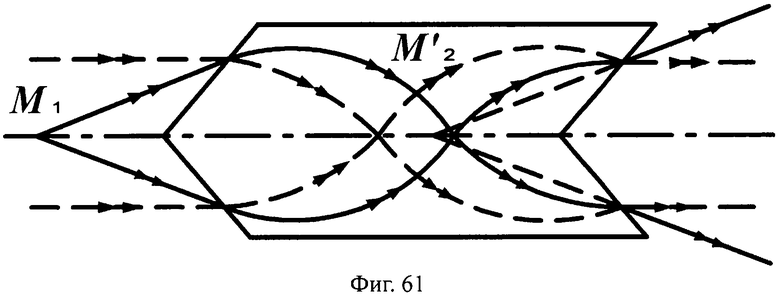
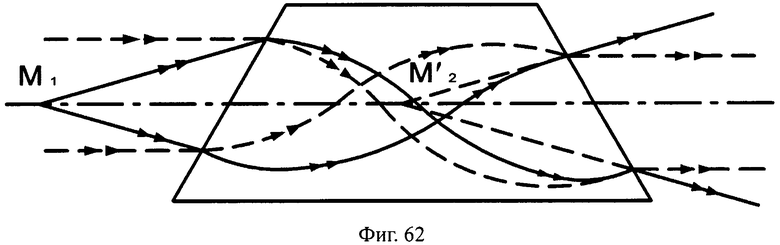
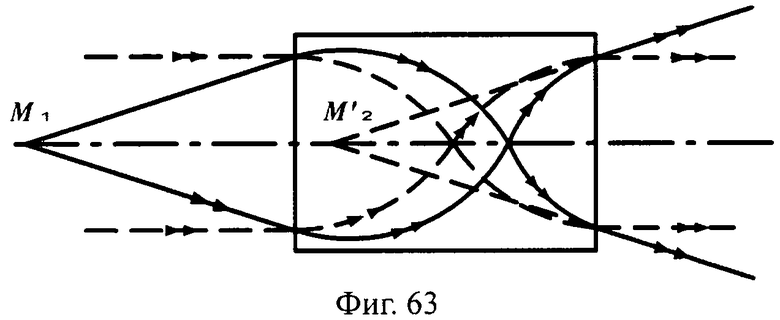
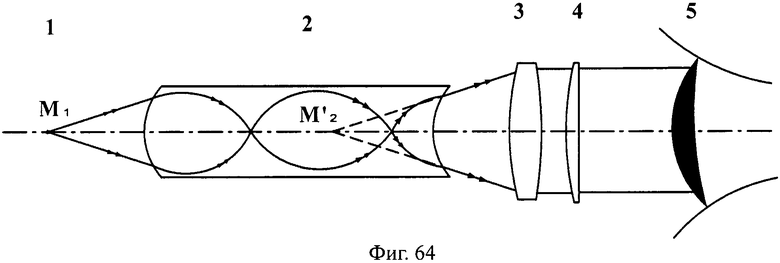
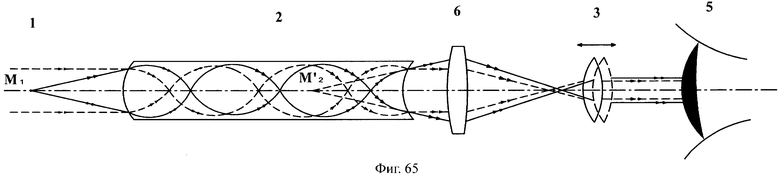
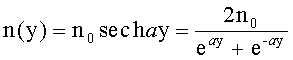 , где n0 - значение показателя преломления на оси; а - постоянная. Толщина линзы d по оптической оси z кратна удвоенному номинальному фокусному расстоянию F, равному
, где n0 - значение показателя преломления на оси; а - постоянная. Толщина линзы d по оптической оси z кратна удвоенному номинальному фокусному расстоянию F, равному 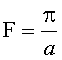 . Линза имеет равные величины переднего sF и заднего s'F' отрезков. При толщине, кратной F, проекция толщины линзы на оптическую ось в любой плоскости, содержащей оптическую ось, для любых двух точек 1-й и 2-й поверхностей, имеющих одинаковую по абсолютной величине высоту относительно оптической оси, но расположенных по разные стороны от оптической оси, равна F. При толщине, кратной 2F, проекция толщины линзы на оптическую ось в любой плоскости, содержащей оптическую ось, для любых двух точек 1-й и 2-й поверхностей, имеющих одинаковую по величине высоту относительно оптической оси и расположенных по одну сторону от оптической оси, равна 2F. Технический результат - возможность выбора разных форм преломляющих поверхностей, упрощение конструкции линзы, наличие одновременно апланатических и телескопических свойств. 4 з.п. ф-лы, 65 ил., 128 табл.
. Линза имеет равные величины переднего sF и заднего s'F' отрезков. При толщине, кратной F, проекция толщины линзы на оптическую ось в любой плоскости, содержащей оптическую ось, для любых двух точек 1-й и 2-й поверхностей, имеющих одинаковую по абсолютной величине высоту относительно оптической оси, но расположенных по разные стороны от оптической оси, равна F. При толщине, кратной 2F, проекция толщины линзы на оптическую ось в любой плоскости, содержащей оптическую ось, для любых двух точек 1-й и 2-й поверхностей, имеющих одинаковую по величине высоту относительно оптической оси и расположенных по одну сторону от оптической оси, равна 2F. Технический результат - возможность выбора разных форм преломляющих поверхностей, упрощение конструкции линзы, наличие одновременно апланатических и телескопических свойств. 4 з.п. ф-лы, 65 ил., 128 табл.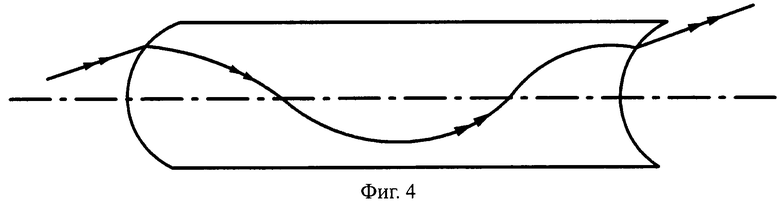
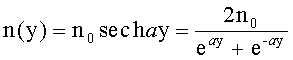 ,
,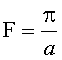 ,
,