Область техники, к которой относится изобретение
Настоящее изобретение относится к системе автоматизированного проектирования и к программе автоматизированного проектирования, которая преобразует форму члена в форму целевой функции с кривой поверхностью.
Уровень техники
Сегодня очевидно стремление сократить процессы от планирования до проектирования и производства для того, чтобы удовлетворять потребительский спрос. Чтобы повысить эффективность процессов проектирования и производства, большую популярность имеют системы машинной графики (CG) и автоматизированного проектирования (CAD). Чтобы изображать формы, имеющие сложные формы с кривыми линиями или кривой поверхностью, такие как автомобили, бытовые электроприборы и т.п., на компьютере, традиционно существовали следующие способы обработки.
Первый - это объемное моделирование, когда простые формы, называемые непроизводными элементами, содержатся в компьютере, и операции такие, чтобы объединять эти формы друг с другом, повторяются так, чтобы выразить сложные формы. Непроизводный элемент - это, например, столбец, куб, шестигранник, тор, шар и т.п., и в объемном моделировании формы представляются посредством операций над множествами этих непроизводных элементов. Следовательно, чтобы сгенерировать сложную форму, требуется много этапов и много точных вычислений.
Второй - это моделирование поверхностей, которое употребляет такой алгоритм, как алгоритм Безье, би-сплайн, рациональный Безье, неравномерный рациональный би-сплайн (NURBS) и т.п., для того, чтобы выполнять такие операции, как отрезание или соединение линий или поверхностей, и посредством повторения этих операций представляются сложные свободные кривые линии или кривые поверхности.
Тем не менее, даже с моделью, в которой нет проблем от точки представления с помощью описанной выше объемной модели или модели поверхностей, в некоторых случаях могут возникать проблемы в случае, когда она используется приложением с нисходящим потоком данных, например CAM, CAE и т.п. Это вызвано различиями между элементом поддержки, который должен поддерживаться сгенерированной машинной графикой, и элементом поддержки, который должен поддерживаться другими приложениями машинной графики, автоматизированного проектирования и с нисходящим потоком данных, и различиями в определении формы и т.п. Модель исправляется с помощью такого приложения, как транслятор, который модифицирует эти различия (японские заявки на патент №№ 2001-250130, Hei 11-65628, Hei 10-69506, Hei 4-134571, Hei 4-117572 и Hei 1-65628).
Раскрытие изобретения
Тем не менее, вышеописанные операции исправления крайне неэффективны для сокращения процессов проектирования и производства. Причины необходимости исправления различны в каждом случае, но момент, который становится проблемой, особенно на стадии производства, состоит в том, что представления всех кривых линий и кривых поверхностей аппроксимируются посредством евклидовой геометрии в традиционной системе машинной графики или автоматизированного проектирования. Например, в случае, когда табличные цилиндрические поверхности седлового типа, показанные на фиг. 6, генерируются операцией развертки, появляется длинная линия в части нижнего уклона седла и короткая линия в центральной части седла. Следовательно, эта операция развертки является преобразованием, сопровождающимся графическим увеличением и сужением для того, чтобы сохранить непрерывность сгенерированной кривой поверхности. Тем не менее, в традиционной системе машинной графики или автоматизированного проектирования это увеличение и сужение не рассматривается, и внутреннее представление приблизительно представляется в качестве цилиндрического типа. Следовательно, если модель машинной графики или модель автоматизированного проектирования, которая фактически приблизительно представляется посредством такой евклидовой геометрии, передается в CAE, появление ошибок в ней становится проблемой при производстве.
Настоящее изобретение было разработано для того, чтобы решать такие проблемы, с целью предоставления системы автоматизированного проектирования и программы автоматизированного проектирования, которая может в значительной степени употреблять модель машинной графики или модель автоматизированного проектирования и может повысить эффективность процессов проектирования и производства.
Система автоматизированного проектирования в соответствии с настоящим изобретением содержит: устройство извлечения информации о точечной последовательности, которое извлекает множество точечных последовательностей на кривой поверхности; делительное устройство, которое генерирует кривую поверхность из точечных последовательностей с помощью другой системы автоматизированного проектирования и делит кривую поверхность на предопределенное число ячеек; вычислительное устройство первой фундаментальной формы для вычисления коэффициентов первой фундаментальной формы, заданных тангенциальным вектором, который формирует касательную плоскость ячейки; вычислительное устройство второй фундаментальной формы для вычисления коэффициентов второй фундаментальной формы, заданных тангенциальным вектором и вектором нормали ячейки; запоминающее устройство, которое сохраняет информацию о точечной последовательности, коэффициенты первой фундаментальной формы и коэффициенты второй фундаментальной формы.
Более того, система автоматизированного проектирования в соответствии с настоящим изобретением, также содержит: вычислительное устройство главной кривизны, которое вычисляет главную кривизну ячейки на основе коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы; вычислительное устройство линии кривизны, которое вычисляет линию кривизны, показывающую главное направление ячейки на основе главной кривизны; устройство анализа характерных точек/характерных линий, которое извлекает точку или линию, которая становится опорной точкой или опорной линией преобразования, заданного шаблонами изменения одной или более характерных величин из пяти характерных величин, показывающих характеристики кривой поверхности, содержащей кривизну Гаусса и среднюю кривизну, вычисленную на основе главной кривизны, главного направления, линии кривизны и коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы; и вычислительное устройство длины охвата, которое вычисляет длину охвата на основе кривизны, вычисленной из коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы.
Кроме того, система автоматизированного проектирования по настоящему изобретению также содержит: устройство воспроизведения, которое преобразует линию кривизны для длины охвата в направлении линии кривизны с характерной точкой или характерной линией в качестве опорной точки преобразования и воспроизводит ячейку или кривую поверхность.
Более того, система автоматизированного проектирования по настоящему изобретению также содержит: устройство преобразования, которое извлекает множество точечных последовательностей на кривой поверхности из воспроизведенной ячейки или кривой поверхности и преобразует точечные последовательности согласно алгоритму графического представления в другой системе автоматизированного проектирования.
В соответствии с программой автоматизированного проектирования по настоящему изобретению на компьютере исполняется: процесс извлечения информации о точечной последовательности для извлечения множества точечных последовательностей на кривой поверхности; делительный процесс для генерации кривой поверхности из точечных последовательностей с помощью другой системы автоматизированного проектирования и деления кривой поверхности на предопределенное число ячеек; вычислительный процесс первой фундаментальной формы для вычисления коэффициентов первой фундаментальной формы, заданных тангенциальным вектором, который формирует касательную плоскость ячейки; вычислительный процесс второй фундаментальной формы для вычисления коэффициентов второй фундаментальной формы, заданных тангенциальным вектором и вектором нормали ячейки; и процесс сохранения для сохранения информации о точечной последовательности, коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы.
Кроме того, в соответствии с программой автоматизированного проектирования по настоящему изобретению на компьютере также выполняют: вычислительный процесс главной кривизны для вычисления главной кривизны ячейки на основе коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы; вычислительный процесс линии кривизны для вычисления линии кривизны, показывающей главное направление ячейки на основе главной кривизны; процесс анализа характерных точек/характерных линий для извлечения точки или линии, которая становится опорной точкой или опорной линией преобразования, заданного шаблонами изменения одной или более характерных величин из пяти характерных величин, показывающих характеристики кривой поверхности, содержащей кривизну Гаусса и среднюю кривизну, вычисленную на основе главной кривизны, главного направления, линии кривизны и коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы; и вычислительный процесс длины охвата для вычисления длины охвата на основе кривизны, вычисленной из коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы.
Более того, в соответствии с программой автоматизированного проектирования по настоящему изобретению на компьютере также выполняют процесс воспроизведения для преобразования линии кривизны для длины охвата в направлении линии кривизны с характерной точкой или характерной линией в качестве опорной точки преобразования и воспроизведения ячейки или кривой поверхности.
Кроме того, в соответствии с программой автоматизированного проектирования по настоящему изобретению на компьютере выполняют процесс преобразования для извлечения множества точечных последовательностей на кривой поверхности из воспроизведенной ячейки или кривой поверхности и преобразования точечных последовательностей согласно алгоритму графического представления в другой системе автоматизированного проектирования.
Система машинной графики по настоящему изобретению содержит: устройство извлечения информации о точечной последовательности, которое извлекает множество точечных последовательностей на кривой поверхности; делительное устройство, которое генерирует кривую поверхность из точечных последовательностей с помощью другой системы машинной графики и делит кривую поверхность на предопределенное число ячеек; вычислительное устройство первой фундаментальной формы для вычисления коэффициентов первой фундаментальной формы, заданных тангенциальным вектором, который формирует касательную плоскость ячейки; вычислительное устройство второй фундаментальной формы для вычисления коэффициентов второй фундаментальной формы, заданных тангенциальным вектором и вектором нормали ячейки; и запоминающее устройство, которое сохраняет информацию о точечной последовательности, коэффициенты первой фундаментальной формы и коэффициенты второй фундаментальной формы.
Кроме того, в соответствии с программой машинной графики по настоящему изобретению на компьютере выполняется: процесс извлечения информации о точечной последовательности для извлечения множества точечных последовательностей на кривой поверхности; делительный процесс для генерации кривой поверхности из точечных последовательностей с помощью другой системы машинной графики и деления кривой поверхности на предопределенное число ячеек; вычислительный процесс первой фундаментальной формы для вычисления коэффициентов первой фундаментальной формы, заданных тангенциальным вектором, который формирует касательную плоскость ячейки; вычислительный процесс второй фундаментальной формы для вычисления коэффициентов второй фундаментальной формы, заданных тангенциальным вектором и вектором нормали ячейки; и процесс сохранения для сохранения информации о точечной последовательности, коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы.
Настоящее изобретение обеспечивает достижение следующих результатов.
Поскольку устройство извлечения информации о точечной последовательности извлекает множество точечных последовательностей на кривой поверхности, делительное устройство генерирует кривую поверхность из точечных последовательностей с помощью другой системы машинной графики или системы автоматизированного проектирования и делит кривую поверхность на предопределенное число ячеек; вычислительное устройство первой фундаментальной формы обеспечивает вычисление коэффициентов первой фундаментальной формы, заданных тангенциальным вектором, который формирует касательную плоскость ячейки; вычислительное устройство второй фундаментальной формы обеспечивает вычисление коэффициентов второй фундаментальной формы, заданных тангенциальным вектором и вектором нормали ячейки; и запоминающее устройство сохраняет информацию о точечной последовательности, коэффициенты первой фундаментальной формы и коэффициенты второй фундаментальной формы, то посредством принятия теории кривой поверхности, которая обеспечивает непрерывность линии свободной формы/поверхности свободной формы, модель машинной графики или модель автоматизированного проектирования могут быть широко употреблены и эффективность процессов проектирования и производства может быть повышена.
Кроме того, поскольку обеспечивается вычислительное устройство главной кривизны, которое вычисляет главную кривизну ячейки на основе коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы; вычислительное устройство линии кривизны, которое вычисляет линию кривизны, показывающую главное направление ячейки на основе главной кривизны; устройство анализа характерных точек/характерных линий, которое извлекает точку или линию, которая становится опорной точкой или опорной линией преобразования, заданного шаблонами изменения одной или более характерных величин из пяти характерных величин, показывающих характеристики кривой поверхности, содержащей кривизну Гаусса и среднюю кривизну, вычисленную на основе главной кривизны, главного направления, линии кривизны и коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы; и вычислительное устройство длины охвата, которое вычисляет длину охвата на основе кривизны, вычисленной из коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы, то модель машинной графики или автоматизированного проектирования, проанализированная посредством теории кривой поверхности, может быть воспроизведена и преобразована в другую модель машинной графики или автоматизированного проектирования.
Более того, поскольку обеспечивается устройство воспроизведения, которое преобразует линию кривизны для длины охвата в направлении линии кривизны с характерной точкой или характерной линией в качестве опорной точки преобразования и воспроизводит ячейку или кривую поверхность, то модель компьютерной графики или автоматизированного проектирования, проанализированная теорией кривой поверхности, может быть воспроизведена.
Кроме того, поскольку обеспечивается устройство преобразования, которое извлекает множество точечных последовательностей на кривой поверхности из воспроизведенной ячейки или кривой поверхности и преобразует точечные последовательности согласно алгоритму графического представления в другой системе машинной графики или автоматизированного проектирования, то модель машинной графики или автоматизированного проектирования, проанализированная теорией кривой поверхности, может быть преобразована в другую модель машинной графики или автоматизированного проектирования.
Краткое описание чертежей
Фиг. 1 - это блок-схема, показывающая конфигурацию системы автоматизированного проектирования варианта осуществления настоящего изобретения.
Фиг. 2 - это пояснительная схема, показывающая ситуацию деления кривой поверхности на ячейку m x n и задания фундаментальных векторов su и sv.
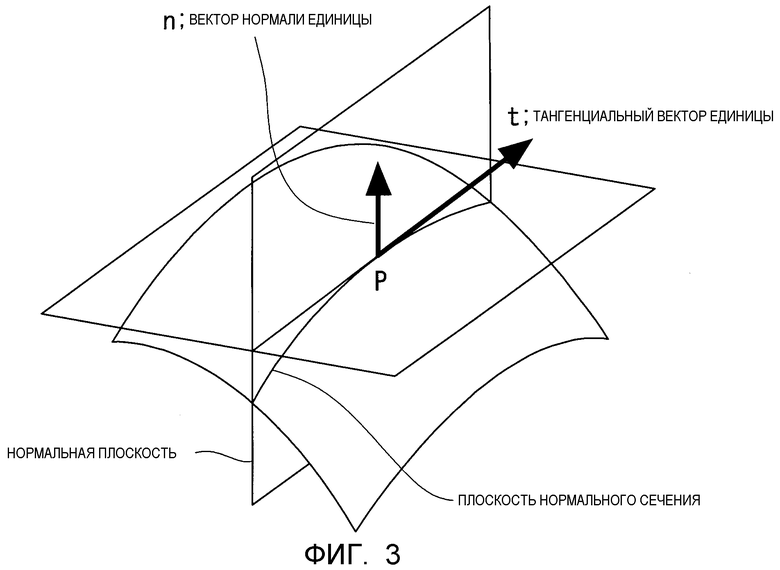
Фиг. 3 - это пояснительная схема, показывающая плоскости, в которых простираются тангенциальный вектор единицы t и вектор нормали единицы n.
Фиг. 4 - это блок-схема последовательности операций способа, показывающая поток обработки от анализа поверхности свободной формы к передаче данных посредством программы 1 анализа.
Фиг. 5 - это пояснительная схема, показывающая сторону изменения кривизны.
Фиг. 6 - это пояснительная схема, показывающая классификации средней кривизны и кривизны Гаусса.
Фиг. 7 - это пояснительная схема, показывающая изоклинальные ортогональные линии.
Фиг. 8 - это пояснительная схема, показывающая линии экстремума главной кривизны.
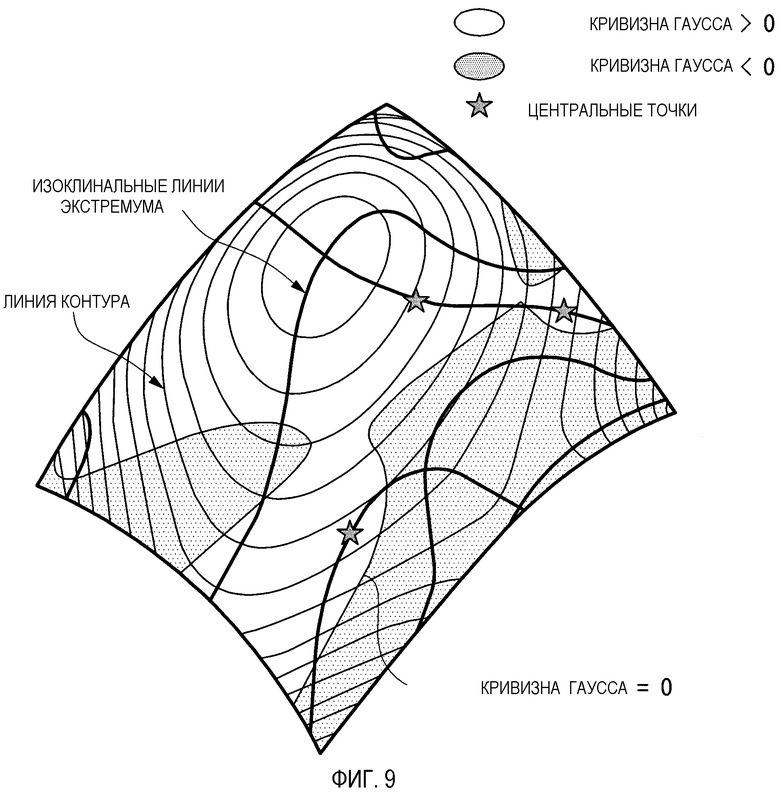
Фиг. 9 - это пояснительная схема, показывающая изоклинальные линии экстремума и стороны распределения кривизны Гаусса.
Фиг. 10 - это пояснительная схема, показывающая линии кривизны.
Осуществление изобретения
Ниже приводится описание варианта осуществления системы автоматизированного проектирования в соответствии с настоящим изобретением, поясняемое чертежами. Фиг. 1 - это блок-схема, показывающая конфигурацию системы автоматизированного проектирования настоящего варианта осуществления. Система автоматизированного проектирования настоящего варианта осуществления содержит: центральный процессор, например, центральное обрабатывающее устройство (CPU) и т.п. (не показан), запоминающее устройство, например, ROM, RAM и т.п. (не показано), базу 10 данных, секцию 11 обработки на графическом дисплее, секцию 12 дисплея, секцию 13 вывода и секцию связи (не показана).
CPU считывает программу 1 анализа, программу 2 преобразования и программу 3 воспроизведения, сохраненные в ROM, и исполняет последовательность процессов, связанных с анализом, преобразованием и воспроизведением поверхности свободной формы. RAM - это полупроводниковая память, в которой главным образом CPU сохраняет данные.
Программа 1 анализа - это программа, которая исполняет в CPU процесс чтения данных 20 значения фактического измерения объекта трехмерной формы посредством автоматизированного тестирования (CAT) и т.п., либо данных 21 другого формата автоматизированного проектирования (графических данных, представленных, например, посредством модели поверхностей, такой как объемная модель, Безье, би-сплайн, рациональный Безье или NURBS), создания таблицы 30 информации о точечной последовательности, таблицы 31 коэффициентов первой фундаментальной формы и таблицы 32 коэффициентов второй фундаментальной формы и последующего сохранения их в базе 10 данных.
Таблица 30 информации о точечной последовательности содержит информацию о точечной последовательности (u, v) для кривой поверхности, выраженную в параметрической форме:
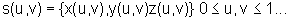(уравнение 1)
как показано на фиг. 2. Например, полагая, что u=0, 1/m, 2/m,... m-1/m (m - натуральное число) и v=0, 1/n, 2/n,... n-1/n (n - натуральное число), кривая поверхность, показанная на фиг. 2, делится на ячейку m x n. В этом случае информацией о точечной последовательности (u, v) становятся последовательности данных mn из идентификаторов ячеек от ID1 до IDmn.
Таблица 31 коэффициентов первой фундаментальной формы содержит коэффициенты первой фундаментальной формы E, F и G, выведенные из следующих уравнений. В случае, если u и v, описанные выше, имеют функциональную зависимость, тогда s (u, v) обозначает кривую линию на кривой поверхности, частичная производная ds/du=su означает тангенциальный вектор кривой линии u=constant, а частичная производная ds/dv=sv означает тангенциальный вектор кривой линии v=constant. При таких условиях фундаментальные векторы su и sv формируют касательную плоскость кривой поверхности. Кроме того, вектор ds, связывающий две точки на кривой поверхности от s (u, v) до s (u+du, v+dv), представляется как:
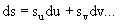(уравнение 2)
При этом квадрат абсолютного значения ds представляется как:
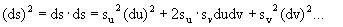(уравнение 3)
Описанные выше коэффициенты первой фундаментальной формы задаются из фундаментального вектора кривой поверхности в следующем уравнении:
(уравнение 4)
Описанные выше коэффициенты первой фундаментальной формы E, F и G уникально определены для соответствующих ячеек таким способом. Таблица 31 коэффициентов первой фундаментальной формы сохраняет значения для соответствующих идентификаторов ячеек от ID1 до IDmn.
Кроме того, объединение вышеуказанного уравнения 3 и уравнения 4 дает:
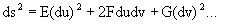(уравнение 5)
Таблица 32 коэффициентов второй фундаментальной формы содержит коэффициенты второй фундаментальной формы L, M и N, выведенные из следующих уравнений. Полагая, что ω - это угол между фундаментальными векторами su и su, тогда их скалярное произведение F и абсолютное значение H векторного произведения фундаментальных векторов представляется следующим образом с помощью коэффициентов первой фундаментальной формы:
(уравнение 6)
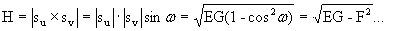(уравнение 7)
Тогда с помощью этого расчетного значения H вектор нормали единицы n на кривой поверхности представляется как:
(уравнение 8)
Кроме того, как показано на фиг. 3, пучок линий тангенциальных векторов в точке P на кривой поверхности находится на этой касательной плоскости и их тангенциальный вектор единицы t представляется следующим уравнением:
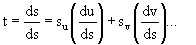(уравнение 9)
Плоскость, определенную t и n, как показано на фиг. 3, называют нормальной плоскостью.
Кривизну k в точке P на данной плоскости нормального сечения называют нормальной кривизной. Дифференцирование t для длины дуги s на плоскости нормального сечения дает:
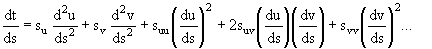(уравнение 10)
Умножение обоих уравнений на вектор нормали и введение следующих коэффициентов второй фундаментальной формы:
(уравнение 11)
дает:
(уравнение 12)
Описанные выше коэффициенты второй фундаментальной формы L, M и N уникально определены для соответствующих ячеек таким способом. Таблица 32 коэффициентов второй фундаментальной формы сохраняет значения для соответствующих идентификаторов ячеек от ID1 до IDmn.
Если уравнение 5 подставлено в уравнение 12, получается следующее уравнение.
(уравнение 13)
Из вышеприведенного нормальная кривизна вычисляется из коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы.
Программа 2 преобразования - это программа, которая исполняет на компьютере процесс считывания необходимой информации для поверхности свободной формы из таблицы 30 информации о точечной последовательности, таблицы 31 коэффициентов первой фундаментальной формы и таблицы 32 коэффициентов второй фундаментальной формы, затем создания данных поверхности свободной формы и преобразования их в форму, которую может интерпретировать другое приложение автоматизированного проектирования.
Программа 3 воспроизведения, аналогично программе 2 считывания, - это программа, которая исполняет на компьютере процесс считывания необходимой информации для поверхности свободной формы из таблицы 30 информации о точечной последовательности, таблицы 31 коэффициентов первой фундаментальной формы и таблицы 32 коэффициентов второй фундаментальной формы, затем создания данных поверхности свободной формы и вывода в секцию 11 обработки на графическом дисплее.
База 10 данных сохраняет вышеописанную таблицу 30 информации о точечной последовательности, таблицу 31 коэффициентов первой фундаментальной формы и таблицу 32 коэффициентов второй фундаментальной формы и записывает в выходном результате программы 1 анализа в ассоциативной связи с идентификатором ячейки, описанным далее.
Секция 11 обработки на графическом дисплее выполняет обработку на графическом дисплее выходных результатов из программы воспроизведения и других приложений автоматизированного проектирования.
Секция 12 дисплея отображает выходные результаты секции 11 обработки на графическом дисплее.
Секция 13 вывода выводит выходные результаты секции 11 обработки на графическом дисплее в секцию связи, другие носители записи и т.п. Секция связи передает такие данные, как информация о точечной последовательности, коэффициенты первой фундаментальной формы и коэффициенты второй фундаментальной формы, сохраненные в базе 1 данных, другим серверам или клиентам посредством такой сети, как LAN, Интернет и т.п.
Далее следует описание последовательности потоков обработки, связанных с анализом, преобразованием и воспроизведением поверхности свободной формы посредством системы автоматизированного проектирования настоящего варианта осуществления, относительно чертежей. Фиг. 4 - это блок-схема последовательности операций способа, показывающая поток обработки от анализа поверхности свободной формы к передаче данных посредством программы 1 анализа.
С помощью действий пользователя CPU принимает команду анализа для данных 20 значения фактического измерения или данных 21 другого формата автоматизированного проектирования, считывает программу 1 анализа из ROM и исполняет процесс анализа поверхности свободной формы. Сначала CPU выполняет процесс извлечения множества точечных последовательностей на кривой поверхности, такой как двухмерная поверхность NURBS, бикубическая поверхность и т.п., содержащихся в данных 20 значения фактического измерения или данных 21 другого формата автоматизированного проектирования. После этого кривая поверхность генерируется из этой точечной последовательности с помощью другой системы автоматизированного проектирования (этап S1 на фиг. 4) и кривая поверхность делится в предопределенном номере ячейки mn, как показано на фиг. 2, после чего соответствующие части ячейки стандартизируются посредством фундаментальных векторов su и sv. Информация о точечной последовательности (u, v), сгенерированная в ходе стандартизации, записывается в таблицу 30 информации о точечной последовательности, содержащуюся в базе 10 данных, в ассоциативной связи с идентификатором ячейки.
Затем CPU исполняет обработку дифференциального геометрического анализа. Т.е. оно выполняет обработку для вычисления коэффициентов первой фундаментальной формы E, F и G, заданных фундаментальными векторами su и sv, которые формируют касательную плоскость ячейки. Вычисленные коэффициенты первой фундаментальной формы E, F и G, аналогично информации о точечной последовательности, записываются в таблицу 31 коэффициентов первой фундаментальной формы, содержащуюся в базе 10 данных, в ассоциативной связи с идентификатором ячейки. Кроме того, CPU выполняет процесс вычисления коэффициентов второй фундаментальной формы L, M и N, заданных фундаментальными векторами su и sv и вектором нормали единицы n ячейки. Вычисленные коэффициенты второй фундаментальной формы L, M и N, аналогично коэффициентам первой фундаментальной формы E, F и G, записываются в таблицу 32 коэффициентов второй фундаментальной формы, содержащуюся в базе 10 данных, в ассоциативной связи с идентификатором ячейки.
Кроме того, CPU выполняет обработку для вычисления интегрируемого условия, которое является условием, когда дифференциальное уравнение, представляющее вышеописанную ячейку, непрерывно в соответствующих границах ячейки, иными словами, условием, когда данное дифференциальное уравнение имеет единственное решение.
Теперь координаты (u, v) кривой поверхности, описанные выше, заменяются на (u1, u2), и устанавливается точка p (u1, u2). Если кривую линию, сформированную посредством фиксирования u2 и перемещения u1, называют кривой линией u1, а кривую линию, сформированную посредством фиксирования u1 и перемещения u2, называют кривой линией u2, полагая, что p (u1, u2) на кривой поверхности - это исходная точка, тогда тангенциальный вектор вдоль кривой линии u1 и кривой линии u2 может быть рассчитан следующим образом:
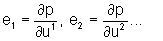(уравнение 14)
Тогда вектор нормали единицы n может быть рассчитан из e1 и e2 следующим образом:
(уравнение 15)
Таким образом, три вектора {e1, e2, n} заданы для соответствующих точек на кривой поверхности.
Для соответствующих точек первые фундаментальные величины E, F и G задаются следующим образом:
(уравнение 16)
Тогда первый фундаментальный тензор (gij, i, j=1, 2) задается следующим образом:
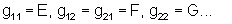(уравнение 17)
Кроме того, четыре числовых совокупности gij, i, j=1, 2, задаются следующим образом.
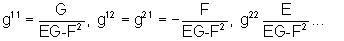(уравнение 18)
Более того, для соответствующих точек вторые фундаментальные величины L, M и N задаются следующим образом:
(уравнение 19)
Тогда второй фундаментальный тензор (hij, i, j = 1, 2) задается следующим образом:
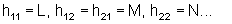(уравнение 20)
Теперь, если динамическая система координат {e1, e2, n} дифференцируется посредством координат (u1, u2) кривой поверхности, получаются структурные уравнения кривой поверхности, показанные посредством следующих двух уравнений (уравнение 21 Гаусса и уравнение 22 Вейнгартена):
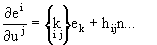(уравнение 21)
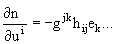(уравнение 22)
(уравнение 23)
где уравнение 23 демонстрирует символ Кристоффеля.
Интегрируемое условие этих структурных уравнений 21 и 22 показано посредством следующих двух уравнений (уравнение Гаусса уравнения 24 и уравнение Майнарди-Кодацци уравнения 25):
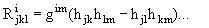(уравнение 24)
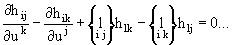(уравнение 25)
(уравнение 26)
где уравнение 26 демонстрирует тензор кривизны Райманна-Кристоффеля.
В случае, когда первый фундаментальный тензор (gij, i, j=1, 2) и второй фундаментальный тензор (hij, i, j=1, 2) применяются в качестве функции координат (u1, u2) кривой поверхности и они удовлетворяют вышеописанному уравнению Гаусса и уравнению Майнарди-Кодацци, форма кривой поверхности, имеющая такие gij и hij, определена уникально (согласно фундаментальной теории Бонне). Следовательно, соответствующие ячейки становятся непрерывными C2.
CPU выполняет эти арифметические процессы и рассчитывает вышеописанное интегрируемое условие (этап S2).
Далее CPU исполняет процесс анализа линии кривизны, процесс анализа характерных линий и процесс преобразования кривизны/длины охвата (шаг S3). Сначала главные кривизны k1 и k2 в ячейке рассчитываются на основе коэффициентов первой фундаментальной формы E, F и G и коэффициентов второй фундаментальной формы L, M и N посредством процесса анализа линии кривизны (этап S4).
То есть сначала рассчитывается экстремум вышеописанной кривизны k1. Форма плоскости нормального сечения, которая является линией пересечения нормальной плоскости и кривой поверхности, изменяется вместе с направлением касания и также изменяется нормальная кривизна. Данная форма возвращается в начальное условие, когда нормальная плоскость наполовину повернута. Теперь, полагая, что:
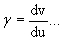(уравнение 27)
и перезаписывая k как функцию k(γ) от γ, получаем:
(уравнение 28)
Из этого квадратного уравнения γ, для dk(γ)/dγ = 0, k(γ) становится экстремумом. Тогда, если уравнение 15 дифференцируется в данном условии для экстремума и k и γ перезаписаны как 
и 
,
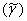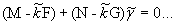(уравнение 29)
получено. Тогда, если оно заменено в уравнении 16,
(уравнение 30)
получено. Следующие зависимости получаются из этих уравнений:
(уравнение 31)
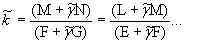(уравнение 32)
Если уравнение 18 модифицировано,
(уравнение 33)
получено. Коэффициент 
- положительный из уравнения 7. Полагая, что корни - это k1 и k2, значение становится главной кривизной, как показано на фиг. 5.
Далее рассчитываются кривизна Гаусса или средняя кривизна на основе главной кривизны (этап S5). Т.е. из зависимости корней и коэффициентов квадратного уравнения,
(уравнение 34)
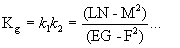(уравнение 35)
выражается. При этом Km - это средняя кривизна, а Kg - кривизна Гаусса. Когда Kg = 0, в этом случае кривая поверхность становится развертывающей поверхностью, как показано на фиг. 6, и линия кривизны на кривой поверхности становится прямой линией. В настоящем варианте осуществления считается, что точка, где кривизна Гаусса становится нулем, является опорной точкой описанного далее преобразования.
В качестве соответствующей точки для опорной точки преобразования, отличной от этой точки, могут быть выбраны, например, линии кривизны, граничные линии (гребневые линии), изоклинальные ортогональные линии, показанные на фиг. 7, линии экстремума главной кривизны, показанные на фиг. 8, изоклинальные линии экстремума, показанные на фиг. 9, или центральные точки. Это точки или линии, которые становятся опорной точкой или опорной линией преобразования, заданного шаблонами изменения одной или более характерных величин из главной кривизны, главного направления, кривизны Гаусса, средней кривизны и линии кривизны, которые являются характерными величинами, показывающими характеристики кривой поверхности. Их можно рассчитать на основе коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы.
Кроме того, линия кривизны, показывающая главное направление ячейки, вычисляется на основе главной кривизны. Т.е., исключая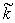 
из уравнения 19, получаем:
(уравнение 36)
или
(уравнение 37)
Оба этих уравнения являются уравнениями линии кривизны и квадратного уравнения, так что γ1 и γ2 имеют следующие зависимости:
(уравнение 38)
В точке на кривой поверхности кривизна становится экстремумом в направлении, определенном γ1 и γ2. Тангенциальный вектор на кривой поверхности - это (sudu + svdv), а скалярное произведение двух тангенциальных векторов, соответствующих γ1 и γ2, становится:
(уравнение 39)
Если внутри скобок {} преобразуется, тогда:
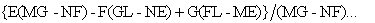(уравнение 40)
становится нулем. Т.е. установлено, что два касательных направления плоскости нормального сечения главной кривизны становятся ортогональными. Это направление называется главным направлением. В случае если это направление и касательная на кривой поверхности совпадают, оно становится линией кривизны, показанной на фиг. 10.
Из вышеприведенного, процесс вычисления линии кривизны, показывающий главное направление ячейки, выполняется.
Далее выполняется процесс преобразования кривизны/длины охвата (этап S6). То есть CPU рассчитывает длину охвата на основе кривизны, которая рассчитана на основе коэффициентов первой фундаментальной формы E, F и G и коэффициентов второй фундаментальной формы L, M и N. В соответствии с линией кривизны, рассчитанной посредством вышеописанного процесса расчета линии кривизны, радиус кривизны рассчитывается из кривизны (1/r), и длина охвата линии кривизны увеличивается и сокращается в каждом интервале вычисления.
Из вышеперечисленного выполняется процесс анализа.
Далее, после того как информация о точечной последовательности, коэффициенты первой фундаментальной формы и коэффициенты второй фундаментальной формы, которые были сгенерированы и извлечены на этапе S1 и этапе S2, были собраны ("Да" на этапе S7), CPU выполняет процесс передачи данных кривой поверхности (этап S9). С другой стороны, в случае если такая информация не была собрана полностью, выполняется процесс оценки базы данных ("Нет" на этапе S7). То есть форма, воспроизведенная на основе главного направления, опорного положения (точка, линия и т.п.), преобразованной величины, которые были рассчитаны на этапах S4-S6, и форма, воспроизведенная на основе информации о точечной поверхности, коэффициентов первой фундаментальной формы и коэффициентов второй фундаментальной формы, сравниваются, и в случае, если они совпадают ("Да" на этапе S8), выполняется процесс передачи данных кривой поверхности (этап S9). Кроме того, в случае, если они не совпадают ("Нет" на этапе S8), выполняется процесс повышения точности посредством аппроксимации и интерполяции. То есть исходная кривая поверхность аппроксимируется и интерполируется, так что она становится дважды дифференцируемой, и вышеописанные процессы снова выполняются, начиная с этапа S1. Затем на этапе, когда сравнительная оценка на этапе S8 приведена в соответствие, поток смещается к процессу передачи данных кривой поверхности.
Данные кривой поверхности передаются программе 2 преобразования или программе 3 воспроизведения, показанной на фиг. 1. Если CPU принимает команду преобразования, оно исполняет программу 2 преобразования. Т.е. сначала полагая, что точка, выбранная в качестве характерной точки или характерной линии, когда кривизна Гаусса становится нулем, является опорной точкой преобразования, линия кривизны - это увеличение и сужение, преобразованное посредством длины охвата в направлении линии кривизны, так что ячейка или кривая поверхность воспроизводится. Затем множество точечных последовательностей на кривой поверхности извлекается из воспроизведенной ячейки или кривой поверхности, и точечные поверхности преобразуются согласно алгоритму графического представления в другой системе автоматизированного проектирования. Преобразованные графические данные воспроизводятся другим приложением 22 автоматизированного проектирования и затем выводятся секции 11 обработки на графическом дисплее. Секция 11 обработки на графическом дисплее выполняет обработку на графическом дисплее данных, выведенных от приложения 22 автоматизированного проектирования, и выводит их на секцию 12 дисплея. Секция 12 дисплея принимает данные для отображения и отображает их.
Кроме того, если CPU принимает команду воспроизведения, оно исполняет программу 3 воспроизведения. Программа воспроизведения командует CPU исполнять процессы в программе преобразования, за исключением процесса преобразования. То есть допуская, что точка, где кривизна Гаусса становится нулем, является опорной точкой преобразования, линия кривизны - это увеличение и сужение, преобразованное посредством длины охвата в направлении линии кривизны, так что ячейка или кривая поверхность воспроизводится. Затем воспроизведенные графические данные выводятся секции 11 обработки на графическом дисплее, и после обработки на дисплее они отображаются в секции 12 дисплея.
Как описано выше, согласно системе автоматизированного проектирования варианта осуществления настоящего изобретения может быть получен результат, при котором поверхность свободной формы может быть проанализирована, преобразована и воспроизведена, одновременно сохраняя непрерывность непрерывной C2. Следовательно, может быть получен результат, при котором полезность модели автоматизированного проектирования может быть в значительной степени увеличена, и эффективность процессов проектирования и производства может быть повышена.
В системе автоматизированного проектирования по варианту осуществления настоящего изобретения описывается последовательность процессов, связанных с анализом, преобразованием и воспроизведением поверхности свободной формы в модели автоматизированного проектирования. Тем не менее, система автоматизированного проектирования по настоящему изобретению не ограничена этим и может быть использована в системе машинной графики или системе и программе для выполнения графического представления с помощью компьютера.
Кроме того, в предлагаемом варианте осуществления системы автоматизированного проектирования, как показано на фиг. 2, в качестве подходящего примера кривая поверхность поделена на ячейки и затем стандартизирована посредством фундаментальных векторов su и sv, так что анализ, преобразование и воспроизведение поверхности свободной формы выполняется параметрической формой u, v, которая использует информацию о точечной последовательности (u, v). Тем не менее, система автоматизированного проектирования по настоящему изобретению не ограничена этим, и могут быть использованы координатные значения для параметров координат (x, y, z).
Описанная выше система автоматизированного проектирования содержит в себе компьютерную систему. Кроме того, этапы последовательности процессов, связанных с вышеупомянутым анализом, преобразованием и воспроизведением поверхности свободной формы, сохраняются в компьютерном считываемом носителе записи в программном формате. Компьютер считывает и исполняет эту программу, чтобы тем самым выполнять вышеописанные процессы. При этом компьютерный считываемый носитель записи - это, например, магнитный диск, магнитооптический диск, CD-ROM, DVD-ROM, полупроводниковая память и т.п. Кроме того, механизм может быть таким, что эта компьютерная программа доставляется в компьютер по линии связи, и компьютер, который принимает эту программу, исполняет ее.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА АВТОМАТИЗИРОВАННОГО ВИРТУАЛЬНОГО ПРОЕКТИРОВАНИЯ ИЗДЕЛИЯ ОДЕЖДЫ ДЛЯ ПОЛЬЗОВАТЕЛЕЙ И СПОСОБ ЕЕ ОСУЩЕСТВЛЕНИЯ | 2019 |
|
RU2718362C1 |
| Плетёная пространственная конструкция Лямина (варианты) | 2020 |
|
RU2753557C1 |
| СПОСОБ ПРОЕКТИРОВАНИЯ ЦЕНТРОБЕЖНЫХ НАСОСОВ | 2013 |
|
RU2542160C1 |
| Способ имитации траекторий движения объектов | 2015 |
|
RU2617144C1 |
| СПОСОБ АВТОМАТИЗИРОВАННОГО УПРАВЛЕНИЯ ПРОЕКТИРОВАНИЕМ БОРТОВЫХ ИНТЕЛЛЕКТУАЛЬНЫХ СИСТЕМ | 2012 |
|
RU2502131C1 |
| СИСТЕМА И СПОСОБ ДЛЯ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ СЛУЖБ ЗДАНИЯ | 2010 |
|
RU2543300C2 |
| АППАРАТУРА И СПОСОБ КОНТРОЛЯ ХАРАКТЕРИСТИК СЕРДЕЧНОЙ ДЕЯТЕЛЬНОСТИ | 1997 |
|
RU2195168C2 |
| СПОСОБ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ СИСТЕМ БЕСПЕРЕБОЙНОГО ЭЛЕКТРОПИТАНИЯ | 2011 |
|
RU2468425C1 |
| Устройство трехмерного проектирования восстановления зуба, способ трехмерного проектирования восстановления зуба и машиночитаемый носитель информации | 2012 |
|
RU2715278C2 |
| СПОСОБ ИМИТАЦИИ ТРАЕКТОРИЙ ДВИЖЕНИЯ ВОЗДУШНЫХ ОБЪЕКТОВ | 2009 |
|
RU2419072C2 |
Изобретение относится к системам автоматизированного проектирования и программам автоматизированного проектирования. Техническим результатом является повышение эффективности процессов проектирования и производства посредством принятия теории кривой поверхности, которая обеспечивает непрерывность линии свободной формы/поверхности свободной формы. Система содержит устройство извлечения информации о точечной последовательности, делительное устройство, вычислительное устройство первой фундаментальной формы, вычислительное устройство второй фундаментальной формы, запоминающее устройство, вычислительное устройство главной кривизны, вычислительное устройство линии кривизны, устройство анализа характерных точек/характерных линий, вычислительное устройство длины охвата, устройство преобразования, устройство воспроизведения. 4 н.п. ф-лы, 10 ил.
| Разборный с внутренней печью кипятильник | 1922 |
|
SU9A1 |
| СПОСОБ АВТОМАТИЧЕСКОГО РАСЧЕТА ФОРМЫ ОБЪЕМНЫХ ТЕЛ | 1998 |
|
RU2158960C2 |
| СПОСОБ ИССЛЕДОВАНИЯ СТРОЕНИЯ ПРОСТРАНСТВ С РАЗМЕРНОСТЬЮ ДО 4-Х ПРЕДСТАВЛЕННЫХ МНОГОПАРАМЕТРОВЫМИ ЦИФРОВЫМИ МАССИВАМИ ДАННЫХ С РАЗМЕРНОСТЬЮ ДО 4-Х | 1995 |
|
RU2118837C1 |
| СИСТЕМА И СПОСОБ ДЛЯ УЛУЧШЕННОГО ПАРАМЕТРИЧЕСКОГО ГЕОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ | 1994 |
|
RU2127449C1 |
| Походная разборная печь для варки пищи и печения хлеба | 1920 |
|
SU11A1 |
