Изобретение относится к неразрушающему контролю прочности, ресурса и качества изделий ракетной, авиационной и другой техники, может быть использовано при контроле статической, длительной и циклической прочности металлических изделий в зависимости от размеров макроскопических дефектов.
Перечень указанных приложений нового технического решения основан на выявленной закономерности формирования упругопластической деформации и разработки новых положений физической кинетики в рамках нелинейной механики разрушения.
Предлагаемое техническое решение является следствием планомерного исследования новой кинетики деформирования твердого тела.
Технический результат изобретения заключается в повышении достоверности результатов контроля прочности и расширении количества информативных характеристик, позволяющих проводить достоверные оценки эксплуатируемой и проектируемой техники.
Технический результат достигается за счет того, что определяют сечение с максимальными напряжениями, на данное сечение устанавливают струнный периметромер с предварительным натяжением струны, нагружают изделие, определяют деформацию и напряжение в указанном сечении, навивают на изделие несколько витков струны периметромера таким образом, чтобы средний виток был расположен в указанном сечении, а остальные размещают симметрично ему, с заданным шагом, определяют интегральную деформацию в сечении, по которой судят об эффективном модуле Еэф продольной упругости материала изделия, а о прочности σр судят по уравнению:
σр=к·10-3[(Еэф·RT)1/2-ЕэфαеТ]·U0/RT),
где к - коэффициент вида напряженного состояния и формы изделия;
R - универсальная газовая постоянная;
Т - температура испытания, °К;
αе- коэффициент теплового расширения, 1/°К;
U0 - истинная энергия активации разрушения, определяют нижнюю границу упругопластической области по соотношению σ=RT и равенству частот (n=γ)-й моды поверхностной волны Рэлея и тепловых колебаний атомов, дополнительно нагружают изделие в упругопластической области через интервалы Δσ, кратные разрушающему эффективному напряжению σэф.р, фиксируют величину пластической деформации на каждой ступени, при этом о качестве изделия дополнительно судят по сравнению измеренной пластической деформации и рассчитанной εip по формуле
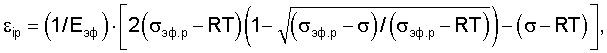
где σ - текущее эффективное напряжение, нагружение изделия производят до достижения нулевого значения скорости роста напряжений в локальных его зонах, фиксируя при этом напряжение пластической неустойчивости материала, по которому судят о концентрации напряжения на дефектах в упомянутой зоне.
Способ основан на том, что при детальном рассмотрении физической кинетики деформирования металла проведено описание поведения макроскопического дефекта. Установлено, что старт, последующий рост макроскопических одиночных трещиноподобных дефектов, естественно разных размеров, присутствующих или возникающих в деформируемом металле, определяет процесс релаксации упругой энергии за счет работы большого количества микроскопических "коротких" трещин нормированных размеров, возникающих в результате сдвиговых процессов (пластической деформации). Поэтому, при анализе кинетики формирования упругопластической деформации, рассматриваются два процесса - упругого и упругопластического деформирования, а также процесс упругопластического деформирования изделия и протекающий на этом фоне процесс старта, роста и разрушения на уровне одиночного макроскопического трещиноподобного дефекта.
Способ основан на введении и определении на новой физической основе локальной концентрации напряжений и деформаций в вершине трещиноподобного макроскопического дефекта и рассмотрении при этом его поведения при локальных и номинальных (напряжения в оболочке) напряжениях. Определение действительной зависимости для локальных напряжений для конкретного изделия гарантируется сохранением начального постоянства теплового состояния за счет поддержания при нагружении определенной скорости роста нагрузки, характерной для данного структурного состояния контролируемого изделия.
Для обоснования предлагаемого решения необходимо привести основные физические закономерности, являющиеся его фундаментальной основой.
При рассмотрении разрушения изделия от наличия трещиноподобных макроскопических дефектов в рамках нелинейной механики разрушения получено уравнение для предельного макроскопического дефекта lкр.м
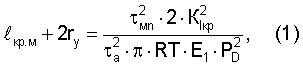
где 2rу - величина зоны пластической деформации в вершине макроскопической трещины,
τмn - время релаксации определенной величины напряжения σо в оболочке изделия,
τа - период тепловых колебаний атомов,
R - универсальная газовая постоянная,
Т - абсолютная температура испытания, °К,
E1 - эффективный модуль продольной упругости,
РD - плотность подвижных микроскопических дефектов,
KIкр - критический коэффициент интенсивности напряжений (вязкость разрушения).
Уравнение (1) имеет универсальный характер. При упругом решении в рамках линейной механики разрушения при подстановке в него РD по уравнению:
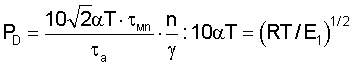
где α - коэффициент температурного расширения,
n - порядковый номер единичного напряжения σо при росте эффективного напряжения по закону σэф.n=σо·n
γ - относительный активационный объем,
получаем при RT/γ=σo, σo·n=σэф.n известное в линейной механике уравнение:
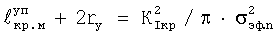
где σэф.n=σf - разрушающее напряжение.
Для нелинейной механики разрушения при подстановке в (1) РD по уравнению:
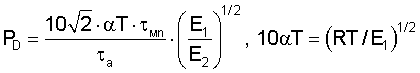
где E2 - релаксированный модуль упругости, учитывающий пластическую деформацию при RT=στ<σэф.n≤σэф.р=σт получаем:
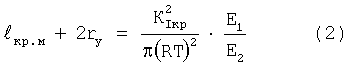
Для критической вязкости разрушения КIкр, постоянной для всех напряжений и длин макроскопических дефектов, на основании уравнения для σэф.n(εip)
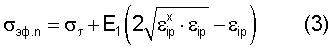
где εip, εх ip - текущая пластическая деформация в оболочке и предельная пластическая деформация при наступлении пластической неустойчивости при σэф.n=σэф.р=σт,εх ip=εо(no-γ)
εо - единичная порция деформации, a no=σэф.р/σо получено уравнение для КIкр при εip=εх ip=εо(no-γ)
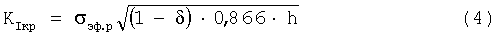
где δ - отношение στ/σэф.р, στ=RT - нормальное напряжение начала сдвиговых процессов,
h - толщина оболочки изделия.
Уравнение (4) отличается от уравнения Красовского А.Я. [1] К2 Ic=σ0,2·E1·δt, если к последнему применить уравнение Розенфильда εip=δt/h [2], a σ0,2=σт=σэф.р по Мизесу при εip=εx ip, коэффициентом (0,866)1/2, что составляет 7,5%. Исходя из уравнений (2), (4) и опускаемых здесь других условий, получены уравнения для 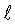 кр.м/h и 2rу
кр.м/h и 2rу
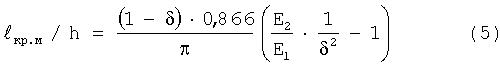
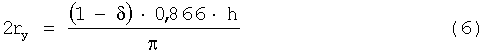
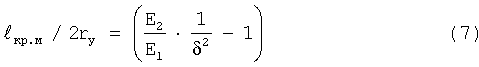
Изложенные положения позволяют рассчитать зависимости σf=f(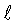 кр.м) как для упругого так и упругопластического решения. На фиг.1 приведено сравнение теоретических и экспериментальных исследований [3].
кр.м) как для упругого так и упругопластического решения. На фиг.1 приведено сравнение теоретических и экспериментальных исследований [3].
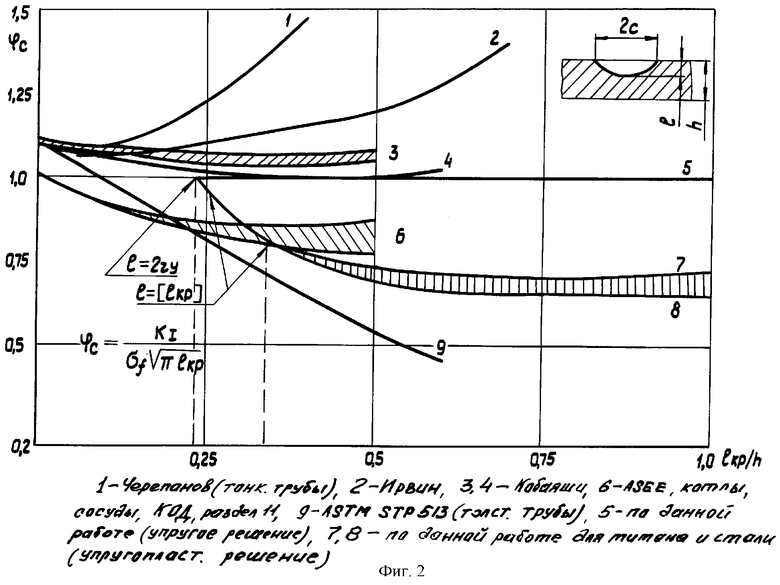
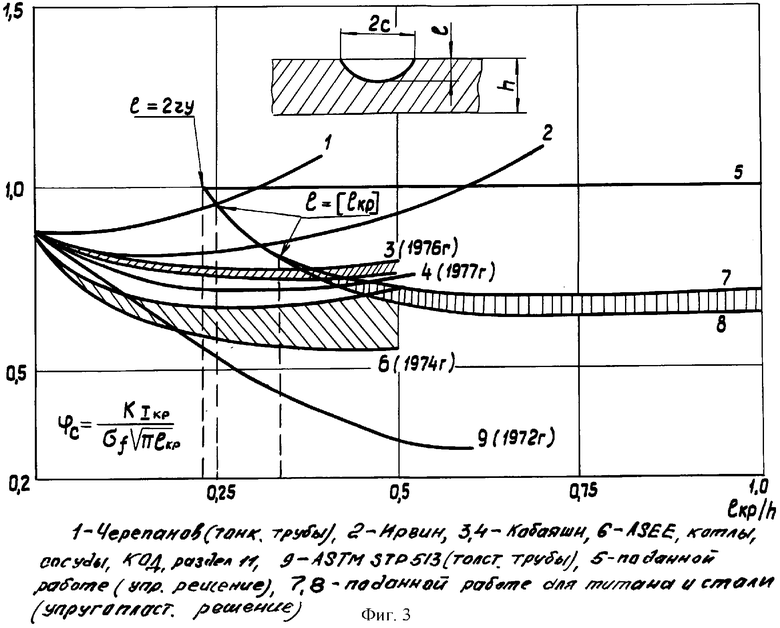
В отечественной и зарубежной практике для учета пластической деформации, геометрических и других факторов используют упражнение с корректирующим множителем KIкр=ϕc·σ+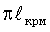 . Результаты сравнения этого уравнения с (4) приведены на фиг.2, 3.
. Результаты сравнения этого уравнения с (4) приведены на фиг.2, 3.
Предпринятый анализ уравнения (7) позволил установить условия деформирования и разрушения на заключительной стадии деформирования оболочки изделия после наступления пластической неустойчивости. Так при
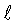 кр.м=2rу получаем Е2=2δ2Е1=const
кр.м=2rу получаем Е2=2δ2Е1=const
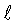 кр.м=0 получаем Е2=δ2Е1=const
кр.м=0 получаем Е2=δ2Е1=const
для всех изделий данного сплава при широком изменении E1
Применяя эти оценки, находим, что при lкр.м=2rу и lкр.м=0 уравнения (2), (4) переходят в известное уравнение
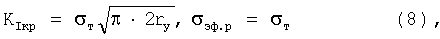
которое совместно с (2) дает критериальное уравнение
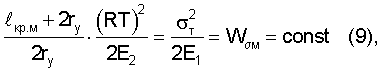
которое согласуется с концепцией плотности энергии деформации и разрушения, выдвинутой σ [4] по уравнению:
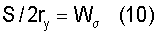 при
при 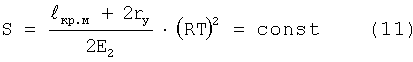
для конкретного контролируемого изделия.
Исходя из концепции плотности энергии деформации и разрушения S определяются параметры нелинейной механики разрушения:
Критический коэффициент вязкости разрушения
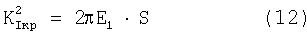
Критический коэффициент интенсивности высвобождения энергии

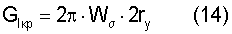
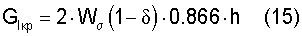
Значение поверхностной энергии
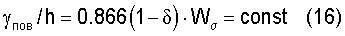
Определяется новое критериальное уравнение
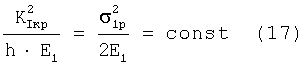
при 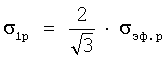
σ1р - разрушающее окружное напряжение.
Или в общем виде:
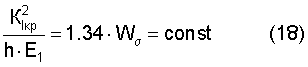
Результаты расчета параметров механики разрушения для цилиндрических корпусов приведены в табл.1
мм
мм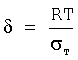
(СП-28)
(СП-28)
(ОТ-4)
(ЧС-ЧВИ)
Перечень исходных положений на этом можно закончить и приступить к обоснованию предлагаемого изобретения.
Основной задачей, которую необходимо решить в предлагаемом изобретении является определение параметров пластической неустойчивости в локальных участках концентраторов напряжений и деформации, обусловленной наличием макроскопических трещиноподобных дефектов. Необходимо определить локальную концентрацию напряжений и деформаций и соответствующие им размеры критических макроскопических дефектов, которые могут расти при повышении локальных напряжений, прежде чем привести к макроскопическому разрушению при номинальных напряжениях в изделии. Для этого принимается, что параметры конечной стадии пластической неустойчивости, возникающей в вершине макроскопической трещины в области, характеризуемой величиной зоны пластической деформации 2rу определяются так же, как при конечной стадии пластической неустойчивости макроскопической оболочки. Для этого рассматриваем процессы высвобождения упругой энергии и развитие критической трещины, при их равной вероятности. Эта ситуация складывается при равенстве времени релаксации этих процессов τу=τе и характеризуется двумя уравнениями [5],
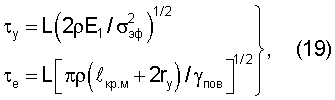
где L - линейная плотность подвижных дефектов, L=PD·a,
a - параметр решетки.
При τу=τe после преобразований (19) с учетом уравнений (5), (6), (16) получаем:
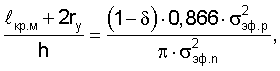
из которого после подстановки выражений для 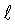 кр.м/h и 2rу/h делаем вывод по уравнению:
кр.м/h и 2rу/h делаем вывод по уравнению:
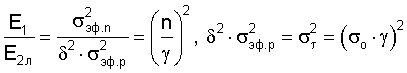 что локальная неустойчивость на макроскопических дефектах характеризуется другим отношением E1/E2л=(n/γ)2 в отличие от отношения этих величин для оболочки изделия, где отношение E1/E2 определяется уравнением
что локальная неустойчивость на макроскопических дефектах характеризуется другим отношением E1/E2л=(n/γ)2 в отличие от отношения этих величин для оболочки изделия, где отношение E1/E2 определяется уравнением
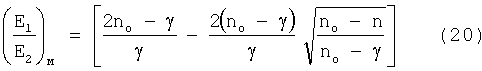
Следовательно, чтобы определить распределение локальных напряжений σл на дефектах в зависимости от номинальных напряжений, необходимо в уравнении (9) изменение текущей пластической деформации определять в зависимости от Е1/Е2л=(n/γ)2.
Текущее значение пластической деформации определяется согласно
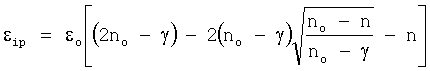
Сравнивая это уравнение с (20) находим, что пластическая и упругопластическая деформации оболочки определяются
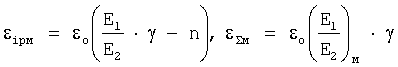
Локальная пластическая и упругопластическая деформации на дефектах εipл, εΣл будут определяться уравнениями:
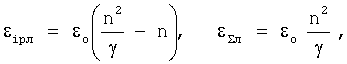
а локальные напряжения на дефектах уравнением:
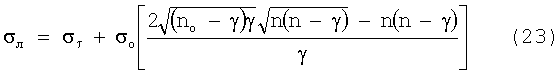
при n=σэф.n/σо, σэф.n - эффективные напряжения в оболочке изделия.
Критические размеры дефектов в зависимости от локальных напряжений σл необходимо определять, так же как и критические дефекты для оболочки по уравнению (2), но с отношением Е1/Е2л, т.е. после его преобразования:
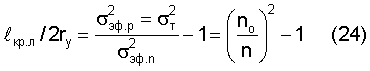
Для обоснования скорости роста локальных и номинальных напряжений в зависимости от времени необходимо взять исходные уравнения (23), (3) и приводимое здесь без вывода уравнение для текущего времени деформирования оболочки, которое является единым для увеличения локальных и номинальных напряжений и отражает постоянство теплового состояния металла.
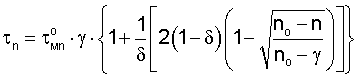
где τo мn - время релаксации упругих напряжений.
Не проводя дифференцирования, отметим, что скорости роста напряжений получены по отношению производных 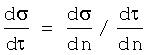 и их уравнения имеют вид:
и их уравнения имеют вид:
для номинальных напряжений σэф.n
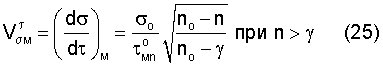
для локальных напряжений σл
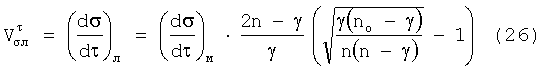
при n>γ
Аналогично можно привести уравнения для скоростей роста напряжения от суммарных деформаций εΣм, εΣл.
для номинального напряжения
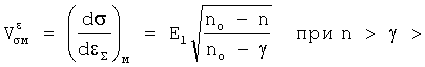
для локальных напряжений
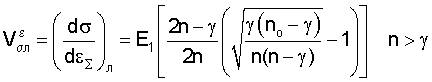
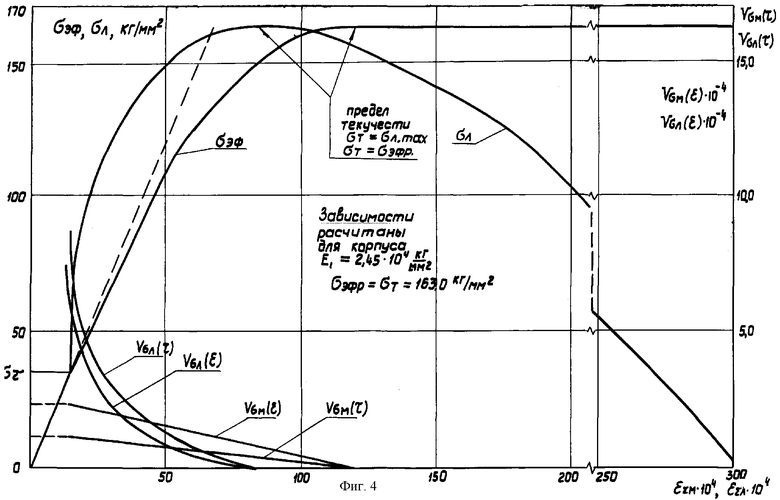
После этого все готово и указанные закономерности можно представить графически. На фиг.4 изображены зависимости σэф.n=f(εΣм), σл=f(εΣл) и изменение четырех скоростей роста напряжений от времени и деформации.
Из фиг.4 видно, что нулевое значение обеих скоростей роста номинального напряжения указывает на максимальное напряжение, равное пределу текучести σт и определяющее пластическую нестабильность оболочки изделия. Нулевое значение двух других скоростей также указывает на максимальное значение концентрации локальных напряжений и пластическую нестабильность в областях, прилегающих к дефектам и численно равную пределу текучести материала σт.
Таким образом полученная закономерность, описываемая рядом уравнений определяет особенность предложенного способа контроля прочности изделий.
Поставленная в формуле изобретения цель - повышение достоверности результатов контроля прочности и расширения перечня диагностических параметров достигается за счет определения зависимости концентрации локальных напряжений на дефектах, позволяющей установить допустимые размеры трещиноподобных дефектов и соответствующие им разрушающие номинальные напряжения оболочки изделий.
Пример практической реализации способа. В качестве примера, подтверждающего новое качество заявленного технического решения, приводим результаты контроля прочности на примере тонкостенного металлического корпуса из высокопрочной стали, представляющего сварную цилиндрическую оболочку диаметром ⊘=209,0 мм и толщиной оболочки h=0,73 мм. В результате нагружения изделия получен эффективный модуль продольной упругости Е1=2.6·105 МПа, структурно-чувствительные параметры и параметры нелинейной механики разрушения, приведенные в таблице 1, пункт 1.
В таблице 2 приведены изменения номинальных и локальных напряжений, определенных по уравнениям (9), (23), и соответствующие им критические размеры дефектов 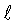 кр.м и
кр.м и 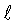 кр.л - рассчитаны по уравнению (2) с соответствующими отношениями (Е1/Е2)м, (Е1/Е2)л. Здесь же приведены упругопластические деформации для номинального и локального состояния, определенные по уравнениям (21), (22)
кр.л - рассчитаны по уравнению (2) с соответствующими отношениями (Е1/Е2)м, (Е1/Е2)л. Здесь же приведены упругопластические деформации для номинального и локального состояния, определенные по уравнениям (21), (22)
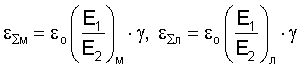
Результаты расчета параметров прочности изделия с толщиной оболочки 0,73 мм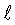 кр.м, мм
кр.м, мм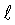 кр.л, мм
кр.л, мм
Прежде чем оценить развитие ситуации из-за наличия в металле изделия макроскопических дефектов необходимо обосновать переход их поведения в локальной и номинальной ситуации. Для этого необходимо преобразовать уравнение (2) для локальной ситуации.
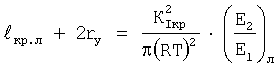
Правую часть этого уравнения представим в ином виде и с учетом уравнения (12) запишем:
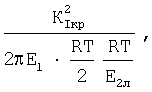
где К2 Iкр/2πЕ1=S - плотность энергии деформации [4],
RT/Е2л=εΣл, а 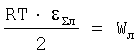 - энергия локальной упругопластической деформации и получаем
- энергия локальной упругопластической деформации и получаем
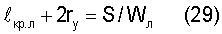
В соответствии с этим для номинальной ситуации:
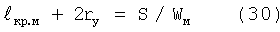
при RT/Е2м=εΣм
Теперь проведем оценку и определим разрушающие номинальные напряжения σэф.f из-за наличия в контролируемом изделии макроскопического дефекта.
Пусть есть первичный трещиноподобный дефект с размером 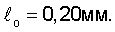 Естественно, в силу опережающего нарастания локальных напряжений (см. табл.2), дефект
Естественно, в силу опережающего нарастания локальных напряжений (см. табл.2), дефект 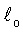 попадает в эту ситуацию и по уравнению (29) подрастает на величину 2rу до
попадает в эту ситуацию и по уравнению (29) подрастает на величину 2rу до 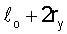 при локальном напряжении σл=149,2 кг/мм2 локализованной энергии при плотности энергии деформации S=8,4·10-2 кг/мм (см. табл.1, п.1).
при локальном напряжении σл=149,2 кг/мм2 локализованной энергии при плотности энергии деформации S=8,4·10-2 кг/мм (см. табл.1, п.1).
Wл=S/(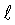 о+2rу)=8,4·10-2/(0,2+0,159)=0,234 кг/мм2
о+2rу)=8,4·10-2/(0,2+0,159)=0,234 кг/мм2
при локализованной упругопластической деформации
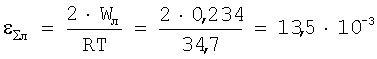
Однако привести к разрушению изделия подрастание 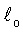 на 2rу не может, так как локальную ситуацию контролируют деформационные процессы в оболочке изделия. Поэтому подросший дефект
на 2rу не может, так как локальную ситуацию контролируют деформационные процессы в оболочке изделия. Поэтому подросший дефект 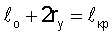 попадает в номинальную ситуацию и ждет, когда в его окрестности наступит необходимое разрушающее напряжение с необходимой упругопластической деформацией εΣм. Эта ситуация развивается по уравнению (30)
попадает в номинальную ситуацию и ждет, когда в его окрестности наступит необходимое разрушающее напряжение с необходимой упругопластической деформацией εΣм. Эта ситуация развивается по уравнению (30)
Wм=S/[(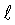 o+2rу)+2rу]=8,4·10-2/0,518=0,162 кг/мм2
o+2rу)+2rу]=8,4·10-2/0,518=0,162 кг/мм2
при 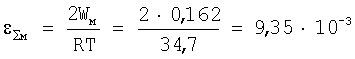 при (Е1/Е2)м по уравнению (2
при (Е1/Е2)м по уравнению (2
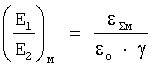
Зная, что для контролируемого изделия εо=3,25·10-5; γ=40,6
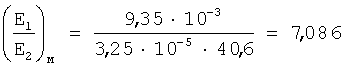
Зная отношение (Е1/Е2)м по уравнению (20), определяем n и номинальное разрушающее напряжение σэф.f, σэф.f=σo·n. Не проводя вычислений, из уравнения (20) определяем n и σэф.f.
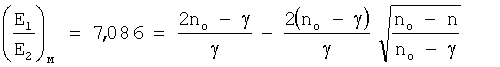
n=189,5, σэф.f=189,5·0,845=160,0 кг/мм2
Таким образом при первичном дефекте 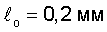 прочность изделия составляет 160,0 кг/мм2 против 165,6 кг/мм2 для бездефектного изделия, что составляет уменьшение прочности на 3,4%. Таким образом можно оценить влияние на прочность любого предлагаемого макроскопического трещиноподобного дефекта или их совокупность для данного контролируемого изделия. Можно установить минимальный размер первичного дефекта, не влияющего на предельную прочность. Для данного изделия таким дефектом является
прочность изделия составляет 160,0 кг/мм2 против 165,6 кг/мм2 для бездефектного изделия, что составляет уменьшение прочности на 3,4%. Таким образом можно оценить влияние на прочность любого предлагаемого макроскопического трещиноподобного дефекта или их совокупность для данного контролируемого изделия. Можно установить минимальный размер первичного дефекта, не влияющего на предельную прочность. Для данного изделия таким дефектом является 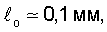 так как прорыв его локальным напряжением на 2rу дает размер дефекта
так как прорыв его локальным напряжением на 2rу дает размер дефекта 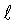 кр.м=0,26 и согласно табл.2 при нем реализуется предельная прочность σэф.р=165,6 кг/мм2. Можно найти максимальный размер первичного дефекта, который после прорыва локальным напряжением приведет к сквозному дефекту, равному толщине стенки. Таким дефектом для данного изделия будет
кр.м=0,26 и согласно табл.2 при нем реализуется предельная прочность σэф.р=165,6 кг/мм2. Можно найти максимальный размер первичного дефекта, который после прорыва локальным напряжением приведет к сквозному дефекту, равному толщине стенки. Таким дефектом для данного изделия будет 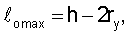
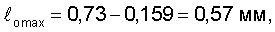 который подрастет до сквозного дефекта при локальном напряжении σл=164,0 кг/мм, что соответствует номинальному напряжению образования сквозного дефекта σэф.f=77,0 кг/мм2.
который подрастет до сквозного дефекта при локальном напряжении σл=164,0 кг/мм, что соответствует номинальному напряжению образования сквозного дефекта σэф.f=77,0 кг/мм2.
Размер сквозного дефекта, но окончательно подрастающего при номинальном напряжении, будет 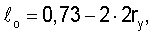
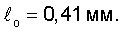 При этом номинальное разрушающее напряжение будет σэф.f=135,0 кг/мм.
При этом номинальное разрушающее напряжение будет σэф.f=135,0 кг/мм.
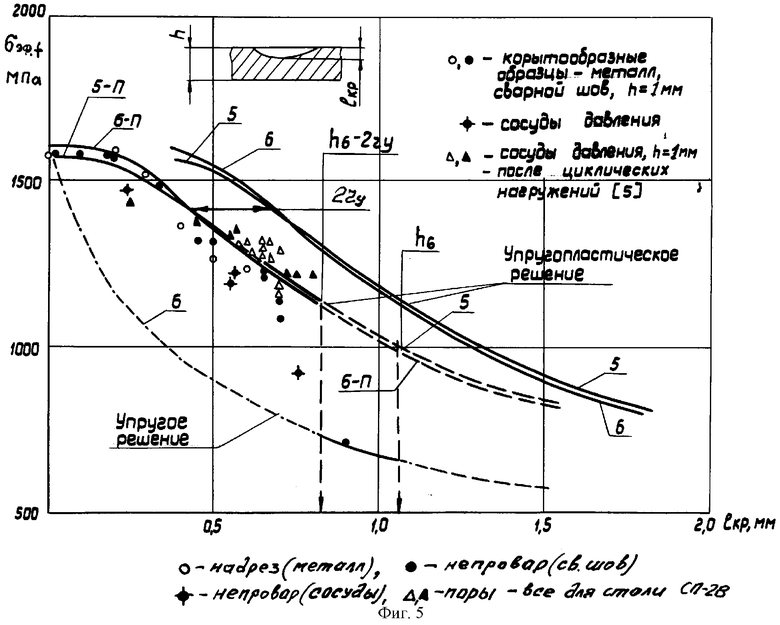
Результаты полной оценки первичных размеров дефектов приведены на фиг.5, где показаны результаты анализа и сравнение их с экспериментом [3] на двух корпусах (см. табл.1, пп.5, 6 с толщиной оболочек h=1,17 мм, и h=1,06). Зависимости с индексом "П" приведены для первичного дефекта, который подрастает при локальных напряжениях и приводит к разрушению при номинальном напряжении. Зависимости без индекса - общее упругопластическое решение и смещены от зависимостей с "П" на величину зоны пластической деформации 2ry по оси 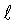 кр.
кр.
В результате определяются две области - интервала по размерам первичных дефектов: первый интервал с нулевого значения первичных дефектов до размера (h-2ry), когда разрушение от их влияния определяется упругопластическим решением; второй интервал с (h-2ry) до 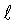 кро=h, когда разрушение определяется величинами только локальных напряжений при упругом решении. В этом заключается выявленная термодинамическая закономерность развития макроскопических дефектов и формирование прочности при их наличии.
кро=h, когда разрушение определяется величинами только локальных напряжений при упругом решении. В этом заключается выявленная термодинамическая закономерность развития макроскопических дефектов и формирование прочности при их наличии.
На основании такого анализа принимаются конкретные решения о размере допустимых дефектов в зависимости от эксплуатационных требований на работу изделия и с фактическими возможностями методов и средств дефектоскопии назначают безопасные коэффициенты запаса прочности.
Практическое значение предлагаемого изобретения заключается в том, что на его основе возможно:
установление оптимальных весовых характеристик изделий из-за возможности установления допустимых коэффициентов запаса прочности с учетом масштабных и геометрических характеристик изделий;
обоснование выбора соответствующих материалов и сплавов при проектировании изделий, представляя предпочтение материалам с большей трещиностойкостью и энергоемкостью за счет развития больших локальных и номинальных упругопластических деформаций;
определение циклической и длительной прочности и планирование необходимого и остаточного ресурса изделий из-за возможного появления неопасных дефектов;
планирование начальной и остаточной надежности изделий, соединение производственных испытаний изделий с системой автоматизированного проектирования изделий и их прочностных расчетов;
возможность переноса метода на развитие кинетики подготовки разрушения других твердых тел, например горных пород и др.
Источники информации
1. Красовский А.Я. и др. Исследование трещиностойкости корпусных сталей при статическом и динамическом нагружении с учетом эффекта масштаба испытуемых образцов / АН УССР. - Ин-т пробл. прочности. Препринт - Киев, 1982.
2. Математические методы в механике разрушения. Дж.Райс. Сб-к "Разрушение", ред. Либовиц. т.2. - М., Мир, 1975, с.280-282.
3. Куркин С.А. Прочность сварных тонкостенных сосудов, работающих под давлением. М., Машиностроение, 1976, 183 с.
4. Миллер К. Ползучесть и разрушение / Иванова B.C. Предисловие к русскому изданию./ М., Металлургия, 1986, С.12-17.
5. Термодинамические аспекты пластического деформирования и разрушения металлов и сплавов. - М., Наука. - 1976, с.170-179.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ПРОЧНОСТИ ИЗДЕЛИЙ | 1987 |
|
RU2297615C2 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ПРОЧНОСТИ ИЗДЕЛИЯ | 1982 |
|
SU1840720A1 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ПРОЧНОСТИ ИЗДЕЛИЙ | 1983 |
|
SU1840508A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РЕСУРСА РАБОТОСПОСОБНОСТИ МЕТАЛЛОВ | 2004 |
|
RU2261436C1 |
| БАЛЛОН ВЫСОКОГО ДАВЛЕНИЯ | 2006 |
|
RU2333417C1 |
| СПОСОБ ГИДРАВЛИЧЕСКОГО ИСПЫТАНИЯ НА УДАР И РЕАБИЛИТАЦИИ ТРУБОПРОВОДА, ОСУЩЕСТВЛЯЕМЫЙ ПРИ ЕГО НАГРУЖЕНИИ ПОВЫШЕННЫМ ДАВЛЕНИЕМ В ПОЛЕВЫХ УСЛОВИЯХ | 2011 |
|
RU2467299C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ СПОСОБНОСТИ ТРУБОПРОВОДА | 2013 |
|
RU2516766C1 |
| Способ оценки циклической трещиностойкости материалов | 1990 |
|
SU1798657A1 |
| Способ неразрушающего контроля качества деталей | 1990 |
|
SU1796985A1 |
| СПОСОБ ПОВЫШЕНИЯ ДОСТОВЕРНОСТИ КОНТРОЛЯ ГЕРМЕТИЧНОСТИ ИЗДЕЛИЙ | 2013 |
|
RU2542684C1 |
Использование: при неразрушающем контроле статической прочности изделий ракетной и авиационной техники. Сущность: нагружают изделие и определяют деформацию и напряжение в сечении с максимальными напряжениями. На изделие навивают несколько витков струны периметромера таким образом, чтобы средний виток был расположен в указанном сечении, а остальные размещают симметрично ему. Определяют интегральную деформацию в сечении, по которой судят об эффективном модуле продольной упругости материала изделия, а прочность вычисляют в соответствии с предлагаемым уравнением. Дополнительно нагружают изделие в упругопластической области через интервалы, кратные разрушающему эффективному напряжению. Фиксируют величину пластической деформации на каждой ступени. При этом о качестве изделия дополнительно судят по сравнению измеренной пластической деформации и рассчитанной в соответствии с расчетной формулой. Нагружение изделия производят до достижения нулевого значения скорости роста напряжений в локальных его зонах. При этом фиксируют напряжение пластической неустойчивости материала. Технический результат изобретения заключается в повышении достоверности результатов контроля. 2 табл., 5 ил.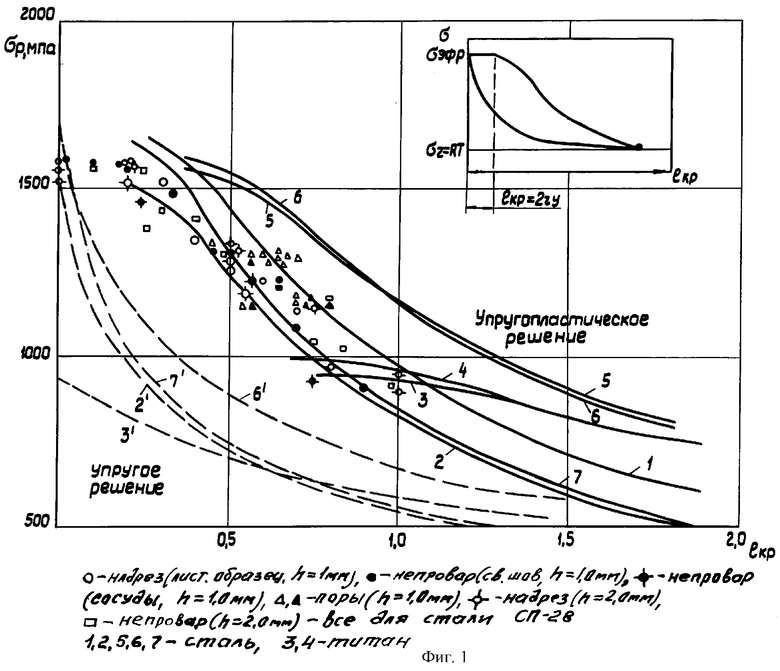
Способ неразрушающего контроля прочности изделий, заключающийся в том, что определяют сечение с максимальными напряжениями, на данное сечение устанавливают струнный периметромер с предварительным натяжением струны, нагружают изделие, определяют деформацию и напряжение в указанном сечении, навивают на изделие несколько витков струны периметромера таким образом, чтобы средний виток был расположен в указанном сечении, а остальные размещают симметрично ему с заданным шагом, определяют интегральную деформацию в сечении, по которой судят об эффективном модуле Еэф продольной упругости материала изделия, а о прочности σр судят по уравнению
σр=к•10-3[(Еэф•RT)1/2-ЕэфαеТ]•(U0/RT),
где к - коэффициент вида напряженного состояния и формы изделия;
R - универсальная газовая постоянная;
Т - температура испытания, К;
αе - коэффициент теплового расширения, 1/К;
U0 - истинная энергия активации разрушения,
определяют нижнюю границу упругопластической области по соотношению σ=RT и равенству частот (n=γ)-й моды поверхностной волны Рэлея и тепловых колебаний атомов, дополнительно нагружают изделие в упругопластической области через интервалы Δσ, кратные разрушающему эффективному напряжению σэф.р, фиксируют величину пластической деформации на каждой ступени, при этом о качестве изделия дополнительно судят по сравнению измеренной пластической деформации и рассчитанной εip по формуле
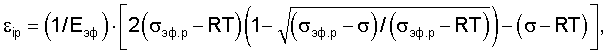
где σ - текущее эффективное напряжение,
нагружение изделия производят до достижения нулевого значения скорости роста напряжений в локальных его зонах, фиксируя при этом напряжение пластической неустойчивости материала, по которому судят о концентрации напряжения на дефектах в упомянутой зоне.
| Сопособ неразрушающего контроля прочности изделий | 1974 |
|
SU606124A1 |
| Способ неразрушающего контроля прочности изделий | 1978 |
|
SU932352A1 |
Авторы
Даты
2007-04-20—Публикация
1989-02-03—Подача