Изобретение относится к неразрушающему контролю прочности, живучести изделий ракетной и авиационной техники и может быть использовано при неразрушающем контроле статической прочности тонкостенных металлических изделий, например полых тел вращения (газонефтепроводов, цилиндрических, конических, сферических резервуаров, теплообменников и т.п.) в различных отраслях народного хозяйства. Изобретение может быть полезно для определения длительной прочности при заданном ресурсе, анализе процессов релаксации, ползучести, формировании под нагрузкой микроскопических коротких трещин, определяющих кинетику развития и размеры критических трещин.
Перечень возможных приложений нового технического решения основан на закономерности формирования упругопластической деформации исходя из закона сохранения энергии и стадийной самоорганизации диссинативных структур при деформировании твердого тела с учетом ангармонизма тепловых колебаний атомов.
В настоящее время техника оценки прочности изделий основана на 100%-ных испытаниях эксплуатационной нагрузкой и выборочных испытаниях до разрушения одного или двух изделий от партии. Выборочные испытания основаны на теории вероятности и даже при малых партиях (до 10 штук) имеют низкую надежность при оптимальных коэффициентах запаса прочности.
Технический результат изобретения заключается в повышении достоверности результатов контроля статической прочности и расширение контрольных нагрузок в области упругопластического деформирования.
Технический результат достигается за счет того, что определяют сечение с максимальными напряжениями, на данное сечение устанавливают струнный периметромер с предварительным натяжением струны, нагружают изделие, определяют деформацию и напряжение в указанном сечении, навивают на изделие несколько витков струны периметромера таким образом, чтобы средний виток был расположен в указанном сечении, а остальные размещают симметрично ему, с заданным шагом, определяют интегральную деформацию в сечении, по которой судят об эффективном модуле Еэф продольной упругости материала изделия, а о прочности σр судят по уравнению
σр=к·10-3[(Еэф·RT)1/2-ЕэфαеТ]·(U0/RT),
где к - коэффициент вида напряженного состояния и формы изделия;
R - универсальная газовая постоянная;
Т - температура испытания, К;
αе- коэффициент теплового расширения, 1/К;
U0 - истинная энергия активации разрушения,
определяют нижнюю границу упругопластической области по соотношению σ=RT и равенству частот (n=γ)ой моды поверхностной волны Рэлея и тепловых колебаний атомов, дополнительно нагружают изделие в упругопластической области через интервалы Δσ, кратные разрушающему эффективному напряжению σэф.р, фиксируют величину пластической деформации на каждой ступени, при этом о качестве изделия дополнительно судят по сравнению измеренной пластической деформации и рассчитанной εip по формуле
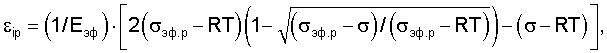
где σ - текущее эффективное напряжение.
Способ основан на том, что теоретически и экспериментально удалось определить точную физическую границу по напряжению и деформации между областями упругого и упругопластического деформирования и придать ей точные физические характеристики как на макроуровне, так и на уровне связи двух атомов. Найденная физическая граница не только ниже известного в настоящее время предела текучести, но значительно ниже известного предела пропорциональности. Способ основан на том, что достигнутый уровень знаний позволяет описать весь диапазон напряженно-деформируемого состояния общими уравнениями, отражающими физическую закономерность, связывающую области упругого и упругопластического деформирования. Рассмотрение всех стадий деформирования металла на единой основе стало возможным после теоретического и экспериментального обоснования того, что параметры чисто упругой деформации контролируют и определяют параметры и величины пластической деформации. Естественно, что фундаментальной основой защищаемого технического решения является уравнение состояния твердого деформируемого тела:
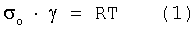
или после раскрытия неопределенности σo·γ=const на основе основного уравнения I и II законов термодинамики ТΔS≥ΔU+ΔL уравнение состояния в общем виде:
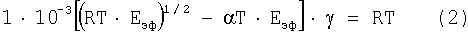
где σo - единичная порция макроскопического напряжения,
γ - относительный активационный объем (число атомов в линейной цепочке активационного объема)
Из уравнений (1) (2) вытекает, что эффективное разрушающее напряжение определяется
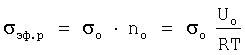
При приложении к изделию единичного напряжения σо возникает единичная порция макроскопической упругой деформации εо, следовательно, текущая упругая деформация определяется:
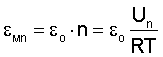
Непосредственно из уравнения (2) при
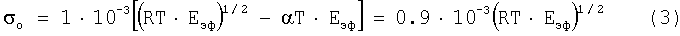
получается уравнение для εо
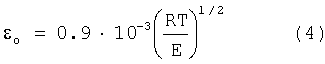
которое при (RT/ρ)1/2=VR1, (E/ρ)1/2=VL записывается
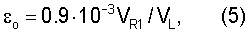
где VR1 - скорость распространения первой нормальной моды поверхностной волны Рэлея,
VL - скорость упругой продольной волны.
Исходя из условия квантования RT·n=Un, (Un - текущая энергия активации на уровне связи двух атомов), получаем периодическое изменение скоростей волны Рэлея
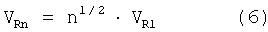
Отсюда при n=no, Un=Uo получаем выражение для известной максимальной скорости рэлеевской волны
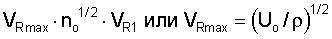
Отметим, что длина волны первой нормальной моды волны Рэлея равна 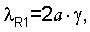 а для всех последующих мод
а для всех последующих мод 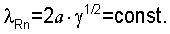 Следовательно, изменение частот рэлеевской волны определяется уравнением
Следовательно, изменение частот рэлеевской волны определяется уравнением
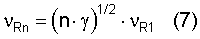
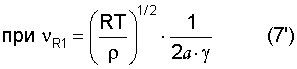
Из уравнения (4) с учетом 0.9·10-3=υR1/υL получаем, что единичная деформация определяется уравнением
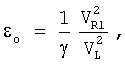
которое с учетом уравнения (6) дает текущее значение упругой деформации
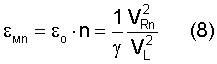
При умножении уравнения (8) на γ получаем уравнение для флуктуации упругой деформации на уровне связи двух атомов:
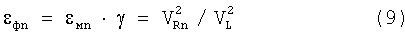
При умножении числителя и знаменателя первой части уравнения (9) на ρ получим уравнение закона Гука для флуктуации упругой деформации на уровне связи двух атомов
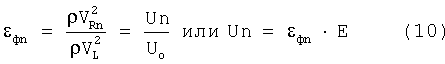
которые для предельного состояния при Un=Uo, εфn=εф.р имеют выражение
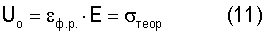
Приведенные выше теоретические уравнения однозначно утверждают, что формирование макроскопической упругой деформации обеспечивают флуктуации упругой деформации на уровне связи двух атомов по уравнению (10) за счет взаимодействия двух волн (L, R), возникающих при воздействии на металл градиента внешней энергии, с решающим влиянием на их взаимодействие тепловых колебаний атомов.
Таким образом, согласно уравнениям, формирование упругой деформации и возрастание напряжения определяются возрастанием числа "n" в интервале 1≤n≤Uo/RT, о чем утверждает уравнение (I). Уравнение (I) утверждает, что если к твердому телу прикладывается единичная, порция макронапряжения σо, то на уровне связи двух атомов увеличивается (локализуется) удельная потенциальная энергия, равная RT, которая за счет термической флуктуации вызывает флуктуацию упругой деформации связи, с удлинением последней, на величину амплитуды тепловых колебаний атомов 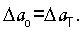 Удлинение связи
Удлинение связи 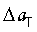 за счет продольных упругих волн, характеризующихся Еэф, рассасывается на все связи линейного активационного объема, содержащего γ атомов
за счет продольных упругих волн, характеризующихся Еэф, рассасывается на все связи линейного активационного объема, содержащего γ атомов 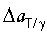 и формирует первую порцию макроскопической упругой деформации
и формирует первую порцию макроскопической упругой деформации
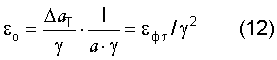
Описанный элементарный процесс продолжается при n=1,2,3...γ и обеспечивает такое состояние, когда на каждую связь будет уложена потенциальная энергия, равная RT, что должно прекратить тепловой колебательный процесс атомов в активационной цепочке 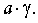 Однако этого не происходит, так как металл включает запасной релаксационный механизм за счет возникновения новых микроскопических дефектов и сдвиговых деформаций. В этом случае напряжение в активационной цепочке уменьшится, и она будет готова принимать новую порцию удельной энергии RT. Поэтому макроскопическое напряжение, при котором возникает такая ситуация, является пороговым напряжением, разделяющим области упругой и упругопластической деформации. Оно равно σr=σo·n, при n=γ, στ=RT. Рассматривая при n=γ уравнения (7) и (7') с учетом
Однако этого не происходит, так как металл включает запасной релаксационный механизм за счет возникновения новых микроскопических дефектов и сдвиговых деформаций. В этом случае напряжение в активационной цепочке уменьшится, и она будет готова принимать новую порцию удельной энергии RT. Поэтому макроскопическое напряжение, при котором возникает такая ситуация, является пороговым напряжением, разделяющим области упругой и упругопластической деформации. Оно равно σr=σo·n, при n=γ, στ=RT. Рассматривая при n=γ уравнения (7) и (7') с учетом 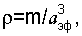 получим условие равенства частот (n=γ)-ой нормальной моды поверхностной волны Рэлея и тепловых колебаний атомов:
получим условие равенства частот (n=γ)-ой нормальной моды поверхностной волны Рэлея и тепловых колебаний атомов:
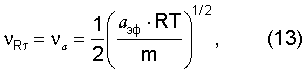
где 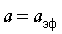 - эффективное межатомное расстояние,
- эффективное межатомное расстояние,
m - эффективная масса атома.
Частота тепловых колебаний атомов не зависит от эффективного модуля продольной упругости Eэф и для сплавов железа имеет при комнатной температуре постоянную величину 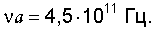
Таким образом установлено, что пороговое напряжение, разделяющее области упругой и упругопластической деформации στ=RT. Это напряжение характеризуется равенством частот (n=γ)-ой нормальной моды поверхностной волны Рэлея и тепловых колебаний атомов.
Отношение напряжения на границе двух областей и разрушающего напряжения - есть фундаментальное отношение для макроскопического и микроскопического уровней:
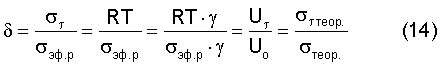
Для решения задачи по формированию упругопластической деформаций при σ>στ=RT воспользуемся известным формализованным математическим аппаратом, учитывающим ангармонизм тепловых колебаний атомов. Примем, что внешняя сила, преодолевающая силу межатомного взаимодействия, определяется уравнением
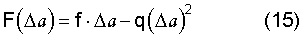
где f - коэффициент упругости связи;
q - коэффициент ангармонизма.
В соответствии с теоретическими положениями на фиг.1 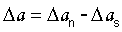 включает в себя упругопластическую деформацию и рассматривается в интервале растягивающей силы:
включает в себя упругопластическую деформацию и рассматривается в интервале растягивающей силы: 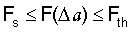
Кроме того, сила Fs соответствует напряжению στ=RT и указывает на нулевой уровень пластической деформации; 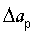 - предельное удлинение межатомной связи при разрушающей флуктуации упругой деформации,
- предельное удлинение межатомной связи при разрушающей флуктуации упругой деформации, 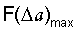 соответствует разрушению металла изделия. Коэффициент ангармонизма при производной
соответствует разрушению металла изделия. Коэффициент ангармонизма при производной 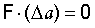 определяется выражением
определяется выражением
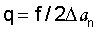
Подставляя (16) в (15) и деля вое на 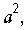 с учетом
с учетом 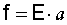 получим:
получим:
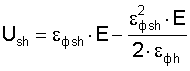
Энергия Ush рассматривается как Ush=Uo-Uτ=Uo-RT·γ
Примем, что величина εфh пропорциональна предельной флуктуации упругой деформации на связи в гуковском приближении без учета антагонизма в соответствии с уравнением (II)
εфh=Kεф.р.=KUо/Е
Решая квадратное уравнение относительно εфsh, в интервале Uо-Uτ,получим
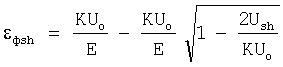
Для определения К необходимо, чтобы выражение под квадратным корнем было равно нулю при Ush=Uo-Uτ. С учетом уравнения (14) получим:
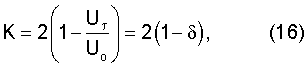
которое определяет начало проявления ангармонизма и возникновение пластической деформации.
В окончательном виде уравнение для текущего значения εфsh
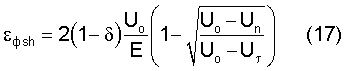
где Un - текущее значение энергии активации на уровне связи.
В уравнении (17): εфsh=εфΣ-εфτ, Uo=σэф.р·γ, σэф.n·γ=Un, RT·γ=Uτ. Уравнение (17) при Un=σэф.n·γ запишем для текущего значения эффективного напряжения:
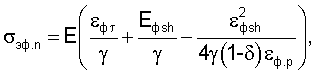
а с учетом выражений εфsh, εфр, Uo, Un, Uτ записать выражения для текущей упругопластической деформации:
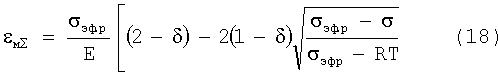
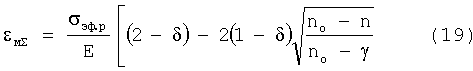
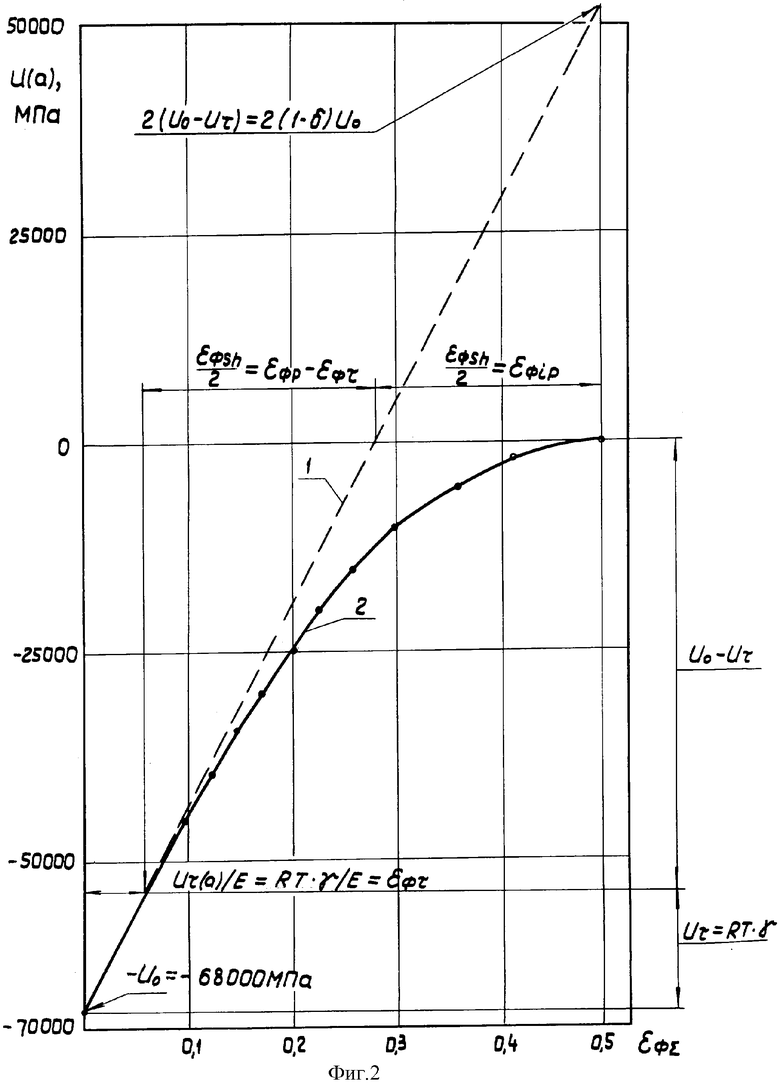
Полученные уравнения (17), (18), (19) определяют, что параметры чисто упругой деформации однозначно определяют кинетику формирования упругопластической деформации. Кроме того, эти уравнения дают возможность по результатам предварительного нагружения изделия в области упругой деформации при σ≤RT с определением Eэф, δ, Uτ построить интегральную зависимость изменения энергии связи двух атомов 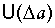 при увеличении растягивающей силы
при увеличении растягивающей силы 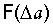 - фиг.2 и истинную зависимость (σэфn-ε) - фиг.3. Графическая интерпритация уравнения (17) - фиг.2 и уравнения (18) - фиг.3 показывает соотношения между упругой и пластической деформациями. Так, при Un-Uo,
- фиг.2 и истинную зависимость (σэфn-ε) - фиг.3. Графическая интерпритация уравнения (17) - фиг.2 и уравнения (18) - фиг.3 показывает соотношения между упругой и пластической деформациями. Так, при Un-Uo, 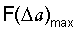 получаем из уравнения (17)
получаем из уравнения (17)
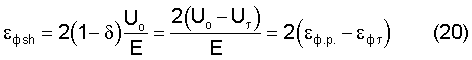
εфsh/2=εф.р.-εфτ
По уравнению (20) устанавливаем, что первая половина εфsh/2 определяет разность упругой деформации; вторая половина определяет фиктивную часть, которая имеет другую природу ее формирования и определяет компаненту необратимой пластической деформации. При нагружении изделия от нуля до разрушения предельная величина εф∑ х определяется по уравнению (20) плюс предельное значение εфτ
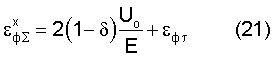
Если все в (21) разделить на 2γ, то получаем предельную величину макроскопической пластической деформации
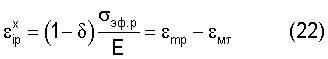
которая равна разности между предельной упругой деформацией и упругой деформацией при στ=RT. Суммарная упругопластическая деформация равна
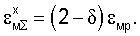
Итак установлено, что текущая величина пластической деформации определяется как разность между текущими значениями упругопластической и упругой деформациями
εip=εm∑-εmn, εmn=σэф.n/E
На этом основании с учетом уравнения (18) запишем основное уравнение для текущего значения пластической деформации

Полученное уравнение (23) определяет завершающую особенность предложенного способа контроля прочности изделий.
Поставленная в изобретении цель - повышение достоверности контроля прочности - достигается за счет контроля процесса испытаний изделий путем сравнения измеренных величин пластической деформации с величинами пластической деформации, рассчитываемых по уравнению (23), с использованием параметров, полученных в области упругой деформации и текущего напряжения в упругопластической области деформирования.
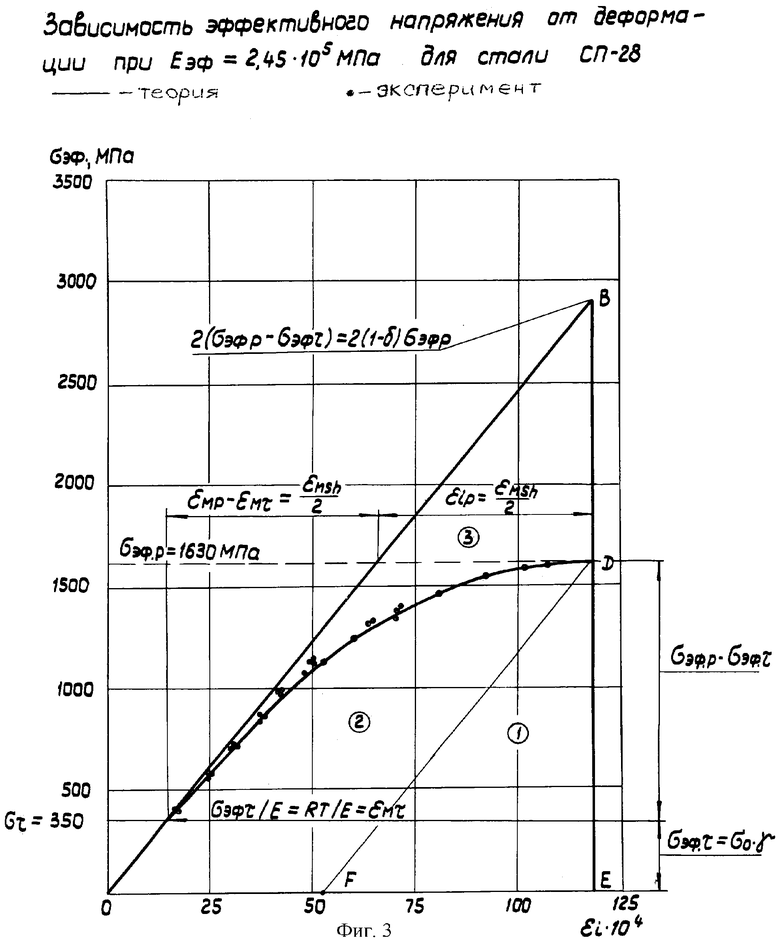
Пример практической реализации способа. В качестве примера, подтверждающего новое качество заявленного технического решения, приводим результаты контроля прочности тонкостенного металлического корпуса из высокопрочной стали, представляющего сварную цилиндрическую оболочку с σв≥1600 МПа. В результате нагружения изделия на участке число упругой деформации в интервале напряжения (170≤σ≤350) МПа получен эффективный модуль предельной упругости Еэф=2,45·105 МПа на основании которого определены структурно-чувствительные параметры металла изделия: σо=8,3 МПа, εо=3,39·10-5, γ=41,8, α=12,5·10-61/град, σэф.р=1630 МПа с отношением δ=RT/σэф.р=0,213.
Результаты испытания изделия, сравнения теоретических и экспериментальных параметров упругопластической деформации приведены в таблице I.
Анализ приведенных упругопластических параметров, полученных экспериментально и определенных теоретически, указывает на хорошую их сходимость, что подтверждает достоверность заявленного способа. Расхождение пластической деформации при напряжениях σ=(690-776)МПа связано с переходной областью напряжений, когда в осевом направлении изделия возникает пластическая деформация из условия σ2/σ1=0.5. Однако уровень пластической деформации в этой области напряжений составляет от 4,5 до 6,0% от суммарной деформации. Невысокая точность уровней пластической деформации при напряжениях σ=(430-517) МПа обусловлена тем, что ее уровень находится на пределе чувствительности датчика измерения деформации ˜2·10-6.
Результаты испытаний изделия и параметры упругопластической деформации
n
εipэ-εipт
εipэ×100%
εмn=σэф.n/Eэф
(23)
В приведенном примере рассматриваются результаты испытаний одного изделия. Для подкрепления результатов на фиг.3 нанесены экспериментальные значения деформации в окружном направлении цилиндрического корпуса, полученные при испытании подобных и других корпусов из высокопрочной стали, которые имели Еэф≈2.45·105 МПа.
В настоящее время в стране и за рубежом интенсивно разрабатывается новый критерий прочности материала - критерий предельной плотности энергии деформации. Поскольку эта энергия является удельной, то она не должна зависеть от условий нагружения и, следовательно, ее можно использовать при решении различных инженерных задач прочности. Суммарную поглощенную энергию w на единицу объема, необходимую для разрушения, рассматривают как состоящую из энергии упругой деформации (we), энергии пластической деформации (wс) и энергии (ws), необходимой для распространения дефектов. Представленное теоретическое обоснование с привлечением результатов испытаний в упругой области дает возможность определить все предельные значения рассмотренных видов удельной энергии в соответствии с текущей и предельной термодинамикой (фиг.3). Так, площадь FDE (1) - изменение потенциальной (свободной) энергии ΔF=We, площадь ODE (2) - энергия пластической деформации - Wc, площадь ОВД (3) - удельная диссипативная энергия - Ws, определяющая процесс образования микроскопических дефектов, площадь ОВЕ - изменение внутренней энергии ΔU в соответствии с основным уравнением термодинамики:
TΔS=ΔU-ΔF, где T·ΔS=Ws+Wc
Все виды удельных энергий связаны с энергией активации разрушения на отрыв - Uo=σтеор.
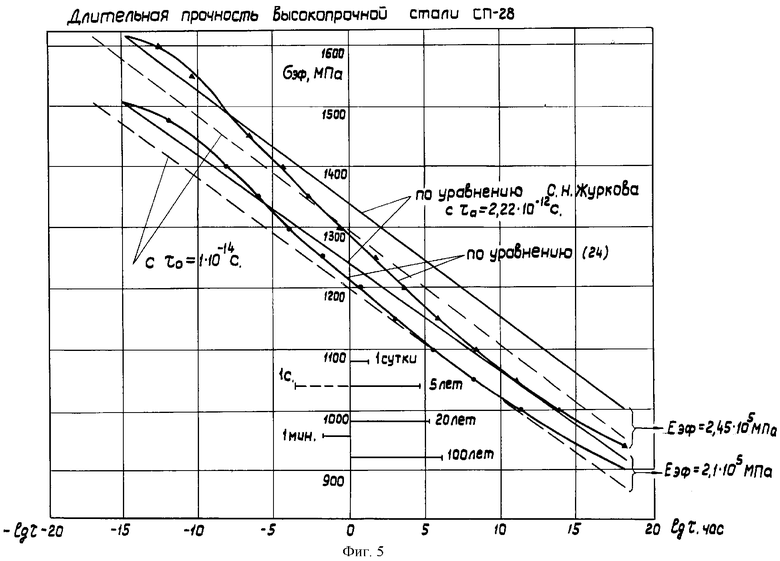
Уравнение длительной прочности С.Н.Журкова
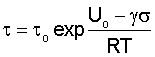
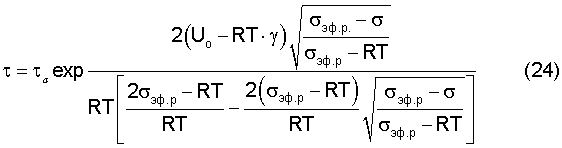
основанное на уравнении Арениуса цепных реакций, стимулировало многочисленные исследования кинетики термофлуктуационных представлений накопления повреждений в напряженном материале. Однако это уравнение не отражает ангармонизма тепловых колебаний атомов и в области эксплуатационных напряжений дает завышенную долговечность. Иная получается картина, когда при постоянном напряжении происходит термофлуктуационное накопление предельной величины упругопластической деформации. На основании приведенных теоретических положений получено уравнение длительной прочности с учетом ангармонизма тепловых колебаний атомов (с учетом пластической деформации):
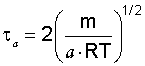 - период тепловых колебаний атомов
- период тепловых колебаний атомов
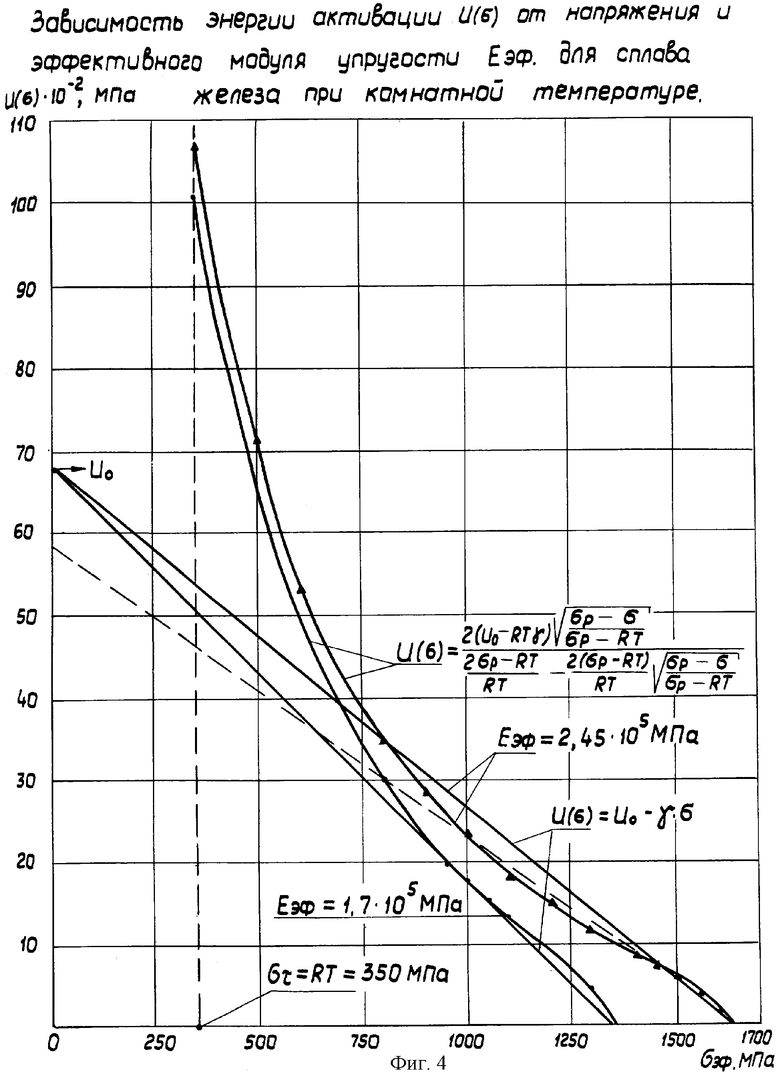
Уравнение (24) резко меняет длительную прочность в сторону ее уменьшения, так как энергия активации
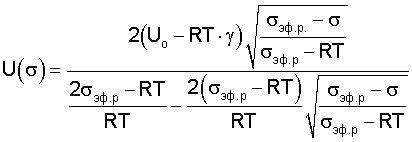
становится меньше, чем энергия активации по С.Н.Журкову
U(σ)=Uo-γσ
Это наглядно представлено на фиг.4, 5 и согласуется с результатами натурных испытаний. Кроме того, например τo в уравнении С.Н.Журкова принимается в интервале от 1·10-14 до 1·10-13 с, чтобы более приблизить расчет по эмпирическому уравнению к экспериментальным результатам, которые дают τo˜1·10-12c. Установлено, что τо в уравнении (24) должно быть равно периоду тепловых колебаний атомов, который при комнатной температуре 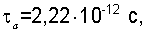 независимо от Еэф. При этом относительный активационный объем γ остается постоянным.
независимо от Еэф. При этом относительный активационный объем γ остается постоянным.
Практическое значение изобретения заключается в том, что на его основе возможно решение следующих практических инженерных задач:
расширение информативности контрольных испытаний изделий за счет определения комплекса деформационно-прочностных характеристик, определение стадийности упругопластической деформации и подобия физико-механических параметров, определяющих границы смены диссипативных структур;
определение текущих и предельных значений удельных значений диссипативной энергии, энергии пластической деформации, свободной (потенциальной) энергии и как их сумму, изменение внутренней энергии в полном соответствии с I и II законами термодинамики;
уточнение основного уравнения термофлуктуационной кинетики разрушения материала с учетом ангармонизма тепловых колебаний атомов (с учетом пластической деформации).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ПРОЧНОСТИ ИЗДЕЛИЙ | 1989 |
|
RU2297616C2 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ПРОЧНОСТИ ИЗДЕЛИЙ | 1983 |
|
SU1840508A1 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ПРОЧНОСТИ ИЗДЕЛИЯ | 1982 |
|
SU1840720A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЗАПАСА ПРОЧНОСТИ НАГРУЖЕННОГО МАТЕРИАЛА | 1998 |
|
RU2167421C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АДГЕЗИОННОЙ ПРОЧНОСТИ ТОНКИХ НАПРЯЖЕННЫХ ПОКРЫТИЙ НА ИЗДЕЛИИ | 2023 |
|
RU2810152C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ | 1999 |
|
RU2146818C1 |
| СПОСОБ ОЦЕНКИ И ПРОГНОЗИРОВАНИЯ ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЙ В ДЕТАЛЯХ ОРГАНИЧЕСКОГО ОСТЕКЛЕНИЯ ПРИ ЛЕТНЫХ ИСПЫТАНИЯХ ВЫСОКОСКОРОСТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА | 2007 |
|
RU2334968C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРЕДЕЛА ВЫНОСЛИВОСТИ МАТЕРИАЛА ПРИ РАСТЯЖЕНИИ-СЖАТИИ | 2015 |
|
RU2599069C1 |
| СПОСОБ ПРОИЗВОДСТВА ТРУБНЫХ МЕТАЛЛОИЗДЕЛИЙ ТЕПЛОВЫДЕЛЯЮЩИХ ЭЛЕМЕНТОВ АТОМНЫХ РЕАКТОРОВ | 2018 |
|
RU2707249C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ СИЛЫ ВНУТРЕННЕГО ТРЕНИЯ ДЛЯ МУЛЬТИАКСИАЛЬНЫХ ТКАНЕЙ | 2011 |
|
RU2467327C1 |
Использование: при неразрушающем контроле статической прочности изделий ракетной и авиационной техники. Сущность: нагружают изделие и определяют деформацию и напряжение в сечении с максимальными напряжениями. На изделие навивают несколько витков струны периметромера таким образом, чтобы средний виток был расположен в указанном сечении, а остальные размещают симметрично ему. Определяют интегральную деформацию в сечении, по которой судят об эффективном модуле продольной упругости материала изделия, а прочность вычисляют в соответствии с предлагаемым уравнением. Дополнительно нагружают изделие в упругопластической области через интервалы, кратные разрушающему эффективному напряжению. Фиксируют величину пластической деформации на каждой ступени. При этом о качестве изделия дополнительно судят по сравнению измеренной пластической деформации и рассчитанной в соответствии с расчетной формулой. Технический результат изобретения заключается в повышении достоверности результатов контроля. 1 табл., 5 ил.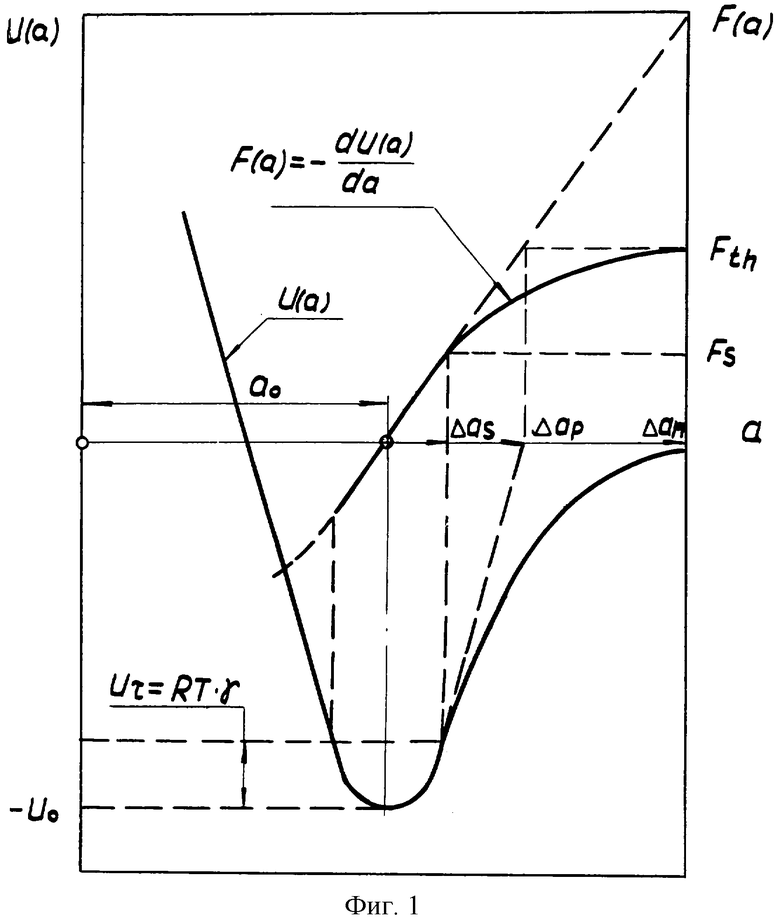
Способ неразрушающего контроля прочности изделий, заключающийся в том, что определяют сечение с максимальными напряжениями, на данное сечение устанавливают струнный периметромер с предварительным натяжением струны, нагружают изделие, определяют деформацию и напряжение в указанном сечении, навивают на изделие несколько витков струны периметромера таким образом, чтобы средний виток был расположен в указанном сечении, а остальные размещают симметрично ему с заданным шагом, определяют интегральную деформацию в сечении, по которой судят об эффективном модуле Еэф продольной упругости материала изделия, а о прочности σр судят по уравнению
σр=к•10-3[(Еэф•RT)1/2-ЕэфαеТ]•(U0/RT),
где к - коэффициент вида напряженного состояния и формы изделия;
R - универсальная газовая постоянная;
Т - температура испытания, К;
αе- коэффициент теплового расширения, 1/К;
U0 - истинная энергия активации разрушения,
определяют нижнюю границу упругопластической области по соотношению σ=RT и равенству частот (n=γ)-й моды поверхностной волны Рэлея и тепловых колебаний атомов, дополнительно нагружают изделие в упругопластической области через интервалы Δσ, кратные разрушающему эффективному напряжению σэф.р, фиксируют величину пластической деформации на каждой ступени, при этом о качестве изделия дополнительно судят по сравнению измеренной пластической деформации и рассчитанной εip по формуле
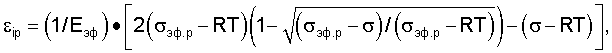
где σ - текущее эффективное напряжение.
| Сопособ неразрушающего контроля прочности изделий | 1974 |
|
SU606124A1 |
| Способ неразрушающего контроля прочности изделий | 1978 |
|
SU932352A1 |
Авторы
Даты
2007-04-20—Публикация
1987-04-03—Подача