Изобретение относится к неразрушающему контролю качества и физико-механических параметров и изделий ракетной и авиационной техники и может быть использовано при неразрушающем контроле прочности тонкостенных металлических изделий, например полых тел вращения (газо-нефтепроводов, цилиндров, конусов, сфер, резервуаров и т.п.) в различных отраслях народного хозяйства.
В настоящее время технология оценки прочности изделий основана на 100%-ых контрольно-технологических испытаниях эксплуатационной нагрузкой при нормальной температуре и последующих выборочных испытаниях до разрушения одного или нескольких изделий от партии. Выборочные испытания обоснованы только при значительных коэффициентах запаса прочности, кроме того их проводят тоже при нормальной температуре.
Известен способ неразрушающего контроля прочности изделий из полимерных материалов, который заключается в определении места возможных максимальных деформаций, возбуждении в этих местах перпендикулярно поверхности изделия упругих колебаний, длина волны которых больше толщины изделия, и измерении времени распространения упругих колебаний на контролируемом участке изделия без нагружения и при нагружении, после чего о деформации судят по относительному изменению времени распространения упругих колебаний, а прочность рассчитывают по математической зависимости, сравнивая данные контролируемого изделия с данными эталона [1]. Основным недостатком такого способа является низкая точность определения прочности, большая длительность измерений и обработки результатов. Кроме того, в этом способе не учитывается в полном объеме влияние всех участков изделия на поведение материала в контролируемой зоне.
Близким по технической сущности является способ оценки прочности [2], суть которого заключается в том, что в контролируемом изделии предварительно определяют сечение с максимальным напряжением и устанавливают на него струнный периметр, который измеряет увеличение длины окружности в процессе роста нагрузки. Способ основан на определении пластической деформации в контролируемом сечении, по которой судят о предельной прочности изделия.
Основным недостатком такого способа является необходимость контроля (нагружения изделия) при напряжении на 10-15% превышающем предел текучести, что является практически недопустимым.
Наиболее близким по технической сущности и достигаемому эффекту к заявляемому является способ неразрушающего контроля прочности. Способ заключается в том, что на сечение с максимальным напряжением навивают по меньшей мере и три витка (центральный н пару дополнительных), изделие нагружают механической нагрузкой, определяют интегральную деформацию и эффективный модуль продольной упругости, а о истинной прочности изделия судят по уравнению. Хотя данный способ позволяет определить предельную прочность с высокой точностью при температурах отличных от нормальной, реализация такой технологии при этих условиях вызывает большие технические трудности, так как требует создания дорогой производственной оснастки, которая бы совмещала необходимость поддержания требуемой температуры и постоянно растущей внешней нагрузки. Кроме того, необходимо разделять суммарную деформацию на силовую и температурную, если струна периметрометра устанавливается до создания требуемой температуры.
Целью настоящего изобретения является упрощение технологии испытаний. Эта цель достигается за счет того, что изделие в заданном диапазоне температур нагревают (охлаждают) с постоянной скоростью изменения температуры на его поверхности, измеряют текущие значения тепловой деформации с помощью термостабилизированной по длине струны периметрометра, а о предельной прочности судят по уравнению
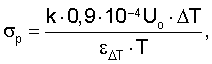
где εΔТ - текущее значение тепловой деформации,
ΔТ - приращение температуры поверхности изделия,
Т - абсолютная температура, K,
Uo - истинная энергия активации разрушения,
k - коэффициент вида напряженного состояния и формы изделия.
Отличительная особенность способа основана на независимости способа постоянного подвода к изделию градиента энергии, зондирующего реально сформированную кристаллическую решетку (структуру) материала. Так, если в способе-прототипе градиент энергии создается изменением внешней механической нагрузки при постоянной температуре, то в заявляемом способе необходимо обеспечить изменение градиента температуры при постоянном или нулевом напряжении в оболочке изделия.
Независимость способа подвода к изделию зондирующей энергии устанавливается уравнением состояния твердого тела
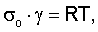 (1)
(1)
где комбинируя параметры σo (силовой фактор) и Т (температурный фактор), можно обосновать два способа контроля прочности: первый - прототип, второй - является предметом предлагаемого изобретения.
Другой отличительной особенностью способа является условие возбуждения двух типов волн в окружном направлении контролируемого изделия (поверхностная волна Рэлея и продольная упругая волна). Отличительная особенность возбуждения продольной волны и определенной нормальной моды поверхностной волны Рэлея заключается в поддержании постоянной скорости нагрева (охлаждения) на поверхности изделия с целью корректного определения коэффициента линейного расширения и связанной с ним тепловой деформации.
Для подтверждения законности отличительного признака в предлагаемом изобретении необходимо показать, что при условии dT/dτ=const возбуждается определенная нормальная мода поверхностной волны Рэлея и продольная волна. Математическое выражение условия возбуждения двух типов волн можно получить из известного уравнения Аррениуса τ=τoexp(-A/RT) или уравнения С.Н.Журкова 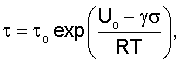 если из выражения для температуры
если из выражения для температуры 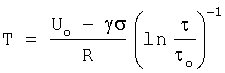 взять вторую производную и приравнять ее нулю на том основании, что скорость роста температуры на поверхности изделия постоянная dT/dτ=const. После математических преобразований получается условие возбуждения двух типов волн
взять вторую производную и приравнять ее нулю на том основании, что скорость роста температуры на поверхности изделия постоянная dT/dτ=const. После математических преобразований получается условие возбуждения двух типов волн
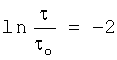 или
или 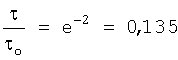
Примем пока без доказательства (ниже оно будет приведено),
что τ=τL - период колебаний атомов в продольной волне,
τо=τRn - период колебаний атомов n-ой нормальной моды поверхностной волны Рэлея. В окончательном виде условие возбуждения двух типов волны можно записать:
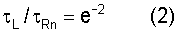
Для доказательства правомочности условия возбуждения двух типов волн необходимо определить номер нормальной моды поверхностной волны Рэлея при условии нагревания (охлаждения) изделия при dT/dτ=const. Кроме того, необходимо показать квантование нормальных мод поверхностной волны Рэлея. Основой для этого по-прежнему является уравнение состояния твердого тела (1). Из обобщенного уравнения I и II законов термодинамики получено выражение для величины единичного напряжения σo
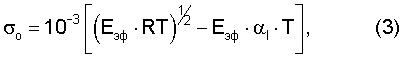
где Еэф - эффективный модуль продольной упругости,
R - универсальная газовая постоянная,
Т - температура испытания,K,
αl - коэффициент линейного удлинения.
Уравнение (3) можно преобразовать, если провести оценку члена 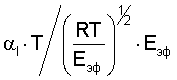 которое дает величину порядка 0,09
которое дает величину порядка 0,09
Поэтому уравнение (3) можно записать в виде:
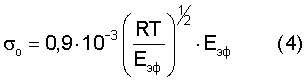
Если принять, что произведение 0,9·10-3(RT/Еэф)1/2 равно единичной деформации εo, возникающей при приложении к телу единичного напряжения σо, то получим уравнение закона Гука в единичных напряжениях и деформациях
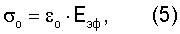
где 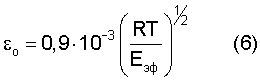
Если преобразовать уравнения (4), (6) с учетом 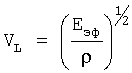
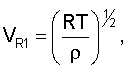 то их можно записать в виде:
то их можно записать в виде:
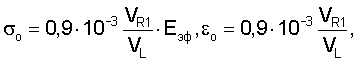
где VL - скорость продольной волны,
VR1 - скорость первой нормальной моды поверхностной волны Рэлея, когда в оболочке корпуса возникает первая порция упругой деформации εо. Используя выражения, вытекающие из уравнения (1), можно показать связь единичной деформации εо со структурно-чувствительным параметром γ, фигурирующим в уравнении Журкова
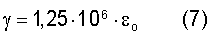
или
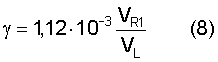
После установления зависимостей для γ покажем его физический смысл на примере установления зависимости между энергией активации разрушения Uo и эффективным модулем продольной упругости. Для этого поступим следующим образом.
Предельная упругая деформация при разрушении определяется
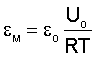
или с учетом уравнения (6)
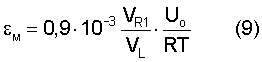
Умножим левую и правую части уравнения (9) на γ, после чего получим выражение:
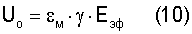
Уравнение (10) записано для момента разрушения. Если учесть, что уравнение состояния (1) предусматривает локализацию энергии RT на одну связь двух атомов в процессе роста напряжения (энергии), то следует предположить локализацию энергии Uo и упругой деформации εm·γ на связи двух атомов в предельном состоянии металла. Это допущение приводит к уравнению упругого взаимодействия (закон Гука) на уровне связи двух атомов в момент разрушения
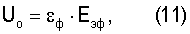
где εф - предельная флуктуация упругой деформации на уровне связи двух атомов.
Уравнение (11), таким образом, отражает флуктуационное уравнение закона Гука для напряжений и деформаций для связи двух атомов. Действительно, если записать выражение для эффективного макронапряжения
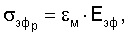
где левую и правую части умножить на γ, то получим
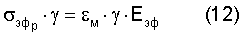
Правая часть уравнения (12) совпадает с уравнением (10), а произведение 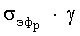 выражает локализованное на одну связь напряжение, которое для момента разрушения представляет теоретическую прочность σтеор., численно равную истинной энергии активации разрушения Uo. Обобщая уравнение (11), (12), получаем флуктуационное уравнение закона Гука для связи двух атомов в предельном состоянии
выражает локализованное на одну связь напряжение, которое для момента разрушения представляет теоретическую прочность σтеор., численно равную истинной энергии активации разрушения Uo. Обобщая уравнение (11), (12), получаем флуктуационное уравнение закона Гука для связи двух атомов в предельном состоянии
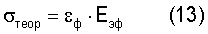
Уравнение (13) можно записать и для текущего напряжения на связи двух атомов
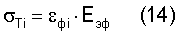
Таким образом, становится понятным, что закон Гука работает до предельного состояния и определяет темп накопления упругой потенциальной энергии для макроскопической среды (оболочки) по уравнению 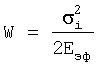 и для уровня связи двух атомов по уравнениям (11), (13). При этом флуктуация упругой деформации εф и макроскопическая деформация εм связаны уравнением:
и для уровня связи двух атомов по уравнениям (11), (13). При этом флуктуация упругой деформации εф и макроскопическая деформация εм связаны уравнением:
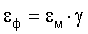
Полученные флуктуационные уравнения (11), (13) дают возможность записать уравнение взаимодействия двух типов волн в предельном состоянии
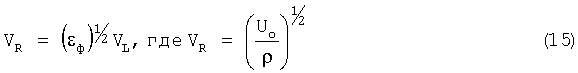
а также и для текущих значений напряжений.
 Согласно экспериментальным данным для высокопрочной стали СП-28 эффективный модуль продольной упругости изменялся в интервале 2,1·105 МПа ≤ Еэф ≤ 2,7·105 МПа, что соответствует изменению VL в интервале 5100 м/с ≤ VL ≤ 5820 м/с и изменению 0,32 ≥ εф ≥ 0,25 при разрушении. Изменению указанных параметров соответствует единственная максимальная скорость поверхностной волны Рэлея VR=2940 м/с. Для корпусов из титанового сплава ОТ-4 получено, что Еэф=1,4·105 МПа и которому соотвествуют при разрушении εф=0,34, VR=3240 м/с.
Согласно экспериментальным данным для высокопрочной стали СП-28 эффективный модуль продольной упругости изменялся в интервале 2,1·105 МПа ≤ Еэф ≤ 2,7·105 МПа, что соответствует изменению VL в интервале 5100 м/с ≤ VL ≤ 5820 м/с и изменению 0,32 ≥ εф ≥ 0,25 при разрушении. Изменению указанных параметров соответствует единственная максимальная скорость поверхностной волны Рэлея VR=2940 м/с. Для корпусов из титанового сплава ОТ-4 получено, что Еэф=1,4·105 МПа и которому соотвествуют при разрушении εф=0,34, VR=3240 м/с.
Становится очевидным, что поверхностная волна Рэлея характеризуется не только максимальной скоростью VR, но и значением минимальной скорости VR1, о чем свидетельствует ее наличие в уравнениях (4, 6, 8, 9). Все промежуточные значения скоростей волны Рэлея, а также флуктуации упругой деформации должны соответствовать дискретным нормальным модам колебаний решетки и определять квантовый характер накопления потенциальной энергии на уровне связи двух атомов в процессе роста нагрузки. Это условие соответствует уравнению
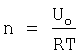
из которого вытекает уравнение квантования скоростей нормальных мод поверхностной волны Рэлея
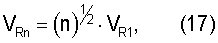
где n=1, 2, 3..., 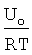
Таким образом, два крайних значения скоростей поверхностной волны Рэлея (VR1, VR) характеризуют начало и конец упругой деформации металла и отвечают двум уровням упругой потенциальной энергии RT и Uо. Все промежуточные дискретные уровни энергии, в том числе уровень энергии начала сдвиговых процессов, должны определяться промежуточными нормальными модами волны Рэлея.
Для получения относительно законченной картины процесса накопления потенциальной энергии в металлических корпусах, подвергаемых нагружению, определим диапазон частот и длин волны нормальных мод волны Рэлея, а также покажем, что относительный активационный объем γ, фигурирующий в уравнении Журкова, однозначно определяет циклические условия Борна-Кармана.
Для исследования характеристик нормальных мод волны Рэлея возьмем зависимости для единичной деформации εо (6, 7)
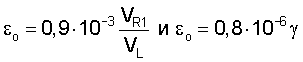
Исключим εо и запишем равенство
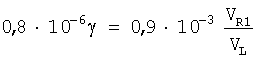 ,
,
которое с учетом дисперсионных уравнений фазовых скоростей VL=νL·λL и VR1 =νR1·λR1 перепишем в виде
0,9·10-3νL·λL·γ=νR1·λR1
Это уравнение распадается на части в соответствии с разложением на нормальные моды колебаний
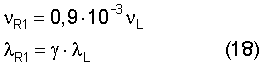
Следовательно, для минимальной скорости волны Рэлея ее частота на три порядка меньше, чем частота продольной волны, а длина волны минимальной скорости увеличивается во столько раз, какова величина γ. Отсюда становится понятным физический смысл коэффициента 1·10-3, который был введен из соображений сходимости экспериментальных и прогнозируемых значений предельной прочности в уравнении для единичного напряжения σо.
Для установления диапазона частот и длин волн последней нормальной моды волны Рэлея, определяющей условие предельной прочности, необходимо записать уравнение для предельного эффективного разрушающего напряжения в оболочке изделия
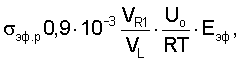
из которого после преобразований можно выделить максимальную скорость волны Рэлея
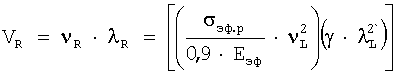
Два множителя этого уравнения, определяющие частоту и длину волны, можно записать как:
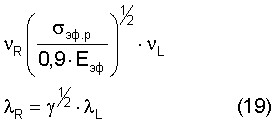
Аналогичным образом можно записать выражение для длины волны и частоты нормальной моды волны Рэлея на уровне начала сдвиговых процессов
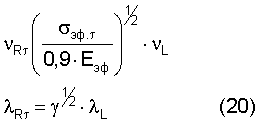
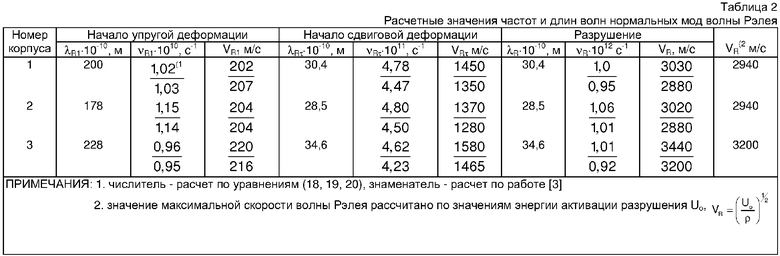
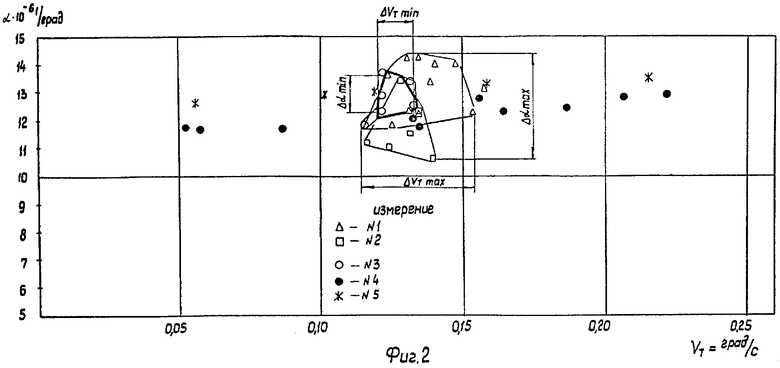
Для подтверждения изложенного подхода проведем расчет частот, длин волн и, соответственно, скоростей нормальных мод волн Рэлея в трех характерных точках деформирования металла (см. фиг.1). В качестве исходных данных возьмем результаты испытаний двух стальных и одного титанового корпусов (табл.1, 2)

Частоты нормальных мод волны Рэлея можно получить также из уравнения, описывающего колебания системы, состоящей из большого числа связанных осцилляторов, представляющих линейную цепочку атомов с натяжением Т [3]

Т - натяжение связей атомов,
m - масса атома,
а=aэф - параметр решетки (эффективный),
n - число атомов в линейной цепочке,
S=1,..., n.
Для этого уравнение (21) преобразуем, вместо T/a примем Δa·Eэф (Δа - удлинение связи двух атомов), а массу атома выразим как 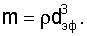
Длину цепочки (число атомов) (n+1) в соответствии циклическими условиями Борна-Кармана заменим на относительный эффективный активационный объем γ. Значение параметра S для трех характерных точек (см. чертеж) назначим в соответствии с квантованием энергии и физическими процессами, протекающими в этих точках
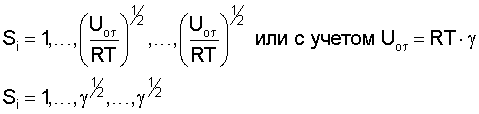
Равенство значений S во второй и третьей точках принято не случайно, а в соответствии с постоянством в этих точках длин волн нормальных мод волны Рэлея и энергии активации сдвига Uoτ.
В этом интервале значение частоты будет расти с ростом натяжения Т, которое увеличивается с ростом эффективного напряжения σэф и в уравнении (21) характеризуется ростом флуктуации упругой деформации εфi на уровне одной связи.
При преобразовании уравнения (21) флуктуацию εфi необходимо заменить с учетом уравнения (17)
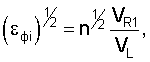
где n=1,..., γ,...,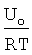
Окончательно уравнение (21) запишем в виде, удобном для расчета
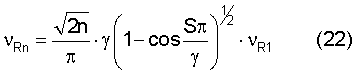
Частоты и скорости нормальных мод волны Рэлея, рассчитанные по этой формуле, приведены в табл.2.
Таким образом, согласно расчету частотный диапазон волны Рэлея изменяется от 1·1010 до 1·1012 Гц и определяет квантовый характер накопления потенциальной энергии как для оболочки корпуса, так и на уровне связи двух атомов. Можно показать по известной формуле Планка
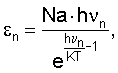
что каждая нормальная мода волны Рэлея переносит единичную энергию, равную RT. При частотах больше 1·1012 Гц равенство εn=RTне выполняется.
Для подтверждения уже известного диапазона частот можно также применить уравнение [3]
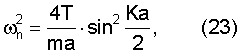
где K - волновой фактор, K=2π/λ,
а=аэф - параметр решетки.
Уравнение (23) эквивалентно уравнению (21), поэтому его следует преобразовать таким же образом, как сделано выше, и получить
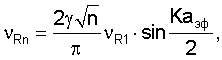
где 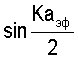 можно заменить на
можно заменить на 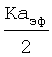 с точностью до 3,0%
с точностью до 3,0%
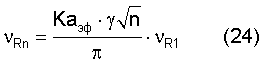
В уравнении (24) необходимо оценить величину волнового вектора К путем его привязки к трем характерным точкам и интервалам между ними. Выше определено, что точка 2 (начало сдвиговых деформаций) и 3 (разрушение) и интервал между ними характеризуются одной длиной волны для волн Рэлея 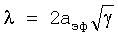 . Поэтому волновой вектор
. Поэтому волновой вектор 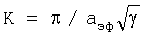 . После этой подстановки в уравнении (24) и спектр частот нормальных мод в точках 2 и 3 и интервале между ними будет определяться уравнением:
. После этой подстановки в уравнении (24) и спектр частот нормальных мод в точках 2 и 3 и интервале между ними будет определяться уравнением:
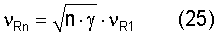
при 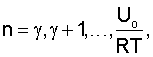
где νR1 - частота первой нормальной моды волны Рэлея.
Иная картина получается для точки 1 (начало упругих деформаций) и интервала до точки 2. Расчет показал, что для выполнения условия дискретного увеличения скоростей нормальных мод волны Рэлея необходимо принять, что длины волны в этом интервале изменяются по закону
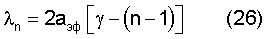
при n=1, 2, 3... (γ-1).
Поэтому для точки 1 и первого интервала, не включая точку 2, частоты будут определяться по уравнению
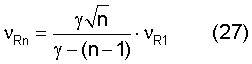
при n=1, 2, 3... (γ-1)
Проведенный анализ гармонического разложения волны Рэлея на нормальные моды колебаний показывает, что в процессе роста напряжения в оболочке корпуса дважды происходит перебор частотного диапазона, что отмечается уменьшением длины волны от 2·аэф·γ до 4·аэф в первом интервале и сохранение постоянства длины волны 2·аэф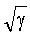 - во втором интервале в присутствии упругих сдвиговых деформаций. Принимая квантовый характер накопления и релаксации энергии и анализируя зависимости, определяющие взаимодействие нормальных мод волны Рэлея с продольными и поперечными волнами, отметим, что в процессе роста нагрузки не происходит гармонического разложения двух последних волн. Действительно, во всех случаях на разных уровнях нагрузки имеют место только максимальные значения скоростей продольных волн, которые характеризуются одной длиной волны λL=2аэф и одной частотой νL, равной
- во втором интервале в присутствии упругих сдвиговых деформаций. Принимая квантовый характер накопления и релаксации энергии и анализируя зависимости, определяющие взаимодействие нормальных мод волны Рэлея с продольными и поперечными волнами, отметим, что в процессе роста нагрузки не происходит гармонического разложения двух последних волн. Действительно, во всех случаях на разных уровнях нагрузки имеют место только максимальные значения скоростей продольных волн, которые характеризуются одной длиной волны λL=2аэф и одной частотой νL, равной 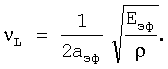
В начале описания физической сущности условия поддержания постоянной скорости роста температуры на поверхности контролируемого изделия было получено условие возбуждения двух типов волн
τL/τRn=e-2
Описанная картина квантования нормальных мод волны Рэлея в характерных трех точках и интервалах между ними дает возможность определить номер нормальной моды волны Рэлея и выявить физическую картину при нагревании изделия с целью получения достоверных значений коэффициентов теплового расширения и тепловой деформации. Необходимое уравнение для определения номера нормальной моды можно получить из выражения для эффективного текущего напряжения
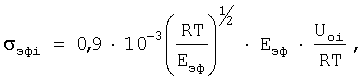
где после преобразования можно получить:
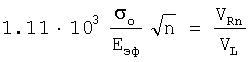
или с учетом выражений 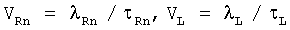
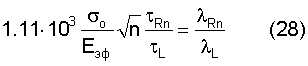
Искать значение n будем вначале в 1 интервале, где длины волн нормальных мод волны Рэлея и продольной волны изменяется как
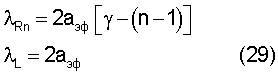
После подстановки τRn/τL=e2 и выражений (29) в уравнение (28) получим необходимое уравнение
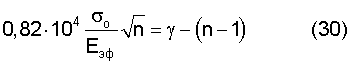
В соответствии с данными табл. 1 исходные значения для расчета:
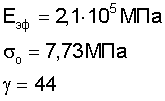
В итоге получаем квадратное уравнение относительно n
n2-90,09n+2025=0, откуда
n1=43, n2=47.
Нормальная мода с n2=47 не имеет смысла, так как она попадает во II интервал, где имеет место другая длина волны λ47=2аэф .
.
Следовательно, имеет смысл нормальная мода с n=43, которая предшествует нормальной моде n=44, на которой происходит сдвиговая деформация. Поэтому условие нагревания изделия с целью контроля прочности с dT/dτ=const возбуждает последнюю нормальную моду поверхностной волны Рэлея чисто упругого деформирования металла с напряжением в стенке изделия из высокопрочной стали σn=σo·43=33 кг/мм2. Если предположить, что напряжения в станке равны нулю, то должна быть нормальная мода с n=45, которая попадает снова во II интервал, где отношение τL/τRn уже не равно e-2.
Таким образом, постоянное увеличение (уменьшение) температуры поверхности изделия с постоянной скоростью возбуждает нормальную моду поверхностной волны Рэлея с длиной волны 4aэф и частотой ν=0,67·1012 Гц.
Постановка параметров других двух корпусов дает нормальную моду n=(γ-1) но с той же длиной волны и частотой.
Далее необходимо обосновать второй отличительный признак предполагаемого изобретения, заключавшийся в расчете разрушающих напряжений по формуле:
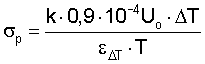
Основой этого уравнения по-прежнему является уравнение состояния (1) в его полной форме, то есть с раскрытием выражения для
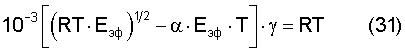
Из уравнения (31) определяем выражение для α
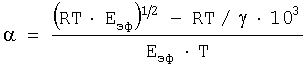
или после преобразований

В случае нагрева (охлаждения) коэффициент линейного удлинения можно заменить на α=εΔТ/ΔТ (εΔТ - величина тепловой деформации за перепад температуры ΔТ). Поэтому замеренная тепловая деформация εΔТ=α·ΔТ в окружном направлении является структурно-чувствительным параметром, которая характеризуется истинным значением при данной температуре коэффициентом линейного удлинения α. На этом основании из уравнения (32) определим значение эффективного модуля продольной упругости Еэф

Подстановка выражения (33) в уравнение (3) дает выражение
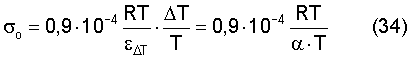
После чего эффективное разрушающее напряжение будет
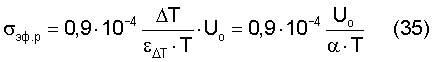
При контроле прочности уравнение для истинного разрушающего напряжения следует записать в общем виде:
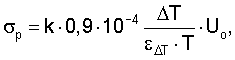
где k - коэффициент напряженного состояния и формы изделия,
εΔТ - приращение тепловой деформации за приращение температуры ΔТ,
Т - абсолютная температура K,
Uо - энергия активации разрушения.
В заключение необходимо обосновать два важных обстоятельства, заключающихся в следующем:
если в уравнении (35) энергию активации разрушения Uo заменить в соответствии с уравнением (10) на εм·γ·Eэф, а εм·Еэф=σэф.р, то получим уравнение
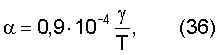
которое выражает связь активационного объема γ с тепловой деформацией 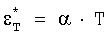 , возникающей при нагревании тела от нуля абсолютной температуры до T K.
, возникающей при нагревании тела от нуля абсолютной температуры до T K.
Замена в уравнении (36) γ=RT/σо дает условие
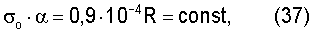
где R - универсальная газовая постоянная.
Второе обстоятельство заключается в соотношении предельной упругой деформации при разрушении εм с тепловой деформацией 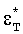 . Для этого в уравнении (35) произведение 0,9·10-4 Uo заменим на отношение
. Для этого в уравнении (35) произведение 0,9·10-4 Uo заменим на отношение 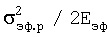 , которое приводим здесь без обоснования. Полученное уравнение
, которое приводим здесь без обоснования. Полученное уравнение
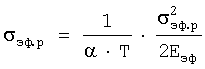
после сокращения и принятия, что σэф.р/Еэф=εм, дает искомое выражение для εм и 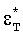
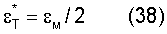
Таким образом, предельная макроскопическая упругая деформация при разрушении определяется выражением:
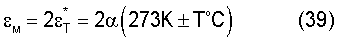
Приведенное теоретическое описание кинетики подготовки металла к разрушению и обоснование особенностей отличительных признаков является достаточным условием для построения новой технологии неразрушающего контроля прочности путем нагрева (охлаждения) изделия, базирующейся на условии dT/dτ=const, необходимого для получения действительных значений коэффициентов линейного удлинения и значений прочности изделия.
Пример практической реализации предложенного способа
Для подтверждения способа контроля прочности проводили нагрев тонкостенных металлических корпусов из высокопрочной стали СП-28 диаметром Dо=209 мм, высотой Н=300 мм с толщиной стенки δ=0,7 мм. Нагрев осуществляли с внутренней стороны с использованием одной кварцевой лампы КГ 230-1000-6У4 N 16-535.718.83, расположенной вдоль центральной оси корпуса. На наружную поверхность устанавливали струнный периметрометр с электрическим выходным сигналом, где охватывающий виток выполняли из проволоки с известным коэффициентом линейного расширения.
На наружную поверхность проволоки, не имеющую контакта с поверхностью корпуса, припаивали термопару. В зоне нахождения точки контроля температуры проволоки периметрометра припаянной к поверхности корпуса второй термопарой измеряли температуру поверхности изделия. Процесс нагрева (характерные точки) контролировали секундомером. Тепловую деформацию оболочки корпуса определяли относительным методом, считывая, что предполагаемый коэффициент линейного удлинения проволоки периметрометра больше, чем тот же коэффициент у оболочки корпуса. Для этого проволоке периметрометра задавали предварительное натяжение, которое в процессе нагрева постепенно уменьшалось. Натяжение (его изменение) контролировали цифровым вольтметром, разрушающая способность датчика деформации позволяла контролировать изменение удлинения с точностью 1 мВ, который соответствовал изменению длины окружности на 1 мкм.
Тепловая деформация оболочки корпуса рассчитывалась по уравнению
εΔТ.К=εΔТ np.-Δε,
где εΔТ np. - деформация проволоки,
Δε - изменение деформации натяжения проволоки периметрометра.
Тепловую деформацию проволоки периметрометра определяли как:
εΔТ np.=αпр.·T
Изменение деформации натяжения проволоки Δε определяли
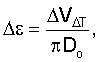
где ΔVΔТ - изменение натяжения в вольтах,
Do - диаметр оболочки контролируемого корпуса.
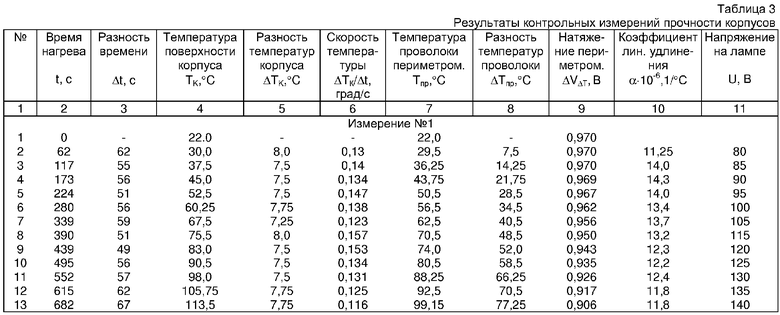
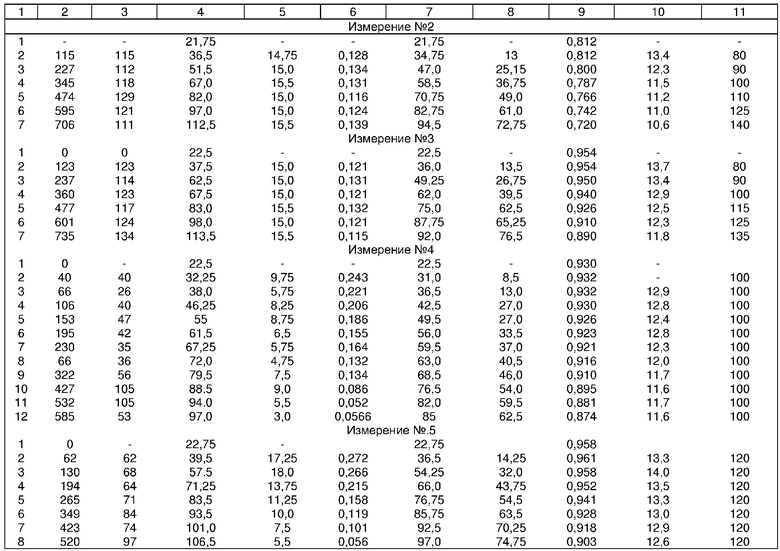
Контрольные замеры тепловой деформации проводили как без обеспечения постоянства скорости нагрева наружной поверхности корпуса, так и с обеспечением dT/dτ=const. Последнее достигалось при подаче на нагреватель различных ступеней напряжения путем их подбора, например, 80, 90, 100, 110, 120, 130 вольт. Результаты контрольных проверок сведены в табл.3.
Измерения 1-3 (табл.3) проведены с приближенной постоянной скоростью изменения температуры на поверхности корпуса. Измерения 4, 5 проведены при постоянном напряжении на лампе, и поэтому скорость роста температуры изменялась в широком интервале. На фиг.2 точки, характеризующие одно измерение при сравнительной постоянной скорости, ограничены множествами, которые характеризуются ΔVTmax, Δαmax.
Три приведенных множества имеют общие точки, соответствующие общему множеству с параметрами ΔVTmin, Δαmin. Геометрическая картинка, характеризующая изменением скорости от 0,12 до 0,157 град/с дает изменение коэффициента теплового удлинения от 12,2·10-6 до до 13,6·10-6 1/град. Таким образом, при контроле прочности обеспечение любой постоянной скорости роста температуры на поверхности изделия дает возможность получить истинный коэффициент теплового удлинения и, естественно, величину предельного разрушающего напряжения.
Расчет разрушающих напряжений по формуле, приведенной в формуле предлагаемого изобретения, представлен в табл.4. Для расчета примем, что в интервале от 20 до 100°С коэффициент α=(12,9±3,7)·10-6 1/град. Здесь же приведем расчет эффективного модуля продольной упругости Еэф.
Таблица 4
Расчетные разрушающие напряжения и эффективный модуль продольной упругости
Приведенный пример показывает достаточно высокую степень точности определения истинной прочности изделий путем их нагрева или охлаждения. При использовании термостабилизированной струны периметрометра и серийно изготавливаемых пирометров с электрическим выходным сигналом для измерения температуры позволит осуществить поставленную цель в предлагаемом способе контроля прочности в более полном объеме.
Разработка и внедрение неразрушающего контроля прочности позволит по сравнению с базовым объектом - способом, прототипом изобретения, обеспечить экономическую эффективность за счет:
- организации многопредметного (группового) способа контроля прочности (то есть параллельного контроля нескольких изделий одновременно),
- возможности получения прочностных характеристик изделий при различных температурах (в том числе эксплуатационных) одновременно,
- разработки автоматизированных средств контроля с применением электронно-управляемых машин,
- сокращения сроков отработки конструкции изделий и их оптимального веса при подготовке их серийного производства.
Источники информации
1. Авторское свидетельство СССР № 606124, кл. G01N 3/00, опубл. 05.05.78, Бюл.17.
2. С.А.Куркин. Прочность сварных тонкостенных сосудов, работающих под давлением. М.: Машиностроение, 1976, с.34-49, 80-98.
3. Пейн Г. Физика колебаний и волн. Пер. с англ. М.: Мир, 1979.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ПРОЧНОСТИ ИЗДЕЛИЙ | 1987 |
|
RU2297615C2 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ПРОЧНОСТИ ИЗДЕЛИЙ | 1989 |
|
RU2297616C2 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ПРОЧНОСТИ ИЗДЕЛИЯ | 1982 |
|
SU1840720A1 |
| СПОСОБ ОБНАРУЖЕНИЯ НЕПРОВАРА | 2001 |
|
RU2212030C2 |
| ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ АКУСТИЧЕСКОЙ ЭМИССИИ | 1996 |
|
RU2110792C1 |
| ВОЛНОВОЙ СПОСОБ КОНТРОЛЯ СВОЙСТВ МАТЕРИАЛОВ | 2007 |
|
RU2335756C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОЧНОСТИ МАТЕРИАЛА ИЗДЕЛИЯ | 2010 |
|
RU2445615C1 |
| СПОСОБ ПОСТРОЕНИЯ КРИВОЙ ПРЕДЕЛЬНОЙ ПЛАСТИЧНОСТИ | 1992 |
|
RU2047414C1 |
| УЛЬТРАЗВУКОВОЙ НАКЛОННЫЙ ПРЕОБРАЗОВАТЕЛЬ | 2007 |
|
RU2356044C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПРОИЗВОДСТВОМ ПЕРЕРАБОТКИ ПОРОХОВОЙ МАССЫ БАЛЛИСТИТНОГО ТИПА | 2004 |
|
RU2273626C2 |
Способ неразрушающего контроля прочности изделий заключается в том, что в заданном сечении с минимальным краевым эффектом измеряют деформацию с помощью струнного периметрометра, возникающую при приложении на изделие внешних воздействий. Определяют эффективный модуль продольной упругости, по которому судят о предельной прочности. Изделие в заданном диапазоне температур нагревают (охлаждают) с постоянной скоростью изменения температур на его поверхности. Измеряют текущие значения тепловой деформации оболочки с помощью термостабилизированной по длине струны периметрометра, а о предельной прочности судят по уравнению
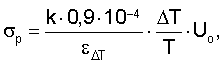
где k - коэффициент напряженного состояния и формы изделия,
Uo - истинная энергия активации разрушения,
ΔT - изменение температуры,
T - абсолютная температура,
εΔT - тепловая деформация оболочки за ΔT°С.
Технический результат - упрощение технологии испытаний. 2 ил.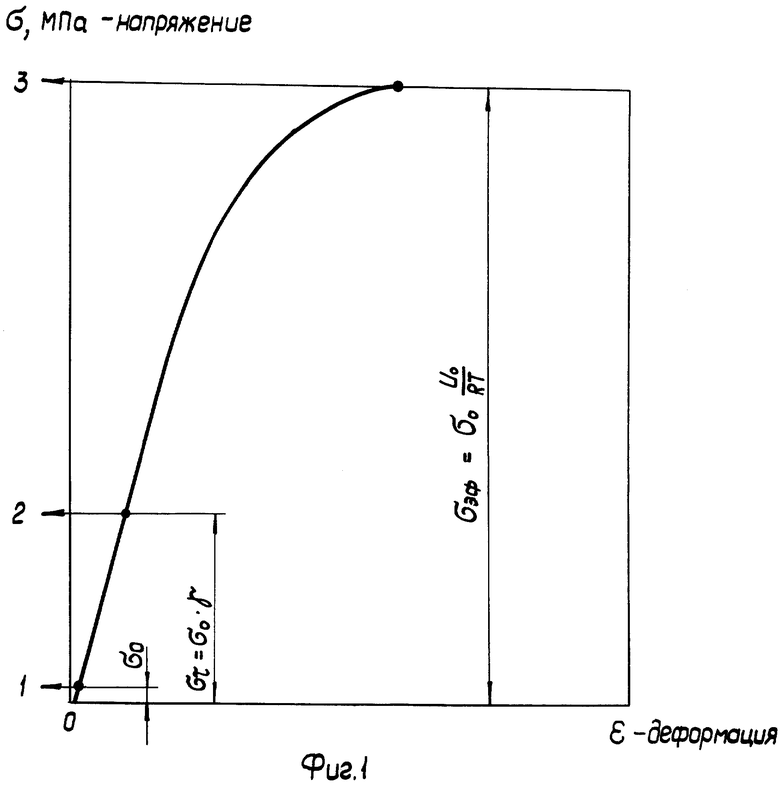
Способ неразрушающего контроля прочности изделий, включающий нагревание изделия с постоянной скоростью изменения температуры на его поверхности и измерение деформации в заданном сечении изделия с минимальным краевым эффектом, отличающийся тем, что, с целью упрощения контроля, в изделии возбуждают продольную упругую волну и поверхностную волну Рэлея с длиной волны и частотой, соответствующей последней нормальной моде упругого деформирования, определяют приращение деформации εΔТ за интервал ΔТ°С приращения температуры, обеспечивающей создание указанных волн, а о прочности σ изделия судят по уравнению:
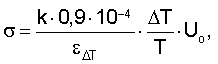
где k - коэффициент напряженного состояния и формы изделия,
Uo - истинная энергия активации разрушения.
| Методы испытания, контроля и исследования машиностроительных материалов т.III, М.: Машиностроение, 1973 г., стр.176-177, 183. |
Авторы
Даты
2007-05-10—Публикация
1983-12-30—Подача