Изобретение относится к способам определения механических свойств материалов путем приложения растягивающих или сжимающих нагрузок, а именно к способам определения модуля упругости Юнга и коэффициента Пуассона.
Известен способ определения модуля упругости [Регистрационный номер заявки № 96116367/03, кл. G01N 33/38, 1998], основанный на том, что изготавливают образцы, содержащие эталонный и исследуемый крупный заполнитель с различной его абсолютной концентрацией. Модуль упругости растворной составляющей определяют по результатам испытаний бетонных образцов на эталонном заполнителе, а модуль упругости исследуемого заполнителя находят из формулы.
Недостатком указанного способа определения модуля упругости является его неприменимость к образцам композиционных материалов, содержащих монодисперсные сферические микро- или наночастицы.
Наиболее близким к заявляемому техническому решению, принятым за прототип, является способ определения модуля упругости углеродных нанотрубок или углеродных волокон, добавленных в эпоксидную матрицу [О.Lourie, H.D.Wagner \\ Evaluation of Young's modulus of carbon nanotubes by micro-Raman spectroscopy \\ Journal of materials research Vol.13, № 9, Sep. 1998], основанный на том, что образец материла подвергают воздействию гелево-неонового лазера. Получают Рамановский спектр образца материала с помощью Renishaw Ramascope. Охлаждают образец до определенной температуры, используя ячейку охлаждения Linkam THMS 600, тем самым вызывая деформацию композиционного материала. Охлаждение выполняют впрыскиванием азота. Снимают Рамановский спектр образца материала. Смещение пика интенсивности образца после охлаждения обусловлено осевым уменьшением длины С-С связи. Вычисляют модуль упругости углеродных нанотрубок или углеродных волокон Еnt по формуле (1):
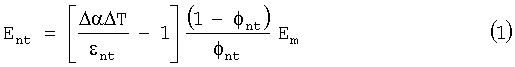



где ω0 и ωq - частоты связи до и после охлаждения; αnt и αm - коэффициенты теплового расширения нанотрубки и матрицы; T0 и Тq - температура до охлаждения и после; φnt - доля объема углеродных нанотрубок или углеродных волокон в составе образца; Еm - модуль упругости матрицы; εnt - деформация длины связи.
Недостатком указанного способа определения модуля упругости является то, что он непригоден для определения коэффициента Пуассона включений, добавленных в эпоксидную матрицу.
Задача изобретения - получение способа определения модуля упругости и коэффициента Пуассона сферических микро- и наночастиц на основе приложения осевых нагрузок к образцу композиционного материала.
Способ определения модуля упругости включает в себя два этапа.
1. Изготавливают образец из полимерной матрицы с добавлением заданного процентного содержания (1-7)% монодисперсных сферических микро- или наночастиц. Процентное содержание микро- или наночастиц в образце материала выбирается исходя из того, что частицы так малы и настолько удалены одна от другой, что взаимодействием между ними можно пренебречь. Сферические частицы равномерно распределены в образце композиционного материала. Размер всех частиц, входящих в состав образца, должен быть одинаков. Проводят экспериментальное одноосное сжатие образца композиционного материала силой n*F, где n=1,9...m.
Определяют продольные и поперечные деформации образца. Строят зависимость продольной деформации от осевого напряжения.
2. Определяют по линейному участку кривой деформирования модуль упругости и коэффициент Пуассона композиционного материала. Вычисляют значения модуля упругости и коэффициента Пуассона материала сферических микро- или наночастиц.
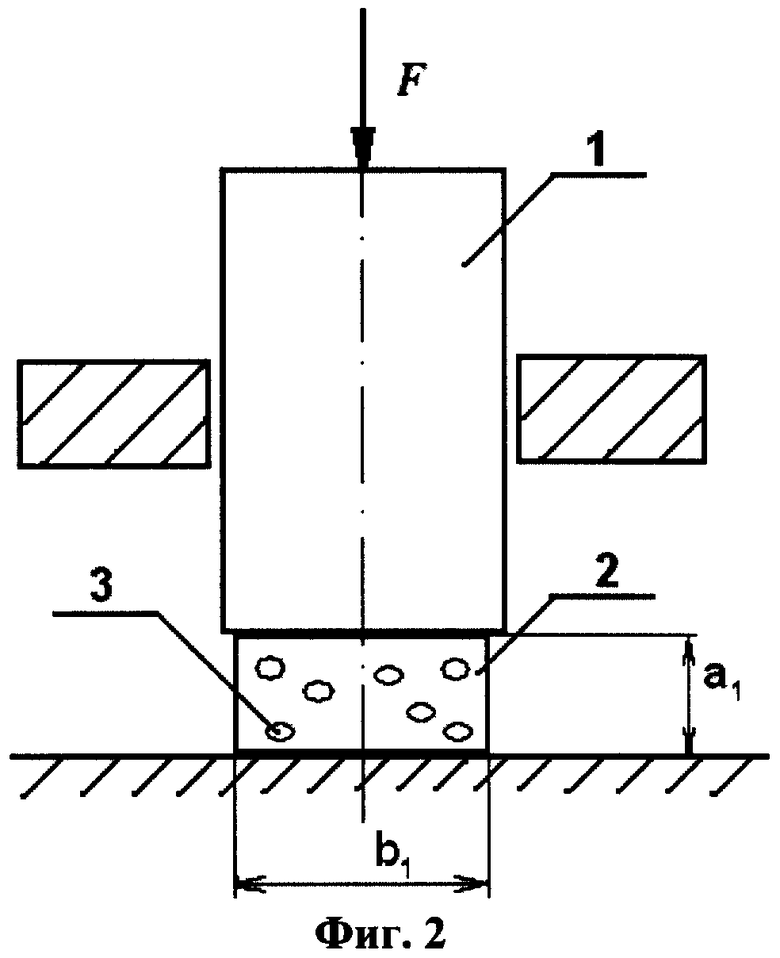
На фиг.1 представлена конструкция для реализации предлагаемого способа.
На фиг.2 представлена схема сжатия пуансоном 1 композиционного материала 2 с упругими сферическими включениями 3 после приложения силы F.
Способ реализуется следующим образом: с помощью пуансона 1 прикладывают силу n*F при n=1, действующую на композиционный материал 2, содержащий сферические включения 3, представляющие собой монодисперсные шарообразные микро- или наночастицы.
Определяют продольную εпр1 и поперечную εпоп1 деформацию (5, 6), осевое напряжение (7)


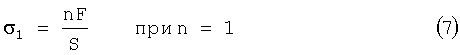
где S - площадь сечения перпендикулярного оси образца композиционного материала.
Продолжают прикладывать силы n*F, где n=2, ...m, находят продольные, поперечные деформации и осевые напряжения. Строят зависимость продольной деформации от осевого напряжения. Для линейного участка кривой деформирования определяют модуль упругости Е (8) и коэффициент Пуассона ν (9) композиционного материала
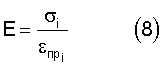
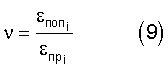
где i - точка на линейном участке кривой деформирования.
Вычисляют модуль сдвига μ (10) и объемный модуль k (11) композиционного материала


По формулам (12), (13) вычисляют модуль сдвига μI и объемный модуль kI сферических микро- или наночастиц [Р.Кристенсен, Введение в механику композитов: Издательство МИР, 1982, с.50-51]
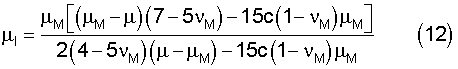
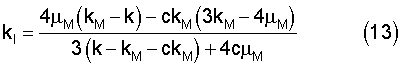
где μM, kM, νM - модуль сдвига, объемный модуль и коэффициент Пуассона полимерной матрицы, с - концентрация (14)

VI - объем монодисперсных сферических микро- или наночастиц, V - объем образца композиционного материала.
Определяют модуль упругости EI (15) и коэффициент Пуассона νI (16) сферических микро- или наночастиц
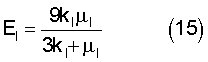
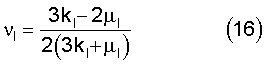
Благодаря предложенному способу стало возможным определять модуль упругости и коэффициент Пуассона для монодисперсных сферических микро- и наночастиц.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИЧЕСКИХ СВОЙСТВ ОДНОРОДНЫХ ИЗОТРОПНЫХ УПРУГИХ МАТЕРИАЛОВ | 1993 |
|
RU2061230C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ МАТЕРИАЛА ПОКРЫТИЯ НА ИЗДЕЛИИ | 2016 |
|
RU2618500C1 |
| ГРАНУЛИРОВАННЫЙ МАГНИТНЫЙ ПОЛИМЕР И ТАМПОНАЖНАЯ СМЕСЬ ДЛЯ ЦЕМЕНТИРОВАНИЯ ОБСАДНЫХ КОЛОНН НА ОСНОВЕ МАГНИТНОГО ПОЛИМЕРА | 2019 |
|
RU2705113C1 |
| Способ защиты электронных блоков от инерционных ударных и вибрационных воздействий | 2017 |
|
RU2666964C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ ЮНГА МАТЕРИАЛА МИКРО- И НАНОЧАСТИЦ | 2012 |
|
RU2494038C1 |
| Способ модифицирования бетона комплексной добавкой, включающей гидротермальные наночастицы SiO и многослойные углеродные нанотрубки | 2020 |
|
RU2750497C1 |
| МНОГОФУНКЦИОНАЛЬНЫЕ НАНОКОМПОЗИТНЫЕ МАТЕРИАЛЫ С ТРЕХМЕРНЫМ АРМИРОВАНИЕМ | 2006 |
|
RU2423394C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ ЮНГА МАТЕРИАЛОВ | 2005 |
|
RU2296972C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИКО-МЕХАНИЧЕСКИХ ХАРАКТЕРИСТИК МОДИФИЦИРОВАННОГО ПОВЕРХНОСТНОГО СЛОЯ МАТЕРИАЛА ИЗДЕЛИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2016 |
|
RU2646442C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АДГЕЗИОННОЙ ПРОЧНОСТИ ТОНКИХ ТВЕРДЫХ ПОКРЫТИЙ НА ИЗДЕЛИЯХ | 2019 |
|
RU2710392C1 |
Изобретение относится к способам определения модуля упругости Юнга материалов, а именно сферических микро- и наночастиц, входящих в состав композиционного материала. Техническим результатом изобретения является возможность определения модуля упругости и коэффициента Пуассона для монодисперсных сферических микро- и наночастиц. Способ определения модуля упругости основан на том, что изготавливают образец из полимерной матрицы с добавлением заданного процентного содержания (1-7)% монодисперсных сферических микро- или наночастиц. Проводят экспериментальное одноосное сжатие образца композиционного материала. Определяют продольные и поперечные деформации образца. Строят зависимость продольных деформаций от осевого напряжения. По линейному участку кривой деформирования определяют модуль упругости и коэффициент Пуассона композиционного материала, и на основании полученных значений модуля упругости и коэффициента Пуассона композиционного материала определяют модуль упругости и коэффициент Пуассона для монодисперсных сферических микро- и наночастиц. 3 з.п. ф-лы, 2 ил.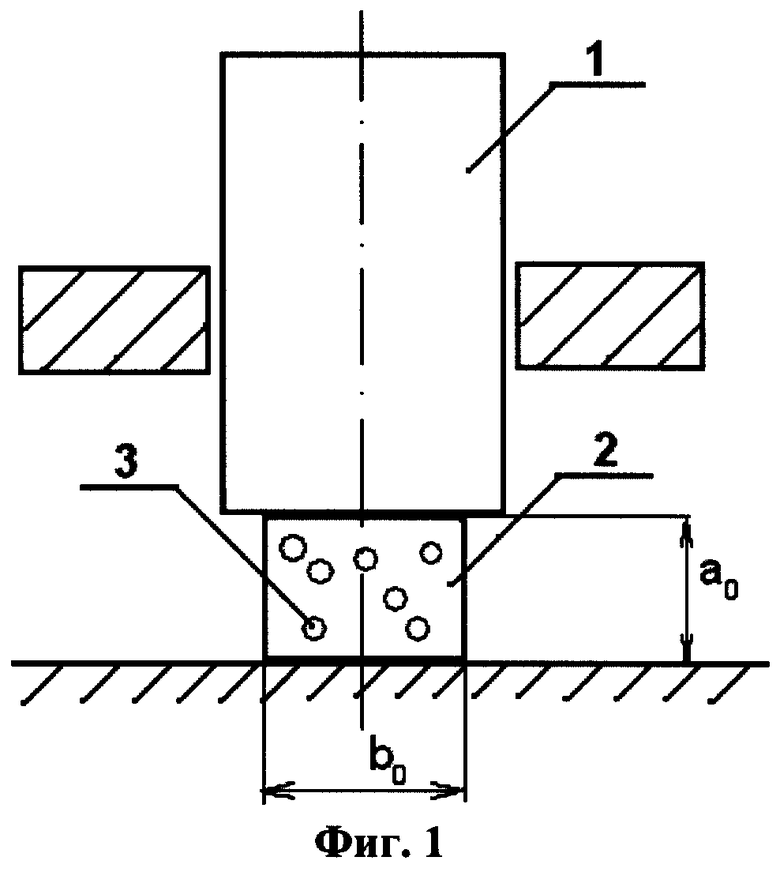
| Способ определения модуля упругости при сжатии слоистого материала | 1980 |
|
SU953502A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ ЗАПОЛНИТЕЛЯ | 1996 |
|
RU2110069C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ МЕТАЛЛИЧЕСКИХ МАТЕРИАЛОВ ПРИ КРИОГЕННЫХ И ПОВЫШЕННЫХ ТЕМПЕРАТУРАХ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2000 |
|
RU2169355C1 |
| Способ определения модуля нормальной упругости | 1987 |
|
SU1497491A1 |
| WO 2004038384, 06.05.2004 | |||
| JP 8233713, 13.09.1996. | |||
Авторы
Даты
2007-04-20—Публикация
2005-10-24—Подача