Изобретение относится к измерительной технике для определения адгезионной прочности тонких защитных покрытий на изделиях машиностроения.
Известен способ определения адгезионной прочности покрытий, заключающийся в том, что в поверхность образца с покрытием известной толщины внедряют сферический индентор с известными упругими характеристиками и радиусом, осуществляют на поверхности серию отпечатков при дискретно возрастающей от отпечатка к отпечатку нормальной нагрузкой, разрезают образец в плоскости нахождения центра отпечатка, определяют с помощью оптической микроскопии отпечаток, в котором впервые обнаруживается отслаивание покрытия, фиксируют значение нагрузки, при которой был получен отпечаток с отслоением, как критическую нагрузку, методом конечных элементов моделируют процесс внедрения сферического индентора при критической нагрузке, определяют величину нормальных растягивающих напряжений на границе раздела покрытие - основной материал, которые считают ответственными за отслаивание покрытия, а значение которых принимают за величину адгезионной прочности. (Патент US 6581441 В1 от 24.06 2003).
Недостатками этого способа является высокая погрешность определения величины адгезионной прочности покрытия, связанная с дискретностью прилагаемой нагрузки при индентировании и невозможностью локализовать плоскость резания отпечатка точно по центру отпечатка, а также высокая трудоемкость процедуры.
Известен способ определения адгезионной прочности покрытия на изделии, заключающийся в том, что измеряют толщину и модуль упругости материала покрытия, помещают изделие в микротвердомер, с помощью которого производят внедрение пирамидального или конического жесткого индентора в поверхность изделия, записывают диаграмму внедрения и анализируют кривую разгружения, по форме и известным текущим координатам которой рассчитывают значение адгезионной прочности покрытия. (P.J. Wei et al. A new method for determining the strain energy release rate of an interface via force-depth data of nanoindentation tests. Nanotechnology, 2009, N. 20, pp. 1-7)
Данный способ по технической сущности и достигаемому результату наиболее близок к предложенному техническому решению и, поэтому, принят за его ближайший прототип.
Согласно этому способу в поверхность с покрытием известной толщины внедряют пирамидальный жесткий индентор, записывают диаграмму внедрения, анализируют кривую изменения величины нагрузки с уменьшением глубины внедрения (так называемую кривую разгружения) известным способом (см. Oliver W.C, Pharr G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, №7, pp. 1564-1583) определяют модуль упругости материала покрытия Е1, рассчитывают тангенс угла наклона (жесткость) K1 кривой разгружения в области малых величин нагрузок, там, где кривая разгружения принимает линейный вид, и определяют величину адгезионной прочности G покрытия по формуле:
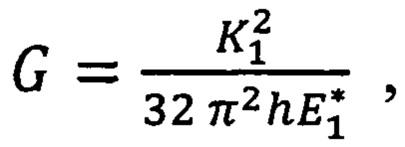
где h - толщина покрытия; 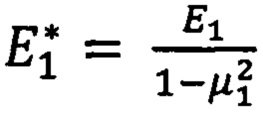 - приведенный модуль упругости материала покрытия,
- приведенный модуль упругости материала покрытия,
μ1 - коффициент Пуассона материала покрытия.
Недостатком этого способа является низкая точность определения адгезионной прочности тонких покрытий, связанная с тем, что измеряемая величина тангенса угла наклона, характеризующая упругость отслоившегося покрытия, не учитывает влияние упругой деформации материала основы, то есть в прототипе показана возможность опредления адгезионной прочности только толстых покрытий, где можно пренеберечь участием материала основы в деформации слоистого тела при индентировании.
Задача, решаемая в предлагаемом способе, заключается в обеспечении возможности с высокой точностью определять адгезионную прочность тонких покрытий за счет учета деформирования при индентировании материала основы, а также расширении номенклатуры исследуемых толщин покрытий за счет возможности определения адгезионной прочности покрытий с толщиной от ультратонких до толстых включительно.
Решение поставленной задачи достигается за счет того, что предложен способ определения адгезионной прочности покрытия, заключающийся в том, что изделие, на поверхности которого имеется покрытие известной толщины, представляет собой слоистое тело, состоящее из основы (подложки) и покрытия, материалы которых (подложки и покрытия) имеют известные значения модулей упругости, помещают в прибор-твердометр, с помощью которого производят нагружение (внедрение) алмазного пирамидального наконечника в поверхность покрытия на глубину, обеспечивающую отслаивание покрытия при разгружении, записывают диаграмму внедрения, представляющее собой график изменения глубины внедрения при возрастании нагрузки и затем при снижении нагрузки до нуля в виде кривых изменения нагрузки от глубины внедрения, фиксируют значения максимальной нагрузки при нагружении Pmax и глубины внедрения smax при этой нагрузке, рассчитывают эффективный модуль упругости 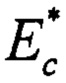 исследуемого слоистого тела, строят теоретические кривые разгружения для слоистого тела, материала покрытия и материала подложки в диапазоне значений экспериментальных данных по нагрузке, совмещают теоретическую кривую разгружения слоистого тела с экспериментальной кривой разгружения путем совпадения значения нагрузки у теоретической кривой разгружения слоистого тела со значением нагрузки Pmax экспериментальной диаграммы внедрения, регистрируют значения нагрузки Радг и глубины внедрения sадг на экспериментальной кривой разгружения, при которых экспериментальная кривая разгружения начинает резко расходится с теоретической кривой разгружения слоистого тела, смещают теоретическую кривую разгружения материала подложки в область нахождения экспериментальной кривой разгружения таким образом, чтобы кривая разгружения материала подложки проходила через точку с координатами [Радг, sадг] и рассчитывают значение адгезионной прочности по формуле:
исследуемого слоистого тела, строят теоретические кривые разгружения для слоистого тела, материала покрытия и материала подложки в диапазоне значений экспериментальных данных по нагрузке, совмещают теоретическую кривую разгружения слоистого тела с экспериментальной кривой разгружения путем совпадения значения нагрузки у теоретической кривой разгружения слоистого тела со значением нагрузки Pmax экспериментальной диаграммы внедрения, регистрируют значения нагрузки Радг и глубины внедрения sадг на экспериментальной кривой разгружения, при которых экспериментальная кривая разгружения начинает резко расходится с теоретической кривой разгружения слоистого тела, смещают теоретическую кривую разгружения материала подложки в область нахождения экспериментальной кривой разгружения таким образом, чтобы кривая разгружения материала подложки проходила через точку с координатами [Радг, sадг] и рассчитывают значение адгезионной прочности по формуле:
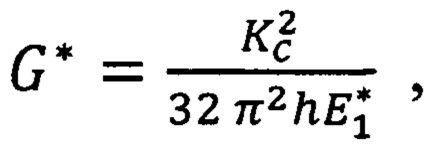
где Кс - тангенс угла наклона прямой линии, полученной путем линейной аппроксимации расчетной кривой упругого деформирования отслоившегося покрытия, которую строят для диапазона нагрузок 0<Pi<Радг по координатам [(sk)i, Pi], используя выражение:
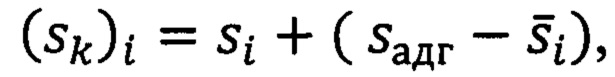
где (sk)i - текущее значение глубины внедрения для расчетной кривой упругого деформирования отслоившегося покрытия,
si - текущее значение глубины внедрения для экспериментальной кривой упругого деформирования отслоившегося покрытия,
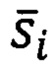 - текущее значение глубины внедрения для смещенной теоретической кривой упругого деформирования материала подложки;
- текущее значение глубины внедрения для смещенной теоретической кривой упругого деформирования материала подложки;
h - толщина покрытия;
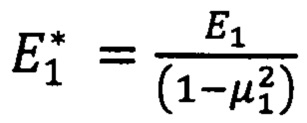 - приведенный модуль упругости материала покрытия.
- приведенный модуль упругости материала покрытия.
При этом теоретически рассчитываемая кривая разгружения слоистого тела рассчитывается по формуле:
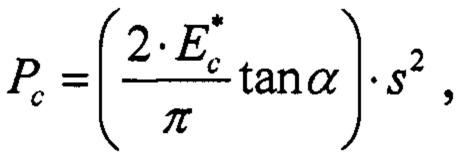
теоретически рассчитываемая кривая разгружения материала покрытия рассчитывается по формуле:

текущие значения глубины внедрения для расчетной кривой разгружения (упругого деформирования) материала подложки в составе слоистого тела рассчитываются по формуле:
(s0)i=(sc)i-(s1)i,
а эффективный модуль упругости исследуемого слоистого тела рассчитывается по формуле:
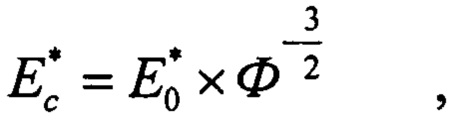
где (sc)i - текущее значение глубины внедрения (упругой деформации) для теоретической кривой разгружения слоистого тела;
(s1)i - текущее значение глубины внедрения (упругой деформации) для теоретической кривой разгружения материала покрытия,
s - текущая глубина индентора, отсчитываемая от свободной поверхности,
α - эквивалентный угол конуса (70,3° для индентора Берковича),
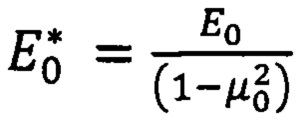 - приведенный модуль упругости материала подложки,
- приведенный модуль упругости материала подложки,
Ф - упруго-геометрический параметр, диапазон существования которого 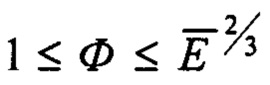 для
для 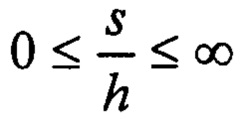 ;
;
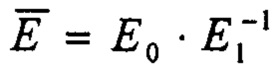 - эффективная упругая константа слоистого тела;
- эффективная упругая константа слоистого тела;
Е1, Е0 - модули нормальной упругости материалов покрытия и подложки;
μ0, и μ1 - коэффициенты Пуассона материала основы и покрытия.
Сущность предлагаемого способа заключается в том, что изделие с покрытием рассматривают как слоистое тело, упругая деформация которого при индентировании рассчитывается по известным зависимостям (Н.А. Воронин. Расчет параметров упругого контакта и эффективных характеристик топокомпозита для случая взаимодействия последнего со сферическим индентором. Трение и износ. 2002, т. 23, №6. с. 583-596.), что позволяет корректно рассчитать жесткость отслаившегося покрытия, с большей точностью и объективностью определить степень адгезионной связи покрытия к основе.
Отличительным признаком изобретения является то, что определение адгезионной прочности покрытия производят без учета вклада упругой деформации материала основы, которая снижает истинное значение адгезионной прочности.
Таким образом, предлагаемый способ позволяет существенно повысить точность и объективность определения адгезионной прочности тонких покрытий за счет учета деформирования при индентировании материала основы, в то время как в прототипе измеряемая величина функционально зависит только от упругой деформации материала покрытия.
Проведенный заявителем анализ техники, включающий поиск по патентным и научно-техническим источникам информации и выявление источников, содержащих сведения об аналогах заявленного изобретения, позволил установить, что заявителем не обнаружен аналог, характеризующийся признаками, идентичными всем существенным признакам заявленного изобретения, а определение из перечня выявленных аналогов прототипа, как наиболее близкого по совокупности признаков аналога, позволил выявить совокупность существенных (по отношению к усматриваемому заявителем техническому результату) отличительных признаков в заявленном объекте, изложенных в формуле изобретения.
Для проверки соответствия заявленного изобретения требованию изобретательского уровня заявитель провел дополнительный поиск известных решений, с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного изобретения, результаты которого показывает, что заявленное изобретение не следует для специалиста явным образом из известного уровня техники, поскольку из уровня техники, определенного заявителем, не выявлено влияние предусматриваемых существенными признаками заявленного изобретения действий на достижение технического результата.
Предлагаемый способ поясняется чертежами, представленными на фиг. 1-3.
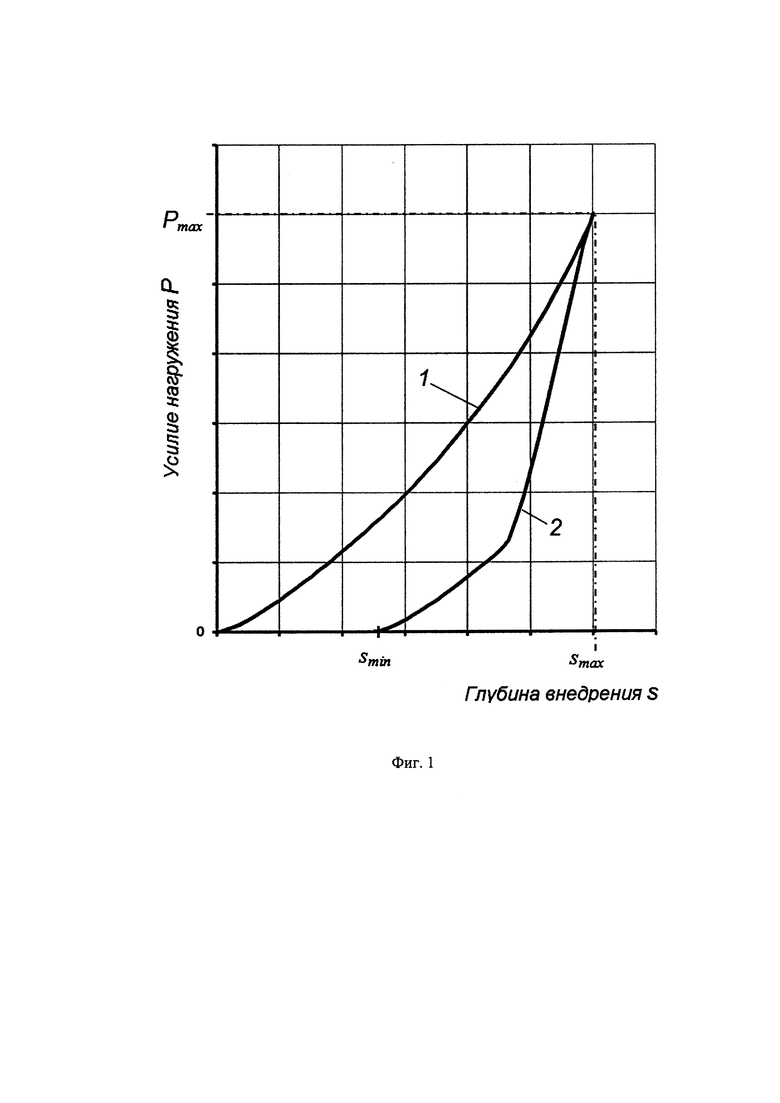
На фиг. 1 изображена экспериментальная диаграмма внедрения алмазного индентора в поверхность изделия с тонким твердым покрытием, в виде зависимости изменения нагрузки Р от величины глубины внедрения s при нагружении и разгружении.
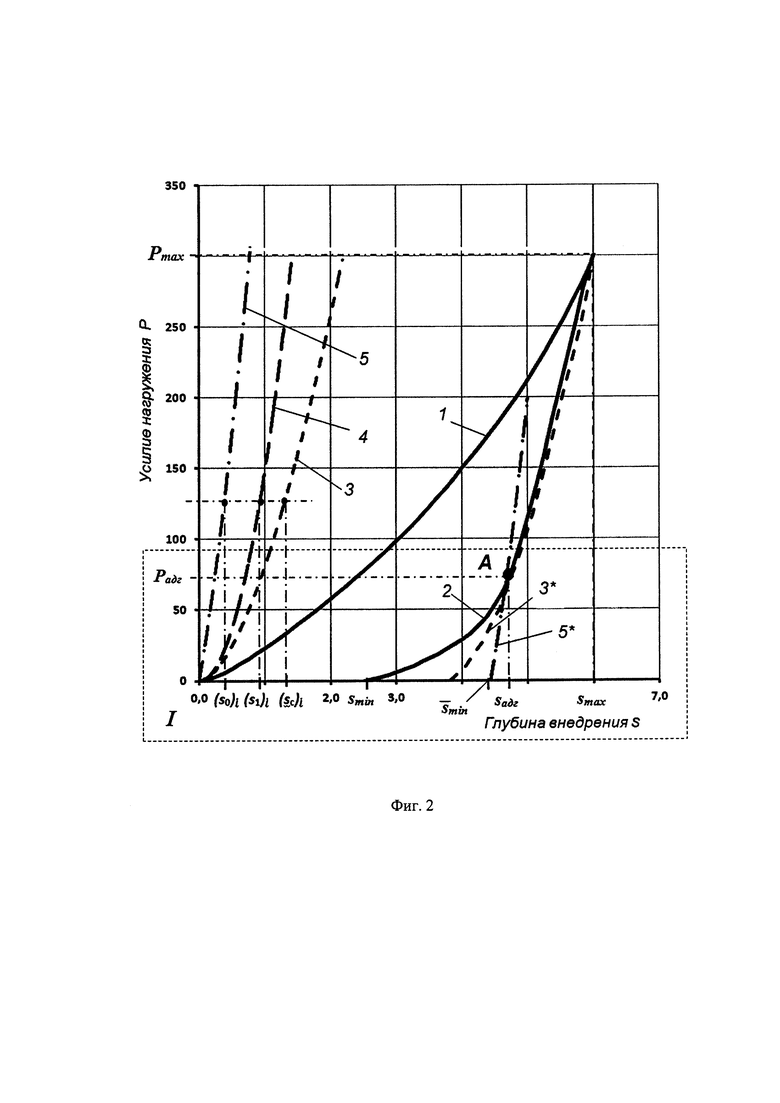
На фиг. 2 изображены кривые нагружения (1) и разгружения (2) из экспериментальной диаграммы внедрения и теоретические кривые разгружения. Графики 3, 4, 5 - теоретические кривые разгружения слоистого тела, материала покрытия и материала основы в составе слоистого тела, соответственно, 3* - кривая разгружения 3, совмещенная с начальной частью кривой разгружения 2, А - точка начала отслаивания покрытия, 5* - кривая разгружения 5, совмещенная с точкой начала отслоения покрытия. Область I - область графика для последующего графического анализа.
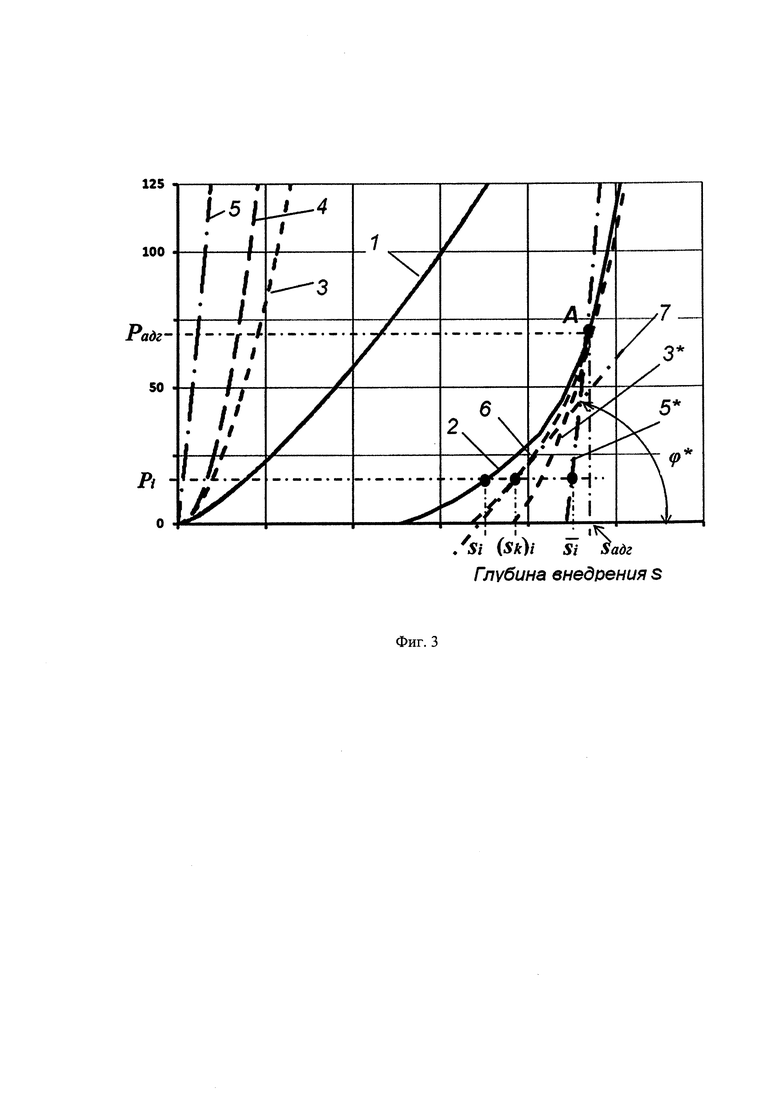
На фиг. 3. изображена в увеличенном масштабе анализируемая область I графика из фиг. 2. 1 - экспериментальная кривая нагружения, 2 - экспериментальная кривая разгружения, 3, 4, 5 - теоретические кривые разгружения (кривые упругого деформирования) слоистого тела, материала покрытия и материала основы в составе слоистого тела, соответственно, 3* - кривая разгружения 3, совмещенная с начальной частью кривой разгружения 2, 5* - кривая разгружения 5, совмещенная с точкой начала отслоения покрытия, 6 - расчетная кривая упругого деформирования отслоившегося покрытия, 7 - линейная аппроксимация расчетной кривой упругого деформирования отслоившегося покрытия, ϕ* - угол наклона линии 7 к оси абсцисс.
Способ определения адгезионной прочности тонких твердых покрытий реализуется следующим образом.
Для исследуемого изделия с тонким твердым покрытием измеряют толщину покрытия h. В случае использования стандартного материала в качестве подложки записывают значения модуля нормальной упругости Е0, коэффициента Пуассона μ0 из справочника. Если материал основы неизвестен, то производят измерение упругих характеристик и объемной твердости с использованием стандартных методик. Определение модуля упругости материала покрытия производят по одной из методик, описанной в технической и научной литературе (см. например, стандарт ISO (International Standard) 14577-4:2007 или патент РФ №2618500. Способ определения модуля упругости материала покрытия на изделии. Авт.Воронин Н.А. 28.04.2016 г. Опубл. 03.05.2017. Бюл. 13). Коэффициент Пуассона материала покрытия записывают из известных опубликованных в научной литературе значений или принимают равной материалу основы. Записывают известные значения упругих характеристик алмазного индентора: модуля Юнга Еи и коэффициента Пуассона μи. С помощью прибора - микро- или нанотвердометра с непрерывной регистрацией нагрузки и глубины внедрения внедряют алмазный наконечник в виде четырехугольной (пирамида Виккерса) или треугольной пирамиды (пирамида Берковича) в исследуемое слоистое тело (поверхность с тонким твердым покрытием) и производят запись диаграммы «нагрузка Р - внедрение s» (см. фиг. 1). Анализируют полученную экспериментальную диаграмму внедрения на наличие резких (скачкообразных) изменений плавности хода кривой нагружения. Если таковые обнаруживаются, то необходим анализ состояния и вида отпечатка на предмет обнаружения поверхностных трещин или отслоения покрытия. Обнаружение разрушений и повреждений в зоне отпечатка и статистически подтверждаемая повторяемость скачков на кривой нагружения является основанием для отказа от применимости описываемого способа определения адгезионной прочности. В случае отсутствия сомнения в плавности кривой нагружения и характерного вида кривой разгружения (с видимым отклонением кривой в конце процесса разгружения в сторону начала координат диаграммы) проводится исследование самого отпечатка и окрестностей отпечатка с помощью усиленной оптики или зондовых высокоразрешающих инструментальных средств на предмет обнаружения вспучивания покрытия в месте индентирования и повреждений покрытия. При наличии вспучивания покрытия, трещин любого вида или локального разрушения покрытия оценка адгезионной прочности с помощью описываемого метода производится не может.
После принятия решения о пригодности экспериментальной диаграммы внедрения для дальнейшего исследования проводится расчет эффективного модуля упругости для исследуемого слоистого тела. Используя известные данные о толщине покрытия, приведенных модулях упругости материалов покрытия и основы, расчет эффективного приведенного модуля упругости слоистого тела ведется по формуле (см. Н.А. Воронин. Расчет параметров упругого контакта и эффективных характеристик топокомпозита для случая взаимодействия последнего со сферическим индентором. Трение и износ. 2002, т. 23, №6. с. 583-596. Н.А. Воронин. Теоретическая оценка композиционной и истинной твердости тонких покрытий. Трение и смазка в машинах и механизмах. 2011, №7. с. 11-21.)

где Ф - упруго-геометрический параметр, диапазон существования которого 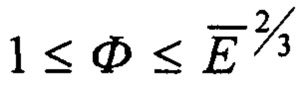 для
для 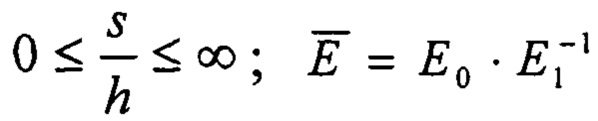 - эффективная упругая константа слоистого тела;
- эффективная упругая константа слоистого тела;
Е1, Е0 - модули нормальной упругости материалов покрытия и основы;
h - толщина покрытия,
s - глубина внедрения в материал с покрытием.
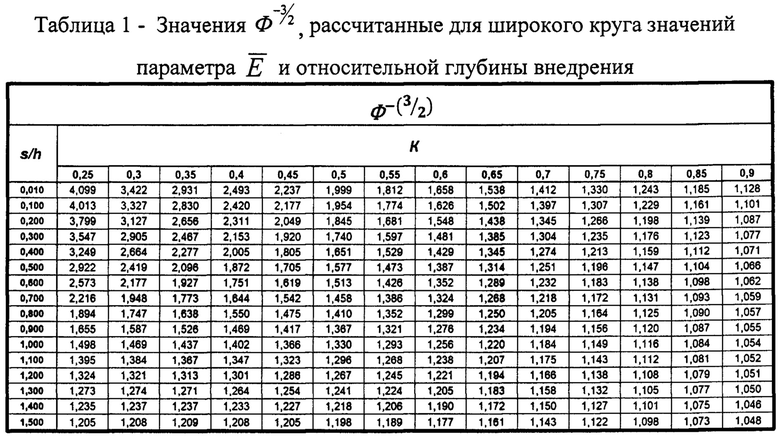
Эффективный модуль упругости слоистого тела может быть рассчитан по формуле (1) или с использованием табулированных значений функции 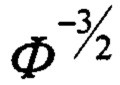 , определенных для широкого круга значений параметра
, определенных для широкого круга значений параметра 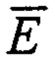 и представленных в таблице 1.
и представленных в таблице 1.
Далее выражение (1) используется для получения зависимости, описывающей теоретическую кривую разгружения слоистого тела в координатах «усилие разгрузки - глубина внедрения» (см. Воронин Н.А. Моделирование диаграммы внедрения для топокомпозитов. Проблемы машиностроения и надежности машин, 2018, №5, с. 57-65.):

где 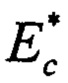 - значение эффективного приведенного модуля упругости слоистого тела;
- значение эффективного приведенного модуля упругости слоистого тела;
α - эквивалентный угол конуса (70,3° для индентора Берковича);
s - глубина индентора в исследуемую поверхность, отсчитываемая от свободной поверхности.
По зависимости (2) строится графически теоретическая кривая разгружения слоистого тела на экспериментальной диаграмме внедрения. Графически полученная зависимость изменения нагрузки от глубины внедрения для слоистого тела представляет собой кривую упругого деформирования (см. фиг. 2, кривая 3), начинающуюся из начала координат.
Используя зависимость (см. Fischer-Cripps А.С. Critical review of analysis and interpretation of nanoindentation test data. Surface & Coatings Technology, 2006, V. 200, p. 4153):
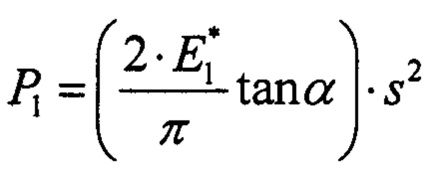
строится графически теоретическая кривая разгружения материала покрытия на экспериментальной диаграмме внедрения. Графически полученная зависимость изменения нагрузки от глубины внедрения для материала покрытия представляет собой кривую упругого деформирования материала покрытия (см. фиг. 2, кривая 4), начинающуюся из начала координат.
На экспериментальной диаграмме внедрения по результатам аналитического решения (3) или графического вычитания из теоретической кривой разгружения слоистого тела теоретической кривой разгружения материала покрытия строится графически расчетная кривая упругого деформирования материала подложки в составе слоистого тела (см. фиг. 2, кривая 5):

где (s0)i - текущее значение глубины внедрения (упругой деформации) для рассчитываемой кривой упругого деформирования материала подложки в составе слоистого тела,
(sc)i - текущее значение глубины внедрения (упругой деформации) для теоретической кривой разгружения слоистого тела и
(s1)i - текущее значение глубины внедрения (упругой деформации) для теоретической кривой разгружения материала покрытия,
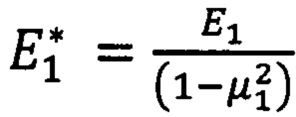 - приведенный модуль упругости материала покрытия.
- приведенный модуль упругости материала покрытия.
На диаграмме внедрения переносим (совмещаем) теоретическую кривую 3 разгружения слоистого тела с экспериментальной кривой разгружения таким образом, чтобы значения максимальной нагрузки Pmax, полученной при построении экспериментальной диаграммы внедрения совпало с таким же значением величины нагрузки, определяемой по аналитической зависимости (2). Кривая 3* на фиг. 2 показывает результат совмещения кривых разгрузки.
Фиксируют (см. фиг. 2, точка А) значение нагрузки Радг и глубины внедрения sадг (см. фиг. 2, точка А) в области экспериментальной кривой разгружения, в которой кривая разгружения начинает резко расходится с теоретической кривой разгружения слоистого тела. Затем переносят (смещают) теоретическую кривую разгружения материала подложки в область нахождения ранее смещенной теоретической кривой разгружения слоистого тела таким образом, чтобы кривая разгружения материала подложки проходила через точку А с координатами [Радг, sадг] и рассчитывают координаты точек (sk)i расчетной кривой упругого деформирования (см. фиг. 3, кривая 4) отслоившегося покрытия для диапазона значений усилия нагружения 0<Pi<Радг, используя выражение:

где (sk)i - текущее значение глубины внедрения расчетной кривой упругого деформирования отслоившегося покрытия,
si - текущее значение глубины внедрения для экспериментальной кривой упругого деформирования отслоившегося покрытия,
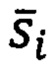 - текущее значение глубины внедрения для смещенной теоретической кривой упругого деформирования материала подложки.
- текущее значение глубины внедрения для смещенной теоретической кривой упругого деформирования материала подложки.
Используя набор данных текущих значений (sk)i строится расчетная кривая упругого деформирования отслоившегося покрытия (фиг. 4, кривая 6) в диапазоне значений усилия нагружения 0<Pi<Радг, осуществляется линейная аппроксимация кривой 6 (см. фиг. 3, кривая 7). По углу наклона кривой 7 к оси абсцисс (фиг. 3, угол ϕ) рассчитывается тангенс угла ϕ, значение которого соответствует жесткости расчетного отслоившегося покрытия Кс. Значение Кс используется для определения адгезионной прочности покрытия G* к основному материалу изделия при подстановки его в выражение:

где Kс - тангенс угла наклона прямой линии, полученной путем линейной аппроксимации кривой упругого деформирования отслоившегося покрытия,
h - толщина покрытия;
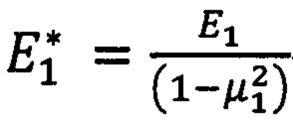 - приведенный модуль упругости материала покрытия.
- приведенный модуль упругости материала покрытия.
Пример. Для примера было произведено определение адгезионной прочности покрытия из нитрида титана (TiN), нанесенного магнетронным способом, толщиной 5 мкм на алюминиевый сплав Д16Т. Модуль Юнга и коэффициент Пуассона алмазной пирамиды Берковича были 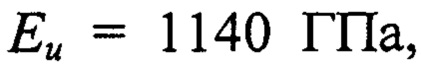
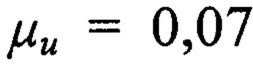 . Приведенные упругие характеристики материала основы изделия E0*=93 ГПа, материала покрытия Е1*=230 ГПа. Запись диаграммы внедрения в материал основы и в поверхность с покрытием производилось на наноиндентометре НаноСкан 4Д с достижением максимальной нагрузки в 500 мН.
. Приведенные упругие характеристики материала основы изделия E0*=93 ГПа, материала покрытия Е1*=230 ГПа. Запись диаграммы внедрения в материал основы и в поверхность с покрытием производилось на наноиндентометре НаноСкан 4Д с достижением максимальной нагрузки в 500 мН.
Расчет адгезионной прочности исследуемой слоистого тела проводился по формуле (5), для случая при котором не учитывался вклад упругой деформации материала подложки, то есть G и когда учитывался - то есть G*.
Результаты расчета дали значения общей (эффективной) адгезионной прочности G=7,9±2,1 Дж/м2, а истинной (расчетной) G*=9,46±2,26 Дж/м2. И эффективная и истинная адгезионная прочность покрытия TiN несколько ниже значений вязкости разрушения покрытий из тугоплавких соединений, известных в научно-технической литературе. Так для покрытий CrN и CrTiN на стальных подложках, эффективная адгезионная прочность находится в диапазоне значений от 10 до 70 Дж/м2 (см. например Wang Q., Zhou F., Yana J. Evaluating mechanical properties and crack resistance of CrN, CrTiN, CrAlN and CrTiAlN coatings by nanoindentation and scratch tests. Surface & Coatings Technology. 2016, V. 285, pp. 203-213.) Однако, если учесть, что ионно-плазменные покрытия получают в процессе высокотемпературного синтеза, который приводит к возникновению высоких остаточных напряжений, можно считать, что полученные значения адгезионной прочности исследуемого в данной работе покрытия достаточно объективно отражают уровень его напряженного состояния.
Результаты экспериментальной проверки свидетельствуют о пригодности предлагаемого способа для практического использования.
Изобретение относится к измерительной технике для определения адгезионной прочности тонких защитных покрытий на изделиях машиностроения. Сущность: производят нагружение и внедрения алмазного пирамидального наконечника в поверхность слоистого тела изделия с покрытием на глубину обеспечивающую отслоение покрытия от основы при разгружении, при этом записывают диаграмму внедрения в виде графиков кривых изменения нагрузки от глубины внедрения при возрастании и затем снижении нагрузки до нуля и фиксируют значения максимальной нагрузки и соответствующей ей глубины внедрения, рассчитывают эффективный модуль упругости слоистого тела, осуществляют графически построение теоретических кривых разгружения независимо материала покрытия, материала основы и слоистого тела в диапазоне значений экспериментальных данных по нагрузке, после чего совмещают теоретическую кривую разгружения слоистого тела с экспериментальной кривой разгружения путем совпадения значения нагрузки у теоретической кривой разгружения слоистого тела со значением нагрузки Рmax экспериментальной диаграммы внедрения, выявляют область расхождения экспериментальной и теоретической кривой разгружения слоистого тела, регистрируют значения в этой области нагрузки Радг и глубины внедрения sадг на экспериментальной кривой разгружения, смещают графически теоретическую кривую разгружения материала основы в область нахождения экспериментальной кривой разгружения таким образом, чтобы кривая разгружения материала основы проходила через точку с координатами [Радг, sадг] и рассчитывают значение адгезионной прочности по формуле. Технический результат: повышение точности и объективности определения адгезионной прочности тонких покрытий. 1 табл., 3 ил.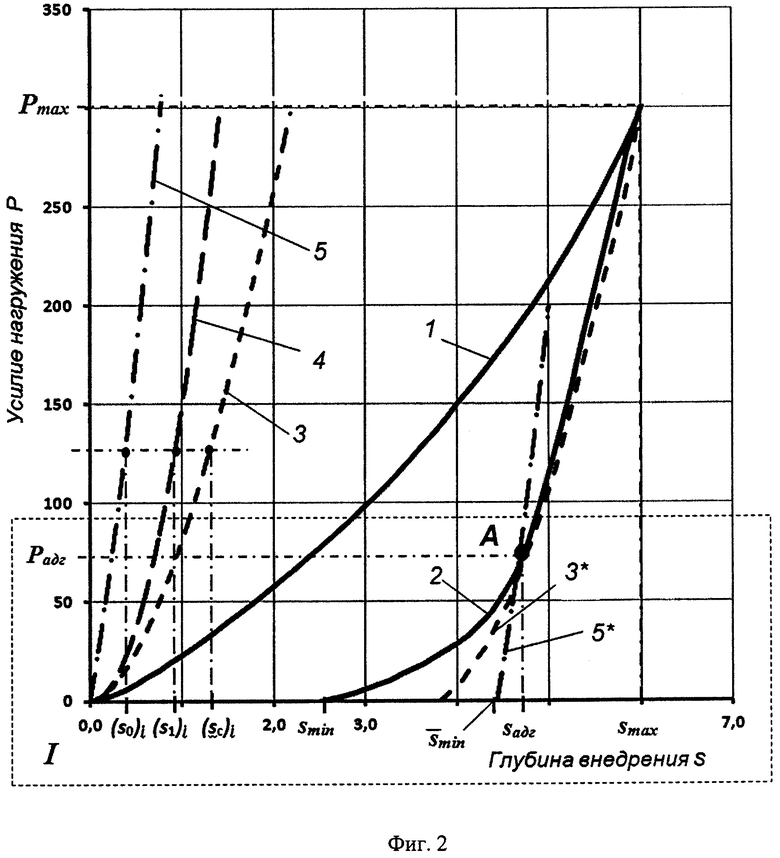
Способ определения адгезионной прочности тонких твердых покрытий на изделиях, включающий нагружение и внедрение алмазного пирамидального наконечника в поверхность слоистого тела изделия с покрытием на глубину отслоения покрытия от основы при разгружении, при этом записывают диаграмму внедрения в виде графиков кривых изменения нагрузки от глубины внедрения при возрастании и затем снижении нагрузки до нуля и фиксируют значения максимальной нагрузки и соответствующей ей глубины внедрения, отличающийся тем, что в нем рассчитывают эффективный модуль упругости слоистого тела по формуле:

осуществляют графически построение теоретических кривых разгружения независимо слоистого тела, материала покрытия и подложки по формулам соответственно:
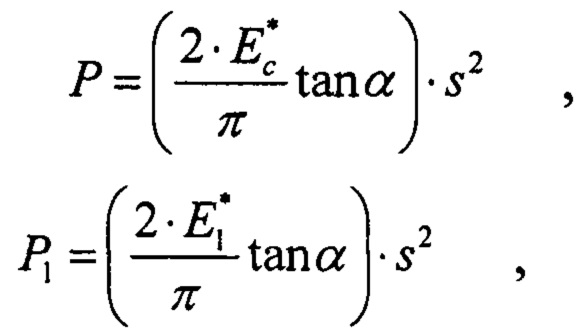
а текущие значения глубины внедрения (s0)i для кривой разгружения (упругого деформирования) материала подложки в составе слоистого тела рассчитываются по формуле
(s0)i=(sc)i-(s1)i,
где (sc)i - текущее значение глубины внедрения (упругой деформации) для теоретически рассчитываемой кривой разгружения слоистого тела и
(s1)i - текущее значение глубины внедрения (упругой деформации) для теоретически рассчитываемой кривой разгружения материала покрытия,
s - текущая глубина индентора, отсчитываемая от свободной поверхности,
α - эквивалентный угол конуса (70,3° для индентора Берковича),
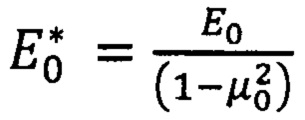 - приведенный модуль упругости материала подложки,
- приведенный модуль упругости материала подложки,
Φ - упруго-геометрический параметр, диапазон существования которого  для
для 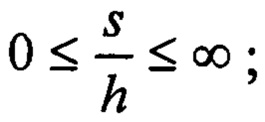
 - эффективная упругая константа слоистого тела;
- эффективная упругая константа слоистого тела;
Е1, Е0 - модули нормальной упругости материалов покрытия и подложки;
μ0 и μ1, - коэффициенты Пуассона материала основы и покрытия, после чего совмещают теоретическую кривую разгружения слоистого тела с экспериментальной кривой разгружения путем совпадения значения нагрузки у теоретической кривой разгружения слоистого тела со значением нагрузки Pmax экспериментальной диаграммы внедрения, выявляют область расхождения экспериментальной и теоретической кривой разгружения слоистого тела, регистрируют значения в этой области нагрузки Радг и глубины внедрения sадг на экспериментальной кривой разгружения, смещают графически теоретическую кривую разгружения материала основы в область нахождения экспериментальной кривой разгружения таким образом, чтобы кривая разгружения материала основы проходила через точку с координатами [Радг, sадг] и рассчитывают значение адгезионной прочности по формуле:

где Kс - тангенс угла наклона прямой линии, полученной путем линейной аппроксимацией расчетной кривой упругого деформирования отслоившегося покрытия, которую строят для диапазона нагрузок 0<Pi<Радг по координатам [(sk)i, Pi], используя выражение:
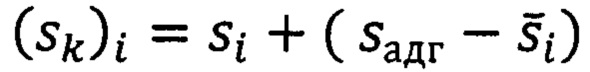
где (sk)i - текущее значение глубины внедрения для расчетной кривой упругого деформирования отслоившегося покрытия,
si - текущее значение глубины внедрения для экспериментальной кривой упругого деформирования отслоившегося покрытия,
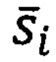 - текущее значение глубины внедрения для смещенной теоретической кривой упругого деформирования материала подложки;
- текущее значение глубины внедрения для смещенной теоретической кривой упругого деформирования материала подложки;
h - толщина покрытия;
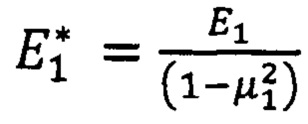 - приведенный модуль упругости материала покрытия.
- приведенный модуль упругости материала покрытия.
| Счетчик числа проходов товара через красильные барки | 1928 |
|
SU13606A1 |
| Устройство для определения адгезионной прочности многослойного керамического теплозащитного покрытия | 2016 |
|
RU2643682C1 |
| Приспособление для механической выгрузки цементного клинкера из шахтной печи | 1928 |
|
SU13618A1 |
| Способ определения адгезионной прочности покрытия | 1982 |
|
SU1052947A1 |
| US 6339958 B1, 22.01.2002. | |||
Авторы
Даты
2019-12-26—Публикация
2019-05-20—Подача