Изобретение относится к области информационных технологий, в частности к способам оптимизации хранения и выборки интервальных и разнородных данных. Изобретение может быть использовано в таких системах, как емкие хранилища данных, системы управления базами данных (СУБД), геоинформационные системы (ГИС).
Известен способ хранения и выборки данных n-мерных интервалов [1]. Этот способ в различных вариантах применяется, в частности, в хранилищах данных и СУБД, являясь в настоящее время одним из самых продуктивных в задачах, связанных с хранением и выборкой данных n-мерных интервалов. Согласно этому способу хранение и выборка данных таких интервалов осуществляется в пространственной структуре данных R-tree, которая является сбалансированным блочным деревом. Элементы данных листового уровня дерева R-tree являются элементами реальных данных - исходными n-мерными интервалами, а элементы данных других уровней являются элементами вспомогательных данных - n-мерными интервалами соответствующих уровней. Элементы данных каждого уровня в отдельности пространственно интегрированы как интервалы соответствующего уровня. Эта интеграция достигается путем объединения элементов данных каждого ненулевого уровня в такие блоки элементов данных, которые с помощью указателей связываются с соответствующими им блоками-предками высшего уровня. Элементы данных нулевого уровня интегрированы в единственный корневой блок.
Недостатком этого способа является то, что в структуре R-tree высокая производительность выполнения интервальных запросов гарантирована быть не может, о чем упоминается и в статье [1]. Это связано с тем, что элементы данных в этой структуре пространственно интегрированы как n-мерные интервалы. При таком способе хранения невозможна одновременная интеграция элементов данных как интервалов по критериям пересечений, вложений, покрытий, касаний и других их взаимных расположений в пространстве. Причиной этого является тот факт, что не существует способа одновременного упорядочения n-мерных интервалов по этим критериям в их собственном n-мерном пространстве. Поэтому блоки элементов данных дерева R-tree могут перекрываться. Это, в свою очередь, не может обеспечить поиск требуемых данных по однозначному пути во время выполнения интервального запроса в R-tree. Более того, эффект перекрывания блоков приводит еще и к следующему дополнительному негативному явлению. Хотя элементы данных каждого уровня дерева R-tree и интегрированы пространственно как n-мерные интервалы, тем не менее из этого вовсе не следует структурная близость пространственно близких интервалов одного и того же уровня в целом дереве. Пространственно близкие интервалы в R-tree могут оказаться структурно далекими, а пространственно далекие интервалы - структурно близкими. В R-tree худший случай выполнения интервальных запросов является максимально медленным с нулевой отдачей и соответствует полному обходу дерева при получении пустого множества результата.
Также известен способ хранения и выборки данных n-мерных интервалов [2]. Согласно этому способу хранение и выборка данных таких интервалов осуществляется в комбинации n структур данных, каждая из которых является двоичным деревом секций. Элементами реальных данных каждого из этих деревьев являются соответствующие базисные проекции исходных n-мерных интервалов. Эти проекции в каждом дереве одновременно являются 2-мерными точками, но отсортированы они по критерию их пересечений. Такой подход обеспечивает оптимальный поиск данных всех n-мерных интервалов, пересекающихся с заданным.
Первым недостатком этого способа является то обстоятельство, что в соответствии с ним хранение и выборка данных осуществляется в n структурах данных, что связано с дополнительными требованиями к используемой памяти и падением производительности с ростом n. Вторым недостатком этого способа является ограничение возможностей осуществления интервальных запросов в каждом дереве. Это ограничение выражается в том, что при таком хранении интервалы являются отсортированными только по критерию их пересечений, но они не интегрированы по критериям вложений, покрытий, касаний и других их взаимных расположений, что не обеспечивает их эффективный поиск по таким критериям.
Способов, позволяющих в одной и той же структуре данных эффективно выполнять любые интервальные запросы, не выявлено.
Задачей изобретения является создание возможности эффективного выполнения в одной и той же пространственной структуре данных любых интервальных запросов с различными условиями взаимного расположения требуемых n-мерных интервалов относительно заданного.
Поставленная задача достигается тем, что в способе хранения и выборки данных n-мерных интервалов, согласно изобретению, формируют такую пространственную структуру данных S, элементами реальных данных которой являются исходные n-мерные интервалы, пространственно интегрированные как 2n-мерные точки, координаты которых совпадают с соответствующими координатами проекций этих интервалов на оси базиса их пространства; определяют линзу, являющуюся 2n-мерным интервалом оператора интервального запроса, представляющего собой инструкцию о выборке данных требуемых n-мерных интервалов с описанием заданного интервала и условий расположения относительно него требуемых, причем линзу определяют согласно розе интервалов, представляющей собой виртуальную двумерную геометрическую диаграмму областей таких 2n-мерных точек в осях xp и уp их пространства, координатами {xp, уp} которых являются соответствующие координаты р-проекций соответствующих этим точкам n-мерных интервалов, где р-проекция n-мерного интервала это его проекция на р-ось базиса его пространства; конструируют и сохраняют на физическом носителе информации оператор интервального запроса о выборке из структуры S данных таких точек, которые покрываются этой линзой; выполняют с помощью этого оператора интервальный запрос к структуре S, результатом которого будет множество данных 2n-мерных точек, одновременно являющихся и данными соответствующих им искомых интервалов.
Такой способ, за счет пространственной интеграции n-мерных интервалов как 2n-мерных точек, позволяет в одной и той же пространственной структуре данных создать возможность эффективного выполнения любых интервальных запросов с различными условиями взаимного расположения требуемых интервалов относительно заданного. Элементы реальных данных такой структуры являются одновременно и n-мерными интервалами и соответствующими им 2n-мерными точками. Эти элементы данных оказываются в 2n-мерном пространстве структуры одновременно интегрированными как 2n-мерные точки пространственно и как n-мерные интервалы по критериям пересечений, вложений, покрытий, касаний и других их взаимных расположений в их собственном n-мерном пространстве. Поэтому такая пространственная структура данных является оптимизированной для выполнения в ней любых интервальных запросов.
В предлагаемом изобретении используется следующая терминология.
Под термином "данные" в контексте излагаемого материала подразумеваются физические данные, то есть информация, представленная в формализованном виде и предназначенная для обработки техническими средствами, например ЭВМ. Физические данные могут сохраняться на физическом носителе информации, модифицироваться, перемещаться, извлекаться, удаляться.
Под каждым из понятий "точка", "отрезок", "прямоугольник", "интервал" подразумеваются наборы физических данных.
Что это за наборы, поясняют следующие ниже примеры.
Точкой называется набор данных, состоящий из одного элемента четких (точных) данных типа: возраст равен 43. Здесь набором данных является {43} - набор данных, состоящий из одного элемента данных, этим элементом являются четкие данные, имеющие точное значение 43.
Отрезком называется набор данных, состоящий из одного элемента нечетких ("размытых", приблизительных, предполагаемых) данных типа: возраст примерно равен 35-40. Здесь набором данных является {35-40} - набор данных, состоящий из одного элемента данных (не из двух, а из одного), этим элементом являются нечеткие данные, имеющие (одно, а не два) интервальное значение 35-40.
И точка и отрезок в этих примерах являются наборами 1-мерных данных.
Набор n-мерных данных это набор данных, состоящий из n элементов данных, этими элементами могут являться как четкие, так и нечеткие данные.
Пример (для двумерного случая, то есть при n=2):
2-мерной точкой называется набор данных, состоящий из двух элементов четких (точных) данных типа: возраст равен 43, а вес равен 85. Здесь набором данных является {43, 85} - набор данных, состоящий из двух элементов данных, этими элементами являются четкие данные, имеющие точные значения 43 и 85.
2-мерным отрезком называется набор данных, состоящий из двух элементов данных, один из которых является элементом четких (точных) данных, а другой - элементом нечетких ("размытых", приблизительных, предполагаемых) данных типа: возраст примерно равен 35-40, а вес равен 80. Здесь набором данных является {35-40, 80} - набор данных, состоящий из двух элементов данных, один из которых является элементом четких данных, имеющих точное значение 80, а другой - элементом нечетких данных, имеющих интервальное значение 35-40.
2-мерным прямоугольником называется набор данных, состоящий из двух элементов нечетких ("размытых", приблизительных, предполагаемых) данных типа: возраст примерно равен 33-35, а вес примерно равен 74-76. Здесь набором данных является {33-35, 74-76} - набор данных, состоящий из двух элементов данных, этими элементами являются нечеткие данные, имеющие интервальные значения 33-35 и 74-76.
n-мерным прямоугольником называется набор n-мерных данных, то есть набор данных, состоящий из n элементов данных, этими элементами могут быть как четкие данные, так и нечеткие.
Любые, рассмотренные выше, точки и отрезки (в том числе и 1-мерные) подпадают под это определение, то есть являются n-мерными прямоугольниками. Поэтому точки и отрезки это тоже наборы n-мерных данных.
Каждому n-мерному прямоугольнику (набору физических данных) соответствует геометрический n-мерный прямоугольник в некотором n-мерном декартовом пространстве, являющийся его геометрическим образом. Такие соответствия виртуальны.
Никакие материальные операции над математическими (абстрактными, логическими) объектами и пространствами ни в формуле изобретения, ни в настоящем его описании не подразумеваются. Все соответствия материальных и геометрических объектов и соответствующие этим соответствиям рисунки приводятся лишь для наглядного разъяснения. Если говорится о любой геометрии n-мерных прямоугольников (наборов данных), то подразумевается геометрия их виртуальных образов в некотором n-мерном декартовом пространстве. Некоторые определения, приведенные ниже, подпадают под это определение как его частные случаи.
n-мерный прямоугольник (набор физических данных) называется ортогональным, если каждое ребро его геометрического образа параллельно какой-либо из осей базиса этого пространства.
n-мерным интервалом называется ортогональный п-мерный прямоугольник.
Так что n-мерный интервал, точно также как и n-мерный прямоугольник, является набором физических n-мерных данных, состоящим из n элементов данных. Поэтому любой n-мерный интервал, также как и любой n-мерный прямоугольник, является материальным объектом - некоторым набором физических данных.
n-мерный интервал может быть точкой, отрезком, прямоугольником, кубом, гиперкубом и т.д. Например, n-мерная точка является n-мерным (ортогональным) прямоугольником, все ребра которого имеют нулевую длину.
n-мерные интервалы могут быть открытыми, закрытыми и частично открытыми.
Открытые n-мерные интервалы это такие интервалы, прямоугольные области геометрических образов которых не включают в себя свои границы.
Закрытые n-мерные интервалы это такие интервалы, прямоугольные области геометрических образов которых включают свои границы.
Частично открытые n-мерные интервалы это такие интервалы, прямоугольные области геометрических образов которых включают в себя не все свои границы, но хотя бы одну из них.
Открытые 1-мерные интервалы (наборы физических данных), также как и их геометрические образы, в настоящем тексте обозначаются как (х, у), закрытые - как [х, у], а частично открытые - как (х, у] или [х, у), в зависимости от того, какой конец этого интервала из него исключен.
Разнородными n-мерными интервалами (по отношению друг к другу) называются такие n-мерные ортогональные прямоугольники, некоторые из которых имеют разное число нулевых ребер.
Например, разнородными n-мерными интервалами (по отношению друг к другу) являются точки, отрезки, прямоугольники, кубы, гиперкубы и т.д.
Разнородные данные это данные разнородных n-мерных интервалов.
Пространством n-мерного интервала называется пространство его геометрического образа, то есть то пространство, которому принадлежит геометрический образ этого интервала.
Областью n-мерных интервалов называется область их геометрических образов.
Координатами n-мерного интервала называются координаты его геометрического образа.
Проекциями n-мерного интервала называются проекции его геометрического образа.
Координатами проекций n-мерного интервала называются координаты проекций его геометрического образа.
р-проекция n-мерного интервала это его проекция на р-ось базиса его пространства. Любая р-проекция n-мерного интервала является 1-мерным интервалом.
Один n-мерный интервал лежит строго левее (правее) другого вдоль р-оси тогда и только тогда, когда р-проекция первого из них лежит на этой оси строго левее (правее) р-проекции второго, а любая другая из остальных проекций первого покрывается соответствующей проекцией второго.
Один n-мерный интервал пересекает слева (справа) другой вдоль р-оси тогда и только тогда, когда их геометрические образы пересекаются, и р-проекция первого из них на этой оси пересекает слева (справа) р-проекцию второго.
Вообще, когда речь идет о пересечениях n-мерных интервалов, их вложениях, покрытиях, касаниях или других их взаимных расположениях в пространстве, то под этими понятиями следует подразумевать соответствующие взаимные расположения их геометрических образов в соответствующем пространстве.
В описываемом способе под структурами данных нужно понимать физические системы закономерно связанных и находящихся во взаимной связи материальных объектов - физических данных. Более точно:
Структура данных это такое хранимое на физическом носителе информации множество, включающее в себя закономерно связанные и находящиеся во взаимной связи элементы реальных и вспомогательных физических данных, над которым эффективно выполняются конкретные алгоритмы. Структура данных материальна.
Любая структура данных имеет свою логику, иначе это была бы не структура, а беспорядочное множество данных.
Реальные данные это исходные данные, то есть такие физические данные, которые, собственно, и интересуют пользователя при сохранении и выборке. Например, данные температур или сигналов биений сердца.
Под вспомогательными данными подразумеваются такие физические данные, которые пользователя не интересуют, но необходимы для организации логических связей внутри структуры (физической системы), обеспечивающих эффективность выполнения конкретных алгоритмов над ее данными (то есть - обеспечивающих функционирование ее собственной логики). Например, формализованные метаданные (данные о данных) или адреса позиций (местоположений) конкретных данных. Формализованные метаданные и адреса также являются физическими данными.
Взаимосвязь элементов структуры может быть реализована, например, с помощью указателей.
Под указателями понимаются адреса тех или иных блоков данных или позиций внутри этих блоков. Так что указатели это физические данные, являющиеся адресами памяти и хранимые на физическом носителе информации точно также как и реальные данные. Указатели являются вспомогательными данными.
Вспомогательными данными могут быть и другие физические данные, отличные от указателей, например метаданные (данные о данных) и т.д. Вся внутренняя организация любой материальной структуры данных обеспечивается такими вспомогательными данными. Здесь под термином "внутренняя организация материальной структуры данных" подразумевается упорядочение ее элементов - физических данных в соответствии с логикой этой структуры.
Под моделью данных в настоящем тексте понимается физическая система, являющаяся еще более общей системой физических данных, чем структура данных. Например, моделями данных (в указанном смысле) являются СУБД и ГИС. Эффективность работы модели данных зависит от структур данных, которые являются частью ее ядра.
Формирование структуры данных это комплекс таких материальных действий, как распределение памяти (выделение места) для хранения данных на физическом носителе информации; поиск данных, сопровождающийся их извлечением и сравнением; вставки, удаления и модификации данных, предваряющиеся их поиском; сохранение данных на физическом носителе информации и т.д. Каждая конкретная структура данных формируется присущим ей способом.
Физическая структура данных в обязательном порядке содержит в себе как минимум один материальный объект. Если таких объектов нет, то нет и материальной структуры. Этим единственным объектом могут быть вспомогательные данные, например, адрес первого выделенного блока памяти. Структура данных пуста, если она не содержит в себе реальных данных.
Если структура данных существует (даже, если она пуста), это означает, что она была сформирована. Любые дальнейшие модификации структуры данных в соответствии с ее логикой, например, вставка данных, удаление данных, обновление данных, являются продолжением процесса ее формирования. В каждый момент завершения любой такой модификации структура данных является вновь сформированной. Любые модификации структуры данных, не соответствующие ее логике, являются процессом ее разрушения.
Пространственная структура данных - это такая структура пространственных (n-мерных) данных, элементы реальных данных которой интегрированы пространственно, то есть по критерию пространственной близости друг к другу. Таким критерием, например, может быть близость центров тяжести объектов, соответствующих этим элементам данных, или близость их ближайших (или наиболее далеких) границ.
Пространственная интеграция (пространственное группирование) физических данных - это такая их организация (упорядочение) на физическом носителе информации, которая соответствует пространственной интеграции их геометрических образов в некотором виртуальном геометрическом пространстве в смысле некоторого пространственного критерия близости. Пространственная интеграция объектов физической системы позволяет минимизировать время доступа между ее ближайшими объектами, в смысле определенного в этой системе пространственного критерия близости. Пространственная интеграция элементов данных в пространственной структуре данных может быть реализована связями между ними и (или) их группами с помощью указателей. Пространственная интеграция элементов данных обеспечивает в пространственной структуре данных возможность их независимого интервального поиска вдоль любой из осей базиса ее пространства.
На основе рассматриваемого в описываемом способе принципа интеграции возможна разработка различных логических структур данных (например, в виде блочных или бинарных деревьев) для реализуемых впоследствии на их основе соответствующих физических структур данных. Любые из этих физических систем подпадают под пространственную структуру, упоминаемую в формуле изобретения, если только принцип интеграции в них тот, который описывается в предлагаемом способе.
Пространство геометрических образов физических данных пространственной структуры данных называется пространством этой структуры.
Пространство пространственной структуры данных является декартовым. Каждая из осей этого пространства соответствует такому множеству уникальных данных, на котором определено отношение порядка. Тип данных каждой оси пространства соответствует типу данных того множества, которому эта ось соответствует. Такими типами данных могут являться числовые, символьные, строковые, временные (даты) и т.д.
Структура пространственных (n-мерных) данных может быть пространственной или нет. Например, такая структура пространственных данных, как двоичное дерево n-мерных данных, не является пространственной структурой данных, поскольку пространственно соседние данные в этой структуре не могут быть интегрированы пространственно. Примерами пространственных структур данных являются KDB-tree, Quad-tree, R-tree.
Запрос это процесс запрашивания данных из структуры данных, включающий в себя их поиск, извлечение и сохранение в виде отдельного множества на физическом носителе информации. Запрос к модели данных по сути является запросом к структуре данных этой модели. Запрос к конкретной структуре данных выполняется способом в соответствии с ее алгоритмами.
Результатом запроса является извлеченное из структуры данных и сохраненное на физическом носителе информации множество данных, удовлетворяющих этому запросу.
Интервальный запрос - это запрос к структуре данных о выборке данных требуемых n-мерных интервалов относительно заданного.
Инструкция запроса - это выражение, описывающее реальные данные, которые требуется получить из структуры данных.
Инструкция не определяет способ поиска данных. Способы их поиска всецело определяются алгоритмами поиска структуры данных, в которой хранятся или возможно хранятся эти данные среди других. Инструкция запроса является командой, которая в соответствии с алгоритмами структуры данных подлежит выполнению техническими средствами, например ЭВМ.
Оператор интервального запроса - это инструкция о выборке данных требуемых n-мерных интервалов, включающая в себя описание заданного интервала и условий расположения относительно него требуемых.
Линзой называется n-мерный интервал оператора интервального запроса, относительно которого осуществляется выборка требуемых. Линза может не являться элементом структуры данных. Это объект, определяемый своими данными и задаваемый в качестве параметра оператора любого интервального запроса.
Условиями оператора интервального запроса являются условия расположения требуемых n-мерных интервалов относительно его линзы. Этими условиями могут являться пересечения, вложения, покрытия, касания и другие требования взаимных расположений выбираемых интервалов относительно линзы.
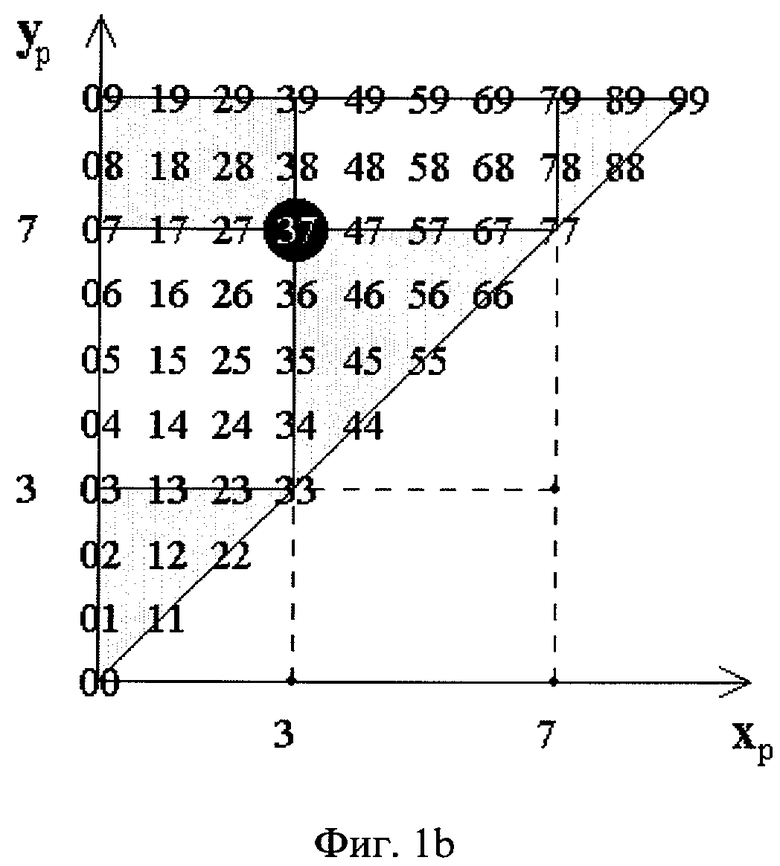
Роза интервалов - это виртуальная двумерная геометрическая диаграмма областей таких 2n-мерных точек в осях xp и уp их пространства, координатами {xp, уp} которых являются соответствующие координаты р-проекций соответствующих этим точкам n-мерных интервалов.
р-проекции всех интервалов в осях розы упорядочены как точки и, кроме того, интегрированы как 1-мерные интервалы по различным критериям своих взаимных расположении на оси р. По существу, роза интервалов - это виртуальный геометрический визуализатор полного и глобального упорядочения в осях хp и уp всех интервалов пространства размерности n в виде точек размерности 2n. Каждая из областей ("лепестков") и комбинаций областей розы интервалов соответствует конкретной группе р-проекций интервалов, расположенных на оси р по определенному критерию относительно такой р-проекции заданного интервала, которая имеет координаты {аp, bp}. Линия уp=xp розы интервалов соответствует точечным (нулевой длины) проекциям интервалов на р-ось. Роза интервалов имеет вид верхнего треугольника, но зеркальным отражением ее областей относительно оси уp=xp она может быть конвертирована в соответствующий нижний треугольник. Обе такие конфигурации розы равноценны. Тип данных осей хp и уp розы интервалов совпадает и соответствует типу данных оси р пространства интервалов.
Из определения розы интервалов ясно, что она является диаграммой для p, пробегающего значения p=0, ..., n-1, поэтому ее можно трактовать как набор из n диаграмм для каждого фиксированного р. В этом смысле розу интервалов можно считать n-мерной.
Роза интервалов виртуальна, для применения описываемого способа не требуется выполнять ее изображение на каком-либо носителе информации или выполнять над ней какие-либо материальные действия. Однако процесс интеграции n-мерных интервалов как 2n-мерных точек в структуре данных сам по себе влечет действия согласно розе интервалов (действия в соответствии с этой виртуальной диаграммой).
Способ иллюстрируется следующими чертежами.
На фигурах 1а и 1b изображена роза интервалов, на которой выделенная черная точка соответствует р-проекции заданного n-мерного интервала и имеет в осях хp и уp этой розы координаты {аp, bp}.
Отмеченные на фигуре 1а области розы означают следующее:
- R1 (серого цвета) - область всех р-проекций n-мерных интервалов, покрывающих р-проекцию заданного;
- R2 (серого цвета) - область всех р-проекций n-мерных интервалов, покрываемых р-проекцией заданного;
- R3 (серого цвета) - область всех р-проекций n-мерных интервалов, лежащих слева от р-проекции заданного;
- R4 (серого цвета) - область всех р-проекций n-мерных интервалов, лежащих справа от р-проекции заданного;
- R5 (белого цвета) - область всех р-проекций n-мерных интервалов, пересекающих слева р-проекцию заданного;
- R6 (белого цвета) - область всех р-проекций n-мерных интервалов, пересекающих справа р-проекцию заданного;
- R7=R1+R2+R5+R6 - область всех р-проекций n-мерных интервалов, пересекающих р-проекцию заданного.
На фигуре 1а точка qp является левой координатой проекции up одной из 2n-мерных линз оператора соответствующего интервального запроса, а точка rp - правой координатой проекции vp этой линзы.
На фигуре 1b изображен конкретный случай розы интервалов для всех возможных р-проекций n-мерных интервалов с целочисленными координатами (от 0 до 9) этих проекций. Координатами заданного интервала на фигуре 1b являются ар=3 и bp=7.
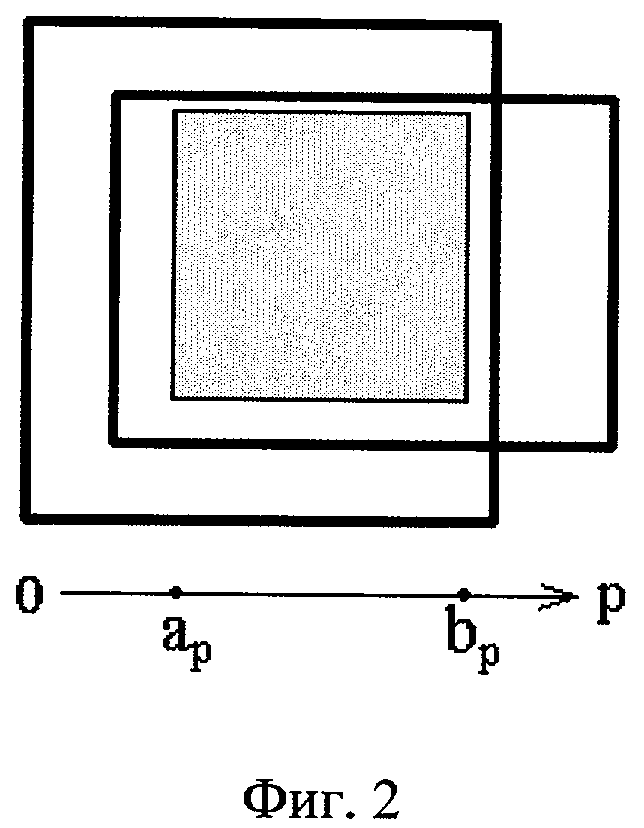
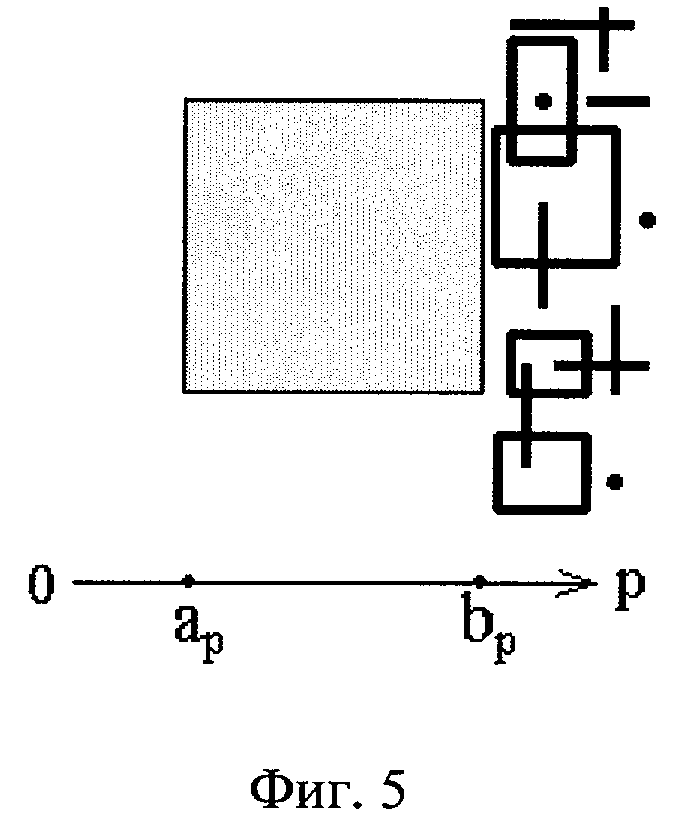
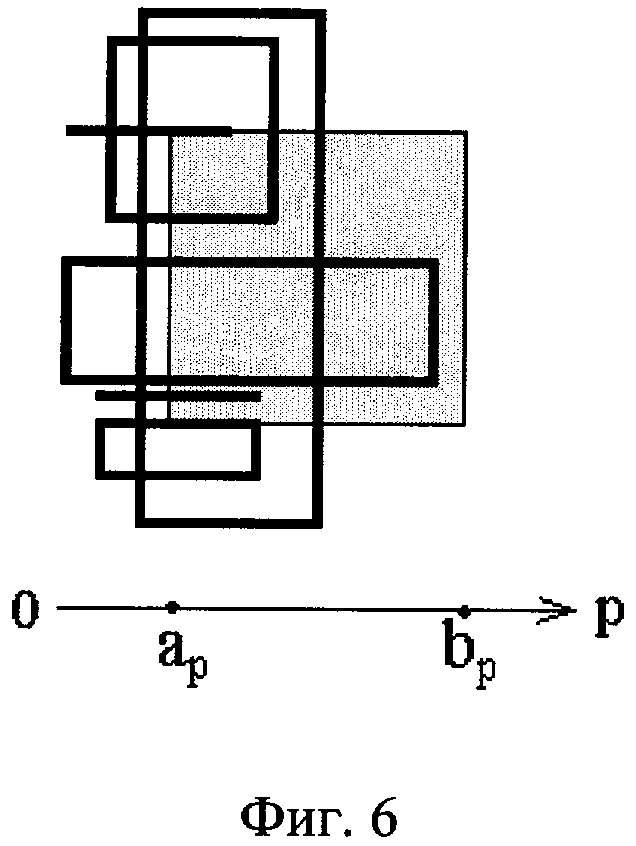
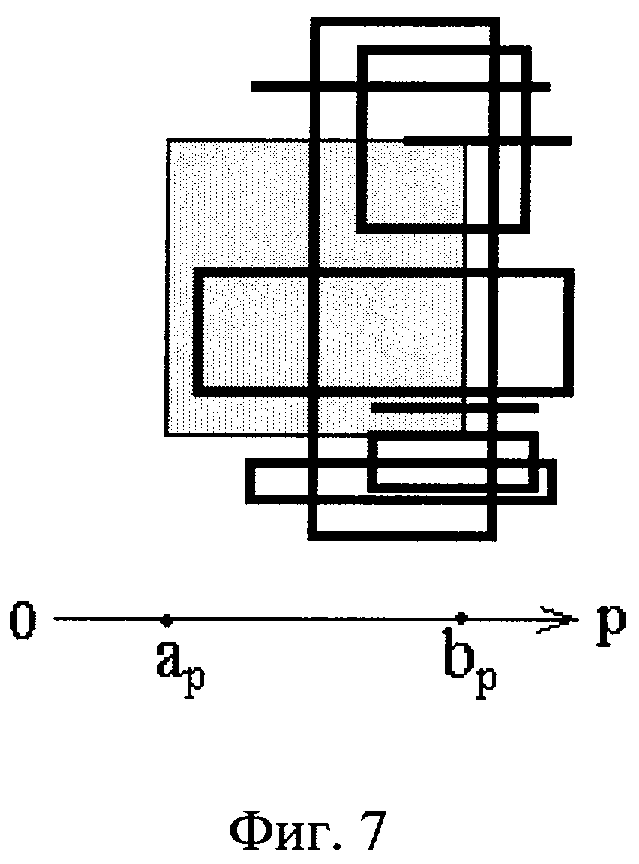
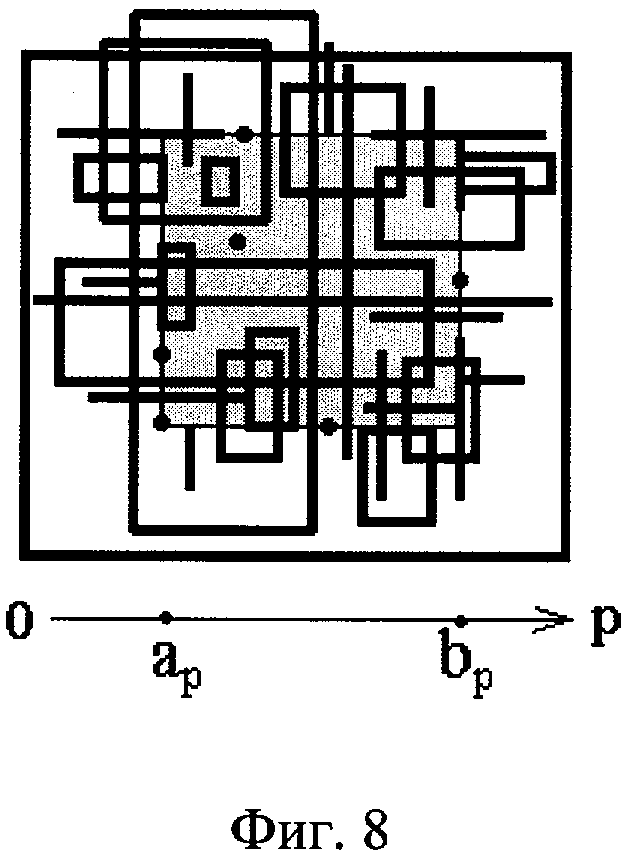
На фигурах 2-8 изображены примеры разнородных 2-мерных интервалов, имеющих различные положения относительно 2-мерного заданного (серого цвета). На каждой из этих фигур показана р-ось 2-мерного пространства этих интервалов. Координаты р-проекции заданного интервала обозначены через ар и bр.
На фигуре 2 изображены примеры 2-мерных интервалов, которые покрывают заданный, исключая те, которых заданный касается изнутри. Такими интервалами для заданного могут быть только 2-мерные интервалы с ненулевыми ребрами.
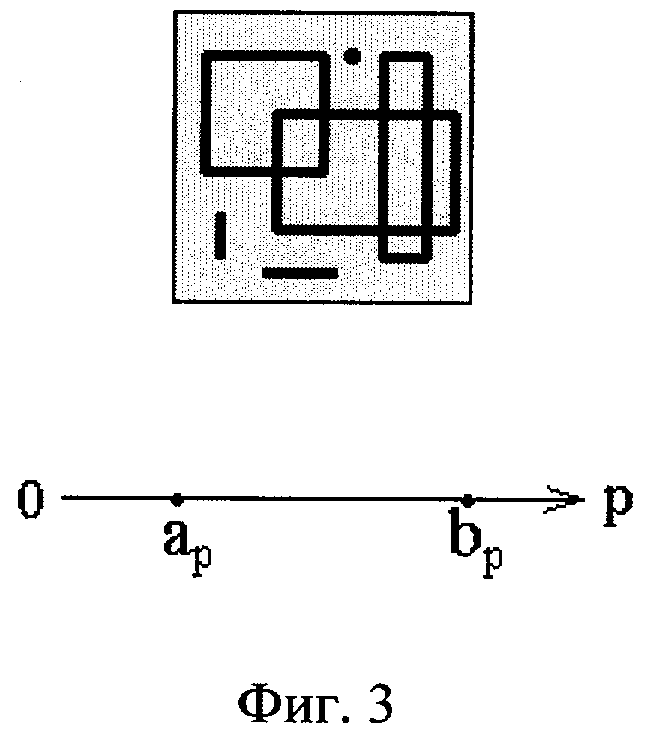
На фигуре 3 изображены примеры 2-мерных интервалов, которые покрывает заданный, исключая те, которые касаются заданного изнутри. Такими интервалами для заданного могут быть 2-мерные интервалы с ненулевыми ребрами, а также точки и отрезки.
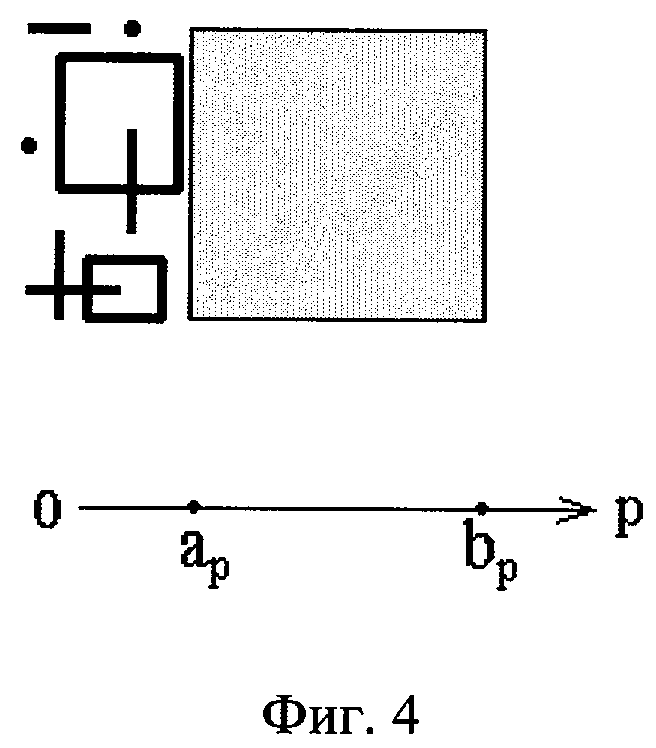
На фигуре 4 изображены примеры 2-мерных интервалов, которые лежат строго слева от заданного вдоль р-оси их пространства. Такими интервалами для заданного могут быть 2-мерные интервалы с ненулевыми ребрами, а также точки и отрезки.
На фигуре 5 изображены примеры 2-мерных интервалов, р-проекции которых лежат справа от р-проекции заданного, исключая те, р-проекции которых касаются р-проекции заданного. Такими интервалами для заданного могут быть 2-мерные интервалы с ненулевыми ребрами, а также точки и отрезки. Но некоторые из них могут не лежать строго справа от заданного. Так что случай, изображенный на этой фигуре, не является зеркальным отображением случая, изображенного на фигуре 4.
На фигуре 6 изображены примеры 2-мерных интервалов, которые пересекаются слева с заданным вдоль р-оси их пространства, исключая те, р-проекции которых касаются р-проекции заданного изнутри и (или) снаружи. Такими интервалами для заданного могут быть только 2-мерные интервалы с ненулевыми ребрами и отрезки, параллельные р-оси.
На фигуре 7 изображены примеры 2-мерных интервалов, р-проекции которых пересекаются справа с р-проекций заданного, исключая те, р-проекции которых касаются р-проекции заданного изнутри и (или) снаружи. Такими интервалами для заданного могут быть только 2-мерные интервалы с ненулевыми ребрами и отрезки, параллельные р-оси пространства интервалов. Но некоторые из них могут вообще не пересекаться с заданным. Так что случай, изображенный на этой фигуре, не является зеркальным отображением случая, изображенного на фигуре 6.
На фигуре 8 изображены примеры 2-мерных интервалов, которые пересекаются с заданным, в том числе те, которые покрывают его, покрываются им, а также касаются его изнутри и (или) снаружи вдоль любой из осей их пространства. Такими интервалами для заданного могут быть 2-мерные интервалы с ненулевыми ребрами, а также точки и отрезки.
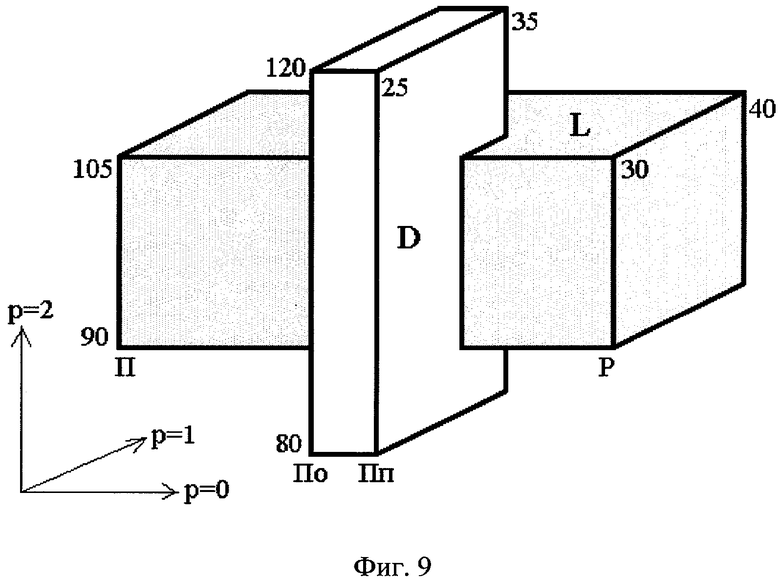
На фигуре 9 в р-осях базиса 3-мерного пространства изображен пример 3-мерного интервала D (белого цвета), который расположен композиционно относительно 3-мерного заданного L (серого цвета). Эта композиция состоит в том, что условие положения интервала D относительно L является комбинацией условий взаимных расположении их проекций: 0-проекция интервала D покрывается 0-проекцией L, 1-проекция D пересекается слева с 1-проекцией L, а 2-проекция D покрывает 2-проекцию L. Оси изображенного на этой фигуре базиса соответствуют столбцам приведенной ниже таблицы нечетких ("размытых", приблизительных, предполагаемых) данных, заданных интервалами: 0-ось соответствует столбцу фамилий, 1-ось - столбцу возрастов, 2-ось - столбцу весов. На фигуре 9 показаны параметры интервалов D и L в осях их пространства. Параметры D соответствуют интервальным данным одной конкретной строки этой таблицы, а параметры L - данным заданного 3-мерного интервала оператора интервального запроса.
Способ осуществляется следующим образом.
Все описываемые примеры рассматриваются в соответствии с розой интервалов (фиг.1а). В семи первых примерах р-проекциями заданного n-мерного интервала {c0, c1, ..., cn-1} являются интервалы cp=[аp, bp], где ар=3 и bp=7 для всех p=0, ..., n-1, а все координаты р-проекций исходных интервалов имеют целочисленные значения от 0 до 9. Этому случаю соответствует роза интервалов, изображенная на фиг.1b.
Пример 1.
Пусть из множества исходных n-мерных интервалов требуется выбрать данные интервалов, которые покрывают заданный, исключая те интервалы, которых заданный касается изнутри.
Пример этого случая при n=2 изображен на фиг.2.
Для получения данных всех интервалов этого запроса формируют такую пространственную структуру данных S (например, R-tree), элементами реальных данных которой являются исходные n-мерные интервалы, пространственно интегрированные как 2n-мерные точки, координаты которых совпадают с соответствующими координатами проекций этих интервалов на оси базиса их пространства. При этом элементы реальных данных структуры S являются одновременно и n-мерными интервалами, и соответствующими им 2n-мерными точками. Эти элементы данных оказываются в 2n-мерном пространстве структуры S одновременно интегрированными как 2n-мерные точки пространственно и как n-мерные интервалы по критериям пересечений, вложений, покрытий, касаний и других их взаимных расположении в их собственном n-мерном пространстве. Среди исходных интервалов структуры S, требуемые, покрывающие заданный, всегда интегрированы в области R1 розы интервалов (фиг.1а) для любой р-оси пространства интервалов. Согласно этому определяют линзу оператора интервального запроса. Определение линз может быть автоматизировано, например, программными средствами. В данном примере линзой может быть 2n-мерный интервал {u0, v0, u1, v1, ..., un-1, vn-1}, р-проекциями которого для всех р=0, ..., n-1 являются
up=(qp, ap) и vp=(bp, rp),
где для всех таких p значения qp выбирают меньшими, чем наименьшие xp в структуре S, а значения rp - большими, чем наибольшие уp в этой структуре (фиг.1а). Например, qp=-∞ и rр=+∞. При таком выборе значений qp и rp р-проекциями линзы оператора интервального запроса являются
up=(-∞, ap) и vp=(bp, +∞).
Затем конструируют и сохраняют на физическом носителе информации оператор интервального запроса о выборке из структуры S данных таких точек, которые покрываются этой линзой. Такой оператор может иметь любую форму, допускаемую синтаксисом языка запросов к структуре S. Например:
"Выбрать из структуры S данные таких точек, которые покрывает линза, определяемая формулами up=(-∞, ар) и vp=(bp, +∞) для всех р=0, ..., n-1".
Равноценным этому является, в частности, оператор, записанный на SQL - стандартном структурированном языке запросов (Structured Query Language):
"SELECT ALL FROM 'S' WHERE x0<a0 AND y0>b0 AND ... AND xn-1<an-1 AND уn-1>bn-1".
После этого с помощью сконструированного оператора выполняют интервальный запрос к структуре S. Результатом этого запроса будет множество данных 2n-мерных точек структуры S, одновременно являющихся изданными соответствующих им искомых интервалов.
Любые другие интервальные запросы выполняют аналогично. Ниже приводятся примеры
- условий взаимного расположения требуемых интервалов относительно заданного в их пространстве,
- формул проекций линз, соответствующих им операторов интервальных запросов к структуре S,
- а также самих этих операторов, записанных на языке SQL.
Пример 2.
Пусть из множества исходных n-мерных интервалов требуется выбрать данные интервалов, которые покрываются заданным, исключая те интервалы, которые касаются заданного изнутри.
Пример этого случая при n=2 изображен на фиг.3. Для любой р-оси пространства интервалов ему соответствует область R2 розы интервалов (фиг.1а). Поэтому р-проекциями линзы оператора интервального запроса для всех p могут являться следующие:
up=(ap, +∞) и vp=(-∞, bp).
Пример SQL-оператора, соответствующего этой линзе:
"SELECT ALL FROM 'S' WHERE x0>a0 AND y0<b0 AND ... AND xn-1>an-1 AND уn-1<bn-1".
Пример 3.
Пусть из множества исходных n-мерных интервалов требуется выбрать данные интервалов, которые лежат строго слева от заданного вдоль р-оси их пространства.
Пример этого случая при n=2 изображен на фиг.4. Для оси p ему соответствует область R3 розы интервалов (фиг.1a), а для остальных осей q≠p - область R2. Поэтому р-проекциями линзы могут являться:
up=(-∞, +∞) и vp=(-∞, ap),
а q-проекциями (q≠p) - такие:
uq=[aq, +∞) и vq=(-∞, bq].
Пример SQL-оператора, соответствующего этой линзе (для 0<p<n-1):
"SELECT ALL FROM 'S' WHERE x0≥a0 AND y0≤b0 AND ... AND yp<ар AND ... AND xn-1≥an-1 AND уn-1≤bn-1".
Пример 4.
Пусть из множества исходных n-мерных интервалов требуется выбрать данные интервалов, р-проекции которых лежат справа от р-проекции заданного, исключая те интервалы, р-проекции которых касаются р-проекции заданного.
Пример этого случая при n=2 изображен на фиг.5. Для оси р ему соответствует область R4 розы интервалов (фиг.1а). Поэтому р-проекциями линзы могут являться:
up=(bp, +∞) и vp=(-∞, +∞),
а остальные ее проекции - произвольны.
Пример SQL-оператора, соответствующего этой линзе:
"SELECT ALL FROM 'S' WHERE xp>bp".
Пример 5.
Пусть из множества исходных n-мерных интервалов требуется выбрать данные интервалов, которые пересекаются слева с заданным вдоль р-оси их пространства, исключая те интервалы, р-проекции которых р-проекция заданного касается изнутри и (или) снаружи.
Пример этого случая при n=2 изображен на фиг.6. Для оси р ему соответствует область R5 розы интервалов (фиг.1а), а для остальных осей q≠p - область R7. Поэтому р-проекциями линзы могут являться:
uр=(-∞, ар) и vp=(ap, bp),
а q-проекциями (q≠p) - такие:
uq=(-∞, bq] и vq=[aq, +∞).
Пример SQL-оператора, соответствующего этой линзе (для 0<р<n-1):
"SELECT ALL FROM 'S' WHERE x0<b0 AND у0>a0 AND ... AND xp<ap AND уp>ap AND уp<bp AND ... AND xn-1≤bn-1 AND уn-1≥an-1".
Пример 6.
Пусть из множества исходных n-мерных интервалов требуется выбрать данные интервалов, р-проекции которых пересекаются справа с р-проекцией заданного, исключая те интервалы, р-проекции которых р-проекция заданного касается изнутри и (или) снаружи.
Пример этого случая при n=2 изображен на фиг.7. Для оси р ему соответствует область R6 розы интервалов (фиг.1а). Поэтому р-проекциями линзы могут являться:
up=(ap, bp) и vp=(bp, +∞),
а остальные ее проекции - произвольны.
Пример SQL-оператора, соответствующего этой линзе:
"SELECT ALL FROM 'S' WHERE xp>ap AND xp<bp AND уp>bp".
Пример 7.
Пусть из множества исходных n-мерных интервалов требуется выбрать данные интервалов, которые пересекаются с заданным, включая касающиеся его изнутри и (или) снаружи.
Пример этого случая при n=2 изображен на фиг.8. Для любой р-оси пространства интервалов ему соответствует область R7 розы интервалов (фиг.1а). Поэтому р-проекциями линзы могут являться:
up=(-∞, bp] и vp=[ap, +∞).
Пример SQL-оператора, соответствующего этой линзе:
"SELECT ALL FROM 'S' WHERE x0≤b0 AND у0>a0 AND ... AND xn-1<bn-1 AND уn-1≥an-1".
Пример 8.
Рассмотрим конкретный случай интервального запроса.
ТНД
Пусть имеется таблица нечетких данных (ТНД), каждый столбец которой способен хранить как точные данные, так и нечеткие ("размытые", приблизительные, предполагаемые), заданные интервалами. Так что данные этой таблицы разнородны. В подобной таблице может быть сколько угодно записей, например, 500 миллионов.
Если данные точно неизвестны, но известен интервал, которому они принадлежат, то этот интервал в этой таблице записывается через тире "-". Например, в столбце "Фамилия" данные "Па-Пб" означают, что точно фамилия человека неизвестна, но известно, что она начинается на "Па". Символ "NULL" означает, что данные неизвестны и расценивается как 1-мерный интервал всех возможных значений соответствующего столбца.
Каждой строке данных рассматриваемой таблицы может быть взаимно однозначно сопоставлен 3-мерный интервал пространства, каждой из осей которого соответствует свой столбец таблицы: 0-оси соответствует столбец фамилий, 1-оси - столбец возрастов, 2-оси - столбец весов.
Пусть в этой таблице требуется найти данные всех людей, у которых фамилии заведомо начинаются на "П", возраст возможно или заведомо лежит в интервале 30-40, включая его концы, а вес возможно или заведомо лежит в интервале 90-105, включая его концы. Эти требования можно сформулировать иначе. Например так: "Из множества данных 3-мерных интервалов требуется выбрать данные интервалов:
- 0-проекции которых покрываются 0-проекцией заданного, включая те, 0-проекции которых касаются 0-проекции заданного изнутри слева и исключая те, 0-проекции которых касаются 0-проекции заданного изнутри справа,
- 1-проекции которых пересекаются с 1-проекцией заданного,
- 2-проекции которых пересекаются с 2-проекцией заданного,
где заданным является 3-мерный интервал, 0-проекция которого есть [П, Р], 1-проекция - [30, 40], а 2-проекция - [90, 105]."
р-проекциями линзы оператора интервального запроса могут являться такие:
u0=[П, Я] и v0=[A, P) (фиг.1а, R2),
u1=(0, 40] и v1=[30, +∞) (фиг.1а, R7),
u2=(0, 105] и v2=[90, +∞) (фиг.1а, R7),
а SQL-оператор интервального запроса, соответственно, может иметь вид:
"SELECT ALL FROM 'ТНД' WHERE х0≥П AND x0≤Я AND у0≥A AND у0<Р AND x1>0 AND x1≤40 AND у1≥30 AND x2>0 AND x2≤105 AND у2≥90".
Этому запросу соответствует пятая строка таблицы, что иллюстрирует фиг.9.
Условия взаимных расположении требуемых интервалов относительно заданного могут быть комбинациями условий любых взаимных расположении р-проекций требуемых интервалов относительно соответствующих р-проекций заданного. В частности, комбинациями условий любых из 13 базовых видов взаимных расположении интервалов классификации Аллена [3] или любых из 16 видов - классификации Фрексы [4].
Поскольку существует конечное число видов взаимных расположении 1-мерных интервалов по отношению к заданному, то параметрические формы операторов интервальных запросов могут быть созданы для размерности не более n заранее. Например, в таком синтаксисе:
"Выбрать из структуры S данные таких точек, которые покрывает линза, определяемая формулами up=(ap, bp) и vp=(cp, dp) для всех р=0, ..., n-1".
Тогда конструирование операторов по патентуемому способу будет состоять из подстановки входных значений условий выборки в параметры ар, bp, cp, dp линз этих форм.
Кроме того, операторы запросов могут включать в себя дополнительные условия. Например, выбор только тех данных, которые соответствуют отрезкам, параллельным конкретной оси пространства интервалов, и, имеющих дополнительный параметр цвета, являющийся зеленым. Или, другой пример, когда в исходные условия включены дополнительные условия взаимных расположений требуемых интервалов относительно второго заданного интервала, отличного от первого. Такие условия соответствуют сложным комбинированным интервальным запросам относительно нескольких линз.
Если уже существующая структура S претерпевает какие-либо модификации, например, за счет вставок, удалений или изменений ее данных, то эти модификации являются новым процессом ее формирования, отличающимся от предыдущего. Поэтому смешанные действия, включающие в себя различные модификации структуры S и интервальные запросы к ней, подпадают под формулу патентуемого способа хранения и выборки данных n-мерных интервалов.
Для реализации предлагаемого способа в качестве структуры S может быть выбрана произвольная пространственная структура данных. Если такой структурой данных является структура, ориентированная на использование памяти блоками (например, R-tree), в которые объединяются ее элементы данных - n-мерные интервалы и которым ставят в соответствие другие интервалы, то последние могут расцениваться как элементы реальных данных более высшего уровня этой структуры. Поэтому k-мерные интервалы любого ее уровня по способу предлагаемого изобретения могут быть представлены как соответствующие им 2k-мерные точки. В этом случае данные элементов данных низших уровней структуры данных оказываются "фрактально вложенными" в данные элементов данных ее высших уровней. Такой подход означает многоуровневое использование предлагаемого способа в одной блочной пространственной структуре данных. Помимо этого, расщепление (split) блоков точечных данных блочной пространственной структуры данных может быть реализовано без перекрытий. Это означает структурную близость пространственно близких элементов реальных данных в такой структуре, что дает возможность во время процессов выборки осуществлять доступ к требуемым множествам по однозначным путям за минимальное время. Все это позволяет блочные пространственные структуры данных полностью оптимизировать для выполнения в них любых интервальных запросов.
Эффективность выполнения интервальных запросов по способу предлагаемого изобретения состоит в том, что в структуре данных способа запрашиваемые элементы реальных данных всегда интегрированы пространственно как точки и интегрированы как интервалы по различным критериям их взаимных расположении в их собственном пространстве, что обеспечивает высокую скорость процессов выборки требуемых данных.
Таким образом, предлагаемое изобретение, в отличие от известных, позволяет в одной и той же пространственной структуре данных эффективно выполнять любые интервальные запросы с различными условиями взаимного расположения требуемых интервалов относительно произвольно заданного. Описанный способ, в частности, открывает пути к созданию конкретных классов эффективных хранилищ и баз нечетких данных, оптимизированных для выполнения в них любых интервальных запросов. Этот способ может эффективно применяться также в таких пространственных моделях данных, как:
- ГИС,
- системы интеллектуального анализа и искусственного интеллекта,
- системы контроля и управления динамическими объектами,
- системы наблюдения и управления процессами,
- системы поддержки принятия решений,
- системы анализа, планирования и оптимизации,
- хронологические, информационные и статистические системы,
- информационные системы транспортных сетей,
- системы поиска и обнаружения закономерностей.
Кроме того, как было показано, любые интервальные запросы выборки данных n-мерных интервалов описанным способом сводятся к простейшим выборкам 2n-мерных точечных данных, покрываемых некоторой линзой. Такие запросы легко конструируются и выполняются с помощью языка SQL. Поэтому описанный способ может быть эффективно использован без реорганизации структур данных действующих пространственных моделей. Это возможно путем создания соответствующих драйверов, которые входные n-мерные интервалы конвертируют в 2n-мерные точки, а входные интервальные запросы интервалов - в интервальные запросы точек, поставляя эти результаты в действующие структуры данных.
Источники информации
1. A.Guttman. "R-trees: a dynamic index structure for spatial searching". Proceedings of the SIGMOD, p.47-57, Boston, Massachusetts, 1984, ISBN: 0-89791-128-8.
2. E.M.McCreight. "Efficient algorithms for enumerating intersecting intervals and rectangles", Technical Report CSL-80-9, 1980.
3. J.F.Allen "Maintaining Knowledge about Temporal Intervals". Communications of the ACM, Vol.26, №11, p.832-843, 1983.
4. С.Freksa. "Temporal reasoning based on semi-intervals". Artificial intelligence 54, p.199-227, 1992.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ВЫБОРКИ ИЗОБРАЖЕНИЙ ИЗ БАЗЫ ИЗОБРАЖЕНИЙ | 2011 |
|
RU2480831C1 |
| СПОСОБ И СИСТЕМА ОРГАНИЗАЦИИ И ФУНКЦИОНИРОВАНИЯ БАЗЫ ДАННЫХ НОРМАТИВНОЙ ДОКУМЕНТАЦИИ | 2008 |
|
RU2386166C2 |
| Способ оперативной идентификации морских целей по их информационным полям на базе нейро-нечетких моделей | 2021 |
|
RU2763125C1 |
| Способ регуляризованного обнаружения полезных сигналов загоризонтной радиолокации при нестационарном ионосферно-пространственном распространении радиоволн | 2023 |
|
RU2817867C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ПЕРЕДАЧИ И ПРИЕМА СИГНАЛОВ С ОГРАНИЧЕННЫМ СПЕКТРОМ (ВАРИАНТЫ) | 2004 |
|
RU2265278C1 |
| СПОСОБ РАСПРЕДЕЛЕННОГО МОНИТОРИНГА КОНТЕЙНЕРОВ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2007 |
|
RU2329470C1 |
| ПОИСКОВАЯ ЭКСПЕРТНАЯ СИСТЕМА | 2012 |
|
RU2485581C1 |
| СПОСОБ АНАЛИЗА ДИНАМИЧЕСКИХ МНОГОПАРАМЕТРИЧЕСКИХ ПРОЦЕССОВ | 2000 |
|
RU2164039C1 |
| Система оперативной идентификации морских целей по их информационным полям на базе нейро-нечетких моделей | 2021 |
|
RU2763384C1 |
| СПОСОБ, А ТАКЖЕ АППАРАТ, УСТРОЙСТВО, СИСТЕМА И НОСИТЕЛЬ ДАННЫХ ДЛЯ ПОЛУЧЕНИЯ И СОЗДАНИЯ ТРАЕКТОРИИ ПРОСТРАНСТВЕННО-ВРЕМЕННОГО ПЕРЕМЕЩЕНИЯ | 2022 |
|
RU2838823C2 |
Изобретение относится к области информационных технологий. Его использование для оптимизации хранения и выборки данных позволяет получить технический результат в виде обеспечения возможности эффективного выполнения в одной пространственной структуре данных любых интервальных запросов. Этот результат достигается благодаря тому, что: формируют пространственную структуру данных с элементами в виде исходных n-мерных интервалов; определяют линзу, являющуюся 2n-мерным интервалом оператора интервального запроса, представляющего собой инструкцию о выборке данных требуемых n-мерных интервалов с описанием заданного интервала и условий расположения относительно него требуемых, причем линзу определяют согласно розе интервалов, представляющей собой виртуальную двумерную геометрическую диаграмму областей таких 2n-мерных точек в осях xp и ур их пространства, координатами {xp, уp} которых являются соответствующие координаты р-проекций соответствующих этим точкам n-мерных интервалов, где р-проекция n-мерного интервала это его проекция на р-ось базиса его пространства; конструируют и сохраняют на физическом носителе информации оператор интервального запроса о выборке из структуры данных таких точек, которые покрываются этой линзой; выполняют с помощью этого оператора интервальный запрос к структуре, результатом чего будет множество данных 2n-мерных точек, одновременно являющихся и данными соответствующих им искомых интервалов. 9 ил., 1 табл.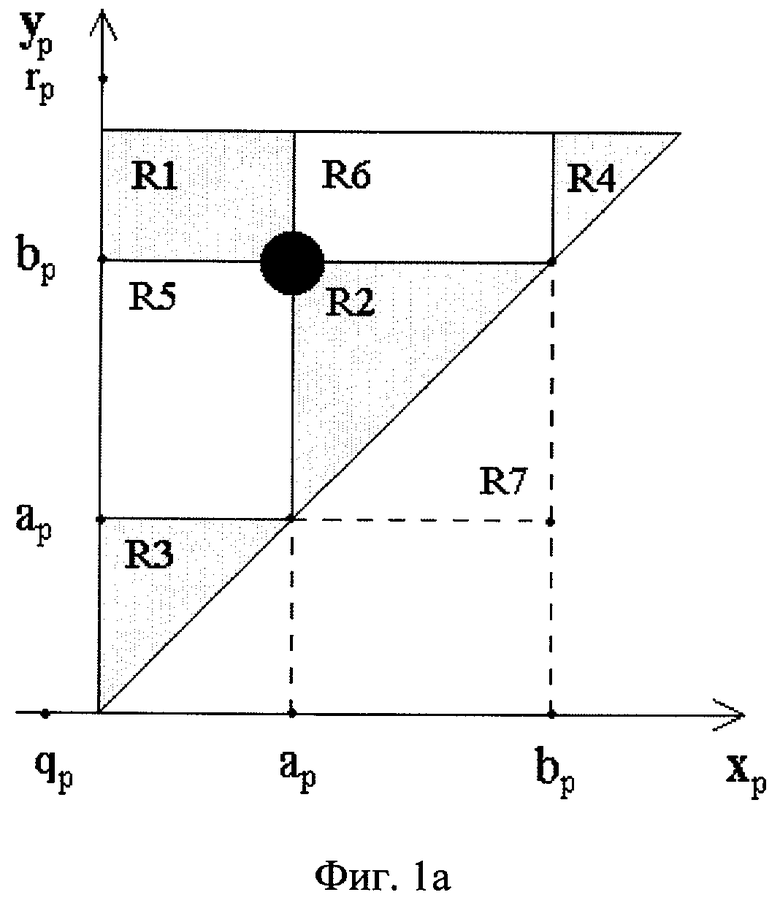
Способ хранения и выборки данных n-мерных интервалов, заключающийся в том, что формируют такую пространственную структуру S данных, элементами реальных данных которой являются исходные n-мерные интервалы, пространственно интегрированные как 2n-мерные точки, координаты которых совпадают с соответствующими координатами проекций этих интервалов на оси базиса их пространства; определяют линзу, являющуюся 2n-мерным интервалом оператора интервального запроса, представляющего собой инструкцию о выборке данных требуемых n-мерных интервалов с описанием заданного интервала и условий расположения относительно него требуемых, причем линзу определяют согласно розе интервалов, представляющей собой виртуальную двумерную геометрическую диаграмму областей таких 2n-мерных точек в осях xp и уp их пространства, координатами {xp, уp} которых являются соответствующие координаты р-проекций соответствующих этим точкам n-мерных интервалов, где р-проекция n-мерного интервала - это его проекция на р-ось базиса его пространства; конструируют и сохраняют на физическом носителе информации оператор интервального запроса о выборке из структуры S данных таких точек, которые покрываются этой линзой; выполняют с помощью этого оператора интервальный запрос к структуре S, результатом которого будет множество данных 2n-мерных точек, одновременно являющихся и данными соответствующих им искомых интервалов.
| СПОСОБ АНАЛИЗА ДИНАМИЧЕСКИХ МНОГОПАРАМЕТРИЧЕСКИХ ПРОЦЕССОВ | 2000 |
|
RU2164039C1 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| Перекатываемый затвор для водоемов | 1922 |
|
SU2001A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Приспособление в пере для письма с целью увеличения на нем запаса чернил и уменьшения скорости их высыхания | 1917 |
|
SU96A1 |
Авторы
Даты
2007-04-27—Публикация
2005-07-12—Подача