Предлагаемое изобретение относится к области измерения и может быть использовано для настройки и калибровки акселерометров и приборов, содержащих акселерометры.
Известен способ определения параметров прецизионных акселерометров, в частности погрешности базовых установочных элементов и угловой деформации основания в плоскости, перпендикулярной оси его вращения, описанный в [1], включающий развороты акселерометра, закрепленного на вертикальном основании, вокруг горизонтальной оси и вокруг измерительной оси на некоторые, заранее заданные углы с одновременным наблюдением выходного сигнала.
Однако для реализации данного способа необходимо осуществлять вращение вокруг измерительной оси акселерометра, что не всегда возможно легко реализовать, т.к. требуется сложное оборудование.
Известен способ определения угловых координат измерительной оси акселерометра - прототип, описание которого приведено в [2]. Сущность данного способа заключается в том, что проводят два разворота акселерометра вокруг первой и второй горизонтальной оси на углы, при которых сигнал акселерометра равен нулю, и после этого, зная углы между осями вращения и осями ортогонального базиса и углы разворотов, вычисляют координаты измерительной оси акселерометра.
Однако способ требует проведения вращения до получения нулевого сигнала с акселерометра. При развороте акселерометра требуется проводить несколько последовательных поворотов (приближений) и замеров сигнала с акселерометра для того, чтобы определить момент нулевого сигнала, что требует больших затрат времени.
Задача изобретения - упрощение способа и увеличение экономичности.
Эта задача достигается тем, что в способе определения угловых координат α, β, γ измерительной оси акселерометра относительно ортогонального базиса X, Y, Z, включающем разворот акселерометра из исходного положения, при котором плоскость XOY расположена в плоскости горизонта, вокруг первой оси OA1, расположенной в плоскости XOY под углом ϕ1 к оси Х базиса, и затем из исходного положения разворот акселерометра вокруг второй оси ОА2, расположенной в плоскости XOY под углом ϕ2 к оси X, дополнительно первый разворот вокруг первой оси OA1 проводят до момента начала изменения сигнала акселерометра в рабочей зоне, фиксируют угол поворота λP1 и сигнал акселерометра U1, возвращают акселерометр в упомянутое исходное положение, второй разворот акселерометра из исходного положения вокруг первой оси OA1 проводят до момента, при котором сигнал акселерометра становится меньше заданного значения Δ, принадлежащего линейной рабочей зоне сигнала акселерометра, при этом фиксируют угол поворота λР2 и сигнал акселерометра U2, не равный сигналу U1, третий разворот акселерометра из исходного положения вокруг второй оси ОА2 проводят до момента начала изменения сигнала акселерометра в рабочей зоне, фиксируют угол λР3 и сигнал акселерометра U3, возвращают акселерометр в исходное положение, четвертый разворот акселерометра из исходного положения проводят вокруг второй оси ОА2 до момента, при котором сигнал акселерометра становится меньше упомянутого заданного значения Δ, при этом фиксируют угол λP4 и сигнал акселерометра U4, не равный сигналу U3, а угловые координаты α, β и γ вычисляют из соотношений:
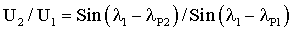
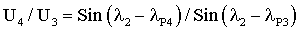
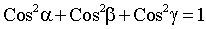
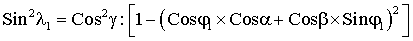
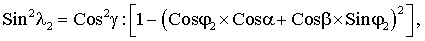
где λ1, λ2 углы поворота (соответственно вокруг осей OA1 и ОА2) акселерометра из исходного положения, при которых сигнал с акселерометра равен нулю.
На чертеже представлена базовая ортогональная система координат OXYZ и орт е (измерительная ось акселерометра), заданный углами α, β и γ, которые он образует с положительными направлениями осей OXYZ. В исходном положении плоскость XOY расположена в плоскости горизонта. Плоскость, заданная векторами OZ и е, образует прямой угол с плоскостью OXY. Вектор OA1 является осью первого разворота, принадлежит плоскости OXY и образует угол ϕ1 с вектором ОХ. Вектор OA2 является осью второго разворота, принадлежит плоскости OXY и образует угол ϕ2 с вектором ОХ. Вектор OB1 показывает положение измерительной оси акселерометра после первого разворота из исходного положения вокруг оси OA1 на угол λP1, при котором сигнал с акселерометра равен U1. Вектор ОВ2 показывает положение измерительной оси акселерометра после второго разворота из исходного положения вокруг оси OA1 на угол λP2, при котором сигнал с акселерометра равен U2. Вектор ОВ3 показывает положение измерительной оси акселерометра после третьего разворота из исходного положения вокруг оси ОА2 на угол λP3, при котором сигнал с акселерометра равен U3. Вектор OB4 показывает положение измерительной оси акселерометра после четвертого разворота из исходного положения вокруг оси ОА2 на угол λР4, при котором сигнал с акселерометра равен U4. λ1 - это угол поворота акселерометра из исходного положения вокруг оси OA1 до положения, при котором измерительная ось акселерометра будет принадлежать плоскости ХОУ (сигнал с акселерометра равен нулю). λ2 - это угол поворота акселерометра из исходного положения вокруг оси ОА2 до положения, при котором измерительная ось акселерометра будет принадлежать плоскости ХОУ (сигнал с акселерометра равен нулю). Угол δ это угол между осью вращения OA1 и измерительной осью акселерометра. Отрезок BD перпендикулярен оси вращения OA1 и является катетом прямоугольного треугольника OBD. Дуга A1C и дуга а являются катетами сферического прямоугольного треугольника A1BC с прямым углом С, а дуга с является его гипотенузой.
Определим сигнал с акселерометра в исходном состоянии. Для этого рассмотрим прямоугольный треугольник OBD с прямым углом D. В нем катет BD можно выразить через гипотенузу е как:
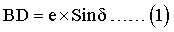
Таким образом, можно представить измеренный сигнал U от полного сигнала акселерометра F в случае, когда плоскость BOA1 перпендикулярна плоскости OXY, плоскость OXY горизонтальна, а вектор е совпадает с измерительной осью акселерометра как:
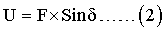
В случае, когда угол между плоскостью BOAi и плоскостью OXY равен μ, измеренный сигнал U можно представить как:
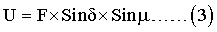
Вместе с тем угол δ, образованный векторами OA1 и е, можно выразить через направляющие косинусы как:
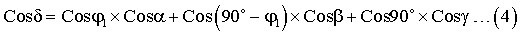
Где Cos90° это сомножитель, определяемый углом между векторами OZ и OA1. Учитывая, что Cos(90°-ϕ1)=Sinϕ1, а Cos90°=0, последнее выражение примет вид:
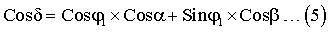
В прямоугольном сферическом треугольнике A1BC гипотенуза с определена углом δ, а катет α - углом (90°-γ). Исходя из формулы синусов для сферических треугольников (Sina/SinA1=Sinc/SinC) получим:
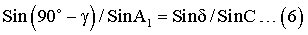
Учитывая, что SinC=1, Sin(90°-γ)=Cosγ, a SinA1=Sinλ1, выражение (6) примет вид:
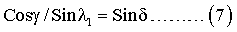
Подставив Sinδ из соотношения (7) в выражение (3), получим:
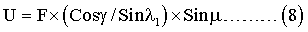
После первого разворота вокруг оси OA1 на угол λP1 угол μ равен λ1-λP1, а сигнал с акселерометра - U1. Подставляя эти значения в выражение (8), получим:
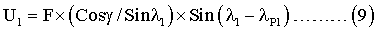
Соответственно после второго разворота вокруг оси OA1 на угол λP2 угол μ равен λ1-λP2, а сигнал с акселерометра - U2. Подставляя и эти значения в выражение (8), получим:
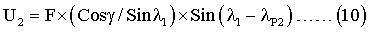
Разделив соотношение (10) на (9) получим:
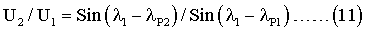
Аналогичным образом получим соотношение для сигналов U3 (третье измерение) и U4 (четвертое измерение) после соответственно третьего разворота вокруг оси ОА2 на угол λP3 и четвертого разворота вокруг оси ОА2 на угол λР4.
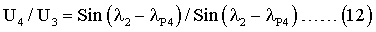
Перепишем выражение (7) как:
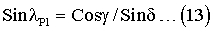
И выразим Sinδ через Cosδ, в результате чего выражение (13) примет вид:
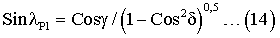
Подставим в выражение (14) Cosδ из соотношения (5), после чего выражение (14) примет вид:
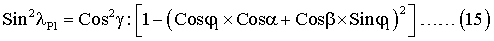
Подставив соответствующие углы λР2 и ϕ2 в данное выражение, получим следующее уравнение для определения координат измерительной оси акселерометра:
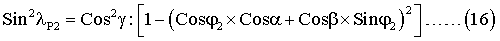
Выражения (11), (12), (15), (16) и равенство Cos2α+Cos2β+Cos2γ=1 при совместном решении позволяют определить углы α, β и γ (координаты измерительной оси акселерометра).
Определение угловых координат α, β и γ измерительной оси е акселерометра осуществляется следующим образом. Пусть поворотная установка имеет платформу, которую можно горизонтировать и устанавливать на нее акселерометр (прибор, в котором установлены акселерометры). Поворотная установка имеет две измерительные оси вращения OA1 и ОА2 с точной фиксацией углов поворота, расположенные под углами ϕ1 и ϕ2 относительно оси X. Выставим плоскость OXY поворотной установки в горизонт - исходное положение. Развернем платформу относительно оси OA1 до момента начала изменения сигнала акселерометра в рабочей зоне, зафиксируем угол поворота λP1 и сигнал акселерометра U1. Возвратим акселерометр в исходное положение (выставим плоскость OXY поворотной установки в горизонт). Развернем платформу (второй разворот акселерометра) вокруг первой оси OA1 до момента, при котором сигнал акселерометра становится меньше заданного значения Δ, принадлежащего линейной рабочей зоне сигнала акселерометра. Зафиксируем угол поворота λP2 и сигнал акселерометра U2, не равный сигналу U1. Возвратим акселерометр в исходное положение. Развернем платформу (третий разворот акселерометра) относительно оси ОА2 до момента начала изменения сигнала акселерометра в рабочей зоне, зафиксируем угол поворота λP3 и сигнал акселерометра U3. Возвратим акселерометр в исходное положение. Развернем платформу (четвертый разворот акселерометра) вокруг первой оси ОА2 до момента, при котором сигнал акселерометра становится меньше упомянутого заданного значения Δ. Зафиксируем угол поворота λР4 и сигнал акселерометра U4 (U4≠U3).
Вычислим углы λ1 и λ2, решая уравнения:
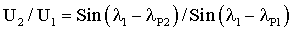 и
и
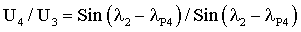
Подставим полученные значения λ1 и λ2 в последние равенства системы уравнений
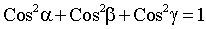
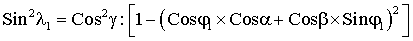
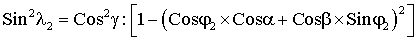
и, решая ее, определим угловые координаты α, β и γ измерительной оси акселерометра е в исходном базисе X, Y, Z.
Эффект от использования предлагаемого способа заключается в том, что он проще известного, т.к. для определения угловых координат акселерометра требуется проводить меньшее количество разворотов акселерометра с последующим измерением угла разворота и сигнала от акселерометра. В то время как в прототипе требуется проводить больше последовательных поворотов с последующими замерами сигнала с акселерометра до тех пор, пока сигнал не уменьшится до определенной очень малой величины. При этом для уменьшения числа итераций по последовательному приближению требуется наличие хорошей квалификации у оператора.
Вместе с тем предложенный способ позволяет увеличить экономичность определения координат измерительной оси за счет того, что сокращается время на проведение работ. Так, например, в случае, если необходимо получить точность прибора на уровне 10-5 по абсолютной величине, диапазон измеряемых ускорений составляет 10 м/с2, а вес одного разряда приращения 4 мм/с. Т.е. величина минимального измеряемого сигнала составит 10 м/с2 ×10-5=0,1 мм/с2. И период следования информационных импульсов (кодовых посылок) от минимального полезного сигнала составит 4 мм/с: 0,1 мм/с2 =40 с. Следовательно, период следования кода, формируемого за счет погрешности, должен быть больше. Учитывая, что трудно (с точки зрения стоимости) бороться с погрешностью, вызванной электронной частью прибора, желательно минимизировать погрешность от неправильной тарировки (измерения координат) датчиков. Это вызывает необходимость увеличивать период следования кода от неправильной установки, примерно, на порядок, т.е. до 400 с. С учетом особенностей работы измерительных приборов (организации цикла измерения, например, с целью защиты от "плавания" периода, вызванного синхронизацией преобразования и передачи информационного кода, вводится измерение нескольких периодов и вычисления среднего), реальное время измерения может быть значительно больше. Учитывая, что операция разворота занимает много времени, и необходимо провести измерение параметров нескольких акселерометров, установленных в приборе, при реализации способа-прототипа потребуется очень много времени, что делает его дорогим в части трудозатрат. Поэтому в случае применения акселерометров, не имеющих нулевой составляющей сигнала (сигнал акселерометра равен нулю при отсутствии ускорения), предлагаемый способ является более экономичным.
Предложенный способ, так же как и способ-прототип, позволяет проводить определение угловых координат акселерометров с линейной зоной преобразования сигнала меньшей чем ускорение свободного падения g.
Определим величину заданного значения Δ, которая позволяет получить точность определения угловых координат у предложенного способа не хуже, чем у прототипа, для датчиков с линейным коэффициентом преобразования, т.е. U2=Δ.
Точность у заявляемого способа определяется погрешностью измерения, а у прототипа - погрешностью измерения плюс допуск на устанавливаемый нулевой сигнал (сигнал при, котором прекращаются действия по изменению наклона для достижения еще более низкого сигнала с акселерометра). Пусть, например, необходима точность Р в определении углов λ1 и λ2, равная 5" (Р=5"). (Погрешности при вычислении углов α, β, γ зависят от погрешностей измерения углов λ1, λ2 и имеют величину одного и того же порядка (зависят от соотношения углов)). Величина искомого угла λ1=45°, линейная зона акселерометра начинается при наклоне на 35° (λP1=35°), погрешность измерения сигнала с акселерометра 0,001 и погрешности при измерении имеют разный знак (т.е. наихудший случай - U2 при измерении увеличивается в (1+0,001) раза, a U1 - уменьшается в (1-0,001) раза). Коэффициент преобразования сигнала акселерометром F=1/Sinδ или, согласно выражению (3), сигнал с акселерометра можно записать как U=Sinμ, тогда для первого измерения U1=Sin(λ1-λP1), для второго измерения U2=Sin(λ1-λP2). Подставляя эти данные в выражение (11), получим:
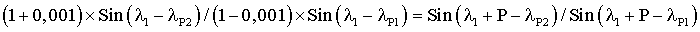
или с учетом цифровых значений:
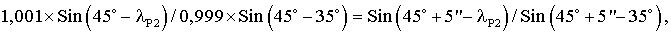
решая данное выражение, получим: λP2=44° 21' 3,36". Таким образом, чтобы получить точность в 5" при использовании способа-прототипа, надо проводить наклоны и измерения сигнала до тех пор, пока сигнал акселерометра станет меньше чем величина, пропорциональная Sin(5"). А при использовании предлагаемого способа надо проводить наклоны и измерения сигнала до тех пор, пока сигнал акселерометра станет меньше, чем величина, пропорциональная Sin(38' 56,64"). Что является значительно более простой задачей. Учитывая, что на практике приходится решать задачу по измерению фактических угловых координат α, β и γ измерительной оси акселерометра, получившихся при изготовлении прибора и отличающихся от заданных α0, β0, γ0 на некоторые небольшие значения, легко предварительно вычислить углы λO1 и λO2, соответственно определить величину сигнала Δ для достижения необходимой точности. Уменьшение допуска на устанавливаемый нулевой сигнал ниже нескольких секунд у способа-прототипа приводит к увеличению операций разворот-измерение.
Предлагаемая совокупность признаков в рассмотренных авторами решениях не встречалась для решения поставленной задачи и не следует явным образом из уровня техники, что позволяет сделать вывод о соответствии технического решения критериям "новизна" и "изобретательский уровень".
Для реализации данного способа необходима платформа с не менее чем двумя рамками карданного подвеса (двумя степенями свободы), например, такая как представлена в [3] с.158.
Литература
1. Патент Российской Федерации № 02117950 от 20.08.98. Способ определения параметров прецизионных акселерометров. G01P 21/00.
2. Патент Российской Федерации № 02164693 от 29.07.99. Способ определения угловых координат измерительной оси акселерометра. G01P 21/00.
3. Савант С.Дж., Ховард Р., Соллоуай С., Савант С.А. Принципы инерциальной навигации. М.: Мир, 1965 г.
Изобретение относится к области измерения и может быть использовано для настройки и калибровки акселерометров и приборов, содержащих акселерометры. Способ определения угловых координат, включающий по два разворота вокруг двух горизонтальных осей, положение которых известно относительно ортогонального базиса, до вхождения измеряемого сигнала в определенные границы с последующим измерением сигналов с акселерометра и углов разворота. Угловые координаты определяются из соответствующих соотношений. В способе сочетаются простота и экономичность, эффект достигается за счет уменьшения числа разворотов и измерений сигнала. Способ позволяет использовать простое технологическое оборудование (с меньшим числом степеней свободы) для калибровки приборов, содержащих акселерометры, или использовать универсальное оборудование, на котором невозможно устанавливать прибор с необходимой ориентацией (например, при несоответствии геометрических размеров оборудования и прибора). 1 ил.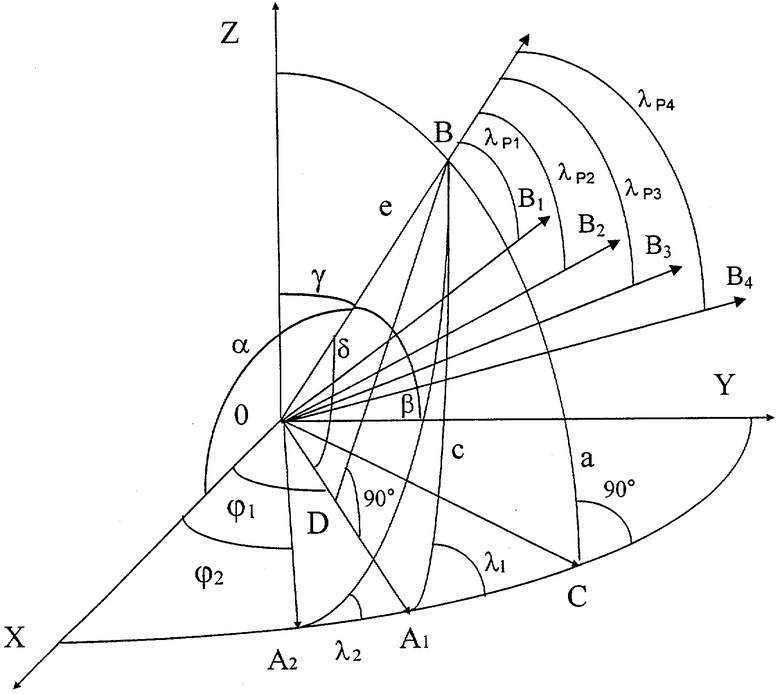
Способ определения угловых координат α, β, γ измерительной оси акселерометра относительно ортогонального базиса X, Y, Z, включающий разворот акселерометра из исходного положения, при котором плоскость XOY расположена в плоскости горизонта, вокруг первой оси OA1, расположенной в плоскости XOY под углом ϕ1 к оси Х базиса и затем из исходного положения разворот акселерометра вокруг второй оси ОА2, расположенной в плоскости XOY под углом ϕ2 к оси X, отличающийся тем, что первый разворот вокруг первой оси ОА1 проводят до момента начала изменения сигнала акселерометра в рабочей зоне, фиксируют угол поворота λP1 и сигнал акселерометра U1, возвращают акселерометр в упомянутое исходное положение, второй разворот акселерометра из исходного положения вокруг первой оси ОА1 проводят до момента, при котором сигнал акселерометра становится меньше заданного значения Δ, принадлежащего линейной рабочей зоне сигнала акселерометра, при этом фиксируют угол поворота λР2 и сигнал акселерометра U2, не равный сигналу U1, третий разворот акселерометра из исходного положения вокруг второй оси ОА2 проводят до момента начала изменения сигнала акселерометра в рабочей зоне, фиксируют угол λР3 и сигнал акселерометра U3, возвращают акселерометр в исходное положение, четвертый разворот акселерометра из исходного положения проводят вокруг второй оси ОА2 до момента при котором сигнал акселерометра становится меньше упомянутого заданного значения Δ, при этом фиксируют угол λР4 и сигнал акселерометра U4, не равный сигналу U3, а угловые координаты α, β и γ вычисляют из соотношений:
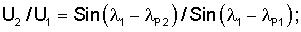
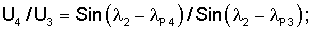
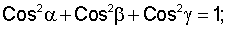
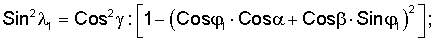
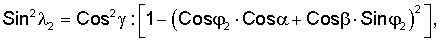
где λ1, λ2 углы поворота, (соответственно, вокруг осей ОА1 и ОА2) акселерометра из исходного положения, при которых сигнал с акселерометра равен нулю.
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВЫХ КООРДИНАТ ИЗМЕРИТЕЛЬНОЙ ОСИ АКСЕЛЕРОМЕТРА | 1999 |
|
RU2164693C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ПРЕЦИЗИОННЫХ АКСЕЛЕРОМЕТРОВ | 1994 |
|
RU2117950C1 |
| US 6823279 В1, 23.11.2004 | |||
| JP 9251031 A, 22.09.1997. | |||
Авторы
Даты
2008-04-27—Публикация
2005-10-31—Подача