Способ обработки трехкратно принятых комбинаций относится к электросвязи, вычислительной технике, а именно к способам повышения достоверности принимаемой информации и может быть использован в системах передачи информации с дублированием сообщений.
Во многих системах передачи данных используют помехоустойчивые двоичные циклические коды.
При передаче данных (исходного сообщения) осуществляют кодирование. Кодирование, в данном случае, означает формирование избыточной информации (избыточных данных или проверочной последовательности). Полученную избыточную информацию дописывают в конец сообщения. Таким образом, в канал связи передают сообщение с избыточностью.
При приеме осуществляют декодирование: сообщение проверяют на наличие ошибок, используя избыточные данные, и при необходимости изменяют. При отсутствии ошибок (избыточная информация соответствует передаваемому сообщению) из принятого сообщения удаляют избыточность, то есть получают исходное сообщение. В случае обнаружения ошибок пытаются получить исходное сообщение, используя избыточность. Однако это не всегда возможно. Получение исходного сообщения возможно только при условии, что ошибок в искаженном сообщении не больше, чем может исправить код при данном объеме избыточности (количестве избыточных бит). При недостаточной избыточности получение исходного сообщения невозможно. Однако теоретически возможно осуществить кодирование сообщения с формированием сколь угодно большого объема избыточности.
Избыточную информацию (проверочную последовательность) для циклического кода получают путем деления полинома информации (сообщения) на образующий полином (обеспечивающий восстановление некоторого количества бит информации). Остаток от деления образует полином избыточной информации.
На приеме производят повторное кодирование принятого сообщения. Если полученная этим кодированием проверочная последовательность (П1) совпадает с принятой из канала связи проверочной последовательностью (П2), то сообщение считают неискаженным. Если сообщение искажено, то последовательности П1 и П2 складывают по модулю два. Полученное значение (синдром) однозначно определяет позиции (вектор ошибки), в которых произошли искажения бит. Исходное сообщение получают сложением по модулю два вектора ошибки, найденного по синдрому, и комбинации, полученной из канала связи.
Для некоторых циклических кодов синдром может показать принципиальную невозможность получения исходного сообщения, то есть невозможность декодирования. Но для большинства кодов при искажении сообщения, большем корректирующей способности используемого кода, происходит ложное декодирование (исправление, не приводящее к получению исходного сообщения).
В результате декодирования можно выделить признак, который показывает изменения, произошедшие с принятой двоичной комбинацией. Признак может принимать следующие значения в порядке увеличения степени искажений (СтИск):
- искажение не обнаружено в комбинации (СтИск=0);
- комбинация исправлена (СтИск=1), возможно ложно;
- комбинация не поддается исправлению (СтИск=2).
Для всего описанного ниже считаем, что принимаемые комбинации - это двоичные сообщения с избыточностью (кодовые блоки), а декодирование - это преобразование комбинации для получения исходного сообщения с получением степени искажения.
Известен способ декодирования повторяющихся сообщений, закодированных двоичными циклическими кодами [1]. Для декодирования необходимо осуществить ряд действий. Во-первых, сформировать суммарную комбинацию путем выбора двоичных элементов принятых комбинаций на одноименных позициях по большинству - мажоритарный принцип. Во-вторых, осуществить декодирование полученной суммарной комбинации, то есть при наличии ошибок произвести соответствующее изменение комбинации для приведения ее к исходному сообщению. Этот способ называется мажоритарным декодированием. Для выбора по мажоритарному принципу необходимо, по крайней мере, три комбинации.
Недостаток известного способа заключается в малой достоверности получаемой информации из-за ошибочного мажоритарного выбора при попадании нескольких искажений в одни и те же позиции в принятых комбинациях.
Известен способ синхронного накопления [2] трех и более кратно принимаемых повторяющихся комбинаций, реализованный в ряде устройств. Результирующая комбинация определяется выбором из комбинаций, получаемых декодированием принятых кодовых блоков, по признаку декодирования: либо комбинация не искажена, либо комбинация исправлена. В нескольких устройствах реализовано декодирование двоичного циклического кода Хемминга, способного исправить ошибку в одной двоичной позиции или определить невозможность декодирования комбинации с четным количеством ошибок - искаженных бит. Комбинация считается успешно принятой, если искажение в ней не обнаружено или комбинация исправлена.
Недостаток известного способа заключается в нерациональном использовании канала связи, так как информация о ранее принятых комбинациях не используется, что приводит к дополнительным затратам времени на повторные передачи информационных комбинаций. То есть, хотя комбинации повторяются несколько раз, предыдущие искаженные комбинации не используются для повышения достоверности приема.
Кроме того, в случае искажения нечетного количества бит (трех, пяти и более) в принятой комбинации, декодирование ложно исправит информационную комбинацию, что приведет к получению комбинации, отличной от исходного сообщения.
Известен способ декодирования повторяющихся комбинаций, реализованный в устройстве и выбранный в качестве прототипа, по которому обнаруживают ошибки в принятых комбинациях путем проверки их на соответствие используемому коду [3]. В случае необнаружения ошибок кодом в первом повторении информация (исходное сообщение) выдается получателю. Если в первом повторении обнаружена ошибка, то принимается второй повтор, который также проверяется на наличие ошибок. В случае необнаружения ошибок во втором повторе информация (исходное сообщение) также выдается получателю. Если и во втором повторе обнаружена ошибка, то выделяется вектор надежности путем сложения по модулю два первого и второго повторов. Если векторы ошибок в первом и втором повторах не содержат единиц в одноименных позициях, то все ошибки кодовых блоков покрываются общим вектором Е. Если вес вектора Е не превышает количества гарантированно обнаруживаемых ошибок, то осуществляется одновременный поиск векторов ошибок для первого и второго кодовых блоков. Так как ошибки могут иметь место только на тех позициях блоков, где у вектора Е стоят единицы, то поиск векторов ошибок двух кодовых блоков сводится к перебору символов только этих позиций. Каждое из чисел-векторов представляет собой тест, который суммируется по модулю два с векторами принятых кодовых блоков. Результаты суммирования проверяются на наличие ошибок кодом. Если в одном из результатов ошибка не обнаруживается, то это свидетельствует о том, что найден один из векторов ошибок и дальнейшее декодирование прекращается. Отказ от декодирования происходит в том случае, если вектор ошибок не найден. Это свидетельствует о том, что ошибка произошла в одноименных разрядах принятых комбинаций и дальнейшее тестирование кодовых блоков бесполезно. Кроме того, отказ от декодирования происходит в том случае, если вес вектора ошибки Е превышает кратность гарантированно обнаруживаемых ошибок кодом. Отказ от декодирования равнозначен запросу следующего кодового блока.
Недостаток известного способа заключается в низкой вероятности приема информации из-за выбранного критерия получения результирующей комбинации. В качестве результирующей получателю выдают комбинацию без искажений (СтИск=0), полученную сложением по модулю два принятой комбинации и найденного для нее вектора ошибки. Если ошибка или ошибки располагаются в одноименных разрядах, то формируют отказ от декодирования, хотя комбинация может быть исправлена кодом (СтИск=1).
Задачей изобретения является увеличение вероятности приема трехкратно принимаемой информации.
Технический результат, достигаемый предлагаемым способом, заключается в увеличении вероятности приема информации за счет использования информации о ранее принятых комбинациях и последующего выбора наиболее достоверной комбинации. Выбор осуществляется путем мажоритарного декодирования и перебора комбинаций с наложением возможных векторов ошибок на принятые искаженные информационные блоки.
Дополнительный технический результат, достигаемый без внесения дополнительной избыточности, заключается в уменьшении времени передачи информации за счет сокращения количества передач информации, в отличие от описанных выше способов.
Признаками предлагаемого способа, общими с прототипом являются:
- выделение лучшей из принятых комбинаций с запоминанием ее и степени ее искажения;
- вычисление вектора надежности путем суммирования по модулю два принятых повторов комбинаций;
- формирование множества векторов ошибок путем перебора единичных символов вектора надежности (единицы там, где одноименные разряды принятых комбинаций различны);
- поиск вектора ошибок для декодированной комбинации, включающий операции: суммирование по модулю два каждого из векторов ошибок с векторами принятых искаженных комбинаций, проверка полученных суммированием комбинаций кодом на наличие ошибок - их декодирование;
- формирование отказа от обработки в случае невозможности получения исходного сообщения.
Признаками предлагаемого способа отличительными от прототипа являются:
- формирование мажоритарной комбинации, которая получается путем выбора двоичных элементов на одноименных позициях принятых комбинаций по большинству;
- декодирование (исправление кодом) мажоритарной комбинаций с запоминанием ее и степени ее искажения;
- анализ степени искажения декодированной мажоритарной комбинации на возможность ее успешного декодирования;
- проверка совпадения исправленной кодом мажоритарной комбинации и исправленной кодом лучшей из принятых из канала связи комбинаций, и при положительном результате проверки выдача комбинации получателю;
- формирование массива исправленных комбинаций, образованных декодированием комбинаций, которые получают суммированием по модулю два векторов однобитовых ошибок и декодированной мажоритарной комбинации;
- проверка наличия в полученном массиве двух одинаково исправленных комбинаций, и при обнаружении - выдача результирующей комбинации получателю;
- проверка наличия одной исправленной комбинации, при обнаружении которой выдают ее в качестве результирующей получателю;
- проверка степени искажения лучшей из принятых комбинаций на возможность ее успешного декодирования, и при положительном результате проверки выдача исправленной кодом лучшей комбинации получателю;
- формирование массива двухбитовых ошибок из вектора надежности;
- поиск вектора двухбитовой ошибки для принятых декодированных искаженных комбинаций;
- формирование массива исправленных комбинаций, образованных декодированием комбинаций, которые получают суммированием по модулю два векторов двухбитовых ошибок и принятых декодированных искаженных комбинаций;
- проверка наличия в полученном массиве двух одинаково исправленных комбинаций, и при обнаружении их - выдача результирующей комбинации получателю.
Предлагаемый способ обработки принятых комбинаций реализует перебор векторов только однобитовых и двухбитовых ошибок, так как перебор векторов трехбитовых ошибок нецелесообразен из-за получения слишком большого числа исправленных комбинаций с большим количеством ложных исправлений.
Выбор наиболее достоверной комбинации посредством перебора возможных вариантов векторов ошибок с наложением их на принятые комбинации и последующим декодированием значительно повышает достоверность приема при синхронном накоплении и мажоритарном декодировании.
Поставленная задача решается при обработке трех принятых искаженных комбинаций при качестве канала, соответствующем корректирующей способности используемого кода. В качестве кода формирования комбинаций используются двоичные циклические коды. Например, в устройствах [2] используется код Хемминга (24, 16), способный исправить все однобитовые ошибки.
При попадании ошибок на одноименные позиции в принимаемых комбинациях использование синхронного накопления и мажоритарного декодирования не достаточно для достоверного приема информации. Поэтому перебор векторов ошибок, реализованный в прототипе, - единственный способ получения правильной комбинации.
Однако в отличие от прототипа поиск двух одинаково исправленных комбинаций (при декодировании сложенных по модулю два векторов ошибок и принятых комбинаций) значительно эффективнее поиска вектора ошибки, дающего комбинацию без ошибок, так как очень часто ошибка попадает в одноименные позиции двух принятых комбинаций.
Отличительной чертой предлагаемого способа является перебор всех двухбитовых ошибок для получения векторов ошибок, при сложении которых по модулю два с принятыми комбинациями и последующего декодирования, возможно получение двух одинаково исправленных комбинаций - комбинации, выдаваемой получателю (исходного сообщения).
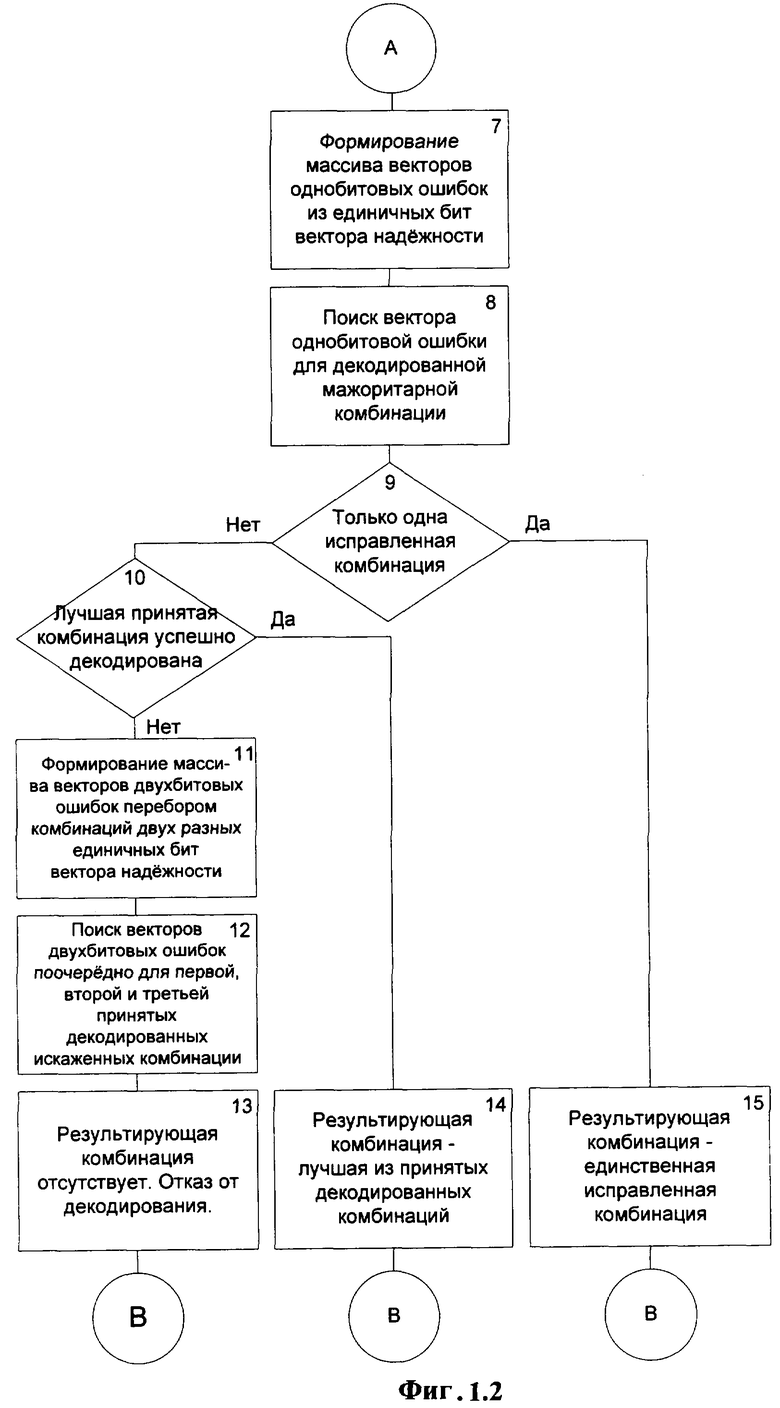
На фигурах 1.1, 1.2 представлена последовательность операций, иллюстрирующая предлагаемый способ обработки трехкратно принятых комбинаций.
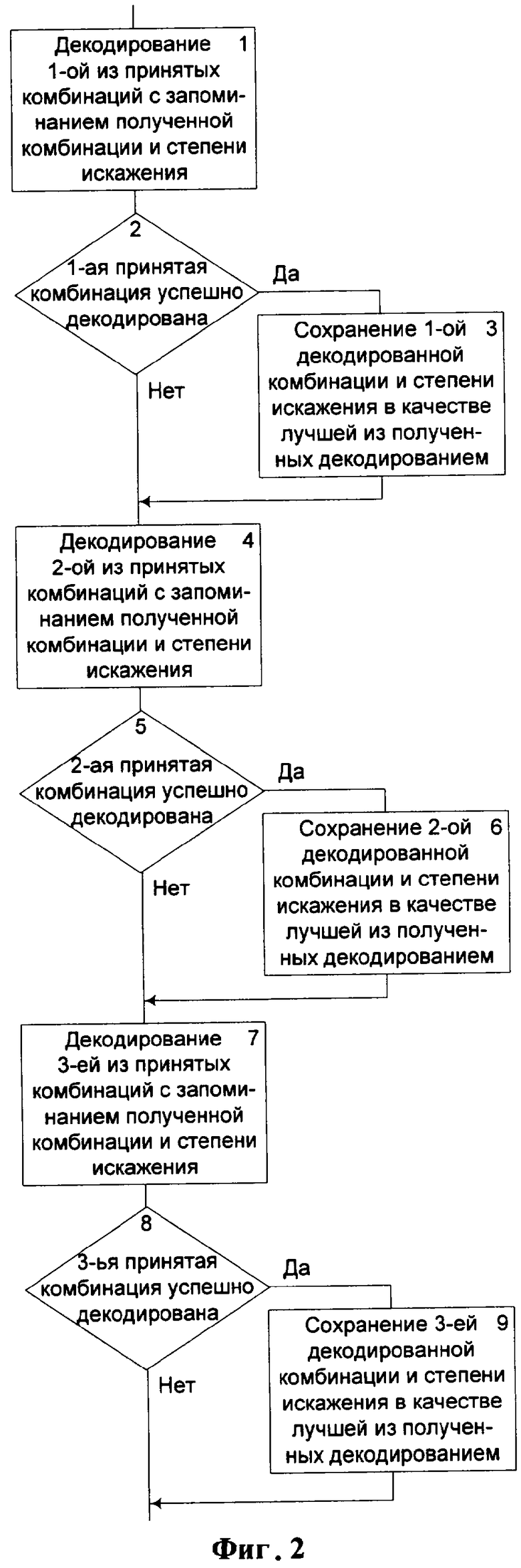
На фигуре 2 - последовательность операций выбора лучшей из принятых комбинаций (пример реализации).
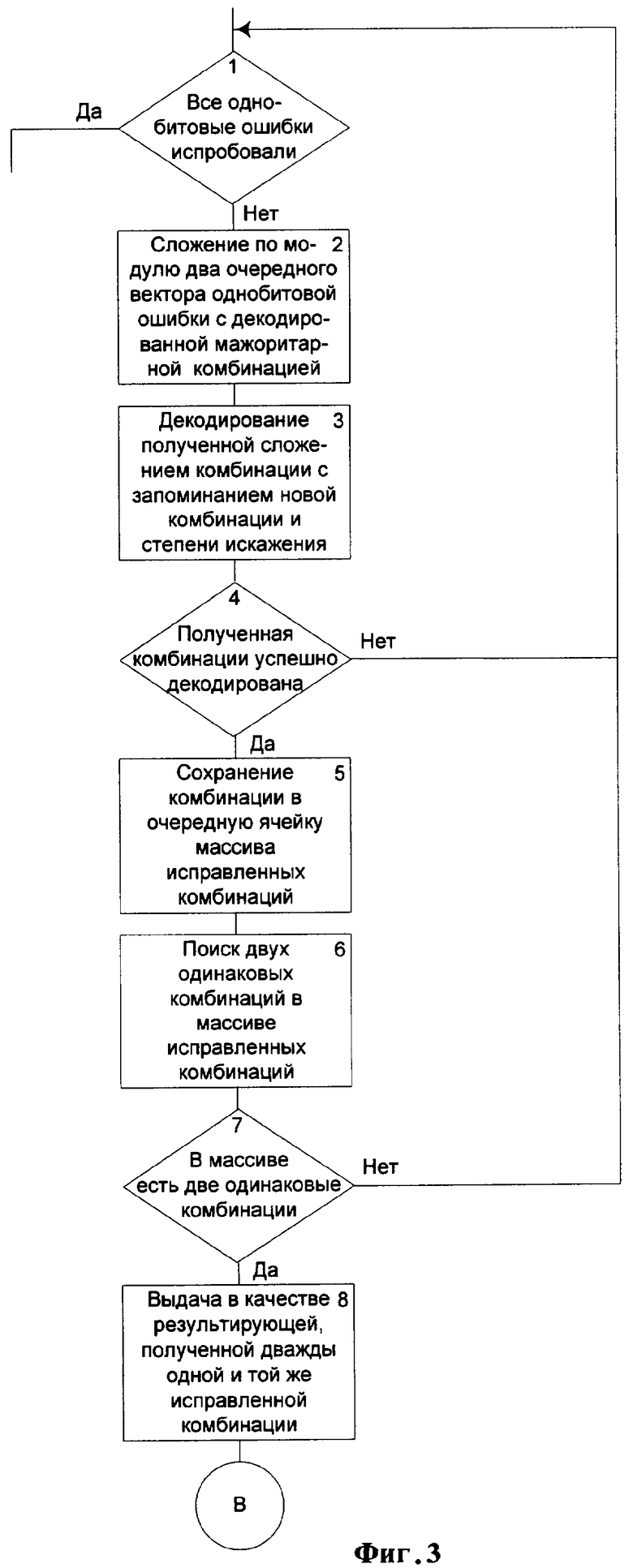
На фигуре 3 - последовательность операций поиска вектора однобитовой ошибки для декодированной мажоритарной комбинации (пример реализации).
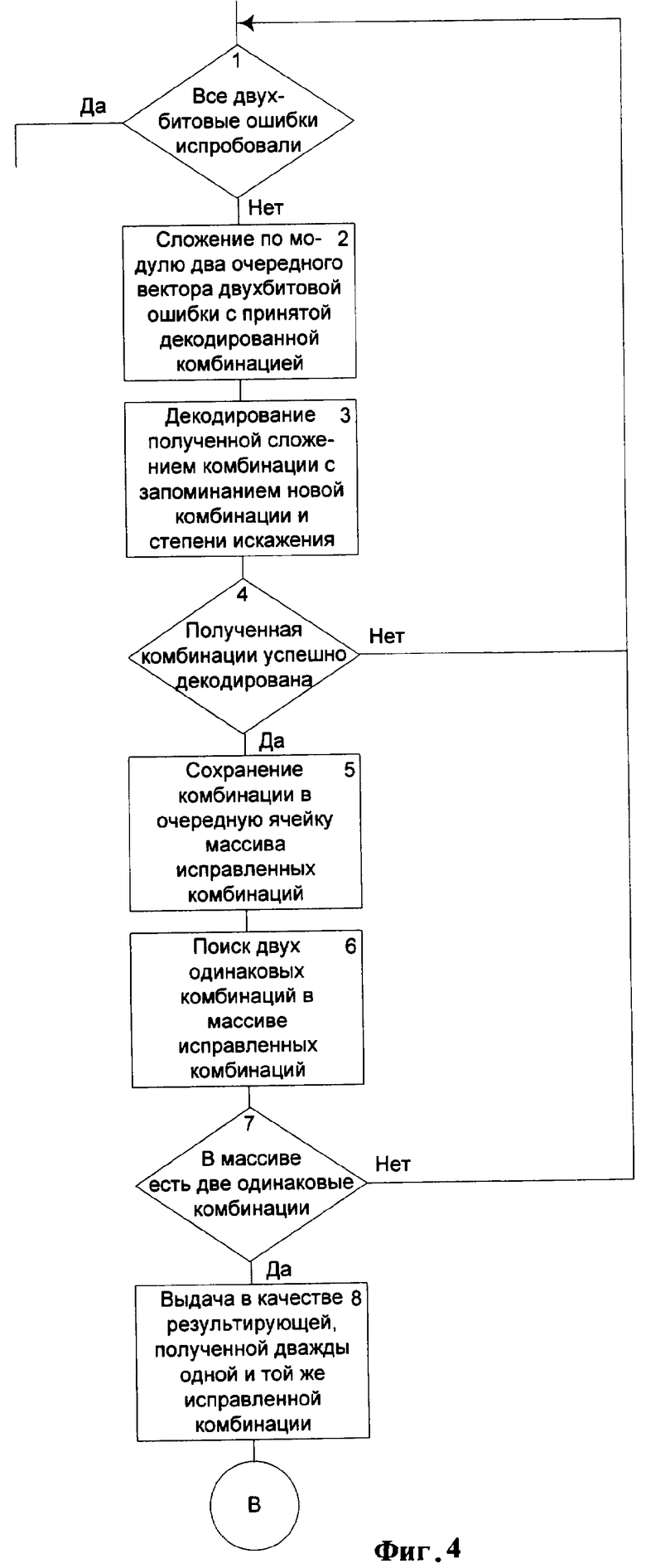
На фигуре 4 - последовательность операций поиска вектора двухбитовой ошибки для одной из принятых декодированных искаженных комбинаций (пример реализации).
Рассмотрим подробно способ обработки трехкратно принятых комбинаций для кода Хемминга (24, 16), способного исправить одну битовую ошибку. Под декодированием будем понимать получение измененной (исправленной) комбинации и признака декодирования - степени искажения.
На фигуре 1 обобщенно представлена последовательность операций, иллюстрирующая предлагаемый способ обработки трехкратно принятых комбинаций на приемной стороне. В блоке 1 из трех принятых из канала связи комбинаций формируют мажоритарную комбинацию путем выбора двоичных элементов на одноименных позициях по большинству. При реализации можно воспользоваться формулой:
Mjr=((K1⊕K2)∧(К1⊕К3))⊕К1, где
Mjr - получаемая мажоритарная комбинация;
K1, K2, К3 - принятые из канала связи комбинации.
Далее декодируют полученную комбинацию с запоминанием новой комбинации (исправленной кодом) и степени ее искажения (СтИск=0, СтИск=1 или СтИск=2).
В блоке 2 осуществляют выбор лучшей из принятых комбинаций с одновременным их декодированием. Пример реализации операции выбора представлен на фигуре 2, описание которой приведено ниже.
В блоке 3 фигуры 1.1 анализируют степень искажения декодированной мажоритарной комбинации. При положительном результате анализа (СтИск=0, СтИск=1) в блоке 4 проверяют совпадение декодированной мажоритарной комбинации с лучшей из принятых комбинаций, полученной в блоке 2. При совпадении комбинаций в блоке 5 выдают получателю результирующую комбинацию - декодированную мажоритарную комбинацию. Иначе в блоке 6 вычисляют вектор надежности суммированием по модулю два принятых комбинаций. В практической реализации эта операция может быть представлена формулой:
VctrN=(К1⊕К2)∨(K1⊕K3), где
VctrN - получаемый вектор надежности;
К1, К2, К3 - принятые из канала связи комбинации.
В блоке 7 формируют массив векторов однобитовых ошибок из предварительно выделенных единичных бит вектора надежности. Вектор однобитовой ошибки - это комбинация, в которой только один единичный бит. В блоке 8 производят поиск вектора однобитовой ошибки для декодированной мажоритарной комбинации, при суммировании которого по модулю два с декодированной мажоритарной комбинацией и последующем исправлении полученной комбинации кодом можно получить исходное сообщение. Пример реализации операции поиска вектора однобитовой ошибки представлен на фигуре 3, описание которой приведено ниже.
В блоке 9 фигуры 1.2 анализируют наличие одной исправленной комбинации, образованной декодированием комбинации, которая получена суммированием по модулю два одного из векторов однобитовой ошибки и декодированной мажоритарной комбинации. Если комбинация обнаружена, ее выдают получателю в качестве результирующей комбинации в блоке 15.
Иначе в блоке 10 проверяют степень искажения лучшей из принятых декодированных комбинаций на ее успешное декодирование: отсутствие искажений (СтИск=0) или исправление комбинации (СтИск=1). Если лучшая комбинация успешно декодирована, ее выдают получателю в качестве результирующей комбинации в блоке 14.
Иначе в блоке 11 формируют массив векторов двухбитовых ошибок перебором всех комбинаций разных единичных бит вектора надежности.
В блоке 12 осуществляют поиск векторов двухбитовых ошибок поочередно для первой, второй и третьей принятых декодированных искаженных комбинаций. Пример реализации поиска вектора двухбитовой ошибки представлен на фигуре 4, описание которой приведено ниже.
Если поиск не сформировал результирующей комбинации, в блоке 13 фигуры 1.2 формируют отказ от обработки.
Поясним примеры возможной реализации некоторых операций из способа обработки трехкратно принятых комбинаций.
На фигуре 2 представлен пример возможной реализации последовательности операций выбора лучшей из декодированных принятых комбинаций.
В блоках 1, 4 и 7 производят декодирование принятых комбинаций с запоминанием полученных исправленных комбинаций и степеней их искажений. В блоках 2, 5 и 8 анализируют успешное декодирование принятых комбинаций. Например, успешным декодирование можно считать при степени искажения, показывающей отсутствие искажений или успешное исправление обнаруженных ошибок. При положительном результате анализа в блоках 3, 6 и 9 сохраняют декодированную комбинацию со степенью ее искажения в качестве лучшей комбинации. Данный способ выбора лучшей комбинации реализован в устройстве [2] и назван синхронным накоплением.
На фигуре 3 представлен пример возможной реализации поиска вектора однобитовой ошибки для декодированной мажоритарной комбинации.
В блоке 1 анализируют перебор всех однобитовых ошибок. Пока не все вектора однобитовых ошибок испробованы, в блоке 2 выполняют суммирование по модулю два очередного вектора с декодированной мажоритарной комбинацией. В блоке 3 выполняют декодирование полученной в блоке 2 комбинации с запоминанием ее и степени ее искажения. В блоке 4 проводят анализ успешного декодирования. Например, успешным декодирование можно считать при степени искажения, показывающей отсутствие искажений или успешное исправление обнаруженных ошибок. При положительном результате анализа в блоке 5 сохраняют комбинацию в очередную ячейку массива исправленных комбинаций. В блоке 6 производят поиск двух одинаковых комбинаций в массиве исправленных комбинаций просмотром и сравнением всех полученных ранее исправленных комбинаций. Если при анализе поиска двух одинаковых комбинаций в блоке 7 получают положительный результат, выдают эту полученную дважды исправленную комбинацию получателю в качестве результирующей комбинации. Иначе продолжают перебор всех векторов однобитовых ошибок.
На фигуре 4 представлен пример возможной реализации поиска вектора двухбитовой ошибки для принятых декодированных комбинаций. Последовательность операций на фигуре 4 во многом сходна с действиями на фигуре 3. Только в блоке 2 производят суммирование по модулю два очередного вектора двухбитовой ошибки с принятой декодированной комбинацией.
Практическая реализация предлагаемого способа подтвердила прогноз по увеличению достоверного приема информации. Для практической реализации был выбран циклический код Хемминга (24, 16), используемый в устройстве [2], и способ передачи данных трехкратно с 225 кодовыми блоками в информационном пакете. Для тестирования использовался имитатор канала, настроенный на 3.12% искажений данных.
При заданном количестве искажений возникают ситуации до четырех искаженных бит в кодовом блоке из 24 бит, то есть до 16,7% искажений в информационной комбинации. Трехбитовые ошибки в кодовых словах вызывают неправильное исправление кодового слова. Это ситуация нередкая. Так что, если пакет данных состоит из 225 кодовых блоков, три из четырех пакетов будут содержать неправильно декодированные блоки Хемминга. Синхронное накопление пакетов данных мало эффективно и 25% пакетов могут не довестись даже с девяти передач пакетов из 225 блоков.
Использование предлагаемого способа значительно повышает достоверность приема данных и на канале с 3.12% искажений гарантирует декодирование 99,97% блоков. По результатам проведенных исследование получено, что не более трех блоков из десяти тысяч будут декодированы неверно. В конечном итоге это приводит к тому, что 94% пакетов данных из 225 блоков доводятся с первой трехкратной передачи. 6% доводятся со второй трехкратной передачи. Для сравнения был взят результат обработки информации, осуществляемой действиями прототипа, где 36% пакетов требовали второй трехкратной передачи кода. Итак, использование предлагаемого способа гарантирует исправление 9997 блоков из 10000, или не более 7% повторных передач пакетов данных из 225 блоков.
Проведенные испытания на канале в 6,25% искажений (это за пределами возможностей кода при данной корректирующей способности) показали доведение 92% пакетов с трехкратной передачей трех пакетов, то есть до девяти вариантов искаженных пакетов.
Источники информации
1. Кларк Дж., мл., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи: Пер. с англ. - М.: Радио и связь, 1987. - 392 с.: ил. - (Стат.теория связи); с.129.
2. Мартынов Ю.М. Обработка информации в системах передачи данных. - М.: Связь, 1969. - 200 с.: ил.
3. Кузнецов С. В., Сорока Л.С., Николаев Ю.И., Александров В.О., Приходько С.И., Рассомахин С.Г., Чипига А.Ф., Малофей О.П. Авторское свидетельство №1522415 А1, МПК Н03М 13/02. Декодирующее устройство.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПЕРЕДАЧИ СООБЩЕНИЙ В СИСТЕМАХ С ОБРАТНОЙ СВЯЗЬЮ И ГИБРИДНЫМ АВТОМАТИЧЕСКИМ ЗАПРОСОМ НА ПОВТОРЕНИЕ | 2022 |
|
RU2786023C1 |
| СПОСОБ СИНДРОМНОГО ДЕКОДИРОВАНИЯ ДЛЯ СВЕРТОЧНЫХ КОДОВ | 2004 |
|
RU2282307C2 |
| СПОСОБ КОДИРОВАНИЯ-ДЕКОДИРОВАНИЯ ИНФОРМАЦИИ В СИСТЕМАХ ПЕРЕДАЧИ ДАННЫХ | 2005 |
|
RU2310273C2 |
| Устройство для мажоритарного декодирования при трехкратном повторении кодовой комбинации | 1985 |
|
SU1305876A1 |
| СПОСОБ КОДИРОВАНИЯ-ДЕКОДИРОВАНИЯ КАСКАДНОЙ КОДОВОЙ КОНСТРУКЦИИ В СИСТЕМАХ ПЕРЕДАЧИ ДАННЫХ | 2009 |
|
RU2420870C1 |
| Устройство для мажоритарного декодирования двоичных кодов при трехкратном повторении сообщения | 1983 |
|
SU1095398A2 |
| Устройство для мажоритарного декодирования циклических кодов при трехкратном повторении комбинации | 1984 |
|
SU1246380A1 |
| Устройство для обнаружения и исправления ошибок | 1990 |
|
SU1785041A1 |
| Устройство для мажоритарного декодирования имитостойких циклических кодов при трехкратном повторении комбинации | 1990 |
|
SU1709538A1 |
| СПОСОБ КОДИРОВАНИЯ-ДЕКОДИРОВАНИЯ ИНФОРМАЦИИ В СИСТЕМАХ ПЕРЕДАЧИ ДАННЫХ | 2014 |
|
RU2562435C1 |
Изобретение относится к электросвязи, вычислительной технике, а именно к способам повышения достоверности принимаемой информации и может быть использовано в системах передачи информации с дублированием сообщений. Сущность способа заключается в увеличении вероятности приема информации за счет использования информации о ранее принятых комбинациях и последующем выборе наиболее достоверной комбинации. Выбор осуществляется путем мажоритарного декодирования и перебора комбинаций с наложением возможных векторов ошибок на принятые искаженные информационные блоки. Технический результат, достигаемый способом, состоит в повышении достоверности приема данных и на канале с количеством искажений, соответствующем исправляющей способности кода, гарантирует декодирование 99,97% информационных кодовых блоков, а на канале с количеством искажений, вдвое превышающем исправляющую способность кода, доведение более 90% информационных сообщений, состоящих из двухсот кодовых блоков, при тройной передаче трехкратно передаваемых сообщений. 4 ил.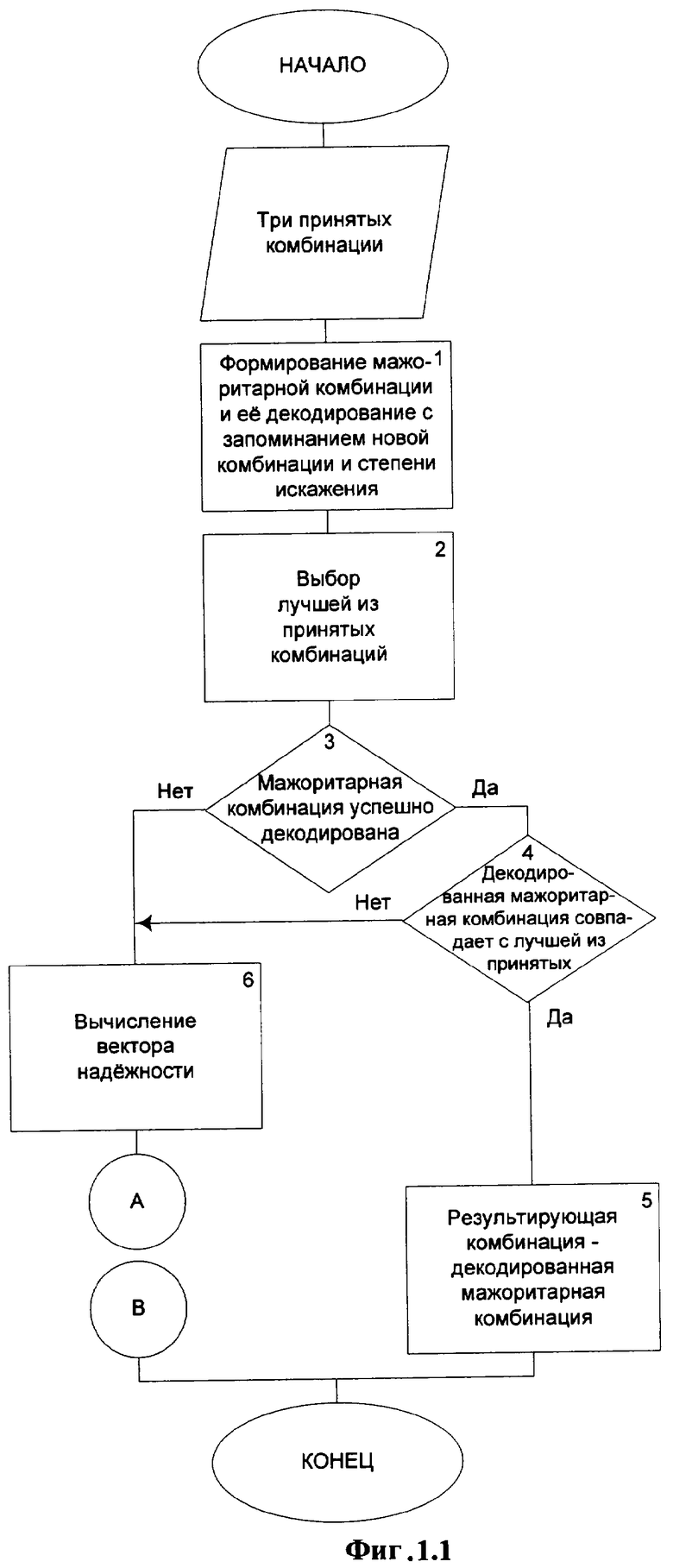
Способ обработки трехкратно принятых комбинаций с использованием операции выделения лучшей из принятых декодированных комбинаций с последующим запоминанием ее и степени ее искажения, а также операции вычисления вектора надежности, формирования из него массива однобитовых ошибок и поиска вектора ошибок для декодированной комбинации, отличающийся тем, что перед выделением лучшей из принятых декодированных комбинаций из них формируют мажоритарную комбинацию, которую декодируют, определяют степень ее искажения, после чего анализируют степень искажения декодированной мажоритарной комбинации на возможность успешного декодирования и при положительном результате анализа проверяют ее на совпадение с лучшей из принятых декодированных комбинаций и при совпадении выдают ее получателю, а операцию вычисления вектора надежности, формирования из него массива однобитовых ошибок и поиска вектора однобитовой ошибки для декодированной комбинации, в качестве которой выбирают декодированную мажоритарную комбинацию, осуществляют при отрицательном результате анализа степени искажения ее на возможность успешного декодирования, при этом в процессе поиска вектора однобитовой ошибки формируют массив исправленных комбинаций, в котором проверяют наличие двух одинаковых исправленных комбинаций и при обнаружении их выдают результирующую комбинацию получателю, по окончании формирования массива анализируют наличие одной исправленной комбинации, при обнаружении которой выдают ее в качестве результирующей получателю, а при необнаружении проверяют степень искажения лучшей из принятых декодированных комбинаций на возможность ее успешного декодирования и при положительном результате проверки выдают получателю, а при отрицательном формируют из вектора надежности массив двухбитовых ошибок, с поочередным использованием которых осуществляют поиск вектора двухбитовой ошибки для принятых декодированных искаженных комбинаций, в процессе которого формируют массив исправленных комбинаций и проверяют наличие в массиве двух одинаковых исправленных комбинаций и при обнаружении их выдают результирующую комбинацию получателю, а при необнаружении выдают получателю отказ от обработки.
| Декодирующее устройство | 1988 |
|
SU1522415A1 |
| Мажоритарное декодирующее устройство корректирующего кода Рида-Маллера | 1980 |
|
SU902283A1 |
| Устройство для исправления пакета ошибок длины два | 1988 |
|
SU1578812A1 |
| Пенообразователь для тушения пожаров | 1984 |
|
SU1353446A1 |
| Дорожная спиртовая кухня | 1918 |
|
SU98A1 |
Авторы
Даты
2008-04-27—Публикация
2006-05-12—Подача