Изобретение относится к области строительства и предназначено для использования в качестве несущих элементов перекрытия зданий и сооружений.
Известна металлическая однопролетная (или многопролетная) неразрезная балка постоянного сечения (прямоугольного, коробчатого или двутаврового), включающая собственно балку, изготовленную из прокатных или сварных профилей, опорные устройства, выполненные по схеме шарнирного опирания или жесткого защемления ее концов, и промежуточные шарнирно подвижные опорные устройства в случае многопролетной балки [1, с.114-116, 120-122].
Недостатком такой балки является неэкономичность из-за перерасхода металла, поскольку большая ее часть остается недонапряженной из-за неравномерного распределения изгибающих моментов вдоль пролета (пролетов) балки.
Задача, на решение которой направлено изобретение, состоит в снижении материалоемкости металлической неразрезной балки за счет изменения ее изгибной жесткости по длине на отдельных участках и рациональном выборе соотношений длин и изгибных жесткостей этих участков.
Это достигается тем, что металлическая неразрезная балка прямоугольного, коробчатого или двутаврового сечений, включающая собственно балку, изготовленную из прокатных или сварных профилей, опорные устройства, изготовленные по схеме шарнирного опирания или жесткого защемления ее концов, выполнена ступенчато-переменной жесткости, при этом участки с большей изгибной жесткостью расположены под эпюрой изгибающих моментов с экстремальными ординатами, а рациональные соотношения длин участков и их изгибных жесткостей подобраны из условия равенства абсолютных значений допускаемых нормальных напряжений в сечениях с наибольшим и наименьшим значениями изгибающих моментов.
В случае равной высоты и симметрии всех сечений металлической неразрезной балки относительно их нейтральной оси отношение изгибных жесткостей смежных участков балки n определяют по формуле 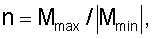 где Мmax и Мmin - экстремальные значения изгибающих моментов в наиболее опасных сечениях балки. При этом в случае действия по всей длине балки равномерно распределенной нагрузки рациональные соотношения длин участков k и их изгибных жесткостей n определяют с помощью аппроксимирующих функций, построенных по результатам точного аналитического расчета:
где Мmax и Мmin - экстремальные значения изгибающих моментов в наиболее опасных сечениях балки. При этом в случае действия по всей длине балки равномерно распределенной нагрузки рациональные соотношения длин участков k и их изгибных жесткостей n определяют с помощью аппроксимирующих функций, построенных по результатам точного аналитического расчета:
- для однопролетной балки, один конец которой жестко защемлен, а другой шарнирно оперт, по формуле
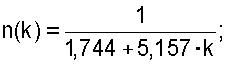
- для жестко защемленной по концам однопролетной балки по формуле
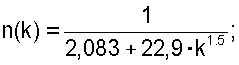
- для двухпролетной балки с равными пролетами и шарнирным опиранием концевых и промежуточных опор по формуле
n(k)=-7,9788·k3+5,3285·k2-0,6077·k+0,5816.
Сущность изобретения поясняется чертежами, представленными на фиг.1...5.
На фиг.1 изображена однопролетная неразрезная балка постоянной изгибной жесткости, один конец которой жестко защемлен, а другой шарнирно оперт, с возможными вариантами поперечных сечений.
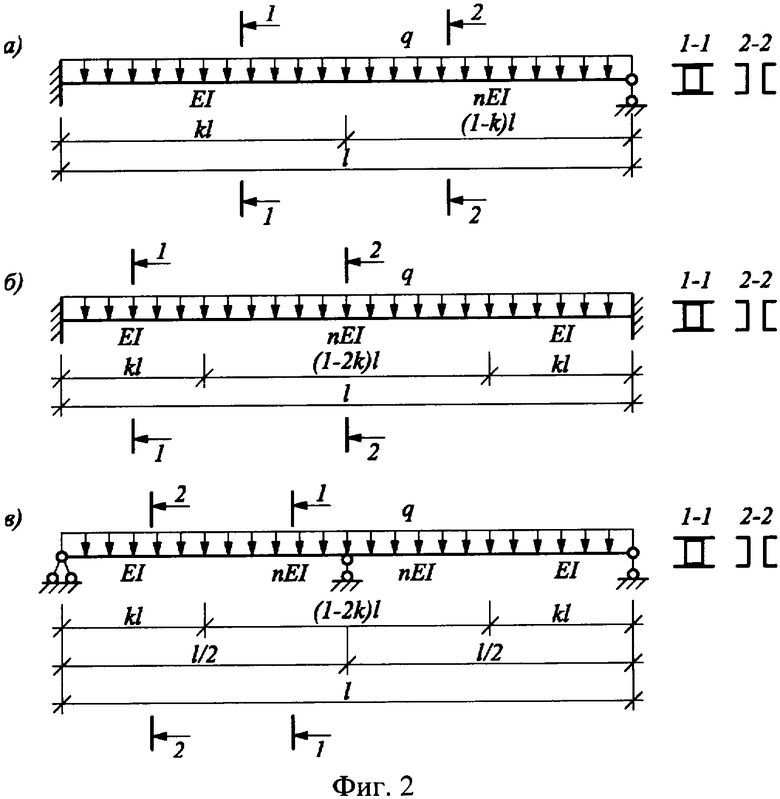
На фиг.2 изображены варианты неразрезных балок ступенчато-переменной жесткости: на схеме а) - балка, один конец которой жестко защемлен, а другой шарнирно оперт; на схеме б) - балка с двумя жестко защемленными концами; на схеме в) - шарнирно опертая двухпролетная балка с равными пролетами. На всех схемах указаны соотношения длин участков с разными изгибными жесткостями и соотношения этих жесткостей.
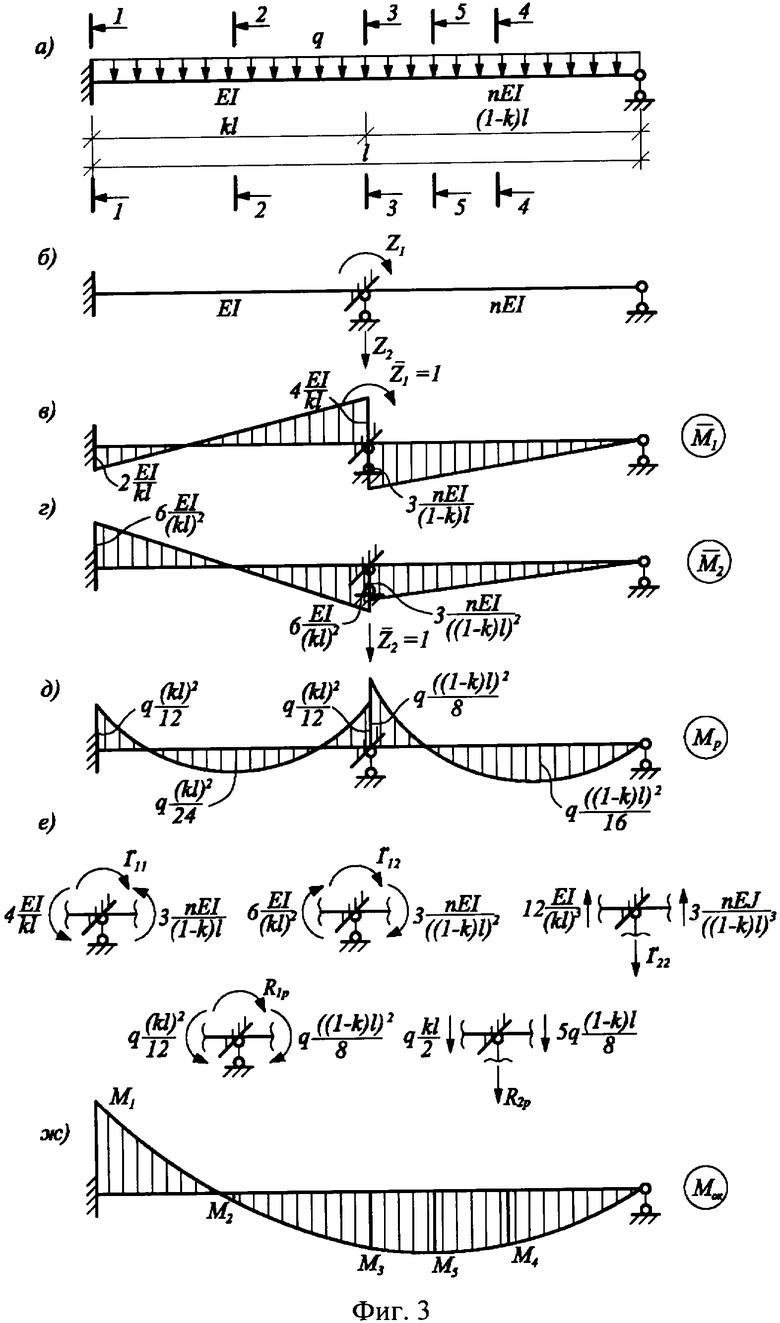
На фиг.3 графически представлены этапы точного решения задачи по определению изгибающих моментов в однопролетной балке ступенчато-переменной жесткости, один конец которой жестко защемлен, а другой шарнирно оперт.
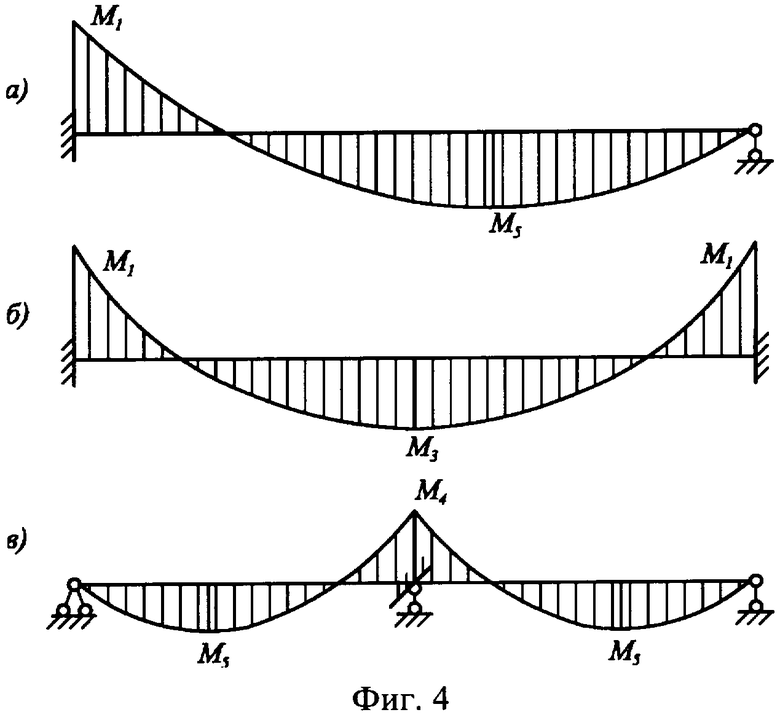
На фиг.4 изображены окончательные эпюры изгибающих моментов в трех неразрезных балках ступенчато-переменной жесткости: на схеме а) - балка, один конец которой жестко защемлен, а другой шарнирно оперт; на схеме б) - балка с обоими жестко защемленными концами; на схеме в) - двухпролетная шарнирно опертая балка с равными пролетами.
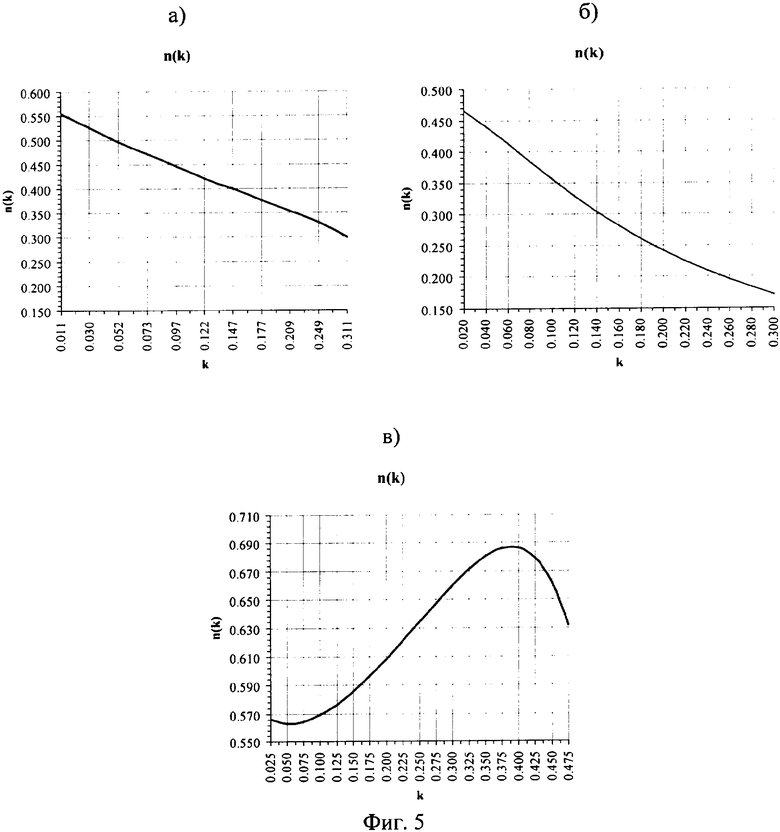
На фиг.5 представлены графики аппроксимирующих функций n(k) для подбора оптимальных соотношений длин участков k и их изгибных жесткостей n для всех трех рассматриваемых схем балок.
Неразрезная металлическая балка (фиг.1) включает в себя собственно балку 1, изготовленную из прокатных или сварных профилей, опорные устройства 2 и 3, выполненные по схеме шарнирного опирания 3 или жесткого защемления 2 ее концов.
Предлагаемая конструкция неразрезной балки ступенчато-переменной жесткости отличается от балки постоянного сечения тем, что имеет два участка с разными изгибными жесткостями. На участке с наибольшими изгибающими моментами площадь поперечного сечения принимают большей, чем на участке с меньшими изгибающими моментами. Реализация указанных конструктивных особенностей неразрезных балок приводит к более экономичному расходу материала. Необходимо лишь подобрать рациональные соотношения длин участков с различными изгибными жесткостями k и соотношения этих жесткостей n.
Рассмотрим теоретическое решение задачи подбора оптимальных соотношений n и k на примере неразрезной балки ступенчато-переменной жесткости, один конец которой жестко защемлен, а другой шарнирно оперт, нагруженной равномерно распределенной нагрузкой интенсивности q.
Разделим балку на два характерных участка (фиг.3, схема а). Изгибную жесткость участка со стороны жесткой заделки обозначим через EI (Е - модуль упругости материала, I - момент инерции сечения), а другого участка - nEI, где n - переменный параметр, определяемый расчетом. Длину участка со стороны жесткой заделки обозначим kl, где k - параметр, также определяемый расчетом.
Для решения этой задачи воспользуемся методом перемещений [2] и запишем систему канонических уравнений для основной системы, представленной на фиг.3 (схема б)
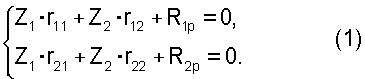
Здесь и далее использованы общепринятые в строительной механике [2] обозначения. Для определения коэффициентов и свободных членов этих уравнений построим эпюры изгибающих моментов единичных и грузового состояний (фиг.3, схемы в, г, д). Вырезая соответствующие узлы балки из эпюр изгибающих моментов единичных и грузового состояний, из условий равновесия этих узлов (фиг.3, схема е) найдем коэффициенты и свободные члены в уравнениях (1):
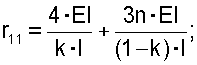
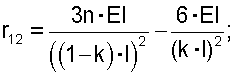
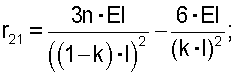
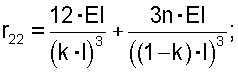
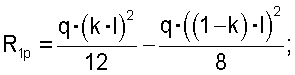
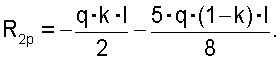
Подставим эти выражения в уравнения (1):
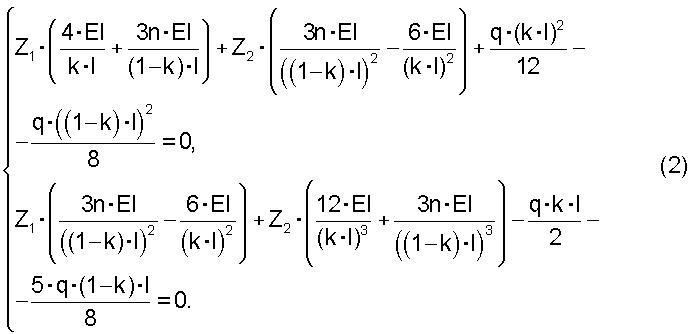
Решая полученную систему уравнений, найдем:
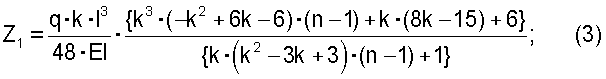
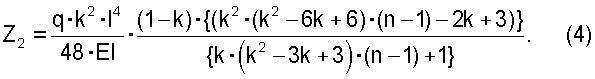
Для построения окончательной эпюры изгибающих моментов (фиг.3, схема ж) следует вычислить изгибающие моменты в характерных сечениях балки по формуле:
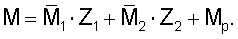
Экстремальные ординаты в этой эпюре моментов будут в сечениях 1-1 и 5-5:
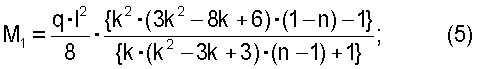
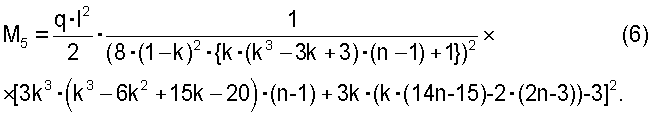
Запишем условие оптимального проектирования балки в виде равенства наибольших нормальных напряжений в сечениях 1-1 и 5-5:
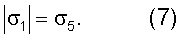
Учитывая, что σ=М/W и W=2I/h, где W - момент сопротивления сечения, h - его высота, это условие примет следующий вид:
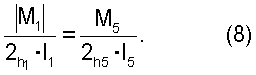
При неизменной высоте сечения h и принятом соотношении жесткостей для характерных участков выражение (8) можно переписать в виде равенства
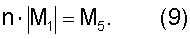
Подставив это равенство в соответствующие выражения для изгибающих моментов в сечениях 1-1 и 5-5 после преобразований, получим:
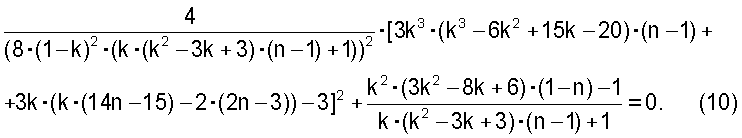
Этой формулой пользоваться неудобно, поэтому по точным значениям n и k, полученным по формуле (10), построена аппроксимирующая функция
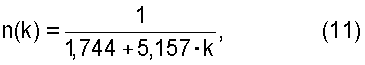
на области определений n∈(0,3; 0,55), которая с погрешностью до 1,5% удовлетворяет точному решению по формуле (10).
График функции (11) построен на фиг.5. Физический смысл этого графика заключается в том, что для каждой его точки с абсциссой k и ординатой n напряжения в сечениях с максимальным и минимальным значениями изгибающих моментов с соответствующими соотношениями изгибных жесткостей и длин участков будут равными.
По формуле (11) или по графику, изображенному на фиг.5, задавшись значением параметра k, можно найти значение параметра n и, наоборот, по параметру n - найти параметр k. Эти соотношения будут наиболее рациональными, поскольку следуют из точного аналитического решения рассматриваемой задачи.
Такие же расчеты были проведены для однопролетной балки с жестко защемленными концами и для двухпролетной шарнирно опертой балки с равными пролетами. При этом были получены следующие результаты
- для однопролетной балки:
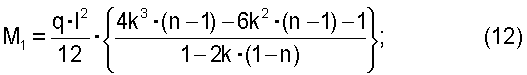
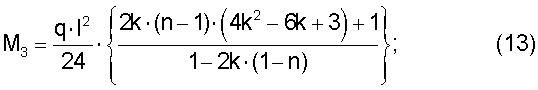
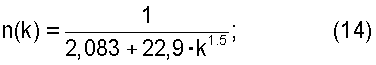
- для двухпролетной балки с равными пролетами:
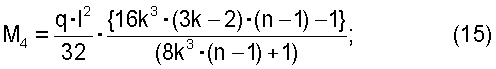
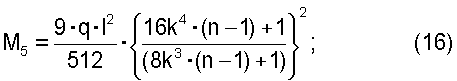
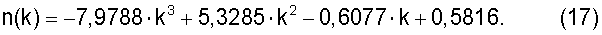
Аналитическое выражение изгибающего момента M5 в обоих случаях находилось путем минимизации функции М, записанной в общем виде на рассматриваемом участке.
Пример реализации изобретения. Поскольку для всех трех рассматриваемых схем балок порядок подбора рациональных соотношений параметров n и k одинаков, рассмотрим только один пример реализации изобретения для однопролетной металлической балки, один конец которой жестко защемлен, а другой шарнирно оперт (фиг.3, схема а).
Для металлической балки, изготовленной из Ст.3, приняты следующие исходные данные: основное сечение балки выполнено из двух швеллеров №30С по ГОСТ 8240-97 (I=2·6045=12090 см4=1,209·10-4 м4, W=2·403=806 см3=8,06·10-4 м3), длина балки l=6 м, модуль упругости материала Е=2·105 МПа; допускаемое напряжение [σ]=30 МПа. Полки швеллеров расположены наружу (фиг.2, сечение 2-2), расстояние между стенками швеллеров - 250 мм. На усиливаемом участке балки вверху и внизу между швеллерами приварены металлические полосы толщиной 28 мм и шириной 250 мм (фиг.2, сечение 1-1).
Момент инерции полученного составного сечения находится по формуле:
I=2I1+2I2=2I10+2I20+2A2·a2,
где 2I10=1,209·10-4 м4 - момент инерции двух швеллеров №30С (взят из сортамента); 2I20 - момент инерции двух полос относительно их горизонтальной центральной оси:

A2 - площадь сечения полосы; а - расстояние межу горизонтальными центральными осями всего сечения и полосы:
2А2·а2=2·0,25·0,028·0,1362=2,589·10-4 м4;
I=1,209·10-4+0,0092·10-4+2,589·10-4=3,8072·10-4 м4.
Найдем отношение моментов инерции основного и составного сечений:
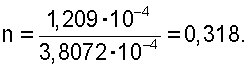
По этому значению параметра n с помощью графика на фиг.5 (схема а) находим значение параметра k=0,26. С учетом этих параметров по формулам (5), (6) находим значения экстремальных изгибающих моментов:
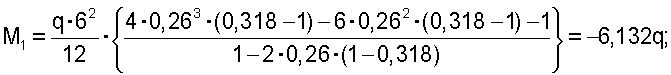
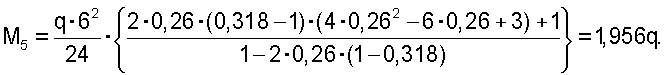
Подставляя полученные значения М1 и M5 в выражение (9) проверяем равенство нормальных напряжений в соответствующих сечениях:
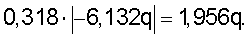
Максимальное нормальное напряжение в сечении 5-5 должно удовлетворять условию прочности σ=М5/W5≤[σ], где W5 - момент сопротивления двух швеллеров №30С, найденный выше. Тогда допускаемый изгибающий момент найдем из неравенства М5≤[σ]·W5. Выразив M5 из выражения (6) путем подстановки в него параметров n и k и приравняв его к допускаемому значению, найдем интенсивность равномерно распределенной нагрузки q:
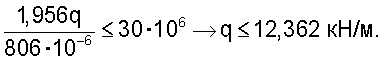
Для дальнейших вычислений примем q=12,36 кН/м.
Сравним материалоемкость балки переменной жесткости с балкой постоянной жесткости, воспринимающей нагрузку q=12,36 кН/м.
Максимальный изгибающий момент в балке постоянного сечения определяется по формуле
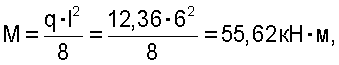
а требуемый момент сопротивления сечения - по формуле
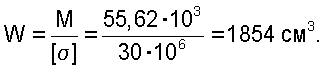
По ГОСТ 8239-89 принимаем два двутавра №40, W=1906 см3, погонная масса m=57 кг.
Сравниваем материалоемкость вариантов:
- масса сечения составленного из двух швеллеров №30С и двух полос длиной 0,26·l=0,26·6=1,56 м, шириной 0,25 м и толщиной 0,028 м
m=2·6·34,44+2·1,56·54,95=584,73 кг;
- масса двух двутавров №40
m=2·6·57=684 кг.
Экономия материала составляет
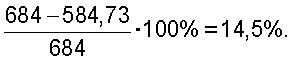
Таким образом, технический результат - сокращение материалоемкости металлических балок - достигается за счет их усиления в наиболее опасных сечениях. При этом рациональные соотношения изгибных жесткостей балок на смежных участках и длин этих участков определяются по аналитическим зависимостям, полученным в предлагаемом изобретении.
Источники информации
1. Васильев А.А. Металлические конструкции. - М.: Стройиздат, 1975. - 424 с.
2. Снитко Н.К. Строительная механика. - М.: Высшая школа, 1972. - 488 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Висячий мост | 1989 |
|
SU1756454A1 |
| Способ мониторинга технического состояния мостовых сооружений в процессе их эксплуатации (варианты) | 2017 |
|
RU2650812C1 |
| РАМНЫЙ МЕТАЛЛИЧЕСКИЙ КАРКАС МНОГОЭТАЖНОГО ЗДАНИЯ И УЗЕЛ РАМНОГО МЕТАЛЛИЧЕСКОГО КАРКАСА | 1998 |
|
RU2146320C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ТЕХНИЧЕСКОГО РЕСУРСА АВАРИЙНОЙ ПОДКРАНОВОЙ БАЛКИ | 2014 |
|
RU2583116C2 |
| РЕШЕТЧАТАЯ ПОДКРАНОВАЯ КОНСТРУКЦИЯ | 1997 |
|
RU2142904C1 |
| СТЕНА ЗДАНИЯ | 1992 |
|
RU2080445C1 |
| МЕТАЛЛИЧЕСКАЯ НЕСУЩАЯ КОНСТРУКЦИЯ ПОКРЫТИЯ | 2007 |
|
RU2361982C1 |
| Металлический каркас многопролетного промышленного здания | 1980 |
|
SU894090A1 |
| ЗДАНИЕ МНОГОФУНКЦИОНАЛЬНОГО НАЗНАЧЕНИЯ | 2007 |
|
RU2345200C2 |
| Дощатая балка | 2022 |
|
RU2796282C1 |
Изобретение относится к области строительства, в частности к металлическим неразрезным балкам. Технический результат изобретения заключается в снижении материалоемкости металлической неразрезной балки за счет изменения ее изгибной жесткости по длине на отдельных участках и рациональном выборе соотношений длин и изгибных жесткостей этих участков. Металлическая неразрезная балка прямоугольного, коробчатого или двутаврового сечения включает собственно балку, изготовленную из прокатных или сварных профилей, опорные устройства, изготовленные по схеме шарнирного опирания или жесткого защемления ее концов. Балка выполнена ступенчато-переменной жесткости, при этом участки с большей изгибной жесткостью расположены под эпюрой изгибающих моментов с экстремальными ординатами, а рациональные соотношения длин участков и их изгибных жесткостей подобраны из условия равенства абсолютных значений допускаемых нормальных напряжений в сечениях с наибольшим и наименьшим значениями изгибающих моментов. 4 з.п. ф-лы, 5 ил.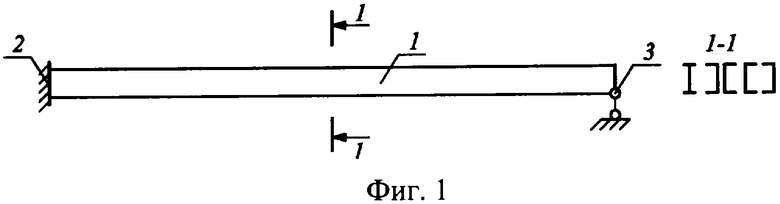
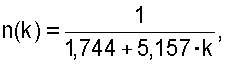
где k - отношение длин смежных участков балки.
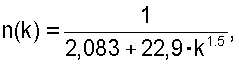
где k - отношение длин смежных участков балки.
n(k)=-7,9788·k3+5,3285·k2-0,6077·k+0,5816,
где k - отношение длин смежных участков балки.
| Файбишенко В.К | |||
| Металлические конструкции | |||
| - М.: Стройиздат, 1984, с.57-62 | |||
| Прибор для промывания газов | 1922 |
|
SU20A1 |
| Механическая топочная решетка с наклонными частью подвижными, частью неподвижными колосниковыми элементами | 1917 |
|
SU1988A1 |
| RU 2004734 С1, 15.12.1993 | |||
| Длинномерная несущая конструкция | 1979 |
|
SU885491A1 |
Авторы
Даты
2008-10-20—Публикация
2007-03-14—Подача