Изобретение относится к экспериментальной аэродинамике летательных аппаратов.
Известен способ определения комплексов вращательных и нестационарных производных продольных аэродинамических сил и моментов модели летательного аппарата, основанный на том, что модель в аэродинамической трубе отклоняют на установочный угол тангажа ϑ0, с помощью двигателя реализуют угловые гармонические колебания модели ϑ(t)=ϑ0+Аϑsinωt относительно неподвижного центра масс с заданными величинами амплитуды Aϑ и частоты ω, во время колебаний измеряют и регистрируют временные зависимости сил Y0(t) и моментов Mz0(t), действующих на модель без потока аэродинамической трубы, затем включают поток и при скорости V потока аналогичным образом измеряют и регистрируют временные зависимости сил и моментов, действующих на модель в потоке, вычисляют амплитуды первых гармоник а1Y, b1Y, a1Mz, b1Mz разложений в ряд Фурье зависимостей Y(t), Mz(t):
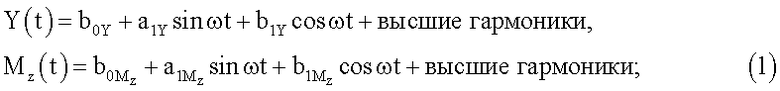
а также аналогичные амплитуды первых гармоник зависимостей Y0(t), Mz0(t), по полученным значениям амплитуд первых гармоник исключают инерционные нагрузки на модель, вычисляют комплексы нестационарных и вращательных производных 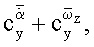
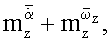 комплексы статических и нестационарных производных
комплексы статических и нестационарных производных 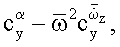
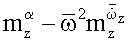 коэффициентов аэродинамических сил и моментов (см. С.М.Белоцерковский, Б.К.Скрипач, В.Г.Табачников. Крыло в нестационарном потоке газа. Стр. 194-196. Изд-во «Наука». Главная редакция физико-математической литературы. Москва. 1971 г.).
коэффициентов аэродинамических сил и моментов (см. С.М.Белоцерковский, Б.К.Скрипач, В.Г.Табачников. Крыло в нестационарном потоке газа. Стр. 194-196. Изд-во «Наука». Главная редакция физико-математической литературы. Москва. 1971 г.).
Данный способ позволяет определить лишь комплексы производных при различных значениях установочного угла атаки α=ϑ0, частоты колебаний ω и амплитуды колебаний угла атаки Аα=Аϑ и не позволяет определить составляющие этих комплексов.
Известно устройство для экспериментального определения комплексов вращательных и нестационарных производных, содержащее испытуемую модель, двигатель, кривошип, шатун, вал, оборудованный измерителем сил и моментов, действующих на модель, датчик угла атаки. Изменение частоты колебаний ω регулируется скоростью вращения вала двигателя, а значение амплитуды Aϑ угловых колебаний модели - радиусом кривошипа (см. С.М.Белоцерковский, Б.К.Скрипач, В.Г.Табачников. Крыло в нестационарном потоке газа. Стр.194. Изд-во «Наука». Главная редакция физико-математической литературы. Москва. 1971 г.).
Устройство работает следующим образом. Модель, жестко закрепленную на валу, отклоняют на заданный начальный угол атаки α=ϑ0 и фиксируют в этом положении. Включают двигатель, с помощью кривошипно-шатунного механизма вращение вала двигателя преобразуется в угловые колебания модели с круговой частотой ω и амплитудой Аϑ. Измеряют силы и моменты, действующие на модель без потока, включают поток и снова измеряют силы и моменты, определяют комплексы вращательных и нестационарных производных. Изменяют установочный угол атаки модели на заданную величину и снова вычисляют указанные комплексы производных. При необходимости испытания повторяются при других заданных значениях частоты ω и амплитуды Аϑ колебаний модели.
Рассмотренное устройство обеспечивает одинаковые значения угловой скорости тангажа и скорости изменения угла атаки, 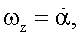 и не позволяет измерить раздельные значения вращательных и нестационарных производных (см. С.М.Белоцерковский, Б.К.Скрипач, В.Г.Табачников. Крыло в нестационарном потоке газа. Стр.195-197. Изд-во «Наука». Главная редакция физико-математической литературы. Москва. 1971 г.).
и не позволяет измерить раздельные значения вращательных и нестационарных производных (см. С.М.Белоцерковский, Б.К.Скрипач, В.Г.Табачников. Крыло в нестационарном потоке газа. Стр.195-197. Изд-во «Наука». Главная редакция физико-математической литературы. Москва. 1971 г.).
За прототип принят способ определения статических и нестационарных производных коэффициентов продольных аэродинамических сил и моментов 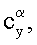
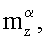
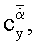
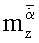 модели летательного аппарата, основанный на том, что модель отклоняют на угол тангажа ϑ0, с помощью двигателя реализуют гармонические вертикальные поступательные колебания модели ΔН(t)=АHcosωt с заданными значениями амплитуды АH и частоты ω при постоянном угле тангажа ϑ0, при колебаниях модели измеряют и регистрируют временные зависимости сил Y0(t) и моментов Mz0(t), действующих на модель без потока аэродинамической трубы, затем включают поток и при скорости V потока аналогичным образом измеряют временные зависимости сил Y(t) и моментов Mz(t), действующих на модель в потоке аэродинамической трубы, вычисляют амплитуды первых гармоник а1Y, b1Y, а1Mz, b1Mz разложений в ряды Фурье зависимостей Y(t), Mz(t):
модели летательного аппарата, основанный на том, что модель отклоняют на угол тангажа ϑ0, с помощью двигателя реализуют гармонические вертикальные поступательные колебания модели ΔН(t)=АHcosωt с заданными значениями амплитуды АH и частоты ω при постоянном угле тангажа ϑ0, при колебаниях модели измеряют и регистрируют временные зависимости сил Y0(t) и моментов Mz0(t), действующих на модель без потока аэродинамической трубы, затем включают поток и при скорости V потока аналогичным образом измеряют временные зависимости сил Y(t) и моментов Mz(t), действующих на модель в потоке аэродинамической трубы, вычисляют амплитуды первых гармоник а1Y, b1Y, а1Mz, b1Mz разложений в ряды Фурье зависимостей Y(t), Mz(t):
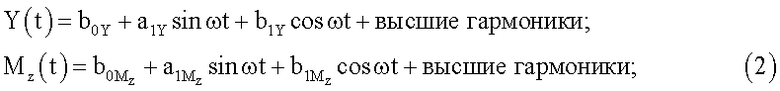
а также аналогичные амплитуды первых гармоник зависимостей Y0(t), Mz0(t), по полученным значениям амплитуд первых гармоник, исключая инерционные нагрузки на модель, вычисляют нестационарные производные 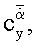
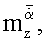 статические производные
статические производные 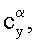
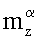 коэффициентов аэродинамических сил и моментов, где
коэффициентов аэродинамических сил и моментов, где 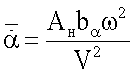 - вычисляемое значение амплитуды безразмерной скорости изменения угла атаки,
- вычисляемое значение амплитуды безразмерной скорости изменения угла атаки, 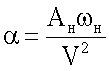 - вычисляемое значение амплитуды приращения угла атаки, bа - средняя аэродинамическая хорда (см. С.М.Белоцерковский, Б.К.Скрипач, В.Г.Табачников. Крыло в нестационарном потоке газа. Стр.194-195. Изд-во «Наука». Главная редакция физико-математической литературы. Москва. 1971 г.).
- вычисляемое значение амплитуды приращения угла атаки, bа - средняя аэродинамическая хорда (см. С.М.Белоцерковский, Б.К.Скрипач, В.Г.Табачников. Крыло в нестационарном потоке газа. Стр.194-195. Изд-во «Наука». Главная редакция физико-математической литературы. Москва. 1971 г.).
За прототип принято устройство для измерения производных 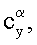
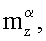
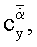
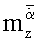 моделей летательных аппаратов. Устройство содержит испытуемую модель, закрепленную на верхнем конце вертикального вала, оборудованного измерителем продольных сил и моментов, действующих на испытуемую модель, механизм поступательных вертикальных колебаний модели, включающий двигатель и преобразователь вращения вала в поступательные колебания вертикального вала, датчик вертикальных перемещений модели.
моделей летательных аппаратов. Устройство содержит испытуемую модель, закрепленную на верхнем конце вертикального вала, оборудованного измерителем продольных сил и моментов, действующих на испытуемую модель, механизм поступательных вертикальных колебаний модели, включающий двигатель и преобразователь вращения вала в поступательные колебания вертикального вала, датчик вертикальных перемещений модели.
Устройство работает следующим образом. Модель жестко закрепляют на валу под установочным углом тангажа ϑ0. Включают двигатель. С помощью кривошипно-шатунного механизма вращение вала двигателя преобразуется в вертикальные поступательные колебания модели ΔH=АHcosωt с частотой ω и амплитудой АH. Во время колебаний измеряют и регистрируют временные зависимости сил Y0(t) и моментов Mz0(t), действующие на модель без потока аэродинамической трубы, затем включают поток и при скорости V потока снова измеряют временные зависимости сил Y(t) и моментов Mz(t). Исключают инерционные нагрузки, действующие на модель, вычисляют аэродинамические силы и моменты, вычисляют статические и нестационарные производные. Изменяют установочный угол тангажа ϑ0 на заданную величину и снова вычисляют указанные производные. При необходимости испытания повторяют при других заданных значениях частот ω и амплитуд АH колебаний модели.
Данные устройство и способ позволяют реализовать колебания модели при постоянном угле тангажа и не позволяют проведение испытаний при скорости тангажа ω≠0 (см. С.М.Белоцерковский, Б.К.Скрипач, В.Г.Табачников. Крыло в нестационарном потоке газа. Стр.193-194. Изд-во «Наука». Главная редакция физико-математической литературы. Москва. 1971 г.).
Задачей изобретения является повышение точности измерения вращательных и нестационарных производных 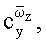
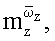
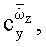
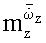 коэффициентов продольных аэродинамических сил и моментов и расширение возможностей экспериментальных исследований в аэродинамических трубах.
коэффициентов продольных аэродинамических сил и моментов и расширение возможностей экспериментальных исследований в аэродинамических трубах.
Технико-экономическим результатом является определение раздельных вращательных и нестационарных, а также новых комплексов статических и нестационарных производных коэффициентов продольных аэродинамических сил и моментов при совместных угловых и поступательных гармонических колебаниях модели летательного аппарата.
Поставленная задача и технический результат достигаются тем, что в способе определения вращательных и нестационарных производных коэффициентов продольных аэродинамических сил и моментов методом вынужденных колебаний модели летательного аппарата, заключающемся в том, что модель отклоняют на установочный угол тангажа ϑ0, создают с помощью двигателя поступательные гармонические колебания модели в вертикальной плоскости, ΔН=АH·cosωt, с амплитудой AH и частотой ω, во время колебаний модели без потока измеряют и регистрируют временные зависимости поступательных перемещений ΔH(t), силы Y0(t) и момента Мz0(t), действующие на модель без потока аэродинамической трубы, затем включают поток и при скорости V потока измеряют и регистрируют временные зависимости поступательных перемещений H(t), силы Y(t) и момента Mz(t), действующих на модель при поступательных колебаниях модели, вычисляют амплитуды первых гармоник разложений в ряды Фурье зависимостей Y0(t), Мz0(t), Y(t), Мz(t), вычитают значения амплитуд, полученных в потоке и без потока, вычисляют статические и нестационарные производные коэффициента подъемной силы и коэффициента момента тангажа, обусловленные изменением угла атаки 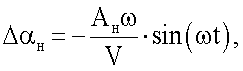 в нем с помощью того же двигателя создают синхронные с поступательными угловые гармонические колебания модели
в нем с помощью того же двигателя создают синхронные с поступательными угловые гармонические колебания модели 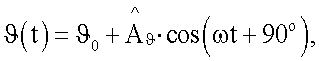 где
где 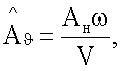 измеряют и регистрируют временные зависимости угловых отклонений ϑ(t) модели, сил Y0(t) и Y(t) и моментов
измеряют и регистрируют временные зависимости угловых отклонений ϑ(t) модели, сил Y0(t) и Y(t) и моментов
Мz0(t) и Мz(t), действующие на модель при совместных поступательных и угловых колебаниях модели без потока и в потоке, вычисляют временные зависимости аэродинамической силы ΔY(t) и момента ΔMz(t), вычисляют амплитуды
А1ΔY(t), B1ΔY(t), А1ΔMz(t), B1ΔMz(t) первых гармоник разложений этих зависимостей в ряд Фурье, вычисляют комплексы вращательных и нестационарных производных аэродинамических сил и моментов
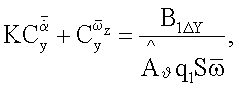
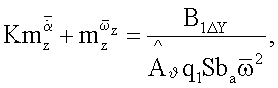
где q - скоростной напор,
S - характерная площадь,
bа - средняя аэродинамическая хорда,
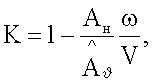
при этом для определения вращательных производных 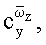
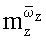 и нестационарных производных
и нестационарных производных 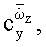
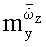
задают амплитуду AH поступательных перемещений из условия 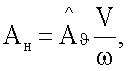 (К=0).
(К=0).
Поставленная задача достигается также тем, что устройство для определения вращательных и нестационарных производных коэффициентов продольных аэродинамических сил и моментов методом вынужденных колебаний модели летательного аппарата, содержащее узел крепления модели на верхнем конце вертикального вала, снабженный измерителем продольных сил и моментов, действующих на испытуемую модель, механизм поступательных вертикальных колебаний модели, включающий двигатель и преобразователь вращения вала в поступательные колебания вертикального вала, датчик вертикальных перемещений модели, снабжено механизмом угловых колебаний модели, узел крепления модели на верхнем конце вертикального вала выполнен в виде осевого шарнира с возможностью колебаний модели по углу тангажа, устройство преобразования вращения вала двигателя в поступательные колебания вертикального вала выполнено в виде синусного механизма, кривошип которого имеет регулируемый радиус R, механизм поступательных вертикальных колебаний модели соединен с механизмом угловых колебаний модели, содержащим синусный механизм, кривошип которого жестко закреплен на шипе кривошипа механизма поступательных колебаний модели, а ось шипа параллельна оси шипа кривошипа механизма поступательных колебаний и смещена по нормали к радиусу R кривошипа этого механизма на заданное расстояние, соединенную с кулисой механизма угловых колебаний вертикальную раздвижную штангу, верхний конец которой выполнен в виде зубчатой рейки, соприкасающейся с шарнирно закрепленным на вертикальном валу рычагом, один конец которого с помощью стержня, оборудованного измерителем осевой силы стержня, шарнирно соединен с моделью, а другой выполнен в виде зубчатого сектора, входящего в зацепление с зубчатой рейкой, нижний конец которой соединен с дистанционно управляемым электроприводом.
На фиг.1, 2 представлены конструктивные схемы устройств, реализующих предлагаемый способ определения вращательных и нестационарных производных коэффициентов продольных аэродинамических сил и моментов.
Устройство состоит из испытуемой модели 1, механизма вертикальных поступательных колебаний модели, включающего вертикальный вал 2, на верхнем конце которого размещены узел крепления модели 3, выполненный в виде осевого шарнира с возможностью колебаний модели по углу тангажа, измеритель 4 продольных сил и моментов, действующих на модель, датчик 5 вертикальных перемещений модели, двигатель 6, устройство преобразования вращения вала двигателя в поступательные колебания вертикального вала, выполненное в виде синусного механизма, включающего кривошип 7 с регулируемым радиусом R, установленный на валу двигателя, и кулису 8, соединенную с нижним концом вертикального вала, и механизма угловых колебаний модели, содержащего синусный механизм, кривошип которого 9 жестко закреплен на кривошипе 7 так, что ось его шипа параллельна оси шипа кривошипа 7 и смещена относительно нее на заданное расстояние е по нормали к радиусу R кривошипа 7, а кулиса 10 соединена с вертикальной раздвижной штангой 11, содержащей дистанционно управляемый электропривод установочных углов атаки 12, выходной шток 13 которого выполнен в виде зубчатой рейки, соприкасающейся с шарнирно закрепленным на вертикальном валу 2 рычагом 14, один конец которого выполнен в виде зубчатого сектора, входящего в зацепление с зубчатой рейкой, а другой с помощью стержня 15, содержащего измеритель 16 осевой силы стержня, соединен с моделью 1, датчик углового положения модели 17, маховик 18 для стабилизации угловой скорости вращения двигателя в условиях переменных нагрузок.
При реализации совместных поступательных и угловых колебаний предлагаемое устройство работает следующим образом.
Модель, шарнирно закрепленную на вертикальном валу 2 с помощью дистанционно управляемого электропривода 12 отклоняют на установочный угол тангажа ϑ0 (равный установочному углу атаки). Устанавливают величину радиуса кривошипа 8 е исходя из условия обеспечения заданной амплитуды угловых колебаний Aϑ, e=rш·Aϑ, где rш - радиус зубчатого сектора рычага 14, устанавливают величину радиуса R кривошипа 7 исходя из условия обеспечения заданной величины коэффициента К (К≤1) в формулах (3), 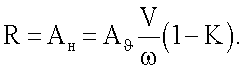 Так как кривошип 7 закреплен на валу двигателя 6, а кривошип 9 закреплен на шипе кривошипа 7 и повернут по отношению к радиусу R на 90° против вращения двигателя, то реализуются поступательные гармонические колебания модели ΔН=R·cos(ωt), где ω - круговая частота вращения двигателя, и синхронные с ними угловые гармонические колебания модели
Так как кривошип 7 закреплен на валу двигателя 6, а кривошип 9 закреплен на шипе кривошипа 7 и повернут по отношению к радиусу R на 90° против вращения двигателя, то реализуются поступательные гармонические колебания модели ΔН=R·cos(ωt), где ω - круговая частота вращения двигателя, и синхронные с ними угловые гармонические колебания модели 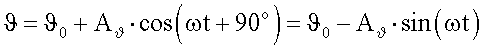 с амплитудой
с амплитудой 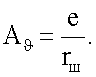
Измеряют и регистрируют временные зависимости угла тангажа ϑ0(t), сил Y0(t) и моментов Mz0(t), действующих на колеблющуюся модель без потока аэродинамической трубы, включают поток и при скорости V потока аналогичным образом измеряют и регистрируют временные зависимости угла тангажа ϑ(t), сил Y(t) и моментов Mz(t) при совместных поступательных и угловых колебаниях модели в потоке аэродинамической трубы, вычисляют амплитуды первых гармоник разложений в ряд Фурье зависимостей ϑ(Y), Y(t), Мz(t) и аналогичные амплитуды зависимостей, измеренных без потока, исключают инерционные нагрузки, вычисляют комплексы вращательных и нестационарных производных 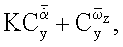
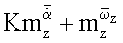 комплексы статических и нестационарных производных
комплексы статических и нестационарных производных 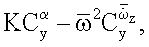
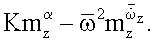
Обозначим:
V - скорость потока в аэродинамической трубе,
bа- средняя аэродинамическая хорда крыла модели,
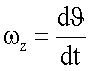 - угловая скорость тангажа модели,
- угловая скорость тангажа модели,
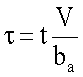 - безразмерное время,
- безразмерное время,
Δαϑ=Δϑ - изменение угла атаки при угловых колебаниях модели,
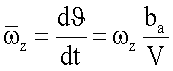 - безразмерная угловая скорость тангажа,
- безразмерная угловая скорость тангажа,
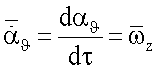
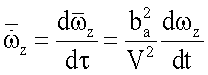 - производная угловой скорости
- производная угловой скорости
ωz(τ) по времени τ,
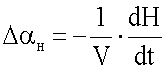 - изменение угла атаки при поступательных колебаниях,
- изменение угла атаки при поступательных колебаниях,
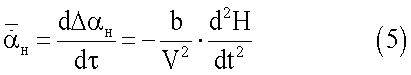
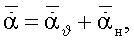
Δα=Δαϑ+Δαн - изменение угла атаки при совместных угловых и поступательных колебаниях,
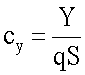 - коэффициент подъемной силы,
- коэффициент подъемной силы,
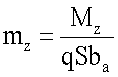 - коэффициент момента тангажа,
- коэффициент момента тангажа,
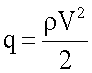 - скоростной напор,
- скоростной напор,
S - характерная площадь.
Известно, что для коэффициентов аэродинамической силы и момента в случае гармонических законов изменения кинематических параметров во времени справедливы формулы Тейлора разложения этих коэффициентов по кинематическим параметрам α, ωz, 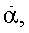
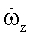
Выражения для коэффициентов cy{t), имеют следующий вид:
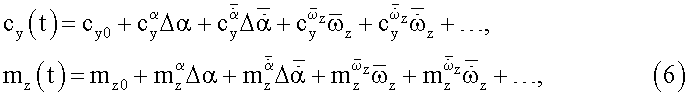
В соответствии с приведенными выше обозначениями при поступательных гармонических колебаниях модели, ΔН=АHcosωt, и синхронных с ними угловых гармонических колебаниях модели, ϑ=ϑ0+Аϑcos(ωt+90°)=ϑ0-А0sinωt, суммарное изменение угла атаки Δα=Δαϑ+ΔαH и безразмерная скорость изменения угла Δα, 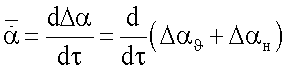 будут определяться соотношениями
будут определяться соотношениями
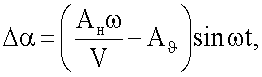
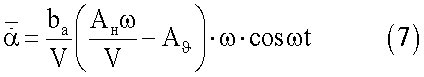
Безразмерная угловая скорость тангажа 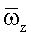 и безразмерное угловое ускорение тангажа при этом определяются соотношениями
и безразмерное угловое ускорение тангажа при этом определяются соотношениями
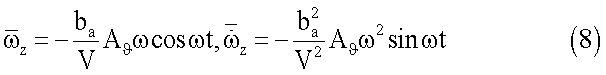
С учетом соотношений (7) и (8) выражения для коэффициентов сy(t), mz(t) (6) принимают вид:
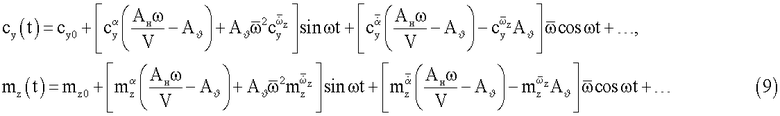
В формуле (9) выражения в квадратных скобках содержат новые комплексы статических и нестационарных производных, а также новые комплексы нестационарных и вращательных производных коэффициентов продольных аэродинамических сил и моментов, измеряемых при двухстепенных угловых и поступательных гармонических колебаниях модели
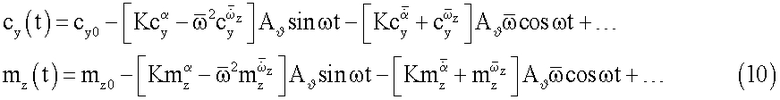
где 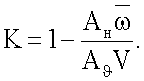
Если совместные угловые и поступательные колебания осуществлять при условии
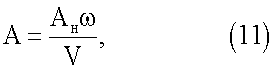
при выполнении которого будет К=0, получим следующие выражения:
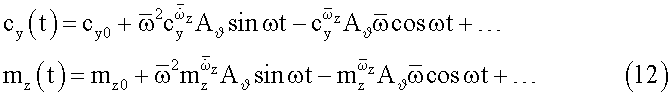
которые позволяют экспериментально измерить вращательные 
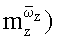 и нестационарные
и нестационарные 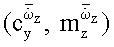 производные аэродинамических коэффициентов сy и mz.
производные аэродинамических коэффициентов сy и mz.
Для этого вычислим коэффициенты А1Y, B1Y, A1Mz, B1Mz разложений в ряд Фурье зависимостей ΔY(t) и ΔMz(t):
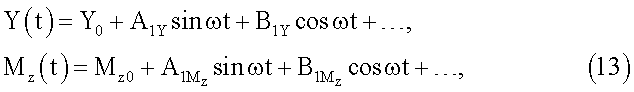
Из соотношений (12) и (13) следуют равенства:
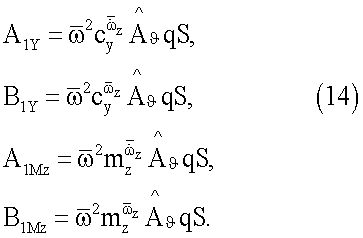
Таким образом, вращательные 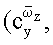
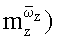 и нестационарные
и нестационарные 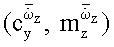 производные определяются по следующим формулам:
производные определяются по следующим формулам:
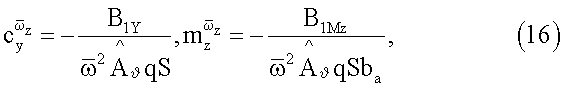
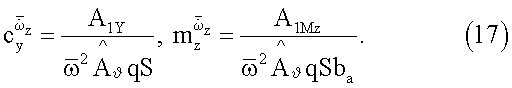
Изобретение относится к экспериментальной аэродинамике летательных аппаратов и может быть использовано при динамических испытаниях моделей различных летательных аппаратов в аэродинамических трубах. В способе рассмотрены совместные гармонические поступательные и угловые колебания модели в потоке аэродинамической трубы. Способ заключается в выборе значений амплитуд колебаний и фазы между поступательными и угловыми колебаниями модели. Устройство содержит узел крепления модели, размещенный на верхнем конце вертикального вала, механизм поступательных колебаний модели и механизм угловых колебаний модели. При этом механизм поступательных колебаний модели включает двигатель и преобразователь вращения вала двигателя в поступательные колебания модели и выполнен в виде синусного механизма, кривошип которого имеет регулируемую длину радиуса. Механизм поступательных колебаний модели соединен с механизмом угловых колебаний модели, содержащим синусный механизм, кривошип которого жестко закреплен на шипе кривошипа механизма поступательных колебаний модели. Ось угловых колебаний параллельна оси шипа кривошипа механизма поступательных колебаний и смещена по нормали к кривошипу этого механизма на заданное расстояние. Конструкции механизмов поступательных и угловых колебаний обеспечивают выполнение необходимого условия равенства сдвига фаз φ поступательных и угловых колебаний значению φ=90°. Технический результат заключается в возможности одновременного измерения раздельных значений вращательных и нестационарных производных аэродинамических сил и моментов, расширении возможностей экспериментальных исследований в аэродинамических трубах. 2 н.п. ф-лы, 2 ил.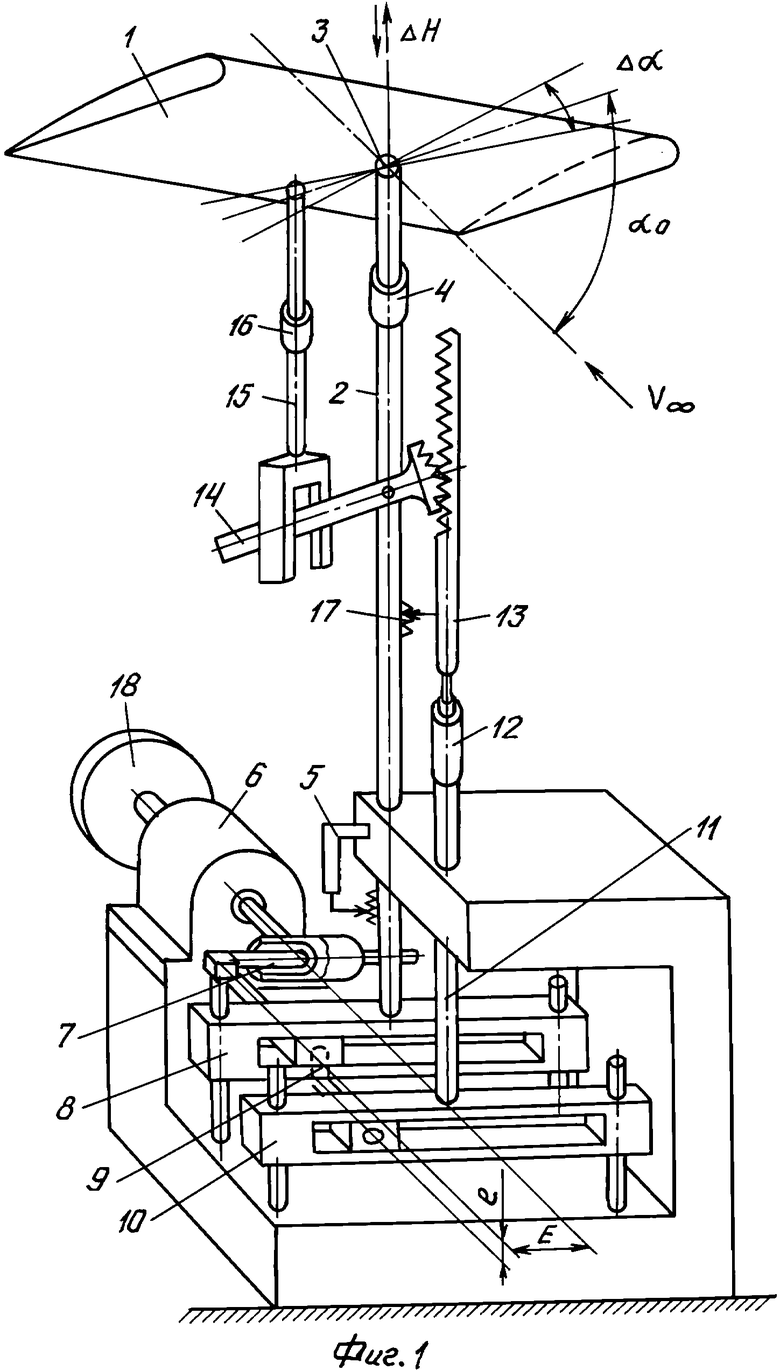
1. Способ определения вращательных и нестационарных производных коэффициентов продольных аэродинамических сил и моментов методом вынужденных колебаний модели летательного аппарата, заключающийся в том, что модель отклоняют на установочный угол тангажа ϑ0, создают с помощью двигателя поступательные гармонические колебания ΔН модели в вертикальной плоскости, ΔН=Ан·cosωt, с амплитудой Ан и частотой ω, во время колебаний модели без потока измеряют и регистрируют временные зависимости поступательных перемещений ΔН(t), силы Y0(t) и момента Mz0(t), действующих на модель без потока аэродинамической трубы, затем включают поток и при скорости V потока измеряют и регистрируют временные зависимости поступательных перемещений H(t), силы Y(t) и момента Mz(t), действующих на модель при поступательных колебаниях модели, вычисляют амплитуды первых гармоник разложений в ряды Фурье зависимостей Y0(t), Mz0(t), Y(t), Mz(t), вычитают значения амплитуд, полученных в потоке и без потока, вычисляют статические и нестационарные производные коэффициента подъемной силы и коэффициента момента тангажа, обусловленные изменением угла атаки 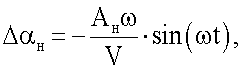 отличающийся тем, что создают синхронные с поступательными колебаниями угловые гармонические колебания модели
отличающийся тем, что создают синхронные с поступательными колебаниями угловые гармонические колебания модели 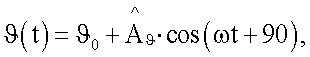 где
где 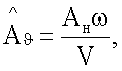 измеряют и регистрируют временные зависимости угловых отклонений ϑ(t) модели, сил Y0(t), Y(t) и моментов Mz0(t), Mz(t), действующих на модель при совместных поступательных и угловых колебаниях модели без потока и в потоке, вычисляют временные зависимости аэродинамической силы ΔY(t) и момента ΔMz(t), вычисляют амплитуды
измеряют и регистрируют временные зависимости угловых отклонений ϑ(t) модели, сил Y0(t), Y(t) и моментов Mz0(t), Mz(t), действующих на модель при совместных поступательных и угловых колебаниях модели без потока и в потоке, вычисляют временные зависимости аэродинамической силы ΔY(t) и момента ΔMz(t), вычисляют амплитуды
A1ΔY(t), B1ΔY(t), A1ΔMz(t), B1ΔMz(t) первых гармоник разложений этих зависимостей в ряд Фурье, вычисляют комплексы вращательных и нестационарных производных аэродинамических сил и моментов:
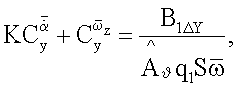
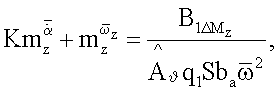
где q - скоростной напор;
S - характерная площадь;
ba - средняя аэродинамическая хорда;
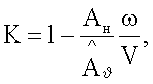
при этом для определения вращательных производных 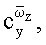
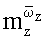 и нестационарных производных
и нестационарных производных 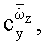
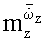 задают амплитуду
задают амплитуду
Ан поступательных перемещений из условия
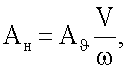 (К=0).
(К=0).
2. Устройство для определения вращательных и нестационарных производных коэффициентов продольных аэродинамических сил и моментов методом вынужденных колебаний модели летательного аппарата, содержащее узел крепления модели на верхнем конце вертикального вала, снабженного измерителем продольных сил и моментов, действующих на испытуемую модель, механизм поступательных вертикальных колебаний модели, включающий двигатель и устройство преобразования вращения вала в поступательные колебания вертикального вала, датчик вертикальных перемещений модели, отличающееся тем, что оно снабжено механизмом угловых колебаний модели, узел крепления модели на верхнем конце вертикального вала выполнен в виде осевого шарнира с возможностью колебаний модели по углу тангажа, устройство преобразования вращения вала двигателя в поступательные колебания вертикального вала выполнено в виде синусного механизма, кривошип которого имеет регулируемый радиус, механизм поступательных вертикальных колебаний модели соединен с механизмом угловых колебаний модели, содержащим синусный механизм, кривошип которого жестко закреплен на шипе кривошипа механизма поступательных колебаний модели, а ось шипа параллельна оси шипа кривошипа механизма поступательных колебаний и смещена по нормали к радиусу кривошипа этого механизма на заданное расстояние, вертикальную раздвижную штангу, соединенную с кулисой механизма угловых колебаний, верхний конец штанги выполнен в виде зубчатой рейки, соприкасающейся с шарнирно закрепленным на вертикальном валу рычагом, один конец которого с помощью стержня, оборудованного измерителем осевой силы стержня, шарнирно соединен с моделью, а другой выполнен в виде зубчатого сектора, входящего в зацепление с зубчатой рейкой, нижний конец которой соединен с дистанционно управляемым электроприводом.
| Белоцерковский С.М., Скрипач Б.К., Табачников В.Г | |||
| Крыло в нестационарном потоке газа | |||
| Приспособление для градации давления в воздухопроводе воздушных тормозов | 1921 |
|
SU193A1 |
| Изд-во: Наука | |||
| Главная редакция физико-математической литературы | |||
| Устройство станционной централизации и блокировочной сигнализации | 1915 |
|
SU1971A1 |
| Устройство для определения коэффициентов вращательных производных | 1974 |
|
SU491062A1 |
| 0 |
|
SU130351A1 | |
| Устройство для определения раздельных значений вращательных производных | 1973 |
|
SU445872A1 |
Авторы
Даты
2009-06-10—Публикация
2007-10-25—Подача