Изобретение относится к радиолокационным методам и может быть использовано в когерентно-импульсных радиолокационных станциях (РЛС) сопровождения цели для формирования доплеровских портретов целей, адекватно отражающих их поперечные линейные размеры.
Известен способ выбора интервала инверсного синтезирования [1], заключающийся в том, что с помощью когерентно-импульсной РЛС излучают в направлении воздушной цели сверхвысокочастотные сигналы, принимают отраженные сигналы, автоматически сопровождают цель по дальности и угловым координатам, определяют дальность R1, угол места ε1 и азимут β1 цели в начальный момент сопровождения, определяют дальность R2, угол места ε2 и азимут β2 цели через интервал ΔТ=1 с, пересчитывают измеренные сферические координаты цели для двух указанных моментов времени в прямоугольные (x1, y1, z1) и (x2,y2,z2), определяют пройденный целью путь ΔR за время ΔT по формуле (фиг.1)
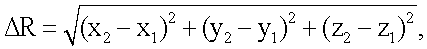
рассчитывают величину угла между начальным и конечным положением линии визирования цели (ЛВЦ) по формуле
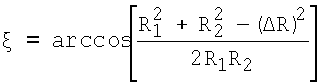 ,
,
рассчитывают скорость цели V по формуле V=ΔR/ΔT, выбирают величину необходимого поперечного разрешения δR⊥, рассчитывают длительность интервала инверсного синтезирования ΔТис по формуле
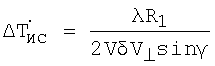 ,
,
где λ - длина волны; γ - угол между линией визирования цели в начальный момент времени и линией пути (вектором линейной скорости) цели, произвольным образом выбирают в пределах интервала ΔT положение интервала инверсного синтезирования ΔТис, считая, что угловая скорость поворота цели 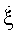 на этом интервале равна
на этом интервале равна 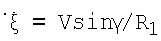 .
.
Недостатком данного способа определения интервала инверсного синтезирования является то, что способ не учитывает влияния траекторных нестабильностей (ТН) полета цели в виде рысканий планера самолета, летящего в турбулентной атмосфере [2]. А вследствие этих случайных квазипериодических рысканий угловая скорость поворота летательного аппарата постоянно и нелинейно изменяется. При изменении угловой скорости поворота цели за счет ТН разрешающая способность δR⊥ соответствующим образом изменяется. Результирующая угловая скорость поворота цели представляет собой векторную сумму угловой скорости поворота цели за счет перемещения ее центра масс по прямолинейной (на малом участке пути) траектории 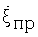 и угловой скорости рысканий планера
и угловой скорости рысканий планера 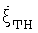 при ТН в турбулентности. Разделить эти две составляющие при оценке реальной угловой скорости не удается. А в результате непредсказуемости величины угловой скорости вращения цели относительно РЛС правильный выбор длительности интервала инверсного синтезирования затруднителен. Известный в настоящее время способ выбора интервала инверсного синтезирования [1] не обеспечивает ни возможности правильного расчета угловой скорости поворота цели
при ТН в турбулентности. Разделить эти две составляющие при оценке реальной угловой скорости не удается. А в результате непредсказуемости величины угловой скорости вращения цели относительно РЛС правильный выбор длительности интервала инверсного синтезирования затруднителен. Известный в настоящее время способ выбора интервала инверсного синтезирования [1] не обеспечивает ни возможности правильного расчета угловой скорости поворота цели 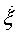 , ни возможности выбора верной величины самого интервала. Если, к примеру, угловые скорости и
, ни возможности выбора верной величины самого интервала. Если, к примеру, угловые скорости и 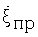 и
и 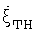 окажутся на произвольно выбранном интервале равными по величине и противоположными по направлению, то ракурс сопровождаемой цели изменяться не будет, и амплитудно-фазовые флюктуации отраженных сигналов, необходимые для реализации инверсного синтезирования, будут минимизированы. Вследствие этого процедура инверсного синтезирования в интересах получения доплеровских портретов целей [3, 4, 5] становится невыполнимой.
окажутся на произвольно выбранном интервале равными по величине и противоположными по направлению, то ракурс сопровождаемой цели изменяться не будет, и амплитудно-фазовые флюктуации отраженных сигналов, необходимые для реализации инверсного синтезирования, будут минимизированы. Вследствие этого процедура инверсного синтезирования в интересах получения доплеровских портретов целей [3, 4, 5] становится невыполнимой.
Задачей изобретения является обеспечение возможности учета характера траекторных нестабильностей полета цели для адаптации процесса выбора интервала инверсного синтезирования и более точной оценки средней угловой скорости поворота цели в пределах выбираемого интервала.
В интересах выполнения указанной задачи предлагается проводить предварительную регистрацию амплитудно-фазовой информации, заключенной в отраженных целью сигналах, на избыточном длительном порядка 10 секунд интервале Δtизб, затем формировать из значений амплитуд принятых сигналов отражательную характеристику (ОХЦ) цели, проводить ее сглаживание (или низкочастотную фильтрацию) для устранения высокочастотной модуляции, вызванной турбовинтовым эффектом, затем получить из ОХЦ корреляционную характеристику цели (КХЦ), провести ее сглаживание для более выраженной локализации экстремумов, определить временное положение двух смежных минимума и максимума, определить временное положение tc точки в КХЦ со среднеарифметическим относительно минимума и максимума значением, рассчитать в соответствии с ранее известным способом [1] длительность интервала инверсного синтезирования и выбрать в пределах интервала Δtизб временное положение рабочего интервала инверсного синтезирования ΔТис так, чтобы точка tc была его серединой.
Предложенный способ выбора интервала инверсного синтезирования обеспечивает устранение двух основных недостатков прототипа. Во-первых, вычисляемая известным способом [1] угловая скорость поворота цели в результате предложенного подхода становится наиболее близкой к реальной средней угловой скорости вращения цели, т.к. ее увеличение и уменьшение на двух смежных половинах рабочего интервала инверсного синтезирования ΔТис компенсируют друг друга. Во-вторых, минимизируется негативное влияние на параметры рабочего интервала инверсного синтезирования ΔТис неизбежно присутствующих в турбулентности ТН полета, которые могут приводить к изменению расчетной 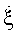 .
.
Сущность предлагаемого способа выбора интервала инверсного синтезирования состоит в следующем.
При сопровождении сложной сосредоточенной воздушной цели фаза и амплитуда принятого сигнала в определенный момент времени определяется взаимным расположением рассеивающих центров (РЦ) поверхности цели в радиальном направлении [6, 7, 8]. При изменении углового положения цели взаимные удаления РЦ в радиальном направлении изменяются и интерференционная картина рассеянного целью поля становится иной. В результате амплитуда и фаза отраженного целью сигнала варьируют. Именно это является причиной изрезанности диаграммы обратного вторичного излучения (ДОВИ) цели, свойства которой известны [9]. В реальных условиях угловое положение летящего самолета изменяется по нелинейному закону, вследствие чего реализацию принятых отраженных сигналов не следует отождествлять с участком ДОВИ, а следует называть реальной отражательной характеристикой цели (ОХЦ), хотя физическая основа получения ДОВИ и ОХЦ общая.
Время, в течение которого воздушная цель сохраняет свое относительно стабильное положение в полете, принято называть интервалом угловой корреляции Тук, величина которого составляет 5-10 мс в квазиоптическом диапазоне длин волн [8, 9]. Величина же интервала инверсного синтезирования [1, 7] занимает диапазон от 0,3 до 1 с. Поэтому отражательная характеристика, используемая в алгоритмах инверсного синтезирования, у сложных сосредоточенных воздушных целей всегда изрезана и тем больше, чем больше произведение угловой скорости поворота 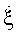 на поперечный размер цели L⊥. А поскольку поперечный размер цели - величина относительно постоянная, то изрезанность ОХЦ в основном определяется угловой скоростью ее поворота
на поперечный размер цели L⊥. А поскольку поперечный размер цели - величина относительно постоянная, то изрезанность ОХЦ в основном определяется угловой скоростью ее поворота 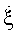 .
.
Еще одним принципиальным отличием ОХЦ от ДОВИ является ее высокочастотная модуляция составляющими турбовинтового эффекта. Факт искажения низкочастотной огибающей ОХЦ турбовинтовыми гармониками является известным [10] и требующим разработки методов устранения этого нежелательного явления, если имеется необходимость использовать низкочастотные флюктуации сигнала, вызванные интерференцией отражений только от элементов конструкции планера (исключая отражения от вращающихся элементов двигателей).
На фиг.2а показана полученная методом натурного эксперимента реальная ОХЦ, изрезанная выбросами турбовинтовых составляющих. Использование такой ОХЦ для оценки угловой скорости поворота цели невозможно. Поэтому предлагается проводить сглаживание высокочастотной модуляции и получать сглаженную планерную ОХЦ. Методы сглаживания являются известными и уже реализованными в современных математических пакетах [11]. Наиболее простым является скользящее усреднение. Его суть состоит в расчете для каждого значения элемента массива среднего значения по данным соседних с ним элементов. Результатом сглаживания является планерная ОХЦ (фиг.2б), т.е. характеристика, зависящая только от формы и размеров планера воздушной цели.
Полученная планерная ОХЦ пригодна для выделения интервалов с различной угловой скоростью поворота цели. Для пояснения идеи выделения таких интервалов рассмотрим фиг.3.
В зависимости от соотношений между величинами 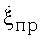 и
и 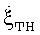 закон изменения совокупной угловой скорости вращения цели может быть различным. Если, к примеру, ТН отсутствуют
закон изменения совокупной угловой скорости вращения цели может быть различным. Если, к примеру, ТН отсутствуют 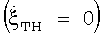 , угловая скорость
, угловая скорость 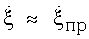 изменяется во времени незначительно. Это должно проявляться в неизменности периода угловых флюктуации и постоянстве угловой ширины лепестков огибающей ОХЦ. Указанная угловая скорость цели
изменяется во времени незначительно. Это должно проявляться в неизменности периода угловых флюктуации и постоянстве угловой ширины лепестков огибающей ОХЦ. Указанная угловая скорость цели 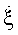 вычисляется по формуле
вычисляется по формуле  .
.
Если курсовой параметр удаленной цели равен нулю, то все угловые флюктуации связаны только с ТН (изменением угла места ε на большой дальности можно пренебречь). В этом случае 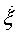 носит квазигармонический характер, и обязательно имеются такие моменты времени, в которых меняется направление поворота. Поскольку в этих точках
носит квазигармонический характер, и обязательно имеются такие моменты времени, в которых меняется направление поворота. Поскольку в этих точках 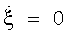 , то соответствующий им интервал корреляции будет максимален в соответствии с наибольшей шириной лепестков ОХЦ.
, то соответствующий им интервал корреляции будет максимален в соответствии с наибольшей шириной лепестков ОХЦ.
Наиболее вероятной является ситуация соизмеримости угловых скоростей 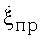 и
и 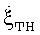 . В этом случае длительность лепестков ОХЦ, число лепестков, сформированных на установленном интервале времени, и поведение интервала корреляции будут определяться модулем разности
. В этом случае длительность лепестков ОХЦ, число лепестков, сформированных на установленном интервале времени, и поведение интервала корреляции будут определяться модулем разности 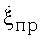 и
и 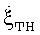 . Модулем
. Модулем  целесообразно оперировать потому, что ширина лепестков (коррелированность сигналов) зависит только от интенсивности флюктуации и инвариантна к направлению поворота цели.
целесообразно оперировать потому, что ширина лепестков (коррелированность сигналов) зависит только от интенсивности флюктуации и инвариантна к направлению поворота цели.
Формирование сложной зависимости  от времени показывает фиг.3. На нем пунктиром обозначено изменение
от времени показывает фиг.3. На нем пунктиром обозначено изменение 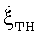 , штрихпунктиром показана величина постоянной угловой скорости
, штрихпунктиром показана величина постоянной угловой скорости 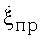 . Модуль разности
. Модуль разности  демонстрируется сплошной линией. При построении графиков были использованы реалистичные параметры линейного и вращательного движения цели: амплитуда рысканий А=2°/с, период рысканий Тр=3 с, скорость цели V=400 м/с, γ=85°, R1=12 км. Рассматривая фиг.3, можно предположить, что в точках А, В, С и D отраженные сигналы будут характеризоваться: максимумом интервала корреляции; минимумом изрезанности ОХЦ; наименьшим числом лепестков ОХЦ в пределах установленного фиксированного интервала.
демонстрируется сплошной линией. При построении графиков были использованы реалистичные параметры линейного и вращательного движения цели: амплитуда рысканий А=2°/с, период рысканий Тр=3 с, скорость цели V=400 м/с, γ=85°, R1=12 км. Рассматривая фиг.3, можно предположить, что в точках А, В, С и D отраженные сигналы будут характеризоваться: максимумом интервала корреляции; минимумом изрезанности ОХЦ; наименьшим числом лепестков ОХЦ в пределах установленного фиксированного интервала.
В указанные моменты времени, соответствующие точкам А, В, С и D, цель минимально изменяет свой ракурс (замирает) за счет взаимокомпенсации угловых скоростей 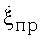 и
и 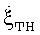 . Минимальные интервалы корреляции отраженных сигналов должны наблюдаться в окрестностях точек F1, F2, E1, E2.
. Минимальные интервалы корреляции отраженных сигналов должны наблюдаться в окрестностях точек F1, F2, E1, E2.
В реальных условиях 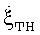 имеет более сложный закон изменения [12, 13]. Однако и в этом случае имеются участки с максимальной и минимальной угловыми скоростями
имеет более сложный закон изменения [12, 13]. Однако и в этом случае имеются участки с максимальной и минимальной угловыми скоростями 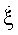 . Это хорошо видно из отражательной характеристики самолета Як-52 (фиг.4), полученной при натурном эксперименте. Курсовой угол цели составлял около 90° при скорости полета 50 м/с и дальности 20 км. Первая половина ОХЦ не содержит низкочастотных флюктуации, что соответствует неизменности углового положения. Вторая половина ОХЦ сильно изрезана. Такое резкое изменение ее параметров объясняется проявлением ТН полета. В серии натурных экспериментов были задействованы самолеты разных габаритов (от 7 до 48 м). Исследование большого числа (более 103) отражательных характеристик целей различных типов при разных условиях локации показало, что ОХЦ с неизменной шириной лепестков в течение 5…10 с встречается крайне редко (1:300).
. Это хорошо видно из отражательной характеристики самолета Як-52 (фиг.4), полученной при натурном эксперименте. Курсовой угол цели составлял около 90° при скорости полета 50 м/с и дальности 20 км. Первая половина ОХЦ не содержит низкочастотных флюктуации, что соответствует неизменности углового положения. Вторая половина ОХЦ сильно изрезана. Такое резкое изменение ее параметров объясняется проявлением ТН полета. В серии натурных экспериментов были задействованы самолеты разных габаритов (от 7 до 48 м). Исследование большого числа (более 103) отражательных характеристик целей различных типов при разных условиях локации показало, что ОХЦ с неизменной шириной лепестков в течение 5…10 с встречается крайне редко (1:300).
Итак, установлено, что интервалам с максимальной угловой скоростью изменения ракурса цели соответствуют участки с наибольшей изрезанностью ОХЦ, т.е. с минимальной шириной лепестков сглаженной планерной ОХЦ и с максимальным числом лепестков на фиксированном по протяженности участке планерной ОХЦ. Наиболее гладким участкам планерной ОХЦ соответствует интервал времени, на котором угловая скорость изменения ракурса цели минимальна.
Для автоматизированного выделения интервалов с различной степенью изрезанности планерной ОХЦ предлагается использовать ее корреляционный анализ. Измерение интервала корреляции τ0 является затруднительным, в связи с чем предлагается оценивать уровень коррелированности по величине коэффициента корреляции (КК) частной выборки элементов ОХЦ для некоторого оценочного интервала τоц. На фиг.5 показаны три автокорреляционные функции, которые соответствуют различному уровню изрезанности планерной ОХЦ в пределах ЧВ одинакового размера. Наименьший интервал корреляции τмин соответствует наибольшей изрезанности ОХЦ, т.е. наибольшей угловой скорости поворота цели. Выбрав некоторую оценочную величину τоц времени корреляции, для различных корреляционных функций можно получить различные КК: ρ(τоц1), ρ(τоц2) и ρ(τоц3). Выбор величины τоц (фиг.5) следует проводить в соответствии с условием τоц<τмин, где τмин - интервал корреляции отражений от воздушной цели максимальных размеров с наибольшей 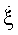 .
.
Для измерения КК может использоваться либо корреляционная функция двух сдвинутых между собой частных выборок (ЧВ), составленных из элементов планерной ОХЦ, либо нормированная автокорреляционная функция (АКФ) частной выборки, также составленной из взятых подряд I элементов планерной ОХЦ. Последовательность коэффициентов автокорреляции (КАК) ЧВ при их сдвигах в пределах генеральной совокупности дискретных отсчетов будем называть корреляционной характеристикой (КХ) амплитудной планерной ОХЦ или корреляционной характеристикой цели.
Если времени τоц соответствует q точек массива (τоц=qTи, где Ти - период повторения импульсов радиолокационной станции, определяющий период дискретизации данных в ОХЦ), выражающего амплитудную планерную ОХЦ, то оценочный КАК R(q) для частной выборки из I дискретных отсчетов рассчитывается по формуле
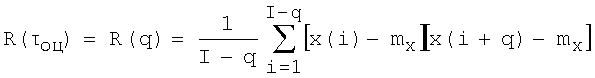 ,
,
где x(i) - величина i-го элемента амплитудной планерной ОХЦ в пределах ЧВ; mх - математическое ожидание амплитуды принимаемого сигнала в пределах амплитудной планерной ОХЦ (определяется как среднее арифметическое всех значений планерной ОХЦ).
Нормированное значение КАК выражается формулой
ρ(q)=R(q)/R(0).
Тогда обобщенная нормированная КХ амплитудной планерной ОХЦ из S принятых сигналов будет определяться по формуле
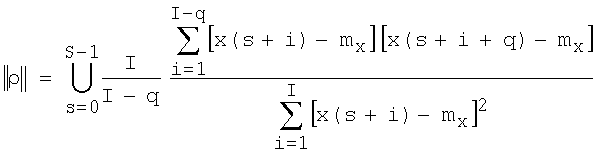 ,
,
где  - знак объединения в массив или вектор данных.
- знак объединения в массив или вектор данных.
Для получения правдоподобных значений оценочных КАК период (параметр сдвига q) дискретизации целесообразно выбирать так, чтобы интервал τмин включал не менее 5 отсчетов амплитудной планерной ОХЦ. Значит, период повторения импульсов локатора, выступающий при формировании ОХЦ и КХ в качестве интервала дискретизации, следует выбирать из условия Ти<τмин/5. Оценка минимально возможного интервала корреляции τмин для статистической модели воздушной цели с нормальным распределением РЦ при 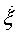 =3°/с, L⊥=40 м и λ=3 см дает τмин=5 мс. Значит, период повторения импульсов должен быть не больше 1 мс, что вполне соответствует техническим характеристикам современных РЛС.
=3°/с, L⊥=40 м и λ=3 см дает τмин=5 мс. Значит, период повторения импульсов должен быть не больше 1 мс, что вполне соответствует техническим характеристикам современных РЛС.
На фиг.6 показана КХ, соответствующая сигналам, отраженным от модели самолета В-52 при его сопровождении РЛС на дальности 30 км при курсовом угле 30°, V=400 м/с, А=2°, максимальной угловой скорости рыскания
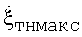 =2,5°/с (
=2,5°/с (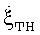 является нелинейной, изменяется с течением времени и принимает максимальное значение
является нелинейной, изменяется с течением времени и принимает максимальное значение 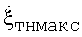 в середине полупериода рыскания цели). Индекс s означает номер отсчета (принятого импульса). Кривая 1 показывает амплитудную планерную ОХЦ, а кривая 3 - истинную КХ, полученную на основе корреляционного анализа планерной ОХЦ. Как видно, истинная КХ имеет сильную изрезанность, что затрудняет ее использование для автоматического определения интервалов с разными угловыми скоростями поворота цели. Поэтому после формирования истинной КХ предлагается проводить ее сглаживание известными методами [11]. Сглаженная КХ показана на фиг.6 кривой 2. Именно она и позволяет правильно выбирать интервалы инверсного синтезирования в интересах минимизации ошибок оценки угловой скорости
в середине полупериода рыскания цели). Индекс s означает номер отсчета (принятого импульса). Кривая 1 показывает амплитудную планерную ОХЦ, а кривая 3 - истинную КХ, полученную на основе корреляционного анализа планерной ОХЦ. Как видно, истинная КХ имеет сильную изрезанность, что затрудняет ее использование для автоматического определения интервалов с разными угловыми скоростями поворота цели. Поэтому после формирования истинной КХ предлагается проводить ее сглаживание известными методами [11]. Сглаженная КХ показана на фиг.6 кривой 2. Именно она и позволяет правильно выбирать интервалы инверсного синтезирования в интересах минимизации ошибок оценки угловой скорости 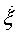 . При моделировании был выбран Ти, равный 384 мкс. Частная выборка (для определения оценочного КК в пределах автокорреляционной функции) включала 150 отсчетов амплитудной планерной ОХЦ. Каждое последующее значение оценочного КК рассчитывалось после сдвига ЧВ на один отсчет в пределах планерной амплитудной ОХЦ. А именно, если первый оценочный КК был рассчитан для ЧВ, включающей с 1-го по 150-й отсчет планерной ОХЦ, то второй - для ЧВ, включающей со 2-го по 151-й отсчеты, и так далее.
. При моделировании был выбран Ти, равный 384 мкс. Частная выборка (для определения оценочного КК в пределах автокорреляционной функции) включала 150 отсчетов амплитудной планерной ОХЦ. Каждое последующее значение оценочного КК рассчитывалось после сдвига ЧВ на один отсчет в пределах планерной амплитудной ОХЦ. А именно, если первый оценочный КК был рассчитан для ЧВ, включающей с 1-го по 150-й отсчет планерной ОХЦ, то второй - для ЧВ, включающей со 2-го по 151-й отсчеты, и так далее.
Анализ полученной сглаженной КХ показал, что она адекватно отражает своими минимумами интервалы с максимальной угловой скоростью поворота цели, а своими максимумами - интервалы с наиболее широкими лепестками амплитудной планерной ОХЦ, что соответствует минимальной угловой скорости вращения цели.
При условии соблюдения целью строго гармонического характера рысканий в турбулентной атмосфере правильно сформированная КХ обладает многими замечательными свойствами. Рассмотрим их на примере КХ из фиг.6. Неопровержимым является то, что имеет место обратная связь (пропорциональность) между минимальным КАК ρмин и 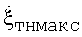 . В зависимости от соотношения между
. В зависимости от соотношения между 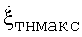 и
и 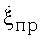 абсолютные уровни минимального КАК в смежных полуволнах КХ различны и незначительно изменяются с течением времени. Так, уровни минимальных КАК рмин в точках глобальных минимумов A1 и С1 отличаются на 0,05. Приблизительно такое же отличие минимальный КАК имеет в точках глобальных минимумов B1 и D1.
абсолютные уровни минимального КАК в смежных полуволнах КХ различны и незначительно изменяются с течением времени. Так, уровни минимальных КАК рмин в точках глобальных минимумов A1 и С1 отличаются на 0,05. Приблизительно такое же отличие минимальный КАК имеет в точках глобальных минимумов B1 и D1.
Согласно теории значение минимального КАК ρмин действительно обратно пропорционально скорости поворота воздушной цели в соответствующий момент времени. Чем меньше ρмин, тем активнее угловые флюктуации.
Разность уровней КАК ρмин в точках локальных (А1, С1) и глобальных (В1, D1) минимумов КХ обратно пропорциональна удвоенной скорости 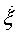 пр. На одном полупериоде
пр. На одном полупериоде 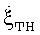 и
и 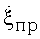 совпадают, на другом - компенсируют друг друга в виду противоположных направлений. Если
совпадают, на другом - компенсируют друг друга в виду противоположных направлений. Если 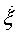 пр=0, все минимумы становятся глобальными, и наблюдается правильное соответствие минимального КАК ρмин угловой скорости
пр=0, все минимумы становятся глобальными, и наблюдается правильное соответствие минимального КАК ρмин угловой скорости 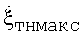 . Это соответствие может использоваться для нахождения численного значения
. Это соответствие может использоваться для нахождения численного значения 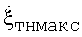 при наличии информации о размерах воздушной цели. В общем случае для определения истинного значения
при наличии информации о размерах воздушной цели. В общем случае для определения истинного значения 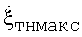 необходимо найти среднее арифметическое смежных глобального и локального минимумов, если таковые имеются.
необходимо найти среднее арифметическое смежных глобального и локального минимумов, если таковые имеются.
Перечислим другие свойства сглаженной КХ.
а) Уровни локальных и глобальных минимумов обратно пропорциональны как максимальной угловой скорости поворота, так и поперечным размерам объекта отражения электромагнитных волн.
б) Отношение уровней локальных и глобальных минимумов пропорционально отношению длительностей интервалов между соответствующими максимумами. Для фиг.6:
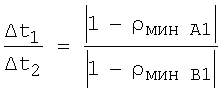 ,
,
в) Точки максимумов сглаженной КХ соответствуют минимальной угловой скорости 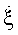 , когда модуль их векторной суммы
, когда модуль их векторной суммы 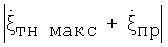 стремится к минимуму.
стремится к минимуму.
г) Ширина интервалов между смежными максимумами КХ, обозначенными точками A, B, C, D, E пропорциональна угловой скорости рысканий при ТН и обратно пропорциональна амплитуде угловых отклонений при рысканиях.
д) Сумма длительностей любых двух смежных интервалов между максимумами равна периоду ТН: 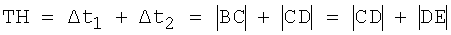 .
.
Однако на практике гармонический характер ТН не наблюдается, и многие свойства КХ нарушаются. При этом экстремумы КХ имеют место всегда. Поэтому сформированная КХ практически может использоваться только для определения моментов минимального, максимального и некоторого среднего уровня изменения ракурса воздушной цели. Как уже отмечалось, два смежных экстремума КХ всегда показывают моменты максимизации и минимизации угловой скорости поворота цели 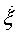 (интервал между ними в идеале равен четвертой части периода рысканий цели). Такими точками, согласно фиг.6, являются точки А и А1 А1 и В, В и В1, B1 и С и т.д. В точках максимума сглаженной КХ две составляющие угловой скорости вращения цели
(интервал между ними в идеале равен четвертой части периода рысканий цели). Такими точками, согласно фиг.6, являются точки А и А1 А1 и В, В и В1, B1 и С и т.д. В точках максимума сглаженной КХ две составляющие угловой скорости вращения цели 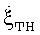 и
и 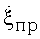 максимально компенсируют друг друга. В точках минимумов КХ эти же две составляющие усиливают друг друга. Нетрудно заметить, что при такой логике среднее арифметическое от значений угловых скоростей в двух смежных экстремумах сглаженной КХ будет определяться только одной составляющей
максимально компенсируют друг друга. В точках минимумов КХ эти же две составляющие усиливают друг друга. Нетрудно заметить, что при такой логике среднее арифметическое от значений угловых скоростей в двух смежных экстремумах сглаженной КХ будет определяться только одной составляющей 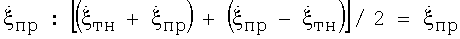 . А данная составляющая может быть рассчитана по параметрам движения цели [1]. Значение среднего арифметического для экстремумов В и В1 фиг.6 соответствует времени, отмеченному точкой tc. Если выбрать интервал инверсного синтезирования ΔТис в окрестности точки tc, то увеличение и уменьшение угловой скорости
. А данная составляющая может быть рассчитана по параметрам движения цели [1]. Значение среднего арифметического для экстремумов В и В1 фиг.6 соответствует времени, отмеченному точкой tc. Если выбрать интервал инверсного синтезирования ΔТис в окрестности точки tc, то увеличение и уменьшение угловой скорости 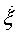 на двух половинах этого интервала будут компенсировать друг друга, сохраняя среднее значение угловой скорости равным
на двух половинах этого интервала будут компенсировать друг друга, сохраняя среднее значение угловой скорости равным 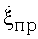 .
.
Для увеличения разрешающей способности в поперечном относительно ЛВЦ направлении выгоднее использовать интервал, где сглаженная КХ имеет минимум. Но тогда пропадает возможность оценки величины 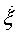 на данном интервале. Поэтому предпочтительнее использовать интервалы инверсного синтезирования в окрестности точки со средним значением КК на участке между двумя смежными экстремумами сглаженной КХ цели.
на данном интервале. Поэтому предпочтительнее использовать интервалы инверсного синтезирования в окрестности точки со средним значением КК на участке между двумя смежными экстремумами сглаженной КХ цели.
Следует заметить, что все данные, которые необходимо будет использовать при инверсном синтезировании нужно также записывать в цифровом виде в память оперативного запоминающего устройства, т.к. первый этап выбора интервала ΔТис заканчивается через 10 секунд, что непременно ведет к утрате параметров, планируемых к использованию в алгоритмах инверсного синтезирования апертуры антенны.
Таким образом, на основе выявления закономерностей изменения параметров отраженных целью сигналов предложен новый весьма полезный подход оценивания поведения летательного аппарата по корреляционным свойствам сигналов в интересах выбора наиболее информативного участка ОХЦ. В данном случае предлагается оценивать и использовать производную КАК по времени, то есть его динамику в процессе сопровождения цели. Корреляционный анализ позволяет безошибочно фиксировать интервалы с максимальной и минимальной угловой скоростью 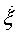 , а в некоторых случаях - определять те из них, где направления
, а в некоторых случаях - определять те из них, где направления 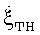 и
и 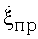 совпадают. Но главный результат заключается в том, что корреляционный анализ позволяет найти интервалы накопления сигналов, в которых угловая скорость поворота воздушной цели определяется только перемещением ее центра масс по прямолинейной траектории. Как видно из описания, предложенный способ выбора интервала инверсного синтезирования существенно превосходит по своей обоснованности прототип [1]. Предложенный способ исключает случайное попадание на интервал, в котором изменения ракурса цели не происходит, или же на интервал, в котором угловая скорость изменения ракурса в несколько раз превышает расчетную.
совпадают. Но главный результат заключается в том, что корреляционный анализ позволяет найти интервалы накопления сигналов, в которых угловая скорость поворота воздушной цели определяется только перемещением ее центра масс по прямолинейной траектории. Как видно из описания, предложенный способ выбора интервала инверсного синтезирования существенно превосходит по своей обоснованности прототип [1]. Предложенный способ исключает случайное попадание на интервал, в котором изменения ракурса цели не происходит, или же на интервал, в котором угловая скорость изменения ракурса в несколько раз превышает расчетную.
Источники информации
1. Стайнберг Б.Д. Формирование радиолокационного изображения самолета в диапазоне СВЧ // ТИИЭР, 1988. №12. Т.76. С.26-46 (прототип).
2. Доброленский Ю.П. Динамика полета в неспокойной атмосфере. М: Машиностроение, 1969. 256 с.
3. Патент РФ №2099742 от 20.12.97 г. Митрофанов Д.Г. Триангуляционный способ построения двумерного радиолокационного изображения в РЛС сопровождения с инверсным синтезированием апертуры. Заявка №95115789. Приоритет 7.09.95 г.
4. Митрофанов Д.Г. Развитие методов формирования доплеровских портретов и двумерных радиолокационных изображений воздушных целей. - М.: Оборонная техника, 1998. №10-11. С.75-81.
5. Митрофанов Д.Г. Синтез радиолокационного изображения цели методом математического моделирования ее доплеровских портретов // Известия вузов. Радиоэлектроника, 1994. Т.37. №3. С.72-76.
6. Финкельштейн М.И. Основы радиолокации. - М.: Радио и связь, 1983. 536 с.
7. Ширман Я.Д., Горшков С.А., Лещенко С.П., Братченко Г.Д., Орленко В.М. Методы радиолокационного распознавания и их моделирование// Зарубежная радиоэлектроника, 1996. №11. С.3-62.
8. Радиоэлектронные системы. Справочник. Основы построения и теория / Под ред. Я.Д.Ширмана. - М.: Радиотехника. 2007. 510 с.
9. Теоретические основы радиолокации/ Под ред. Я.Д.Ширмана. - М.: Сов. радио, 1970. 560 с.
10. Митрофанов Д.Г., Прохоркин А.Г. Методы компенсации влияния составляющих турбинного эффекта при построении изображений воздушных целей // Радиотехника, 2006. №9. С.32-37.
11. Кирьянов Д.В. Mathcad 12. СПб.: БХВ-Петербург, 2005. 576 с.
12. Доброленский Ю.П. Динамика полета в неспокойной атмосфере. - М.: Машиностроение, 1969. 225 с.
13. Справочник по радиолокации. Под ред. М.И.Сколника. Пер. с англ. - М.: Сов. радио, 1967. Т.1. Основы радиолокации. - 456 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ИДЕНТИФИКАЦИИ ВОЗДУШНОГО РАДИОЛОКАЦИОННОГО ОБЪЕКТА НАБЛЮДЕНИЯ С ВЫБОРОМ ИНТЕРВАЛА МАКСИМИЗАЦИИ УГЛОВОЙ СКОРОСТИ ЕГО ПОВОРОТА ПРИ ТРАЕКТОРНЫХ НЕСТАБИЛЬНОСТЯХ ДВИЖЕНИЯ | 2010 |
|
RU2427001C1 |
| СПОСОБ ВЫБОРА ПОЛОЖЕНИЯ ИНТЕРВАЛА ИНВЕРСНОГО СИНТЕЗИРОВАНИЯ АПЕРТУРЫ ПРИ НАЛИЧИИ ТРАЕКТОРНЫХ НЕСТАБИЛЬНОСТЕЙ ПОЛЕТА ВОЗДУШНОГО ОБЪЕКТА С ВОЗМОЖНОСТЬЮ ОЦЕНКИ УГЛОВОЙ СКОРОСТИ ЕГО ПОВОРОТА ОТНОСИТЕЛЬНО РАДИОЛОКАЦИОННОЙ СТАНЦИИ | 2009 |
|
RU2409823C1 |
| СПОСОБ РАСПОЗНАВАНИЯ ЛОЖНЫХ ВОЗДУШНЫХ ЦЕЛЕЙ | 2007 |
|
RU2348053C1 |
| УСТРОЙСТВО КЛАССИФИКАЦИИ РАДИОЛОКАЦИОННЫХ ОБЪЕКТОВ НАБЛЮДЕНИЯ ПО ИНТЕНСИВНОСТИ АМПЛИТУДНЫХ ФЛЮКТУАЦИЙ | 2010 |
|
RU2425395C2 |
| Способ оценки пространственного размера воздушной цели по частотной протяженности доплеровского портрета | 2018 |
|
RU2679396C2 |
| СПОСОБ ИЗВЛЕЧЕНИЯ ИЗ ДОПЛЕРОВСКИХ ПОРТРЕТОВ ВОЗДУШНЫХ ОБЪЕКТОВ ПРИЗНАКОВ ИДЕНТИФИКАЦИИ С ИСПОЛЬЗОВАНИЕМ МЕТОДА СВЕРХРАЗРЕШЕНИЯ | 2015 |
|
RU2589737C1 |
| РАДИОЛОКАЦИОННЫЙ СПОСОБ ВЫЯВЛЕНИЯ ЗАКОНА ИЗМЕНЕНИЯ УГЛОВОЙ СКОРОСТИ ПОВОРОТА СОПРОВОЖДАЕМОГО ВОЗДУШНОГО ОБЪЕКТА ПО ПОСЛЕДОВАТЕЛЬНО ПРИНЯТЫМ ОТРАЖЕНИЯМ СИГНАЛОВ С ПЕРЕСТРОЙКОЙ НЕСУЩЕЙ ЧАСТОТЫ | 2013 |
|
RU2525829C1 |
| СПОСОБ ВНЕШНЕГО РАДИОЛОКАЦИОННОГО ВЫЯВЛЕНИЯ ФАКТА НАЛИЧИЯ ТРАЕКТОРНЫХ НЕСТАБИЛЬНОСТЕЙ ПОЛЕТА ВОЗДУШНОГО ОБЪЕКТА С МАЛЫМ КУРСОВЫМ УГЛОМ ПЕРЕМЕЩЕНИЯ | 2009 |
|
RU2410717C2 |
| СПОСОБ ПОСТРОЕНИЯ ДВУМЕРНОГО РАДИОЛОКАЦИОННОГО ИЗОБРАЖЕНИЯ ВОЗДУШНОЙ ЦЕЛИ ПО ТРАЕКТОРНЫМ НЕСТАБИЛЬНОСТЯМ ЕЕ ПОЛЕТА | 2000 |
|
RU2180445C2 |
| СПОСОБ ЭКСПЕРИМЕНТАЛЬНОЙ ПРОВЕРКИ ИНФОРМАЦИОННЫХ И ИДЕНТИФИКАЦИОННЫХ ВОЗМОЖНОСТЕЙ ДОПЛЕРОВСКИХ ПОРТРЕТОВ ВОЗДУШНЫХ ОБЪЕКТОВ | 2014 |
|
RU2571957C1 |
Изобретение относится к радиолокационным методам и может быть использовано в когерентно-импульсных радиолокационных станциях сопровождения цели для проведения инверсного синтезирования апертуры антенны, которое обеспечивает построение радиолокационных изображений целей в интересах их дальнейшего распознавания. Достигаемым техническим результатом изобретения является обеспечение возможности учета характера траекторных нестабильностей полета цели. Сущность изобретения заключается в том, что для наиболее обоснованного выбора длительности и положения интервала инверсного синтезирования предлагается анализировать сглаженную амплитудную отражательную характеристику воздушной цели, сформированную на избыточном, длительностью до 10 секунд интервале сопровождения. В процессе анализа получают корреляционную характеристику цели, которая после сглаживания указывает интервалы с максимальной и минимальной угловыми скоростями поворота цели относительно радиолокатора. Это позволяет определять интервал, на котором минимизировано влияние траекторных нестабильностей полета на совокупную угловую скорость вращения цели. Анализ базируется на том, что суммарная угловая скорость поворота цели является суперпозицией угловой скорости ее вращения за счет прямолинейного движения 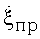 и угловой скорости рысканий ее планера
и угловой скорости рысканий ее планера 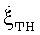 при траекторных нестабильностях полета, связанных наличием бокового ветра в турбулентной атмосфере. 6 ил.
при траекторных нестабильностях полета, связанных наличием бокового ветра в турбулентной атмосфере. 6 ил.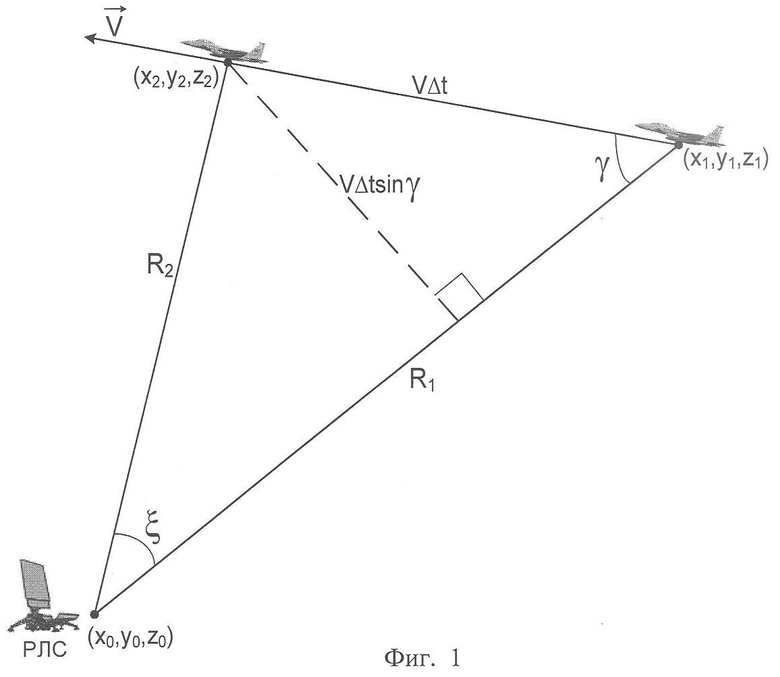
Способ выбора интервала инверсного синтезирования с рассчитываемой угловой скоростью поворота цели относительно радиолокатора, заключающийся в том, что с помощью когерентно-импульсной радиолокационной станции (РЛС) излучают в направлении воздушной цели сверхвысокочастотные сигналы, принимают отраженные сигналы, автоматически сопровождают цель по дальности и угловым координатам, определяют дальность R1, угол места ε1 и азимут β1 цели в начальный момент сопровождения, определяют дальность R2, угол места ε2 и азимут β2 цели через интервал ΔТ=1 с, пересчитывают измеренные сферические координаты цели для двух указанных моментов времени в прямоугольные (x1, y1, z1) и (х2, y2, z2), определяют пройденный целью путь ΔR за время ΔТ по формуле
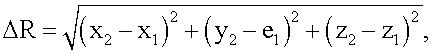
рассчитывают величину угла между начальным и конечным положением линии визирования цели по формуле
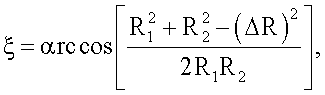
рассчитывают скорость цели V по формуле V=ΔR/ΔT, выбирают величину необходимой разрешающей способности δR⊥, в поперечном относительно линии визирования цели направлении, рассчитывают длительность интервала инверсного синтезирования ΔТис по формуле
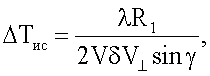
где λ - длина волны; γ - угол между линией визирования цели в начальный момент времени и линией пути цели, выбирают в пределах интервала ΔТ положение интервала инверсного синтезирования ΔТис, считая, что угловая скорость поворота цели 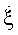 на этом интервале равна
на этом интервале равна 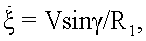 отличающийся тем, что период повторения импульсов Ти излучаемых сверхвысокочастотных сигналов когерентно-импульсной РЛС выбирают не более 1 мс, в процессе приема отраженных сигналов проводят регистрацию, перевод в цифровую форму и запись в оперативное запоминающее устройство когерентно-импульсной РЛС значений амплитуды и точного времени приема каждого отраженного импульсного сигнала на избыточном длительном порядка 10 с интервале Δtизб, формируют из значений амплитуд и времен приема импульсов двумерный массив M1 из S столбцов, в каждый s-й столбец которого записывают информацию об амплитуде и времени приема s-го сигнала из S сигналов, принятых за интервал Δtизб, вектор элементов строки массива M1 с величинами амплитуд отраженных сигналов принимают за отражательную характеристику цели, устраняют методом скользящего усреднения высокочастотную турбовинтовую модуляцию отражательной характеристики цели, в результате получают планерную отражательную характеристику цели, заменяют значения отражательной характеристики цели в массиве M1 соответствующими значениями планерной отражательной характеристики цели, задают величину оценочного времени корреляции τоц=3 мс, вычисляют значение q=G(τоц/Ти), где G(τоц/Tи) - функция нахождения целой части числа τоц/Ти, определяют число элементов I частной выборки отраженных сигналов, выполняя условие, чтобы I входило в диапазон от 50 до 200, последовательно смещают частную выборку сигналов на один отсчет в пределах планерной отражательной характеристики цели от первого положения, соответствующего участку планерной отражательной характеристики цели с первого по I-й отсчет, до (S-I+1)-го положения, соответствующего участку планерной отражательной характеристики цели с (S-I+1)-го по S-й отсчет, для каждого k-го положения частной выборки рассчитывают величину оценочного нормированного коэффициента автокорреляции по формуле
отличающийся тем, что период повторения импульсов Ти излучаемых сверхвысокочастотных сигналов когерентно-импульсной РЛС выбирают не более 1 мс, в процессе приема отраженных сигналов проводят регистрацию, перевод в цифровую форму и запись в оперативное запоминающее устройство когерентно-импульсной РЛС значений амплитуды и точного времени приема каждого отраженного импульсного сигнала на избыточном длительном порядка 10 с интервале Δtизб, формируют из значений амплитуд и времен приема импульсов двумерный массив M1 из S столбцов, в каждый s-й столбец которого записывают информацию об амплитуде и времени приема s-го сигнала из S сигналов, принятых за интервал Δtизб, вектор элементов строки массива M1 с величинами амплитуд отраженных сигналов принимают за отражательную характеристику цели, устраняют методом скользящего усреднения высокочастотную турбовинтовую модуляцию отражательной характеристики цели, в результате получают планерную отражательную характеристику цели, заменяют значения отражательной характеристики цели в массиве M1 соответствующими значениями планерной отражательной характеристики цели, задают величину оценочного времени корреляции τоц=3 мс, вычисляют значение q=G(τоц/Ти), где G(τоц/Tи) - функция нахождения целой части числа τоц/Ти, определяют число элементов I частной выборки отраженных сигналов, выполняя условие, чтобы I входило в диапазон от 50 до 200, последовательно смещают частную выборку сигналов на один отсчет в пределах планерной отражательной характеристики цели от первого положения, соответствующего участку планерной отражательной характеристики цели с первого по I-й отсчет, до (S-I+1)-го положения, соответствующего участку планерной отражательной характеристики цели с (S-I+1)-го по S-й отсчет, для каждого k-го положения частной выборки рассчитывают величину оценочного нормированного коэффициента автокорреляции по формуле
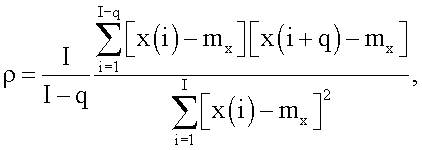
где x(i) - величина i-го элемента частной выборки в соответствующем k-м положении, состоящей из I элементов, mx - математическое ожидание амплитуды принимаемого сигнала в пределах планерной отражательной характеристики цели, связывают рассчитанный на k-м шаге нормированный коэффициент автокорреляции с временем начала соответствующей частной выборки, составляют из рассчитанных нормированных коэффициентов автокорреляции и соответствующих им времен двумерный массив М2, в первой строке которого располагают с первого по К-й нормированные коэффициенты автокорреляции, принимают вектор элементов этой строки за корреляционную характеристику цели, сглаживают корреляционную характеристику цели методом скользящего усреднения, в результате получают сглаженную корреляционную характеристику цели, заменяют значения корреляционной характеристики цели массива М2 соответствующими значениями сглаженной корреляционной характеристики, находят в пределах этой сглаженной корреляционной характеристики точки экстремумов, выбирают из них два смежных экстремума, находят их среднее арифметическое Z, определяют на интервале между используемыми экстремумами m-й элемент первой строки массива М2, наиболее близкий по значению сглаженного нормированного коэффициента автокорреляции к рассчитанной величине Z, принимают соответствующее ему m-е значение времени приема сигнала за середину интервала инверсного синтезирования tc, определяют время tн начала интервала инверсного синтезирования апертуры ΔТис по формуле tн=tс-ΔТис/2.
| СТАЙНБЕРГ Б.Д | |||
| Формирование радиолокационного изображения самолета в диапазоне СВЧ | |||
| ТИИЭР, 1988, т.76, №12, с.26-40 | |||
| СПОСОБ ИЗМЕРЕНИЯ ПОПЕРЕЧНЫХ РАЗМЕРОВ РАДИОЛОКАЦИОННЫХ ОБЪЕКТОВ РЛС В РЕАЛЬНОМ МАСШТАБЕ ВРЕМЕНИ | 1999 |
|
RU2150714C1 |
| СПОСОБ ПОСТРОЕНИЯ ДВУМЕРНОГО РАДИОЛОКАЦИОННОГО ИЗОБРАЖЕНИЯ ВОЗДУШНОЙ ЦЕЛИ ПО ТРАЕКТОРНЫМ НЕСТАБИЛЬНОСТЯМ ЕЕ ПОЛЕТА | 2000 |
|
RU2180445C2 |
| СПОСОБ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ ПО КУРСУ В УГЛОМЕРНОЙ ДВУХПОЗИЦИОННОЙ РАДИОЛОКАЦИОННОЙ СИСТЕМЕ | 2006 |
|
RU2308093C1 |
| US 4855747 А, 08.08.1989 | |||
| СПОСОБ ДЕКОДИРОВАНИЯ ВИДЕОСИГНАЛА | 2012 |
|
RU2628160C1 |
| СМЕСИ О-АЦИЛ-ИЗЕТИОНАТОВ И ПАВ НА ОСНОВЕ N-АЦИЛ-АМИНОКИСЛОТ | 2013 |
|
RU2606113C2 |
| US 2005062639 А1, 24.03.2005. | |||
Авторы
Даты
2009-06-27—Публикация
2007-11-06—Подача