Изобретение относится к цифровой вычислительной технике и может быть использовано в системах цифровой обработки сигналов при решении задач оптимальной нелинейной фильтрации.
Известно устройство - расширенный калмановский фильтр [1, 2], недостатком которого является ограниченность функциональных возможностей, обусловленная линейной структурой обрабатываемых процессов, и устройство [3], недостатком которого является эвристическое задание параметра регуляризации.
Наиболее близким по технической сущности к заявленному изобретению является цифровой итеративный фильтр [3], содержащий первый и второй блоки формирования суммы, первый, второй, третий и четвертый блоки формирования матричных функций, первый и второй блоки формирования разности, первую и вторую линии задержки, первый и второй блоки коррекции, блок формирования и выдачи априорных данных. Недостатком данного устройства является низкая точность формируемых оценок параметров информационного процесса.
Улучшение точностных характеристик фильтрации параметров случайных процессов является актуальным направлением.
Заявленное изобретение направлено на повышение точности при формировании оценки параметров информационного процесса в измерительных системах, что весьма важно при радиолокационном сопровождении целей. Цифровой интеллектуальный итеративный фильтр содержит блоки: первый, второй, третий блоки формирования разности; первый, второй, третий блоки коррекции; блок формирования и выдачи априорных данных; первый, второй, третий блоки формирования суммы; первый, второй, третий, четвертый, пятый и шестой блоки формирования матричных функций; первую, вторую и третью линии задержки; первый и второй блоки расчета параметра регуляризации, при этом первый, второй, третий и четвертый выходы блока формирования и выдачи априорных данных соединены соответственно со вторым, третьим, четвертым и пятым информационным входами первого, второго и третьего блоков коррекции, кроме того, первый, второй, пятый выходы блока формирования и выдачи априорных данных соединены соответственно с третьим, вторым и пятым информационными входами первого и второго блоков расчета параметра регуляризации, первый информационный выход первого блока коррекции соединен с первым информационным входом первого блока формирования суммы, выход которого соединен с информационным входом первого блока формирования матричной функции и четвертым информационным входом первого блока расчета параметра регуляризации, выход которого соединен с девятым информационным входом второго блока коррекции, выход первого блока формирования матричной функции соединен с информационным входом первой линии задержки, выход которой соединен со вторым информационным входом первого блока формирования суммы, с седьмым информационным входом первого блока коррекции и с информационным входом второго блока формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом первого блока коррекции, первый информационный выход второго блока формирования матричной функции соединен со вторым информационным входом блока формирования разности, выход которого соединен с первым информационным входом первого блока коррекции; второй информационный выход первого блока коррекции соединен с восьмым информационным входом второго блока коррекции, первый информационный выход которого соединен с первым информационным входом второго блока формирования суммы, выход которого соединен с информационным входом третьего блока формирования матричной функции и с четвертым информационным входом второго блока расчета параметра регуляризации, выход которого соединен с девятым информационным входом третьего блока коррекции, выход третьего блока формирования матричной функции соединен с информационным входом второй линии задержки, выход которой соединен со вторым информационным входом второго блока формирования суммы, седьмым информационным входом второго блока коррекции и с информационным входом четвертого блока формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом второго блока коррекции, первый информационный выход четвертого блока формирования матричной функции соединен со вторым информационным входом второго блока формирования разности, выход которого соединен с первым информационным входом второго блока коррекции; второй информационный выход второго блока коррекции соединен с восьмым информационным входом третьего блока коррекции, первый информационный выход которого соединен с первым информационным входом третьего блока формирования суммы, выход которого является выходом устройства и соединен с информационным входом пятого блока формирования матричной функции, выход которого соединен с информационным входом третьей линии задержки, выход которой соединен со вторым информационным входом пятого блока формирования суммы, седьмым информационным входом третьего блока коррекции и с информационным входом шестого блока формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом третьего блока коррекции, первый информационный выход шестого блока формирования матричной функции соединен со вторым информационным входом третьего блока формирования разности, выход которого соединен с первым информационным входом третьего блока коррекции.
Одним из способов повышения точности оценки параметров динамических систем является использование методов решения некорректных задач на основе принципов регуляризации. Эффективность применения регуляризации для случая непрерывных систем доказана и получила свое выражение в виде метода А.Н.Тихонова [4] и его разновидности в виде метода итерационной регуляризации [5]. Получим уравнения фильтрации с использованием метода итерационной регуляризации для дискретной системы [6, 9].
Пусть динамика оцениваемых параметров описывается системой разностных уравнений в дискретном времени
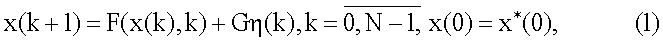
где х(k)=[х1(k),х2(k),…,хM(k)]T∈EM - вектор состояния исследуемой системы; η(k)=[η1(k),η2(k),…(ηM(k)]T∈EM - вектор неизвестных внешних воздействий; переходная функция 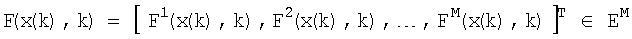 - непрерывная вместе с частными производными вектор-функция своих аргументов;
- непрерывная вместе с частными производными вектор-функция своих аргументов;
G∈ЕM×ЕM - матрица интенсивности внешних воздействий; k, N, М - натуральные числа. Предполагается, что матрица 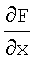 - имеет обратную.
- имеет обратную.
Наблюдаемый сигнал, получаемый на выходе модели измерительной системы, описывается дискретным уравнением

где y(k)=[yl(k),y2(k),…,yL(k)]T∈EL - вектор наблюдения,
n(k)=[nl(k),n2(k),…,nL(k)]T∈EL - вектор дискретного белого гауссовского шума с известными локальными характеристиками
M[n(k)]=0,
M[n(k)nT(l)]=Wδ(k-l),
W - ковариационная матрица размерности L×L, δ(·)- векторная дельта-функция; H(x(k))=[Hl(x(k)),H2(x(k)),…,HL(x(k))]T∈EL - сигнальная вектор-функция, непрерывна вместе с частными производными; L, l - натуральные числа.
Поставим задачу синтеза, рекуррентного фильтра оценки х*(k), оптимального в смысле минимума функционала, характеризующего ошибку измерения
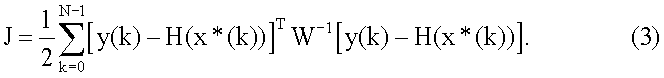
В силу непрерывности вектор-функции F(·) решение уравнения (1) непрерывно зависит от η(k), поэтому функционал ошибки (3) на каждом решении системы (1) непрерывно зависит от η(k). Таким образом, задача определения оценки х*(k), доставляющей минимум (3), равносильна задаче определения

Задача (1), (2), (4) является некорректно поставленной обратной задачей [7]. Найти значения векторов х*(k), η*(k), 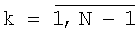 путем решения совокупности уравнений (1), (2), (4) в условиях некорректности исходной задачи достаточно сложно, в связи с этим широкое распространение получили итерационные градиентные методы. Однако использование таких методов может привести к расходящейся последовательности приближений.
путем решения совокупности уравнений (1), (2), (4) в условиях некорректности исходной задачи достаточно сложно, в связи с этим широкое распространение получили итерационные градиентные методы. Однако использование таких методов может привести к расходящейся последовательности приближений.
Поэтому применение любого итерационного метода для решения задачи (1), (2), (4) требует определения регуляризирующего семейства операторов, в котором параметром регуляризации является номер итерации.
В соответствии с общим определением регуляризирующего семейства операторов по А.Н.Тихонову [7] будем говорить, что итерационный метод
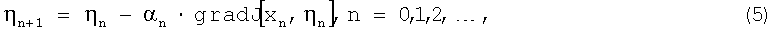
в котором числовой параметр αn удовлетворяет условиям:

где Δ(ηn) - невязка, порождает регуляризирующее семейство операторов, в котором параметром является номер итерации, если для любого начального приближения η0 и для любого значения погрешности исходных данных σ, удовлетворяющего условию 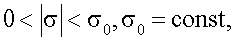 существует номер n(σ) такой, что
существует номер n(σ) такой, что
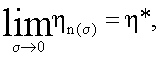
то есть полученные приближения сходятся к точному решению в норме пространства 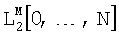 при стремлении погрешности исходных данных к нулю.
при стремлении погрешности исходных данных к нулю.
Согласно [8] выражение для определения градиента в точке ηn(k) имеет вид
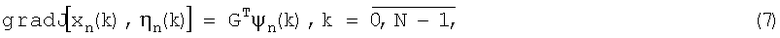
где хn(k) - решение задачи (1) при ηn(k), а вектор Ψn(k) определяется из условий
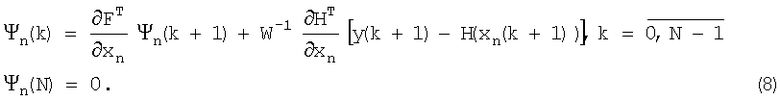
Зная выражение для градиента (7) функционала (3), можно переписать выражение (6) для параметра регуляризации [9] в следующем виде
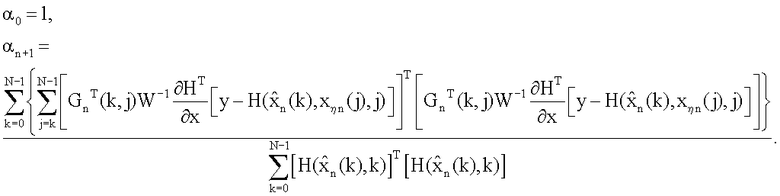
Выбор последовательности параметров αn, удовлетворяющей условию
(9), позволит реализовать фильтр цифровой обработки измерительной информации повышенной точности.
Для реализации итерационного метода (5) требуется определить градиент функционала (3), определяемый выражением (7). Приняв за нулевое приближение 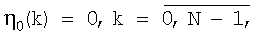 запишем итерационную последовательность (5) в развернутой форме для
запишем итерационную последовательность (5) в развернутой форме для 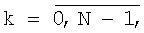
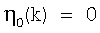 ,
,
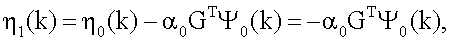

В результате с учетом (7) имеем последовательность дискретных двухточечных краевых задач (ДДТКЗ) вида
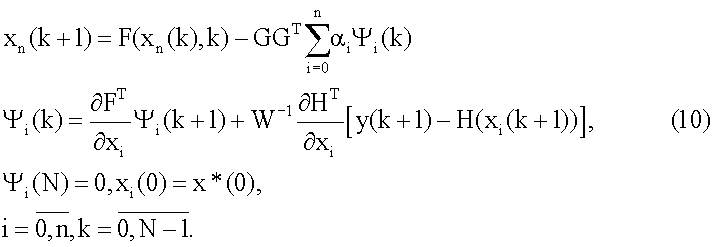
Введем обозначение 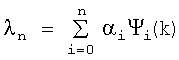 и помножим каждое из уравнений для сопряженных векторов Ψi на величину αi, тогда уравнения (10)
и помножим каждое из уравнений для сопряженных векторов Ψi на величину αi, тогда уравнения (10)
принимают следующий вид
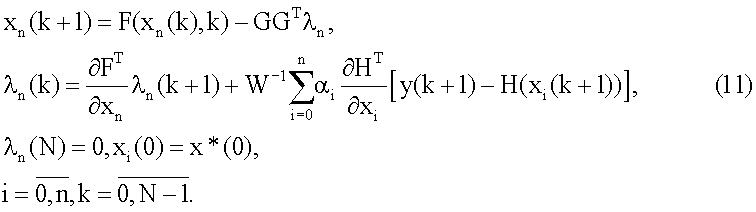
Для получения алгоритма рекуррентного оценивания вектора состояния необходимо воспользоваться методом инвариантного погружения в дискретном варианте. Заметим, что уравнение для вектор-функций λ в ДДТКЗ (9) записано в обратном времени. Это требует его преобразования к виду, отражающему зависимость λn(k+1) от λn(k) и хn(k). Производя соответствующие преобразования с учетом выражения для
хn(k+1) из (11) и используя разложение в ряд Тейлора в окрестности F(xn(k),k), получим следующую последовательность ДДТКЗ
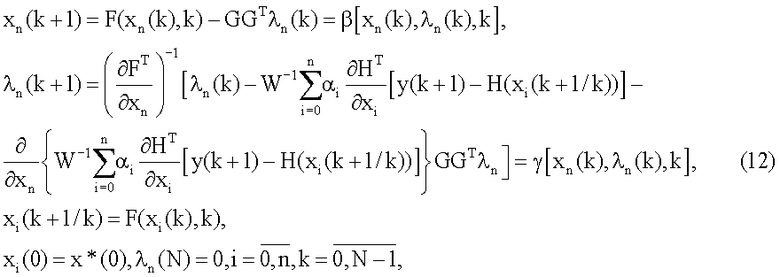
где функции β и γ вводятся для сокращения записи.
Заменим условие на конце λn(N)=0 более общим условием λn(N)=с и пусть N и с - переменные величины. Тогда значение вектора xn(N) определяется как функция величин N и с
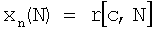 .
.
Изменение величины N на N+1 дает приращение Δс, тогда
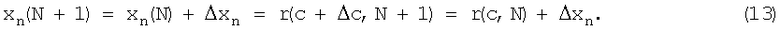
Запишем выражение для r(с+Δс,N+1), используя аппарат конечных разностей
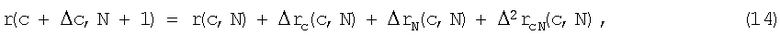
или, учитывая (13), получим
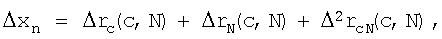
где
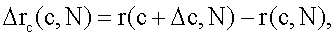
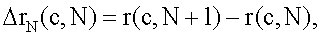
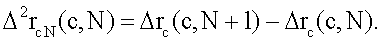
Согласно (12) выражения для Δxn и Δc имеют вид
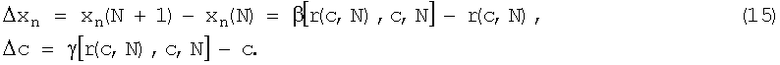
Разрешить разностное уравнение (14) относительно r(c,N), т.е. найти общее аналитическое решение не удается, и обычно обращаются к приближенным методам. Предположим, что r(c,N) линейна по с
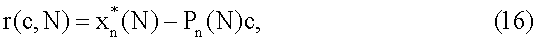
где 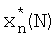 - оценка вектора состояния в момент N, Рn(N) - некоторая матрица размерности М×М.
- оценка вектора состояния в момент N, Рn(N) - некоторая матрица размерности М×М.
Вычислим разности, входящие в выражение (14), используя выражение (16)
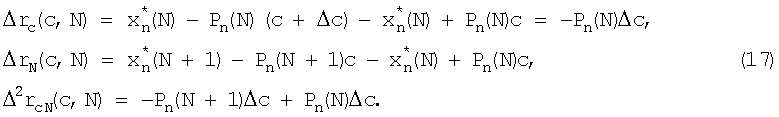
Подставив выражения (15), (16), (17) в (14), получим
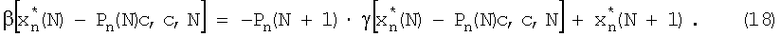
Разлагая β и γ в ряд Тейлора в окрестности 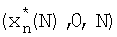 и пренебрегая членами порядка выше первого, можно записать уравнение (18) в виде
и пренебрегая членами порядка выше первого, можно записать уравнение (18) в виде
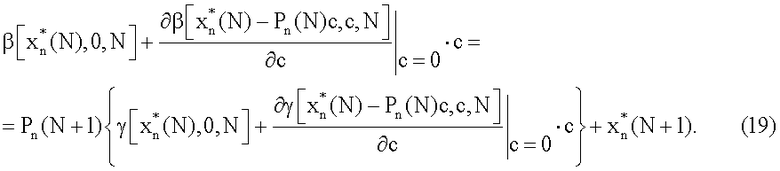
Соотношение (19) выполняется при c→0, поэтому, приравнивая коэффициенты при первой и нулевой степени с, получим разностные уравнения для 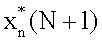 и Рn(N+1)
и Рn(N+1)
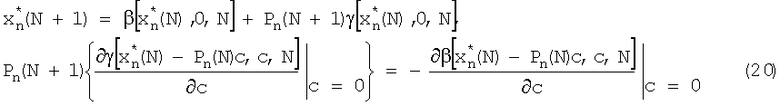
Запишем ДДТКЗ (12) для случая, когда k=N, при этом учтем, что это все ДДТКЗ для i=0,…,n-1 являются разрешенными и, соответственно, оценки хi представляют собой известные функции параметра k. Таким образом, имеем
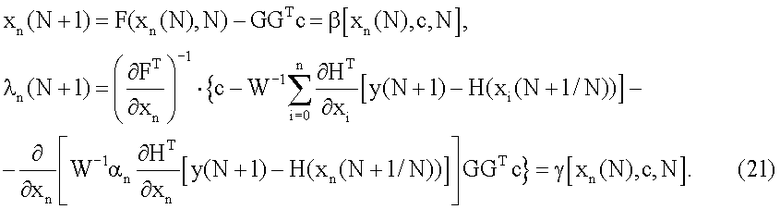
Тогда уравнение (20) преобразуется следующим образом
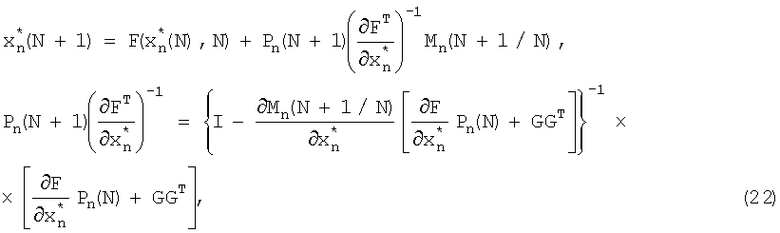
где
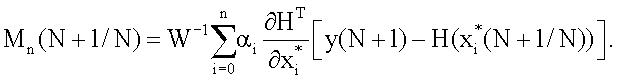
Введем обозначения
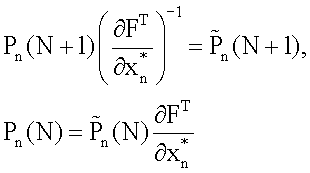
Тогда уравнение (22) запишем в виде
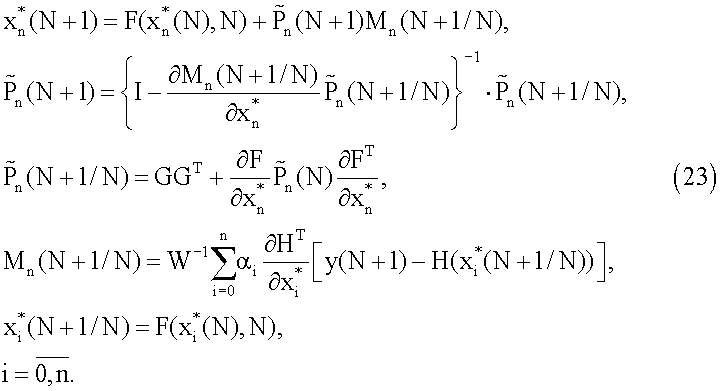
Поскольку разницы в переобозначении матриц Рn и 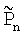 нет, запишем последовательность уравнений для оценки
нет, запишем последовательность уравнений для оценки 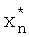 процесса (1), предполагая, что N постоянно изменяется и k=N, а также учитывая условие (7), налагаемое на параметр регуляризации, в виде
процесса (1), предполагая, что N постоянно изменяется и k=N, а также учитывая условие (7), налагаемое на параметр регуляризации, в виде
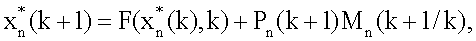
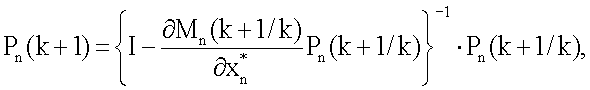
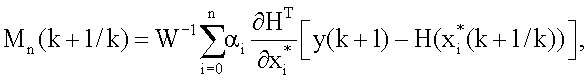
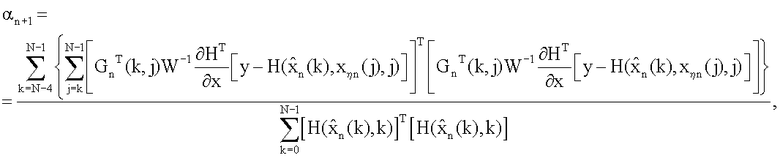
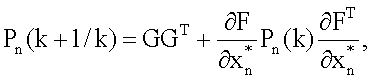
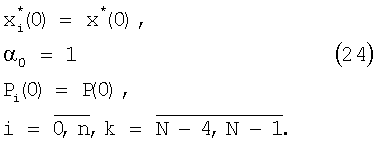
Последовательность уравнений (24) представляет собой цифровой интеллектуальный рекурсивный фильтр, который позволяет осуществить процесс цифровой обработки измерительной информации для дискретных динамических систем. Если сравнить полученные уравнения с уравнениями цифрового итеративного фильтра [3], то становится ясно, что они отличны друг от друга за счет возникновения связи между параметром регуляризации и блоком коррекции, а также дополнительных связей последовательности параметров αi, изменяющих общий коэффициент обратной связи в уравнении для оценки 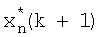 , с оценками
, с оценками 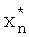 , сигнальной вектор - функцией Н и матрицами G, W. To есть в фильтре (24) в отличии от фильтра [3] параметр регуляризации согласован в соответствии с принципом невязки с ошибками измерений, что позволяет получить более точную процедуру оценивания. Алгоритм (24) дает оптимальную для нелинейной системы оценку параметров в смысле минимума функционала, характеризующего среднеквадратическую ошибку измерительного канала.
, сигнальной вектор - функцией Н и матрицами G, W. To есть в фильтре (24) в отличии от фильтра [3] параметр регуляризации согласован в соответствии с принципом невязки с ошибками измерений, что позволяет получить более точную процедуру оценивания. Алгоритм (24) дает оптимальную для нелинейной системы оценку параметров в смысле минимума функционала, характеризующего среднеквадратическую ошибку измерительного канала.
Вычисление параметра регуляризации организовано следующим образом: пределы интегрирования [0,t] изменены на [t-3s,t], где t означает текущее время, s - шаг вычислений; для дискретного времени необходимо брать [N-1,N-4]. Исследования показали [6], что использование данных больше чем на три шага назад обеспечивает повышение точности получаемых оценок на доли процента при увеличении количества необходимых арифметических операций в несколько раз.
Следует отметить, что для реализации 2-й итерации разработанного алгоритма (24) необходимо, чтобы 1-я итерация была реализована, для реализации 3-й - 1-я и 2-я. То есть количество арифметических операций, необходимых для вычисления итерации алгоритма, включат в себя число арифметических операций предыдущих итераций. Анализ вычислительных затрат, требуемых на реализацию разработанного алгоритма оценки, позволяют сделать вывод о возможности его реализации в реальном масштабе времени на основе использования современной вычислительной техники.
Исследования показали, что эффективность каждой повторной обработки по отношению к предыдущей падает. Между тем, объем вычислений резко увеличивается. На основании анализа результатов численного моделирования можно рекомендовать трехкратную итеративную обработку данных.
Оценка эффективности функционирования разработанного фильтра произведена на основе численного моделирования задачи определения неизвестного постоянного параметра d дискретной нелинейной системы третьего порядка
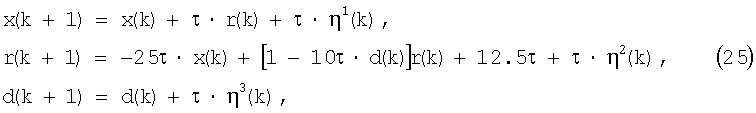
где параметр τ имеет смысл интервала времени, через который поступает измерительная информация в виде

Графики оценок параметра d=0.2 для 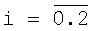 приводятся на фиг.1 при τ=0.3 при общем интервале Т=5. Видно, что оценка интеллектуального рекурсивного фильтра превосходит по точности оценку итеративного фильтра. Численное моделирование показало, что точность определения параметра d с помощью цифрового интеллектуального рекурсивного фильтра выше на 10.8% по сравнению с цифровым итеративным фильтром.
приводятся на фиг.1 при τ=0.3 при общем интервале Т=5. Видно, что оценка интеллектуального рекурсивного фильтра превосходит по точности оценку итеративного фильтра. Численное моделирование показало, что точность определения параметра d с помощью цифрового интеллектуального рекурсивного фильтра выше на 10.8% по сравнению с цифровым итеративным фильтром.
Таким образом, как следует из соотношений (24), введение новых структурных элементов и связей позволяет в совокупности с общими признаками получить технический результат, состоящий в уменьшении дисперсии ошибок полученных на выходе фильтра оценок входных процессов.
Заявленное устройство может быть применено в информационных системах, связанных со сбором и обработкой информации, например в информационных системах радиолокационных и радионавигационных комплексов.
Сущность изобретения поясняется фиг.2-8, где представлены структурные схемы интеллектуального рекурсивного цифрового фильтра, первого и второго блоков коррекции, блока расчета точностных характеристик, блока расчета параметра регуляризации, первого блока формирования произведения числителя параметра регуляризации, блока расчета прогноза.
На фиг.2 представлена структурная схема цифрового интеллектуального рекурсивного фильтра. Устройство содержит первый блок 1, второй блок 7 и третий блок 14 формирования разности, первый блок 2, второй блок 8 и третий блок 15 коррекции, первый блок 3, второй блок 9, третий блок 16 формирования суммы, первую линию задержки 5, вторую линию задержки 11 и третью линию задержки 18, первый блок 4, второй блок 6, третий блок 10, четвертый блок 12, пятый блок 17 и шестой блок 19 формирования матричных функций, блок 13 формирования и выдачи априорных данных и первый блок 20, а также второй блок 21 расчета параметра регуляризации.
На фиг.3 представлена структурная схема первого блока коррекции, которая содержит блок 2.1 формирования частных производных, блок 2.2 транспонирования матричной функции, блок 2.3 формирования произведения, блок 2.4 вычисления точностных характеристик, блок 2.5 формирования произведения.
На фиг.4 представлена структурная схема второго блока коррекции, который содержит блок 8.1 формирования частных производных, блок 8.2 транспонирования матричной функции, блок 8.3 формирования произведения, блок 8.4 формирования суммы, блок 8.5 расчета точностных характеристик, блок 8.6 формирования произведения.
На фиг.5 представлена структурная схема блока расчета точностных характеристик, входящего в первый и второй блоки коррекции, который содержит блок 14 формирования частных производных матричной функции, блок 21 транспонирования матриц, блок 22 формирования произведения, линию 23 задержки, блок 24 транспонирования матриц, блок 25 формирования произведения, блок 26 формирования суммы, блок 27 формирования частных производных матричной функции, блок 28 формирования произведения, блок 29 формирования разности, устройство 30 обращения матриц, блок 31 формирования произведения.
На фиг.6 представлена структурная схема блока расчета параметра регуляризации, который содержит блок формирования матричной функции 14.1, линии задержки 14.2, 14.4, 14.7, 14.8, 14.12, 14.13, 14.16, 14.17, 14.18, 14.24, 14.25, 14.26, 14.29, 14.30, 14.31, 14.32, 14.40, 14.41, 14.42, 14.43, блоки 14.3, 14.9, 14.11, 14.19, 14.22, 14.23, 14.33, 14.37, 14.38, 14.39 формирования произведения числителя параметра регуляризации, блоки 14.5, 14.14, 14.27, 14.44 транспонирования, блоки 14.6, 14.15, 14.28, 14.45 формирования произведения, блоки 14.10, 14.20, 14.21, 14.34, 14.35, 14.36 расчета прогноза, блоки 14.46, 14.47 формирования суммы, блок 14.48 формирования отношения.
На фиг.7 представлена структурная схема первого блока формирования произведения числителя параметра регуляризации, входящего в первый блок формирования параметра регуляризации, который содержит блок 14.3.1 формирования матричной функции, блок 14.3.2 частных производных матричной функции, блок 14.3.3 транспонирования матриц, блок 14.3.4, блок 14.3.5 формирования произведения, блоки 14.3.6 и 14.3.7 транспонирования матриц и блок 14.3.8 формирования произведения.
На фиг.8 представлена структурная схема первого блока расчета прогноза, который входит в состав блока формирования произведения числителя параметра регуляризации, он включает блоки 14.10.1 и 14.10.5 формирования произведения, блоки 14.10.2 и 14.10.6 формирования суммы, блок 14.10.3 формирования частных производных матричной функции, блок 14.10.4 формирования матричной функции.
Информационные входы линий задержки 14.2, 14.7, 14.16, 14.29 (фиг.6) соединены с информационным выходом блока 3 формирования суммы (фиг.2), первые информационные входы линий задержки 14.4, 14.12, 14.24, 14.40 соединены с первым информационным выходом блока 14.1 формирования матричной функции 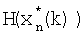 , информационный вход которого соединен с информационным выходом блока 3, информационный выход первой линии задержки 14.2 соединен со вторым информационным входом первого блока 14.3 формирования произведения числителя параметра регуляризации, первый и третий его информационные входы соединены со вторым и первым информационными выходами блока 13 формирования и выдачи априорных данных соответственно, а четвертый информационный вход - со входом устройства, первый информационный выход первого блока 14.3 формирования произведения числителя параметра регуляризации соединен с шестым и седьмым информационными входами второго блока 14.46 формирования суммы, первый информационный выход которого соединен с первым информационным входом блока 14.48 формирования отношения, первый выход блока 14.48 формирования отношения является выходом блока 14; первый информационный выход второй линии задержки 14.4 соединен с первым информационным входом первого блока транспонирования 14.5 и первым информационным входом первого блока 14.6 формирования произведения, первый информационный выход блока 14.5 соединен со вторым информационным входом блока 14.6 формирования произведения, первый информационный выход которого соединен с четвертым информационным входом первого блока 14.47 формирования произведения, первый информационный выход которого соединен со вторым информационным входом блока 14.48 формирования отношения; первый информационный выход третьей 14.7 линии задержки соединен с первым информационным входом четвертой 14.8 линии задержки, первый информационный выход которой соединен со вторым информационным входом второго блока 14.9 формирования произведения числителя параметра регуляризации и вторым информационным входом первого блока 14.10 расчета прогноза, второй информационный выход которого соединен со вторым информационным входом третьего блока 14.11 формирования произведения числителя параметра регуляризации, третьи и четвертые информационные входы блоков 14.9, 14.11, соединены с первым информационным выходом блока 13 и входом устройства, первый информационный выход блока 14.9 соединен с третьим и четвертым информационными входами блока 14.46, первый информационный выход блока 14.11 соединен с десятым информационным входом блока 14.46; первый информационный выход пятой 14.12 линии задержки соединен с первым информационным входом шестой 14.13 линии задержки, первый информационный выход которой соединен с первым информационным входом второго блока 14.14 транспонирования и первым информационным входом второго блока 14.15 формирования произведения, первый информационный выход второго 14.14 блока транспонирования соединен со вторым информационным входом блока 14.15, первый информационный выход которого соединен с третьим информационным входом блока 14.47 формирования суммы; первый информационный выход седьмой линии задержки 14.16 соединен с первым информационным входом восьмой линии задержки 14.17, первый информационный выход которой соединен с первым информационным входом девятой 14.18 линии задержки, первый информационный выход которой соединен со вторыми информационными входами четвертого 14.19 блока формирования произведения числителя параметра регуляризации и второго блока 14.20 расчета прогноза, второй информационный выход которого соединен со вторыми информационными входами третьего блока 14.21 расчета прогноза и 14.23 формирования произведения числителя параметра регуляризации, второй информационный вход блока 14.22 расчета прогноза соединен со вторым информационным выходом третьего блока 14.21 вычисления, третьи и четвертые информационные входы блоков 14.19, 14.22 и 14.23 соединены с первым информационным выходом блока 13 и входом устройства соответственно, первый информационный выход блока 14.19 соединен с одиннадцатым и двенадцатым информационными входами второго блока 14.46 формирования суммы, первые информационные выходы блоков 14.23, 14.22 соединены с тринадцатым и четырнадцатым информационными входами первого блока 14.46 соответственно; первый информационный выход десятой линии задержки 14.24 соединен с первым информационным входом одиннадцатой линии задержки 14.25, первый информационный выход которой соединен с первым информационным входом двенадцатой 14.26 линии задержки, первый информационный выход которой соединен с первыми информационным входом третьего блока 14.27 транспонирования матричной функции и первым информационным входом третьего блока 14.28 формирования произведения, первый информационный выход третьего блока 14.27 транспонирования соединен со вторым информационным входом третьего блока 14.28 формирования произведения, первый информационный выход которого соединен с первым информационным входом первого блока 14.47 формирования суммы; первый информационный выход тринадцатой линии задержки 14.29 соединен с первым информационным входом четырнадцатой линии задержки 14.30, первый информационный выход которой соединен с первым информационным входом пятнадцатой 14.31 линии задержки, первый информационный выход которой в свою очередь соединен с первым информационным входом шестнадцатой линии задержки 14.32, выход которой соединен со вторым информационным входом седьмого блока 14.33 формирования произведения числителя параметра регуляризации и вторым информационным входом четвертого блока 14.34 расчета прогноза, второй информационный выход которого соединен со вторым информационным входом девятого блока 14.38 формирования произведения числителя параметра регуляризации и вторым информационным входом пятого блока 14.35 расчета прогноза, второй информационный выход последнего соединен со вторым информационным входом десятого блока 14.39 формирования произведения числителя параметра регуляризации и со вторым информационным входом шестого блока расчета прогноза 14.36, второй информационный выход которого соединен со вторым информационным входом восьмого блока 14.37 формирования произведения числителя параметра регуляризации, третьи и четвертые информационные входы блоков 14.33, 14.37, 14.38, 14.39 соединены соответственно с первым информационным выходом блока 13 и входом устройства, первый информационный выход блока 14.33 соединен с восьмым и девятым информационными входами блока 14.46 формирования суммы, первый информационный выход блока 14.37 формирования произведения числителя параметра регуляризации соединен с пятым информационным входом блока 14.46, первые информационные выходы блоков 14.38 и 14.39 формирования произведения числителя параметра регуляризации соединены со вторым и первым информационными входами блока 14.46 соответственно; первый информационный выход семнадцатой линии задержки 14.40 соединен с первым информационным входом восемнадцатой линии задержки 14.41, первый информационный выход которой соединен с первым информационным входом девятнадцатой 14.42 линии задержки, первый информационный выход которой в свою очередь соединен с первым информационным входом двадцатой линии задержки 14.43, информационный выход которой соединен с первыми информационными входами четвертого блока 14.44 транспонирования и четвертого блока 14.45 формирования произведения, первый информационный выход блока 14.44 соединен со вторым информационным входом блока 14.45, первый информационный выход которого соединен со вторым информационным входом блока 14.47; первые информационные входы второго 14.9, четвертого 14.19 и седьмого 14.33 блоков формирования произведения числителя параметра регуляризации соединены со входом устройства, а первые информационные входы третьего 14.11, пятого 14.22, шестого 14.23, восьмого 14.37, девятого 14.38 и десятого 14.39 блоков формирования произведения числителя параметра регуляризации соединены соответственно с первыми информационными выходами первого 14.10, третьего 14.21, второго 14.20, шестого 14.36, четвертого 14.34 и пятого 14.35 блоков расчета прогноза; первые информационные входы первого 14.10, второго 14.20 и четвертого 14.34 блоков расчета прогноза соединены со вторым информационным выходом блока 13, а первые информационные входы третьего 14.21, пятого 14.35, шестого 14.36 блоков расчета прогноза соединены с первыми информационными выходами соответственно второго 14.20, четвертого 14.34 и пятого 14.35 блоков расчета прогноза, третьи информационные входы блоков расчета прогноза соединены с пятым информационным выходом блока 13. Структура второго блока расчета параметра регуляризации аналогична.
, информационный вход которого соединен с информационным выходом блока 3, информационный выход первой линии задержки 14.2 соединен со вторым информационным входом первого блока 14.3 формирования произведения числителя параметра регуляризации, первый и третий его информационные входы соединены со вторым и первым информационными выходами блока 13 формирования и выдачи априорных данных соответственно, а четвертый информационный вход - со входом устройства, первый информационный выход первого блока 14.3 формирования произведения числителя параметра регуляризации соединен с шестым и седьмым информационными входами второго блока 14.46 формирования суммы, первый информационный выход которого соединен с первым информационным входом блока 14.48 формирования отношения, первый выход блока 14.48 формирования отношения является выходом блока 14; первый информационный выход второй линии задержки 14.4 соединен с первым информационным входом первого блока транспонирования 14.5 и первым информационным входом первого блока 14.6 формирования произведения, первый информационный выход блока 14.5 соединен со вторым информационным входом блока 14.6 формирования произведения, первый информационный выход которого соединен с четвертым информационным входом первого блока 14.47 формирования произведения, первый информационный выход которого соединен со вторым информационным входом блока 14.48 формирования отношения; первый информационный выход третьей 14.7 линии задержки соединен с первым информационным входом четвертой 14.8 линии задержки, первый информационный выход которой соединен со вторым информационным входом второго блока 14.9 формирования произведения числителя параметра регуляризации и вторым информационным входом первого блока 14.10 расчета прогноза, второй информационный выход которого соединен со вторым информационным входом третьего блока 14.11 формирования произведения числителя параметра регуляризации, третьи и четвертые информационные входы блоков 14.9, 14.11, соединены с первым информационным выходом блока 13 и входом устройства, первый информационный выход блока 14.9 соединен с третьим и четвертым информационными входами блока 14.46, первый информационный выход блока 14.11 соединен с десятым информационным входом блока 14.46; первый информационный выход пятой 14.12 линии задержки соединен с первым информационным входом шестой 14.13 линии задержки, первый информационный выход которой соединен с первым информационным входом второго блока 14.14 транспонирования и первым информационным входом второго блока 14.15 формирования произведения, первый информационный выход второго 14.14 блока транспонирования соединен со вторым информационным входом блока 14.15, первый информационный выход которого соединен с третьим информационным входом блока 14.47 формирования суммы; первый информационный выход седьмой линии задержки 14.16 соединен с первым информационным входом восьмой линии задержки 14.17, первый информационный выход которой соединен с первым информационным входом девятой 14.18 линии задержки, первый информационный выход которой соединен со вторыми информационными входами четвертого 14.19 блока формирования произведения числителя параметра регуляризации и второго блока 14.20 расчета прогноза, второй информационный выход которого соединен со вторыми информационными входами третьего блока 14.21 расчета прогноза и 14.23 формирования произведения числителя параметра регуляризации, второй информационный вход блока 14.22 расчета прогноза соединен со вторым информационным выходом третьего блока 14.21 вычисления, третьи и четвертые информационные входы блоков 14.19, 14.22 и 14.23 соединены с первым информационным выходом блока 13 и входом устройства соответственно, первый информационный выход блока 14.19 соединен с одиннадцатым и двенадцатым информационными входами второго блока 14.46 формирования суммы, первые информационные выходы блоков 14.23, 14.22 соединены с тринадцатым и четырнадцатым информационными входами первого блока 14.46 соответственно; первый информационный выход десятой линии задержки 14.24 соединен с первым информационным входом одиннадцатой линии задержки 14.25, первый информационный выход которой соединен с первым информационным входом двенадцатой 14.26 линии задержки, первый информационный выход которой соединен с первыми информационным входом третьего блока 14.27 транспонирования матричной функции и первым информационным входом третьего блока 14.28 формирования произведения, первый информационный выход третьего блока 14.27 транспонирования соединен со вторым информационным входом третьего блока 14.28 формирования произведения, первый информационный выход которого соединен с первым информационным входом первого блока 14.47 формирования суммы; первый информационный выход тринадцатой линии задержки 14.29 соединен с первым информационным входом четырнадцатой линии задержки 14.30, первый информационный выход которой соединен с первым информационным входом пятнадцатой 14.31 линии задержки, первый информационный выход которой в свою очередь соединен с первым информационным входом шестнадцатой линии задержки 14.32, выход которой соединен со вторым информационным входом седьмого блока 14.33 формирования произведения числителя параметра регуляризации и вторым информационным входом четвертого блока 14.34 расчета прогноза, второй информационный выход которого соединен со вторым информационным входом девятого блока 14.38 формирования произведения числителя параметра регуляризации и вторым информационным входом пятого блока 14.35 расчета прогноза, второй информационный выход последнего соединен со вторым информационным входом десятого блока 14.39 формирования произведения числителя параметра регуляризации и со вторым информационным входом шестого блока расчета прогноза 14.36, второй информационный выход которого соединен со вторым информационным входом восьмого блока 14.37 формирования произведения числителя параметра регуляризации, третьи и четвертые информационные входы блоков 14.33, 14.37, 14.38, 14.39 соединены соответственно с первым информационным выходом блока 13 и входом устройства, первый информационный выход блока 14.33 соединен с восьмым и девятым информационными входами блока 14.46 формирования суммы, первый информационный выход блока 14.37 формирования произведения числителя параметра регуляризации соединен с пятым информационным входом блока 14.46, первые информационные выходы блоков 14.38 и 14.39 формирования произведения числителя параметра регуляризации соединены со вторым и первым информационными входами блока 14.46 соответственно; первый информационный выход семнадцатой линии задержки 14.40 соединен с первым информационным входом восемнадцатой линии задержки 14.41, первый информационный выход которой соединен с первым информационным входом девятнадцатой 14.42 линии задержки, первый информационный выход которой в свою очередь соединен с первым информационным входом двадцатой линии задержки 14.43, информационный выход которой соединен с первыми информационными входами четвертого блока 14.44 транспонирования и четвертого блока 14.45 формирования произведения, первый информационный выход блока 14.44 соединен со вторым информационным входом блока 14.45, первый информационный выход которого соединен со вторым информационным входом блока 14.47; первые информационные входы второго 14.9, четвертого 14.19 и седьмого 14.33 блоков формирования произведения числителя параметра регуляризации соединены со входом устройства, а первые информационные входы третьего 14.11, пятого 14.22, шестого 14.23, восьмого 14.37, девятого 14.38 и десятого 14.39 блоков формирования произведения числителя параметра регуляризации соединены соответственно с первыми информационными выходами первого 14.10, третьего 14.21, второго 14.20, шестого 14.36, четвертого 14.34 и пятого 14.35 блоков расчета прогноза; первые информационные входы первого 14.10, второго 14.20 и четвертого 14.34 блоков расчета прогноза соединены со вторым информационным выходом блока 13, а первые информационные входы третьего 14.21, пятого 14.35, шестого 14.36 блоков расчета прогноза соединены с первыми информационными выходами соответственно второго 14.20, четвертого 14.34 и пятого 14.35 блоков расчета прогноза, третьи информационные входы блоков расчета прогноза соединены с пятым информационным выходом блока 13. Структура второго блока расчета параметра регуляризации аналогична.
Первый, второй и пятый информационные выходы блока 13 формирования и выдачи априорных данных (фиг.2) соединены соответственно с третьим, вторым и пятым информационными входами первого блока 14 и второго блока 21 расчета параметра регуляризации, выход которого соединен с девятым информационным входом третьего блока 15 коррекции, а первый, второй, третий, четвертый информационные выходы блока 13 формирования и выдачи априорных данных соединены соответственно со вторым, третьим, четвертым, пятым информационными входами первого блока 2, второго блока 8 и третьего блока 15 коррекции, второй информационный выход первого блока 2 коррекции соединен с восьмым информационным входом второго блока 8 коррекции, второй информационный выход второго блока 8 коррекции соединен с восьмым информационным входом третьего блока 15 коррекции, выход которого соединен с первым информационным входом третьего блока 16 формирования суммы, выход которого является выходом устройства и соединен с информационным входом пятого блока 17 формирования матричной функции, выход которого соединен с информационным входом третьей линии задержки 18 выход которой соединен со вторым информационным входом третьего блока 16 формирования суммы, с седьмым информационным входом третьего блока 15 коррекции и с информационным входом шестого блока 19 формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом третьего блока 15 коррекции; первый информационный выход шестого блока 19 формирования матричной функции соединен со вторым информационным входом третьего блока 14 формирования разности, выход которого соединен с первым информационным входом третьего блока 15 коррекции; выход первого блока 20 расчета параметра регуляризации соединен с девятым информационным входом второго блока 8 коррекции, выход которого соединен с первым информационным входом второго блока 9 формирования суммы, выход которого соединен с четвертым информационным входом второго блока 21 расчета параметра регуляризации и с информационным входом третьего блока 10 формирования матричной функции, выход которого соединен с информационным входом второй линии 11 задержки, выход которой соединен со вторым информационным входом второго блока 9 формирования суммы, с седьмым информационным входом второго блока 8 коррекции и с информационным входом четвертого блока 12 формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом блока 8 коррекции; первый информационный выход четвертого блока 12 формирования матричной функции соединен со вторым информационным входом второго блока 7 формирования разности, выход которого соединен с первым информационным входом второго блока 8 коррекции; первый информационный выход первого блока 2 коррекции соединен с первым информационным входом первого блока 3 формирования суммы, выход которого соединен с четвертым информационным входом первого блока 14 расчета параметра регуляризации и с информационным входом первого блока 4 формирования матричной функции, выход которого соединен с информационным входом первой линии 5 задержки, выход которой соединен со вторым информационным входом первого блока 3 формирования суммы, с седьмым информационным входом первого блока 2 коррекции и информационным входом второго блока 6 формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом первого блока 2 коррекции; первый информационный выход второго блока 6 формирования матричной функции соединен со вторым информационным входом блока 1 формирования разности, выход которого соединен с первым информационным входом первого блока 2 коррекции; первый информационный вход первого блока 1 формирования разности, первый информационный вход второго блока 7 формирования разности и первый информационный вход третьего блока 14 формирования разности, а также первый информационный вход первого блока 20 расчета параметра регуляризации и первый информационный вход второго блока 21 расчета параметра регуляризации являются входами устройства.
Первый и четвертый информационные выходы блока 13 формирования и выдачи априорных данных соединены с третьим и четвертым информационными входами блока 2.3 формирования произведения (фиг.3); информационный выход первого блока 1 формирования разности соединен с первым информационным входом блока 2.3 формирования произведения; второй информационный выход второго блока 6 формирования матричной функции соединен с информационным входом блока 2.1 формирования частных производных, выход которого соединен с информационным входом блока 2.2 транспонирования матричной функции, выход которого соединен со вторым информационным входом блока 2.3, выход которого соединен с первым информационным входом блока 2.4 расчета точностных характеристик, выход которого соединен с первым информационным входом блока 2.5 формирования произведения, выход которого является выходом первого блока 2 коррекции; информационный выход линии задержки 5 (фиг.2) соединен со вторым информационным входом блока 2.4 расчета точностных характеристик; второй и третий выходы блока 13 формирования и выдачи априорных данных соединены с третьим и четвертым информационными входами блока 2.4 расчета точностных характеристик; выход блока 2.3 формирования произведения соединен со вторым информационным входом блока 2.5 формирования произведения и вторым информационным входом блока 8.4 формирования суммы (фиг.4).
Информационный выход второго блока 7 формирования разности соединен с первым информационным входом блока 8.3 формирования произведения (фиг.4). Первый информационный выход блока 13 формирования выдачи априорных данных соединен с третьим информационным входом блока 8.3 формирования произведения; выход блока 14.48 соединен со вторым информационным входом блока 8.3 формирования произведения; второй информационный выход четвертого блока 12 формирования матричной функции соединен с первым информационным входом блока 8.1 формирования частных производных, выход которого соединен с информационным входом блока 8.2 транспонирования матричной функции, выход которого соединен с четвертым информационным входом блока 8.3, выход которого соединен с первым информационным входом блока 8.4 формирования суммы, второй информационный вход которого соединен с информационным выходом блока 2.3 (фиг.3), выход блока 8.4 формирования суммы соединен с первым информационным выходом блока 8.5, а также со вторым информационным выходом блока 8.6 формирования произведения; третий и четвертый информационные выходы блока 13 формирования выдачи априорных данных соединены со вторым и третьим информационными входами блока 8.5 расчета точностных характеристик; информационный выход линии задержки 11 соединен с четвертым информационным входом блока 8.5 расчета точностных характеристик, выход которого соединен с первым информационным входом блока 8.6 формирования произведения, выход которого является выходом второго блока 8 коррекции (фиг.2).
Выход блока 2.3 формирования произведения (фиг.3) соединен с информационным входом блока 27 формирования частных производных (фиг.5), выход которого соединен с информационным входом блока 28 формирования произведения, выход которого соединен с первым информационным входом блока 29 формирования разности, выход которого соединен с информационным входом устройства 30 обращения матриц, выход которого соединен с первым информационным входом блока 31 формирования произведения, выход которого является выходом блока 2.4 (фиг.3) расчета точностных характеристик; четвертый выход блока 13 формирования и выдачи априорных данных соединяется с вторым информационным входом блока 29 формирования разности; выход блока 31 формирования произведения соединен с информационным входом линии 23 задержки, выход которой соединен с третьим информационным входом блока 22 формирования произведения, выход которого соединен со вторым информационным входом блока 26 формирования суммы, выход которого соединен со вторыми информационными входами блоков 28 и 31 формирования произведения; выход первой линии задержки 5 (фиг.2) соединен с информационным входом блока 14 формирования частных производных, выход которого соединен с информационным входом блока 21 транспонирования матриц и первым информационным входом блока 22 формирования произведения, второй информационный вход которого соединен с выходом блока 21; третий информационный выход блока 13 формирования и выдачи априорных данных соединен с информационным входом блока 24 транспонирования матриц и вторым информационным входом блока 25 формирования произведения, первый информационный вход которого соединен с информационным выходом блока 24; выход блока 25 соединен с информационным входом блока 26 формирования суммы.
Блок 8.5 расчета точностных характеристик (фиг.5) имеет структуру и связи, аналогичные блоку 2.4.
Первый и второй информационные выходы блока 13 формирования и выдачи априорных данных соединены с четвертым информационным входом блока 14.3.5 (фиг.7) и информационным входом блока 14.3.6 транспонирования матричной функции, информационный выход которого соединен с третьим информационным входом блока 14.3.5, информационный выход которого соединен с информационным входом блока 14.3.7 транспонирования матричной функции и вторым информационным входом блока 14.3.8 формирования произведения, информационный выход которого является выходом первого блока формирования произведения числителя параметра регуляризации, информационный выход блока 14.3.7 соединен с первым информационным входом блока 14.3.8; первый информационный вход блока 14.3.5 соединен с информационным входом блока 14.3.4, второй информационный вход блока 14.3.5 соединен с информационным выходом блока 14.3.3 транспонирования матричной функции, информационный вход которого соединен с информационным выходом блока 14.3.2 формирования частных производных матричной функции, информационный выход которого в свою очередь соединен с информационным входом блока формирования матричной функции; структура всех блоков формирования произведения числителя параметра регуляризации идентична, они различаются только связями между информационным входом блока 14.3.1 (соединен либо с информационным выходом соответствующей линии задержки, либо первым информационным выходом блока расчета прогноза) и блоком 14.3.6 (информационный вход которого соединен либо со вторым информационным выходом блока 13 формирования и выдачи априорных данных, либо вторым информационным выходом блока расчета прогноза).
Первый информационный вход блока формирования 14.10.1 произведения, который является первым информационным входом первого блока расчета прогноза (фиг.8), соединен с информационным выходом линии задержки, второй информационный вход блока 14.10.1 соединен с пятым информационным выходом блока 13 формирования и выдачи априорных данных, с этим же информационным выходом соединен первый информационный вход блока 14.10.2 формирования суммы и второй информационный выход блока 14.10.5, третий информационный вход блока 14.10.1 соединен с информационным выходом блока 14.10.3 формирования частных производных матричной функции, второй информационный вход которой соединен с пятым информационным входом блока 13 формирования и выдачи априорных данных, а первый информационный вход с информационным первым выходом блока 14.10.4 формирования матричной функции, второй информационный выход которой соединен с первым информационным входом блока 14.10.5 формирования произведения и вторым информационным входом блока 14.10.6 формирования суммы, информационный выход блока 14.10.5 соединен с первым информационным входом блока 14.10.6; информационный выход блока 14.10.1 соединен со вторым информационным входом блока 14.10.2, его информационный выход является вторым информационным выходом блока расчета прогноза и соединен с третьим информационным входом блока 14.3.6 второго блока формирования произведения числителя параметра регуляризации (фиг.2); структура последующих блоков расчета прогноза аналогична, различаются только связями между третьим информационным входом блока 14.3.5 (он соединен либо со вторым информационным входом предыдущего блок прогноза, либо с пятым информационным выходом блока 13 формирования и выдачи априорных данных) и первым информационным входом блока 14.3.1 (он соединен или с информационным выходом линии задержки, или первым информационным выходом предыдущего блока прогноза).
Устройство работает следующим образом (фиг.2). В исходном состоянии в блоке 13 формирования и выдачи априорных данных записаны значения матриц W-1, G, I, а также значения α0, Δt - значение шага дискретизации. Значение оценки информационного процесса в (k+1)-й момент времени 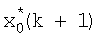 с выхода блока 3 формирования суммы поступает на вход блока 20 вычисления параметра регуляризации и вход блока 4 формирования матричной функции, на остальные входы блока 20 поступают значения y,G,W-1, с выхода блока 4 формирования матричной функции значение
с выхода блока 3 формирования суммы поступает на вход блока 20 вычисления параметра регуляризации и вход блока 4 формирования матричной функции, на остальные входы блока 20 поступают значения y,G,W-1, с выхода блока 4 формирования матричной функции значение 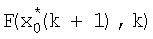 поступает на вход линии задержки 5, с выхода которой значение
поступает на вход линии задержки 5, с выхода которой значение 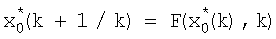 поступает на вход блока 3 формирования суммы, вход блока 2 коррекции и вход блока 6 формирования матричной функции
поступает на вход блока 3 формирования суммы, вход блока 2 коррекции и вход блока 6 формирования матричной функции 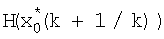 , значение которой с выхода блока 6 поступает на вход блока 2 и на вход блока 1, на выходе блока 1 формируется значение
, значение которой с выхода блока 6 поступает на вход блока 2 и на вход блока 1, на выходе блока 1 формируется значение 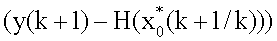 невязки измерения, которое поступает на вход блока 2 коррекции, на остальные входы которого поступают значения α0, G, W-l, I; в блоке 2 формируется произведение матричного коэффициента усиления и невязки измерения, которое суммируется в блоке 3 со значением
невязки измерения, которое поступает на вход блока 2 коррекции, на остальные входы которого поступают значения α0, G, W-l, I; в блоке 2 формируется произведение матричного коэффициента усиления и невязки измерения, которое суммируется в блоке 3 со значением 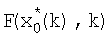 ; на выходе блока 20, начиная с третьего момента времени, формируется значение α1 параметра регуляризации (до этого имеем α1=0.5), которое поступает на вход второго блока 8 коррекции, на остальные входы блока 20 поступают значения α0, G, W-1, I; с одного из выходов блока 2 коррекции значение М0(k+1/k) поступает на вход блока 8 коррекции, в котором формируется значение
; на выходе блока 20, начиная с третьего момента времени, формируется значение α1 параметра регуляризации (до этого имеем α1=0.5), которое поступает на вход второго блока 8 коррекции, на остальные входы блока 20 поступают значения α0, G, W-1, I; с одного из выходов блока 2 коррекции значение М0(k+1/k) поступает на вход блока 8 коррекции, в котором формируется значение
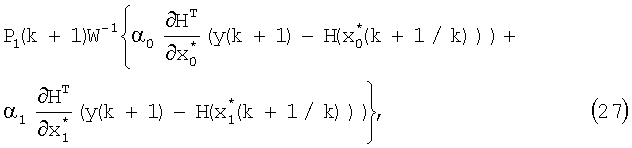
которое поступает на вход блока 9 формирования суммы; значение 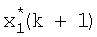 на выходе блока 9 поступает на вход блока 21 вычисления параметра регуляризации и вход блока 10 формирования матричной функции, с выхода блока 10 значение
на выходе блока 9 поступает на вход блока 21 вычисления параметра регуляризации и вход блока 10 формирования матричной функции, с выхода блока 10 значение 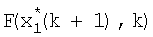 поступает на вход линии задержки 11, на выходе которой формируется значение
поступает на вход линии задержки 11, на выходе которой формируется значение 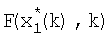 , которое суммируется со значением (27) в блоке 9, на выходе которого формируется значение
, которое суммируется со значением (27) в блоке 9, на выходе которого формируется значение 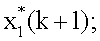 с выхода блока 11 значение
с выхода блока 11 значение 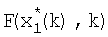 поступает на вход блока 8 коррекции, на вход блока 9 и на вход блока 12 формирования матричной функции, на выходе которого формируется значение
поступает на вход блока 8 коррекции, на вход блока 9 и на вход блока 12 формирования матричной функции, на выходе которого формируется значение 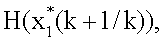 которое подается на вход блока 8 и вход блока 7, на другой вход которого поступает входное колебание; невязка измерения
которое подается на вход блока 8 и вход блока 7, на другой вход которого поступает входное колебание; невязка измерения 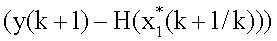 с выхода блока 7 поступает на вход блока 8, на остальные входы которого поступают значения α1, G, W-1, I; с одного из выходов блока 8 коррекции значение M1(k+1/k) поступает на вход блока 15 коррекции, в котором формируется значение
с выхода блока 7 поступает на вход блока 8, на остальные входы которого поступают значения α1, G, W-1, I; с одного из выходов блока 8 коррекции значение M1(k+1/k) поступает на вход блока 15 коррекции, в котором формируется значение
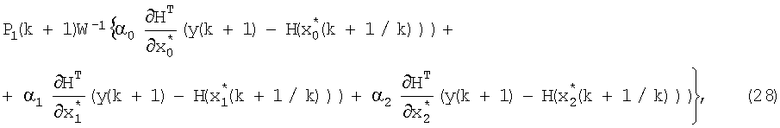
которое поступает на вход блока 16 формирования суммы; значение 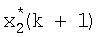 на выходе блока 16 поступает на вход блока 17 формирования матричной функции, с выхода блока 17 значение
на выходе блока 16 поступает на вход блока 17 формирования матричной функции, с выхода блока 17 значение 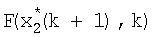 поступает на вход линии задержки 18, на выходе которой формируется значение
поступает на вход линии задержки 18, на выходе которой формируется значение 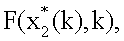 которое суммируется со значением (28) в блоке 16, на выходе которого формируется значение
которое суммируется со значением (28) в блоке 16, на выходе которого формируется значение 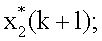 с выхода блока 18 значение
с выхода блока 18 значение 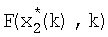 поступает на вход блока 15 коррекции, на вход блока 16 и на вход блока 19 формирования матричной функции, на выходе которого формируется значение
поступает на вход блока 15 коррекции, на вход блока 16 и на вход блока 19 формирования матричной функции, на выходе которого формируется значение 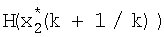 , которое подается на вход блока 15 и вход блока 14, на другой вход которого поступает входное колебание; невязка измерения
, которое подается на вход блока 15 и вход блока 14, на другой вход которого поступает входное колебание; невязка измерения 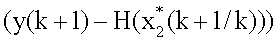 с выхода блока 14 поступает на вход блока 15, на остальные входы которого поступают значения α1, G, W-1, I.
с выхода блока 14 поступает на вход блока 15, на остальные входы которого поступают значения α1, G, W-1, I.
Первый блок 2 коррекции работает следующим образом (фиг.3). Значения матричной функции 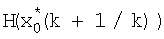 поступают на вход блока 2.1 формирования частных производных, с выхода которого значения
поступают на вход блока 2.1 формирования частных производных, с выхода которого значения 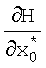 поступают на вход блока транспонирования матричной функции 2.2, с выхода которого значения
поступают на вход блока транспонирования матричной функции 2.2, с выхода которого значения 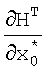 , невязка измерения
, невязка измерения 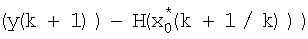
и значения W-1, α0 поступают на входы блока 2.3 формирования произведения, с выхода которого значение M0(k+1/k) поступает на вход блока 2.4 расчета точностных характеристик, на другие входы которого поступают значения G, I, 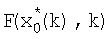 и на выходе которого формируется значение P1(k+1), которое поступает на вход блока 2.5 формирования произведения, на другой вход которого поступает значение M0(k+1/k) с выхода блока 2.3. Выход блока 2.5 является выходом блока 2 коррекции.
и на выходе которого формируется значение P1(k+1), которое поступает на вход блока 2.5 формирования произведения, на другой вход которого поступает значение M0(k+1/k) с выхода блока 2.3. Выход блока 2.5 является выходом блока 2 коррекции.
Второй блок 8 коррекции работает следующим образом (фиг.4). Значение матричной функции 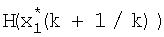 поступает на вход блока 8.1 формирования частных производных, с выхода которого значения
поступает на вход блока 8.1 формирования частных производных, с выхода которого значения 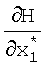 поступают на вход блока транспонирования матричной функции 8.2, с выхода которого значения
поступают на вход блока транспонирования матричной функции 8.2, с выхода которого значения 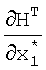 , а также значение невязки измерения
, а также значение невязки измерения 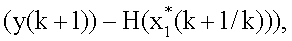 α1, W-1 поступают на вход блока 8.3 формирования произведения, с выхода которого значение
α1, W-1 поступают на вход блока 8.3 формирования произведения, с выхода которого значение 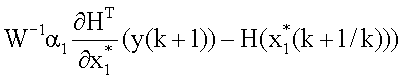 поступает на вход блока 8.4 суммирования, на другой вход которого поступает значение M0(k+1/k); значение
поступает на вход блока 8.4 суммирования, на другой вход которого поступает значение M0(k+1/k); значение
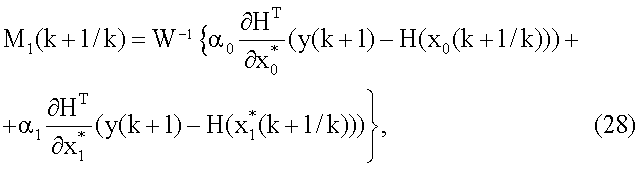
с выхода блока 8.4 поступает на вход блока 8.5 расчета точностных характеристик, на другие входы которого поступают значения G, W-1, 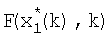 , а на выходе формируется значение P1(k+l), которое умножается на (28) в блоке 8.6 формирования произведения; выход блока 8.6 является выходом блока 8 коррекции. Третий блок 15 коррекции работает аналогично.
, а на выходе формируется значение P1(k+l), которое умножается на (28) в блоке 8.6 формирования произведения; выход блока 8.6 является выходом блока 8 коррекции. Третий блок 15 коррекции работает аналогично.
Первый блок 2.4 расчета точностных характеристик работает следующим образом (фиг.6). Значение матричной функции 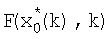 поступает на вход блока 14 формирования частных производных, с выхода которого значение
поступает на вход блока 14 формирования частных производных, с выхода которого значение 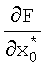 поступает на вход блока 21 транспонирования матричной функции и на вход блока 22 формирования произведения, на вход которого также поступает значение
поступает на вход блока 21 транспонирования матричной функции и на вход блока 22 формирования произведения, на вход которого также поступает значение 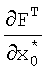 с выхода блока 21 и значение Р0(k) с выхода линии задержки 23, на вход которой с выхода блока 31 формирования произведения, являющегося выходом блока 2.3, поступает значение P0(k+1); значение
с выхода блока 21 и значение Р0(k) с выхода линии задержки 23, на вход которой с выхода блока 31 формирования произведения, являющегося выходом блока 2.3, поступает значение P0(k+1); значение 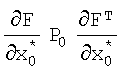 с выхода блока 22 поступает на вход блока 26 формирования суммы, на другой вход которого поступает значение GGT, сформированное в блоке 25 формирования произведения, на вход которого поступает значение G и значение Gт, сформированное в блоке 24 транспонирования матриц, на вход которого также поступает значение G; значение матричной функции
с выхода блока 22 поступает на вход блока 26 формирования суммы, на другой вход которого поступает значение GGT, сформированное в блоке 25 формирования произведения, на вход которого поступает значение G и значение Gт, сформированное в блоке 24 транспонирования матриц, на вход которого также поступает значение G; значение матричной функции
M0(k+l/k) поступает на вход блока 27 формирования частных производных, с выхода которого значение 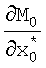 поступает на вход блока 28, на другой вход которого поступает значение P0(k+1/k), сформированное на выходе блока 26; значение
поступает на вход блока 28, на другой вход которого поступает значение P0(k+1/k), сформированное на выходе блока 26; значение 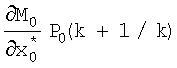 поступает на вход блока 29 формирования разности, на другой вход которого поступает значение I; с выхода блока 29 значение
поступает на вход блока 29 формирования разности, на другой вход которого поступает значение I; с выхода блока 29 значение  поступает на вход устройства 30 обращения матриц, выход которого соединен с входом блока 31 формирования произведения, на другой вход которого поступает значение P0(k+1/k) с выхода блока 26. Блок расчета точностных характеристик 8.5 второго блока коррекции работает аналогичным образом. На выходе блока 8.5 формируется значение P1(k+1).
поступает на вход устройства 30 обращения матриц, выход которого соединен с входом блока 31 формирования произведения, на другой вход которого поступает значение P0(k+1/k) с выхода блока 26. Блок расчета точностных характеристик 8.5 второго блока коррекции работает аналогичным образом. На выходе блока 8.5 формируется значение P1(k+1).
Блок расчета параметра регуляризации работает следующим образом. В исходном состоянии на вход блока расчета параметра регуляризации поступает 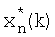 - значение оценки информационного процесса, где k - текущий момент времени, которое соответственно передается на линии задержки 14.2, 14.7, 14.16, 14.29 (фиг.6) и блок формирования матричной функции
- значение оценки информационного процесса, где k - текущий момент времени, которое соответственно передается на линии задержки 14.2, 14.7, 14.16, 14.29 (фиг.6) и блок формирования матричной функции 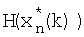 , с выхода которого значение
, с выхода которого значение 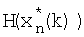 поступает на вход 14.4, 14.12, 14.24 и 14.40 линий задержки; в следующей итерации фильтра на эти же блоки поступает текущее значение оценки информационного процесса, с выходов линий задержки 14.2, 14.7, 14.16, 14.29 и 14.4, 14.12, 14.24, 14.40 на линии задержки 14.8, 14.17, 14.30 и 14.13, 14.25, 14.41 поступают соответственно к-1 значение оценки и матричной функции
поступает на вход 14.4, 14.12, 14.24 и 14.40 линий задержки; в следующей итерации фильтра на эти же блоки поступает текущее значение оценки информационного процесса, с выходов линий задержки 14.2, 14.7, 14.16, 14.29 и 14.4, 14.12, 14.24, 14.40 на линии задержки 14.8, 14.17, 14.30 и 14.13, 14.25, 14.41 поступают соответственно к-1 значение оценки и матричной функции 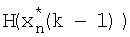 , эти же значения оценок и матричной функции поступают на входы блоков 14.3 формирования произведения
, эти же значения оценок и матричной функции поступают на входы блоков 14.3 формирования произведения
числителя коэффициента регуляризации и блоков 14.5 транспонирования матричной функции, 14.6 формирования произведения; далее на входы линий задержки 14.2, 14.7, 14.16, 14.29 опять поступает текущее значение оценки информационного процесса, с этих линий задержки к-1 значение оценки поступает на 14.8, 14.17, 14.30 линий задержки, с выхода которых к-2 значение оценки информационного процесса поступает дальше на вход блока 14.9 и линий задержки 14.18, 14.31; аналогично и для и 14.4, 14.12, 14.24, 14.40, а также 14.13, 14.25, 14.41 линий задержки, только для матричной функции Н; в результате на n+5 и последующих итерациях 31 будем иметь на выходах линий задержки 14.2, 14.8, 14.18, 14.32 значения к-1, к-2, к-3, к-4 оценок информационного процесса соответственно и на выходах 14.4, 14.13, 14.26, 14.43 линий задержки значения матричной функции для тех же оценок. Эти значения оценок информационного процесса поступают на блоки 14.3, 14.9, 14.19, 14.33 формирования произведения числителя коэффициента регуляризации и 14.10, 14.20, 14.34 формирования прогноза; в блоки 14.3, 14.9, 14.19, 14.33 поступают из 13 блока G, W-1 и у со входа устройства, с выхода этих блоков значения
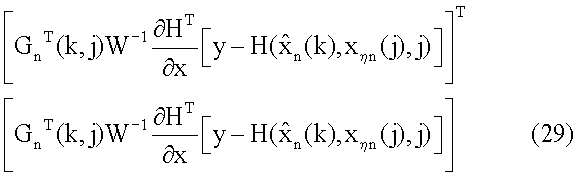
для 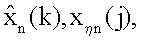 для j=k, поступают на вход блока 14.46 формирования суммы; с выхода 14.10 блока на 14.11 блок поступает значение прогноза для k-1 момента времени, в блок 14.11 поступают значения G, W-1, y, с выхода 14.11 блока на вход 14.46 блока поступает выражение, аналогичное (29), с 14.20 блока в 14.23 блок и 14.21 блок поступает значение прогноза для k-2 момента времени, в блок 14.23 передаются значения G, W-1, y, с 14.23 блока на вход 14.45 блока поступает выражение, аналогичное (29), с выхода блока 14.21 поступает значение прогноза для k-1 момента времени, в блок 14.22 поступают значения G, W-1, у, с выхода 14.22 блока на 14.46 блок поступает выражение, аналогичное (29), на входах 14.34, 14.35, 14.36 блоков имеем
для j=k, поступают на вход блока 14.46 формирования суммы; с выхода 14.10 блока на 14.11 блок поступает значение прогноза для k-1 момента времени, в блок 14.11 поступают значения G, W-1, y, с выхода 14.11 блока на вход 14.46 блока поступает выражение, аналогичное (29), с 14.20 блока в 14.23 блок и 14.21 блок поступает значение прогноза для k-2 момента времени, в блок 14.23 передаются значения G, W-1, y, с 14.23 блока на вход 14.45 блока поступает выражение, аналогичное (29), с выхода блока 14.21 поступает значение прогноза для k-1 момента времени, в блок 14.22 поступают значения G, W-1, у, с выхода 14.22 блока на 14.46 блок поступает выражение, аналогичное (29), на входах 14.34, 14.35, 14.36 блоков имеем 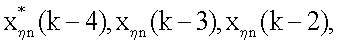 с выходов этих блоков имеем значения для k-3, k-2, k-1 момента времени, которые поступают на блоки 14.38, 14.39, 14.37 соответственно, кроме того, блок 14.36 использует результаты работы 14.35 блока, а 14.35 блок 14.36 блока и, наконец, в 14.34 блок передаются начальные значения, на входы блоков 14.37, 14.38, 14.39 поступают значения G, W-1, y, с выхода блоков 14.37, 14.38, 14.39 в блок 14.46 поступают выражения, аналогичные (29); с линий задержки 14.4, 14.13, 14.26, 14.43 на вход блоков 14.5, 14.14, 14.27, 14.44 транспонирования матричной функции и 14.6, 14.15, 14.28, 14.45 формирования произведения передается
с выходов этих блоков имеем значения для k-3, k-2, k-1 момента времени, которые поступают на блоки 14.38, 14.39, 14.37 соответственно, кроме того, блок 14.36 использует результаты работы 14.35 блока, а 14.35 блок 14.36 блока и, наконец, в 14.34 блок передаются начальные значения, на входы блоков 14.37, 14.38, 14.39 поступают значения G, W-1, y, с выхода блоков 14.37, 14.38, 14.39 в блок 14.46 поступают выражения, аналогичные (29); с линий задержки 14.4, 14.13, 14.26, 14.43 на вход блоков 14.5, 14.14, 14.27, 14.44 транспонирования матричной функции и 14.6, 14.15, 14.28, 14.45 формирования произведения передается 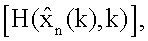 после чего с выхода блоков 14.6, 14.15, 14.28, 14.45 на вход блока 14.45 формирования сумм поступают значения
после чего с выхода блоков 14.6, 14.15, 14.28, 14.45 на вход блока 14.45 формирования сумм поступают значения 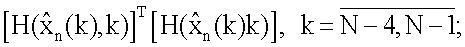 с блока 14.46 в блок 14.47 формирования отношения передается значение
с блока 14.46 в блок 14.47 формирования отношения передается значение 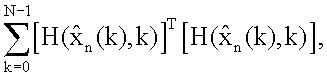 на вход 14.47 блока с 14.45 блока поступает
на вход 14.47 блока с 14.45 блока поступает 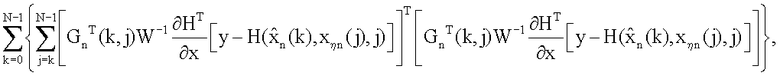 , на выходе блока 14.47 формирования отношения получаем значение коэффициента регуляризации αn+1. Второй блок 21 расчета параметра регуляризации работает аналогично.
, на выходе блока 14.47 формирования отношения получаем значение коэффициента регуляризации αn+1. Второй блок 21 расчета параметра регуляризации работает аналогично.
Первый блок формирования произведения числителя параметра регуляризации 14.3 (фиг.7) работает следующим образом. На вход блока 14.3.1 формирования матричной функции поступает значение оценки информационного процесса 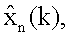 с выхода блока на вход блоков 14.3.2 формирования частных производных матричной функции и блока 14.3.4, далее с выхода блока 14.3.2 значения поступают на вход блока 14.3.3 транспонирования матричной функции, откуда на вход блока 14.3.5 формирования произведения поступает
с выхода блока на вход блоков 14.3.2 формирования частных производных матричной функции и блока 14.3.4, далее с выхода блока 14.3.2 значения поступают на вход блока 14.3.3 транспонирования матричной функции, откуда на вход блока 14.3.5 формирования произведения поступает 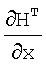 , на другие входы поступают значения GT,W-1 и значение
, на другие входы поступают значения GT,W-1 и значение 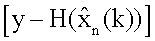 c выхода блока 14.3.4, на один из входов которого поступает у, значение GT поступает на вход блока 14.3.5 с выхода блока 14.3.6 транспонирования матричной функции, на вход которого соответственно с выхода 13 блока поступает значение G; с выхода блока 14.3.5 имеем значение
c выхода блока 14.3.4, на один из входов которого поступает у, значение GT поступает на вход блока 14.3.5 с выхода блока 14.3.6 транспонирования матричной функции, на вход которого соответственно с выхода 13 блока поступает значение G; с выхода блока 14.3.5 имеем значение 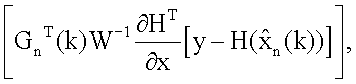 которое поступает соответственно на вход блоков 14.3.7 транспонирования матричной функции и 14.3.8 формирования произведения, в результате на выходе устройства будем иметь значения
которое поступает соответственно на вход блоков 14.3.7 транспонирования матричной функции и 14.3.8 формирования произведения, в результате на выходе устройства будем иметь значения 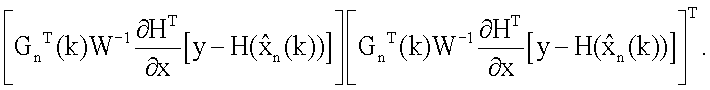
Первый блок расчета прогноза работает следующим образом. На вход блоков 14.10.4 формирования матричной функции и 14.10.3 формирования частных производных поступает значение оценки информационного процесса 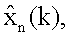 с выхода блока 14.10.4 значение
с выхода блока 14.10.4 значение 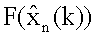 поступает на другой вход блока 14.10.3 и блоков 14.10.5 формирования произведения, 14.10.6 формирования суммы, с выхода блока 14.10.3 значение
поступает на другой вход блока 14.10.3 и блоков 14.10.5 формирования произведения, 14.10.6 формирования суммы, с выхода блока 14.10.3 значение 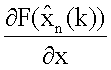 поступает на вход блока 14.10.1 формирования произведения, на другие входы которого поступают значения Gn(k) и Δt, с выхода этого блока на вход блока 14.10.2 формирования суммы передается значение
поступает на вход блока 14.10.1 формирования произведения, на другие входы которого поступают значения Gn(k) и Δt, с выхода этого блока на вход блока 14.10.2 формирования суммы передается значение 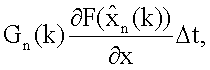
на другой вход блока 10.2 поступает значение Gn(k), в результате на выходе 14.10.2 блока, выход которого является первым выходом блока расчета прогноза, имеем прогноз Gn(j),j=k+1; на второй вход блока 14.10.5 поступает значение Δt, с выхода которого значение 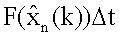 поступает на второй вход блока 14.10.6, выход которого является вторым выходом блока расчета прогноза, с выхода которого имеем xηn(j). Остальные блоки расчета прогноза работают аналогично.
поступает на второй вход блока 14.10.6, выход которого является вторым выходом блока расчета прогноза, с выхода которого имеем xηn(j). Остальные блоки расчета прогноза работают аналогично.
Источники информации
1. А.А.Венгеров, В.А.Щаренский. Прикладные вопросы оптимальной линейной фильтрации. - М.: Энергоиздат, 1982. - 96 с.
2. А.Фарина, Ф.Студер. Цифровая обработка радиолокационной информации. Сопровождение целей. - М.: Радио и связь, 1993. - 118 с.
3. Патент №2209506. Россия. 2003. Цифровой итеративный фильтр. // Костоглотов А.А., Фасоля А.А., Кузнецов А.А., Черемсин А.И., Черных А.С.
4. Костоглотов А.А. Синтез интеллектуальных измерительных процедур на основе принципа регуляризации А.Н.Тихонова. // Измерительная техника, №1, 2001. С.8-12.
5. Костоглотов А.А. Метод последовательных приближений в теории фильтрации. // Автоматика и вычислительная техника, №3, 2000. С.53-63.
6. Костоглотов А.А., Кузнецов А.А. Синтез интеллектуальной измерительной процедуры на основе метода минимальных ошибок. // Измерительная техника, №7, 2005. С.8-13.
7. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. - М.: Наука, 1986. - 288 с.
8. Васильев Ф.П. Методы решения экстремальных задач. - М.: Наука, 1981. - 106 с.
9. Костоглотов А.А. Цифровая интеллектуальная измерительная процедура. // Измерительная техника, №7, 2002. С.16-21.
| название | год | авторы | номер документа |
|---|---|---|---|
| ЦИФРОВОЙ ИНТЕЛЛЕКТУАЛЬНЫЙ РЕКУРСИВНЫЙ ФИЛЬТР | 2007 |
|
RU2357357C2 |
| ЦИФРОВОЙ ИНТЕЛЛЕКТУАЛЬНЫЙ МНОГОКАСКАДНЫЙ ФИЛЬТР | 2010 |
|
RU2436228C1 |
| ЦИФРОВОЙ МНОГОИТЕРАЦИОНАЛЬНЫЙ ФИЛЬТР | 2011 |
|
RU2452080C1 |
| ЦИФРОВОЙ РЕКУРСИВНЫЙ ФИЛЬТР | 2003 |
|
RU2257667C2 |
| УСТРОЙСТВО ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ ДИНАМИЧЕСКИХ СИСТЕМ НА ОСНОВЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ | 2011 |
|
RU2464615C1 |
| Устройство идентификации параметров динамических звеньев информационно-управляющих систем | 2014 |
|
RU2632681C2 |
| Устройство оценки параметров с использованием априорной информации в форме интеграла действия | 2016 |
|
RU2657477C1 |
| Экстраполятор с адаптацией по целевому функционалу | 2021 |
|
RU2780197C1 |
| Устройство идентификации параметров акселерометра | 2014 |
|
RU2628279C2 |
| УСТРОЙСТВО КОНТУРА ФАЗОВОЙ АВТОПОДСТРОЙКИ ЧАСТОТЫ С ОБРАТНОЙ СВЯЗЬЮ НА ОСНОВЕ ОБЪЕДИНЕННОГО ПРИНЦИПА МАКСИМУМА | 2013 |
|
RU2547635C1 |
Изобретение относится к цифровой вычислительной технике и может быть использовано в системах цифровой обработки сигналов для решения задач оптимальной нелинейной фильтрации. Техническим результатом является повышение точности оценки параметров информационного процесса в измерительных системах. Устройство содержит шесть блоков формирования матричных функций, три блока коррекции, три блока формирования разности, три блока формирования суммы, три линии задержки, блок формирования и выдачи априорных данных, два блока расчета параметра регуляризации. 8 ил.
Цифровой интеллектуальный итеративный фильтр, содержащий первый, второй и третий блоки формирования разности, первый, второй и третий блоки коррекции, блок формирования и выдачи априорных данных, первый, второй и третий блоки формирования суммы, первый, второй, третий, четвертый, пятый и шестой блоки формирования матричных функций, первую, вторую и третью линии задержки, при этом первый, второй, третий и четвертый выходы блока формирования и выдачи априорных данных соединены соответственно со вторым, третьим, четвертым и пятым информационным входами первого, второго и третьего блока коррекции, первый информационный выход первого блока коррекции соединен с первым информационным входом первого блока формирования суммы, выход которого соединен с информационным входом первого блока формирования матричной функции, выход первого блока формирования матричной функции соединен с информационным входом первой линии задержки, выход которой соединен со вторым информационным входом первого блока формирования суммы, с седьмым информационным входом первого блока коррекции и с информационным входом второго блока формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом первого блока коррекции, первый информационный выход второго блока формирования матричной функции соединен со вторым информационным входом первого блока формирования разности, выход которого соединен с первым информационным входом первого блока коррекции, второй информационный выход первого блока коррекции соединен с восьмым информационным входом второго блока коррекции, первый информационный выход которого соединен с первым информационным входом второго блока формирования суммы, выход которого соединен с информационным входом третьего блока формирования матричной функции, выход третьего блока формирования матричной функции соединен с информационным входом второй линии задержки, выход которой соединен со вторым информационным входом второго блока формирования суммы, седьмым информационным входом второго блока коррекции и с информационным входом четвертого блока формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом второго блока коррекции, первый информационный выход четвертого блока формирования матричной функции соединен со вторым информационным входом второго блока формирования разности, выход которого соединен с первым информационным входом второго блока коррекции, второй информационный выход второго блока коррекции соединен с восьмым информационным входом третьего блока коррекции, первый информационный выход которого соединен с первым информационным входом третьего блока формирования суммы, выход которого является выходом устройства и соединен с информационным входом пятого блока формирования матричной функции, выход которого соединен с информационным входом третьей линии задержки, выход которой соединен со вторым информационным входом третьего блока формирования суммы, седьмым информационным входом третьего блока коррекции и с информационным входом шестого блока формирования матричной функции, второй информационный выход которого соединен с шестым информационным входом третьего блока коррекции, первый информационный выход шестого блока формирования матричной функции соединен со вторым информационным входом третьего блока формирования разности, выход которого соединен с первым информационным входом третьего блока коррекции, первый информационный вход первого блока формирования разности, первый информационный вход второго блока формирования разности, первый информационный вход третьего блока формирования разности являются входами устройства, отличающийся тем, что в него введены первый и второй блоки расчета параметра регуляризации, первые информационные входы которых являются входами устройства, третий, второй и пятый информационные входы первого и второго блоков расчета параметра регуляризации соединены соответственно с первым, вторым и пятым выходами блока формирования и выдачи априорных данных, четвертый информационный вход первого блока расчета параметра регуляризации соединен с выходом первого блока формирования суммы, четвертый информационный вход второго блока расчета параметра регуляризации соединен с выходом второго блока формирования суммы, выходы первого и второго блоков расчета параметра регуляризации соединены с девятыми входами соответственно второго и третьего блока коррекции.
| ЦИФРОВОЙ РЕКУРСИВНЫЙ ФИЛЬТР | 2003 |
|
RU2257667C2 |
| ЦИФРОВОЙ ИТЕРАТИВНЫЙ ФИЛЬТР | 2001 |
|
RU2209506C2 |
| Цифровой рекурсивный фильтр | 1984 |
|
SU1188856A1 |
| Цифровой рекурсивный фильтр | 1985 |
|
SU1302420A1 |
| Бесколесный шариковый ход для железнодорожных вагонов | 1917 |
|
SU97A1 |
| US 4893264 А, 09.01.1990. | |||
Авторы
Даты
2009-07-20—Публикация
2007-11-16—Подача