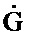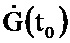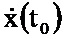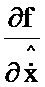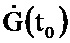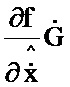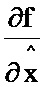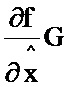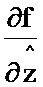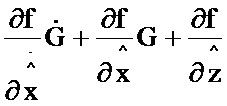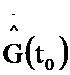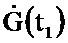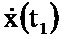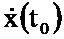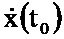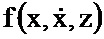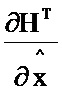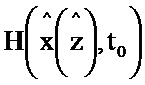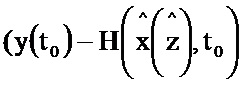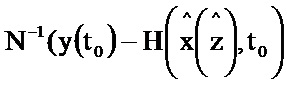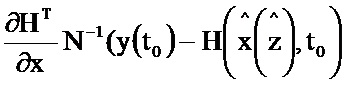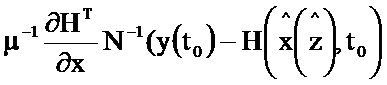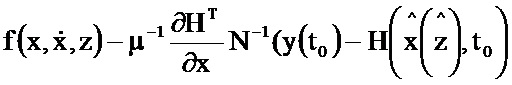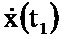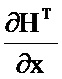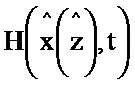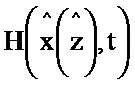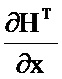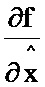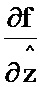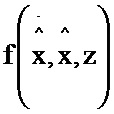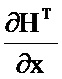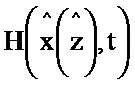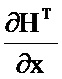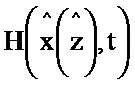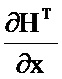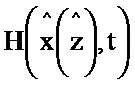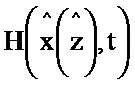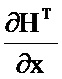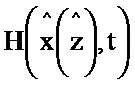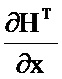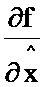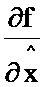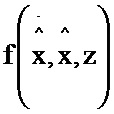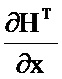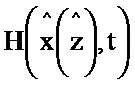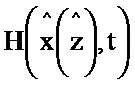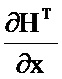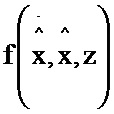Изобретение относится к измерительной технике и предназначено для определения параметров динамических звеньев информационно-управляющих систем и может быть использовано для уточнения динамики модели конкретного динамического звена в реальном масштабе времени.
Известно устройство идентификации параметров динамических систем, в основе которого лежит фильтр Калмана [1]. Его эффективное функционирование возможно в случае априорной определенности законов распределения внешних воздействий, что является существенным недостатком.
Наиболее близким по технической сущности к заявленному изобретению можно отнести устройство идентификации параметров динамических систем на основе вариационных принципов [2]. Однако известное устройство имеет сложную схемную реализацию, что объясняется задействованием функциональных блоков одновременно для реализации всех четырех уравнений алгоритма идентификации, что приводит к последовательной обработке данных и как следствие уменьшению быстродействия в процессе идентификации указанным устройством.
Цель изобретения - увеличить быстродействие в процессе идентификации параметров динамических звеньев информационно-управляющих систем.
Указанный технический результат достигается за счет декомпозиции уравнений идентификации на подсистемы, каждая из которых реализуется параллельно и отдельными блоками в составе устройства. Устройство идентификации параметров сообщений информационно-управляющих систем содержит следующие блоки: первый блок формирования функции z, второй блок формирования функции Р, третий блок формирования функции G, четвертый блок формирования функции х, пятый блок формирования функции  , шестой блок формирования функции
, шестой блок формирования функции 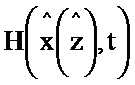 , седьмой блок формирования функции
, седьмой блок формирования функции 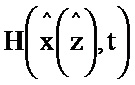 , восьмой блок формирования функции
, восьмой блок формирования функции  , девятый блок формирования функции
, девятый блок формирования функции 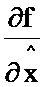 , десятый блок формирования функции
, десятый блок формирования функции 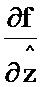 , одиннадцатый блок формирования функции
, одиннадцатый блок формирования функции 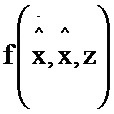 , двенадцатый блок формирования функции
, двенадцатый блок формирования функции  и тринадцатый блок формирования функции
и тринадцатый блок формирования функции 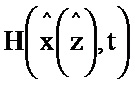 ; первый, второй, третий, четвертый, пятый, шестой, седьмой, восьмой, девятый, десятый, одиннадцатый, двенадцатый, тринадцатый, четырнадцатый, пятнадцатый и шестнадцатый блоки умножения; первый и второй блоки транспонирования; первый, второй, третий, четвертый и пятый блоки формирования разности; первый, второй, третий, четвертый, пятый и шестой блоки интегрирования; первый блок дифференцирования по ∂х; первый блок формирования суммы.
; первый, второй, третий, четвертый, пятый, шестой, седьмой, восьмой, девятый, десятый, одиннадцатый, двенадцатый, тринадцатый, четырнадцатый, пятнадцатый и шестнадцатый блоки умножения; первый и второй блоки транспонирования; первый, второй, третий, четвертый и пятый блоки формирования разности; первый, второй, третий, четвертый, пятый и шестой блоки интегрирования; первый блок дифференцирования по ∂х; первый блок формирования суммы.
Сущность изобретения поясняется фиг. 1-фиг. 5, где представлены: первый, второй, третий и четвертый блоки формирования функций z, P, G, х соответственно.
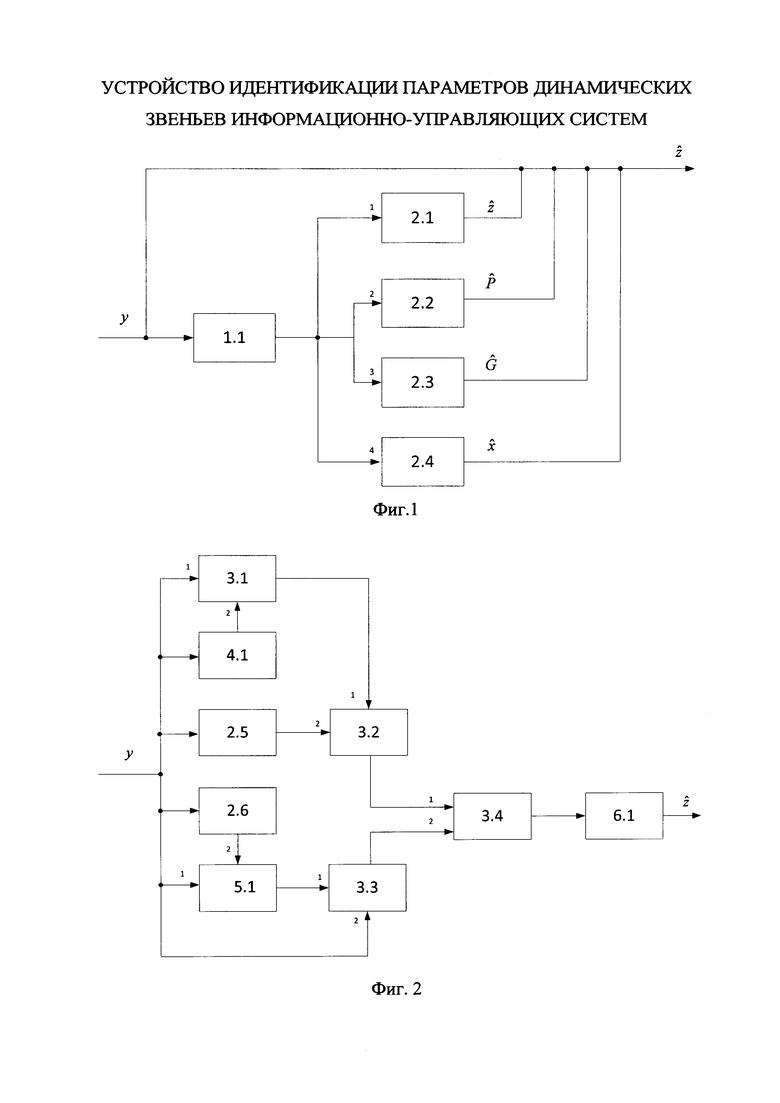
На фигуре 1 представлена система функций z, P, G, х, формирующих процедуру идентификации, которая содержит: первый блок хранения констант 1.1; первый блок формирования функции z 2.1; второй блок формирования функции Р 2.2; третий блок формирования функции G 2.3; четвертый блок формирования функции х 2.4. При этом на информационный вход первого блока хранения констант, который является входом устройства, поступает значение наблюдаемой величины, первый информационный выход которого соединен с информационным входом первого блока формирования функции z, второй информационный выход соединен с информационным входом второго блока формирования функции Р, третий информационный выход соединен с информационным входом третьего блока формирования функции G, четвертый информационный выход соединен с информационным входом четвертого блока формирования функции х; информационный выход первого блока формирования функции z, который является выходом устройства, соединен с информационным входом первого блока хранения констант; информационные выходы второго, третьего и четвертого блоков формирования функции P, G, x соответственно соединены с информационным входом первого блока хранения констант.
На фигуре 2 представлена структурная схема первого блока формирования функции z, который содержит: первый блок транспонирования 4.1; пятый блок формирования функции  2.5; первый блок умножения 3.1; второй блок умножения 3.2; шестой блок формирования функции
2.5; первый блок умножения 3.1; второй блок умножения 3.2; шестой блок формирования функции 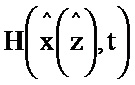 2.6; первый блок формирования разности 5.1; третий блок умножения 3.3; четвертый блок умножения 3.4; первый блок интегрирования 6.1. При этом информационный вход первого блока формирования функции z соединен с первым информационным входом первого блока транспонирования, информационным входом пятого блока формирования функции
2.6; первый блок формирования разности 5.1; третий блок умножения 3.3; четвертый блок умножения 3.4; первый блок интегрирования 6.1. При этом информационный вход первого блока формирования функции z соединен с первым информационным входом первого блока транспонирования, информационным входом пятого блока формирования функции  , информационным входом шестого блока формирования функции
, информационным входом шестого блока формирования функции 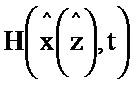 , информационным входом первого блока формирования разности, со вторым информационным входом третьего блока умножения; информационный выход первого блока транспонирования соединен со вторым информационным входом первого блока умножения, выход которого соединен с первым информационным входом второго блока умножения; информационный выход пятого блока формирования функции
, информационным входом первого блока формирования разности, со вторым информационным входом третьего блока умножения; информационный выход первого блока транспонирования соединен со вторым информационным входом первого блока умножения, выход которого соединен с первым информационным входом второго блока умножения; информационный выход пятого блока формирования функции  соединен со вторым информационным входом второго блока умножения; информационный выход шестого блока формирования функции
соединен со вторым информационным входом второго блока умножения; информационный выход шестого блока формирования функции 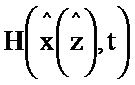 соединен со вторым информационным входом первого блока формирования разности, информационный выход которого соединен с первым информационным входом третьего блока умножения; информационные выходы второго и третьего блоков умножения соединены с первым и вторым информационными входами четвертого блока умножения соответственно, выход которого соединен с информационным входом первого блока интегрирования; с выхода первого блока интегрирования снимается значение
соединен со вторым информационным входом первого блока формирования разности, информационный выход которого соединен с первым информационным входом третьего блока умножения; информационные выходы второго и третьего блоков умножения соединены с первым и вторым информационными входами четвертого блока умножения соответственно, выход которого соединен с информационным входом первого блока интегрирования; с выхода первого блока интегрирования снимается значение  .
.
На фигуре 3 представлена структурная схема второго блока формирования функции Р 2.2, который содержит: пятый блок умножения 3.5; шестой блок умножения 3.6; второй блок транспонирования 4.2; седьмой блок формирования функции 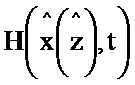 2.7; седьмой блок умножения 3.7; восьмой блок формирования функции
2.7; седьмой блок умножения 3.7; восьмой блок формирования функции  2.8; восьмой блок умножения 3.8; первый блок дифференцирования по ∂х 7.1; девятый блок умножения 3.9; десятый блок умножения 3.10; одиннадцатый блок умножения 3.11; третий блок формирования разности 5.3; второй блок формирования разности 5.2; второй блок интегрирования 6.2. При этом информационный вход блока формирования функции Р соединен с информационными входами седьмого и восьмого блоков формирования функций
2.8; восьмой блок умножения 3.8; первый блок дифференцирования по ∂х 7.1; девятый блок умножения 3.9; десятый блок умножения 3.10; одиннадцатый блок умножения 3.11; третий блок формирования разности 5.3; второй блок формирования разности 5.2; второй блок интегрирования 6.2. При этом информационный вход блока формирования функции Р соединен с информационными входами седьмого и восьмого блоков формирования функций 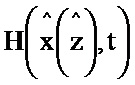 и
и  соответственно, вторым блоком транспонирования, первым и вторым информационными входами пятого и десятого блоков умножения, первым информационным входом шестого блока умножения и второго блока разности, вторым информационным входом седьмого блока умножения; информационный выход седьмого блока формирования функции
соответственно, вторым блоком транспонирования, первым и вторым информационными входами пятого и десятого блоков умножения, первым информационным входом шестого блока умножения и второго блока разности, вторым информационным входом седьмого блока умножения; информационный выход седьмого блока формирования функции 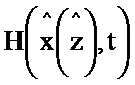 соединен со вторым информационным входом второго блока формирования разности, выход которого соединен с первым информационным входом седьмого блока умножения, выход которого соединен с информационным входом восьмого блока умножения; информационный выход восьмого блока формирования функции
соединен со вторым информационным входом второго блока формирования разности, выход которого соединен с первым информационным входом седьмого блока умножения, выход которого соединен с информационным входом восьмого блока умножения; информационный выход восьмого блока формирования функции  соединен со вторым информационным входом восьмого блока умножения; информационный выход второго блока транспонирования соединен со вторым информационным входом шестого блока умножения, выход которого соединен с первым информационным входом девятого блока умножения; информационный выход десятого блока умножения соединен с первым информационным входом одиннадцатого блока умножения; информационный выход пятого блока умножения соединен с первым информационным входом третьего блока формирования разности; информационный выход восьмого блока умножения соединен с информационным входом первого блока дифференцирования по ∂х, выход которого соединен со вторым информационным входом девятого блока умножения, выход которого соединен со вторым информационным входом одиннадцатого блока умножения, выход которого соединен со вторым информационным входом третьего блока формирования разности, выход которого соединен с информационным входом второго блока интегрирования; с выхода второго блока интегрирования снимается значение P.
соединен со вторым информационным входом восьмого блока умножения; информационный выход второго блока транспонирования соединен со вторым информационным входом шестого блока умножения, выход которого соединен с первым информационным входом девятого блока умножения; информационный выход десятого блока умножения соединен с первым информационным входом одиннадцатого блока умножения; информационный выход пятого блока умножения соединен с первым информационным входом третьего блока формирования разности; информационный выход восьмого блока умножения соединен с информационным входом первого блока дифференцирования по ∂х, выход которого соединен со вторым информационным входом девятого блока умножения, выход которого соединен со вторым информационным входом одиннадцатого блока умножения, выход которого соединен со вторым информационным входом третьего блока формирования разности, выход которого соединен с информационным входом второго блока интегрирования; с выхода второго блока интегрирования снимается значение P.
На фигуре 4 представлена структурная схема третьего блока формирования функции G 2.3, который содержит: девятый блок формирования функции 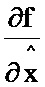 2.9; двенадцатый блок умножения 3.12; десятый блок формирования функции
2.9; двенадцатый блок умножения 3.12; десятый блок формирования функции 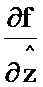 2.10; тринадцатый блок умножения 3.13; первый блок формирования суммы 8.1; третий блок интегрирования 6.3; четвертый блок интегрирования 6.4. При этом информационный вход третьего блока формирования функции G соединен с информационным входом девятого и десятого блоков формирования функции
2.10; тринадцатый блок умножения 3.13; первый блок формирования суммы 8.1; третий блок интегрирования 6.3; четвертый блок интегрирования 6.4. При этом информационный вход третьего блока формирования функции G соединен с информационным входом девятого и десятого блоков формирования функции 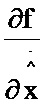 и
и 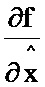 соответственно, вторыми информационными входами двенадцатого и тринадцатого блоков умножения, третьим информационным входом первого блока формирования суммы; информационный выход девятого блока формирования
соответственно, вторыми информационными входами двенадцатого и тринадцатого блоков умножения, третьим информационным входом первого блока формирования суммы; информационный выход девятого блока формирования  соединен с первым информационным входом двенадцатого блока умножения, выход которого соединен с первым информационным входом первого блока формирования суммы; информационный выход десятого блока формирования функции
соединен с первым информационным входом двенадцатого блока умножения, выход которого соединен с первым информационным входом первого блока формирования суммы; информационный выход десятого блока формирования функции 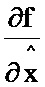 соединен с первым информационным входом тринадцатого блока умножения, выход которого соединен со вторым информационным входом первого блока формирования суммы, информационный выход которого соединен с информационным входом третьего блока интегрирования, выход которого соединен с информационным входом четвертого блока интегрирования; с выхода четвертого блока интегрирования снимается значение G.
соединен с первым информационным входом тринадцатого блока умножения, выход которого соединен со вторым информационным входом первого блока формирования суммы, информационный выход которого соединен с информационным входом третьего блока интегрирования, выход которого соединен с информационным входом четвертого блока интегрирования; с выхода четвертого блока интегрирования снимается значение G.
На фигуре 5 представлена структурная схема четвертого блока формирования функции  2.4, который содержит: одиннадцатый блок формирования функции
2.4, который содержит: одиннадцатый блок формирования функции 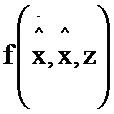 2.11; двенадцатый блок формирования функции
2.11; двенадцатый блок формирования функции  2.12; четвертый блок формирования разности 5.4; тринадцатый блок формирования функции
2.12; четвертый блок формирования разности 5.4; тринадцатый блок формирования функции 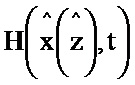 2.13; четырнадцатый блок умножения 3.14; пятнадцатый блок умножения 3.15; шестнадцатый блок умножения 3.16; пятый блок формирования разности 5.5; пятый блок интегрирования 6.5; шестой блок интегрирования 6.6. При этом информационный вход четвертого блока формирования функции
2.13; четырнадцатый блок умножения 3.14; пятнадцатый блок умножения 3.15; шестнадцатый блок умножения 3.16; пятый блок формирования разности 5.5; пятый блок интегрирования 6.5; шестой блок интегрирования 6.6. При этом информационный вход четвертого блока формирования функции  соединен с информационными входами одиннадцатого, двенадцатого и тринадцатого блоков формирования функций
соединен с информационными входами одиннадцатого, двенадцатого и тринадцатого блоков формирования функций 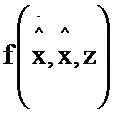 ,
,  ,
, 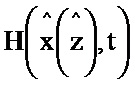 соответственно, первым информационным входом четвертого блока формирования разности, вторыми информационными входами четырнадцатого и шестнадцатого блоков умножения; первый информационный выход тринадцатого блока формирования функции
соответственно, первым информационным входом четвертого блока формирования разности, вторыми информационными входами четырнадцатого и шестнадцатого блоков умножения; первый информационный выход тринадцатого блока формирования функции 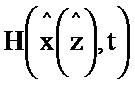 соединен со вторым информационным входом четвертого блока формирования разности, а второй информационный выход соединен с первым информационным входом четырнадцатого блока умножения, выход которого соединен с первым информационным входом пятнадцатого блока умножения; информационный выход двенадцатого блока формирования функции
соединен со вторым информационным входом четвертого блока формирования разности, а второй информационный выход соединен с первым информационным входом четырнадцатого блока умножения, выход которого соединен с первым информационным входом пятнадцатого блока умножения; информационный выход двенадцатого блока формирования функции  соединен со вторым информационным входом пятнадцатого блока умножения, выход которого соединен с первым информационным входом шестнадцатого блока умножения, выход которого соединен со вторым информационным входом пятого блока формирования разности; информационный выход одиннадцатого блока формирования функции
соединен со вторым информационным входом пятнадцатого блока умножения, выход которого соединен с первым информационным входом шестнадцатого блока умножения, выход которого соединен со вторым информационным входом пятого блока формирования разности; информационный выход одиннадцатого блока формирования функции 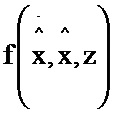 соединен с первым информационным входом пятого блока формирования разности, выход которого соединен с информационным входом пятого блока интегрирования, выход которого соединен с информационным входом шестого блока интегрирования; с выхода шестого блока интегрирования снимается значение
соединен с первым информационным входом пятого блока формирования разности, выход которого соединен с информационным входом пятого блока интегрирования, выход которого соединен с информационным входом шестого блока интегрирования; с выхода шестого блока интегрирования снимается значение  .
.
Пояснить работу устройства позволяют следующие математические выкладки [3-5]:
Пусть уравнение состояния динамической системы известно и имеет следующий вид
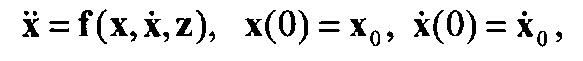
где 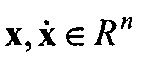 - аналог обобщенной координаты и скорости динамической системы,
- аналог обобщенной координаты и скорости динамической системы,
z∈Rm - вектор неизвестных постоянных параметров,
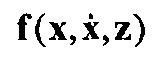 - вектор-функция, непрерывная вместе со своими частными производными,
- вектор-функция, непрерывная вместе со своими частными производными,
n, m - натуральные числа.
Динамика идентифицируемых параметров z описывается уравнением
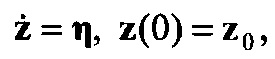
где η∈Rm - вектор неизвестных неслучайных возмущений, удовлетворяющий требованиям физической реализуемости 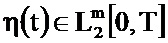 .
.
Уравнение наблюдения имеет вид
y=H(x, t)+n(t),
где y∈Rk - вектор наблюдения,
H(x, t) - непрерывная вместе с частными производными вектор-функция,
k - натуральное число,
n(t) - вектор белого гауссовского шума.
Поставим задачу определения оценки  вектора z из условия минимума функционала невязки
вектора z из условия минимума функционала невязки
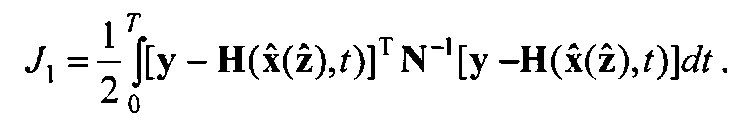
Согласно [5] для рассмотренной постановки задачи получены рекуррентные уравнения последовательной идентификации, которые имеют вид
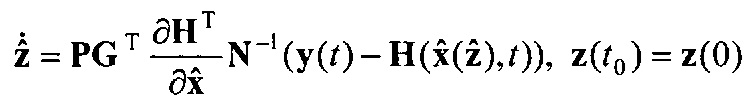
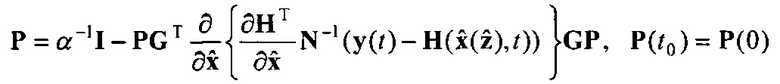
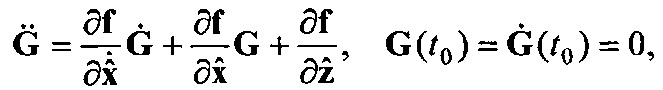
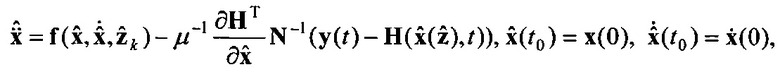
где N - матрица односторонней спектральной плотности шума наблюдения,
G - матрица чувствительности системы по вектору параметров z,
Р - некоторая матрица размера m×m.
Устройство работает следующим образом. В исходном состоянии на информационный вход блока 1.1 поступает значение y(t0) (см. фиг. 1). В блоке 1.1 хранятся начальные значения и константы величин μ-1, x(t0), 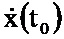 , z(t0), N-1, P(t0), G(t0),
, z(t0), N-1, P(t0), G(t0), 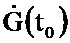 , α-1, I. В момент времени t0 с информационного выхода блока 1.1 соответствующие значения поступают на блоки 2.1, 2.2, 2.3, 2.4 на информационных выходах которых формируются оценки
, α-1, I. В момент времени t0 с информационного выхода блока 1.1 соответствующие значения поступают на блоки 2.1, 2.2, 2.3, 2.4 на информационных выходах которых формируются оценки 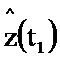 , P(t1), G(t1),
, P(t1), G(t1), 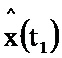 . Полученные оценки с информационных выходов блоков 2.1, 2.2, 2.3, 2.4 поступают на информационный вход блока 1.1.
. Полученные оценки с информационных выходов блоков 2.1, 2.2, 2.3, 2.4 поступают на информационный вход блока 1.1.
В следующий момент времени t1 на информационный вход блока 1.1 поступает значение y(t1), при этом в блоке 1.1 хранятся значения μ-1, x(t1), 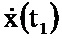 , z(t1), N-1, P(t1), G(t1),
, z(t1), N-1, P(t1), G(t1), 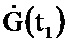 . С информационного выхода блока 1.1 соответствующие значения поступают на блоки 2.1, 2.2, 2.3, 2.4, на информационный выходах которых формируются оценки функций
. С информационного выхода блока 1.1 соответствующие значения поступают на блоки 2.1, 2.2, 2.3, 2.4, на информационный выходах которых формируются оценки функций 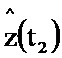 , P(t2), G(t2),
, P(t2), G(t2), 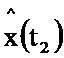 .
.
Описанная процедура идентификации осуществляется до момента времени Т.
Блок формирования функции z работает следующим образом (см. фиг. 2). В момент времени t0 на информационный вход блока 2.1 поступает значение y(t0), μ-1, P(t0), G(t0), x(t0), N-1, z(t0). При этом на первый информационный вход 3.1 поступает значение P(t0), на второй информационный вход блока 3.1 поступает значение GT(t0), на информационный вход блока 4.1 поступает значение G(t0), на информационном выходе блока 3.1 формируется выражение P(t0), GT(t0) и поступает на первый информационный вход блока 3.2; на информационный вход блока 2.5 поступает значение x(t0), на информационном выходе которого формируется функция  и поступает на второй информационный вход блока 3.2, на информационном выходе которого формируется выражение P(t0), G(t0),
и поступает на второй информационный вход блока 3.2, на информационном выходе которого формируется выражение P(t0), G(t0),  и поступает на первый информационный вход блока 3.4; на информационный вход блока 2.3 поступает значение x(t0), z(t0), на информационном выходе которого формируется функция
и поступает на первый информационный вход блока 3.4; на информационный вход блока 2.3 поступает значение x(t0), z(t0), на информационном выходе которого формируется функция 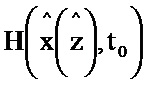 и поступает на второй информационный вход блока 5.1, на первый информационный вход блока 5.1 поступает значение y(t0), на выходе которого формируется выражение
и поступает на второй информационный вход блока 5.1, на первый информационный вход блока 5.1 поступает значение y(t0), на выходе которого формируется выражение 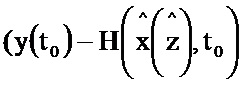 и поступает на первый информационный вход блока 3.3, на второй информационный вход блока 3.3 поступает значение N-1, на информационном выходе которого формируется выражение
и поступает на первый информационный вход блока 3.3, на второй информационный вход блока 3.3 поступает значение N-1, на информационном выходе которого формируется выражение 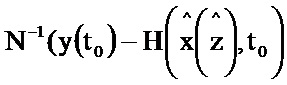 и поступает на второй информационный вход блока 3.4, на информационном выходе которого формируется выражение
и поступает на второй информационный вход блока 3.4, на информационном выходе которого формируется выражение 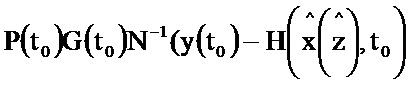 и поступает на информационный вход блока 6.1, на выходе которого формируется оценка z(t0).
и поступает на информационный вход блока 6.1, на выходе которого формируется оценка z(t0).
В следующий момент времени t1 на информационный вход блока 2.1 поступает значение y(t1), P(t1), G(t1), x(t1), N-1 и повторяется описанная процедура формирования оценки  до момента времени Т.
до момента времени Т.
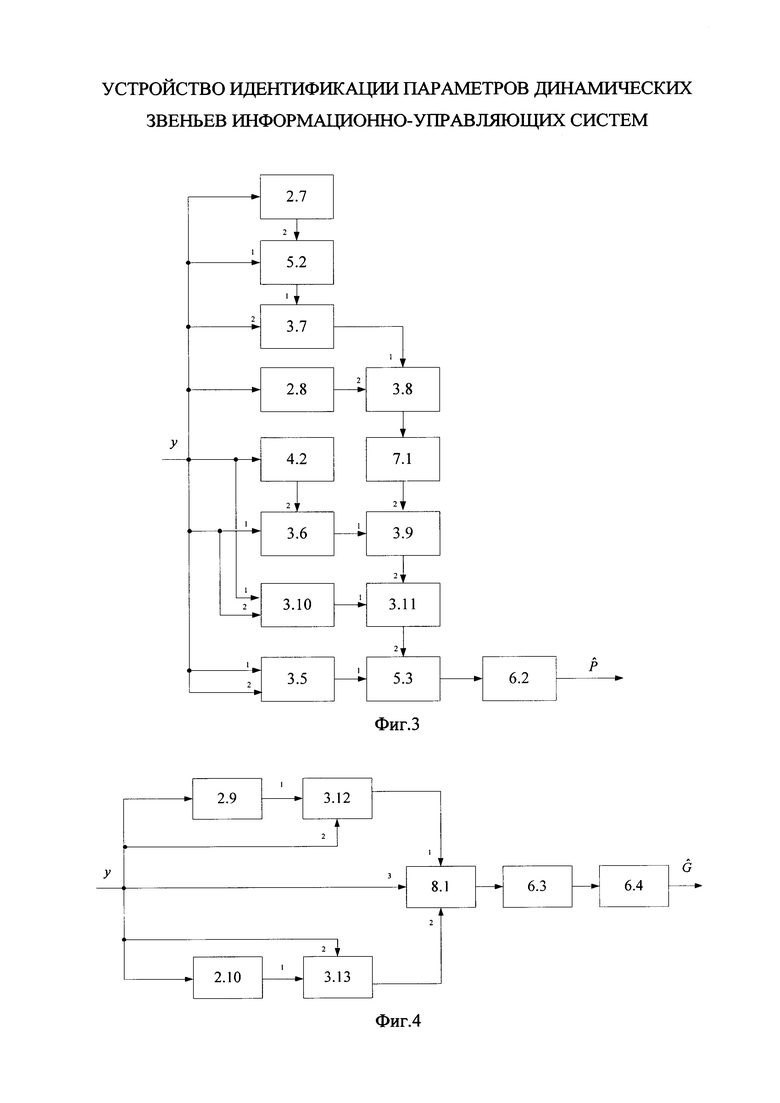
Блок формирования функции Р работает следующим образом (см. фиг. 3). В момент времени t0 на информационный вход блока 2.2 поступает значение y(t0), α-1, I, P(t0), G(t0), x(t0), z(t0). При этом на информационный вход блока 2.7 поступает значение x(t0), z(t0) на информационном выходе которого формируется значение H(x(z),t) и поступает на второй информационный вход блока 5.2, на первый информационный вход блока 5.2 поступает значение y(t0), на информационном выходе которого формируется выражение 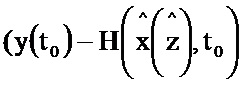 и поступает на первый информационный вход блока 3.7, на второй информационный вход блока 3.7 поступает значение N-1, на выходе которого формируется выражение
и поступает на первый информационный вход блока 3.7, на второй информационный вход блока 3.7 поступает значение N-1, на выходе которого формируется выражение 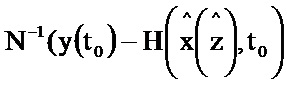 и поступает на первый информационный вход блока 3.8; на информационный вход блока 2.8 поступает значение x(t0), на выходе которого формируется выражение
и поступает на первый информационный вход блока 3.8; на информационный вход блока 2.8 поступает значение x(t0), на выходе которого формируется выражение 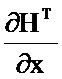 и поступает на второй информационный вход блока 3.8, на выходе которого формируется выражение
и поступает на второй информационный вход блока 3.8, на выходе которого формируется выражение 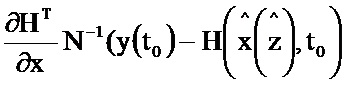 и поступает на информационный вход блока 7.1, на выходе которого формируется значение
и поступает на информационный вход блока 7.1, на выходе которого формируется значение 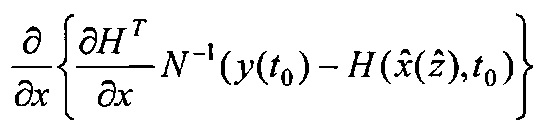 и поступает на второй информационный вход блока 3.9; на информационный вход блока 4.2 и первый информационный вход блока 3.10 поступает значение G(t0); на первый информационный вход блока 3.6 и второй информационный вход блока 3.10 поступает значение P(t0); на информационном выходе блока 4.2 формируется выражение GT(t0) и поступает на второй информационный вход блока 3.6, на выходе которого формируется выражение P(t0)GT(t0) и поступает на первый информационный вход блока 3.9, на выходе которого формируется выражение
и поступает на второй информационный вход блока 3.9; на информационный вход блока 4.2 и первый информационный вход блока 3.10 поступает значение G(t0); на первый информационный вход блока 3.6 и второй информационный вход блока 3.10 поступает значение P(t0); на информационном выходе блока 4.2 формируется выражение GT(t0) и поступает на второй информационный вход блока 3.6, на выходе которого формируется выражение P(t0)GT(t0) и поступает на первый информационный вход блока 3.9, на выходе которого формируется выражение 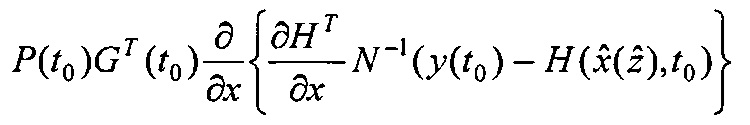 и поступает на второй информационный вход блока 3.11; на информационном выходе блока 3.10 формируется выражение P(t0)G(t0) и поступает на первый информационный вход блока 3.11, на информационном выходе которого формируется выражение
и поступает на второй информационный вход блока 3.11; на информационном выходе блока 3.10 формируется выражение P(t0)G(t0) и поступает на первый информационный вход блока 3.11, на информационном выходе которого формируется выражение 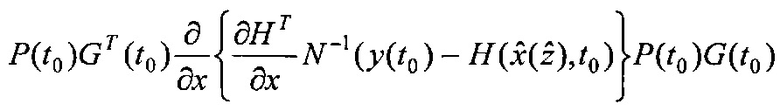 и поступает на второй информационный вход блока 5.3; на первый информационный вход блока 3.5 поступает значение α-1, на второй информационный вход блока 3.5 поступает значение I, на информационном выходе которого формируется выражение α-1I и поступает на первый информационный вход блока 5.3, на информационном выходе которого формируется выражение
и поступает на второй информационный вход блока 5.3; на первый информационный вход блока 3.5 поступает значение α-1, на второй информационный вход блока 3.5 поступает значение I, на информационном выходе которого формируется выражение α-1I и поступает на первый информационный вход блока 5.3, на информационном выходе которого формируется выражение 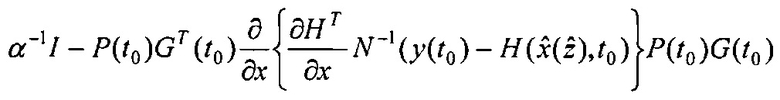 и поступает значение 6.2, на информационном выходе которого формируется оценка P(t0).
и поступает значение 6.2, на информационном выходе которого формируется оценка P(t0).
В следующий момент времени t1 на информационный вход блока 2.2 поступает значение y(t1), α-1, I, P(t1), x(t1), z(t1) и повторяется описанная процедура формирования оценки Р до момента времени Т.
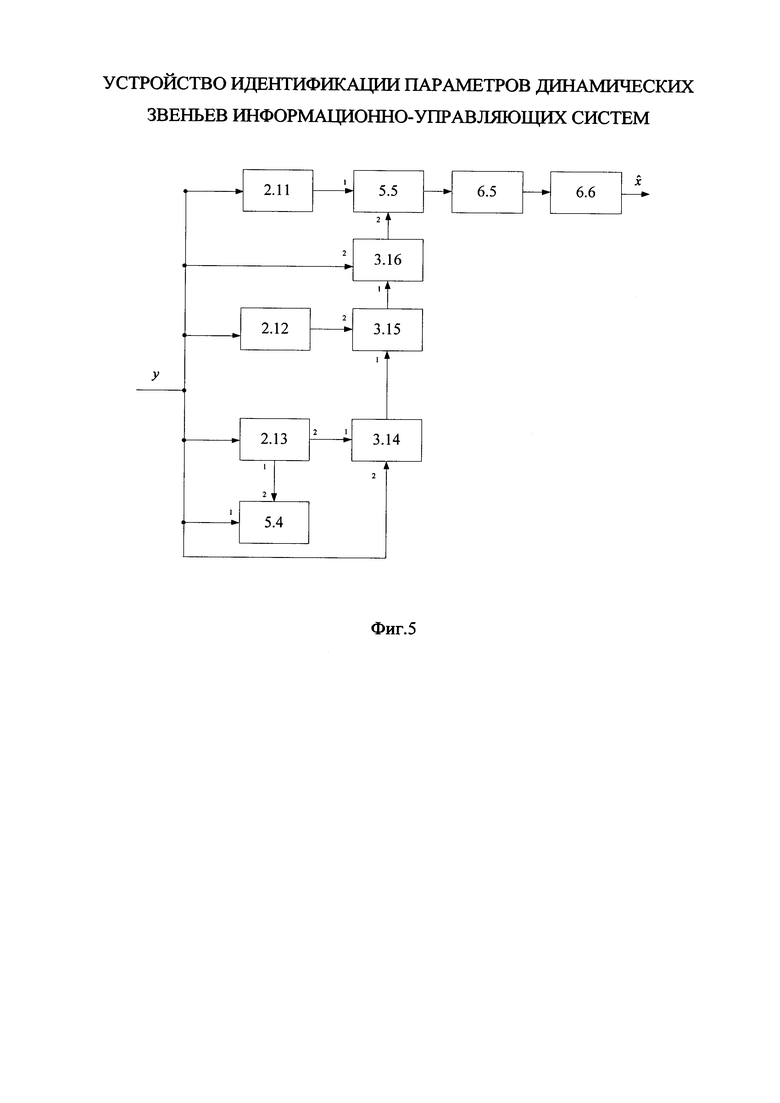
Блок формирования функции 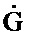 , G работает следующим образом (см. фиг. 4). В момент времени t0 на информационный вход блока 2.3 поступает значение
, G работает следующим образом (см. фиг. 4). В момент времени t0 на информационный вход блока 2.3 поступает значение 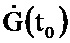 , G(t0),
, G(t0), 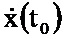 , x(t0), z(t0). При этом на информационный вход блока 2.9 поступают значение
, x(t0), z(t0). При этом на информационный вход блока 2.9 поступают значение  , на выходе которого формируется значение функции
, на выходе которого формируется значение функции 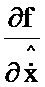 и поступает на первый информационный вход блока 3.12; на второй информационный вход блока 3.12 поступает значение
и поступает на первый информационный вход блока 3.12; на второй информационный вход блока 3.12 поступает значение 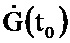 на выходе которого формируется значение
на выходе которого формируется значение 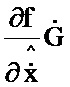 и поступает на первый информационный вход блока 8.1; на информационный вход блока 2.10 поступает значение x(t0), на выходе которого формируется значение функции
и поступает на первый информационный вход блока 8.1; на информационный вход блока 2.10 поступает значение x(t0), на выходе которого формируется значение функции 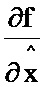 и поступает на первый информационный вход блока 3.13; на второй информационный вход блока 3.13 поступает значение G(t0), на выходе которого формируется значение
и поступает на первый информационный вход блока 3.13; на второй информационный вход блока 3.13 поступает значение G(t0), на выходе которого формируется значение 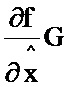 и поступает на второй информационный вход блока 8.1; на третий информационный вход блока 8.1 поступает значение
и поступает на второй информационный вход блока 8.1; на третий информационный вход блока 8.1 поступает значение 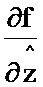 , на выходе которого формируется значение
, на выходе которого формируется значение 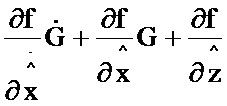 и поступает на информационный вход блока 6.3, на выходе которого формируется значение
и поступает на информационный вход блока 6.3, на выходе которого формируется значение 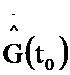 и поступает на информационный вход блока 6.4, на выходе которого формируется значение G(t0).
и поступает на информационный вход блока 6.4, на выходе которого формируется значение G(t0).
В следующий момент времени t1, на информационный вход блока 2.3 поступает значение 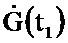 , G(t1),
, G(t1), 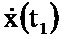 , x(t1), z(t1) и повторяется описанная процедура формирования оценки G до момента времени Т.
, x(t1), z(t1) и повторяется описанная процедура формирования оценки G до момента времени Т.
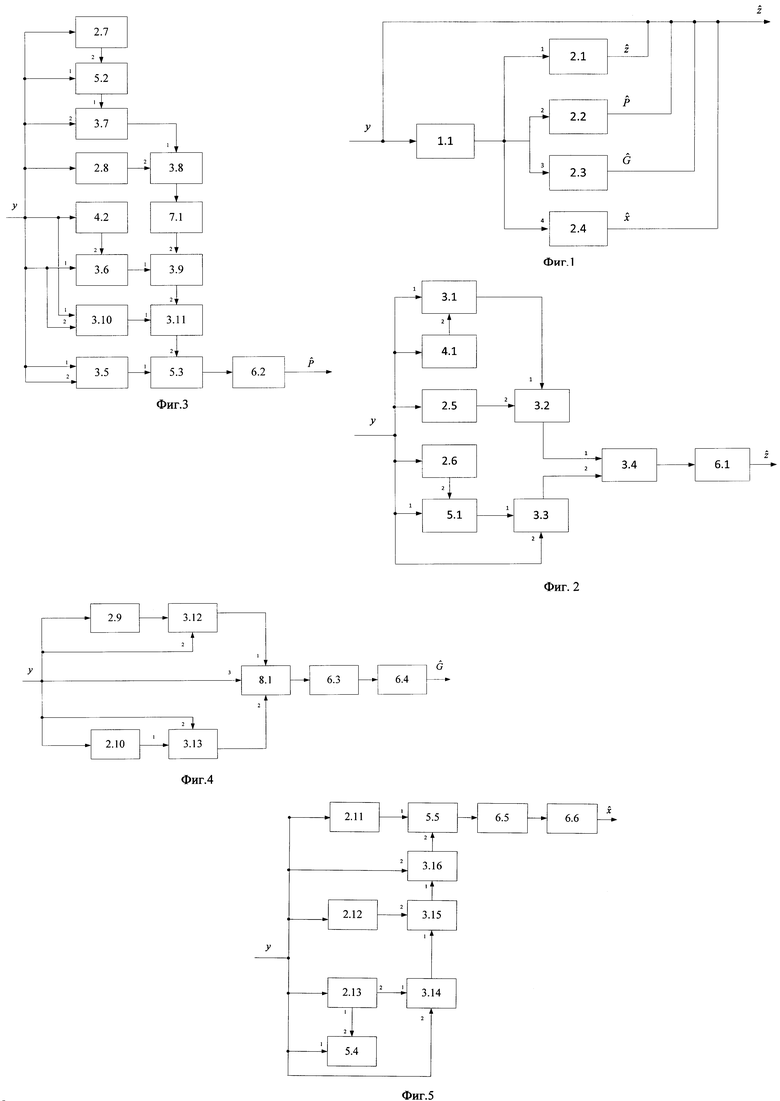
Блок формирования функции х работает следующим образом (см. фиг. 5). В момент времени t0 на информационный вход блока 2.4 поступает значение P(t0), 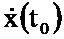 , x(t0), y(t0), μ-1, z(t0), x(t0), N-1. При этом на первый информационный вход блока 2.11 поступают значение
, x(t0), y(t0), μ-1, z(t0), x(t0), N-1. При этом на первый информационный вход блока 2.11 поступают значение 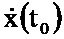 , x(t0), z(t0), на выходе которого формируется значение функции
, x(t0), z(t0), на выходе которого формируется значение функции 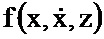 и поступает на первый информационный вход блока 5.5; на информационный вход блока 2.12 поступает значение x(t0) на выходе которого формируется значение
и поступает на первый информационный вход блока 5.5; на информационный вход блока 2.12 поступает значение x(t0) на выходе которого формируется значение 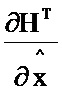 и поступает на второй информационный вход блока 3.15; на информационный вход блока 2.13 поступает значение x(t0), z(t0), t0 на выходе которого формируется значение функции
и поступает на второй информационный вход блока 3.15; на информационный вход блока 2.13 поступает значение x(t0), z(t0), t0 на выходе которого формируется значение функции 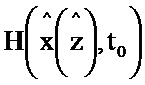 и поступает на второй информационный вход блока 5.4; на первый информационный вход блока 5.4 поступает значение y(t0), на выходе которого формируется значение
и поступает на второй информационный вход блока 5.4; на первый информационный вход блока 5.4 поступает значение y(t0), на выходе которого формируется значение 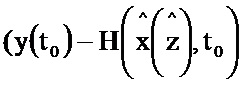 и поступает на первый информационный вход блока 3.14; на второй информационный вход блока 3.14 поступает значение N-1, на выходе которого формируется значение
и поступает на первый информационный вход блока 3.14; на второй информационный вход блока 3.14 поступает значение N-1, на выходе которого формируется значение 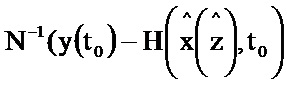 и поступает на первый информационный вход блока 3.15, на выходе которого формируется значение
и поступает на первый информационный вход блока 3.15, на выходе которого формируется значение 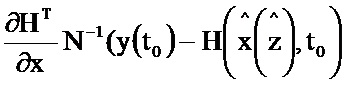 и поступает на первый информационный вход блока 3.16; на второй информационный вход блока 3.16 поступает значение μ-1, на выходе которого формируется значение
и поступает на первый информационный вход блока 3.16; на второй информационный вход блока 3.16 поступает значение μ-1, на выходе которого формируется значение 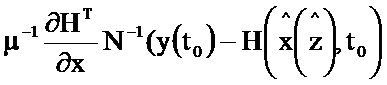 и поступает на второй вход блока 5.5 на выходе которого формируется значение
и поступает на второй вход блока 5.5 на выходе которого формируется значение 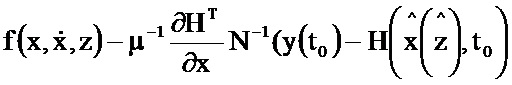 и поступает на вход блока 6.5, с выхода которого полученное значение поступает на вход блока 6.6, на выходе которого формируется оценка x(t1).
и поступает на вход блока 6.5, с выхода которого полученное значение поступает на вход блока 6.6, на выходе которого формируется оценка x(t1).
В следующий момент времени t1 на информационный вход блока 2.5 поступает значение P(t1), 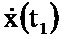 , x(t1), y(t1), μ-1, z(t1), x(t1), N-1 и повторяется описанная процедура формирования оценки х до момента времени Т.
, x(t1), y(t1), μ-1, z(t1), x(t1), N-1 и повторяется описанная процедура формирования оценки х до момента времени Т.
Литература
1. Браммер К., Зиффлинг Г. Фильтр Калмана - Бьюси. М.: Наука, 1982, 210 с.
2. Патент РФ №2464615 от 20.10.2012 г. Устройство идентификации параметров динамических систем на основе вариационных принципов. // Андрашитов Д.С., Костоглотов А.А., Кузнецов А.А., Лазаренко С.В., Сметанникова Н.А.
3. Костоглотов А.А. Метод идентификации параметров голономных систем на основе аппарата асинхронного варьирования. / Изв. РАН. Теория и системы управления. 2003 г. №2. - С. 86-92.
4. Андрашитов Д.С., Костоглотов А.А., Лазаренко С.В. Регуляризированный алгоритм многопараметрической вариационной идентификации динамических систем. // Сервис в России и за рубежом, №8 (27) http://www.rguts.ru/electronic_journal/number27/contents.
5. Андрашитов Д.С., Костоглотов А.А., Лазаренко С.В., Дерябкин И.В. Вариационный метод многопараметрической идентификации динамических систем на основе итерационной регуляризации. // Успехи современной радиоэлектроники. №6, 2012, С. 67-72.
Устройство идентификации параметров динамических звеньев информационно-управляющих систем содержит следующие блоки: первый блок формирования функции z, второй блок формирования функции Р, третий блок формирования функции G, четвертый блок формирования функции х, пятый блок формирования функции 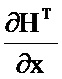 , шестой блок формирования функции
, шестой блок формирования функции 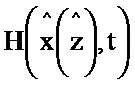 , седьмой блок формирования функции
, седьмой блок формирования функции 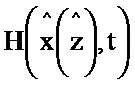 , восьмой блок формирования функции
, восьмой блок формирования функции 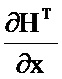 , девятый блок формирования функции
, девятый блок формирования функции 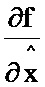 , десятый блок формирования функции
, десятый блок формирования функции 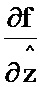 , одиннадцатый блок формирования функции
, одиннадцатый блок формирования функции 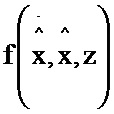 , двенадцатый блок формирования функции
, двенадцатый блок формирования функции 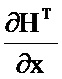 и тринадцатый блок формирования функции
и тринадцатый блок формирования функции 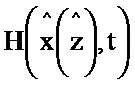 ; первый, второй, третий, четвертый, пятый, шестой, седьмой, восьмой, девятый, десятый, одиннадцатый, двенадцатый, тринадцатый, четырнадцатый, пятнадцатый и шестнадцатый блоки умножения; первый и второй блоки транспонирования; первый, второй, третий, четвертый и пятый блоки формирования разности; первый, второй, третий, четвертый, пятый и шестой блоки интегрирования; первый блок дифференцирования по ∂х; первый блок формирования суммы; при этом первый информационный вход первого блока хранения констант является входом устройства, а информационный выход первого блока формирования функции z является выходом устройства, отличающееся тем, что в устройство введены первый, второй, третий и четвертый блоки формирования функции z, P, G, x, причем информационный вход первого блока формирования функции z соединен с первым информационным входом первого блока транспонирования, информационным входом пятого блока формирования функции
; первый, второй, третий, четвертый, пятый, шестой, седьмой, восьмой, девятый, десятый, одиннадцатый, двенадцатый, тринадцатый, четырнадцатый, пятнадцатый и шестнадцатый блоки умножения; первый и второй блоки транспонирования; первый, второй, третий, четвертый и пятый блоки формирования разности; первый, второй, третий, четвертый, пятый и шестой блоки интегрирования; первый блок дифференцирования по ∂х; первый блок формирования суммы; при этом первый информационный вход первого блока хранения констант является входом устройства, а информационный выход первого блока формирования функции z является выходом устройства, отличающееся тем, что в устройство введены первый, второй, третий и четвертый блоки формирования функции z, P, G, x, причем информационный вход первого блока формирования функции z соединен с первым информационным входом первого блока транспонирования, информационным входом пятого блока формирования функции 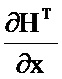 , информационным входом шестого блока формирования функции
, информационным входом шестого блока формирования функции 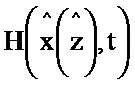 , информационным входом первого блока формирования разности, со вторым информационным входом третьего блока умножения; информационный выход первого блока транспонирования соединен со вторым информационным входом первого блока умножения, выход которого соединен с первым информационным входом второго блока умножения; информационный выход пятого блока формирования функции
, информационным входом первого блока формирования разности, со вторым информационным входом третьего блока умножения; информационный выход первого блока транспонирования соединен со вторым информационным входом первого блока умножения, выход которого соединен с первым информационным входом второго блока умножения; информационный выход пятого блока формирования функции 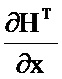 соединен со вторым информационным входом второго блока умножения; информационный выход шестого блока формирования функции
соединен со вторым информационным входом второго блока умножения; информационный выход шестого блока формирования функции 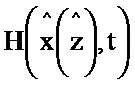 соединен со вторым информационным входом первого блока формирования разности, информационный выход которого соединен с первым информационным входом третьего блока умножения; информационные выходы второго и третьего блоков умножения соединены с первым и вторым информационными входами четвертого блока умножения соответственно, выход которого соединен с информационным входом первого блока интегрирования; с выхода первого блока интегрирования снимается значение
соединен со вторым информационным входом первого блока формирования разности, информационный выход которого соединен с первым информационным входом третьего блока умножения; информационные выходы второго и третьего блоков умножения соединены с первым и вторым информационными входами четвертого блока умножения соответственно, выход которого соединен с информационным входом первого блока интегрирования; с выхода первого блока интегрирования снимается значение  ; информационный вход блока формирования функции Р соединен с информационными входами седьмого и восьмого блоков формирования функций
; информационный вход блока формирования функции Р соединен с информационными входами седьмого и восьмого блоков формирования функций 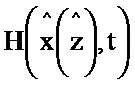 и
и 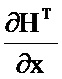 соответственно, вторым блоком транспонирования, первым и вторым информационными входами пятого и десятого блоков умножения, первым информационным входом шестого блока умножения и второго блока разности, вторым информационным входом седьмого блока умножения; информационный выход седьмого блока формирования функции
соответственно, вторым блоком транспонирования, первым и вторым информационными входами пятого и десятого блоков умножения, первым информационным входом шестого блока умножения и второго блока разности, вторым информационным входом седьмого блока умножения; информационный выход седьмого блока формирования функции 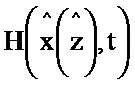 соединен со вторым информационным входом второго блока формирования разности, выход которого соединен с первым информационным входом седьмого блока умножения, выход которого соединен с информационным входом восьмого блока умножения; информационный выход восьмого блока формирования функции
соединен со вторым информационным входом второго блока формирования разности, выход которого соединен с первым информационным входом седьмого блока умножения, выход которого соединен с информационным входом восьмого блока умножения; информационный выход восьмого блока формирования функции 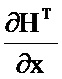 соединен со вторым информационным входом восьмого блока умножения; информационный выход второго блока транспонирования соединен со вторым информационным входом шестого блока умножения, выход которого соединен с первым информационным входом девятого блока умножения; информационный выход десятого блока умножения соединен с первым информационным входом одиннадцатого блока умножения; информационный выход пятого блока умножения соединен с первым информационным входом третьего блока формирования разности; информационный выход восьмого блока умножения соединен с информационным входом первого блока дифференцирования по ∂х, выход которого соединен со вторым информационным входом девятого блока умножения, выход которого соединен со вторым информационным входом одиннадцатого блока умножения, выход которого соединен со вторым информационным входом третьего блока формирования разности, выход которого соединен с информационным входом второго блока интегрирования; с выхода второго блока интегрирования снимается значение Р; информационный вход третьего блока формирования функции G соединен с информационным входом девятого и десятого блоков формирования функции
соединен со вторым информационным входом восьмого блока умножения; информационный выход второго блока транспонирования соединен со вторым информационным входом шестого блока умножения, выход которого соединен с первым информационным входом девятого блока умножения; информационный выход десятого блока умножения соединен с первым информационным входом одиннадцатого блока умножения; информационный выход пятого блока умножения соединен с первым информационным входом третьего блока формирования разности; информационный выход восьмого блока умножения соединен с информационным входом первого блока дифференцирования по ∂х, выход которого соединен со вторым информационным входом девятого блока умножения, выход которого соединен со вторым информационным входом одиннадцатого блока умножения, выход которого соединен со вторым информационным входом третьего блока формирования разности, выход которого соединен с информационным входом второго блока интегрирования; с выхода второго блока интегрирования снимается значение Р; информационный вход третьего блока формирования функции G соединен с информационным входом девятого и десятого блоков формирования функции 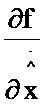 и
и 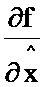 соответственно, вторыми информационными входами двенадцатого и тринадцатого блоков умножения, третьим информационным входом первого блока формирования суммы; информационный выход девятого блока формирования
соответственно, вторыми информационными входами двенадцатого и тринадцатого блоков умножения, третьим информационным входом первого блока формирования суммы; информационный выход девятого блока формирования  соединен с первым информационным входом двенадцатого блока умножения, выход которого соединен с первым информационным входом первого блока формирования суммы; информационный выход десятого блока формирования функции
соединен с первым информационным входом двенадцатого блока умножения, выход которого соединен с первым информационным входом первого блока формирования суммы; информационный выход десятого блока формирования функции 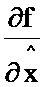 соединен с первым информационным входом тринадцатого блока умножения, выход которого соединен со вторым информационным входом первого блока формирования суммы, информационный выход которого соединен с информационным входом третьего блока интегрирования, выход которого соединен с информационным входом четвертого блока интегрирования; с выхода четвертого блока интегрирования снимается значение G; информационный вход четвертого блока формирования функции
соединен с первым информационным входом тринадцатого блока умножения, выход которого соединен со вторым информационным входом первого блока формирования суммы, информационный выход которого соединен с информационным входом третьего блока интегрирования, выход которого соединен с информационным входом четвертого блока интегрирования; с выхода четвертого блока интегрирования снимается значение G; информационный вход четвертого блока формирования функции  соединен с информационными входами одиннадцатого, двенадцатого и тринадцатого блоков формирования функций
соединен с информационными входами одиннадцатого, двенадцатого и тринадцатого блоков формирования функций 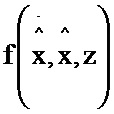 ,
, 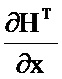 ,
, 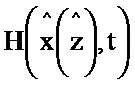 соответственно, первым информационным входом четвертого блока формирования разности, вторыми информационными входами четырнадцатого и шестнадцатого блоков умножения; первый информационный выход тринадцатого блока формирования функции
соответственно, первым информационным входом четвертого блока формирования разности, вторыми информационными входами четырнадцатого и шестнадцатого блоков умножения; первый информационный выход тринадцатого блока формирования функции 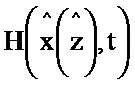 соединен со вторым информационным входом четвертого блока формирования разности, а второй информационный выход соединен с первым информационным входом четырнадцатого блока умножения, выход которого соединен с первым информационным входом пятнадцатого блока умножения; информационный выход двенадцатого блока формирования функции
соединен со вторым информационным входом четвертого блока формирования разности, а второй информационный выход соединен с первым информационным входом четырнадцатого блока умножения, выход которого соединен с первым информационным входом пятнадцатого блока умножения; информационный выход двенадцатого блока формирования функции 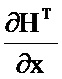 соединен со вторым информационным входом пятнадцатого блока умножения, выход которого соединен с первым информационным входом шестнадцатого блока умножения, выход которого соединен со вторым информационным входом пятого блока формирования разности; информационный выход одиннадцатого блока формирования функции
соединен со вторым информационным входом пятнадцатого блока умножения, выход которого соединен с первым информационным входом шестнадцатого блока умножения, выход которого соединен со вторым информационным входом пятого блока формирования разности; информационный выход одиннадцатого блока формирования функции 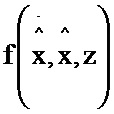 соединен с первым информационным входом пятого блока формирования разности, выход которого соединен с информационным входом пятого блока интегрирования, выход которого соединен с информационным входом шестого блока интегрирования; с выхода шестого блока интегрирования снимается значение
соединен с первым информационным входом пятого блока формирования разности, выход которого соединен с информационным входом пятого блока интегрирования, выход которого соединен с информационным входом шестого блока интегрирования; с выхода шестого блока интегрирования снимается значение  .
.

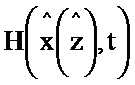
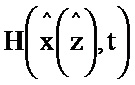

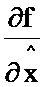
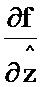
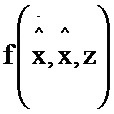

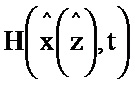

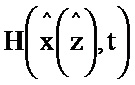

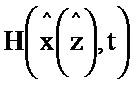

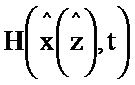

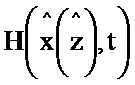

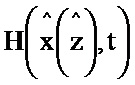

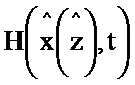

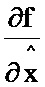
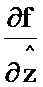

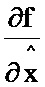

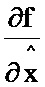

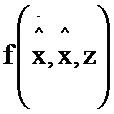

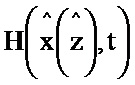

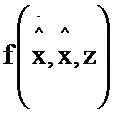

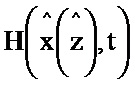
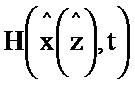

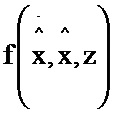

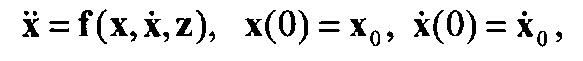
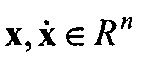 - аналог обобщенной координаты и скорости динамической системы,
- аналог обобщенной координаты и скорости динамической системы,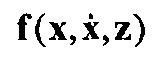 - вектор-функция, непрерывная вместе со своими частными производными,
- вектор-функция, непрерывная вместе со своими частными производными,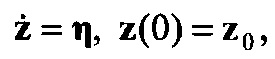
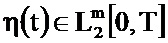

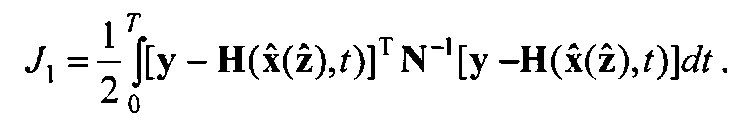
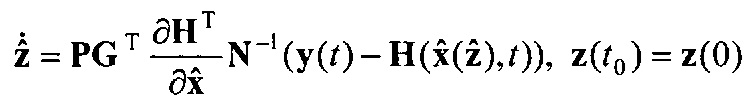
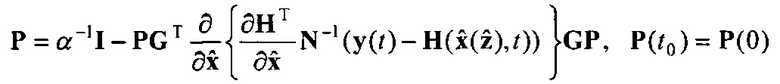
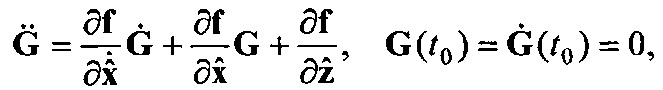
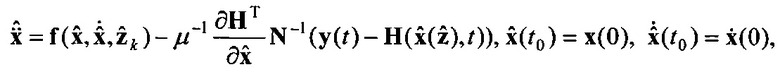
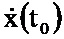
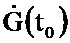
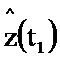
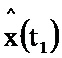
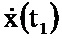
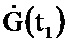
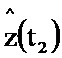
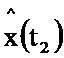


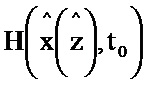
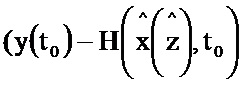
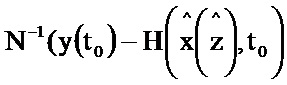
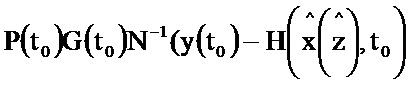

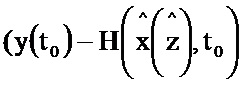
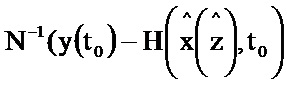
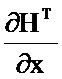
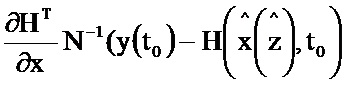
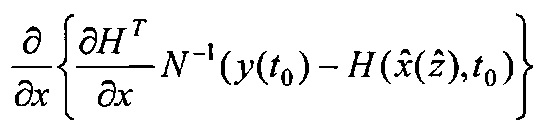 и поступает на второй информационный вход блока 3.9; на информационный вход блока 4.2 и первый информационный вход блока 3.10 поступает значение G(t0); на первый информационный вход блока 3.6 и второй информационный вход блока 3.10 поступает значение P(t0); на информационном выходе блока 4.2 формируется выражение GT(t0) и поступает на второй информационный вход блока 3.6, на выходе которого формируется выражение P(t0)GT(t0) и поступает на первый информационный вход блока 3.9, на выходе которого формируется выражение
и поступает на второй информационный вход блока 3.9; на информационный вход блока 4.2 и первый информационный вход блока 3.10 поступает значение G(t0); на первый информационный вход блока 3.6 и второй информационный вход блока 3.10 поступает значение P(t0); на информационном выходе блока 4.2 формируется выражение GT(t0) и поступает на второй информационный вход блока 3.6, на выходе которого формируется выражение P(t0)GT(t0) и поступает на первый информационный вход блока 3.9, на выходе которого формируется выражение 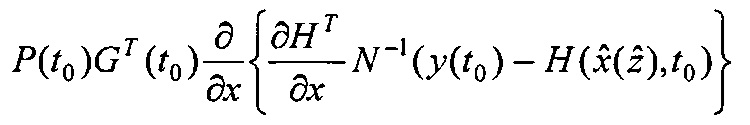 и поступает на второй информационный вход блока 3.11; на информационном выходе блока 3.10 формируется выражение P(t0)G(t0) и поступает на первый информационный вход блока 3.11, на информационном выходе которого формируется выражение
и поступает на второй информационный вход блока 3.11; на информационном выходе блока 3.10 формируется выражение P(t0)G(t0) и поступает на первый информационный вход блока 3.11, на информационном выходе которого формируется выражение 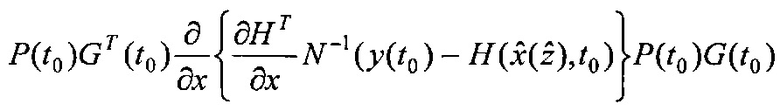 и поступает на второй информационный вход блока 5.3; на первый информационный вход блока 3.5 поступает значение α-1, на второй информационный вход блока 3.5 поступает значение I, на информационном выходе которого формируется выражение α-1I и поступает на первый информационный вход блока 5.3, на информационном выходе которого формируется выражение
и поступает на второй информационный вход блока 5.3; на первый информационный вход блока 3.5 поступает значение α-1, на второй информационный вход блока 3.5 поступает значение I, на информационном выходе которого формируется выражение α-1I и поступает на первый информационный вход блока 5.3, на информационном выходе которого формируется выражение 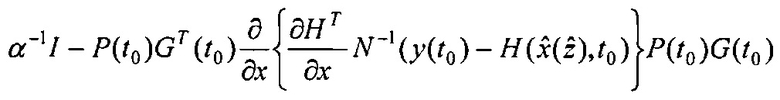 и поступает значение 6.2, на информационном выходе которого формируется оценка P(t0).
и поступает значение 6.2, на информационном выходе которого формируется оценка P(t0).