Область техники, к которой относится изобретение
Настоящее изобретение относится к устройству кодирования с исправлением ошибок и к способу кодирования с исправлением ошибок, используемому в нем, и, в частности, к системе блочного кодирования с исправлением ошибок, в которой информационная серия разделяется на блоки, имеющие предварительно определенную длину, и избыточная серия независимо добавляется к каждому блоку, к способу кодирования с низкой плотностью проверок на четность (НППЧ), используемому в его схеме, и его устройству.
Предшествующий уровень техники
Технологии кодирования с исправлением ошибок, достигающие большого выигрыша от кодирования, были внедрены в системы спутниковой связи и мобильных телекоммуникаций, чтобы соответствовать требованиям, касающимся конструкции системы, таких как снижение потребляемой мощности и размеров антенн. Код с низкой плотностью проверок на четность известен как код с исправлением ошибок, достигающий очень большого выигрыша от кодирования, и использовался в различных системах связи и запоминающих устройствах, таких как магнитные запоминающие устройства.
Код с низкой плотностью проверок на четность не относится к одному конкретному способу кодирования с исправлением ошибок, но он представляет собой общий термин для кодов с исправлением ошибок, отличающихся разреженной проверочной матрицей (большинство элементов в матрице равно 0, и количество элементов «1» очень мало). Посредством выбора разреженной проверочной матрицы и использования способа итеративного декодирования, такого как алгоритм сумма-произведений, код с низкой плотностью проверок на четность может реализовать систему кодирования с исправлением ошибок, способную достигать очень большого выигрыша от кодирования, близкого к теоретическому пределу (например, смотрите непатентные документы 1 и 2).
Технические проблемы, касающиеся кода с низкой плотностью проверок на четность, следующие. Большое количество вычислений, необходимое для способа кодирования (способа вычисления последовательности избыточных битов из последовательности информационных битов), и трудно оценить эффективность характеристик частоты появления ошибок (полученный выигрыш от кодирования) в области, где вероятность ошибок низкая, особенно в области зоны насыщения. В наиболее типичном устройстве кодирования, в котором система кодирования составляется матричным умножением на порождающую матрицу кода, количество требуемых операций Исключающее-ИЛИ пропорционально квадрату длины кода.
Далее, когда устройство кодирования снабжается проверочной матрицей кода, проверочная матрица преобразуется при помощи элементарного матричного преобразования, так что оно частично образует диагональную матрицу, такую как выражение (1), и устройство реализуется при помощи преобразованной проверочной матрицы.
[Выражение 1]
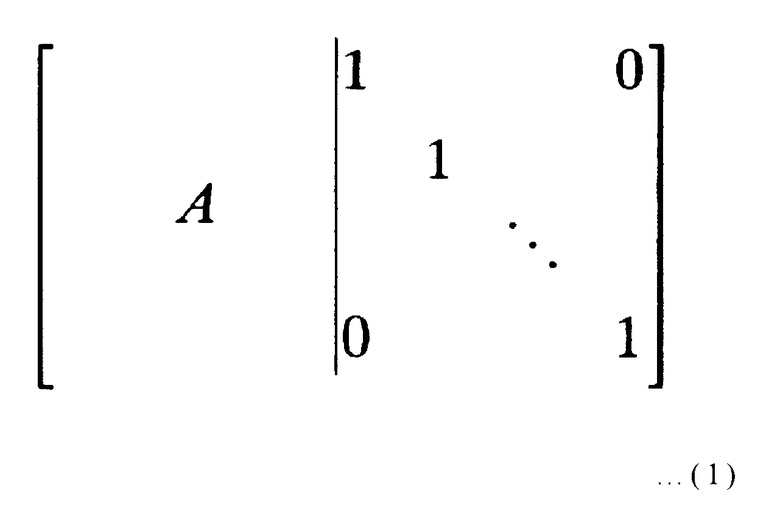
Более конкретно, когда часть, обозначенная А в выражении (1), представляет собой матрицу размера r x k (где r и k представляют положительные целые числа), и с1, с2, …, сk представляют собой серию информационных битов из k битов, каждый бит pi (где i представляет целое число от 1 до r включительно) из строки p1, p2, …, pr избыточных битов из r битов, которые соответствуют серии информационных битов из k битов, может быть получен при помощи следующего выражения (2):
[Выражение 2]
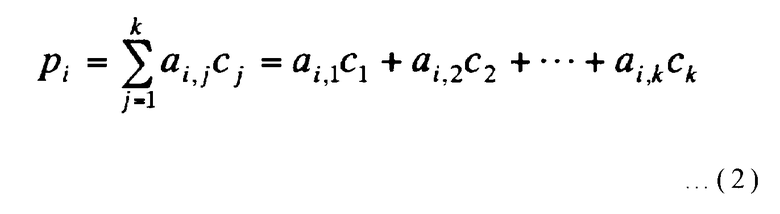
Здесь ai, j в выражении (2) представляет (i, j) элемент матрицы А размером r x k (где i представляет целое число от 1 до r включительно, и j представляет целое число от 1 до k включительно). Поэтому, чтобы образовать устройство кодирования кода с исправлением ошибок, матрица А размером r x k хранится в запоминающем устройстве, таком как память, и операции Исключающее-ИЛИ должны быть выполнены столько раз, чему равно количество «1» в элементах матрицы.
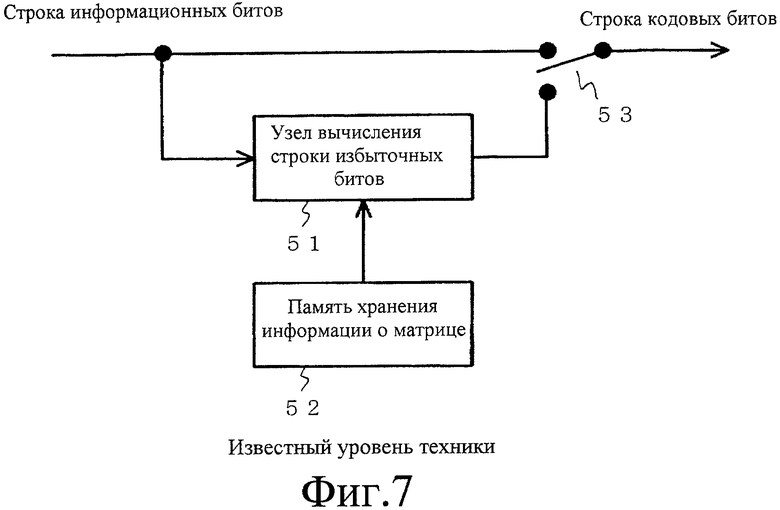
Фиг.7 изображает пример обычного устройства кодирования, относящегося к коду с низкой плотностью проверок на четность. Позиция 51 на фиг.7 представляет собой узел вычисления строки избыточных битов, который выполняет вычисления по выражению (2), позиция 52 на фиг.7 представляет собой память, которая хранит матрицу А в выражении (1), и позиция 53 на фиг.7 представляет собой переключатель.
В отношении снижения требуемого объема памяти и узлов Исключающее-ИЛИ в устройстве кодирования известны способ, в котором объем памяти уменьшается, и упрощаются операции Исключающее-ИЛИ посредством ограничения проверочной матрицы до матрицы, образованной матрицей циклических перестановок в виде блочной матрицы, и наложения регулярности на матрицу А (например, смотрите патентный документ 1), и способ составления кодов с низкой плотностью проверок на четность, в которых минимизируется количество «1» в элементах матрицы А, тогда как максимизируется выигрыш от кодирования, получаемый посредством итеративного кодирования (например, смотрите непатентный документ 3).
Далее, в качестве кодов с исправлением ошибок, с которыми легко может быть реализовано устройство кодирования, известны циклические коды, в которых строки избыточных битов вычисляются посредством использования только схемы деления многочленов; циклические коды представляются кодом Рида-Соломона (РС) и кодом Боуза-Чоудхури-Хоквингема (БЧХ-кодом), в частности. Далее, как и с вышеупомянутыми циклическими кодами, устройство кодирования легко может быть реализовано посредством использования сверточных кодов.
Однако в циклических кодах или сверточных кодах, имеющих большую длину кодового ограничения, очень большое количество вычислений, необходимых для декодирования с мягким решением, которое выполняет декодирование с точностью, близкой к оптимальной, представляя проблему, и нельзя получить достаточный выигрыш от кодирования по сравнению с кодами с низкой плотностью проверок на четность, в которых декодирование легко может быть выполнено с точностью, близкой к оптимальной, используя узел итеративного декодирования, применяющий вышеупомянутый алгоритм сумма-произведений, который вызывает проблему. В качестве относительно простых кодов, которые могут декодироваться с точностью, близкой к оптимальной, используя итеративное декодирование, и использоваться для устройства кодирования, известны турбокоды (например, смотрите патентный документ 2), однако турбокоды имеют низкую скорость кодирования (отношение длины строки информационных битов и длины строки кодовых битов), поэтому они не пригодны для системы, в которой требуется высокая скорость кодирования.
Известен тот факт, что оценка характеристик частоты появления ошибок кодов с низкой плотностью проверок на четность и предсказание эффективности характеристик частоты появления ошибок может, как правило, выполняться системой, называемой «эволюцией плотности» в области, где вероятность ошибки достаточно высока (например, смотрите непатентный документ 4). Предсказание эффективности характеристик частоты появления ошибок в области, где вероятность ошибок низкая, особенно в области, называемой зоной насыщения, оценивается экспериментальным способом, использующим моделирование на компьютере.
Как описано выше, обычное устройство кодирования, относящееся к коду с низкой плотностью проверок на четность, реализуется при помощи запоминающих устройств, которые хранят матрицу А по выражению (1), и узлов обработки операций, которые выполняют операцию по выражению (2). Далее, оценка характеристик частоты появления ошибок выполняется экспериментально.
[Патентный документ 1]
Публикация патента Японии Kokai № JP-P2003-115768A (стр.10-11, фиг.4-7)
[Патентный документ 2]
Патент США 5446747 (стр.2, фиг.1)
[Непатентный документ 1]
Gallager R., “Low-Density Parity-Check Codes”, MIT Press, 1963 г.
[Непатентный документ 2]
MacKay D. J. C., “Good Error-Correcting Codes Based on Very Sparse Matrices”, труды Института инженеров по электротехнике и радиоэлектронике (ИИЭР) по теории информации, том 45, № 2, Март 1999 г., стр.399-431.
[Непатентный документ 3]
Richardson T. J., and Urbanke, R. L., “Efficient Encoding of Low-Density Parity-Check Codes”, труды ИИЭР по теории информации, том 47, № 2, сентябрь 2001 г., стр.638-656.
[Непатентный документ 4]
Richardson, T. J., Shokrollahi, M. A. and Urbanke, R. L., “Design of Capacity-Approaching Irregular Low-Density Parity-Check Codes”, труды ИИЭР по теории информации, том 47, № 2, сентябрь 2001 г., стр.619-637.
Сущность изобретения
Проблемы, решаемые изобретением
Так как обычное устройство кодирования с исправлением ошибок, относящееся к коду с низкой плотностью проверок на четность, описанному выше, реализуется посредством запоминающих устройств, которые хранят матрицу А по выражению (1), и узлов обработки операций, которые выполняют операцию по выражению (2), размер устройства кодирования очень большой по сравнению с устройствами, применяющими циклические коды, такие как код Рида-Соломона или сверточные коды. В частности, в условиях, когда являются высокими требования к размеру устройства и потреблению мощности, таких как спутниковая связь и мобильные телекоммуникации, требуется дальнейшее снижение количества запоминающих устройств и узлов Исключающее-ИЛИ.
Далее, хотя устройство кодирования может быть реализовано относительно легко с использованием турбокодов, трудно применить такое устройство в системе, которая требует высоких скоростей кодирования, так как турбокоды имеют низкие скорости кодирования. Из-за проблем, описанных выше, чтобы получить большой выигрыш от кодирования, используя коды с низкой плотностью проверок на четность, большое количество вычислений требуется для процесса кодирования, и конфигурация устройства становится сложной, особенно в системах связи, в которых требуются высокие скорости кодирования.
Далее, в обычном устройстве кодирования с исправлением ошибок оценка характеристик частоты появления ошибок должна выполняться экспериментально. Предсказание характеристик частоты появления ошибок в области, где вероятность ошибок низкая, особенно в области, называемой «зоной насыщения», или предсказание вероятности ошибок, в которых наблюдается эффект насыщения, представляет собой важный вопрос при оценке надежности системы связи. Экспериментальный способ, использующий моделирование на компьютере, является эффективным, однако, он занимает много времени, чтобы экспериментально моделировать характеристики области с вероятностью ошибок 10-12, учитывая возможности современных компьютеров.
Следовательно, задачей настоящего изобретения является решение вышеописанных проблем и обеспечение устройства кодирования с исправлением ошибок, в котором конструкция устройства простая, итеративное декодирование используется для достижения декодирования с точностью, близкой к оптимальной, и простое математическое выражение используется для выполнения оценки характеристики области зоны насыщения без использования каких-либо экспериментов на компьютере, и способа кодирования с исправлением ошибок, используемого в нем.
Средство решения проблем
Устройство кодирования с исправлением ошибок согласно настоящему изобретению представляет собой устройство кодирования с исправлением ошибок, которое использует код с низкой плотностью проверок на четность и содержит (m-1) узлов умножения многочленов (где m представляет целое число, равное или большее двух), которые, соответственно, принимают блок, имеющий длину n (где n представляет целое число, равное или большее двух), строки информационных битов, разделенной на (m-1) блоков строк битов, имеющих длину n, и один блок строки битов, имеющий длину (n-r) (где r представляет целое число от 1 до n включительно), выполняет умножение многочленов и, соответственно, выводит серию битов, имеющих длину n; узел сумматора, который суммирует каждый выход (m-1) узлов умножения многочленов; и узел деления многочленов, который выполняет деление многочленов выходного результата узла сумматора и блока, имеющего длину (n-r), и выводит серию избыточных битов, имеющую длину r.
Способ кодирования с исправлением ошибок согласно настоящему изобретению представляет собой способ кодирования с исправлением ошибок, в котором используется код с низкой плотностью проверок на четность; (m-1) узлов умножения многочленов (где m представляет целое число, равное или большее двух), соответственно, принимают блок, имеющий длину n (где n представляет целое число, равное или большее двух), строки информационных битов, разделенной на (m-1) блоков строк битов, имеющих длину n, и один блок строки битов, имеющий длину (n-r) (где r представляет целое число от 1 до n включительно), выполняет умножение многочленов и, соответственно, выводит серию битов, имеющую длину n; узел сумматора добавляет каждый выход (m-1) узлов умножения многочленов; и узел деления многочленов выполняет деление многочленов выходного результата узла сумматора и блока, имеющего длину (n-r), и выводит серию избыточных битов, имеющую длину r.
Другими словами, чтобы достичь задачи, описанной выше, устройство кодирования с исправлением ошибок согласно настоящему изобретению содержит (m-1) узлов умножения многочленов, которые дополнительно делят строку информационных битов, имеющую длину K (где K представляет целое число), которая была разделена на блоки для кодирования с исправлением ошибок, на (m-1) блоков, имеющих длину n, и один блок, имеющий длину (n-r) (где m и n представляют целые числа, равные или большие двух, и r представляет целое число от 1 до n включительно), принимают (m-1) блоков, которые имеют длину n, из числа разделенных строк информационных битов, выполняют умножение многочленов и выводят серию, имеющую длину n; узел сумматора, который суммирует каждый выход (m-1) узлов умножения многочленов; и узел деления многочленов, который принимает выходной результат узла сумматора и блок, имеющий длину (n-r), выполняет деление многочленов и выводит серию избыточных битов, имеющую длину r.
Имея описанную выше конфигурацию, устройство кодирования с исправлением ошибок настоящего изобретения может быть реализовано с простой конструкцией устройства, так как оно образовано из узлов умножения многочленов и узла деления многочленов, и могут быть уменьшены количество вычислений, необходимое для обработки кодирования, и размер устройства. Далее, количество кодовых слов с минимальным весом в устройстве кодирования с исправлением ошибок настоящего изобретения может быть сделано небольшим посредством выбора коммутационного соединения в узлах умножения многочленов и коммутационного соединения в узле деления многочленов.
Поэтому в устройстве кодирования с исправлением ошибок настоящего изобретения размер устройства небольшой, конструкция устройства простая, и большой выигрыш от кодирования может быть получен с использованием способа итеративного декодирования, способствуя повышению надежности и снижению потребляемой мощности в системах связи.
Далее, так как точная аппроксимация минимального расстояния и количества кодовых слов с минимальным весом делается возможной посредством того, что выполняется переключение коммутационного соединения в узлах умножения многочленов и узле деления многочленов в устройстве кодирования с исправлением ошибок настоящего изобретения, можно легко вычислить хорошую аппроксимацию характеристик частоты появления ошибок, особенно вероятность ошибок в области зоны насыщения, в типовой системе связи, в которой применяется настоящее изобретение. Поэтому становится возможным количественно оценивать надежность системы связи, даже когда занимает очень много времени выполнение экспериментальной оценки с использованием моделирования на компьютере или когда количество вычислений слишком большое для выполнения этого.
Выгоды изобретения
В настоящем изобретении с конфигурацией и функционированием, описанными ниже, конструкция устройства может быть сделана простой, декодирование с точностью, близкой к оптимальной, может достигаться с использованием итеративного декодирования, и оценка характеристик области зоны насыщения может выполняться с использованием простого математического выражения без использования каких-либо экспериментов на компьютере.
Краткое описание чертежей
Фиг.1 представляет собой блок-схему, изображающую конфигурацию устройства кодирования с исправлением ошибок согласно примеру настоящего изобретения.
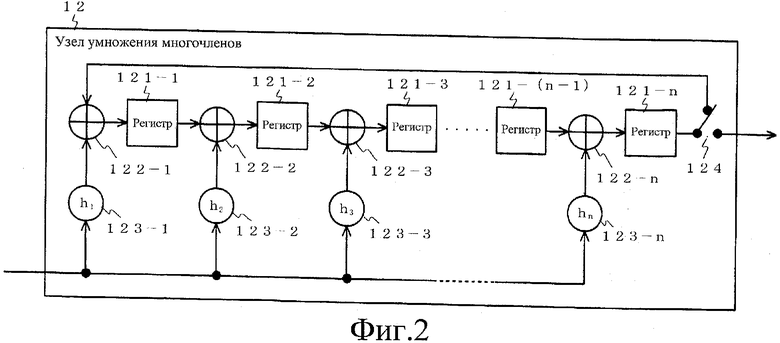
Фиг.2 представляет собой блок-схему, изображающую конфигурацию узла умножения многочленов (n-1)-го порядка, изображенного на фиг.1.
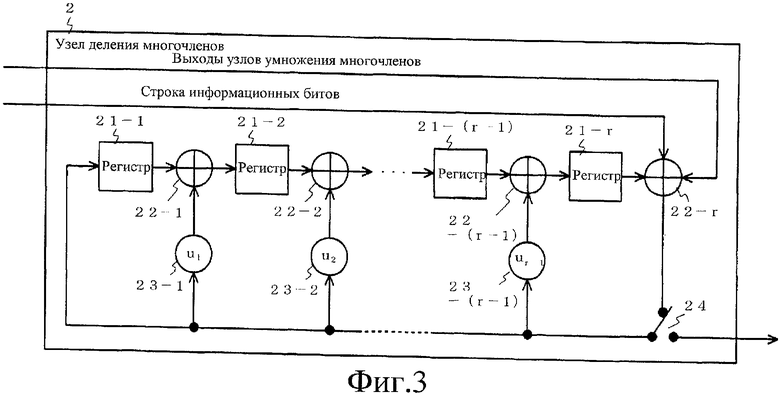
Фиг.3 представляет собой блок-схему, изображающую конфигурацию узла деления многочленов r-го порядка, показанного на фиг.1.
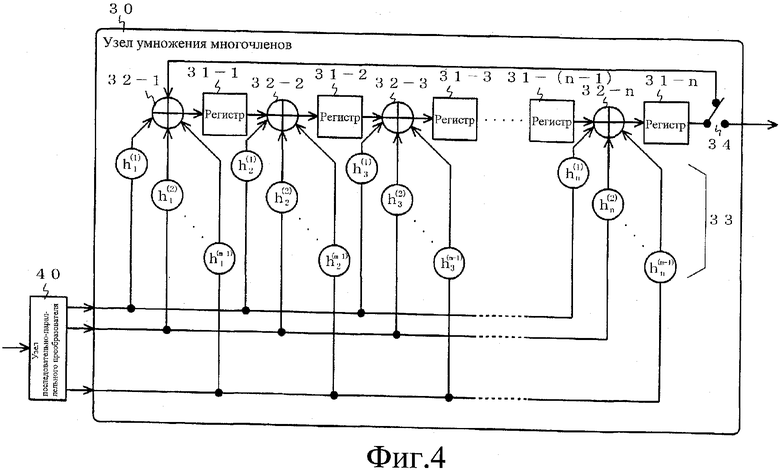
Фиг.4 представляет собой блок-схему, изображающую подробную конфигурацию блока 1 умножения многочленов, показанного на фиг.1.
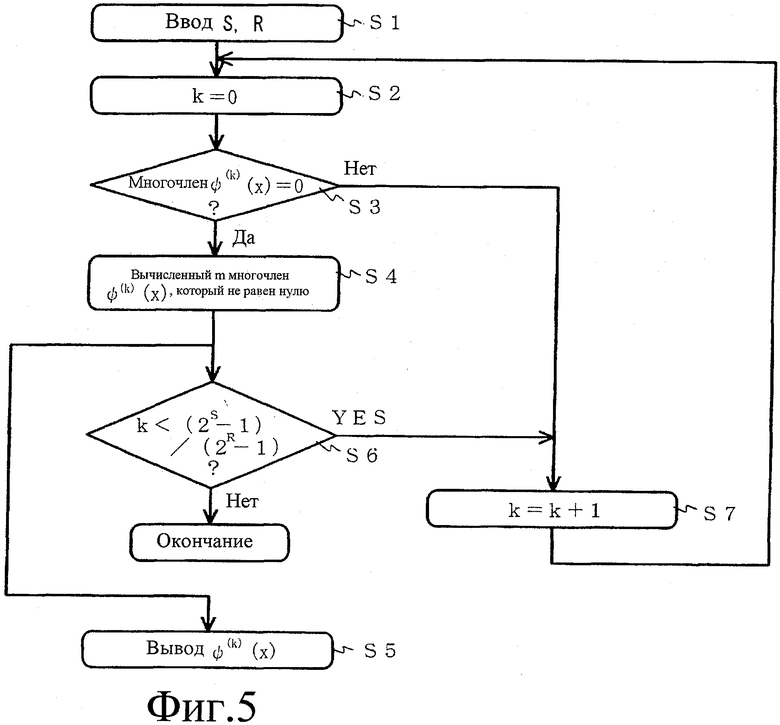
Фиг.5 представляет собой блок-схему последовательности операций, изображающую пример способа вычисления m многочленов, которые не равны нулю, согласно примеру настоящего изобретения.
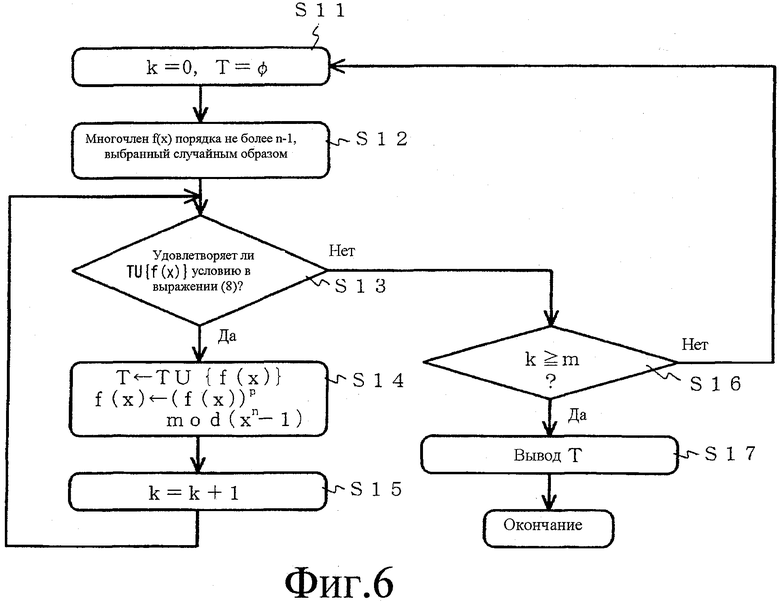
Фиг.6 представляет собой блок-схему последовательности операций, изображающую пример способа вычисления многочленов согласно другому примеру настоящего изобретения.
Фиг.7 представляет собой блок-схему, изображающую пример обычного устройства кодирования с исправлением ошибок, относящегося к коду с низкой плотностью проверок на четность.
Объяснение ссылочных символов
1: блок умножения многочленов
2: узел деления многочленов r-го порядка
3, 4, 24, 34, 124: переключатель
11, 40: узел последовательно-параллельного преобразователя
12, 12-1 - 12-(m-1): узел умножения многочленов (n-1)-го порядка
13: узел сумматора
21-1 - 21-r, 31-1 - 31-n, 121-1 - 121-n: регистр
22-1 - 22-r, 32-1 - 32-n, 122-1 - 122-n: узел операции Исключающее-ИЛИ
23-1 - 23-(r-1), 33, 123-1 - 123-n: переключатель, указывающий скоммутированное или нескоммутированное состояние
Предпочтительные варианты для осуществления изобретения
Ниже описываются примеры настоящего изобретения с ссылкой на чертежи. Фиг.1 представляет собой блок-схему, изображающую конфигурацию устройства кодирования с исправлением ошибок согласно примеру настоящего изобретения. На фиг.1 устройство кодирования с исправлением ошибок согласно примеру настоящего изобретения образовано блоком 1 умножения многочленов, содержащим узел 11 последовательно-параллельного (Пос-Пар) преобразователя, узлы 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка в количестве m-1 и узел 13 сумматора, узлом 2 деления многочленов r-го порядка и переключателями 3 и 4 и представляет собой устройство, которое преобразует строку информационных битов из (nm-r) битов в строку кодовых битов из nm битов (где m и n представляют целые числа, равные или большие двух, и r представляет целое число от 1 до n включительно).
Как описано ниже, блок 1 умножения многочленов конфигурируется так, как показано на фиг.4, однако, чтобы упростить объяснение, заявители предполагают, что блок 1 умножения многочленов составлен из узлов 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка в количестве m-1.
Способ (или система) кодирования настоящего изобретения представлена в качестве схемы систематического кодирования, в которой (nm-r) битов с первого бита строки кодовых битов совпадает со строкой информационных битов, тогда как остальные r битов становятся строкой избыточных битов для исправления ошибок.
(m-1) узлов 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка дополнительно делят строку информационных битов, имеющую длину K (где K представляет целое число), которая была разделена на блоки для кодирования с исправлением ошибок, на (m-1) блоков, имеющих длину n, и один блок, имеющий длину (n-r) (где m и n представляют целые числа, равные или большие двух, и где r представляет целое число от 1 до n включительно), принимают каждый из (m-1) блоков, имеющих длину n, из разделенных строк информационных битов, выполняют умножение многочленов (n-1)-го порядка, и каждый выводит серию (или последовательность), причем каждая имеет длину n.
Узел 13 сумматора складывает каждый выход (m-1) узлов 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка. Узел 2 деления многочленов r-го порядка принимает блок, имеющий длину (n-r), и выходной результат узла 13 сумматора, выполняет деление многочленов r-го порядка и выводит серию избыточных битов, имеющую длину r.
Фиг.2 представляет собой блок-схему, изображающую конфигурацию узла умножения многочленов (n-1)-го порядка. На фиг.2 узел 12 умножения многочленов (n-1)-го порядка составлен из регистров 121-1 - 121-n в количестве n и узлов 122-1 - 122-n Исключающее-ИЛИ в количестве n, максимум. Узлы 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка на фиг.1 все конфигурируются идентично этому узлу 12 умножения многочленов (n-1)-го порядка.
Узел 12 умножения многочленов (n-1)-го порядка принимает/выводит n битов и последовательно принимает строку входных битов из n битов. После того как он примет все биты, переключатель 124 переключается и последовательно выводится содержимое n регистров 121-1 - 121-n.
На фиг.2 позиции 123-1 - 123-n представляют собой переключатели, в которых выполняется коммутационное соединение или коммутационное разъединение под действием предварительно определенной строки битов из n битов (h1, h2, …, hn). Когда hj равен 1, в элементе, обозначенном hj, выполняется коммутационное соединение, и когда hj равен 0, в элементе, обозначенном hj, выполняется коммутационное разъединение (j представляет собой целое число от 1 до m включительно). Как выбирается эта строка битов из n битов (h1, h2, …, hn), описывается ниже.
Фиг.3 представляет собой блок-схему, изображающую конфигурацию узла деления многочленов r-го порядка, показанного на фиг.1. На фиг.3 узел 2 деления многочленов r-го порядка составлен из регистров 21-1 - 21-r в количестве r, узлов 22-1 - 22-r Исключающее-ИЛИ в количестве r, максимум, и переключателя 24.
Узел 2 деления многочленов r-го порядка принимает результирующие n битов операций Исключающее-ИЛИ между (n-r) информационными битами и каждым выходным битом (m-1) узлов 121-1 - 121-n умножения многочленов (n-1)-го порядка и выводит r битов. После того как он примет (n-r) информационных битов, узел 2 деления многочленов r-го порядка переключает переключатель 24 и последовательно выводит результаты операций Исключающее-ИЛИ между остальными r битами с каждого выхода узлов 121-1 - 121-(m-1) умножения многочленов (n-1)-го порядка и содержимым r регистров 21-1 - 21-r на фиг.3 (в этот момент ввод строки информационных битов устанавливается в 0).
Выходные r биты узла 2 деления многочленов r-го порядка становятся строкой избыточных битов из r битов для строки информационных битов из (nm-r) битов. На фиг.3 позиции 23-1 - 23-(r-1) представляют собой переключатели, в которых выполняется коммутационное соединение или коммутационное разъединение под действием предварительно определенной строки битов из (r-1) битов (u1, u2, …, ur-1). Когда uj равен 1, в элементе, обозначенном uj, выполняется коммутационное соединение, и когда uj равен 0, в элементе, обозначенном uj, выполняется коммутационное разъединение (j представляет собой целое число от 1 до (r-1) включительно). Как выбирается эта строка битов из (r-1) битов (u1, u2, …, ur-1), описывается ниже.
Фиг.4 представляет собой блок-схему, изображающую подробную конфигурацию блока 1 умножения многочленов, показанного на фиг.1. На фиг.4 регистры являются совместно используемыми. Позиция 33 на фиг.4 представляет переключатель, который соединяется или разъединяется под действием строки предварительно определенных битов из n(m-1) битов. Когда этот же способ применяется для выбора этой строки битов из n(m-1) битов и строки битов, которая определяет состояние коммутационного соединения переключателей в узлах 12 умножения многочленов (n-1)-го порядка на фиг.2, зависимость между входом и выходом, показанная на фиг.4, совпадает с зависимостью между входом и выходом блока 1 умножения многочленов, реализованного с использованием узлов 12 умножения многочленов (n-1)-го порядка в количестве (m-1) на фиг.2.
Проверочная матрица, которая соответствует устройству кодирования с исправлением ошибок согласно примеру настоящего изобретения, показанному на фиг.1, указывается в следующем выражении:
[Выражение 3]
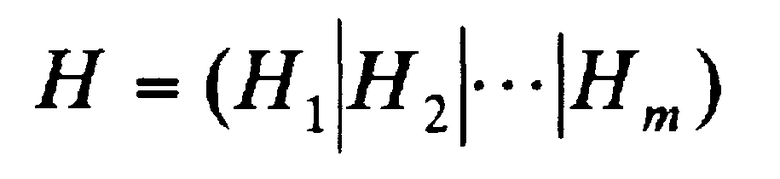

Проверочная матрица в выражении (3) представляет собой линейное расположение циклических матриц размера n x n в количестве m, и Hi в выражении (3) обозначает циклическую матрицу размера n x n (где i представляет собой целое число от 1 до m включительно). Циклическая матрица выражается следующим образом.
[Выражение 4]
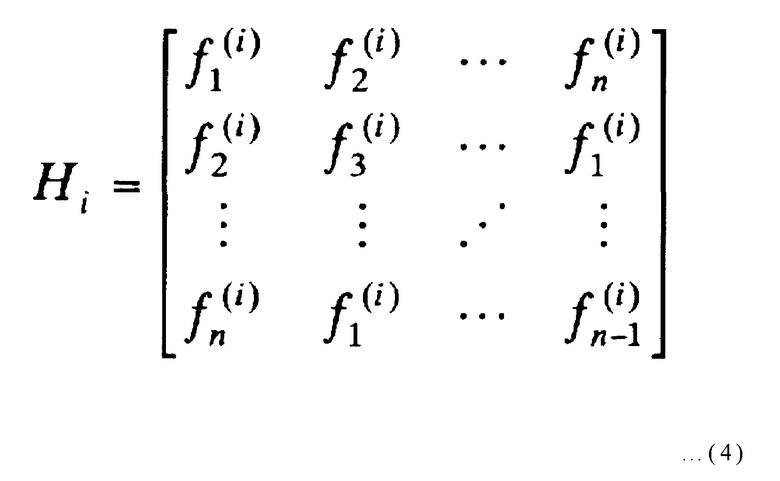
В выражении (4) положения векторов первой строки сдвигаются на один бит влево во второй строке, и после этого положения векторов первой строки сдвигаются на (k-1) битов влево в k-ой строке (где k представляет целое число от двух до n включительно).
Векторы первой строки циклической матрицы размера n x n в выражении (4) выражаются следующим выражением:
[Выражение 5]
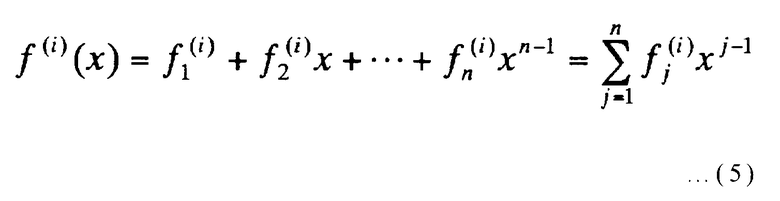
В выражении (5) векторы первой строки циклической матрицы размера n x n выражаются многочленом порядка (n-1) или менее как f(i)(x) (где i представляет собой целое число от 1 до m включительно).
Выбор строки n битов, которая определяет коммутационное соединение между узлами 12 умножения многочленов (n-1)-го порядка: 12-1 - 12-(m-1) и узлом 2 деления многочленов r-ого порядка, определяется выбором m многочленов порядка (n-1) или менее: f(1)(x), f(2)(x), …, f(m)(x). Сначала описывается способ выбора m многочленов порядка (n-1) или менее: f(1)(x), f(2)(x), …, f(m).
Что касается многочлена f(x) порядка (n-1) или менее, множество s(f(x)) определяется следующим выражением:
[Выражение 6]
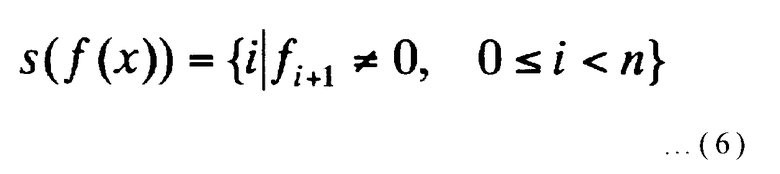
Здесь коэффициент члена порядка i f(x) обозначается как fi+1. Множество s(f(x)) представляет собой подмножество целых чисел от 0 до (n-1) включительно, определенное многочленом f(x).
Далее, для целых чисел v от 1 до (n-1) включительно подмножество λ v(f(x)) декартова произведения s(f(x))×s(f(x)) определяется следующим выражением:
[Выражение 7]
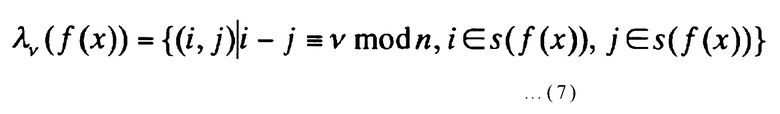
Одним из условий для выбора m многочленов порядка не более, (n-1): f(1)(x), f(2)(x), …, f(m)(x) является то, что m многочленов удовлетворяет следующему выражению для всех целых чисел v от 1 до (n-1) включительно:
[Выражение 8]
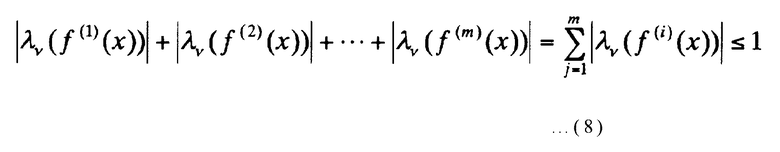
Здесь, количество элементов в множестве А обозначается как |A|. Вторым условием для выбора m многочленов порядка не более (n-1): f(1)(x), f(2)(x), …, f(m)(x) является то, что каждый из (m-1) многочленов f(2)(x), …, f(m)(x) делится на многочлен f(1)(x), при этом многочлен (xn-1) используется в качестве делителя. Далее, факторы-многочлены в количестве (m-1) выражаются как g(2)(x), g(3)(x), …, g(m)(x), что указывается следующим выражением:
[Выражение 9]
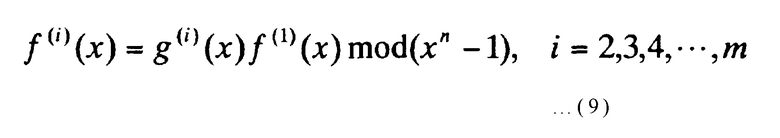
Первое условие [выражение (8)] для выбора m многочленов порядка не более (n-1): f(1)(x), f(2)(x), …, f(m)(x) представляет собой необходимое условие для достижения декодирования с точностью, близкой к оптимальной, используя итеративное декодирование кода с низкой плотностью проверок на четность, обычно алгоритм сумма-произведений и т.д. Фактически, посредством выполнения этого условия [выражение (8)] максимальное количество 1, включенных в каждый вектор строки проверочной матрицы, показанной в выражении (3), становится равным (nm)1/2, и проверочная матрица становится разреженной матрицей.
Второе условие [выражение (9)] представляет собой необходимое условие, чтобы устройство кодирования с исправлением ошибок, показанное на фиг.1, точно вычисляло строку избыточных битов. Примеры многочленов, которые удовлетворяют обоим условиям [выражения (8) и (9)], описываются ниже.
Ниже описывается коммутационное соединение в узле 12 умножения многочленов (n-1)-го порядка, показанном на фиг.2. Как упомянуто выше, коммутационное соединение переключателей 123-1 - 123-n в узле 12 умножения многочленов (n-1)-го порядка на фиг.2 определяется предварительно определенной строкой битов (h1, h2, …, hn). Когда hj равен 1, элемент, обозначенный hj, соединяется, и, когда hj равен 0, элемент, обозначенный hj, разъединяется (j представляет собой целое число от 1 до m включительно).
Эта строка битов из n битов (h1, h2, …, hn) выбирается следующим образом. Как упомянуто ранее, устройство кодирования с исправлением ошибок содержит узлы 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка, и строка n битов, которая определяет коммутационное соединение в узлах 12-i умножения многочленов (n-1)-го порядка, выражается следующим образом.
[Выражение 10]
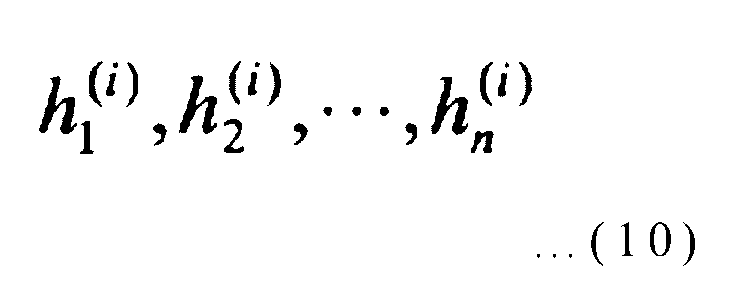
(где i представляет целое число от 1 до (m-1) включительно). Эта строка n битов определяется следующим выражением (11), используя (m-1) многочленов g(2)(x), g(3)(x), …, g(m)(x), указанных в выражении (9):
[Выражение 11]
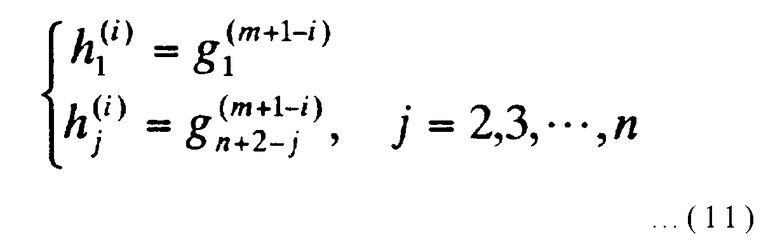
Где
[Выражение 12]
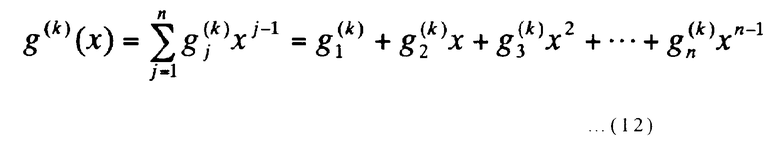
(где k представляет собой целое число от 2 до m включительно). Далее, битовая строка из n(m-1) битов, которая определяет коммутационное соединение переключателей на фиг.4, аналогично определяется выражением (10).
[Выражение 13]
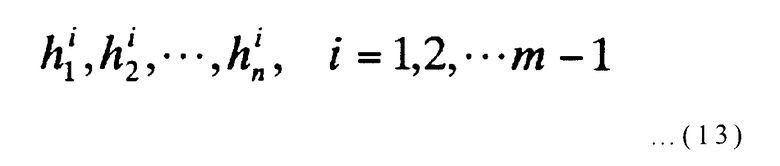
Ниже описывается коммутационное соединение в узле 2 деления многочленов r-го порядка, показанном на фиг.3. В переключателях 23-1 - 23-(r-1) на фиг.3 выполняется коммутационное соединение или разъединение посредством предварительно определенной битовой строки из (r-1) битов (u1, u2, …, ur-1). Когда uj равен 1, элемент, обозначенный uj, соединяется, и, когда uj равен 0, элемент, обозначенный uj, разъединяется (j представляет собой целое число от 1 до (r-1) включительно). Битовая строка из (r-1) битов (u1, u2, …, ur-1) определяется следующим выражением, используя вышеупомянутый многочлен f(1)(x):
[Выражение 14]
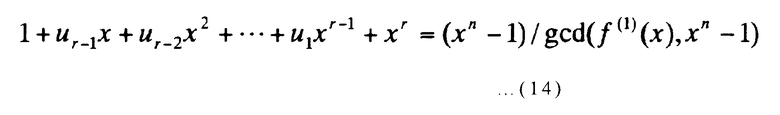
Здесь gcd(f(1)(x), xn-1) представляет наибольший общий многочлен из f(1)(x) и (xn-1), и порядок этого наибольшего общего многочлена равен (n-r). Как упомянуто ранее, r представляет собой количество избыточных битов устройства кодирования настоящего изобретения. Другими словами, количество информационных битов устройства кодирования с исправлением ошибок настоящего изобретения равно количеству битов, полученному добавлением порядкового номера наибольшего общего многочлена f(1)(x) и (xn-1) к n(m-1).
Ниже описывается принцип действия настоящего примера. Устройство кодирования с исправлением ошибок, показанное на фиг.1, последовательно принимает строку информационных битов, имеющую длину K=(nm-r) битов (где m и n представляют целые числа, равные или большие двух, и r представляет целое число от 1 до n включительно), которая была разбита на блоки для кодирования с исправлением ошибок. Серия информационных битов делится на первый блок, включающий в себя от первого бита до n(m-1)-го бита, и второй блок, включающий в себя от (n(m-1)+1)-го бита до (nm-r)-го бита.
Блок 1 умножения многочленов, составленный из (m-1) узлов 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка, последовательно принимает первый блок, и, после переключения переключателя 3, второй блок последовательно принимается узлом 2 деления многочленов r-го порядка. Первый блок, имеющий длину n(m-1) в строке информационных битов, принятой блоком 1 умножения многочленов, преобразуется узлом 11 последовательно-параллельного преобразователя в (m-1) битов, и каждый бит преобразованных (m-1) битов последовательно подается на узлы 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка.
Количество узлов 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка равно (m-1), и i-ый бит (где i представляет целое число от 1 до (m-1) включительно) последовательно-параллельно преобразованных (m-1) битов подается на i-ый узел 12-i умножения многочленов (n-1)-го порядка. Другими словами, первый блок дополнительно делится на (m-1) блоков, имеющих длину n, узлом 11 последовательно-параллельного преобразователя, и каждый из (m-1) блоков, имеющих длину n, принимается каждым из (m-1) узлов 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка.
Каждый из узлов 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка принимает разделенные n биты, и их выходное количество битов равно n битов. Побитовая операция Исключающее-ИЛИ каждого выхода (m-1) узлов 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка превращает в n-битовый выход блока 1 умножения многочленов.
Ниже описывается принцип действия узла 12 умножения многочленов (n-1)-го порядка, показанного на фиг.2. Содержимое всех регистров 121-1 - 121-n инициализируется в нуль, и они последовательно принимают строку из n битов бит за битом. В течение этого времени переключатель 124 устанавливается так, что существует обратная связь. После того как будут приняты все из n битов, переключатель 124 переключается, и содержимое регистров 121-1 - 121-n последовательно выводится.
Устройство кодирования с исправлением ошибок, показанное на фиг.1, использует узлы 12 умножения многочленов (n-1)-го порядка в количестве (m-1). Так как операция Исключающее-ИЛИ каждого выхода узлов 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка превращает в выход блока 1 умножения многочленов, каждый регистр (121-1 - 121-n) может совместно использоваться с другими узлами 12-1 - 12-(m-1) умножения многочленов (n-1)-го порядка.
Конфигурация блока 1 умножения многочленов, показанного на фиг.4, может достигаться так, как описано выше. Принцип действия конфигурации по фиг.4 одинаков с описанным принципом действия за исключением того, что регистры 31-1 - 31-n являются совместно используемыми, и требуемый выходной результат может быть получен с этой конфигурацией, показанной на фиг.4.
Ниже описывается узел 2 деления многочленов r-го порядка, показанный на фиг.3. Содержимое всех регистров 21-1 - 21-r инициализируется в нуль, и они последовательно и одновременно принимают последнюю половину (n-r) битов строки информационных битов и n-битовый выход блока 1 умножения многочленов бит за битом. В течение этого времени переключатель 24 на фиг.3 устанавливается так, что существует обратная связь. После того как будет принята (n-r)-битовая строка информационных битов, переключатель 24 переключается, и операции Исключающее-ИЛИ остальных r битов выхода блока 1 умножения многочленов и содержимое каждого регистра (21-1 - 21-r) последовательно выводятся (вход строки информационных битов устанавливается в нуль в это время).
r-битовый выход узла 2 деления многочленов r-го порядка, показанного на фиг.3, становится строкой избыточных битов для строки информационных битов из (nm-r) битов. Когда количество r избыточных битов совпадает с n, то это означает, что количество битов строки информационных битов, принятой узлом 2 деления многочленов r-порядка, равно нулю, и в этом случае узел 2 деления многочленов r-го порядка просто выводит n-битовый выход блока 1 умножения многочленов.
Ниже описывается выходной переключатель 4 устройства кодирования с исправлением ошибок, показанный на фиг.1. Строка информационных битов из (nm-r) битов становится выходной битовой строкой устройства кодирования с исправлением ошибок одновременно с тем, как она принимается блоком 1 умножения многочленов или узлом 2 деления многочленов r-го порядка. В этот момент времени, если необходимо, с первого по n(m-1)-ый бит информационных битов, принятых блоком 1 умножения многочленов, переупорядочиваются так, что их порядок совпадает с порядком битов, указанным проверочной матрицей, показанной в выражении (3), перед выводом.
После того как будут выведены все (nm-r) биты строки информационных битов, переключатель 4 переключается так, что становится активным выход узла 2 деления многочленов r-го порядка, и r-битовый выход узла 2 деления многочленов r-го порядка выводится в качестве выхода устройства кодирования с исправлением ошибок. Как описано, настоящим примером является устройство систематического кодирования, в котором с первого по n(m-r) биты строки кодовых битов совпадают со строкой информационных битов, и остальные r биты становятся строкой избыточных битов для исправления ошибок.
Имея такую конфигурацию, устройство кодирования с исправлением ошибок, использующее код с низкой плотностью проверок на четность со скоростью кодирования, равной или большей, чем (n-1)/n, может быть составлено из максимум 2n регистров и 2n узлов Исключающее-ИЛИ в настоящем примере.
Далее, как описано ниже, устройство кодирования с исправлением ошибок, в котором выигрыш от кодирования является большим, и характеристики частоты появления ошибок в области зоны насыщения могут вычисляться простым математическим оценочным выражением (или формулой), может быть составлено из конфигурации настоящего примера.
Ниже описывается конкретный пример вычисления многочленов, которые удовлетворяют вышеупомянутым условиям [выражения (8) и (9)]. Далее, используя данный пример, объясняется, как может быть получен большой выигрыш от кодирования и как могут быть вычислены характеристики частоты появления ошибок в области зоны насыщения простым математическим оценочным выражением.
α представляет собой примитивный элемент конечного поля GF(22S) (где S представляет собой положительное целое число), и R представляет собой делитель S, но не равен ни 1, ни S. Далее, n представляется посредством (2S+1)(2R-1), и m - посредством (2S-2S-R)/(2R-1). Многочлен ψ (k)(x) порядка не более (n-1) определяется следующим выражением:
[Выражение 15]
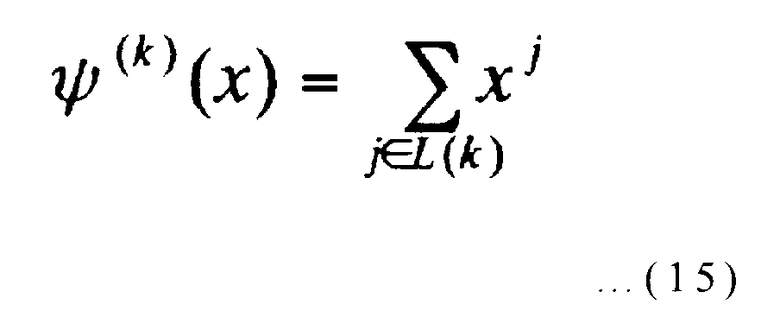
(где k представляет целые числа от 0 до (2S-1)/(2R-1)-1 включительно).
Здесь L(K) представляет собой подмножество целых чисел от 0 до (n-1) включительно, и оно определяется следующим выражением:
[Выражение 16]
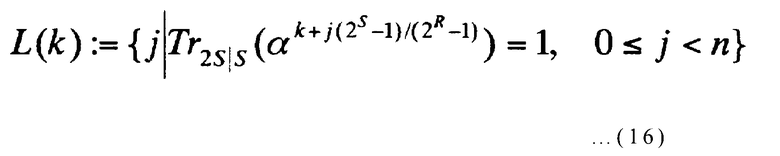
Отметьте, что Tr2S|S в выражении (16) представляет след от конечного поля GF(22S) на GF(2S). Существует количество m многочленов ψ (k)(x), которые не равны нулю, где k представляет целые числа от 0 до (2S-1)/(2R-1)-1 включительно.
Фиг.5 представляет собой блок-схему последовательности операций, изображающую пример способа вычисления m многочленов, которые не равны нулю. Равен ли многочлен ψ (k)(x) нулю или нет (где k представляет целые числа от 0 до (2S-1)/(2R-1)-1 включительно) может определяться тем, что равен ли нулю или нет след αk(2S+1) (где α представляет собой элемент конечного поля GF(2S)) на GF(2R). Другими словами, он может определяться следующим выражением:
[Выражение 17]
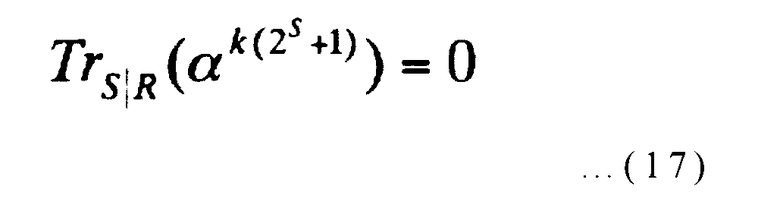
Так как (2S-1)/(2R-1), умноженное на m, равно 22S-1, множество L(k) в выражении (16) соответствует множеству элементов, которые являются подмножеством конечного поля GF(22S), значения которого совпадают друг с другом при возведении в m-ую степень, и следы которого на конечное поле GF(2S) равны 1. Далее, даже когда значение вышеуказанного следа не равно нулю, вышеупомянутое выражение действует до тех пор, пока значение следа одинаково для каждого k (где k представляет целые числа от 0 до (2S-1)/(2R-1)-1 включительно). Поэтому многочлены ψ (k)(x) определяются множеством элементов, значения которых совпадают друг с другом при возведении в m-ую степень, и следы которых на конечное поле GF(2S) представляют собой предварительно определенное значение, отличное от нуля, и совпадают друг с другом в подмножестве конечного поля GF(22S) (этапы S1-S7 на фиг.5).
После того как m многочленов, которые представляют собой выход блок-схемы последовательности операций на фиг.5, надлежащим образом упорядочены, они представляются как f(1)(x), f(2)(x), …, f(m)(x). Эти m многочленов f(1)(x), f(2)(x), …, f(m)(x) удовлетворяют вышеупомянутым условиям [выражения (8) и (9)]. В данном случае, эти m многочленов должны быть упорядочены так, что, в частности, многочлен f(1)(x) представляет собой минимальный многочлен, что означает, что среди многочленов ψ (k)(x), которые не равны нулю, номер порядка их наибольшего общего многочлена с (xn-1) является наименьшим.
Длина N строки кодовых битов в устройстве кодирования с исправлением ошибок согласно настоящему примеру, составленному многочленами, выбранными так, как описано, равна следующему.
N=nm=(2S+1)(2S-2S-R)
Длина K строки информационных битов не меньше, чем
n(m-1)=(2S+1)(2S-2S-R-2R+1)
Точнее говоря, как описано выше, фактически, это номер бита, полученный посредством добавления номера порядка наибольшего общего многочлена f(1)(x) и (xn-1) к n(m-1).
Далее, минимальное расстояние d представляется посредством d=2R+1, и число Ad строк кодовых битов с весом d составляет, по меньшей мере, (2S+1)(2S-2S-R). В действительности, число Ad строк кодовых битов с весом d очень близко к (2S+1)(2S-2S-R), поэтому это хорошая аппроксимация. Кроме того, число строк кодовых битов с весом d очень небольшое, и этот факт имеет хорошее влияние на характеристики частоты появления ошибок, как описано ниже.
Используя аппроксимации минимального расстояния d и число строк кодовых битов с весом d, примерное значение вероятности Pb битовой ошибки, когда схемой модуляции является двухкратная фазовая манипуляция (2-ФМн), и каналом является канал с аддитивным гауссовым шумом, может вычисляться по следующему выражению:
[Выражение 18]
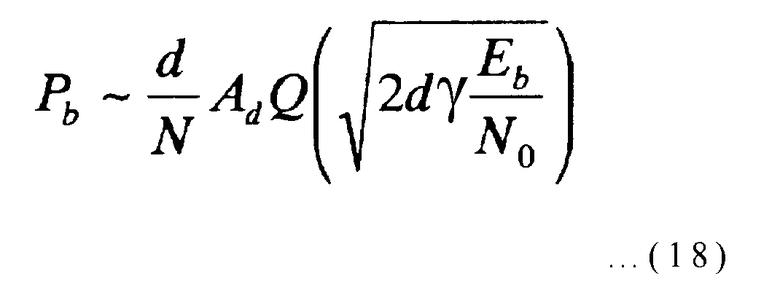
Здесь d представляет минимальное расстояние (d=2R+1), Ad представляет число строк кодовых битов с весом d, N представляет длину строки кодовых битов, и γ представляет скорость кодирования (γ=K/N). Далее, Eb/No представляет отношение сигнал-шум (ОСШ) на бит в канале с аддитивным гауссовым шумом, и Q представляет гауссову Q функцию, которая может быть выражена следующим выражением:
[Выражение 19]
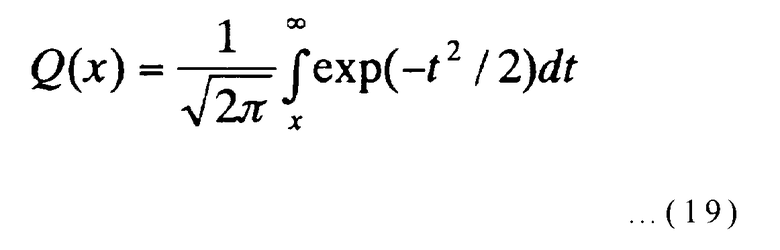
Соответствующей подстановкой (2R+1) и (2S+1)(2S-2S-R) вместо N и d и (2S+1)(2S-2S-R) вместо Ad в выражении (18) может быть вычислено примерное значение вероятности Pb битовой ошибки. Эта аппроксимация очень точная в области зоны насыщения, и она эффективна для оценки характеристики области зоны насыщения, когда занимает слишком много времени выполнение экспериментальной оценки, используя моделирование на компьютере, или когда количество вычислений слишком большое для их выполнения.
Увеличение минимального расстояния d является эффективным для улучшения вероятности ошибки, используя выражение (18), и получения большего выигрыша от кодирования. Имеются многочлены в количестве m, которые не равны нулю, из числа многочленов ψ (k)(x) (k=0, 1, …, (2S-1)/(2R-1)-1), указанных выражением (15). Вместо использования всех m многочленов, как описано, можно увеличить минимальное расстояние примерно до (2R+1) посредством использования только частей многочленов. Этот способ описывается ниже.
m' многочленов выбираются из m многочленов ψ (k)(x) (где k представляет целые числа от 0 до (2S-1)/(2R-1)-1) включительно, которые не равны нулю. После того как они будут надлежащим образом упорядочены, предположим, что они представлены как f(1)(x), f(2)(x), …, f(m')(x). В этом случае многочлен ψ (k)(x) и многочлен ψ (r(k)(x) не должен выбираться вместе одновременно. Здесь r(k) представляет остаток, когда (2xk) делится на (2S-1)/(2R-1).
Эти m' многочленов f(1)(x), f(2)(x), …, f(m')(x) удовлетворяют вышеупомянутым условиям [выражения (8) и (9)], и длина N строки кодовых битов в устройстве кодирования настоящего изобретения, составленной многочленами, выбранными так, как описано, составляет N=nm'. Минимальное расстояние равно или меньше, чем 2R+1, и число строк кодовых битов с весом 2R+1 равно, по меньшей мере, значению, полученному умножением биномиального коэффициента m' и 2 на n. Значение, полученное подстановкой нижней границы строк кодовых битов с этим весом 2R+1 в выражение (18), может обеспечивать очень хорошую аппроксимацию характеристик частоты появления ошибок, когда вероятность ошибки относительно низка (когда отношение сигнал-шум канала относительно высокое). Используя этот способ, скорость кодирования становится более низкой по сравнению со случаем, когда используются все m многочленов, однако, взамен улучшаются характеристики ошибок.
Настоящий пример дополнительно описывается с использованием приведенных в качестве примера конкретных значений. В настоящем примере, описанном выше, заявители предполагают S=6 и R=3. В этом случае n=455 и m=8. Далее, многочлены ψ (k)(x) выражения (15) (где k представляет целые числа от 0 до 8 включительно) могут быть выражены следующим образом.
[Выражение 20]
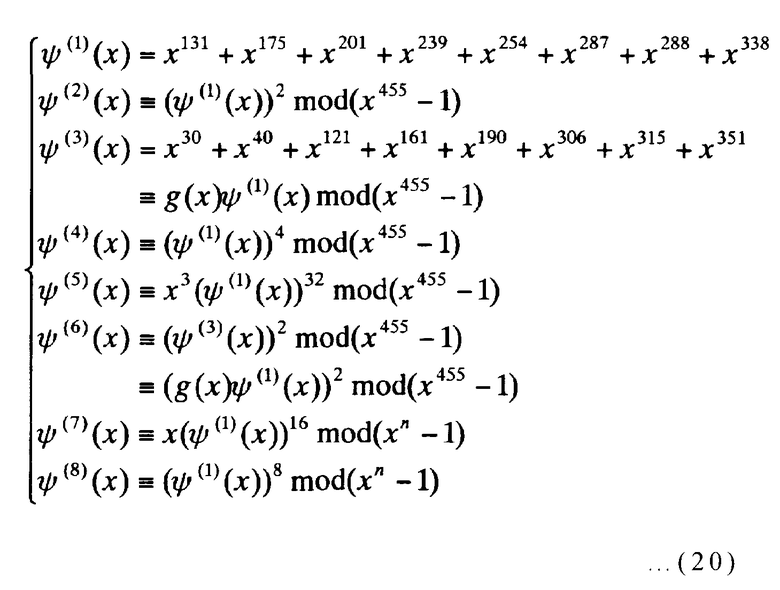
Далее, ψ (0)(x)=0 и g(x) представляет фактор-многочлен, когда ψ (3)(x) делится на ψ (1)(x), используя (x455-1) в качестве делителя.
Когда восемь многочленов f(1)(x), f(2)(x), …, f(8)(x) представляются посредством f(k)(x)=ψ (k)(x) (где k=1, 2, …, 8), эти восемь многочленов удовлетворяют вышеупомянутым условиям [выражения (8) и (9)]. В этом случае длина N строки кодовых битов равна 3640 битов; длина K строки информационных битов равна 3288 битов; скорость кодирования γ равна примерно 0,9; минимальное расстояние равно 9; и число А9 строк кодовых битов с весом 9 равно или больше 3640.
Подставив эти значения в выражение (18) и вычислив вероятность ошибки, может быть обнаружен тот факт, что отношение сигнал-шум на бит, необходимое для достижения вероятности битовой ошибки 10-12 после декодирования, составляет примерно 5 децибел. Это может достигаться посредством использования способа итеративного декодирования.
Также легко может быть вычислено отношение сигнал-шум, необходимое для достижения еще меньшей частоты появления битовой ошибки, используя способ итеративного декодирования. Далее, в сравнении со случаем, когда этот код кодируется с использованием кода Рида-Соломона с этой же скоростью кодирования и декодируется с использованием обычного способа декодирования с ограниченным расстоянием, может быть получен выигрыш от кодирования 2,0 децибела (дБ) или более, когда вероятность битовой ошибки после декодирования составляет 10-6.
Когда четыре многочлена из восьми многочленов ψ (1)(x), ψ (2)(x), …, ψ (8)(x) используются и представляются как f(1)(x)= ψ (1)(x), f(2)(x)=ψ (4)(x), f(3)(x)=ψ (7)(x), f(4)(x)=ψ (3)(x), эти четыре многочлена также удовлетворяют вышеупомянутым условиям [выражения (8) и (9)]. В этом случае длина N строки кодовых битов равна 1820 битов; длина K строки информационных битов равна 1468 битов; скорость кодирования γ равна примерно 0,8; минимальное расстояние равно 16 или менее; и число А16 строк кодовых битов с весом 16 равно 2730 или больше.
Подставив эти значения в выражение (18) и вычислив вероятность ошибки, может быть обнаружен тот факт, что отношение сигнал-шум на бит, необходимое для достижения вероятности битовой ошибки 10-12 после декодирования, равно примерно 4,4 децибела, и это может быть достигнуто использованием способа итеративного декодирования. Также легко может быть вычислено отношение сигнал-шум, необходимое для достижения даже меньших частот появления битовых ошибок, используя способ итеративного декодирования. Далее, по сравнению со случаем, когда этот код кодируется с использованием кода Рида-Соломона с такой же скоростью кодирования и декодируется с использованием обычного способа декодирования с ограниченным расстоянием, может быть получен выигрыш от кодирования 2,0 децибела (дБ) или более, когда вероятность битовой ошибки после декодирования составляет 10-6.
Фиг.6 представляет собой блок-схему последовательности операций, изображающую способ вычисления многочленов согласно другому примеру настоящего изобретения. На фиг.6 k представляет неотрицательное целое число, и Т представляет множество многочлена (многочленов) порядка (порядков) не более чем (n-1) (где n представляет целое число, равное или большее двух). Далее, p представляет степени двух, такие как 2 и 4. В начальном состоянии k=0; T представляет собой пустое множество; и многочлены порядка (порядков) не более чем (n-1) f(x) выбираются случайным образом.
Когда эти многочлены удовлетворяют вышеупомянутому условию [выражение (8)] (в выражении (8) m равно 1, и f(1)(x) равно f(x)), f(x) добавляется к элементам множества Т, и значение k увеличивается на единицу. При k-ой итеративной обработке на фиг.6 (где k представляет целое число, равное или большее двух), когда следующий многочлен (выражение (21)), вычисленный из множества многочленов Т, и многочлены f(x), описанные выше, удовлетворяют вышеупомянутому условию [выражение (8)] (m в выражении (8) равно k), f(k)(x) добавляется к элементам множества Т, и значение k увеличивается на единицу.
[Выражение 21]
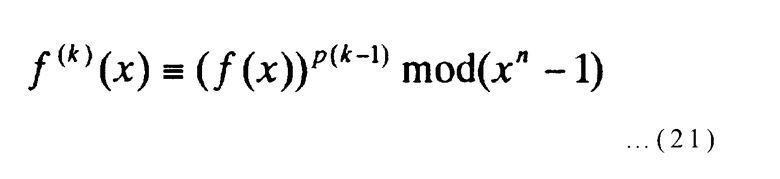
Как только количество многочленов, включенных в множество многочленов Т, достигает предварительно определенного количества m (где m представляет целое число, равное или большее двух), Т выводится и обработка завершается (этапы S11-S17 на фиг.6).
На фиг.6, как описано выше, посредством многочленов f(x), которые выбираются случайным образом в начальном состоянии, может быть получено следующее выражение:
[Выражение 22]
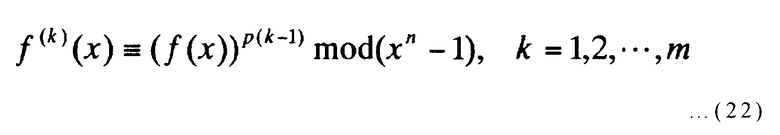
Тогда выход Т блок-схемы последовательности операций по фиг.6 равен T={f(1)(x), f(2)(x), …, f(m)(x)}, и они удовлетворяют вышеупомянутым условиям [выражения (8) и (9)]. Далее, когда количество членов, которые не равны нулю в многочленах f(x), выбранных в начальном состоянии, представлено посредством w, каждый из многочленов, включенных в Т, имеет w членов, которые не равны нулю.
Длина N строки кодовых битов в устройстве кодирования с исправлением ошибок согласно настоящему примеру, составленному m многочленами f(1)(x), f(2)(x), …, f(m)(x), которые представляют собой выход блок-схемы последовательности операций на фиг.6, равна N=nm, и длина K строки информационных битов составляет по меньшей мере n(m-1). Говоря точнее, как описано выше, это, фактически, представляет собой количество битов, полученное посредством добавления номера порядка наибольшего общего многочлена f(1)(x) и (xn-1) к n(m-1).
Когда p равно 2, минимальное расстояние d равно d=w+1, и число Ad строк кодовых битов с весом d составляет по меньшей мере n(m-1). В большинстве случаев значение, полученное заменой нижней границы числа строк кодовых битов на этот минимальный вес в выражении (18), может обеспечить очень хорошую аппроксимацию характеристик частоты появления ошибок, когда вероятность ошибок относительно низкая (когда отношение сигнал-шум канала относительно высокое).
Далее, когда p не равно 2, число строк кодовых битов с весом 2w представляет собой, по меньшей мере, значение, полученное умножением биномиального коэффициента m и 2 на n, и в большинстве случаев значение, полученное заменой нижней границы числа строк кодовых битов на этот минимальный вес 2w в выражении (18), может обеспечивать очень хорошую аппроксимацию характеристик частоты появления ошибок, когда вероятность ошибок относительно низкая (когда отношение сигнал-шум канала относительно высокое).
Ниже дополнительно описывается настоящий пример с использованием конкретных значений в качестве примера. Когда n=255, m=4 и p=4 в настоящем примере, посредством f5(x), выраженного ниже,
[Выражение 23]
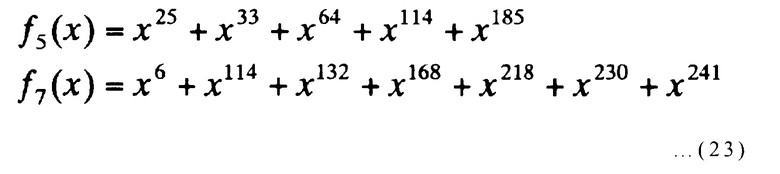
может быть получено следующее выражение:
[Выражение 24]
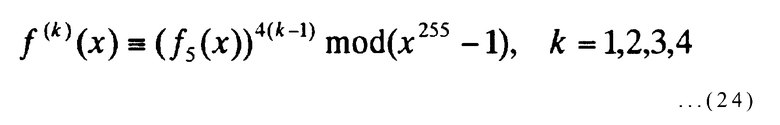
Тогда, в качестве выхода обработки, описанной на фиг.6, например, может быть получено Т={f(1)(x), f(2)(x), f(3)(x), f(4)(x)}.
Эти многочлены удовлетворяют вышеупомянутым условиям [выражения (8) и (9)]. В этом случае длина N строки кодовых битов равна 1020 битов; количество K информационных битов равно 769 битов; скорость кодирования равна примерно 0,754; минимальное расстояние равно 10 или меньше; и число A10 строк кода с весом 10 равно 1530 или более.
Посредством подстановки их в выражение (18) и вычисления вероятности ошибок может быть обнаружен тот факт, что отношение сигнал-шум на бит, необходимое для достижения вероятности битовой ошибки 10-12 после декодирования, составляет примерно 5,6 децибел, и оно может достигаться использованием способа итеративного декодирования. Также легко может быть вычислено отношение сигнал-шум, необходимое для достижения даже меньшей частоты появления битовой ошибки, с использованием способа итеративного декодирования.
Затем посредством f7(x) в выражении (23) может быть получено следующее выражение:
[Выражение 25]
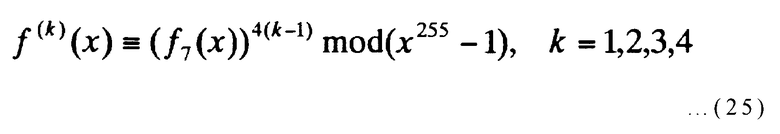
Тогда, в качестве выхода обработки, изображенной на фиг.6, может быть получено Т={f(1)(x), f(2)(x), f(3)(x), f(4)(x)} как в случае с f(5)(x), описанном выше. Эти многочлены удовлетворяют вышеупомянутым условиям [выражения (8) и (9)]. В этом случае длина N строки кодовых битов, количество K информационных битов и скорость кодирования равны 1020, 769 и 0,754, соответственно, точно такие же как в случае с f(5)(x), описанном выше, за исключением того, что минимальное расстояние другое: 14 или менее. Далее, число А14 строк кода с весом 14 равно 1530 или более.
В результате подстановки их в выражение (18) и вычисления вероятности ошибки может быть обнаружен тот факт, что отношение сигнал-шум на бит, необходимое для достижения вероятности битовой ошибки 10-12 после декодирования, равно примерно 5,0 децибел, и оно может достигаться использованием способа итеративного декодирования. Также легко может быть вычислено отношение сигнал-шум, необходимое для достижения даже меньшей частоты появления битовой ошибки, с использованием способа итеративного декодирования.
Когда вероятность битовой ошибки после декодирования составляет 10-12, в сравнении с устройством, составленным посредством f5(x), описанного выше, может ожидаться увеличение выигрыша от кодирования на 0,6 децибел. С другой стороны, когда вероятность битовой ошибки после декодирования составляет 10-6 в сравнении с устройством, составленным посредством f5(x), выигрыш от кодирования уменьшается на 0,4 децибела. В этом случае конструкция устройства кодирования с исправлением ошибок должна выбираться в соответствии с требованиями на систему связи, и посредством выбора многочленов устройство кодирования с исправлением ошибок согласно настоящему изобретению способно удовлетворять широкому диапазону требований.
Промышленная применимость
Настоящее изобретение может быть применено к технологии исправления ошибок для удовлетворения требований, относящихся к конструкции системы, таких как снижение потребляемой мощности и размера антенн в системах спутниковой связи и мобильной телекоммуникации, или к технологии исправления ошибок для повышения надежности запоминающих устройств, таких как магнитные запоминающие устройства.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО КОДИРОВАНИЯ, СПОСОБ КОНФИГУРИРОВАНИЯ КОДА С ИСПРАВЛЕНИЕМ ОШИБОК И ПРОГРАММА ДЛЯ НИХ | 2011 |
|
RU2527207C2 |
| СПОСОБ И УСТРОЙСТВО КОДИРОВАНИЯ С ИСПРАВЛЕНИЕМ ОШИБОК | 2007 |
|
RU2408979C2 |
| СПОСОБ И ДЕКОДИРУЮЩЕЕ УСТРОЙСТВО ИСПРАВЛЕНИЯ ДВУХ ОШИБОК В ПРИНИМАЕМОМ КОДЕ | 2006 |
|
RU2336559C2 |
| УСТРОЙСТВО КОДИРОВАНИЯ-ДЕКОДИРОВАНИЯ ИНФОРМАЦИИ | 1994 |
|
RU2115231C1 |
| Запоминающее устройство с исправлением ошибок | 1984 |
|
SU1226536A1 |
| СИСТЕМА ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ С ИСПРАВЛЕНИЕМ ОШИБОК | 1991 |
|
RU2007042C1 |
| УСОВЕРШЕНСТВОВАННЫЙ ПОДХОД К ДЕКОДИРОВАНИЮ m-МАССИВА И ИСПРАВЛЕНИЮ ОШИБОК | 2004 |
|
RU2380736C2 |
| Декодер циклического кода | 1988 |
|
SU1599996A1 |
| ДЕКОДЕР С ИСПРАВЛЕНИЕМ ОШИБОК | 1993 |
|
RU2054224C1 |
| Логическое запоминающее устройство | 1978 |
|
SU771720A1 |
Устройство кодирования с исправлением ошибок, в котором конструкция устройства простая; используется итеративное декодирование для достижения декодирования с точностью, близкой к оптимальной; и простое математическое выражение используется для выполнения оценки характеристик области зоны насыщения без использования каких-либо экспериментов на компьютере. В блоке 1 умножения многочленов узлы (12-1-12-(m-1)) умножения многочленов (n-1)-го порядка дополнительно делят строку информационных битов, которая была разделена на блоки для кодирования с исправлением ошибок, на (m-1) блоков, имеющих длину n, и один блок, имеющий длину (n-r) (где тип представляют целые числа, равные или большие двух, и где г представляет целое число от 1 до n включительно); принимают блоки, которые имеют длину n, разделенных строк информационных битов; и выводят серию, имеющую такую же длину. Узел 2 деления многочленов r-го порядка принимает добавление выходов от соответствующих узлов (12-1-12-(m-1)) умножения многочленов (n-1)-го порядка и также принимает блок, имеющий длину (n-r), и выводит серию избыточных битов, имеющую длину r. Технический результат - достижение декодирования с точностью, близкой к оптимальной, и упрощение математического выражения для выполнения характеристики области зоны насыщения. 2 н. и 3 з.п. ф-лы, 7 ил.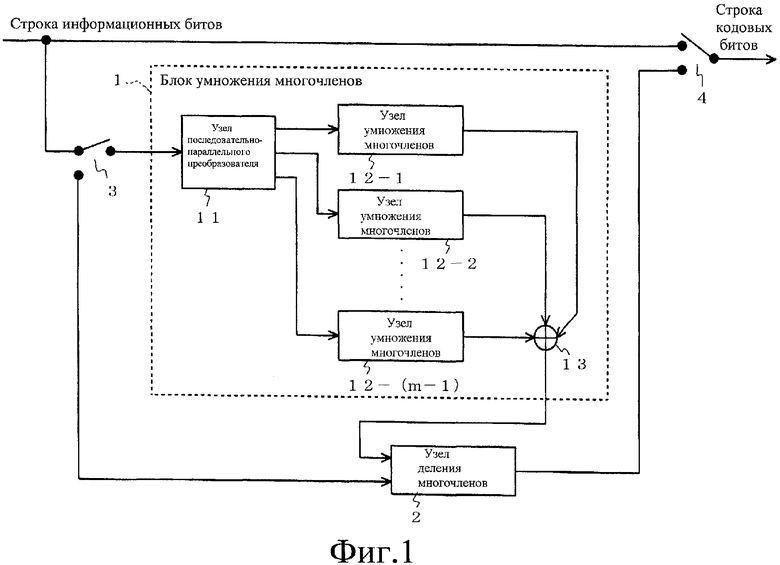
1. Устройство кодирования с исправлением ошибок, использующее код с низкой плотностью проверок на четность, отличающееся тем, что содержит:
переключатель для переключения первого блока, имеющего длину n(m-1) (где n и m представляют целые числа, равные или большие двух), где первый блок разделен на (m-1) блоков строк битов, имеющих длину n, и второго блока, имеющего длину n-r строки информационных битов (где r представляет целое число от 1 до n включительно);
узел последовательно-параллельного преобразователя для преобразования первого блока в (m-1) битов, где каждый бит из преобразованных (m-1) битов последовательно передается в (m-1) узлов умножения многочленов (n-1)-го порядка; (m-1) узлов умножения многочленов, которые принимают первый блок, выполняют умножение многочленов и выводят, соответственно, серию битов, имеющую длину n;
узел сумматора, который добавляет каждый выход упомянутых (m-1) узлов умножения многочленов; узел деления многочленов, который выполняет деление многочленов выходного результата упомянутого узла сумматора и упомянутого второго блока, имеющего длину (n-r), и выводит серию избыточных битов, имеющую длину r;
переключатель для переключения таким образом, что становится активным выход узла деления многочленов, и выводится r-битовый выход узла деления многочленов;
причем упомянутый узел деления многочленов и упомянутые узлы умножения многочленов включают в себя схему, в которой регистры и схемы Исключающее-ИЛИ, подсоединенные к выходам упомянутых регистров, подсоединены последовательным образом во множестве каскадов; и
выходная логика упомянутых схем Исключающее-ИЛИ устанавливается коммутационным соединением, определяемым в соответствии с предварительно определенной операцией многочленов, так что выходная логика упомянутых схем Исключающее-ИЛИ является не инвертированной или инвертированной.
2. Устройство кодирования с исправлением ошибок по п.1, в котором коммутационный многочлен, который задает коммутационное соединение в упомянутом узле деления многочленов, представляет собой минимальный многочлен из числа многочленов, определенных множеством элементов, значения которых совпадают друг с другом при возведении в m-ю степень, и проекции которых на конечное поле из 2S элементов представляют собой значение, отличное от нуля, и совпадают друг с другом в подмножестве конечного поля из 22S (где S представляет положительное целое число) элементов, и фактор-многочлен, когда многочлен, определенный подмножеством другого конечного поля, делится на упомянутый минимальный многочлен, представляет собой многочлен коммутационного соединения, который задает коммутационное соединение в упомянутых узлах умножения многочленов.
3. Устройство кодирования с исправлением ошибок по п.1, в котором коммутационные многочлены, которые задают коммутационное соединение в упомянутом узле деления многочленов, выбираются случайным образом, и каждый из (m-1) коммутационных многочленов, которые задают коммутационное соединение в упомянутых (m-1) узлах умножения многочленов, определяется степенью упомянутых многочленов, выбранных случайным образом, которые отличны друг от друга.
4. Способ кодирования с исправлением ошибок, использующий код с низкой плотностью проверок на четность, отличающийся тем, что содержит этапы, на которых:
переключают, посредством переключателя, первый блок, имеющий длину n(m-1) (где n и m представляют целые числа, равные или большие двух), где первый блок разделен на (m-1) блоков строк битов, имеющих длину n, и второй блок, имеющий длину n-r строки информационных битов (где r представляет целое число от 1 до n включительно);
в узле последовательно-параллельного преобразователя, преобразовывают первый блок в (m-1) битов, где каждый бит из преобразованных (m-1) битов последовательно передается в (m-1) узлов умножения многочленов (n-1)-го порядка;
в (m-1) узлах умножения многочленов принимают первый блок и выполняют умножения многочленов и, соответственно, вывод серии битов, имеющей длину n;
в узле сумматора добавление каждого выхода упомянутых (m-1) узлов умножения многочленов;
в узле деления многочленов выполнение деления многочленов выходного результата упомянутого узла сумматора и упомянутого второго блока, имеющего длину (n-r), и вывод серии избыточных битов, имеющей длину r;
переключают, посредством переключателя, таким образом, что становится активным выход узла деления многочленов, и выводится r-битовый выход узла деления многочленов;
причем коммутационный многочлен, который задает коммутационное соединение в упомянутом узле деления многочленов, представляет собой минимальный многочлен из числа многочленов, определенных множеством элементов, значения которых совпадают друг с другом при возведении в m-ю степень, и проекции которых на конечное поле из 2S элементов представляют собой значение, отличное от нуля, и совпадают друг с другом в подмножестве конечного поля из 22S (где S представляет положительное целое число) элементов, и фактор-многочлен, когда многочлен, определенный подмножеством другого конечного поля, делится на упомянутый минимальный многочлен, представляет собой коммутационный многочлен, который задает коммутационное соединение в упомянутых узлах умножения многочленов.
5. Способ кодирования с исправлением ошибок по п.4, в котором коммутационные многочлены, которые задают коммутационное соединение в упомянутом узле деления многочленов, выбираются случайным образом, и каждый из (m-1) коммутационных многочленов, которые задают коммутационное соединение в упомянутых (m-1) узлах умножения многочленов, определяется степенями упомянутых многочленов, выбранных случайным образом, которые отличны друг от друга.
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| СИСТЕМА ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ С ИСПРАВЛЕНИЕМ ОШИБОК | 1991 |
|
RU2007042C1 |
| US 2003079172 А1, 24.04.2003 | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Подмости | 1979 |
|
SU806839A1 |
Авторы
Даты
2009-11-20—Публикация
2005-11-29—Подача