УСТРОЙСТВО КОДИРОВАНИЯ, СПОСОБ КОНФИГУРИРОВАНИЯ КОДА С ИСПРАВЛЕНИЕМ ОШИБОК И ПРОГРАММА ДЛЯ НИХ Российский патент 2014 года по МПК H03M13/19 

ОБЛАСТЬ ТЕХНИКИ

Настоящее изобретение относится к устройству кодирования, устройству конфигурирования кода с исправлением ошибок и их программе. Более точно, настоящее изобретение относится к устройству кодирования и тому подобному, которое строит многие разновидности квазициклических кодов контроля четности с низкой плотностью, с небольшой областью хранения.

УРОВЕНЬ ТЕХНИКИ

Для передачи и хранения цифровых сигналов, таких как спутниковая связь, мобильная связь, оптические диски, и тому подобное, снижение потребляемой электрической энергии, уменьшение размера антенны, улучшения скорости передачи (или емкости хранения), и тому подобное, требуются во все времена. Для того чтобы удовлетворять такие потребности, применяются технологии кодирования с исправлением ошибок, имеющие большую эффективность кодирования. Среди таковых, код контроля четности с низкой плотностью (указываемый ссылкой как код LDPC в дальнейшем) известен в качестве кода с исправлением ошибок, имеющего большую эффективность кодирования, и он все больше и больше применяется к различным видам описанных выше цифровых систем связи и запоминающих устройств.

Устройство кодирования, использующее код LDPC, генерирует блочную проверочную матрицу квазициклического кода LDPC и передает ее в кодировщик. Кодировщик выполняет обработку кодированием над входным сообщением, которое является цифровым сигналом, используя проверочную матрицу для генерирования кодового слова, и выдает его в модулятор. Модулятор передает его в тракт передачи, такой как оптическое волокно, посредством несущей волны. В качестве альтернативы, тракт передачи может быть заменен носителем информации, таким как оптический диск.

Здесь отметим, что код LDPC означает не только одиночную систему кодирования с исправлением ошибок, но используется в качестве общего термина для кодов с исправлением ошибок, имеющих такую характеристику, что проверочная матрица является разреженной (большая часть компонентов в матрице имеет значение 0, и мало количество компонентов 1). В числе таковых, квазициклический код LDPC может составлять систему кодирования ошибок, имеющую большую эффективность кодирования, благодаря использованию способа повторного декодирования, такого как алгоритм sum-product или алгоритм min-sum. В дальнейшем, это будет далее описано более подробно.

Выражение 1 показывает блочную матрицу r×n (r и n - натуральные числа, удовлетворяющие rn, и k=n-r), которая показывает блочную проверочную матрицу квазициклического кода LDPC. В матрице циклической перестановки, в качестве каждого из компонентов блочной матрицы, показанной в выражении 1, порядок u(i, j) показывает целое число между 0 и m-1 (m - целое число 1 или большее) или символ -∞ (i - целое число между 0 и r-1, а j - целое число между 0 и n-1).

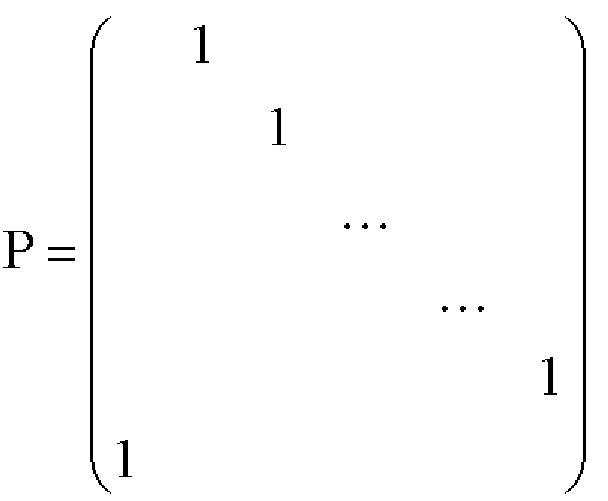
Кроме того, выражение 2 показывает матрицу P циклической перестановки m×m, показанную в выражении 1. P - матрица перестановок, в которой по одной «1» существует в каждой строке и каждом столбце, а другие компоненты имеют значение «0». Кроме того, каждая вектор-строка у P циклически сдвигается вправо от вектор-строки ее верхнего уровня. Только первый компонент вектор-строки самого верхнего каскада имеет значение «1», а другие компоненты имеют значение «0» (компонент на дальнем левом краю рассматривается в качестве 0-ого компонента).

Когда u является целым числом между 0 и m-1, «Pˆu» показывает матрицу циклической перестановки, в которой только u-ый компонент самой верхней вектор-строки имеет значение «1», а другие компоненты имеют значение «0». Здесь «u» названо в качестве порядка матрицы Pˆu циклической перестановки. Когда порядок u имеет значение «0», Pˆu является единичной матрицей, в которой только диагональные компоненты имеют значение «1». Таким образом, это, в частности, выражается как «I». Кроме того, для того чтобы упростить нотацию, матрица Pˆ-∞ циклической перестановки порядка -∞ должна показывать нулевую матрицу, в которой все компоненты имеют значение «0».

В этой связи, «A с верхним индексом B» (например, A в степени B) выражается как «AˆB», а «A с нижним индексом B» выражено в качестве «A_B» в строках текста, отличных от числовых выражений.

(Выражение 1)

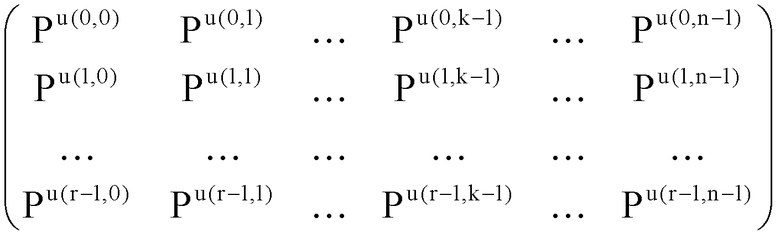
(Выражение 2)

Длина кода квазициклического кода LDPC, имеющего блочную матрицу в виде выражения 1 в качестве проверочной матрицы, имеет значение n×m битов. Среди битовых последовательностей из m×m битов, последовательности, чье матричное произведение с выражением 1 становится нулевым, рассматриваются в качестве набора строки битов передачи. На приемной стороне, делается вывод, есть или нет ошибка в строке битов приема, в зависимости от того, является ли нулевым матричное произведение строки битов приема и проверочной матрицы по выражению 1. Когда ошибка есть, обработка декодированием для исправления ошибки выполняется посредством использования проверочной матрицы с использованием алгоритма sum-product или min-sum, упомянутого выше.

Благодаря вышеприведенной обработке, квазициклический код LDPC, имеющий проверочную матрицу, показанную в выражении 1, определяется в зависимости от того, каким образом каждый порядок u(i, j) должен выбираться относительно каждого (i, j). Для определения порядка u(i, j), три момента, то есть способность исправления ошибок высока, обработка кодированием может легко выполняться, и емкость запоминающего устройства для сохранения значений каждого из порядков u(i, j) мала, могут браться в качестве руководящих принципов для определения порядка u(i, j). Технический вопрос, который должен быть преодолен, состоит в том, чтобы предоставить способ определения порядков u(i, j), который удовлетворяет трем моментам, и предоставить эффективное и экономичное устройство кодирования кода LDPC, имеющего проверочную матрицу, определенную согласно определенным порядкам u(i, j).

Среди таковых, известно, что способность исправления ошибок, в качестве первого руководящего принципа, должна зависеть от распределения весов относительно строчных и столбцовых блоков проверочной матрицы и количества коротких циклов. Распределение c(w) весов касательно строчного блока показывает, относительно положительного целого числа w, количество строчных блоков i, где количество столбцовых блоков j, удовлетворяющих u(i, j)≠-∞, соответствует w (i - целое число между 0 и r-1, j - целое число между 0 и n-1). Распределение v(w) весов касательно столбцового блока показывает количество столбцовых блоков j, где количество строчных блоков i, удовлетворяющих u(i, j)≠-∞, соответствует w.

Известно, что распределения v(w) и c(w) весов, требуемые в показателях способности исправления ошибок, могут быть вычислены посредством эволюции плотности, и тому подобного. Кроме того, цикл проверочной матрицы означает замкнутый контур, сформированный ветвями, осуществляющими соединение между вершинами, имея «1» в компонентах проверочной матрицы в качестве вершин. Количество ветвей в цикле показывает длину цикла.

Фиг. 11 - пояснительная схема, показывающая пример цикла (замкнутого контура) в проверочной матрице. На фиг. 11 проиллюстрированы цикл 801 длиной 4 и цикл 802 длиной 6. В случае использования алгоритма sum-product или min-sum, описанного выше, считается, что условие для достижения высокой способности исправления ошибок состоит в том, чтобы не иметь короткого цикла, равного или меньшего, чем длина 4, такого как цикл 801. То есть, касательно способности исправления ошибок в качестве первого руководящего принципа, необходимо принимать во внимание не только распределение весов, но также и количество коротких циклов.

В качестве технологии для преодоления описанного выше технического вопроса, есть способ, показанный в Непатентном документе 3. Эта технология определяет порядки u(i, j) как в выражении 3 (l - целое число, удовлетворяющее 0<l<r-1) касательно столбцового блока j, где j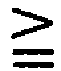k (k показывает n-r).

(Выражение 3)

(Выражение 4)

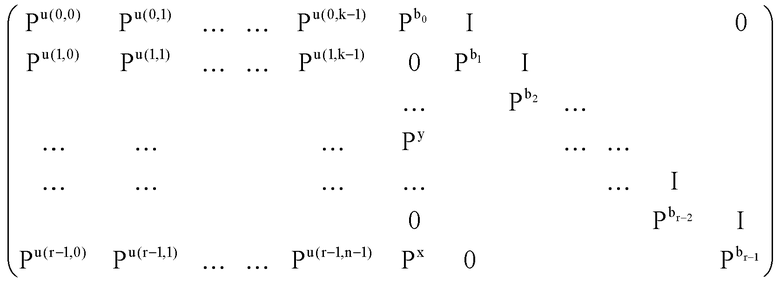
В выражении 3 и выражении 4, порядки b_0, b_1,..., b_r1, x определены, чтобы быть способными легко применять способ кодирования, изображенный в Непатентном документе 4. Для значений касательно порядков u(i, j) значения 0i<r, 0j<k, иных, чем приведенные выше, сначала делается вывод, справедливо или нет u(i, j)=-∞. Затем, значение u(i, j) определяется относительно (i, j), которое удовлетворяет u(i, j)≠-∞.

Фиг. 12 - блок-схема алгоритма, показывающая пример способа определения u(i, j) согласно технологиям, изображенным в Непатентных документах 3 и 4. В процессе обработки, показанном на фиг. 12, сначала определяются b_0, b_1,..., b_r1, x и y (этап S901), и определяются распределение c(w) весов касательно строчного блока и распределение v(w) весов касательно столбцового блока проверочной матрицы (w - целое число). Впоследствии, вычисляются распределения v(w) и c(w) весов (этап S902), а строчные и столбцовые блоки i и j, удовлетворяющие u(i, j)≠-∞, определяются согласно распределениям весов (этап S903).

Строчные и столбцовые блоки не обязательно определяются единственным образом. Кроме того, как описано выше, все блоки согласно распределениям весов, вычисленным на этапе S902, не обязательно имеют высокую способность исправления ошибок. Это в общем принимается во внимание, и строчные и столбцовые блоки i и j, удовлетворяющие u(i, j)≠-∞, определяются подряд из тех, которые сопровождают одни и те же распределения весов, посредством использования случайных чисел, при этом обращая внимание на количество коротких циклов.

Благодаря обработке вплоть до этапа S903, может быть определено, все или нет u(i, j) имеют значение -∞. В последствии, столбцовые блоки подряд выбираются из одного с наименьшим весом (этап S904), и числовое значение u(i, j*) касательно выбранного столбцового блока j* определяется таким образом, чтобы количество коротких циклов матрицы по выражению 4 становилось меньшим (этап S905). Обработка этапов с S904 по 905 повторяется до тех пор, пока не определены все u(i, j) (этап S906). Тем самым, последовательно определяются числовые значения u(i, j) относительно (i, j), удовлетворяющие u(i, j)≠-∞.

Есть следствия в качестве Патентных документов, имеющие отношение к этому. Среди них, в Патентном документе 1, изображена технология, которая уменьшает масштаб схемы устройства кодирования посредством выполнения обработки маскированием над проверочной матрицей контроля четности согласно специфичному правилу. В патентном документе 2, изображен способ генерирования проверочной матрицы, который получает множество составных показателей с помощью одиночной проверочной матрицы посредством компоновки маскированной квазициклической матрицы и матрицы циклической перестановки в предписанных положениях. В Патентном документе 3, изображен способ кодирования/декодирования, который выполняет кодирование, используя матрицу контроля четности, составленную подматрицами, имеющими специфичную регулярность по весам строк и столбцов.

Патентный документ 1: WO 2007/072721.

Патентный документ 2: WO 2007/080827.

Патентный документ 3: Публикация 2008-508776 заявки на выдачу патента Японии.

Непатентный документ 1: Robert Gallager, «Low-density-parity-check Codes», IEEE Transoperations on InformationTheory, January, 1962, pp 21-28.

Непатентный документ 2: D. J. C. Mackay, «Good Error-Correcting Codes Based on very sparse matrices», IEEE Transoperations on InformationTheory, March, 1999, pp 339-431.

Непатентный документ 3: Myung, Yang, Kim, «Quasi-Cyclic LDPC Codes for Fast Encoding», IEEE Transoperations on InformationTheory, August, 2005, pp 2894-2901.

Непатентный документ 4: Richardson, Urbanke, «Efficient Encoding Of Low-density-parity-check Codes», IEEE Transoperations on InformationTheory, February, 2001, pp 638-656.

В проверочной матрице в виде выражения 4, определенного описанной выше технологией, между значениями каждого из порядков u(i, j) наблюдают не регулярность, а случайность. Таким образом, необходимо иметь область хранения размера (k_r) log (2_m), для того чтобы сохранять проверочную матрицу, требуемую в конструкции устройства кодирования или декодирования. Однако, когда есть регулярность между значениями каждого из порядков u(i, j), характеристика частоты появления ошибок ухудшается.

Поэтому много областей хранения требуется для сохранения проверочной матрицы, требуемой в устройстве кодирования и устройстве декодирования квазициклического кода LDPC. В частности, в системе связи, которая использует множество разных кодов LDPC разных скоростей кодирования, длин кадра, характеристики частоты появления ошибок, и тому подобного, согласно факторам, таким как состояние тракта связи, есть такие проблемы, что по-прежнему большее количество областей хранения требуются для сохранения проверочной матрицы, и время, требуемое для переключения устройства кодирования, становится большим.

Патентные документы 1 и 2 предназначены для преодоления описанных выше проблем и эффективны в уменьшении области хранения, требуемой для использования множества кодов LDPC. Однако нет специального соображения, предпринятого для укорачивания времени, требуемого для переключения, так что они не преодолевают такой проблемный момент. Этот момент не учитывается технологиями в Патентном документе 3 и Непатентных документах с 1 по 4, так что он не может быть преодолен комбинированием таких технологий.

Задача настоящего изобретения состоит в том, чтобы предложить устройство кодирования, способ конфигурирования кода с исправлением ошибок и их программу, которые могут уменьшать область хранения, требуемую для использования множества кодов контроля четности с низкой плотностью (LDPC), и сокращать время для переключения во время использования таковых надлежащим образом.

РАСКРЫТИЕ ИЗОБРЕТЕНИЯ

Для того чтобы решить вышеизложенную задачу, устройство кодирования согласно настоящему изобретению является устройством кодирования для построения квазициклического кода контроля четности с низкой плотностью, которое включает в себя: модуль генерирования проверочной матрицы, который генерирует блочную проверочную матрицу квазициклического кода контроля четности с низкой плотностью, которая имеет матрицу циклической перестановки, где количество строк и количество столбцов оба имеют значение q-1, или нулевую матрицу в качестве компонентов (q - целое число 4 или большее, и является степенью 2), количество строчных блоков имеет значение r, а количество столбцовых блоков имеет значение q+1 (r - целое число между 4 и q включительно), и компоненты i-ого строчного блока и j-ого столбцового блока (i - целое число между 0 и r-1, j - целое число между 0 и q, крайний левый столбец матрицы определен в качестве 0-ого столбца, а крайняя верхняя строка определена в качестве 0-ой строки) соответствуют нулевой матрице или матрице циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i в качестве аргумента; и модуль кодирования, который генерирует и выдает кодовое слово посредством блочной проверочной матрицы из введенного сообщения, при этом, модуль генерирования проверочной матрицы дополнительно включает в себя: блок назначения порядка, который предписывает значение функции λ(j-i) блочной проверочной матрицы посредством коэффициента самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней; блок определения распределения весов, который предписывает количество компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока блочной проверочной матрицы и количество компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого строчного блока блочной проверочной матрицы посредством использования заданного шаблона маски; первый блок изменения порядка, который берет полную сумму компонентов k_r-ого блока (k_r - целая часть (q+1-r)/2) блочной проверочной матрицы в качестве матрицы циклической перестановки; и второй блок изменения порядка, который предписывает количество компонентов строчного блока, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока, за исключением k_r-ого столбцового блока блочной проверочной матрицы.

Для того чтобы решить вышеизложенную задачу, способ конфигурирования кода с исправлением ошибок согласно настоящему изобретению является способом конфигурирования кода с исправлением ошибок для построения квазициклического кода контроля четности с низкой плотностью, который включает в себя: генерирование посредством модуля генерирования проверочной матрицы блочной проверочной матрицы квазициклического кода контроля четности с низкой плотностью, которая имеет матрицу циклической перестановки, где количество строк и количество столбцов оба имеют значение q-1, или нулевую матрицу в качестве компонентов (q - целое число 4 или большее, и является степенью 2), количество строчных блоков имеет значение r, а количество столбцовых блоков имеет значение q+1 (r - целое число между 4 и q включительно), и компоненты i-ого строчного блока и j-ого столбцового блока (i - целое число между 0 и r-1, j - целое число между 0 и q, крайний левый столбец матрицы определен в качестве 0-ого столбца, а крайняя верхняя строка определена в качестве 0-ой строки) соответствуют нулевой матрице или матрице циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i в качестве аргумента; и генерирование и выдачу, модулем кодирования, кодового слова посредством блочной проверочной матрицы из введенного сообщения. Способ дополнительно включает в себя: при генерировании блочной проверочной матрицы, предписание, блоком назначения порядка, значения функции λ(j-i) блочной проверочной матрицы посредством коэффициента самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней; предписание, блоком определения распределения весов, количества компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока блочной проверочной матрицы и количества компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого строчного блока блочной проверочной матрицы посредством использования заданного шаблона маски; взятие, первым блоком изменения порядка, полной суммы компонентов k_r-ого блока (k_r - целая часть (q+1-r)/2) блочной проверочной матрицы в качестве матрицы циклической перестановки; и предписание, вторым блоком изменения порядка, количества компонентов строчного блока, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока, за исключением k_r-ого столбцового блока блочной проверочной матрицы.

Для того чтобы решить вышеизложенную задачу, программа конфигурирования кода с исправлением ошибок согласно настоящему изобретению является программой конфигурирования кода с исправлением ошибок для построения квазициклического кода контроля четности с низкой плотностью, которая побуждает компьютер выполнять: функцию генерирования блочной проверочной матрицы квазициклического кода контроля четности с низкой плотностью, которая имеет матрицу циклической перестановки, где количество строк и количество столбцов оба имеют значение q-1, или нулевую матрицу в качестве компонентов (q - целое число 4 или большее, и является степенью 2), количество строчных блоков имеет значение r, а количество столбцовых блоков имеет значение q+1 (r - целое число между 4 и q включительно), и компоненты i-ого строчного блока и j-ого столбцового блока (i - целое число между 0 и r-1, j - целое число между 0 и q, крайний левый столбец матрицы определен в качестве 0-ого столбца, а крайняя верхняя строка определена в качестве 0-ой строки) соответствуют нулевой матрице или матрице циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i в качестве аргумента; и функцию генерирования и выдачи кодового слова посредством блочной проверочной матрицы из введенного сообщения. Программа дополнительно побуждает компьютер, при генерировании блочной проверочной матрицы, выполнять: функцию предписания значения λ(j-i) функции блочной проверочной матрицы посредством коэффициента самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней; функцию предписания количества компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока блочной проверочной матрицы и количества компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого строчного блока блочной проверочной матрицы посредством использования заданного шаблона маски; функцию взятия полной суммы компонентов k_r-ого блока (k_r - целая часть (q+1-r)/2) блочной проверочной матрицы в качестве матрицы циклической перестановки; и функцию предписания количества компонентов строчного блока, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока, за исключением k_r-ого столбцового блока блочной проверочной матрицы.

Как описано выше, настоящее изобретение сконструировано в качестве конструкции, в которой: порядки матрицы циклической перестановки имеют значения λ(j-i), когда компоненты i-ой строки и j-ого столбца блочной проверочной матрицы не являются нулевой матрицей; порядки матрицы циклической перестановки имеют значения λ(j-i), когда компоненты i+1-ой строки и j+1-ого столбца блочной проверочной матрицы не являются нулевой матрицей; и порядки матрицы циклической перестановки имеют значения λ(j-i), когда компоненты i+2-ой строки и j+2-ого столбца блочной проверочной матрицы, компоненты i+3-ей строки и j+3-его столбца блочной проверочной матрицы, и после этого, не являются нулевой матрицей. Таким образом, область хранения, требуемая для сохранения проверочной матрицы, сгенерированной настоящим изобретением, может быть уменьшена до приблизительно (q+1-r)×r битов. Кроме того, использование шаблона маски дает возможность генерировать много видов проверочных матриц разных скоростей кодирования из одних и тех же данных и, кроме того, мгновенно переключать проверочные матрицы.

Тем самым, можно предоставить устройство кодирования, способ конфигурирования кода с исправлением ошибок и их программу, которые демонстрируют превосходные характеристики, такие как способность уменьшать область хранения, требуемую для использования множества кодов контроля четности с низкой плотностью (LDPC), и сокращать время для переключения во время использования таковых надлежащим образом.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Фиг. 1 - пояснительная схема, показывающая систему связи, которая включает в себя устройство кодирования согласно первому примерному варианту осуществления настоящего изобретения;

фиг. 2 - пояснительная схема, показывающая более подробную структуру модуля генерирования проверочной матрицы, показанного на фиг. 1;

фиг. 3 - блок-схема алгоритма, показывающая операции для генерирования блочной проверочной матрицы, выполняемые модулем генерирования проверочной матрицы, показанным на фиг. 2;

фиг. 4 - блок-схема алгоритма, показывающая подробности обработки, выполняемой вторым блоком изменения порядка, показанным в качестве этапа S104 на фиг. 3;

фиг. 5 - пояснительная схема для описания структуры модуля кодирования, показанного на фиг. 1;

фиг. 6 - пояснительная схема, показывающая пример проверочной матрицы, получаемой посредством операций, показанных в специфичном примере работы;

фиг. 7 - пояснительная схема, показывающая пример проверочной матрицы, получаемой посредством операций, показанных в специфичном примере работы;

Фиг. 8 - пояснительная схема, показывающая систему связи, которая включает в себя устройство кодирования согласно второму примерному варианту осуществления настоящего изобретения;

фиг. 9 - пояснительная схема, показывающая более подробную структуру модуля генерирования проверочной матрицы, показанного на фиг. 8;

фиг. 10 - блок-схема алгоритма, показывающая операции для генерирования блочной проверочной матрицы, выполняемые модулем генерирования проверочной матрицы, показанным на фиг. 8;

фиг. 11 - пояснительная схема для описания примера циклов (замкнутых контуров) длиной 4 и длиной 6 в проверочной матрице; и

фиг. 12 - блок-схема алгоритма, показывающая пример способа определения u(i, j) согласно технологиям, изображенным в Непатентных документах с 3 по 4.

НАИЛУЧШИЕ ВАРИАНТЫ ДЛЯ ОСУЩЕСТВЛЕНИЯ ИЗОБРЕТЕНИЯ

<ПЕРВЫЙ ПРИМЕРНЫЙ ВАРИАНТ ОСУЩЕСТВЛЕНИЯ>

В дальнейшем, конструкция по первому примерному варианту осуществления настоящего изобретения будет описана посредством ссылки на фиг. 1 прилагаемых чертежей.

Сначала будет описано базовое содержание примерного варианта осуществления, а более специфичное его содержание будет описано в дальнейшем.

Как показано на фиг. 1, устройство 10 кодирования согласно примерному варианту осуществления включает в себя: модуль 11 генерирования проверочной матрицы, который генерирует блочную проверочную матрицу квазициклического кода контроля четности с низкой плотностью (LDPC), которая является матрицей циклической перестановки, где количество строк и количество столбцов оба имеют значение q-1, или нулевой матрицей в качестве компонентов (q - целое число 4 или большее, и является степенью 2), количество строчных блоков имеет значение r, а количество столбцовых блоков имеет значение q+1 (r - целое число между 4 и q включительно), и компоненты i-ого строчного блока и j-ого столбцового блока (i - целое число между 0 и r-1, j - целое число между 0 и q, крайний левый столбец матрицы определен в качестве 0-ого столбца, а крайняя верхняя строка определена в качестве 0-ой строки) соответствуют нулевой матрице или матрице циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i в качестве аргумента; и модуль 12 кодирования, который генерирует и выдает кодовое слово посредством блочной проверочной матрицы из введенного сообщения.

Кроме того, модуль 11 генерирования проверочной матрицы включает в себя: блок 11a назначения порядка, который предписывает значение функции λ(j-i) блочной проверочной матрицы посредством коэффициента самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней; блок 11b определения распределения весов, который предписывает количество компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока блочной проверочной матрицы и количество компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого строчного блока блочной проверочной матрицы посредством использования заданного шаблона маски; первый блок 11c изменения порядка, который берет полную сумму компонентов k_r-ого блока (k_r - целая часть (q+1-r)/2) блочной проверочной матрицы в качестве матрицы циклической перестановки; и второй блок 11d изменения порядка, который предписывает количество компонентов строчного блока, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока, за исключением k_r-ого столбцового блока блочной проверочной матрицы.

Кроме того, модуль 12 кодирования включает в себя: память 33 сохранения матричных данных, которая хранит блочную проверочную матрицу, сгенерированную модулем генерирования проверочной матрицы, и шаблон маски; устройства 31 умножения r фрагментов матриц, которые вычисляют матричные произведения строк битов информации сообщения и матрицы циклической перестановки, чей порядок является значением функции λ(j-i), имеющей в качестве аргумента целое число j-i, предписанное коэффициентом самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней; и селектор 32, который переключает входные сигналы в устройства матричного умножения согласно шаблону маски, сохраненному в памяти сохранения матричных данных.

Кроме того, память 33 сохранения матричных данных включает в себя: функцию, которая удерживает номера строк всех строчных блоков, чьи компоненты в столбцовых блоках являются ненулевыми матрицами циклической перестановки во всех столбцовых блоках из множества блочных проверочных матриц; и функцию, которая изменяет входные сигналы в селектор для каждой из блочных проверочных матриц.

Посредством обеспечения такой структуры, устройство 10 кодирования может уменьшать область хранения, требуемую при использовании множества кодов LDPC, различимым образом и сокращать служебные сигналы или данные, требуемые для их переключения.

В дальнейшем, это будет описано подробнее.

Фиг. 1 - пояснительная схема, показывающая систему 1 связи, которая включает в себя устройство 10 кодирования согласно первому примерному варианту осуществления настоящего изобретения. Система 1 связи составлена из: устройства 10 кодирования, которое генерирует кодовое слово из сообщения, которое является цифровым сигналом, введенным из устройства связи, запоминающего устройства, или тому подобного; модулятора 21, который модулирует кодовое слово, выведенное из устройства 10 кодирования, и загружает его в несущую волну; тракта 22 передачи, который передает несущую волну, выданную из модулятора 21; демодулятора 23, который извлекает кодовое слово из несущей волны, переданной через тракт 22 передачи; и устройства 24 декодирования, которое декодирует извлеченное кодовое слово и получает исходное сообщение. В качестве альтернативы, тракт 22 передачи может быть заменен носителем информации, таким как оптический диск или магнитный диск.

Устройство 10 кодирования включает в себя: модуль 11 генерирования проверочной матрицы, который генерирует блочную проверочную матрицу квазициклического кода LDPC; и модуль 12 кодирования, который генерирует кодовое слово из введенного сообщения посредством использования блочной проверочной матрицы. Выражение 5 показывает блочную проверочную матрицу, сгенерированную модулем 11 генерирования проверочной матрицы.

(Выражение 5)

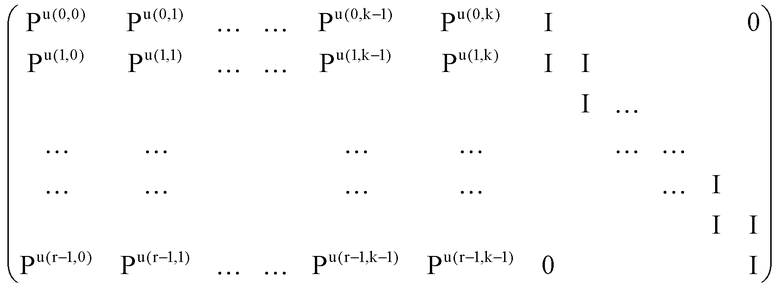
В этой связи, в выражении 5, u(i, j), определенное в отношении 0i<r, k<j<n в выражении 1, описанном выше, определяется как u(i, j)=0, только когда применяется j=k+i, или j=k+1+i, и определяется как u(i, j)=-∞ в других случаях.

Для того чтобы упросить разъяснения в дальнейшем, q определяется в качестве степени 2 (q=2ˆs; s - целое число 2 или большее), r определено в качестве положительного целого числа между 4 и q, включительно, а k определено в качестве q+1-r. Кроме того, каждое из количества строк и количества столбцов матрицы P циклической перестановки, показанной на фиг. 2, определено в качестве q-1. Выражение 5 является блочной матрицей, в которой количество строчных блоков имеет значение r, а количество n столбцовых блоков имеет значение (q+1).

Фиг. 2 - пояснительная схема, показывающая более подробную структуру модуля 11 генерирования проверочной матрицы, показанного на фиг. 1. Кроме того, фиг. 3 - блок-схема алгоритма, показывающая операции для генерирования блочной проверочной матрицы (выражение 5), выполняемые модулем 11 генерирования проверочной матрицы, показанным на фиг. 2. Операции предназначены для определения u(i, j) для фрагментов r×(k+1) компонентов блочной проверочной матрицы, показанной в выражении 5 (i - целое число между 0 и r-1, j - целое число между 0 и k).

Модуль 11 генерирования проверочной матрицы включает в себя операционные блоки, такие как блок 11a назначения порядка, блок 11b определения распределения весов, первый блок 11c изменения порядка и второй блок 11d изменения порядка.

Блок 11a назначения порядка сначала назначает u(i, j)=λ(j-i) всем u(i, j) (этап S101). Отметим, что λ(t) - положительное целое число, определенное благодаря процедуре, описанной следующей, когда t+r+(q/2) не может быть поделено на q+1 для целого числа t. Когда t+r+(q/2) является кратным q+1, определяется, что λ(t)=-∞.

Будет описан способ для определения λ(t) для целого числа t. β определено в качестве примитивного элемента поля Галуа, GF(qˆ2). Для всех целых чисел h, удовлетворяющих -(q-2)/2h (q-2)/2, многочлен выражения 6, имеющий βˆh в качестве нуля, определен как g(x), а коэффициент его члена порядка t определен как g_t.

(Выражение 6)

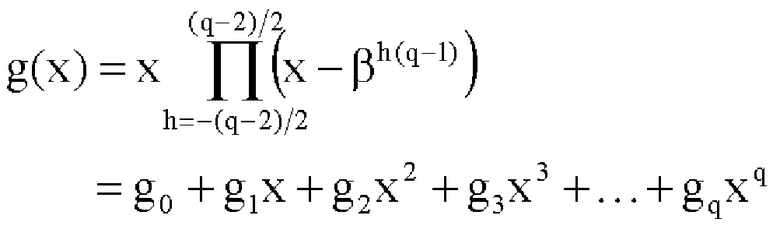
Коэффициент g_t выражения 6, упомянутый выше, имеет значение g_0=0, и он имеет значение g_t=g_(q+1-t) для случаев 0<tq. Такой многочлен, у которого нет никаких изменений, даже когда его коэффициент члена низкого порядка и коэффициент члена высокого порядка находятся в обратной очередности, называется самодвойственным многочленом. Кроме того, касательно 0<tq, коэффициент g_t может быть выражен степенью βˆt посредством использования примитивного элемента β. Показательная функция выражена в качестве μ(t). То есть g_t=(βˆ(q+1))ˆμ(t). Аргумент t у μ(t) расширен до всех целых чисел за исключением кратных q+1, чтобы иметь значение μ(t)=μ(t mod (q+1)). Кроме того, что касается целого числа t, при котором t+r+(q/2) не может делиться на q+1, λ(t), упомянутое выше, определено в качестве выражения 7 посредством использования целого числа μ(t).

(Выражение 7)

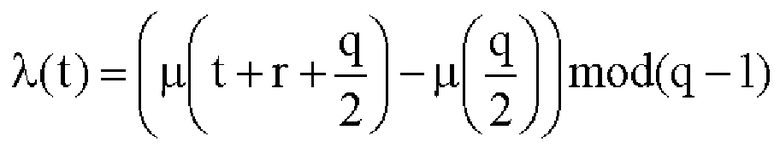
Кроме того, что касается целого числа t, при котором t+r+(q/2) может делиться на q+1, оно определено в качестве λ(t)=-∞ для целей удобства. Как описано выше, целочисленное значение λ(t) вычисляется на этапе S101, и u(i, j)= λ(j-i) устанавливается для всех u(i, j). Посредством этого, выражение 1, упомянутое выше, может быть выражено в виде выражения 8, показанного ниже.

(Выражение 8)

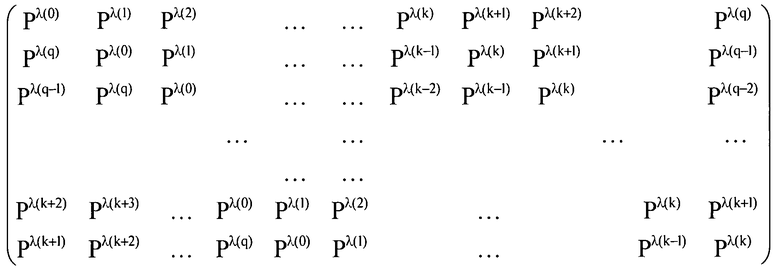
Затем, блок 11b определения распределения весов определяет распределение весов касательно строчных блоков и столбцовых блоков проверочной матрицы выражения 8, упомянутого выше (этап S102). Ввиду повышения возможности исправления ошибок, нормально, распределение весов определяется посредством использования эволюции плотности. Однако способ в материалах настоящей заявки не ограничен эволюцией плотности. Должно быть отмечено, что вес столбца определен как 2 для всех блоков с k+1-ого столбцового блока по q-ый столбцовый блок.

Все u(i, j) уже определены в качестве λ(j-i) на этапе S101. Однако часть u(i, j) превращается этапами с S103 по 104, показанными в последующем, в -∞ для приведения в соответствие распределению весов, вычисленному на этапе S102.

Поскольку λ(k)=λ(k+1)=0 из выражения 7, упомянутого выше, матрица по выражению 8 становится находящейся в форме матрицы по выражению 5 посредством превращения u(i, j) относительно 0i<r, k<j<n в u(i, j)= -∞ в случае, где j≠k+i, и j≠k+1+i. Поэтому должно быть отмечено, что u(i, j) относительно 0i<r, k<j<n изменяется в качестве u(i, j)=-∞ в случае, где j≠k+i, и j≠k+1+i.

Первый блок 11c изменения порядка превращает часть u(i, k_r) в -∞, так что полная сумма компонентов k_r-ого столбцового блока становится матрицей циклической перестановки (этап S103). Отметим здесь, что k_r показывает целочисленные значения, показанные в следующем выражении 9.

(Выражение 9)

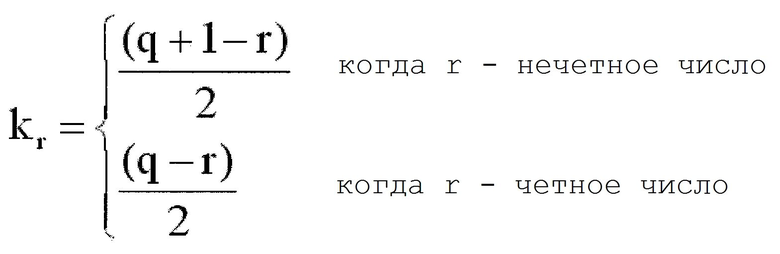
То есть, k_r показывает целую часть (q+1-r)/2. Пример способа превращения части u(i, k_r) в -∞, так чтобы полная сумма компонентов k_r-ого столбцового блока становилась матрицей циклической перестановки, будет описан позже.

Второй блок 11c изменения порядка превращает часть u(i, k_r) в -∞ для каждого столбцового блока j, иного чем k_r-ый столбцовый блок, для которого обработка выполняется на этапе S103 (этап S104). В это время, это делается для удовлетворения распределения весов, определенного на этапе S102, и для уменьшения количества коротких циклов, описанных на фиг. 10, как можно меньше. Подробности обработки этапа S104 также будут описаны позже.

Операции модуля 11 генерирования проверочной матрицы будут описаны дополнительно. Как описано выше, модуль 11 генерирования проверочной матрицы определяет все u(i, j) проверочной матрицы, показанной в выражении 5 (i - целое число между 0 и r-1, а j - целое число между 0 и k). Как описано выше, оно определяется на этапе S101 в качестве u(i, j)=λ(j-i) согласно λ(t), показанному в выражении 7. На следующем этапе S102, часть u(i, j) превращается из λ(j-i) в -∞ согласно заданному распределению весов проверочной матрицы. Относительно каждого из i и j, m(i, j) определяется в качестве 1 или 0, а матрица следующего выражения 10 выражается как H(m). Кроме того, u(i, j)*m(i, j) в выражении 10 определено, как в выражении 11.

(Выражение 10)

(Выражение 11)

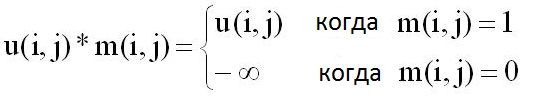
Как очевидно из выражения 10 и выражения 11, принимается во внимание, что m(i, j) обозначает, следует или нет менять значение u(i, j) с λ(j-i) на -∞ согласно его значению. То есть для каждого из i и j, посредством установки m(i, j), чтобы придерживалось распределений c(w) и v(w) весов, блочная матрица H(m) по выражению 10 становится требуемой проверочной матрицей. Что касается положительного целого числа w, распределение c(w) весов относительно строчных блоков показывает количество строк i, где количество столбцов j, удовлетворяющих u(i, j)*m(i, j)≠-∞, соответствует w, и распределение v(w) весов относительно столбцовых блоков показывает количество столбцов j, где количество строк i, удовлетворяющих u(i, j)*m(i, j)≠-∞, соответствует w. Благодаря изменению значения m(i, j), матрица H(m) также изменяется. Поэтому может быть выражено множество проверочных матриц.

Как описано выше, что касается m(i, j) при 0i<r и k<jq, оно определено в качестве m(i, j)=1, только когда j=k+i, или j=k+1+i, и оно зафиксировано в качестве m(i, j)=0 в других случаях. Таким образом, в этом случае, количество требуемых битов для выражения одиночной проверочной матрицы имеет значение k×r битов. Как описано, m(i, j) действует для маскирования каждого компонента блочной матрицы исходного выражения 5, и m(i, j) названо шаблоном маски.

На этапе S103, первый блок 11c изменения порядка определяет строку i, удовлетворяющую u(i, k_r)=-∞ относительно k_r-ого столбца (k_r является таким, как показано в выражении 9). Использование описанного выше способа эквивалентно определению значения m(i, k_r) относительно всех 0i<r. Вес k_r-ого столбца устанавливается имеющим значение нечетного числа 3 или большего. Для того чтобы упростить пояснения, вес k_r-ого столбца установлен в качестве 3, и описан способ установки значения m(i, k_r), так чтобы полная сумма k_r-столбцового блока матрицы H(m), показанной в выражении 10, становилась матрицей циклической перестановки, посредством установки t. Прежде всего, в случае, где r - нечетное число, значение m(i, k_r) определяется следующим выражением 12.

(Выражение 12)

Благодаря установке значений способом, описанным выше, полная сумма каждого из компонентов k_r-ого столбцового блока матрицы H(m), показанной в выражении 10, становится матрицей циклической перестановки, чей порядок имеет значение u((r+1)/2, k_r). Кроме того, в случае, где r - четное число 6 или большее, значение m(i, k_r) определяется посредством следующего выражения 13.

(Выражение 13)

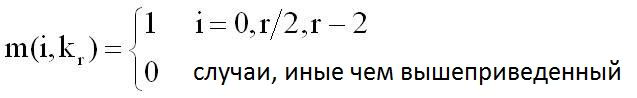
В это время, полная сумма каждого из компонентов k_r-ого столбцового блока матрицы H(m), показанной в выражении 10, становится матрицей циклической перестановки, чей порядок имеет значение u(r/2, k_r). Наконец, в случае, где r имеет значение 4, определено, что m(0, k_4)=1, m(1, k_4)=0, m(2, k_4)=1, и m(3, k_4)=1. В это время, полная сумма каждого из компонентов k_4-ого столбцового блока матрицы H(m) становится матрицей циклической перестановки, чей порядок имеет значение u(3, k_4).

На следующем этапе S104, второй блок 11d изменения порядка определяет значения m(i, j) для всех столбцов j за исключением k_r-ого столбца. Фиг. 4 - блок-схема алгоритма, показывающая подробности обработки, выполняемой вторым блоком 11d изменения порядка, показанным в качестве этапа S104 на фиг. 3. Прежде всего, второй блок 11d изменения порядка осуществляет установку в качестве m(i, j)=0 для всех столбцов j за исключением k_r-ого столбца, в качестве начального состояния (этап S201).

Впоследствии, второй блок 11d изменения порядка определяет строки i, удовлетворяющие m(i, j)=1, для каждого столбца j (этапы с S202 по 204). Сначала, в случае, где вес столбца j (количество строк i, удовлетворяющих m(i, j)=1, является нулевым), выбирается номер i строки, удовлетворяющей u(i, j)≠-∞ и имеющей наименьший вес среди строчных блоков H(m) (i - целое число между 0 и r-1) касательно матрицы H(m), показанной в выражении 10, и он определяется в качестве m(i, j)=1 (этап S205).

Затем, выбирается номер i строки, удовлетворяющей u(i, j)≠-∞ и имеющей самую длинную минимальную длину цикла в матрице H(m), и при котором количество циклов минимальной длины становится минимальным, и он определяется в качестве m(i, j)=1 (этап S206). В случае, где номер i строки не определен уникально, он определяется случайным образом из номеров строк, удовлетворяющих описанному выше условию.

После этого, обработка по этапам с S204 по 206 продолжается (этапы с S207 по 208) до тех пор, пока вес столбца j (количество номеров i строк, удовлетворяющих m(i, j)=1) не совпадает с весом (вес столбца j выражен в качестве wt(j) на фиг. 4), определенным для каждого столбца на этапе S102 по фиг. 3. Проверочная матрица H(m) получается посредством выполнения обработки до этого для всех столбцов за исключением столбца k_r (этапы с S209 по 210).

Для того чтобы упростить обработку кодированием, проверочная матрица, вычисленная в описанной выше процедуре, используется посредством замены k-ого столбцового блока столбцовым блоком, полученным равномерным циклическим сдвигом каждого из компонентов k_r-ого столбцового блока, так что полная сумма k_r-ого столбцового блока становилась единичной матрицей. Кроме того, блочная проверочная матрица r×n относительно целого числа n, которое не соответствует q+1, генерируется посредством генерирования блочной матрицы r×(q+1) описанным выше средством касательно n<q+1 и выбором n-фрагментов столбцовых блоков, содержащих в себе r-фрагментов столбцовых блоков на правом краю из числа q+1-фрагментов столбцовых блоков.

Фиг. 5 - пояснительная схема для описания структуры модуля 12 кодирования, показанного на фиг. 1. С помощью способа генерирования проверочной матрицы, описанного выше, можно осуществлять изменения в отношении кода, имеющего еще один параметр, простым изменением шаблона m(i, j) маски. Таким образом, как будет описано далее, модуль 12 кодирования может конструироваться, чтобы быть совместимым, посредством простого изменения шаблона маски.

Модуль 12 кодирования включает в себя такое же количество устройств 31_0, 31_1,..., 31_(r-1) матричного умножения, как количество r строчных блоков проверочной матрицы, показанной в выражении 5. Модуль 12 кодирования также включает в себя селекторы 32_0, 32_1,..., 32_(r-1) для отбора входных данных в r фрагментов устройств 31 матричного умножения и память 33 сохранения матричных данных для выдачи данных r битов, которые должны быть сигналом переключения селекторов. Кроме того, модуль 12 кодирования также включает в себя устройства 34, 35_0, 35_1,..., 35_(r-2) вычисления исключающего ИЛИ и селектор 36.

Кроме того, модуль 12 кодирования может изменять проверочную матрицу кода LDPC, чтобы она использовалась согласно данным, удерживаемым в памяти 33 сохранения матричных данных. В этом случае, область хранения, требуемая для сохранения одиночного фрагмента матричных данных, имеет k×r битов.

В дальнейшем, описан пример случая, где модуль 12 кодирования выполняет кодирование строки битов информации входного сообщения посредством квазициклического кода LDPC с проверочной матрицей, показанной в выражении 10, добавляет (q-1)×r битов с битами четности во входные данные количества битов информации в (q-1)×k битов и выводит таковые. В этом случае, один кадр составлен битами информации и избыточными битами. Суммарное количество битов одного кадра становится qˆ2-1 битами, поскольку k=q+1-r, как описано выше.

Биты четности из (q-1)×r битов определены таким образом, чтобы произведение проверочной матрицы и матрицы кадра становилось нулевым. Модуль 12 кодирования вводит биты информации k-раз каждыми (q-1) битами и вводит каждые из таковых в r-фрагментов устройств 31 матричного умножения через селектор 32.

i-е устройство 31_i матричного умножения (i - целое число между 0 и r-1) включает в себя регистр внутри него. Когда строка битов информации, составленная j-ыми q-1 битами из числа k-раз вводов данных битов информации, вводится в селектор 32 (j - целое число между 0 и k-1), i-ое устройство 31_i матричного умножения вычисляет матричное произведение выходных данных селектора 32 и матрицы Pˆu(i, j), и результаты, полученные сложением вычисленного результата и данных, удерживаемых внутри регистра устройства 31l матричного умножения, сохраняются в тот же самый регистр.

Здесь отметим, что начальное значение внутри регистра устройства 31l матричного умножения установлено в 0, и «сложение» в материалах настоящей заявки означает операцию исключающего ИЛИ каждого бита. Кроме того, селектор 32 принимает строку битов информации, составленную j-ыми q-1 битами, нулевым битом и выходными данными устройства 34 вычисления исключающего ИЛИ, и берет шаблон m(i, j) маски, сохраненный в память 33 сохранения матричных данных, в качестве сигнала переключения. Селектор 32 выдает строку битов информации, составленную j-ыми q-1 битами в устройство 31l матричного умножения, как описано выше, когда m(i, j)=1, и выдает нулевой бит в устройство 31l матричного умножения, когда m(i, j)=0.

Когда строка битов информации из (q-1)×k битов записана как a_0ˆ(j), a_1ˆ(j),..., a_(q-2)ˆ(j), j=0, 1,..., и k-1, q-1-битные данные b_0ˆ(i), b_1ˆ(i),..., b_(q-2)ˆ(i), i=0, 1,..., r-1, удерживаемые внутри регистра устройства 31_i матричного умножения на стадии, где все биты информации полностью введены, соответствуют данным, выраженным в качестве матрицы в следующем выражении 14.

(Выражение 14)

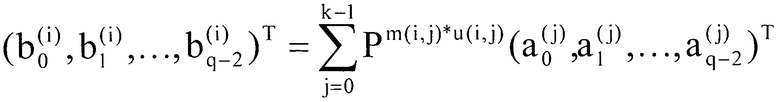
В выражении 14, T показывает транспонированную матрицу. b_0ˆ(i), b_1ˆ(i),..., b_(q-2)ˆ(i),..., i=0, 1,..., r-1 складываются по каждому биту посредством исключающего ИЛИ 34 и становятся битами p_0ˆ(0), p_1ˆ(0),..., p_(q-2)ˆ(0) четности q-1 битов, показанных в выражении 15.

(Выражение 15)

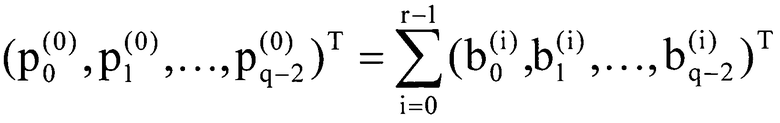
Биты p_0ˆ(0), p_1ˆ(0),..., p_(q-2)ˆ(0) четности, показанные в выражении 15, вводятся в селектор 32_i (i - целое число между 0 и r-1), выбранный согласно сигналу m(i, k) переключения, выдаваемому памятью 33 сохранения матричных данных, и вводятся в r-фрагментов устройств 31 матричного умножения. Как результат, данные b_0ˆ(i), b_1ˆ(i),..., b_(q-2)ˆ(i), i=0, 1,..., r-1, удерживаемые внутри регистра устройства 31_i матричного умножения (i - целое число между 0 и r-1), обновляются, как показано в следующем выражении 16.

(Выражение 16)

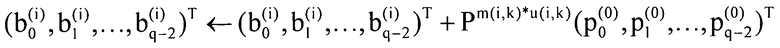
Модуль 12 кодирования использует обновленные данные b_0ˆ(i), b_1ˆ(i),..., b_(q-2)ˆ(i),..., i=0, 1,..., r-1 для расчета строки p_0ˆ(i), p_1ˆ(i),..., p_(q-2)ˆ(i),..., битов четности, i=1, 2,..., r-1, составленной оставшимися (q-1)×(r-1) битами, посредством обратной подстановки, как показано в выражении 17.

(Выражение 17)

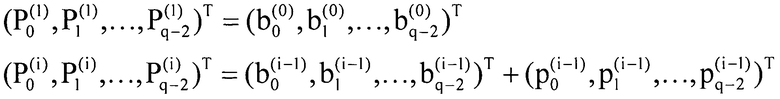
Матричное произведение векторов, составленных строкой a_0ˆ(j), a_1ˆ(j),..., a_(q-2)ˆ(j), j=0, 1,..., k-1 битов информации из (q-1)×k битов, (q-1)×r-битной строкой p_0ˆ(i), p_1ˆ(i),..., p_(q-2)ˆ(i),..., i=1, 2,..., r-1 битов четности, рассчитанное посредством этого благодаря описанной выше процедуре и проверочной матрице по выражению 10, становится нулевым. Модуль 12 кодирования может использоваться в качестве устройства кодирования, соответствующего другой проверочной матрице, простым увеличением области хранения для k×r битов благодаря изменению шаблона маски, удерживаемого в запоминающем устройстве сохранения матричных данных, данным образом.

(Специфичный пример работы)

В дальнейшем, содержание работы модуля 11 генерирования проверочной матрицы будет описано посредством использования специфичных примеров числовых значений, и будет описан пример проверочной матрицы, сгенерированной модулем 11 генерирования проверочной матрицы согласно примерному варианту осуществления. При условии, что q имеет значение 2ˆ6 (=64), модуль 11 генерирования проверочной матрицы может генерировать проверочную матрицу кода LDPC, чья длина кода имеет значение qˆ2-1=4095 битов или меньше.

Таким образом определяется, что β является примитивным элементом поля Галуа, GF(2ˆ6), и βˆ6+β+1=0. В это время, шестьдесят четыре целых числа μ(1), μ(2),..., μ(64), выведенные из коэффициента g_t членов порядка t (t - целое число между 1 и 64) многочлена g(x) по выражению 7, имеют значения 0, 61, 39, 57, 22, 13, 60, 49, 25, 42, 17, 24, 23, 55, 7, 33, 27, 48, 53, 19, 62, 32, 59, 46, 36, 44, 41, 45, 31, 12, 52, 1, 1, 52, 12, 31, 45, 41, 44, 36, 46, 59, 32, 62, 19, 53, 48, 27, 33, 7, 55, 23, 24, 17, 42, 25, 49, 60, 13, 22, 57, 39, 61 и 0, соответственно.

При условии, что количеством r строчных блоков является 18, λ(0), λ(1),..., λ(64) по выражению 7 имеют значения 6, 54, 22, 23, 16, 41, 24, 48, 59, 12, 21, 56, 38, 60, 62, -∞, 62, 60, 38, 56, 21, 12, 59, 48, 24, 41, 16, 23, 22, 54, 6, 32, 26, 47, 52, 18, 61, 31, 58, 45, 35, 43, 40, 44, 30, 11, 51, 0, 0, 51, 11, 30, 44, 40, 43, 35, 45, 58, 31, 61, 18, 52, 47, 26 и 32, соответственно.

Как в операциях блока 11a назначения порядка (этапа S101), показанных на фиг. 2-3, оно устанавливается в u(i, j)=λ(j-i) для всех u(i, j) (0i<18, 0j<65). Что касается m(i, j) при 0i<18, 48j<65, оно определяется как m(i, j)=1, только когда j=47+i, или j=48+i, и фиксируется как m(i, j)=0 в других случаях.

Распределение весов блока 11b определения распределения весов (этапа S102) определено как v(2)=17, v(3)=12, v(8)=7, v(0)=29 и c(7)=18. Поскольку k_18=23 согласно выражению 9, восемнадцать порядков u(0, 23), u(1, 23),..., u(17, 23) 23-его столбцового блока имеют значения 48, 59, 12, 21, 56, 38, 60, 62, -∞, 62, 60, 38, 56, 21, 12, 59, 48 и 24, соответственно.

Согласно выражению 13, m(i, 23) имеет значение 1, только когда i=0, 9, 16, и оно имеет значение 0 в других случаях. Посредством второго блока 11d изменения порядка (этапа S104), определяются шаблоны m(i, j) маски относительно столбцовых блоков с 0-ого столбцового блока по 47-ой столбцовый блок, за исключением 23-его столбцового блока.

Из распределения весов, описанного выше, v(0)=29. Таким образом, есть двадцать девять столбцов столбцовых блоков веса 0 из числа всех шестидесяти пяти столбцовых блоков, и столбцовые блоки с 0-ого столбцового блока по 28-ой столбцовый блок (за исключением 23-его столбцового блока) и 47-ой столбцовый блок определены в качестве нуля. Каждое значение m(i, j) относительно других восемнадцати столбцовых блоков с 29-ого столбцового блока по 46-ой столбцовый блок определяется посредством процедуры на фиг. 4, чтобы придерживаться распределения весов, описанного выше.

Затем, столбцовый блок, полученный равномерным циклическим сдвигом каждого компонента 23-его столбцового блока и 47-ого столбцового блока, заменяется и используется, так чтобы полная сумма 23-го столбцового блока проверочной матрицы становилась единичной матрицей.

Фиг. 6 - пояснительная схема, показывающая пример проверочной матрицы, получаемой посредством описанного выше примера работы. Для того чтобы упростить изображение, только часть порядка матрицы P циклической перестановки показана в качестве каждого компонента матрицы по фиг. 6. Кроме того, пустое место показывает матрицу всех нулей (порядок=-∞). Проверочная матрица по фиг. 6 становится проверочной матрицей квазициклического кода LDPC со скоростью кодирования 1/2, имеющей длину кода в 2268 битов, а информационную длину в 1134 битов.

Будет описан еще один пример генерирования проверочной матрицы, когда количество r столбцовых блоков имеет значение 6. Совершенно таким же образом, как описанный выше пример генерирования, при условии, что q имеет значение 2ˆ6 (=64), а β, удовлетворяющее βˆ6+β+1=0 - примитивный элемент поля Галуа, GF(2ˆ6), проверочная матрица генерируется из многочлена g(x) по выражению 7. Согласно выражению 7, λ(0), λ(1),..., λ(64) имеют значения 40, 43, 35, 45, 58, 31, 61, 18, 52, 47, 26, 32, 6, 54, 22, 23, 16, 41, 24, 48, 59, 12, 21, 56, 38, 60, 62, -∞, 62, 60, 38, 56, 21, 12, 59, 48, 24, 41, 16, 23, 22, 54, 6, 32, 26, 47, 52, 18, 61, 31, 58, 45, 35, 43, 40, 44, 30, 11, 51, 0, 0, 51, 11, 30 и 44, соответственно.

Эта последовательность является такой же, как последовательность, полученная циклическим сдвигом последовательности случая, где r=18, показанного на фиг. 6, в правом направлении двенадцать раз. Благодаря операциям блока 11a назначения порядка (этап S101), показанным на фиг. 2-3, оно устанавливается в u(i, j)=λ(j-i) для всех u(i, j) (0i<6, 0j<65). Что касается m(i, j) при 0i<6, 60j<65, оно определяется как m(i, j)=1, только когда j=59+i, или j=60+i, и оно фиксируется как m(i, j)=0 в других случаях.

Распределение весов блока 11b определения распределения весов (этап S102) определено как v(2)=5, v(3)=20, v(6)=11, v(0)=29, c(22)=2, и c(23)=4. Поскольку k_6=29 согласно выражению 9, шесть порядков u(0, 29), u(1, 29),..., u(5, 29) 29-ого столбцового блока имеют значение 60, 62, -∞, 62, 60 и 38, соответственно.

Согласно выражению 13, m(i, 29) имеет значение 1, только когда i=0, 3, 4, и оно имеет значение 0 в других случаях. Посредством второго блока 11d изменения порядка (этап S104), определяются шаблоны m(i, j) маски относительно столбцовых блоков с 0-ого столбцового блока по 59-ый столбцовый блок, за исключением 29-ого столбцового блока.

Из распределения весов, описанного выше, v(0)=29. Таким образом, есть двадцать девять столбцов столбцовых блоков веса 0 из числа всех шестидесяти пяти столбцовых блоков, и столбцовые блоки с 0-ого столбцового блока по 28-ой столбцовый блок определены в качестве нуля. Кроме того, после того, как 29-ый столбцовый блок определен описанным выше образом, каждое значение m(i, j) относительно других тридцати столбцовых блоков с 30-ого столбцового блока по 59-ый столбцовый блок определяется посредством процедуры на фиг. 4, чтобы придерживаться распределения весов, описанного выше.

Затем, столбцовый блок, полученный равномерным циклическим сдвигом каждого компонента 29-ого столбцового блока и 59-ого столбцового блока, заменяется и используется, так чтобы полная сумма 29-го столбцового блока проверочной матрицы становилась единичной матрицей. Фиг. 7 - пояснительная схема, показывающая пример проверочной матрицы, получаемой посредством описанного выше примера работы. Для того, чтобы упростить изображение, только часть порядка матрицы P циклической перестановки показана в качестве каждого компонента матрицы по фиг. 7. Кроме того, пустое место показывает матрицу всех нулей (порядок=-∞). Проверочная матрица по фиг. 7 становится проверочной матрицей квазициклического кода LDPC со скоростью кодирования 5/6, имеющей длину кода в 2268 битов, а информационную длину в 1890 битов.

На фиг. 6 и фиг. 7 показаны две разновидности проверочных матриц разных скоростей кодирования, в которых количество r столбцовых блоков проверочной матрицы по фиг. 6 имеет значение 18, и количество r столбцовых блоков проверочной матрицы по фиг. 7 имеет значение 6. Обе основаны на одних и тех же данных, генерируемых модулем 11 генерирования проверочной матрицы согласно примерному варианту осуществления. Числовые значения компонентов, которые не имеют значение -∞, определены последовательностью μ(1), μ(2),..., μ(64), обусловленной коэффициентом многочлена g(x). Таким образом, обработка кодированием может выполняться для обеих устройством кодирования, показанным на фиг. 5 посредством изменения шаблонов m(i, j) маски.

(Операции первого примерного варианта осуществления в целом)

Далее, будут описаны операции описанного выше примерного варианта осуществления в целом. Способ конфигурирования кода с исправлением ошибок согласно примерному варианту осуществления используется устройством кодирования, которое составлено: модулем генерирования проверочной матрицы, который генерирует блочную проверочную матрицу квазициклического кода контроля четности с низкой плотностью, которая имеет матрицу циклической перестановки, где количество строк и количество столбцов оба имеют значение q-1, или нулевую матрицу в качестве компонентов (q - целое число 4 или большее, и является степенью 2), количество строчных блоков имеет значение r, а количество столбцовых блоков имеет значение q+1 (r - целое число между 4 и q включительно), и компоненты i-ого строчного блока и j-ого столбцового блока (i - целое число между 0 и r-1, j - целое число между 0 и q, крайний левый столбец матрицы определен в качестве 0-ого столбца, а крайняя верхняя строка определена в качестве 0-ой строки) соответствуют нулевой матрице или матрице циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i в качестве аргумента; и модулем кодирования, который генерирует и выдает кодовое слово посредством блочной проверочной матрицы из введенного сообщения, причем: блок назначения порядка модуля генерирования проверочной матрицы предписывает значение функции λ(j-i) блочной проверочной матрицы посредством коэффициента самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней (фиг. 3: этап S101); блок определения распределения весов модуля генерирования проверочной матрицы предписывает количество компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока блочной проверочной матрицы и количество компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого строчного блока блочной проверочной матрицы посредством использования заданного шаблона маски (фиг. 3: этап S102); первый блок изменения порядка модуля генерирования проверочной матрицы берет полную сумму компонентов k_r-ого блока (k_r - целая часть (q+1-r)/2) блочной проверочной матрицы в качестве матрицы циклической перестановки (фиг. 3: этап S103); и второй блок изменения порядка модуля генерирования проверочной матрицы предписывает количество компонентов строчного блока, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока, за исключением k_r-ого столбцового блока блочной проверочной матрицы (фиг. 3: этап S104).

Кроме того, блочная проверочная матрица, сгенерированная модулем генерирования проверочной матрицы, и шаблон маски сохраняются в память сохранения матричных данных модуля кодирования; селектор модуля кодирования переключает входные сигналы согласно шаблону маски, сохраненному в памяти сохранения матричных данных; и устройства матричного умножения модуля кодирования вычисляют матричные произведения строк битов информации сообщения и матрицы циклической перестановки, имеющей в качестве порядка значение функции λ(j-i), имеющей целое число j-i, предписанное коэффициентом самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней, в качестве аргумента.

Отметим здесь, что каждый из описанных выше операционных этапов может быть вставлен в программу, которая должна выполняться устройством 10 кодирования в качестве компьютера, который непосредственно выполняет каждый из этапов. Программа может быть записана на постоянном носителе записи, таком как DVD, CD или флэш-память. В таком случае, программа считывается с носителя записи компьютером и выполняется.

С такой конструкцией и операциями, примерный вариант осуществления может давать следующие результаты.

Согласно примерному варианту осуществления, порядок матрицы циклической перестановки имеет значение λ(j-i), когда компоненты i-ого строчного и j-ого столбцового блоков блочной проверочной матрицы не являются нулевой матрицей. Она также является матрицей циклической перестановки с порядком λ(j-i), когда компоненты i+1-ого строчного и j+1-ого столбцового блоков блочной проверочной матрицы не являются нулевой матрицей. Это является таким же для компонентов i+2-ого строчного и j+2-ого столбцового блока, компонентов i+3-его строчного и j+3-его столбцового блока, и т.д. Таким образом, область хранения, требуемая для сохранения проверочной матрицы, сгенерированной посредством настоящего изобретения, занимает порядка (q+1-r)×r битов, так что она требует значительно меньшей области хранения.

Кроме того, можно генерировать проверочную матрицу квазициклического кода LDPC различных типов, не изменяя порядок в случае матрицы циклической перестановки, посредством простого выбора, являются ли компоненты проверочной матрицы матрицей циклической перестановки или нулевой матрицей. Таким образом, есть эффект способности сокращать время (служебные данные), требуемое для переключения устройств кодирования и декодирования, даже в системе связи, которая надлежащим образом использует множество кодов LDPC разных параметров, таких как скорость кодирования, длина кадра, характеристика частоты появления ошибок, и тому подобное.

(ВТОРОЙ ПРИМЕРНЫЙ ВАРИАНТ ОСУЩЕСТВЛЕНИЯ)

В дополнение к конструкции устройства 10 кодирования согласно первому примерному варианту осуществления, устройство 110 кодирования согласно второму примерному варианту осуществления настоящего изобретения сконструировано так, что: блок 11b определения распределения весов модуля генерирования проверочной матрицы определяет все компоненты q+1-n фрагментов столбцовых блоков из числа q+1-r фрагментов столбцовых блоков за исключением r-1 фрагмента столбцового блока на правом конце и k_r-ого столбцового блока q+1 фрагментов столбцовых блоков блочной проверочной матрицы; и модуль генерирования проверочной матрицы включает в себя блок 111e вычеркивания столбцовых блоков, который вычеркивает q+1-n фрагментов столбцовых блоков, чьи все компоненты являются нулевой матрицей.

При этой конструкции, можно получать такой же результат, как по первому примерному варианту осуществления. Кроме того, количество столбцовых блоков проверочной матрицы, которая должна быть сгенерирована, может устанавливаться в произвольное количество из r+1 и q+1, включительно, так что можно генерировать еще более широкие разновидности проверочных матриц.

В дальнейшем, это будет далее описано более подробно.

Фиг. 8 - пояснительная схема, показывающая систему 101 связи, включающую в себя устройство 110 кодирования согласно второму примерному варианту осуществления настоящего изобретения. Система 101 связи имеет такую же конструкцию, как система 1 связи, описанная в первом примерном варианте осуществления настоящего изобретения за исключением того момента, что устройство 10 кодирования заменено устройством 110 кодирования. Устройство 110 кодирования включает в себя модуль 111 генерирования проверочной матрицы и модуль 12 кодирования, такой же, как по первому примерному варианту осуществления.

Фиг. 9 - пояснительная схема, показывающая более подробную структуру модуля 111 генерирования проверочной матрицы, показанного на фиг. 8. Кроме того, фиг. 10 - блок-схема алгоритма, показывающая операции для генерирования блочной проверочной матрицы, выполняемые модулем 111 генерирования проверочной матрицы, показанным на фиг. 8. Модуль 111 генерирования проверочной матрицы имеет такую же конструкцию, как у модуля 11 генерирования проверочной матрицы (показанного на фиг. 2) согласно первому примерному варианту осуществления за исключением того момента, что блок 11b определения распределения весов модуля 11 генерирования проверочной матрицы согласно первому примерному варианту осуществления заменен блоком 111b определения распределения весов, и что дополнительно предусмотрен блок 111e вычеркивания столбцовых блоков.

Модуль 111 генерирования проверочной матрицы может генерировать блочную проверочную матрицу, в которой количество строчных блоков имеет значение r, количество столбцовых блоков имеет значение q+1 (q - степень 2), а компоненты i-ого строчного блока и j-ого столбцового блока (i - целое число между 0 и r-1, j - целое число между 0 и q) являются нулевой матрицей или матрицей циклической перестановки q-1, имеющей значение функции λ(j-i) в качестве порядка.

Работа блока 11a назначения порядка (этап S101) является такой же, как у модуля 11 генерирования проверочной матрицы (показанного на фиг. 3). При восприятии этого, блок 111b определения распределения весов может устанавливать количество столбцовых блоков проверочной матрицы, которые должны быть сгенерированы, в качестве произвольного количества из r+1 и q+1, включительно, посредством установки столбцовых блоков с нулевым весом среди столбцовых блоков за исключением фрагмента r-1 столбцового блока на правом конце и k_r-ого столбцового блока (этап S302).

Последующие операции первого блока 11c изменения порядка и второго блока 11d изменения порядка (этапы с S103 по 104) являются такими же, как описанные на фиг. 2-3. Затем, модуль 111 генерирования проверочной матрицы вычеркивает столбцовые блоки с нулевым весом посредством блока 111e вычеркивания столбцовых блоков после этого (этап S305), и его работа заканчивается.

Нет изменения минимального значения длины цикла, даже когда количество строк и столбцов матрицы циклической перестановки и нулевой матрицы в качестве компонентов блочной проверочной матрицы устанавливается в произвольное число умножения q-1. Таким образом, можно генерировать блочную проверочную матрицу, имеющую матрицу циклической перестановки или нулевую матрицу, чье количество строк и столбцов является произвольным положительным умножением q-1, посредством использования модулей, показанных на фиг. 8-10.

Кроме того, что касается проверочной матрицы, генерируемой модулем 111 генерирования проверочной матрицы, в которой количество r строчных блоков, количество n столбцовых блоков, и количество строк и количество столбцов, которые должны быть ее компонентами, оба имеют значение t×(q-1) (t - положительное целое число), модуль 12 кодирования, показанный на фиг. 5, может вычислять и выдавать избыточные биты из r×t×(q-1) битов для битов информации из (n-r)×t×(q-1) битов.

Несмотря на то, что настоящее изобретение было описано посредством ссылки на специфичные примерные варианты осуществления, проиллюстрированные на чертежах, настоящее изобретение не ограничено только такими примерными вариантами осуществления, описанными выше. Любые другие известные конструкции могут применяться до тех пор, пока с их помощью могут достигаться результаты настоящего изобретения.

Новое техническое содержание описанного выше примерного варианта осуществления может быть обобщено, как изложено ниже. Несмотря на то, что часть или целая часть примерных вариантов осуществления может быть обобщена, как изложено ниже, в качестве новой технологии, настоящее изобретение не обязательно ограничено только изложенным ниже.

(Дополнительное примечание 1)

Устройство кодирования для построения квазициклического кода контроля четности с низкой плотностью, которое включает в себя: модуль генерирования проверочной матрицы, который генерирует блочную проверочную матрицу квазициклического кода контроля четности с низкой плотностью, которая имеет матрицу циклической перестановки, где количество строк и количество столбцов оба имеют значение q-1, или нулевую матрицу в качестве компонентов (q - целое число 4 или большее, и является степенью 2), количество строчных блоков имеет значение r, а количество столбцовых блоков имеет значение q+1 (r - целое число между 4 и q включительно), и компоненты i-ого строчного блока и j-ого столбцового блока (i - целое число между 0 и r-1, j - целое число между 0 и q, крайний левый столбец матрицы определен в качестве 0-ого столбца, а крайняя верхняя строка определена в качестве 0-ой строки) соответствуют нулевой матрице или матрице циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i в качестве аргумента; и модуль кодирования, который генерирует и выдает кодовое слово, посредством блочной проверочной матрицы, из введенного сообщения, при этом, модуль генерирования проверочной матрицы дополнительно включает в себя: блок назначения порядка, который предписывает значение функции λ(j-i) блочной проверочной матрицы посредством коэффициента самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней; блок определения распределения весов, который предписывает количество компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока блочной проверочной матрицы и количество компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого строчного блока блочной проверочной матрицы посредством использования заданного шаблона маски; первый блок изменения порядка, который берет полную сумму компонентов k_r-ого блока (k_r - целая часть (q+1-r)/2) блочной проверочной матрицы в качестве матрицы циклической перестановки; и второй блок изменения порядка, который предписывает количество компонентов строчного блока, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока, за исключением k_r-ого столбцового блока блочной проверочной матрицы.

(Дополнительное примечание 2)

Устройство кодирования как изображенное в дополнительном примечании 1, в котором: блок определения распределения весов модуля генерирования проверочной матрицы определяет все компоненты q+1-n фрагментов столбцовых блоков из числа q+1-r фрагментов столбцовых блоков за исключением r-1 фрагментов столбцовых блоков на правом конце и k_r-ого столбцового блока q+1 фрагментов столбцовых блоков блочной проверочной матрицы в качестве нулевых матриц; и модуль генерирования проверочной матрицы включает в себя блок вычеркивания столбцовых блоков, который вычеркивает q+1-n фрагментов столбцовых блоков, чьи все компоненты являются нулевыми матрицами.

(Дополнительное примечание 3)

Устройство кодирования как изображенное в дополнительном примечании 1 или 2, в котором модуль кодирования включает в себя: память сохранения матричных данных, которая хранит блочную проверочную матрицу, сгенерированную модулем генерирования проверочной матрицы, и шаблон маски; устройства умножения r фрагментов матриц, которые вычисляют матричные произведения строк битов информации сообщения и матрицы циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i, предписанное коэффициентом самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней, в качестве аргумента; и селектор, который переключает входные сигналы в устройства матричного умножения согласно шаблону маски, сохраненному в памяти сохранения матричных данных.

(Дополнительное примечание 4)

Устройство кодирования как изображенное в дополнительном примечании 3, в котором память сохранения матричных данных включает в себя: функцию, которая удерживает номера строк всех строчных блоков, чьи компоненты в столбцовых блоках являются ненулевыми матрицами циклической перестановки во всех столбцовых блоках из множества блочных проверочных матриц; и функцию, которая изменяет входные сигналы в селектор для каждой из блочных проверочных матриц.

(Дополнительное примечание 5)

Способ конфигурирования кода с исправлением ошибок для построения квазициклического кода контроля четности с низкой плотностью, который включает в себя: генерирование, модулем генерирования проверочной матрицы, блочной проверочной матрицы квазициклического кода контроля четности с низкой плотностью, которая имеет матрицу циклической перестановки, где количество строк и количество столбцов оба имеют значение q-1, или нулевую матрицу в качестве компонентов (q - целое число 4 или большее, и является степенью 2), количество строчных блоков имеет значение r, а количество столбцовых блоков имеет значение q+1 (r - целое число между 4 и q включительно), и компоненты i-ого строчного блока и j-ого столбцового блока (i - целое число между 0 и r-1, j - целое число между 0 и q, крайний левый столбец матрицы определен в качестве 0-ого столбца, а крайняя верхняя строка определена в качестве 0-ой строки) соответствуют нулевой матрице или матрице циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i в качестве аргумента; и генерирование и выдачу, модулем кодирования, кодового слова посредством блочной проверочной матрицы из введенного сообщения.

Способ дополнительно включает в себя: при генерировании блочной проверочной матрицы, предписание, блоком назначения порядка, значения функции λ(j-i) блочной проверочной матрицы посредством коэффициента самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней; предписание, блоком определения распределения весов, количества компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока блочной проверочной матрицы и количества компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого строчного блока блочной проверочной матрицы посредством использования заданного шаблона маски; взятие, первым блоком изменения порядка, полной суммы компонентов k_r-ого блока (k_r - целая часть (q+1-r)/2) блочной проверочной матрицы в качестве матрицы циклической перестановки; и предписание, вторым блоком изменения порядка, количества компонентов строчного блока, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока, за исключением k_r-ого столбцового блока блочной проверочной матрицы.

(Дополнительное примечание 6)

Способ конфигурирования кода с исправлением ошибок как изображенный в дополнительном примечании 5, который включает в себя: сохранение блочной проверочной матрицы, сгенерированной модулем генерирования проверочной матрицы, и шаблона маски в память сохранения матричных данных модуля кодирования; переключение входных сигналов, селектором модуля кодирования, согласно шаблону маски, сохраненному в памяти сохранения матричных данных; и вычисление, устройством матричного умножения модуля кодирования, матричных произведений строк битов информации сообщения и матрицы циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i, предписанное коэффициентом самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней, в качестве аргумента.

(Дополнительное примечание 7)

Программа конфигурирования кода с исправлением ошибок для построения квазициклического кода контроля четности с низкой плотностью, которая побуждает компьютер выполнять: функцию генерирования блочной проверочной матрицы квазициклического кода контроля четности с низкой плотностью, которая имеет матрицу циклической перестановки, где количество строк и количество столбцов оба имеют значение q-1, или нулевую матрицу в качестве компонентов (q - целое число 4 или большее, и является степенью 2), количество строчных блоков имеет значение r, а количество столбцовых блоков имеет значение q+1 (r - целое число между 4 и q включительно), и компоненты i-ого строчного блока и j-ого столбцового блока (i - целое число между 0 и r-1, j - целое число между 0 и q, крайний левый столбец матрицы определен в качестве 0-ого столбца, а крайняя верхняя строка определена в качестве 0-ой строки) соответствуют нулевой матрице или матрице циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i в качестве аргумента; и функцию генерирования и выдачи кодового слова, посредством блочной проверочной матрицы, из введенного сообщения, и программа дополнительно побуждает компьютер, при генерировании блочной проверочной матрицы, выполнять: функцию предписания значения λ(j-i) функции блочной проверочной матрицы посредством коэффициента самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней; функцию предписания количества компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока блочной проверочной матрицы и количества компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого строчного блока блочной проверочной матрицы посредством использования заданного шаблона маски; функцию взятия полной суммы компонентов k_r-ого блока (k_r - целая часть (q+1-r)/2) блочной проверочной матрицы в качестве матрицы циклической перестановки; и функцию предписания количества компонентов строчного блока, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока, за исключением k_r-ого столбцового блока блочной проверочной матрицы.

(Дополнительное примечание 8)

Программа конфигурирования кода с исправлением ошибок как изображенная в дополнительном примечании 7, которая побуждает компьютер выполнять: функцию сохранения сгенерированной блочной проверочной матрицы и шаблона маски в памяти сохранения матричных данных модуля кодирования; функцию переключения входных сигналов согласно шаблону маски, сохраненному в памяти сохранения матричных данных; и функцию вычисления матричных произведений строк битов информации сообщения и матрицы циклической перестановки, чей порядок является значением функции λ(j-i), имеющей в качестве аргумента целое число j-i, предписанное коэффициентом самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(qˆ2), в качестве корней.

Несмотря на то, что настоящее изобретение было описано до этого посредством ссылки на варианты осуществления (и ПРИМЕРЫ), настоящее изобретение не ограничено только вариантами осуществления (и ПРИМЕРАМИ). Различные изменения и модификации, приходящие на ум специалистам в данной области техники, могут быть применены к конструкциям и деталям настоящего изобретения, не выходя из объема настоящего изобретения.

Эта заявка испрашивает право на приоритет на основании заявки № 2010-102479 на выдачу патента Японии, поданной 27 апреля 2010 года, и ее раскрытие настоящим включено в состав посредством ссылки во всей своей полноте.

ПРОМЫШЛЕННАЯ ПРИМЕНИМОСТЬ

Настоящее изобретение может применяться в качестве технологии исправления ошибок для удовлетворения требований в показателях конструкции системы, таких как достижение высокой надежности, вследствие снижения частоты появления ошибочных битов, и уменьшение потребляемой электрической энергии в различных видах систем связи или в качестве технологии исправления ошибок для улучшения надежности, касающейся запоминающего устройства, такого как магнитная запись.

ПОЗИЦИОННЫЕ ОБОЗНАЧЕНИЯ

1, 101 Система связи

10, 110 Устройство кодирования

11, 111 Модуль генерирования проверочной матрицы

11a Блок назначения порядка

11b, 111b Блок определения распределения весов

11c Первый блок изменения порядка

11d Второй блок изменения порядка

12 Модуль кодирования

21 Модулятор

22 Тракт передачи

23 Демодулятор

24 Устройство декодирования

30 Устройство матричного умножения

32, 36 Селектор

33 Память сохранения матричных данных

34, 35 Устройство вычисления исключающего ИЛИ

111e Блок вычеркивания столбцовых блоков.

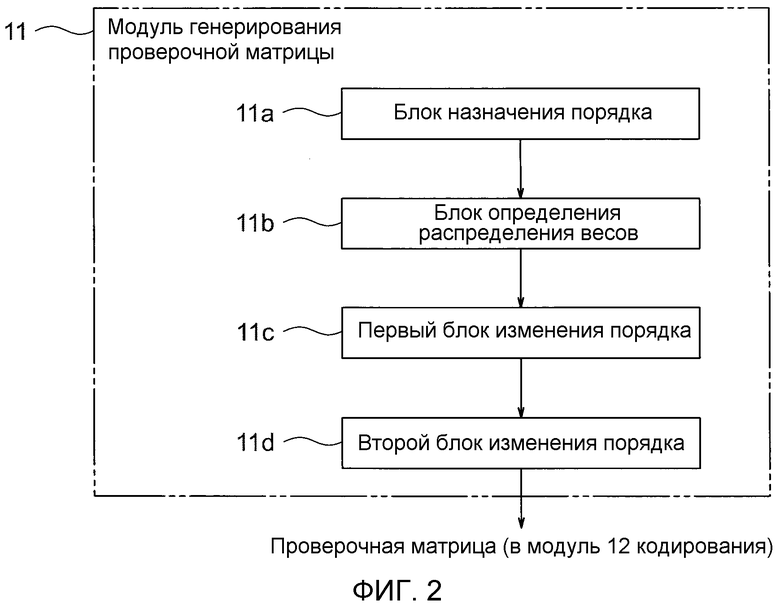
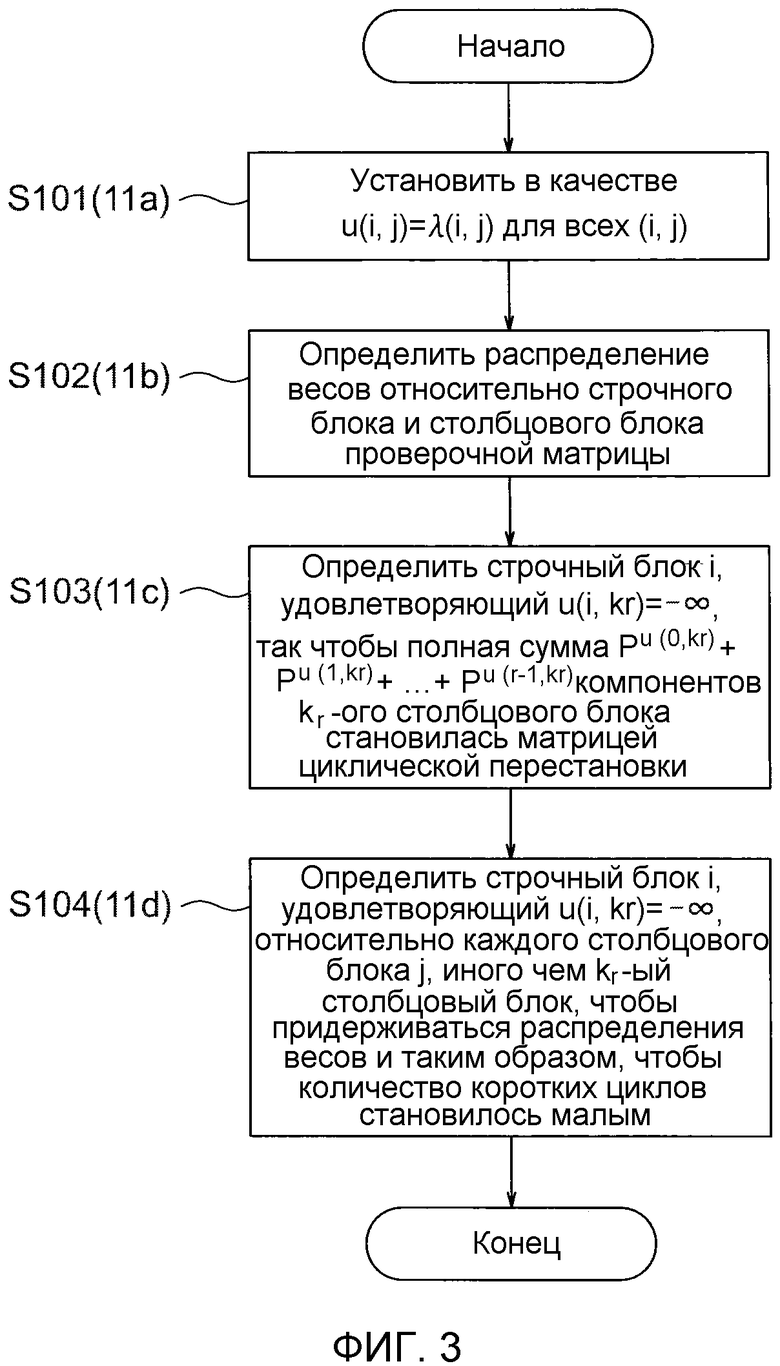
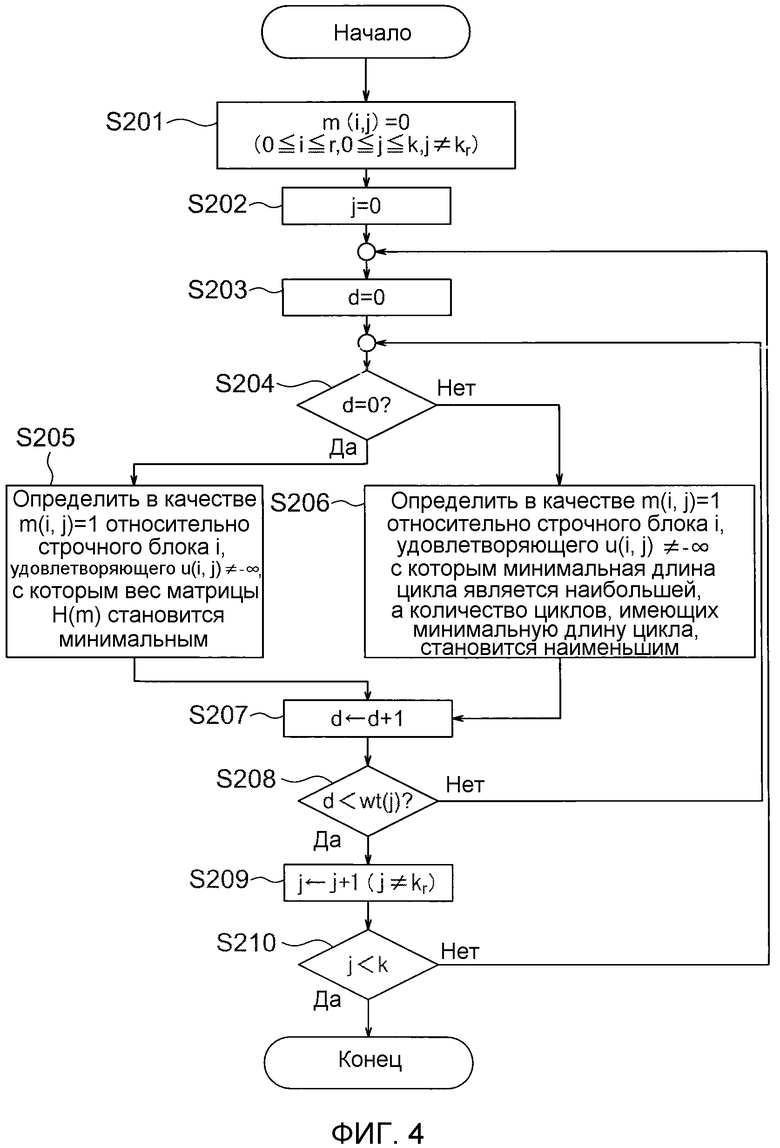
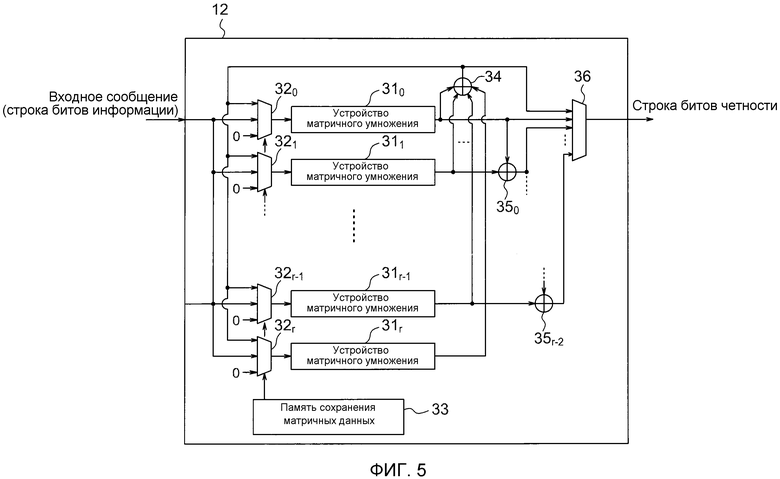
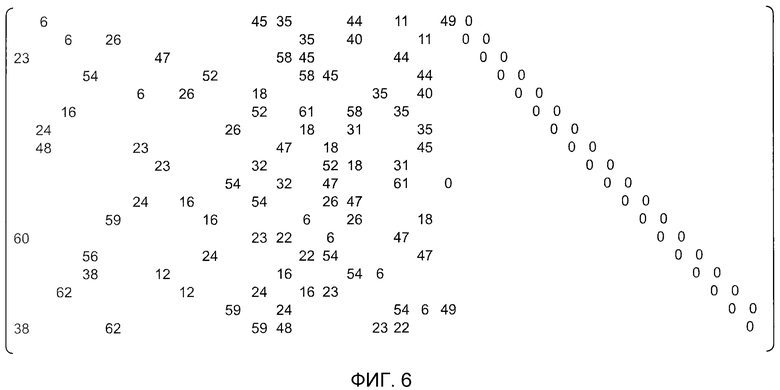
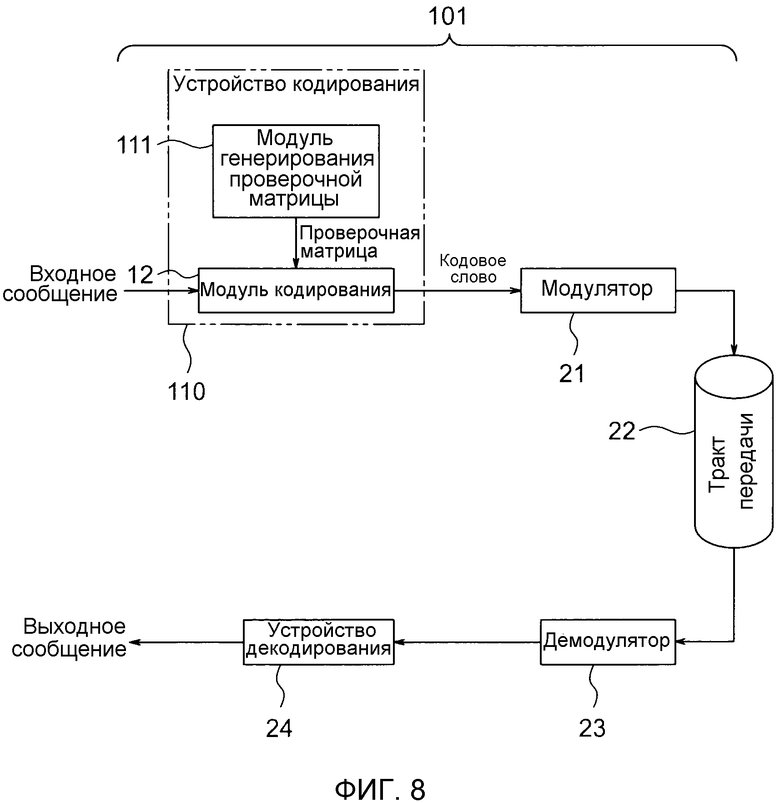
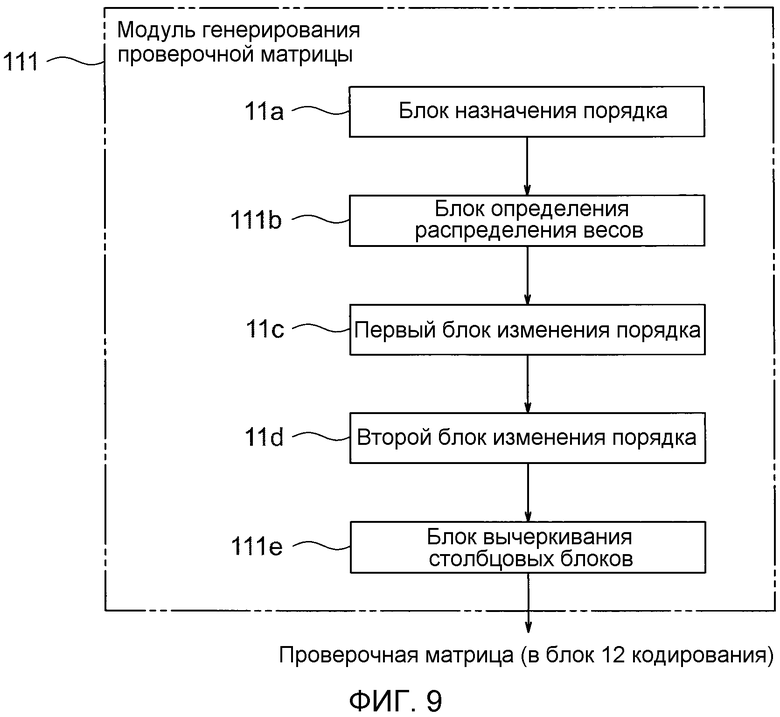
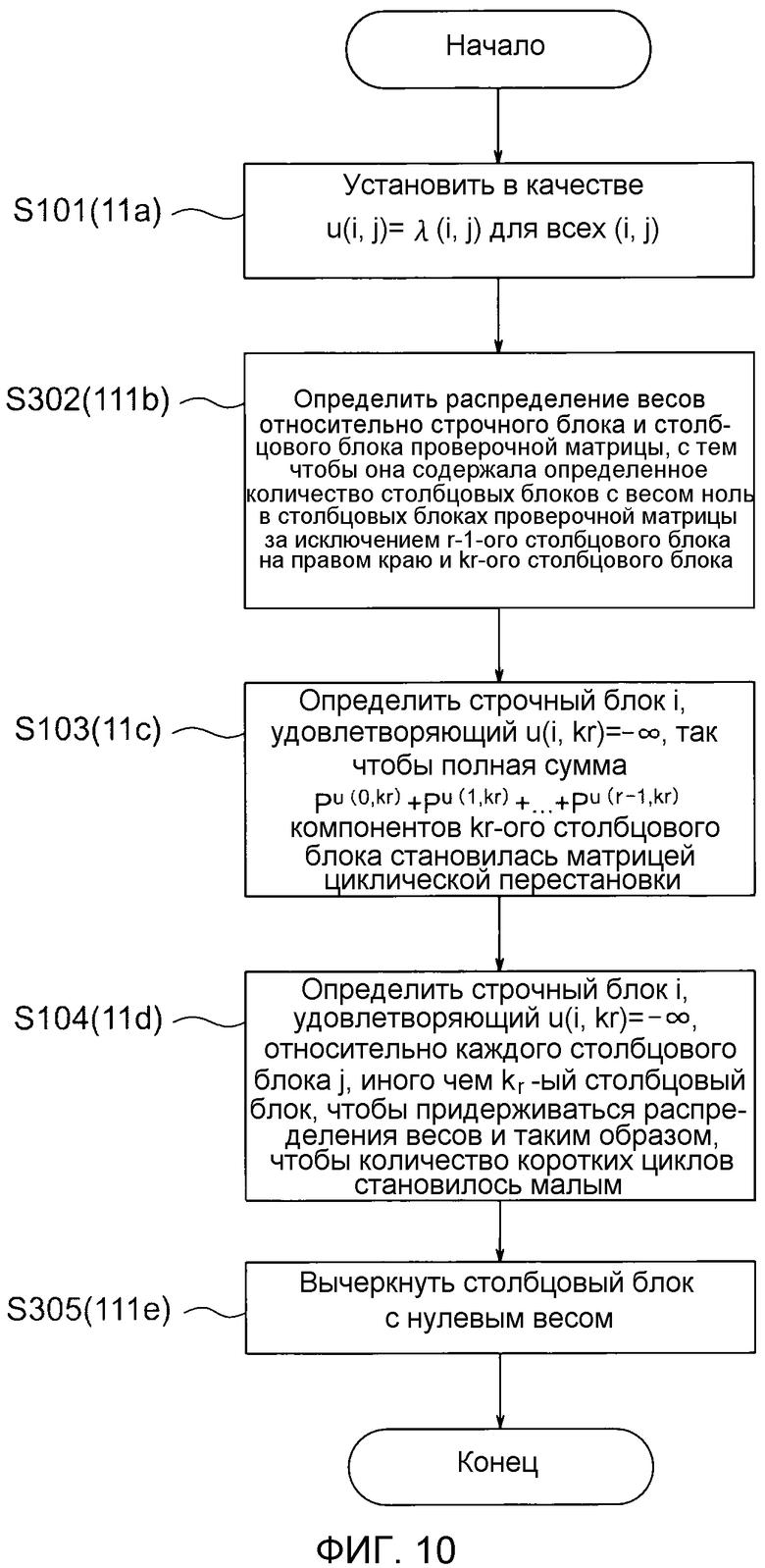
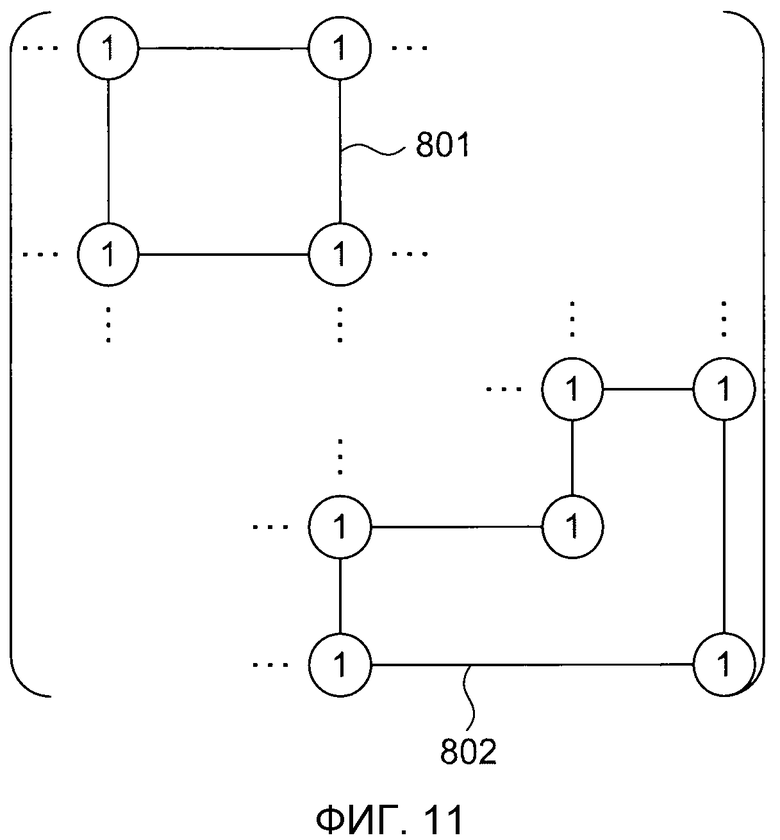
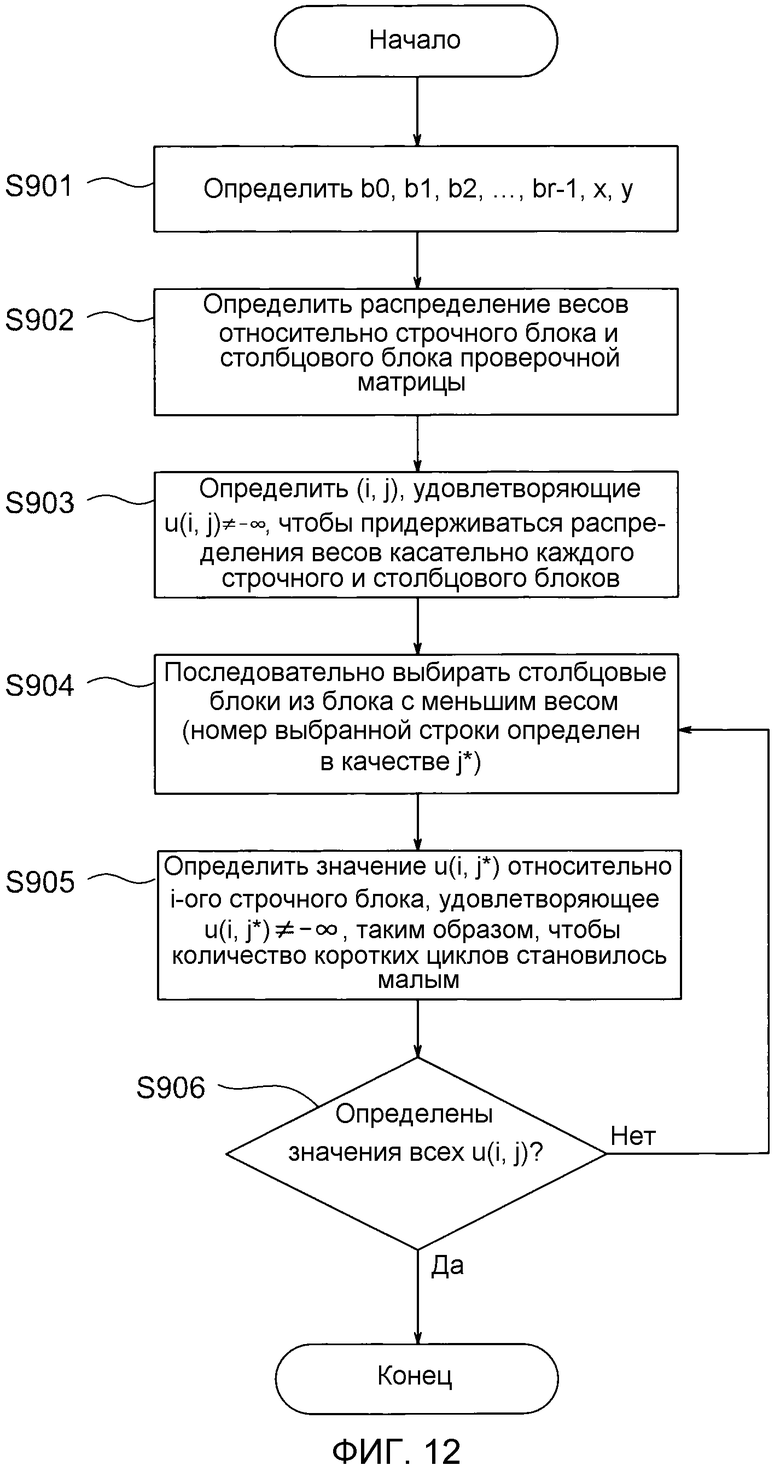
Изобретение относится к средствам кодирования. Технический результат заключается в уменьшении области хранения, требуемой для хранения множества кодов контроля четности с низкой плотностью. Устройство кодирования содержит модуль генерирования проверочной матрицы, который генерирует блочную проверочную матрицу; и модуль кодирования, который генерирует и выдает кодовое слово из входного сообщения посредством проверочной матрицы. Модуль генерирования проверочной матрицы включает в себя: блок назначения порядка, который предписывает значения функции блочной проверочной матрицы посредством коэффициентов самодвойственного многочленного выражения; блок определения распределения веса, который предписывает количество компонентов, которые являются ненулевыми матрицами, из числа компонентов каждого блока блочной проверочной матрицы с использованием шаблона маски; первый блок изменения порядка, который рассматривает сумму компонентов k_r-го строчного блока блочной проверочной матрицы в качестве матрицы циклической перестановки; и второй блок изменения порядка, который предписывает количество компонентов строчного блока, которые являются ненулевыми матрицами, из числа компонентов каждого строчного блока, исключая упомянутый k_r-й строчный блок блочной проверочной матрицы. 3 н. и 5 з.п. ф-лы, 12 ил.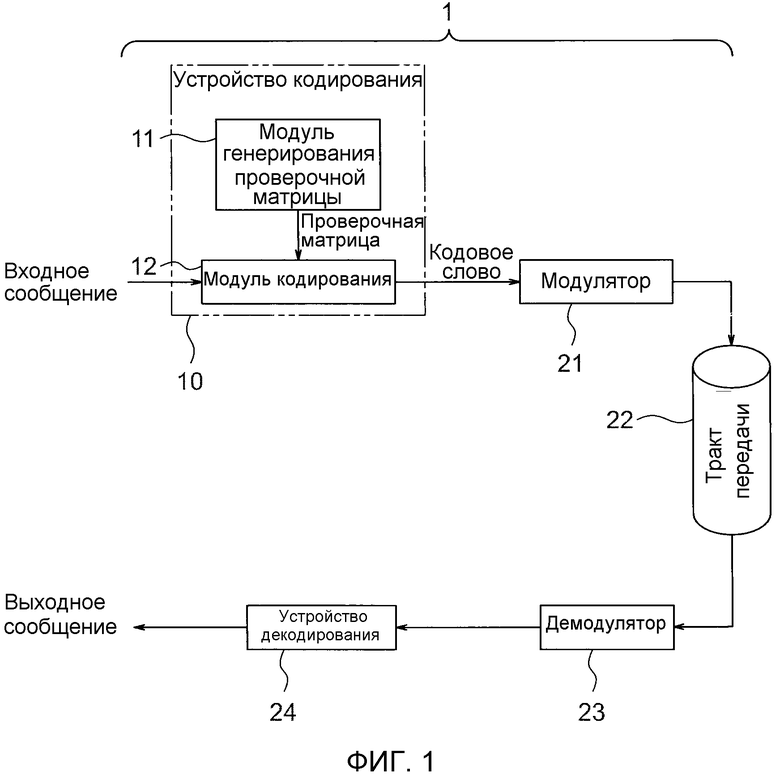

1. Устройство кодирования для построения квазициклического кода контроля четности с низкой плотностью, содержащее:
средство генерирования проверочной матрицы для генерирования блочной проверочной матрицы квазициклического кода контроля четности с низкой плотностью, которая имеет матрицу циклической перестановки, где количество строк и количество столбцов оба имеют значение q-1, или нулевую матрицу в качестве компонентов (q - целое число 4 или большее, и является степенью 2), количество строчных блоков имеет значение r, а количество столбцовых блоков имеет значение q+1 (r - целое число между 4 и q включительно), и компоненты i-ого строчного блока и j-ого столбцового блока (i - целое число между 0 и r-1, j - целое число между 0 и q, крайний левый столбец матрицы определен в качестве 0-го столбца, а крайняя верхняя строка определена в качестве 0-й строки) соответствуют нулевой матрице или матрице циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i в качестве аргумента; и
средство кодирования для генерирования и выдачи кодового слова посредством блочной проверочной матрицы из введенного сообщения, при этом,
средство генерирования проверочной матрицы дополнительно содержит:
средство назначения порядка для предписания значения функции λ(j-i) блочной проверочной матрицы посредством коэффициента самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(q^2), в качестве корней;
средство определения распределения весов для предписания количества компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока блочной проверочной матрицы и количества компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого строчного блока блочной проверочной матрицы посредством использования заданного шаблона маски;
первое средство изменения порядка для взятия полной суммы компонентов k_r-го блока (k_r - целая часть (q+1-r)/2) блочной проверочной матрицы в качестве матрицы циклической перестановки; и второе средство изменения порядка для предписания количества компонентов строчного блока, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока, за исключением k_r-го столбцового блока блочной проверочной матрицы.

2. Устройство кодирования по п.1, в котором: средство определения распределения весов средства генерирования проверочной матрицы определяет все компоненты q+1-n фрагментов столбцовых блоков из числа q+1-r фрагментов столбцовых блоков за исключением r-1 фрагментов столбцовых блоков на правом конце и k_r-го столбцового блока q+1 фрагментов столбцовых блоков блочной проверочной матрицы в качестве нулевых матриц; и
средство генерирования проверочной матрицы содержит средство вычеркивания столбцовых блоков для вычеркивания q+1-n фрагментов столбцовых блоков, чьи все компоненты являются нулевыми матрицами.

3. Устройство кодирования по п.1 или 2, в котором средство кодирования содержит:
средство памяти сохранения матричных данных для хранения блочной проверочной матрицы, сгенерированной средством генерирования проверочной матрицы, и шаблона маски;
средство умножения r фрагментов матриц для вычисления матричных произведений строк битов информации сообщения и матрицы циклической перестановки, чей порядок является значением функции λ(j-i), имеющей в качестве аргумента целое число j-i, предписанное коэффициентом самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(q^2), в качестве корней; и
средство селектора для переключения входных сигналов в средство матричного умножения согласно шаблону маски, сохраненному в средство памяти сохранения матричных данных.

4. Устройство кодирования по п.3, в котором средство памяти сохранения матричных данных содержит:
функцию, которая удерживает номера строк всех строчных блоков, чьи компоненты в столбцовых блоках являются ненулевыми матрицами циклической перестановки во всех столбцовых блоках из множества блочных проверочных матриц; и
функцию, которая изменяет входные сигналы в средство селектора для каждой из блочных проверочных матриц.

5. Способ конфигурирования кода с исправлением ошибок для построения квазициклического кода контроля четности с низкой плотностью, содержащий этапы, на которых:
генерируют, модулем генерирования проверочной матрицы, блочную проверочную матрицу квазициклического кода контроля четности с низкой плотностью, которая имеет матрицу циклической перестановки, где количество строк и количество столбцов оба имеют значение q-1, или нулевую матрицу в качестве компонентов (q - целое число 4 или большее, и является степенью 2), количество строчных блоков имеет значение r, а количество столбцовых блоков имеет значение q+1 (r - целое число между 4 и q включительно), и компоненты i-го строчного блока и j-го столбцового блока (i - целое число между 0 и r-1, j - целое число между 0 и q, крайний левый столбец матрицы определен в качестве 0-го столбца, а крайняя верхняя строка определена в качестве 0-й строки) соответствуют нулевой матрице или матрице циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i в качестве аргумента; и
генерируют и выдают, модулем кодирования, кодовое слово посредством блочной проверочной матрицы из введенного сообщения, и дополнительно содержащий этапы, на которых:
при генерировании блочной проверочной матрицы,
предписывают, блоком назначения порядка, значение функции λ(j-i) блочной проверочной матрицы посредством коэффициента самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(q^2), в качестве корней;
предписывают, блоком определения распределения весов, количество компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока блочной проверочной матрицы и количество компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого строчного блока блочной проверочной матрицы посредством использования заданного шаблона маски;
берут, первым блоком изменения порядка, полную сумму компонентов k_r-го блока (k_r - целая часть (q+1-r)/2) блочной проверочной матрицы в качестве матрицы циклической перестановки; и
предписывают, вторым блоком изменения порядка, количество компонентов строчного блока, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока, за исключением k_r-го столбцового блока блочной проверочной матрицы.

6. Способ конфигурирования кода с исправлением ошибок по п.5, содержащий этапы, на которых:
сохраняют блочную проверочную матрицу, сгенерированную модулем генерирования проверочной матрицы, и шаблон маски в память сохранения матричных данных модуля кодирования;
переключают входные сигналы, селектором модуля кодирования, согласно шаблону маски, сохраненному в памяти сохранения матричных данных; и
вычисляют, устройством матричного умножения модуля кодирования, матричные произведения строк битов информации сообщения и матрицы циклической перестановки, чей порядок является значением функции λ(j-i), имеющей в качестве аргумента целое число j-i, предписанное коэффициентом самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(q^2), в качестве корней.

7. Машиночитаемый носитель записи, содержащий программу конфигурирования кода с исправлением ошибок для построения квазициклического кода контроля четности с низкой плотностью, которая при выполнении на компьютере предписывает компьютеру выполнять:
функцию генерирования блочной проверочной матрицы квазициклического кода контроля четности с низкой плотностью, которая имеет матрицу циклической перестановки, где количество строк и количество столбцов оба имеют значение q-1, или нулевую матрицу в качестве компонентов (q - целое число 4 или большее, и является степенью 2), количество строчных блоков имеет значение r, а количество столбцовых блоков имеет значение q+1 (r - целое число между 4 и q включительно), и компоненты i-го строчного блока и j-го столбцового блока (i - целое число между 0 и r-1, j - целое число между 0 и q, крайний левый столбец матрицы определен в качестве 0-го столбца, а крайняя верхняя строка определена в качестве 0-й строки) соответствуют нулевой матрице или матрице циклической перестановки, чей порядок является значением функции λ(j-i), имеющей целое число j-i в качестве аргумента; и
функцию генерирования и выдачи кодового слова, посредством блочной проверочной матрицы, из введенного сообщения, и дополнительно предписывает компьютеру, при генерировании блочной проверочной матрицы, выполнять:
функцию предписания значения λ(j-i) функции блочной проверочной матрицы посредством коэффициента самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(q^2), в качестве корней;
функцию предписания количества компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока блочной проверочной матрицы и количества компонентов, которые должны быть ненулевой матрицей, из числа компонентов каждого строчного блока блочной проверочной матрицы посредством использования заданного шаблона маски;
функцию взятия полной суммы компонентов k_r-го блока (k_r - целая часть (q+1-r)/2) блочной проверочной матрицы в качестве матрицы циклической перестановки; и
функцию предписания количества компонентов строчного блока, которые должны быть ненулевой матрицей, из числа компонентов каждого столбцового блока, за исключением k_r-го столбцового блока блочной проверочной матрицы.

8. Машиночитаемый носитель записи, содержащий программу конфигурирования кода с исправлением ошибок по п.7, которая предписывает компьютеру выполнять:
функцию сохранения сгенерированной блочной проверочной матрицы и шаблона маски в памяти сохранения матричных данных модуля кодирования;
функцию переключения входных сигналов согласно шаблону маски, сохраненному в памяти сохранения матричных данных; и
функцию вычисления матричных произведений строк битов информации сообщения и матрицы циклической перестановки, чей порядок является значением функции λ(j-i), имеющей в качестве аргумента целое число j-i, предписанное коэффициентом самодвойственного многочлена, имеющего q-1 фрагментов элементов поля Галуа, GF(q^2), в качестве корней.