Предлагаемое устройство относится к вычислительной технике и может быть использовано для достоверной параллельной реализации систем логических функций в средствах криптографической защиты информации, искусственного интеллекта, системах автоматизированного проектирования интегральных схем и др.
Известно вычислительное устройство, включающее в себя сумматор, выход которого подключен к второму входу регистра результата, регистр для хранения булевых переменных, выход которого подключен к блоку конъюнкций, регистры для фиксации очередных строк матриц, описывающих структуру соответствующей конъюнкции, выходы которых подключены также к блоку конъюнкций, выход которого подключен к третьему входу регистра результата, выход которого является шиной выдачи результата вычислений (Малюгин В.Д. Параллельные логические вычисления посредством арифметических полиномов. / В.Д.Малюгин - М.: Наука. Физматлит, 1997. - с.156-157).
Недостаток известного устройства - отсутствие функциональной возможности контроля ошибок логических вычислений.
Наиболее близким по сущности технического решения к заявляемому устройству является вычислительное устройство, содержащее блок конъюнкций, входы которого являются шиной подачи значений булевых переменных, выходы которого подключены к блоку памяти, выходы которого подключены к входам коммутатора, выходы которого подключены к многоместному сумматору, выходы которого являются выходами устройства выдачи результата вычислений (Малюгин В.Д. Параллельные логические вычисления посредством арифметических полиномов. / В.Д.Малюгин - М.: Наука. Физматлит, 1997. - с.154-155).
Недостаток известного устройства - отсутствие функциональной возможности контроля ошибок логических вычислений.
Цель изобретения - расширение функциональных возможностей устройства за счет обеспечения контроля ошибок логических вычислений.
Поставленная цель достигается тем, что в самопроверяемом модулярном вычислителе систем логических функций, содержащем блок конъюнкций, входы которого являются входами устройства для подачи n булевых переменных, выходы подключены к первому блоку памяти, предназначенному для хранения коэффициентов первого полинома избыточной модулярной числовой нормальной формы, первый сумматор, дополнительно введены второй сумматор, блок вычисления остатка по модулю, элемент ИЛИ-НЕ, элемент И, регистр памяти и второй блок памяти, входы которого соединены с выходами блока конъюнкций, при этом второй блок памяти предназначен для хранения коэффициентов второго полинома избыточной модулярной числовой нормальной формы, выходы первого блока памяти подключены к входам первого сумматора, выходы которого подключены к (s+1)-му, (s+2)-му, …, (d+s)-му входам (старшие разряды слева, d - количество реализуемых булевых функций, составляющих информационные разряды разделимого AN-кода, s - количество избыточных булевых функций, соответствующих избыточным разрядам разделимого AN-кода) блока вычисления остатка по модулю и информационным входам регистра памяти, выходы которого являются выходами устройства выдачи значений d булевых функций, выходы второго блока памяти подключены к входам второго сумматора, выходы которого подключены к 1-му, 2-му, …, s-му входам (старшие разряды слева) блока вычисления остатка по модулю, выходы которого подключены к входам элемента ИЛИ-НЕ, выход которого подключен к первому входу элемента И, второй вход которого соединен с входом подачи синхроимпульсов устройства, а выход подключен к синхровходу регистра памяти.
Структурная схема предлагаемого устройства представлена на фиг.1.
Пусть дана система булевых функций (СБФ): f1(Х), f2(X), …, fd(X) от n булевых переменных X=x1, x2, …, xn (xi∈{0,1}, i=1, 2, …, n):
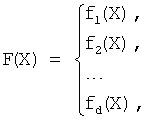
где F(X) - значение, принимаемое d-выходной БФ.
Таблица истинности реализуемой СБФ имеет вид:
где 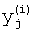 - значения, принимаемые j-й БФ на i-м наборе переменных, Y(i) - целые неотрицательные числа, записанные в двоичной системе счисления:
- значения, принимаемые j-й БФ на i-м наборе переменных, Y(i) - целые неотрицательные числа, записанные в двоичной системе счисления:
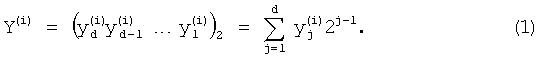
Известно, что СБФ можно однозначно представить в модулярной числовой нормальной форме (Финько О.А. Реализация систем булевых функций большой размерности методами модулярной арифметики. / Автоматика и телемеханика, 2004, №6. - с.37-60); (Финько, О.А. Поисковые методы гибкой параллельной достоверной реализации логических функций криптографических
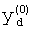
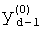
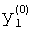
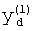
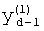
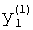
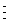
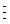
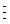
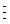
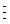
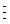
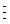
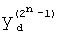
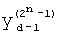
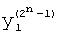
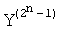
алгоритмов в кн. Криптографическая защита информации: коллективная монография под ред. Е.М.Сухарева. - М.: Радиотехника, 2007. - с.97-118):
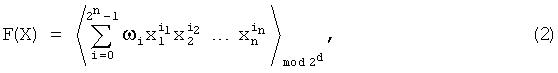
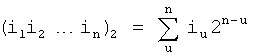 (iu=∈0, 1);
(iu=∈0, 1);  ,
,
где 2d - значение модуля, d - количество реализуемых булевых функций, 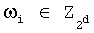 - коэффициенты полинома.
- коэффициенты полинома.
Коэффициенты ωi (i=0,1,…,2n-1) полинома (2) находятся матричным способом:


где 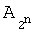 и
и 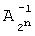 - матрицы прямого и инверсного арифметического преобразования; Y - вектор истинности значений функции F(X) и W - вектор коэффициентов модулярной формы арифметического полинома W(X),
- матрицы прямого и инверсного арифметического преобразования; Y - вектор истинности значений функции F(X) и W - вектор коэффициентов модулярной формы арифметического полинома W(X), 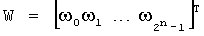 , T - символ транспонирования.
, T - символ транспонирования.
Матрица 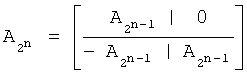 является n-й кронекеровской степенью
является n-й кронекеровской степенью 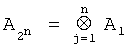 базовой матрицы
базовой матрицы 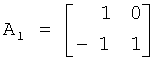 ;
; 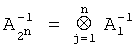 .
.
Преобразования (3) и (4) являются модулярной формой прямого и обратного матричного числового преобразования.
Известная форма (2) не позволяет контролировать ошибки, которые возникают при вычислении систем логических функций.
Для обеспечения контроля логических вычислений дополним реализуемую СБФ f1(X), f2(X), …, fd(X) избыточными булевыми функциями 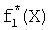 , …,
, …, 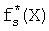 , получив избыточную систему fd(X), …, fs+1(X),
, получив избыточную систему fd(X), …, fs+1(X), 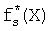 , …,
, …, 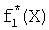 , где s - количество избыточных булевых функций. Так же как и для СБФ f1(X), f2(X), …, fd(X), значения которых интерпретируются в виде целых неотрицательных чисел, записанных в двоичной системе счисления (1), избыточная СБФ
, где s - количество избыточных булевых функций. Так же как и для СБФ f1(X), f2(X), …, fd(X), значения которых интерпретируются в виде целых неотрицательных чисел, записанных в двоичной системе счисления (1), избыточная СБФ 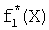 , …,
, …, 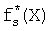 представляется как:
представляется как:
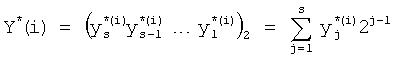 ,
,
где 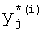 - значения, принимаемые j-й БФ на i-м наборе переменных, Y*(i) - целые неотрицательные числа, записанные в двоичной системе счисления.
- значения, принимаемые j-й БФ на i-м наборе переменных, Y*(i) - целые неотрицательные числа, записанные в двоичной системе счисления.
Рассмотрим полученную избыточную СБФ по правилу задания разделимого AN-кода (Дадаев Ю.Г. Арифметические коды, исправляющие ошибки. / Ю.Г.Дадаев - М: Советское радио, 1969. - 168 с.), где кодовое слово R, формируется из выражения:
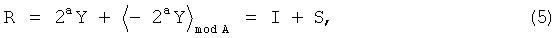
Y - исходное число, здесь - вектор значений реализуемых БФ, I=2aY - информационная часть кода, 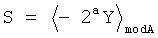 - проверочные символы кодовой комбинации, 2 - основание системы счисления, a - количество двоичных разрядов, необходимое для записи чисел, не превосходящих А - генератора кода, получим:
- проверочные символы кодовой комбинации, 2 - основание системы счисления, a - количество двоичных разрядов, необходимое для записи чисел, не превосходящих А - генератора кода, получим:
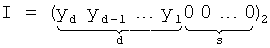 ,
, 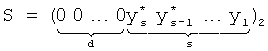 .
.
Отсюда:
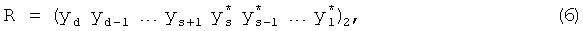
здесь d - количество информационных символов кодового слова (количество реализуемых булевых функций), s - количество проверочных символов (количество избыточных булевых функций), причем количество проверочных символов зависит от выбора численного значения генератора и определяется следующим образом:
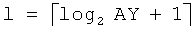 , s=l-d,
, s=l-d,
где l - общая длина кода,  - целая часть числа •.
- целая часть числа •.
Таким образом, требуется реализовать таблицу истинности, представленную в табл.2.
Используя преобразования (3), (4), построим полиномы избыточной модулярной числовой AN-формы:

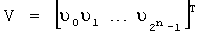 ,
,
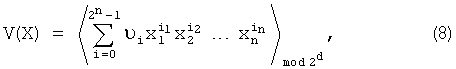
где V - вектор коэффициентов информационного модулярного полинома (8), 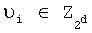 (i=0, 1, …, 2n-1).
(i=0, 1, …, 2n-1).

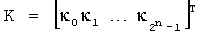 ,
,
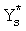
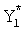
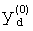
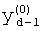
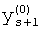
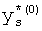
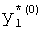
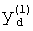
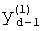
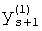
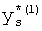
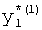
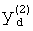
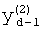
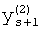
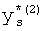
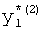
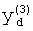
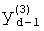
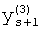
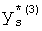
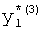
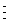
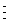
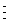
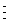
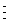
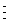
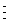
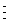
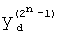
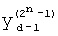
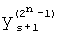
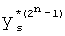
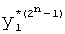
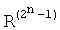
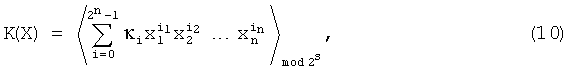
где K - вектор коэффициентов проверочного модулярного полинома (10) и 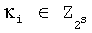 (i=0, 1, …, 2n-1).
(i=0, 1, …, 2n-1).
Как известно, выбор генератора А арифметического AN-кода, не только определяет арифметическое расстояние кода D, но и его корректирующие свойства. Так код с D=2 гарантировано обнаруживает онократную ошибку (в одной булевой функции).
В процессе реализации систем БФ выполняется классическая процедура контроля ошибок в соответствии со свойствами и выбранными параметрами AN-кода.
Принцип контроля заключается в выполнении следующего правила:

что соответствует правильному результату, а выражение
 ,
,
являются признаком ошибки вычислений.
ПРИМЕР
Пусть дана таблица истинности СБФ, представленная в табл.3.
Полином имеет вид:
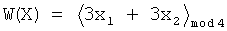 .
.
Применив арифметический разделимый AN-код с А=3, построим избыточную СБФ (табл.4).
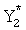
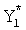
В соответствии с (7):
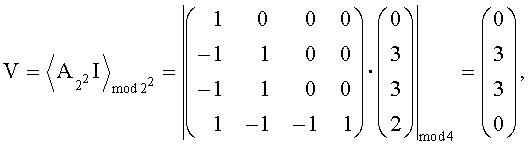
где смысл обозначения 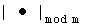 аналогичен обозначению
аналогичен обозначению 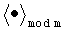 . Таким образом получим полином (8):
. Таким образом получим полином (8): 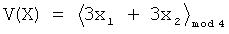 .
.
Используя преобразования (9) построим полином (10):
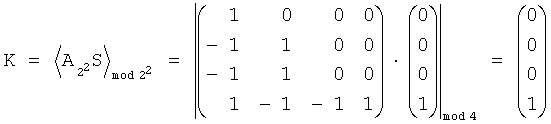 ,
,
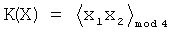 .
.
Пример обнаружения однократной ошибки (звездочкой * обозначается ошибка) продемонстрируем на таблице 5.
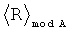
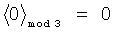
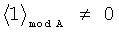
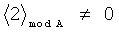
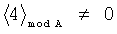
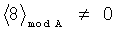
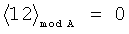
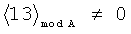
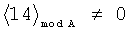
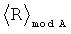
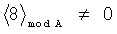
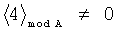
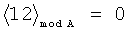
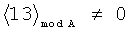
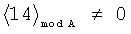
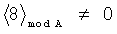
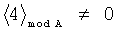
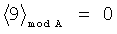
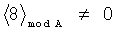
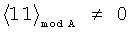
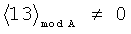
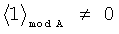
Предлагаемое устройство включает: входы 8.1, …, 8.n подачи значений булевых переменных, блок 1 конъюнкций, блоки памяти 2.1 и 2.2, сумматоры 3.1 и 3.2, блок 4 вычисления остатка по модулю, элемент ИЛИ-НЕ 5, регистр памяти 6, элемент И 7, выходы 9.1, …, 9.d выдачи значений булевых функций: f1(X), f2(X), …, fd(X), вход 10 шины подачи синхроимпульсов. Блок 1 конъюнкций предназначен для вычисления конъюнкций: 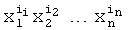 , где
, где 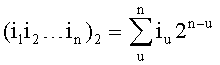 (iu∈0, 1);
(iu∈0, 1);
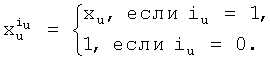
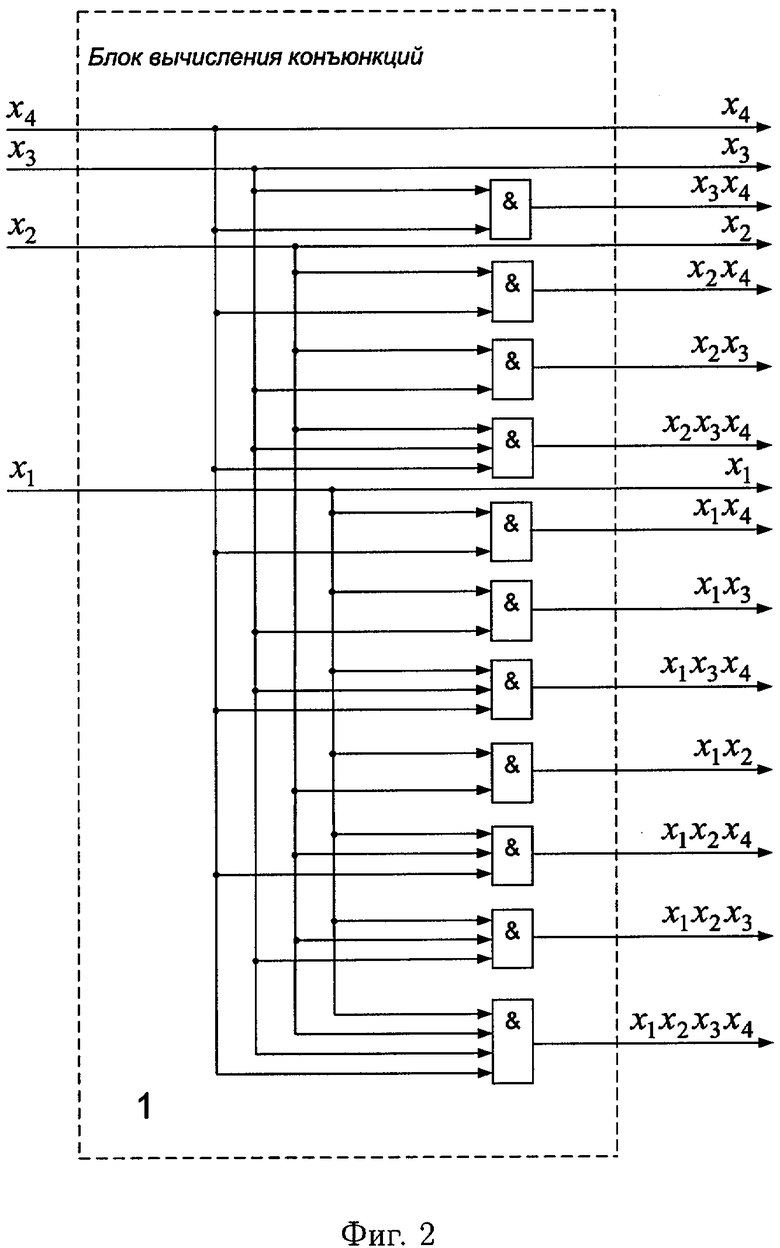
Принцип построения блока 1 конъюнкций для случая четырех булевых переменных поясняется с помощью фиг.2.
Входы 8.1, …, 8.n подачи значений булевых переменных x1, x2, …, xn являются входами блока конъюнкций 1, выходы которого подключены к входам блоков 2.1 и 2.2 памяти, выходы блока памяти 2.1 подключены к сумматору 3.1, выходы которого подключены к (s+1)-му, (s+2)-му, …, (d+s)-му входам (старшие разряды слева) блока 4 вычисления остатка по модулю и информационным входам регистра памяти 6, выходы которого являются выходами устройства выдачи значений d булевых функций: f1(X), f2(X), …, fd(X), выходы блока памяти 2.2 подключены к входам сумматора 3.2, выходы которого подключены к 1-му, 2-му, …, s-му входам блока 4 вычисления остатка по модулю, выходы которого подключены ко входам элемента 5 ИЛИ-НЕ, выход которого подключен к первому входу элемента 7 И, второй вход которого соединен с входом 10 подчи синхроимпульсов устройства, а выход 7 подключен к синхровходу регистра памяти 6.
Предлагаемое устройство работает следующим образом.
В исходном состоянии в блоки 2.1 и 2.2 памяти занесены коэффициенты: 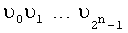 ;
; 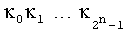 модулярных полиномов (8) и (10) соответственно, полученных в результате преобразований (7), (8), регистр 6 памяти обнулен. В момент времени, соответствующий началу преобразования, на входы 8.1, …, 8.n блока конъюнкций 1 поступают значения булевых переменных x1, x2, …, xn. На выходе блока 1 конъюнкций образуются результаты вычисления конъюнкций
модулярных полиномов (8) и (10) соответственно, полученных в результате преобразований (7), (8), регистр 6 памяти обнулен. В момент времени, соответствующий началу преобразования, на входы 8.1, …, 8.n блока конъюнкций 1 поступают значения булевых переменных x1, x2, …, xn. На выходе блока 1 конъюнкций образуются результаты вычисления конъюнкций 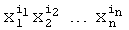 , которые поступают на входы блоков 2.1 и 2.2 памяти. С выходов блоков 2.1 и 2.2 памяти на сумматоры 3.1 и 3.2 поступают произведения
, которые поступают на входы блоков 2.1 и 2.2 памяти. С выходов блоков 2.1 и 2.2 памяти на сумматоры 3.1 и 3.2 поступают произведения 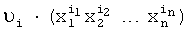 , где i=0, 1, …, 2n-1 и
, где i=0, 1, …, 2n-1 и 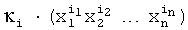 , где i=0, 1, …, 2n-1. С выходов сумматора 3.1 на (s+1)-ый, (s+2)-ой, …, (d+s)-ый входы (старшие разряды слева) блока 4 вычисления остатка по модулю и на информационные входы регистра памяти 6 поступает числовой результат вычисления полинома V(X), с выходов сумматора 3.2 на 1-ый, 2-ой, …, s-ый входы (старшие разряды слева) блока 4 вычисления остатка по модулю поступает числовой результат вычисления полинома K(Х). С выходов блока 4 вычисления остатка по модулю на входы элемента ИЛИ-НЕ 5 поступает результат вычисления
, где i=0, 1, …, 2n-1. С выходов сумматора 3.1 на (s+1)-ый, (s+2)-ой, …, (d+s)-ый входы (старшие разряды слева) блока 4 вычисления остатка по модулю и на информационные входы регистра памяти 6 поступает числовой результат вычисления полинома V(X), с выходов сумматора 3.2 на 1-ый, 2-ой, …, s-ый входы (старшие разряды слева) блока 4 вычисления остатка по модулю поступает числовой результат вычисления полинома K(Х). С выходов блока 4 вычисления остатка по модулю на входы элемента ИЛИ-НЕ 5 поступает результат вычисления 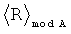 . На выходе элемента 5 ИЛИ-НЕ образуется сигнал «1» при выполнении равенства (11) (ошибки нет) и «0» в противном случае. Синхроимпульс с входа 10 устройства через элемент 7 И поступает на синхровход регистра 6 памяти при отсутствии ошибок вычислений в соответствии с (11). Таким образом при отсутствии ошибок вычислений в регистр 6 памяти записывается численный результат вычисления полинома V(X), интерпритируемый как результат реализации f1(X), f2(X), …, fd(X). При этом результат реализации СБФ соответствует размещению от младшего разряда справа (f1(X)) к старшим разрядам слева (fd(X)).
. На выходе элемента 5 ИЛИ-НЕ образуется сигнал «1» при выполнении равенства (11) (ошибки нет) и «0» в противном случае. Синхроимпульс с входа 10 устройства через элемент 7 И поступает на синхровход регистра 6 памяти при отсутствии ошибок вычислений в соответствии с (11). Таким образом при отсутствии ошибок вычислений в регистр 6 памяти записывается численный результат вычисления полинома V(X), интерпритируемый как результат реализации f1(X), f2(X), …, fd(X). При этом результат реализации СБФ соответствует размещению от младшего разряда справа (f1(X)) к старшим разрядам слева (fd(X)).
| название | год | авторы | номер документа |
|---|---|---|---|
| МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2007 |
|
RU2373564C2 |
| ПОЛИНОМИАЛЬНЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ С ОБНАРУЖЕНИЕМ ОШИБОК | 2015 |
|
RU2586574C1 |
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2012 |
|
RU2485575C1 |
| МОДУЛЯРНЫЙ ПОЛИНОМИАЛЬНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2586575C1 |
| Логический вычислитель в системе остаточных классов | 2016 |
|
RU2637488C1 |
| АРИФМЕТИЧЕСКИЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2011 |
|
RU2461868C1 |
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2579991C1 |
| ОТКАЗОУСТОЙЧИВЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2018 |
|
RU2680035C1 |
| СПОСОБ ПОВЫШЕНИЯ ДОСТОВЕРНОСТИ КРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫ КАНАЛОВ СВЯЗИ РОБОТОТЕХНИЧЕСКИХ КОМПЛЕКСОВ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ | 2023 |
|
RU2809279C1 |
| Устройство поддержки защищенных логических вычислений | 2016 |
|
RU2625049C1 |
Устройство относится к вычислительной технике и может быть использовано для достоверной параллельной реализации систем логических функций в средствах криптографической защиты информации, искусственного интеллекта, системах автоматизированного проектирования интегральных схем. Техническим результатом является расширение функциональных возможностей устройства за счет обеспечения контроля ошибок логических вычислений. Устройство содержит блок конъюнкций, два блока памяти, два сумматора, блок вычисления остатка по модулю, элемент ИЛИ-НЕ, элемент И, регистр памяти. 2 ил., 5 табл.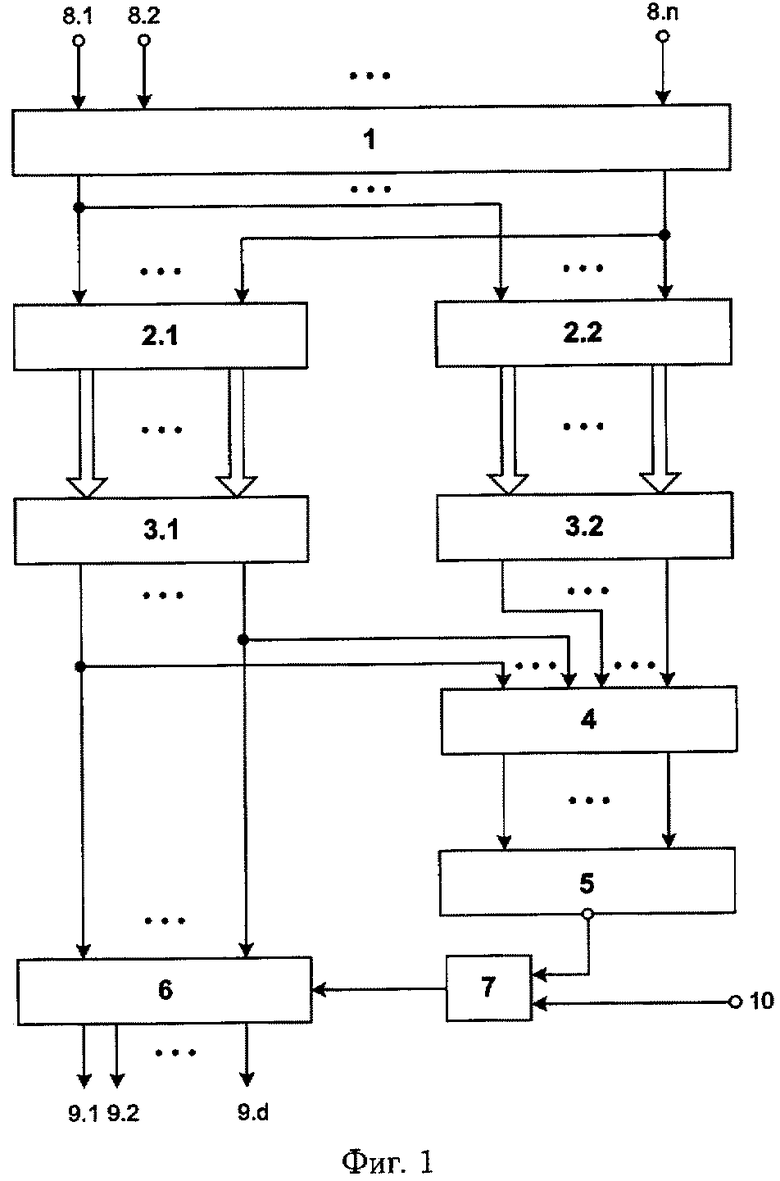
Самопроверяемый модулярный вычислитель систем логических функций, содержащий блок конъюнкций, входы которого являются входами устройства для подачи n булевых переменных, выходы которого подключены к первому блоку памяти, предназначенному для хранения коэффициентов первого полинома избыточной модулярной числовой нормальной формы, первый сумматор, отличающийся тем, что дополнительно введены второй блок памяти, входы которого соединены с выходами блока конъюнкций, при этом второй блок памяти предназначен для хранения коэффициентов второго полинома избыточной модулярной числовой нормальной формы, выходы первого блока памяти подключены к входам первого сумматора, выходы которого подключены к (s+1)-му, (s+2)-му, …, (d+s)-му входам (d - количество реализуемых булевых функций, составляющих информационные разряды разделимого AN-кода, s - количество избыточных булевых функций, соответствующих избыточным разрядам разделимого AN-кода) блока вычисления остатка по модулю и информационным входам регистра памяти, выходы которого являются выходами устройства выдачи значений d булевых функций, выходы второго блока памяти подключены к входам второго сумматора, выходы которого подключены к 1-му, 2-му, …, s-му входам блока вычисления остатка по модулю, выходы которого подключены к входам элемента ИЛИ-НЕ, выход которого подключен к первому входу элемента И, второй вход которого соединен с входом подачи синхроимпульсов устройства, а выход подключен к синхровходу регистра памяти.
| RU 2007141074 А, 20.05.2009 | |||
| МНОГОФУНКЦИОНАЛЬНЫЙ ЛОГИЧЕСКИЙ МОДУЛЬ | 1991 |
|
RU2020555C1 |
| Универсальный логический модуль с самоконтролем | 1988 |
|
SU1644125A1 |
| JP 57108932 А, 07.07.1982. | |||
Авторы
Даты
2011-04-27—Публикация
2009-06-08—Подача