Предлагаемое устройство относится к вычислительной технике и может быть использовано как специализированный вычислитель - универсальный в классе логических вычислений.
Известно специализированное вычислительное устройство, включающее в себя сумматор, выход которого подключен к второму входу регистра результата, регистр для хранения булевых переменных, выход которого подключен к блоку конъюнкций, регистры для фиксации очередных строк матриц, описывающих структуру соответствующей конъюнкции, выходы которых подключены также к блоку конъюнкций, выход которого подключен к третьему входу регистра результата, выход которого является шиной выдачи результата вычислений (Малюгин В.Д. Параллельные логические вычисления посредством арифметических полиномов. - М.: Наука. Физматлит, 1997. - С.156-157).
Недостаток известного устройства - большая длительность вычислений.
Наиболее близким по сущности технического решения к заявляемому устройству является специализированное вычислительное устройство, содержащее блок конъюнкций, входы которого являются шиной подачи значений булевых переменных, выходы которого подключены к блоку памяти, выходы которого подключены к входам коммутатора, выходы которого подключены к многоместному сумматору, выходы которого являются выходами устройства выдачи результата вычислений (Малюгин В.Д. Параллельные логические вычисления посредством арифметических полиномов. - М.: Наука. Физматлит, 1997. - С.154-155).
Недостаток известного устройства - большая длительность вычислений.
Цель изобретения - уменьшение длительности вычислений.
Поставленная цель достигается тем, что в специализированное устройство для логических вычислений (СУЛВ), содержащее коммутатор, входы которого являются входами устройства подачи n булевых переменных, блок конъюнкций, выходы которого подключены к первому блоку памяти, многоместный сумматор, выходы которого являются выходами устройства выдачи значений булевых функций, с целью уменьшения длительности вычислений введены 2k-1 блоков памяти, где k - количество булевых переменных разложения, 2n-k мультиплексоров, при этом входы (k+1)…n коммутатора подключены ко входам блока конъюнкций, выходы которого подключены ко входам второго, третьего и так далее, 2k-го блоков памяти соответственно, первые выходы блоков памяти подключены к информационным входам первого мультиплексора, вторые выходы блоков памяти подключены к информационным входам второго мультиплексора и так далее, (n-k)-е выходы блоков памяти подключены к информационным входам 2n-k-го мультиплексора соответственно, выходы мультиплексоров подключены ко входам многоместного сумматора, а первый, второй и так далее, k-й адресные входы мультиплексоров соединены соответственно с первым, вторым и так далее, k-м выходами коммутатора.
Структурная схема предлагаемого СУЛВ представлена на фиг.1. Пусть дана система булевых функций (СБФ): f1(x), f2(х), …, fd(х) от n булевых переменных x=x1,x2,…,xn (xi∈{0,1}, i=1,2,…,n):
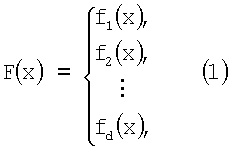
где F(х) - значение, принимаемое d-выходной БФ.
Известно, что СБФ (1) можно однозначно представить в числовой нормальной форме (ЧНФ):
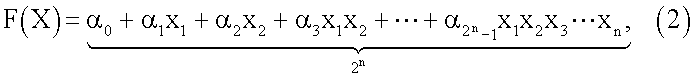
где α0,α1,α2,…αn∈Z, Z - множество целых чисел, F(x) при представлении в двоичной системе счисления интерпретируется как результат вычисления СБФ.
Пример 1. Пусть СБФ (1) задана формулами:
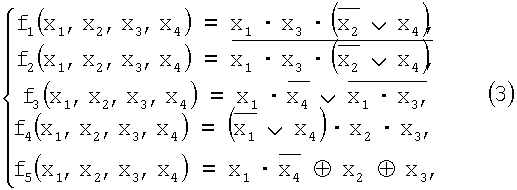
тогда ЧНФ (2) будет иметь вид:
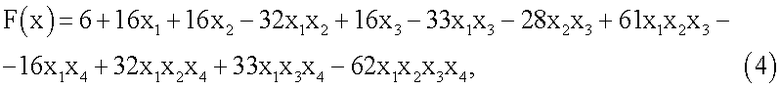
присвоив булевым переменным значения x1=1, x2=1, x3=1, x4=1, получим
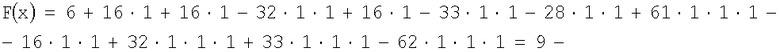
результат вычисления СБФ (3)
Так как число 9 в двоичной системе счисления запишется как (01001)2, то f1(x)=1, f2(x)=0, f3(x)=0, f4(x)=1, f5(x)=0 (значения f1(x) находится в младшем разряде (справа), а f5(x) -в старшем разряде слева)).
Известно, что СБФ (1) может быть единственным образом представлена на основе модулярной ЧНФ (2) в виде:
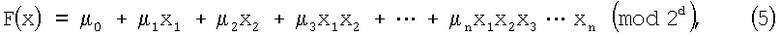
где d - количество реализуемых булевых функций, 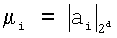 ,
,
(mod 2d) - указывает на то, что вычисление (5) выполняется в конечном кольце 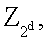
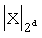 - получение наименьшего неотрицательного вычета от x по модулю 2d.
- получение наименьшего неотрицательного вычета от x по модулю 2d.
Пример 2. Пусть дана ЧНФ (4) СБФ (3), тогда модулярная форма (5) будет иметь вид:
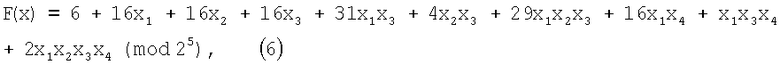
присвоив булевым переменным значения: x1=1, x2=1, x3=1, x4=1, получим:
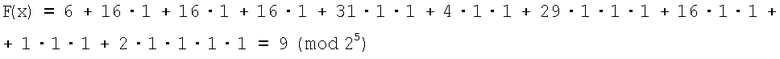 - результат вычисления СБФ (3).
- результат вычисления СБФ (3).
Известно, что любую СБФ, зависящую от n аргументов, можно разложить по переменным и представить в виде:

где
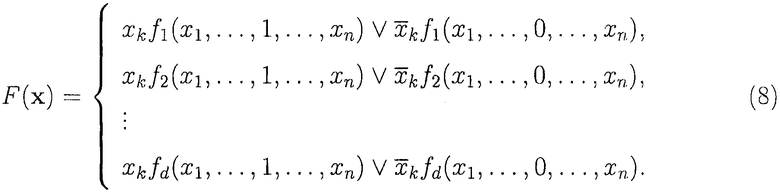
Обобщим (7) для произвольного количества переменных разложения, получим:
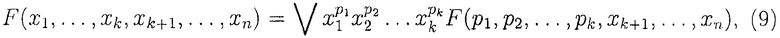
где 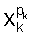 - степень аргументов xk, pk - двоичная переменная величина такая, что
- степень аргументов xk, pk - двоичная переменная величина такая, что
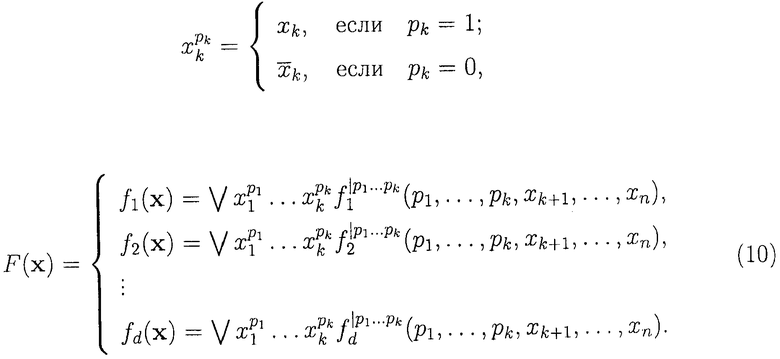
Придав фиксированные значения переменным разложения: 0…0; 0…1; …; 1…1, разложение (9) можно записать в виде
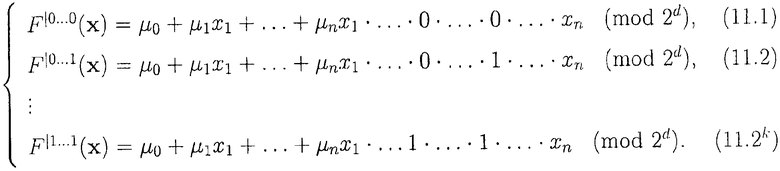
Пример 3. Пусть дана СБФ (3). Разложим каждую функцию по переменным x1, x3. Тогда СБФ будет иметь вид:

Объединим подфункции, полученные в результате разложения, в системы 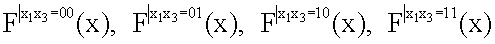 и присвоим булевым переменным значения x2=1, x4=1, представим каждую систему подфункций в ЧНФ:
и присвоим булевым переменным значения x2=1, x4=1, представим каждую систему подфункций в ЧНФ:
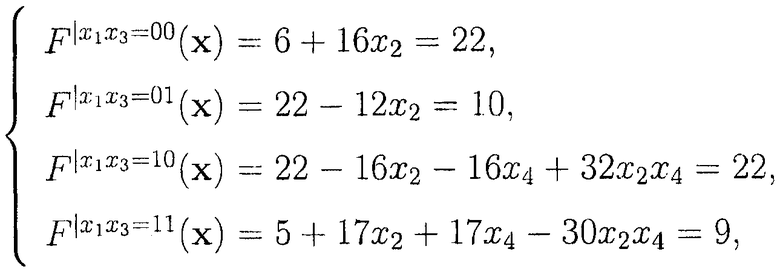
а затем в модулярной ЧНФ:
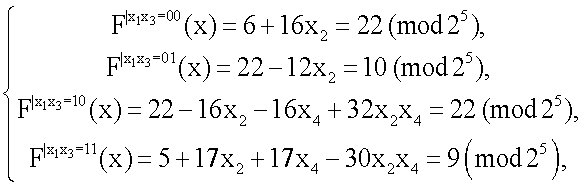
Результат вычисления 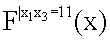 соответствует результату вычисления F(x).
соответствует результату вычисления F(x).
Таким образом, для нахождения искомого результата достаточно вычислить только одну систему подфункций, представленную модулярной ЧНФ в соответствии с координатами, определяемыми значениями переменных разложения. В данном примере координатами системы подфункций являются значения переменных разложения x1=1, x3=1.
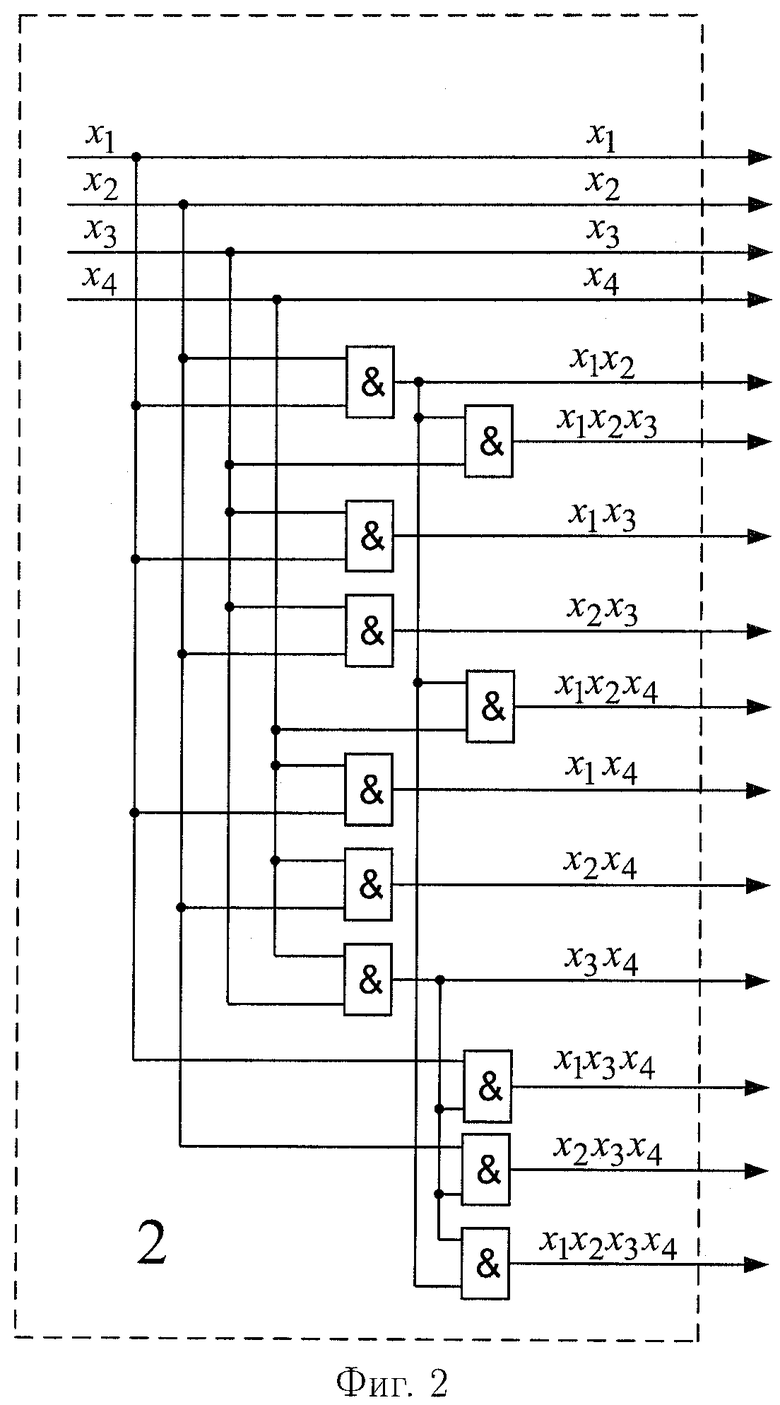
Предлагаемое устройство СУЛВ включает: входы 6.1,…,6.n подачи значений булевых переменных, коммутатор 1, блок 2 конъюнкций, блоки 3.1,…,3.2k памяти, мультиплексоры 4.1,…,4.2n-k, сумматор 5, выходы 7.1,…,7d выдачи значений булевых функций: fd(x),…,f1(x).
Входы 6.1,…,6.n подачи значений булевых переменных x1,x2,…,xn, которые являются входами устройства, являются и входами коммутатора 1, выходы (k+1)…n которого подключены ко входам блока 2 конъюнкций, выходы которого подключены ко входам блоков 3.1,…,3.2k памяти соответственно, первые выходы блоков 3.1,…,3.2k памяти подключены к информационным входам мультиплексора 4.1, вторые выходы блоков 3.1,…,3.2k памяти подключены к информационным входам мультиплексора 4.2 и так далее, (n-k)-e выходы блоков 3.1,…,3.2k памяти подключены к информационным входам мультиплексора 4.2n-k соответственно, выходы мультиплексоров 4.1,…,4.2n-k подключены ко входам многоместного сумматора 5, а первый, второй и так далее, k-й адресные входы мультиплексоров 4.1,…,4.2n-k соединены соответственно с первым, вторым и так далее, k-м выходами коммутатора 1. Выходы 7.1,…,7.d многоместного сумматора 5 являются выходами устройства выдачи значений булевых функций: fd(x),…,f1(x). Предлагаемое устройство работает следующим образом.
В исходном состоянии в блоки 3.1,…,3.2k памяти занесены группы коэффициентов: 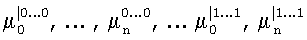 модулярных ЧНФ (11.1), (11.2),…,(11.2k) соответственно, полученных в результате разложения (9). В момент времени, соответствующий началу преобразования, на входы 6.1,…,6.n коммутатора 1 поступают значения булевых переменных x1,x2,…,xn. В коммутаторе 1 под воздействием внешних сигналов управления, в соответствии с заранее выполненным разложением (9) из состава поступивших переменных x1,x2,…,xn выделяются переменные разложения xi1,…,xik, которые поступают на адресные входы мультиплексоров 4.1,…,4.2n-k, а остальные - информационные переменные xik+1,…,xin - подаются далее на входы блока 2 конъюнкций. Блок 2 конъюнкций предназначен для вычисления конъюнкций: xik+1; xik+2; xik+1·xik+2;…; xik+1·xik+2·…·xin, которые поступают на входы блоков 3.1,…,3.2k памяти, с первых выходов которых коэффициенты
модулярных ЧНФ (11.1), (11.2),…,(11.2k) соответственно, полученных в результате разложения (9). В момент времени, соответствующий началу преобразования, на входы 6.1,…,6.n коммутатора 1 поступают значения булевых переменных x1,x2,…,xn. В коммутаторе 1 под воздействием внешних сигналов управления, в соответствии с заранее выполненным разложением (9) из состава поступивших переменных x1,x2,…,xn выделяются переменные разложения xi1,…,xik, которые поступают на адресные входы мультиплексоров 4.1,…,4.2n-k, а остальные - информационные переменные xik+1,…,xin - подаются далее на входы блока 2 конъюнкций. Блок 2 конъюнкций предназначен для вычисления конъюнкций: xik+1; xik+2; xik+1·xik+2;…; xik+1·xik+2·…·xin, которые поступают на входы блоков 3.1,…,3.2k памяти, с первых выходов которых коэффициенты 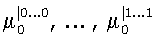 поступают на информационные входы мультиплексора 4.1, со вторых выходов блоков 3.1,…,3.2k памяти коэффициенты
поступают на информационные входы мультиплексора 4.1, со вторых выходов блоков 3.1,…,3.2k памяти коэффициенты 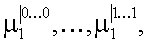 , значения соответствующих конъюнкций которых равны 1, поступают на информационные входы мультиплексора 4.2 и так далее, с (n-k)-x выходов блоков 3.1,…,3,2k памяти коэффициенты
, значения соответствующих конъюнкций которых равны 1, поступают на информационные входы мультиплексора 4.2 и так далее, с (n-k)-x выходов блоков 3.1,…,3,2k памяти коэффициенты 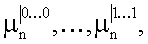 значения соответствующих конъюнкций которых равны 1, поступают на информационные входы мультиплексора 4.2n-k. Общая задача мультиплексоров 4.1,…,4.2n-k заключается в том, чтобы в соответствии со значениями булевых переменных xi1…,xik, поступивших на адресные входы и определяющих параметр разложения, подать на входы многоместного сумматора 5 значения коэффициентов
значения соответствующих конъюнкций которых равны 1, поступают на информационные входы мультиплексора 4.2n-k. Общая задача мультиплексоров 4.1,…,4.2n-k заключается в том, чтобы в соответствии со значениями булевых переменных xi1…,xik, поступивших на адресные входы и определяющих параметр разложения, подать на входы многоместного сумматора 5 значения коэффициентов 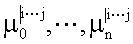 одной из подсистем БФ, представленной в модулярной ЧНФ. После преобразований в многоместном сумматоре 5 на выходы устройства поступают вычисленные значения СБФ в следующем порядке: fd(x), fd-1(x), …, f1(x).
одной из подсистем БФ, представленной в модулярной ЧНФ. После преобразований в многоместном сумматоре 5 на выходы устройства поступают вычисленные значения СБФ в следующем порядке: fd(x), fd-1(x), …, f1(x).
Длительность функционирования СВУ - прототипа определяется как:
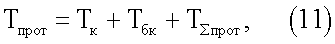
где Tк - длительность функционирования коммутатора,
Tбк - длительность функционирования блока конъюнкций,
Т∑прот - длительность функционирования многоместного сумматора прототипа,
T∑прот=ΔτЛЭ4dlog22n = ΔτЛЭ4dn, где ΔτЛЭ - время задержки одного двухвходового логического элемента (ЛЭ), n - количество булевых переменных, d - количество реализуемых булевых функций.
Длительность функционирования предлагаемого СУЛВ определяется как:
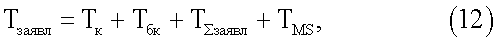
T∑заявл - длительность функционирования многоместного сумматора предлагаемого СУЛВ,
T∑заявл=ΔτЛЭ4dlog22n-k=ΔτЛЭ4d(n-k), где k - количество булевых переменных разложения,
TMS - длительность функционирования мультиплексора,
TMS=ΔτЛЭ(k+log2(k+1)).
Из (11) и (12) видно, что общей и у прототипа, и у предлагаемого СУЛВ является сумма длительностей Tк+Tбк=Tк,бк. Длительность функционирования предлагаемого устройства отличается от длительности функционирования прототипа уменьшенной длительностью функционирования T∑заявл сумматора 5. При допущении, что коммутатор 1 конструктивно представляет схему последовательно соединенных мультиплексора и демультиплексора, а блок 2 конъюнкций построен по принципу, представленному на фиг.2, коэффициент выигрыша в уменьшении длительности вычислений предлагаемого СУЛВ по отношению к прототипу с учетом длительности функционирования TMS мультиплексора будет определяться выражением:
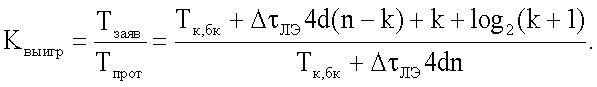
Например, при значениях: d=10, n=16, k=1 минимальный выигрыш в уменьшении длительности вычислений предлагаемого СУЛВ по отношению к прототипу составит 6 процентов, при значениях: d=10, n=16, k=4 выигрыш составит 24 процента, при значениях: d=10, n=16, k=8 выигрыш составит 48 процентов. Получаемый выигрыш достигается за счет обеспечения замены вычисления всей СБФ вычислением только одной системы подфункций, выбранной из состава разложения.
| название | год | авторы | номер документа |
|---|---|---|---|
| АРИФМЕТИЧЕСКИЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2011 |
|
RU2461868C1 |
| САМОПРОВЕРЯЕМЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ ЛОГИЧЕСКИХ ФУНКЦИЙ | 2009 |
|
RU2417405C2 |
| МОДУЛЯРНЫЙ ПОЛИНОМИАЛЬНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2586575C1 |
| Логический вычислитель в системе остаточных классов | 2016 |
|
RU2637488C1 |
| ПОЛИНОМИАЛЬНЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ С ОБНАРУЖЕНИЕМ ОШИБОК | 2015 |
|
RU2586574C1 |
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2012 |
|
RU2485575C1 |
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2579991C1 |
| Устройство решения систем логических уравнений | 2017 |
|
RU2654137C1 |
| ОТКАЗОУСТОЙЧИВЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2018 |
|
RU2680035C1 |
| Устройство для моделирования конечных автоматов | 1980 |
|
SU955080A1 |
Изобретение относится к вычислительной технике и может быть использовано как специализированный вычислитель систем булевых функций. Техническим результатом является уменьшение длительности вычислений. Поставленная цель достигнута за счет обеспечения вычисления не всей системы булевых функций, представленной в модулярной числовой нормальной форме, а лишь одной системы подфункций, представленной в модулярной числовой нормальной форме, полученной в результате примененного к системе булевых функций разложения. Устройство содержит коммутатор, блок конъюнкций, 2k блоков памяти, где k - количество булевых переменных разложения,
2n-k мультиплексоров, сумматор. 2 ил.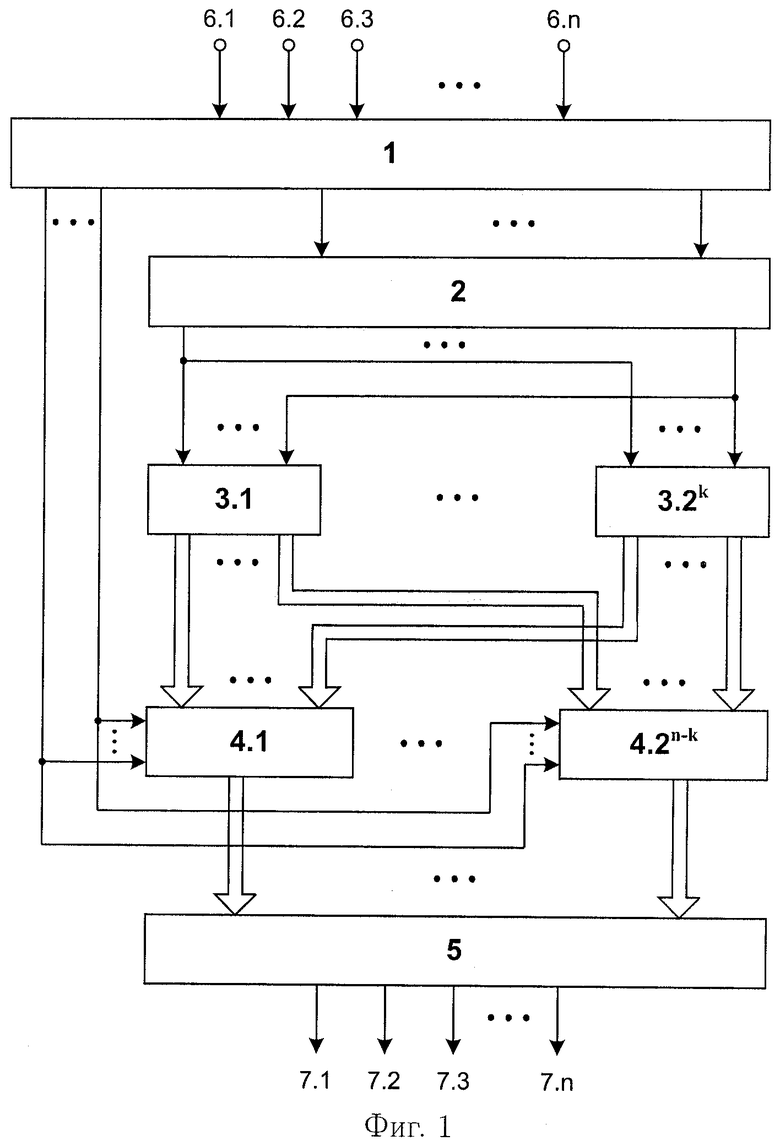
Устройство для вычисления булевых функций, содержащее коммутатор, входы которого являются входами устройства для подачи n булевых переменных, предназначенный для выделения переменных разложения системы булевых функций, блок конъюнкций, выходы которого подключены к первому блоку памяти, многовходовый сумматор, выходы которого являются выходами устройства выдачи значений булевых функций, отличающееся тем, что дополнительно введены 2k-1 блоков памяти, где k - количество булевых переменных разложения, при этом 2k блоков памяти предназначены для хранения 2k групп коэффициентов модулярных числовых нормальных форм, полученных в результате заранее выполненного разложения системы булевых функций, 2n-k мультиплексоров, при этом с (k+1)-го по n-ый выходы коммутатора подключены к входам блока конъюнкций, выходы которого подключены к входам со второго по 2k-ый блоков памяти соответственно, первые (n-k)-ые выходы блоков памяти подключены к информационным входам соответственно первого 2n-k-ого мультиплексора, выходы мультиплексоров, на которые поступают значения коэффициентов одной из подсистем булевых функций, представленной в модулярной числовой нормальной форме, в соответствии со значениями булевых переменных, определяющих параметр разложения, подключены к входам многовходового сумматора, с первого по k-ый адресные входы мультиплексоров соединены соответственно с первого по k-ый выходами коммутатора, на которых формируются значения булевых переменных, определяющие параметр разложения.
| МАЛЮГИН В.Д | |||
| Параллельные логические вычисления посредством арифметических полиномов | |||
| - М.: Наука, Физматлит, 1997, с.154-155 | |||
| УСТРОЙСТВО ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ | 2005 |
|
RU2288500C1 |
| МНОГОФУНКЦИОНАЛЬНЫЙ ЛОГИЧЕСКИЙ МОДУЛЬ | 1990 |
|
RU2018922C1 |
| Блок вычисления логических функций | 1990 |
|
SU1800465A1 |
| US 6070182 A, 30.05.2000 | |||
| JP 8007083 A, 12.01.1996. | |||
Авторы
Даты
2009-11-20—Публикация
2007-11-06—Подача