Область техники, к которой относится изобретение
Предлагаемое устройство относится к вычислительной технике и может быть использовано для обеспечения отказоустойчивости наиболее важных узлов средств криптографической защиты информации.
Уровень техники
а) Описание аналога
Известно вычислительное устройство, содержащее шифраторы, выходы которых подключены ко входам устройств сравнения, выходы которых подключены ко входам устройства управления, выходы которого подключены к постоянным запоминающим устройствам (ПЗУ), предназначенным для хранения констант ортогональных базисов и общего модуля системы, выходы которых подключены ко входам умножителей, к которым также подключены выходы шифраторов, на входы которых поступают значения наименьших неотрицательных вычетов по системе попарно простых и упорядоченных модулей системы, значения первого из которых поступают на вход первого умножителя и входы устройств сравнения. Выходы умножителей и выход ПЗУ, предназначенного для хранения констант общего модуля системы, подключены ко входам сумматора по общему модулю, выход которого является шиной выдачи результата вычислений (Финько, О.А. Контроль и реконфигурация аналого-цифровых устройств, функционирующих в системе остаточных классов / О.А. Финько // Электронное моделирование. Том №22.4.2000. - С. 92-103).
Недостаток известного устройства - отсутствие функциональных возможностей обеспечения отказоустойчивости устройства при вычислении двоичных псевдослучайных последовательностей (ПСП), идентичных ПСП, получаемым посредством классических генераторов на линейных рекуррентных регистрах сдвига (ЛРРС).
б) Описание ближайшего аналога (прототипа)
Наиболее близким по сущности технического решения заявленному устройству является вычислительное устройство, включающее в себя регистр памяти, входы которого являются входами устройства, к которому подключена шина подачи булевых переменных, блок памяти, предназначенный для хранения коэффициентов линейного числового полинома (ЛЧП), ко входу которого подключена шина подачи коэффициентов ЛЧП, блок памяти, предназначенный для хранения оснований системы, ко входу которого подключена шина подачи оснований системы, выходы которого вместе с выходами блока памяти хранения коэффициентов ЛЧП подключены ко входам блоков вычисления наименьших неотрицательных вычетов числа (коэффициентов ЛЧП) по основаниям системы, выходы которых вместе с выходами регистра памяти подключены ко входам множителей, выходы которых подключены ко входам многоместных сумматоров, выходы которых подключены ко входам блока решения системы сравнений с одним неизвестным, выход которого подключен ко входам блока сравнения и блока оператора маскирования, выход блока сравнения подключен ко второму входу блока оператора маскирования, выходы которого являются выходами устройства выдачи значений булевых функций (БФ) (Патент РФ №2579991, публ. 10.04.2016).
Недостаток известного устройства - отсутствие функциональных возможностей обеспечения отказоустойчивости устройства при вычислении двоичных ПСП, идентичных ПСП, получаемым посредством классических генераторов на ЛРРС.
Раскрытие изобретения
а) Технический результат, на достижение которого направлено изобретение
Цель изобретения - расширение функциональных возможностей устройства за счет обеспечения его отказоустойчивости при вычислении двоичных ПСП, идентичных ПСП, получаемым посредством классических генераторов на ЛРРС.
б) Совокупность существенных признаков
Поставленная цель достигается тем, что в отказоустойчивый специализированный вычислитель систем БФ, содержащий регистр памяти, входы которого являются входами устройства, к которому подключена шина подачи т булевых переменных, блок памяти, предназначенный для хранения коэффициентов ЛЧП, ко входу которого подключена шина подачи коэффициентов ЛЧП, блок памяти, предназначенный для хранения оснований системы, ко входу которого подключена шина подачи оснований системы, выходы которого вместе с выходами блока памяти хранения коэффициентов ЛЧП подключены ко входам блоков вычисления наименьших неотрицательных вычетов числа (коэффициентов ЛЧП) по основаниям системы, выходы которых вместе с выходами регистра памяти подключены ко входам множителей, выходы которых подключены ко входам многоместных сумматоров, оператор маскирования; дополнительно введены блок памяти, предназначенный для хранения модулей системы, блоки памяти, предназначенные для хранения ортогональных базисов, выходы которых вместе с выходами многоместных сумматоров являются входами множителей, выходы которых вместе с выходами блока памяти, предназначенного для хранения модулей системы, являются входами многоместного сумматора по модулю системы, выход которого подключен ко входам блока контроля и управления и блока оператора маскирования, первый выход блока контроля и управления подключен ко второму входу блока оператора маскирования, выходы которого являются выходами устройства выдачи значений т БФ, второй выход блока контроля и управления подключен к входам блоков памяти, предназначенным для хранения ортогональных базисов и блока памяти, предназначенного для хранения модулей системы.
Структурная схема предлагаемого устройства представлена на фиг. 1.
в) Причинно-следственная связь между признаками и техническим результатом Благодаря новой совокупности существенных признаков в устройстве реализована возможность:
- обнаружения возникающей ошибки;
- коррекции обнаруженной ошибки;
- восстановления достоверности функционирования посредством осуществления реконфигурации системы.
Доказательства соответствия заявленного изобретения условиям патентоспособности «новизна» и «изобретательский уровень»
Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности «новизна».
Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность отличительных существенных признаков, обуславливающих тот же технический результат, который достигнут в заявленном способе. Следовательно, заявленное изобретение соответствует условию патентоспособности «изобретательский уровень».
Краткое описание чертежей
Заявленное устройство поясняется чертежами, на которых показано:
фиг. 1 - отказоустойчивый специализированный вычислитель систем БФ;
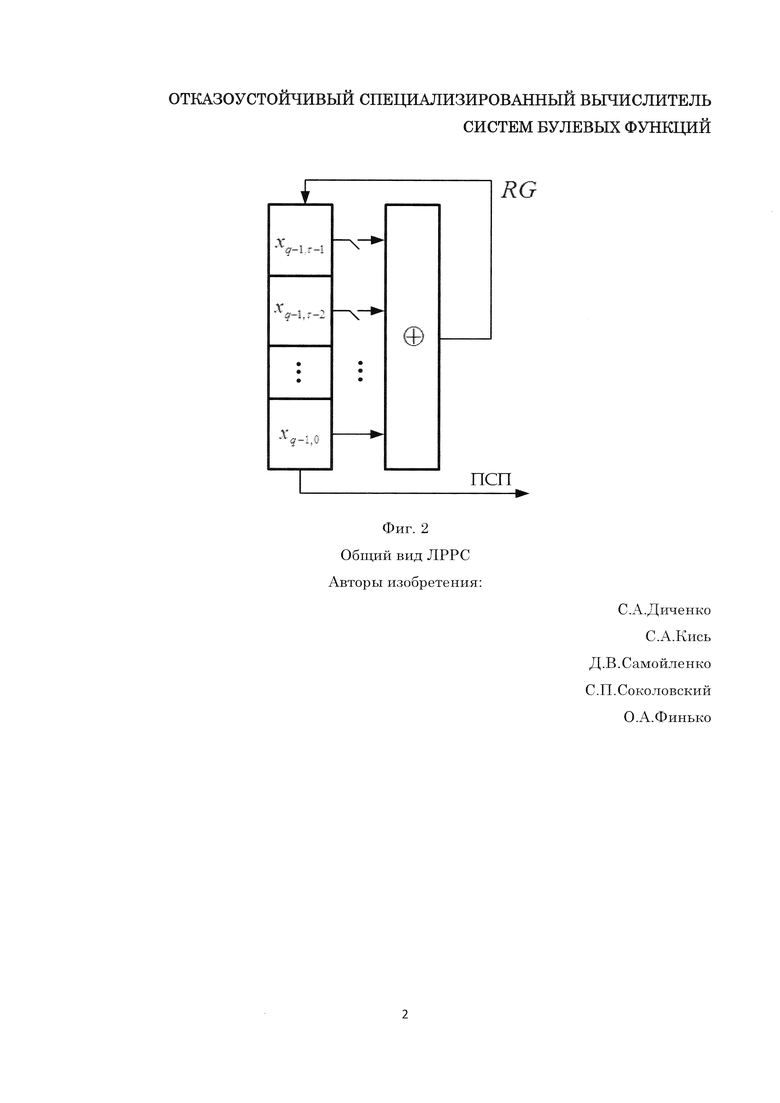
фиг. 2 - общий вид ЛРРС;
фиг. 3 - общий вид ЛРРС (частный случай: образующий полином - трином).
Осуществление изобретения
Предлагаемое устройство предназначено для вычисления двоичных ПСП, идентичных ПСП, получаемым посредством классических генераторов на ЛРРС, с функцией обеспечения отказоустойчивости. Работа устройства основана на представлении систем рекурсивных характеристических уравнений ЛЧП.
Алгоритмы и устройства генерации ПСП, основанные на использовании рекуррентных логических выражений и неприводимых полиномов, наиболее простым по структуре из которых является ЛРРС (фиг. 2), считаются наиболее распространенными и проверенными практикой (Бабаш, А.В. Криптография / А.В. Бабаш, Г.П. Шанкин. - М.: СОЛОН-Р, 2002. - 575 с).
Структура ЛРРС определяется образующим многочленом:
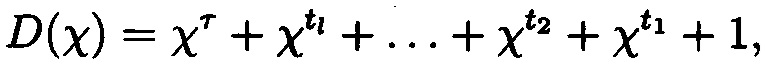
где τ, ti∈N  а также полученным на его основе характеристическим уравнением:
а также полученным на его основе характеристическим уравнением:
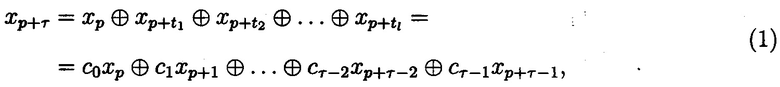
где xр, xp+ti, cj∈{0,1}; р∈N; 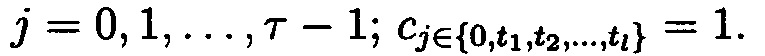
В терминах линейной алгебры очередной элемент ПСП xp+τ выражения (1) вычисляется произведением (Песошин, В.А. Генераторы псевдослучайных и случайных чисел на регистрах сдвига: моногр. / В.А. Песошин, В.М. Кузнецов. - Казань: Казан. Гос. техн. ун-т, 2007. - 296 с.):
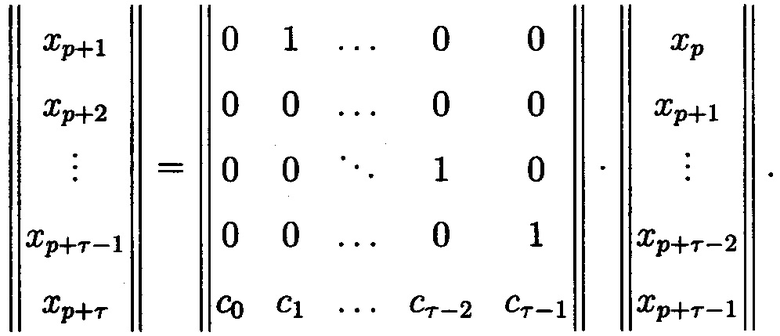
Для осуществления контроля ошибок вычислений в области цифровой схемотехники известны решения, основанные на использовании методов избыточного модулярного кодирования (Согомонян, Е.С. Самопроверяемые устройства и отказоустойчивые системы [Текст] / Е.С. Согомонян, Е.В. Слабаков. - М.: Радио и связь, 1989. - 208 с.). Для применения этих методов к генераторам ПСП необходимо предварительно решить задачу распараллеливания процесса вычислений ПСП.
Решение задачи основано на применении классических параллельных алгоритмов вычисления рекурсий (Ортега, Дж. Введение в параллельные и векторные методы решения линейных систем [Текст] / Дж. Ортега. - М.: Мир, 1991. - 365 с.).
В частности, ЛРРС длины τ реализующий данный метод, имеет т ячеек памяти, значения которых совместно образуют (начальное) состояние (xq-1,0, …, xq-1,t, …, xq-1,τ-1). После первого такта работы ЛРРС выдаст xq-1,0 и перейдет в состояние (xq-1,1, …, xq,0), где xq,0=xq-1,0⊕ xq-1,t. Продолжая таким образом, ЛРРС генерирует ДСП. Общий вид данного ЛРРС представлен на фиг. 3.
Так, например, для характеристического уравнения:

где xp+τ, xp+t, xp∈{0,1}, соответствующего триному D(χ)=χτ+χt+1 (где τ - степень тринома; τ, t∈N; τ≥3; 1≤t≤τ-1).
Для рекурсии (2) построим систему характеристических уравнений (3):

Реализация системы (3) позволяет одновременно получить q-й блок ПСП, состоящий из τ элементов. Выразим правые части системы (3) через заданные начальные условия и представим ее как систему булевых функций (БФ)(4) от τ переменных:
булевых функций (БФ)(4) от τ переменных:
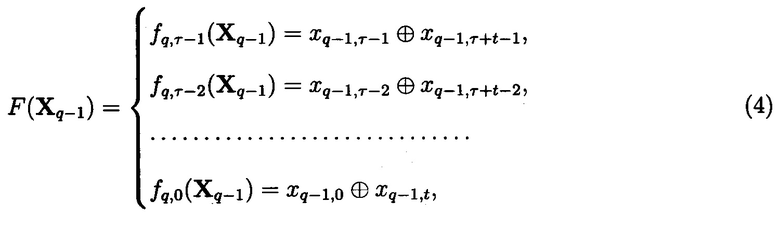
где Xq-1=[xq-1,0, …, xq-1,τ-2 xq-1,τ-1] - вектор начальных условий.
Используем правило представления БФ ƒj ЛЧП (Малюгин, В.Д. Параллельные логические вычисления посредством арифметических полиномов [Текст] / В.Д. Малюгин. - М.: Наука. Физматлит, 1997. - 190 с):
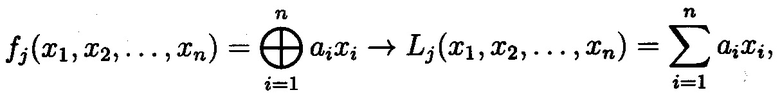
где результат вычисления БФ ƒj(x1, …, хn) соответствует значению младшего разряда двоичного представления результата вычисления Lj(x1, …, хn).
Получим систему ЛЧП:
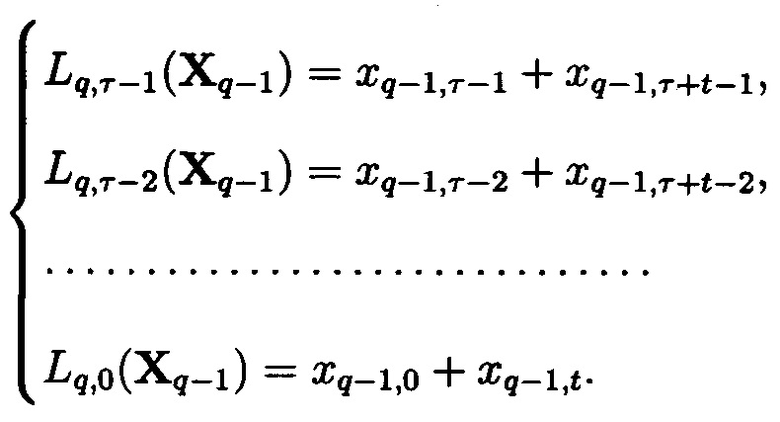
Получим общий ЛЧП:
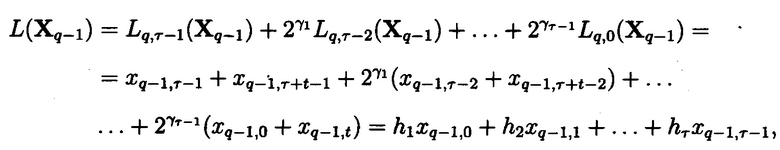
где 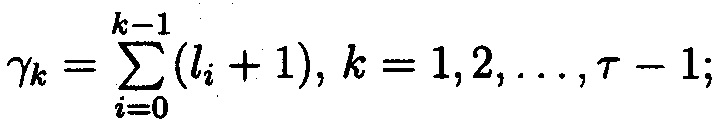 hj∈Z, или
hj∈Z, или

Окончательный результат образуется путем реализации оператора маскирования 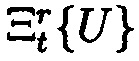 .
.
Оператор маскирования 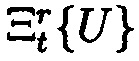 служит для определения значения t-ой БФ представления U=(аr … аt … а2а1)2 (запись (…)2 означает запись в 2-ичной системе счисления), то есть
служит для определения значения t-ой БФ представления U=(аr … аt … а2а1)2 (запись (…)2 означает запись в 2-ичной системе счисления), то есть 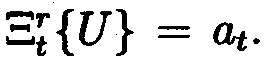 (Шмерко, В.П. Теоремы Малюгина: новое понимание в логическом управлении, проектировании СБИС и структурах данных для новых технологий [Текст] / В.П. Шмерко // Автоматика и телемеханика. - 2004. - №6. - С. 104-112).
(Шмерко, В.П. Теоремы Малюгина: новое понимание в логическом управлении, проектировании СБИС и структурах данных для новых технологий [Текст] / В.П. Шмерко // Автоматика и телемеханика. - 2004. - №6. - С. 104-112).
Таким образом, полученный ЛЧП (5) позволяет реализовать q-й блок ПСП длины τ. Значения полученного блока ПСП будут являться начальным заполнением для ЛЧП, реализующего следующий блок последовательности длиной равной τ.
Пример 1 Для 6-ти разрядного ЛРРС, структура которого определяется образующим триномом D(χ)=χ6+χ+1 и характеристическим уравнением x6=х0⊕x1, система уравнений участка ПСП длины τ=6 примет вид:
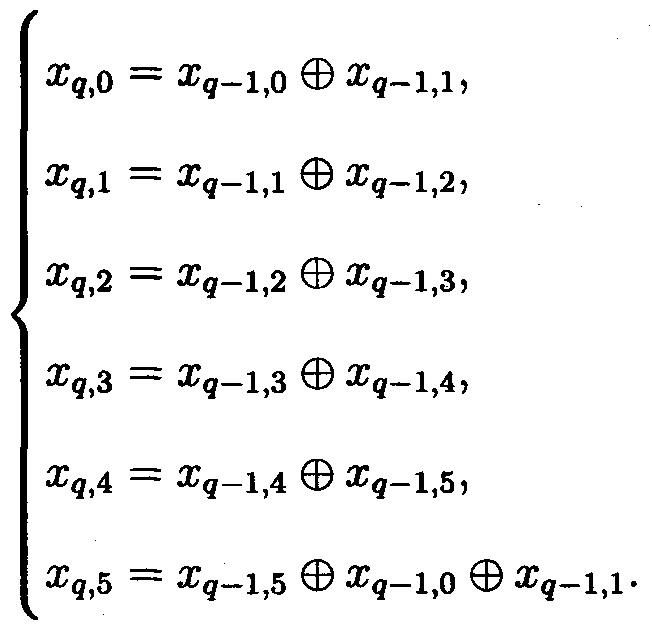
Запишем систему характеристических уравнений, как систему БФ:

Получим систему ЛЧП:

Получим обший ЛЧП:
U=L(Xq-1)=1025xq-1,0+1029xq-1,1+20xq-1,2++80хq-1,3+320xq-1,4+1280xq-1,5.
Пусть xqq-1,1=xq-1,2=xq-1,5=0, xq-1,1=xq-1,3=xq-1,4, тогда

Таким образом, посредством одного ЛЧП получим q-блок ПСП длины τ=6 идентичной ПСП, получаемой посредством классического генератора на ЛРРС.
В модулярной арифметике (МА) целое неотрицательное число А может быть однозначно представлено набором остатков по основаниям МА р1<р2< … <рη<pη+1< … <рκ.

где Pη=р1р2 … рη>А;  |⋅|р - наименьший неотрицательный вычет числа «⋅» по модулю р; р1<р2< … <рη<pη+1< … <рκ - попарно простые; j=1, 2, …, η, η+1, …, κ (Акушский, И.Я. Машинная арифметика в остаточных классах [Текст] / И.Я. Акушский, Д.И. Юдицкий. - М.: Советское радио, 1968. - 440 с.).
|⋅|р - наименьший неотрицательный вычет числа «⋅» по модулю р; р1<р2< … <рη<pη+1< … <рκ - попарно простые; j=1, 2, …, η, η+1, …, κ (Акушский, И.Я. Машинная арифметика в остаточных классах [Текст] / И.Я. Акушский, Д.И. Юдицкий. - М.: Советское радио, 1968. - 440 с.).
При этом остатки МА α1, α2, …, αη считаются информационными, a αη+i, …, ακ - контрольными (избыточными). Сама МА является в этом случае расширенной, где Рκ=Pηpη+1 … рκ, и охватывает полное множество состояний, представляемых всеми к вычетами. Эта область будет являться полным диапазоном МА [0,Рκ) и состоять из рабочего диапазона [0,Рη), где Рη=р1р2 … рη, определяемого неизбыточными основаниями МА, и диапазона, определяемого избыточными основаниями [Pη,Pκ), представляющего недопустимую область. Это означает, что операции над числом А выполняются в диапазоне [0,Рκ). Поэтому, если результат операции МА выходит за пределы Pη, то делается вывод об ошибке вычислений. Полученные числа меньшие Pη будем называть правильными, равные или большие Рη - неправильными (Акушский, И.Я. Машинная арифметика в остаточных классах [Текст] / И.Я. Акушский, Д.И. Юдицкий. - М.: Советское радио, 1968. - 440 с.).
Для осуществления контроля ошибок арифметических вычислений при реализации ЛЧП (5) рассмотрим систему, заданную основаниями р1, p2, … , pη, … , рκ. Представим каждый коэффициент hi ЛЧП (5) в виде (6), построим систему малоразмерных ЛЧП вида:

Малоразмерность ЛЧП системы (7) будет обеспечиваться малой величиной коэффициентов 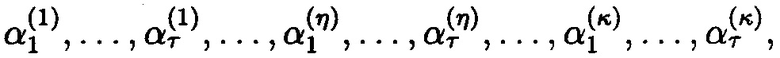 определяемых выбранными основаниями системы p1, …, pη, …, рκ.
определяемых выбранными основаниями системы p1, …, pη, …, рκ.
Подставив в (7) значения остатков системы по соответствующим основаниям для каждого коэффициента hi ЛЧП (5), а также значения переменных xq-1,0, …, xq-1,τ-1 получим избыточный модулярный код (МК), представленный системой ЛЧП (7):
(u(1), u(2), …, u(η), …, u(κ))МК,
где u(1), u(2), …, u(η), …, u(κ) - целые числа.
Решим систему выражений с одним неизвестным:

Так как основания р1, p2, … , pη, … , рκ попарно просты, то в соответствии с известными положениями теории чисел единственным решением системы (8) является выражение:

где 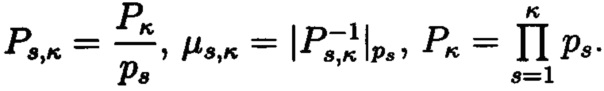
Вхождение результата вычисления (9) в рабочий диапазон (контрольное выражение):

означает отсутствие обнаруживаемых ошибок вычислений.
Пример 2 Пусть q-й блок участка ПСП представлен одним ЛЧП вида:
L(Хq-1)=65xq-1,0+69x q-1,1+20x q-1,2+80x q-1,3.
Выберем основания системы: p1=2, р2=3, р3=5, р4=11, р5=13, где р5 - контрольное основание.
Рабочий и полный диапазоны системы в этом случае равны: Р4=р1р2р3р4=330 и Р5=Р4р5=4290 соответственно.
Представим каждый коэффициент ЛЧП в виде набора остатков по выбранным основаниям системы:
h1=65=(1,2,0,10,0)МA,
h2=69=(1,0,4,3,4)МA,
h3=20=(0,2,0,9,7)МA,
h4=80=(0,2,0,3,2)МA.
Построим систему (7):

Пусть xq-1,0=xq-1,1=xq-1,3=1, xq-1,2=0, тогда u(1)=2, u(2)=4, u(3)=4, u(4)=16, и u(5)=6, получим избыточный МК: (2,4,4,16,6)МК.
Решим систему (8):

в соответствии с (9) получим: U=214.
Так как результат вычисления U удовлетворяет 0≤U<330, то будем считать, что при вычислениях ошибка допущена не была, либо произошла необнаруживаемая ошибка.
Восстановление достоверного функционирования генератора ПСП в случае возникновения долговременного отказа возможно путем исправления ошибки или реконфигурации оборудования генератора (активного резервирования). Первый вариант является неприемлемым, так как не гарантирует непроникновения необнаруживаемых ошибок в результат шифрования. Благодаря применению методов избыточного модулярного кодирования стало возможным применить вариант реконфигурации оборудования путем исключения из процесса функционирования отказавшего оборудования.
После локализации неисправного оборудования, например, одного канала функционирования МА, операция реконфигурации выполняется вычислением из системы:
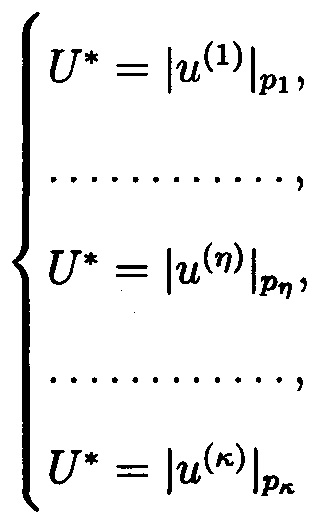
по «правильным» основаниям МА:
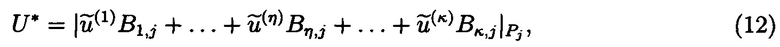
где 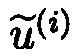 - ошибочный остаток; Bi,j - ортогональные базисы; i,j=1, …, η,…, κ; i≠j;
- ошибочный остаток; Bi,j - ортогональные базисы; i,j=1, …, η,…, κ; i≠j; 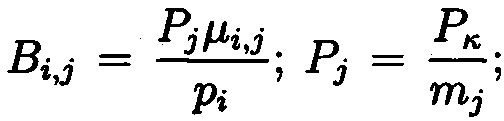 μi,j вычисляется из сравнения:
μi,j вычисляется из сравнения: 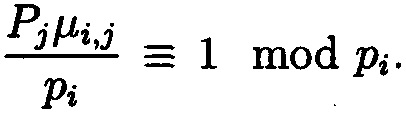 Составляется табл. 1, содержащая значения ортогональных базисов и модулей системы для условий возникновения однократной ошибки по каждому основанию МА.
Составляется табл. 1, содержащая значения ортогональных базисов и модулей системы для условий возникновения однократной ошибки по каждому основанию МА.
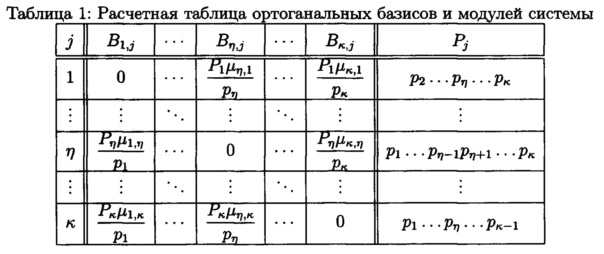
Пример 3 Допустим, что при вычислении решения системы (11) обнаружена ошибка, например, по основанию p2. В соответствии с (12) вычислим U*, используя табл. 1. Получим:

Предлагаемое устройство содержит: шину 13 подачи значений τ булевых переменных xq-1,0, xq-1,1, …, xq-1,τ-1, шину 14 подачи коэффициентов h1, …, hτ ЛЧП, шину 15 подачи оснований системы (информационные: p1, …, pη; контрольные: pη+i,…,рκ), регистр памяти 1, блок памяти 2 коэффициентов h1, …, hτ ЛЧП, блоки 3.1.1, …, 3.1.τ, …, 3.η.1, …, 3η.τ, …, 3.κ.1, …, 3.κ.τ вычисления наименьших неотрицательных вычетов числа (коэффициентов ЛЧП) по основаниям системы, множители 4.1.1, …, 4.1.τ, …, 4.η.1, …, 4η.τ, …, 4.κ.1, …, 4.κ.τ, блок памяти 5 оснований p1, …, рη, pη+1, …, рκ системы, многоместные сумматоры 6.1, …, 6.η, …, 6.κ, блоки памяти ортогональных базисов 7.1, …, 7.η, …, 7.κ, множители 8.1, …, 8.η, …, 8.κ, блок памяти модулей системы 9, многоместный сумматор по модулю системы 10, блок контроля и управления 11, блок оператора маскирования 12, выходы 16.1, …, 16.τ выдачи значений τ БФ ƒq,0(Xq-1), …, ƒq,τ-1(Xq-1) соответственно.
Шина 13 подачи значений τ булевых переменных xq-1,0, xq-1,1, …, xq-1,τ-1 является входом регистра памяти 1, шина 14 подачи коэффициентов ЛЧП является входом блока памяти 2 коэффициентов h1, …, hτ ЛЧП, предназначенного для их хранения, шина 15 подачи оснований системы является входом блока памяти 5 оснований p1, …, рη, pη+1, …, рκ системы, предназначенного для их хранения, выходы блоков памяти 2 и 5 являются входами блоков 3.1.1, …, 3.1.τ, …, 3.η.1, …, 3η.τ, …, 3.κ.1, …, 3.κ.τ вычисления наименьших неотрицательных вычетов числа (коэффициентов ЛЧП) по соответствующим основаниям системы, выходы которых вместе с выходами регистра памяти 1 являются входами множителей 4.1.1, …, 4.1.τ, …, 4.η.1, …, 4η.τ, …, 4.κ.1, …, 4.κ.τ, выходы которых являются входами многоместных сумматоров 6.1, …, 6.η, …, 6.κ, выходы которых являются входами множители 8.1, …, 8.η, …, 8.κ, ко вторым входам которых присоединены выходы блоков памяти ортогональных базисов 7.1, …, 7.η, …, 7.κ, предназначенных для их хранения; выходы множителей 8.1, …, 8.η, …, 8.κ являются входами многоместного сумматора по модулю системы 10, ко второму входу которого присоединен выход блока памяти модулей системы 9, предназначенного для их хранения; выход многоместного сумматора по модулю системы 10 подключен к входам блока контроля и управления 11 и блока оператора маскирования 12, выход блока управления и контроля 11 является вторым входом блока оператора маскирования 12, выходы которого являются выходами устройства выдачи значений τ БФ ƒq,0(Xq-1), …, ƒq,τ-1(Xq-1) соответственно.
Предлагаемое устройство работает следующим образом.
В исходном состоянии в блоки 2 и 5 памяти занесены по шинам 13 и 14 коэффициенты h1, …, hτ ЛЧП и основания p1, …, рη, pη+1, …, рκ системы соответственно, с их выходов на входы блоков 3.1.1, …, 3.1.τ, …, 3.η.1, …, 3η.τ, …, 3.κ.1, …, 3.κ.τ вычисления наименьших неотрицательных вычетов числа (коэффициентов ЛЧП) по основаниям системы поступают коэффициенты ЛЧП (5) и основания системы. В момент времени, соответствующий началу преобразований, на входы регистра памяти 1 из шины 13 поступают значения булевых переменных xq-1,0, xq-1,1, …, xq-1,τ-1. С выходов регистра памяти 1 и блоков 3.1.1, …, 3.1.τ, …, 3.η.1, …, 3η.τ, …, 3.κ.1, …, 3.κ.τ вычисления наименьших неотрицательных вычетов числа (коэффициентов ЛЧП) по основаниям системы на входы множителей 4.1.1, …, 4.1.τ, …, 4.η.1, …, 4η.τ, …, 4.κ.1, …, 4.κ.τ поступают наименьшие неотрицательные вычеты 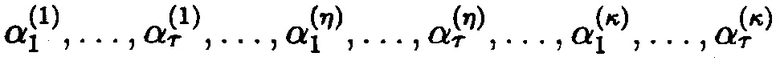 и значения булевых переменных xq-1,0, xq-1,1, …, xq-1,τ-1. С выходов множителей 4.1.1, …, 4.1.τ, …, 4.η.1, …, 4η.τ, …, 4.κ.1, …, 4.κ.τ на входы многоместных сумматоров 6.1, …, 6.η, …, 6.κ поступают произведения
и значения булевых переменных xq-1,0, xq-1,1, …, xq-1,τ-1. С выходов множителей 4.1.1, …, 4.1.τ, …, 4.η.1, …, 4η.τ, …, 4.κ.1, …, 4.κ.τ на входы многоместных сумматоров 6.1, …, 6.η, …, 6.κ поступают произведения  С выходов многоместных сумматоров 6.1, …, 6.η, …, 6.κ и блоков памяти ортогональных базисов 77.1, …, 7.η, …, 7.κ на входы множителей 8.1, …, 8.η, …, 8.κ поступают числовые результаты вычисления ЛЧП u(1), …, u(η), …, u(κ) и значения ортогональных базисов B1,j,…, Bη,j, …, Bκ,j соответственно. С выходов множителей 8.1, …, 8.η, …, 8.κ, а также блока памяти модулей системы 9 на входы многоместного сумматора по модулю системы 10 поступают произведения u(1)B1,j, …, u(η)Bη,j, …, u(κ)Bκ,j и значение модуля системы Рκ. Значения u(1), …, u(η), …, u(κ) являются избыточным МК, представленным системой ЛЧП (7): (u(1), u(2), …, u(η), …, u(κ))МК, где u(1), …, u(η), …, u(κ) - целые числа. С выхода многоместного сумматора по модулю системы 10 на входы блока управления и контроля 11 и блока оператора маскирования 12 поступает числовой результат вычисления (9). Вхождение результата вычисления (9) в рабочий диапазон (контрольное выражение): 0≤U≤Рη означает отсутствие обнаруживаемых ошибок вычислений. Таким образом, при отсутствии ошибок вычислений с блока управления и контроля 11 на вход блока оператора маскирования 12 поступает сигнал, разрешающий выполнять операцию маскирования, в противном случае - запрещающий. С выхода блока оператора маскирования 12 получим значения БФ ƒq,0(Xq-1), …, ƒq,τ-1(Xq-1), которые соответствуют элементам q-то блока ПСП xq-1,0, xq-1,1, …, xq-1,τ-1. В случае запрещающего сигнала (при обнаружении ошибки вычислений) выполняется локализация неисправного оборудования, с блока управления и контроля 11 на блоки памяти ортогональных базисов 7.1, …, 7.η, …, 7.κ и блок памяти модулей системы 9 поступает информация об используемых при повторных вычислениях ортогональных базисов и модулей системы. Вычисления выполняются согласно (9) и табл. 1.
С выходов многоместных сумматоров 6.1, …, 6.η, …, 6.κ и блоков памяти ортогональных базисов 77.1, …, 7.η, …, 7.κ на входы множителей 8.1, …, 8.η, …, 8.κ поступают числовые результаты вычисления ЛЧП u(1), …, u(η), …, u(κ) и значения ортогональных базисов B1,j,…, Bη,j, …, Bκ,j соответственно. С выходов множителей 8.1, …, 8.η, …, 8.κ, а также блока памяти модулей системы 9 на входы многоместного сумматора по модулю системы 10 поступают произведения u(1)B1,j, …, u(η)Bη,j, …, u(κ)Bκ,j и значение модуля системы Рκ. Значения u(1), …, u(η), …, u(κ) являются избыточным МК, представленным системой ЛЧП (7): (u(1), u(2), …, u(η), …, u(κ))МК, где u(1), …, u(η), …, u(κ) - целые числа. С выхода многоместного сумматора по модулю системы 10 на входы блока управления и контроля 11 и блока оператора маскирования 12 поступает числовой результат вычисления (9). Вхождение результата вычисления (9) в рабочий диапазон (контрольное выражение): 0≤U≤Рη означает отсутствие обнаруживаемых ошибок вычислений. Таким образом, при отсутствии ошибок вычислений с блока управления и контроля 11 на вход блока оператора маскирования 12 поступает сигнал, разрешающий выполнять операцию маскирования, в противном случае - запрещающий. С выхода блока оператора маскирования 12 получим значения БФ ƒq,0(Xq-1), …, ƒq,τ-1(Xq-1), которые соответствуют элементам q-то блока ПСП xq-1,0, xq-1,1, …, xq-1,τ-1. В случае запрещающего сигнала (при обнаружении ошибки вычислений) выполняется локализация неисправного оборудования, с блока управления и контроля 11 на блоки памяти ортогональных базисов 7.1, …, 7.η, …, 7.κ и блок памяти модулей системы 9 поступает информация об используемых при повторных вычислениях ортогональных базисов и модулей системы. Вычисления выполняются согласно (9) и табл. 1.
| название | год | авторы | номер документа |
|---|---|---|---|
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2579991C1 |
| УСТРОЙСТВО ПАРАЛЛЕЛЬНОГО ФОРМИРОВАНИЯ q-ЗНАЧНЫХ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ НА АРИФМЕТИЧЕСКИХ ПОЛИНОМАХ | 2021 |
|
RU2762209C1 |
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2012 |
|
RU2485575C1 |
| СПОСОБ ПОВЫШЕНИЯ ДОСТОВЕРНОСТИ КРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫ КАНАЛОВ СВЯЗИ РОБОТОТЕХНИЧЕСКИХ КОМПЛЕКСОВ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ | 2023 |
|
RU2809279C1 |
| САМОПРОВЕРЯЕМЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ ЛОГИЧЕСКИХ ФУНКЦИЙ | 2009 |
|
RU2417405C2 |
| Устройство формирования систем двукратных производных кодовых дискретно-частотных сигналов | 2016 |
|
RU2626331C1 |
| МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2007 |
|
RU2373564C2 |
| СПОСОБ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ ОДНОМЕРНЫХ МАССИВОВ ДАННЫХ НА ОСНОВЕ КОМПЛЕКСИРОВАНИЯ КРИПТОГРАФИЧЕСКИХ МЕТОДОВ И МЕТОДОВ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ | 2022 |
|
RU2786617C1 |
| АРИФМЕТИЧЕСКИЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2011 |
|
RU2461868C1 |
| СПОСОБ И УСТРОЙСТВО ИМИТОУСТОЙЧИВОЙ ПЕРЕДАЧИ ИНФОРМАЦИИ ПО КАНАЛАМ СВЯЗИ | 2017 |
|
RU2669144C1 |


Изобретение относится к вычислительной технике и может быть использовано для отказоустойчивой параллельной реализации систем булевых функций в средствах криптографической защиты информации. Техническим результатом является обеспечение отказоустойчивости при вычислении двоичных псевдослучайных последовательностей, идентичных псевдослучайным последовательностям, получаемым посредством классических генераторов на линейных рекуррентных регистрах сдвига. Устройство содержит регистр памяти, блок памяти для хранения коэффициентов линейного числового полинома (ЛЧП), блок памяти для хранения оснований системы, блоки вычисления наименьших неотрицательных вычетов числа (коэффициентов ЛЧП) по основаниям системы, множители, многоместные сумматоры, оператор маскирования, блок памяти модулей системы, блоки памяти ортогональных базисов, многоместный сумматор по модулю системы, блок контроля и управления. 3 ил., 1 табл.
Отказоустойчивый специализированный вычислитель систем БФ, содержащий регистр памяти, входы которого являются входами устройства, к которому подключена шина подачи τ булевых переменных, блок памяти, предназначенный для хранения коэффициентов ЛЧП, к входу которого подключена шина подачи коэффициентов ЛЧП, блок памяти, предназначенный для хранения оснований системы, к входу которого подключена шина подачи оснований системы, выходы которого вместе с выходами блока памяти хранения коэффициентов ЛЧП подключены к входам блоков вычисления наименьших неотрицательных вычетов числа (коэффициентов ЛЧП) по основаниям системы, выходы которых вместе с выходами регистра памяти подключены к входам множителей, выходы которых подключены к входам многоместных сумматоров, оператор маскирования; отличающийся тем, что введены блок памяти, предназначенный для хранения модулей системы, блоки памяти, предназначенные для хранения ортогональных базисов, выходы которых вместе с выходами многоместных сумматоров являются входами множителей, выходы которых вместе с выходами блока памяти, предназначенного для хранения модулей системы, являются входами многоместного сумматора по модулю системы, выход которого подключен к входам блока контроля и управления и блока оператора маскирования, первый выход блока контроля и управления подключен ко второму входу блока оператора маскирования, выходы которого являются выходами устройства выдачи значений τ БФ, второй выход блока контроля и управления подключен к входам блоков памяти, предназначенным для хранения ортогональных базисов, и блока памяти, предназначенного для хранения модулей системы.
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2579991C1 |
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2012 |
|
RU2485575C1 |
| САМОПРОВЕРЯЕМЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ ЛОГИЧЕСКИХ ФУНКЦИЙ | 2009 |
|
RU2417405C2 |
| МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2007 |
|
RU2373564C2 |
| US 2009116644 А1, 07.05.2009 | |||
| US 20080021942 A1, 24.01.2008 | |||
| МЕТАЛЛОПОРИСТЫЙ ПРОПИТАННЫЙ КАТОД ДЛЯ МАГНЕТРОНА | 2007 |
|
RU2342732C1 |
Авторы
Даты
2019-02-14—Публикация
2018-04-25—Подача