Уровень техники
Последующее относится к беспроводным сетям. Оно находит конкретное применение с установкой безопасной передачи информации в пределах беспроводной сети датчиков на теле. Однако следует принять во внимание, что изобретение может также найти применение в обеспечении безопасной передачи данных между другими беспроводными устройствами и другими беспроводными повторителями сигналов.
Мобильные сети датчиков на теле (BSN) привлекли внимание из-за медицинского применения и в целом используются для контроля за пациентом и наблюдения. BSN включает в себя узлы сбора данных и, по выбору, узлы управления. Узлы датчиков питаются от аккумулятора, имеют ограниченные вычислительные возможности и память и основываются на прерывистой беспроводной связи по радиочастоте. Традиционно большая группа (например, тысячи) имеющих возможность взаимодействия узлов разворачивается в медицинском помещении, например больнице, и затем, разным образом, спонтанно соединяются для создания различных разъединенных BSN. BSN обычно состоит из небольшого подмножества (от 2 до 50 узлов) от всех узлов, например узлы, назначенные конкретному пациенту в медицинском помещении. Априори размер и членство BSN неизвестно: узлы BSN могут присутствовать в момент создания BSN или могут быть впоследствии добавлены или удалены. Некоторые узлы имеют ограниченную мобильность после создания BSN, а другие являются высоко мобильными и часто перемещаются по разным независимым BSN, созданным в том же самом помещении (например, узлы сбора данных и управления, переносимые людьми, датчики, одетые на отдельных лиц и т.д.). Некоторые узлы могут быть оставлены без присутствия оператора. Время жизни BSN ограничено несколькими днями, неделями, месяцами и т.д. Время жизни узлов датчиков обычно дольше, чем время жизни экземпляра BSN. BSN создают в общественных помещениях или помещениях с враждебной средой, где передача данных может мониторироваться и узлы датчиков подвержены захвату и манипуляции недобросовестного лица. Перекрестное взаимодействие между узлами сетей BSN, ассоциированных с различными пациентами, может подвергнуть риску медицинскую достоверность регистрируемых данных.
Эти сложные функциональные требования равным образом накладывают сложные ограничения безопасности на конструкцию BSN. Службы безопасности для BSN включают в себя аутентификацию и конфиденциальность передачи данных. Обычно службы управления ключами предоставляют и управляют основными данными безопасности для удовлетворения ранее упомянутых служб безопасности. Вычислительные ограничения и ограничения на передачу данных узлов датчиков BSN делают непрактичным использование любого решения безопасности на основе криптографии с открытым ключом. Узкоспециализированная сущность BSN и функциональные требования BSN делают обычные интерактивные решения на основе серверов неподходящими.
Управление ключами на основе схем предварительного распределения ключей (KPS) является одним вариантом для BSN. Необходимость однозначной аутентификации узла и установки ключей, независимо от членства BSN и размера, налагает строгие требования на KPS для сетей BSN. Однако существующие предложения KPS ограничены для BSN. Во-первых, предварительное распределение ключей по всей сети не предлагает достаточной безопасности или не может управляться в BSN. Во-вторых, простая KPS не является ни масштабируемой, ни управляемой в BSN. В-третьих, устойчивость и масштабируемость KPS Блундо (Blundo)
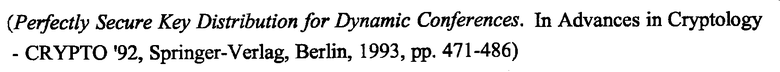
ограничена памятью и вычислительной мощностью узлов датчиков. В-четвертых, предварительное случайное распределение ключей не предлагает хороших свойств связи для BSN с ограниченным числом узлов. В конечном счете, детерминистическая KPS Кемтепа (Camtepe) и Йенера (Yener) на основе теории комбинаторной схемы

имеет соответствующие свойства связи и небольшую устойчивость для BSN, но не предоставляет уникальных парных ключей.
Басани (Basagni) и др.

представляет схему управления ключами для обеспечения безопасности передач данных датчиков с помощью периодического обновления группового симметричного ключа, совместно используемого всеми узлами датчиков. Эта схема предполагает устойчивые к вмешательству датчики и инфраструктуру управления, соединенную с распределенными сетями датчиков (DSN), предположения, которые не применимы для сетей BSN (крупномасштабная DSN может рассматриваться как соединение многочисленных сетей BSN с одиночными функциональными и сетевыми отличиями. Альтернативно BSN рассматриваются как многочисленные разъединенные части крупномасштабной DSN).
Перриг (Perrig) и др.
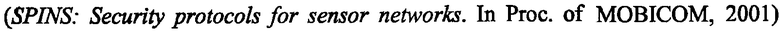
предлагает SPINS, архитектуру безопасности, специально спроектированную для сетей датчиков. В SPINS каждый узел датчика совместно использует секретный ключ с базовой станцией. Два узла датчика не могут непосредственно установить секретный ключ. Однако они могут использовать базовую станцию как надежную третью сторону для установления секретного ключа. В сетях BSN базовая станция может не быть доступной в момент установки ключа.
Блундо и др. предлагает KPS на полиномиальной основе для извлечения групповых ключей. Для групп из двух пользователей схема предварительного распределения ключей Блундо может использоваться для установки парных ключей в BSN. Сервер настройки случайно формирует симметричный двумерный со степенью λ полином 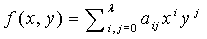 над конечным полем Fq, где q - это простое число, достаточно большое, чтобы вмещать криптографический ключ. По свойству симметрии
над конечным полем Fq, где q - это простое число, достаточно большое, чтобы вмещать криптографический ключ. По свойству симметрии 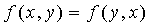 . Сервер настройки вычисляет и распределяет полиномиальную часть
. Сервер настройки вычисляет и распределяет полиномиальную часть 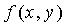 для каждого датчика u, т.е.
для каждого датчика u, т.е. 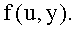 Каждый датчик u имеет уникальный идентификатор. После фазы внедрения для двух произвольных узлов u и v узел u может вычислить общий ключ
Каждый датчик u имеет уникальный идентификатор. После фазы внедрения для двух произвольных узлов u и v узел u может вычислить общий ключ 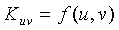 , вычисляя
, вычисляя 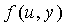 в точке v, и узел v может вычислить тот же самый ключ
в точке v, и узел v может вычислить тот же самый ключ 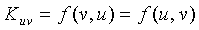 , вычисляя
, вычисляя 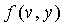 в точке u.
в точке u.
Устойчивость α KPS Блундо равна 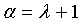 , т.е. злоумышленнику необходимо осуществить взлом α датчиков, чтобы суметь сформировать парные ключи невзломанных датчиков. Каждый узел u датчика требует хранения полиномиальной части
, т.е. злоумышленнику необходимо осуществить взлом α датчиков, чтобы суметь сформировать парные ключи невзломанных датчиков. Каждый узел u датчика требует хранения полиномиальной части 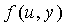 со степенью λ, которая занимает
со степенью λ, которая занимает 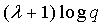 области памяти. Следует принять во внимание, что λ ограничено памятью m, доступной в датчиках, т.е.
области памяти. Следует принять во внимание, что λ ограничено памятью m, доступной в датчиках, т.е. 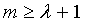 ключей. Во время процесса установки парных ключей нет коммуникационных накладных расходов. Для того, чтобы установить парный ключ, оба узла датчика должны вычислить полином в идентификаторе (ID) другого узла датчика. Это требует λ умножений по модулю и λ сложений по модулю в Fq, что может быть затратным в датчиках с ограниченными возможностями центрального процессора (CPV).
ключей. Во время процесса установки парных ключей нет коммуникационных накладных расходов. Для того, чтобы установить парный ключ, оба узла датчика должны вычислить полином в идентификаторе (ID) другого узла датчика. Это требует λ умножений по модулю и λ сложений по модулю в Fq, что может быть затратным в датчиках с ограниченными возможностями центрального процессора (CPV).
Лиу (Liu) и др.

описывают модификацию полиномиального вычисления для приспособления к ограничениям, накладываемым центральными процессорами с низкой битовой скоростью без команды деления, и, таким образом, уменьшают вычислительные требования на датчики. Это достигается уменьшением длины в битах коэффициентов двумерного полинома степени λ до logq' и с помощью выбора q' формы q'=2k+1.
Лиу и др. показывают, что ключ из logq бит может компоноваться с помощью конкатенации t частичных ключей, сформированных с помощью двумерных полиномиальных частей 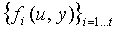 степени λ с коэффициентами в Fq', где
степени λ с коэффициентами в Fq', где 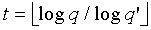 , без значительной потери безопасности, т.е. результирующий logq-битовый ключ обладает аналогичной энтропией, как если он был сформирован с помощью двумерного полинома степени λ с коэффициентами из Fq. Объединенное множество t двумерных полиномов
, без значительной потери безопасности, т.е. результирующий logq-битовый ключ обладает аналогичной энтропией, как если он был сформирован с помощью двумерного полинома степени λ с коэффициентами из Fq. Объединенное множество t двумерных полиномов 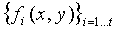 степени λ с коэффициентами из Fq' упоминается как t-полиномиальное множество
степени λ с коэффициентами из Fq' упоминается как t-полиномиальное множество 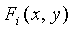 . T-полиномиальное множество
. T-полиномиальное множество 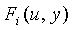 , вычисленное в точке u, в дальнейшем в данном документе это часть t-полиномиального множества.
, вычисленное в точке u, в дальнейшем в данном документе это часть t-полиномиального множества.
Недостатком этой методики является то, что полиномиальная функция над Fq' может вмещать только максимальное число q'-1 датчиков (вместо q-1). Конкретно, t полиномов над Fq', скомбинированных параллельно (т.е. t-полиномиальное множество) могут лишь вмещать максимум N'=q'-1 узлов. Например, для 8-битовых центральных процессоров, q'=28+1 предлагает оптимальную вычислительную производительность, но тогда число N' максимальных узлов равно 256. Еще сохраняющееся свойство - это то, что каждый двумерный полином 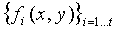 над Fq' и, таким образом, t-полиномиальное множество является устойчивым против λ- объединения. Технология полиномиального разбиения может применяться к любой основанной на полиномах KPS при некоторой нижней границе по λ, налагаемой q, q' и полным числом полиномов над Fq', используемым схемой KPS.
над Fq' и, таким образом, t-полиномиальное множество является устойчивым против λ- объединения. Технология полиномиального разбиения может применяться к любой основанной на полиномах KPS при некоторой нижней границе по λ, налагаемой q, q' и полным числом полиномов над Fq', используемым схемой KPS.
Сбалансированная схема неполных блоков (BIBD) является расположением v отдельных объектов в b блоках из условия, что каждый блок содержит точно k отдельных объектов, каждый объект присутствует точно в r разных блоках, и каждая пара отдельных объектов присутствует вместе в точно t блоках. Схема может быть выражена как (v, k, t) или эквивалентно (v, b, r, k, t), где: r(v-1)=r(k-1) и bk=vr.
В симметричной BIBD (SPIBD) b=v и, таким образом, k=r. SPIBD имеет четыре свойства: каждый блок содержит k=r элементов, каждый элемент присутствует в k=r блоках, каждая пара элементов присутствует в t блоках и каждая пара блоков пересекается в t элементах.
При заданной схеме D=(v, k, t) блока с множеством S из │S│=v объектов и множеством B ={B1, B2,…Bb} из │B│=b блоков, где каждый блок включает в себя в точности k объектов, комплементарная схема 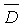 имеет комплементарные блоки
имеет комплементарные блоки 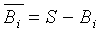 в качестве своих блоков для 1≤i≤b.
в качестве своих блоков для 1≤i≤b. 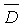 является BIBD с параметрами (v, b, b-r, v-k, b-2r+t), где b-2r+t>0. Если D=(v, k, t) является SBIBD, тогда
является BIBD с параметрами (v, b, b-r, v-k, b-2r+t), где b-2r+t>0. Если D=(v, k, t) является SBIBD, тогда 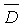 является также SBIBD.
является также SBIBD.
Конечные проективные плоскости (FPP) являются подмножеством SPIBD особого интереса для предварительного распределения ключей. FPP является SPIBD с параметрами (n2+n+1, n+1, 1). FPP существует для любой простой степени n, где n≥2. FPP порядка n имеет четыре свойства: (i) каждый блок содержит в точности n+1 точек, (ii) каждая точка присутствует в точности в n+1 блоках, (iii) существует в точности n2+n+1 точек, и (iv) существует в точности n2+n+1 блоков. Камтеп и Йенер
применяют схему SBIBD для предварительного распределения ключей в SN.
Рассмотрим FPP с параметрами (n2+n+1, n+1, 1), с элементами, принадлежащими множеству S, где │S│=n2+n+1. Используя терминологию Эсченауэра (Eschenauer) и Глигора (Gligor)

S ассоциируется с совокупностью ключей, т.е. каждый элемент в S ассоциируется с отдельным случайным ключом. Дополнительно каждый блок FPP ассоциируется с кольцом ключей. Свойства FPP гарантируют, что любая пара колец ключей (блоков) имеет 1 случайный ключ (элемент) совместно.
Для сети датчиков (SN) из N узлов с общим числом N колец ключей, FPP с n2+n+1≥N блоков должна строиться посредством использования множества S. Это предоставляет n2+n+1≥N колец ключей, при этом каждое имеет K=n+1 ключей и один ключ совместно. Размер памяти, необходимый на узлах, равен тогда (n+1)×logq (эквивалентно m=n+1). Умному злоумышленнику нужно захватить α=K=n+1 узлов, чтобы суметь взломать SN.
Каждый узел датчика SN численности N принимает разное кольцо ключей. Заметим, что каждые два узла совместно используют совместный конкретный ключ. Действительно, из-за свойств плоскостей FPP, каждые n+1 датчиков совместно используют один и тот же конкретный ключ. Следовательно, ключи этой KPS не могут использоваться для однозначной аутентификации узла. Второй связанной проблемой является то, что не всегда возможно отыскать FPP, в которой (i) n является простой степенью и (ii) n2+n+1≥N, с ограничением m≥n+1.
Камтеп и Йенер решают вышеуказанную проблему созданием гибридной схемы, которая включает в себя n2+n+1 блоков плоскости FPP (n2+n+1, n+1, 1), где n<m-1 (т.е. теперь размер кольца ключей m≥K>n+1) и N-n2+n+1 произвольно выбранных (n+1) - элементных подблоков плоскости 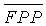 (n2+n+1, n2, n2-n). Побочными эффектами являются: (i) K>n+1, (ii) некоторые конкретные ключи совместно используются более, чем n+1 узлами, (iii) некоторые пары узлов могут совместно использовать до совместных n2-n ключей и (iv), по меньшей мере, N-n2+n+1 блоков не имеют совместного ключа. Таким образом, из-за (iv), по меньшей мере, N-n2+n+1 не могут непосредственно установить совместный ключ, и из-за (i), (ii) и (iii) α≤n+1<K≤m, т.е. устойчивость сети снижается.
(n2+n+1, n2, n2-n). Побочными эффектами являются: (i) K>n+1, (ii) некоторые конкретные ключи совместно используются более, чем n+1 узлами, (iii) некоторые пары узлов могут совместно использовать до совместных n2-n ключей и (iv), по меньшей мере, N-n2+n+1 блоков не имеют совместного ключа. Таким образом, из-за (iv), по меньшей мере, N-n2+n+1 не могут непосредственно установить совместный ключ, и из-за (i), (ii) и (iii) α≤n+1<K≤m, т.е. устойчивость сети снижается.
Недавно было предложено множество схем управления случайными ключами на основе предварительного распределения ключей для обеспечения безопасности инфраструктуры передачи данных крупномасштабных DSN. Такие схемы управления предполагают возможность соединения со всей DSN на основе предположений, что узел датчика может беспроводным образом соединяться с минимальным уровнем соседних узлов (например, узлами в диапазоне беспроводной передачи данных) и что узлы датчиков имеют очень ограниченную мобильность после применения. Эти схемы нацелены на максимальную безопасную связь по всей DSN и устойчивость сети при удовлетворении функциональным ограничениям сетей DSN. В схемах управления предварительным распределением случайных ключей каждый узел принимает до применения случайное подмножество ключей из большой совокупности ключей. Для того чтобы согласовать ключ для безопасной передачи данных с некоторой вероятностью, два соседних узла находят один общий ключ в их подмножествах и используют этот ключ как их совместно используемый секретный ключ. Два узла датчиков, которые не находят общий ключ, используют другие надежные узлы в своем окружении и даже некоторые непрямые передачи, чтобы помогать устанавливать общий ключ. Схемы предварительного распределения случайных парных ключей, основанные на схемах Блома (Blom)

или Блундо, улучшают предшествующее с помощью повышения устойчивости сети и дополнительного предоставления аутентификации узлов.
Однако схемы предварительного распределения случайных ключей не подходят для обеспечения безопасности BSN. Во-первых, из-за малой степени соседствующих узлов, BSN не всегда позволяет двум произвольным узлам прямо или косвенно устанавливать общий ключ. Во-вторых, из-за возможности захватов узлов, аутентификация узлов должна выполняться напрямую без каких-либо посредников.
Так как независимые BSN не соединены, централизованные или распределенные глобальные системы обнаружения проникновения (IDS), предлагаемые для DSN или для специальных сетей, не могут использоваться в BSN. Взломанный узел может быть обнаружен в BSN, но традиционные системы и способы не распространяют эффективно эту информацию остальным узлам в других BSN. Следовательно, BSN намного более уязвимы к атакам репликации узлов, чем крупномасштабная DSN. В больницах, например, атаки интеллектуального злоумышленника являются наибольшей угрозой для безопасности BSN. Хотя в литературе не четко сформулировано, устойчивость сети в отношении захватов узлов и репликации узлов предыдущих схем предварительного распределения ключей сильно зависит от существования IDS, эффективной по всей DNS. Отсутствие устойчивости сети определяется как число λ узлов, которые злоумышленнику необходимо захватить, чтобы взломать некоторую часть всех передач данных DSN. Интеллектуальный злоумышленник не беспокоится о захвате и вмешательстве в λ узлов, чтобы осуществить атаку. Интеллектуальный злоумышленник лишь захватывает один или малую часть узлов и использует расшифрованные ключи для атаки на сеть. В действительности, чтобы продолжать быть необнаруженным, злоумышленник не пытается прерывать сетевые операции сети, но пытается считать или модифицировать конфиденциальную информацию или даже ввести ложные сообщения. Таким способом злоумышленник может получить и/или ввести требуемую информацию даже без необходимости затрат своих собственных ресурсов, чтобы взломать другие сетевые передачи данных.
В конечном итоге механизм установки ключей, поддерживаемый соседями, необходим в некоторых схемах для достижения высокой степени безопасного соединения DSN. Злоумышленник с соответствующими ключами может получить помощь от одного или более прилегающих узлов, узлов, смежных с такими узлами, и так далее, чтобы установить ключи с полным окружением соседей. Если безопасное соединение жертвуется, чтобы улучшить безопасность посредством ограничения помощи установки ключей для окрестности соседей узла, злоумышленник все еще может продвигаться и пытаться атаковать настолько много соседних узлов, насколько это возможно. Эффективная и безопасная схема управления ключами должна принимать во внимание интеллектуального злоумышленника, особенно в установках BSN.
Что необходимо, это схема предварительного распределения ключей, которая дает возможность аутентификации, конфиденциальности и целостных услуг и обеспечивает улучшенное безопасное сетевое соединение, устойчивость и масштабируемость, связанные с оптимальным уровнем производительности. Также необходима схема управления ключами, которая управляет использованием предварительно распределяемых ключей, подходящая для функциональных условий BSN. Настоящее изобретение рассматривает улучшенное устройство и способ, которые преодолевают вышеупомянутые ограничения и другие.
Краткое описание изобретения
Согласно одному аспекту беспроводная сеть для контроля пациента содержит сеть датчиков на теле, состоит из одного или более беспроводных датчиков, оперативно соединенных с пациентом, которые собирают и передают информацию, связанную со здоровьем пациента, в беспроводную сеть. Сервер настройки конфигурирует один или более беспроводных датчиков с помощью материала ключей до того, как один или более датчиков будут использованы в беспроводной сети. Мобильная базовая станция распределяет сертификат ключа в один или более датчиков, ассоциированных с сетью датчиков не теле, при этом два датчика формируют уникальный парный ключ, базируясь, по меньшей мере, частично на предварительно распределенном материале ключей и сертификате ключей, распределяемом базовой станцией.
Согласно другому аспекту беспроводная сеть включает в себя сеть, которая состоит из одного или более беспроводных узлов, и сервер настройки, который конфигурирует один или более беспроводных узлов с помощью материала ключей до того, как один или более узлов будут использоваться в беспроводной сети. Базовая станция распределяет сертификат ключей в один или более датчиков, ассоциированных с сетью, при этом два узла формируют уникальный парный ключ, базируясь частично, по меньшей мере, на предварительно распределенном материале ключей и сертификате ключей, распределяемом базовой станцией.
Согласно другому аспекту способ вычисляет и распределяет части t-полиномиальных множеств, используя комбинаторное распределение, для того, чтобы максимизировать масштабируемость, устойчивость и уровень производительности беспроводной системы, которая включает в себя предварительное распределение ключа безопасности через сервер настройки в узел u датчика и узел v датчика, которые передают данные в беспроводной системе.
Согласно еще одному аспекту способ определяет датчик u в системе мобильных датчиков, что включает в себя образование конечной проективной плоскости (n2+n+1, n+1, 1) из множества n-1 взаимно ортогональных Латинских квадратов порядка n, где n является простой степенью. Общая часть t-полиномиального множества эффективно обнаруживается, и точка вычисления части t-полиномиального множества эффективно выводится датчиком v из идентификатора датчика u.
Одним преимуществом настоящего изобретения является то, что оно предоставляет ключи безопасности большому множеству узлов датчиков, оптимизируя передачу данных, эффективность вычислений и хранения для аккумулятора, мощности центрального процессора и узлов с ограниченной памятью.
Другим преимуществом является то, что оно обеспечивает улучшенную силу защиты для предварительно распределяемых безопасных ключей большому множеству узлов датчиков.
Другим преимуществом является то, что безопасность предусмотрена прозрачной для пользователей беспроводной сети.
Другим преимуществом является то, что обеспечивается безопасность, которая допускает однозначную идентификацию идентичности любой произвольной пары узлов датчиков (большого множества датчиков) и установку надежных связей независимо от плотности беспроводного окружения соседей датчиков или размера.
Другим преимуществом является то, что безопасность уменьшает степень, до которой может быть взломана беспроводная сеть.
Многочисленные дополнительные преимущества и выгоды станут видны специалистам в данной области техники при прочтении последующего подробного описания предпочтительных вариантов осуществления.
Краткое описание чертежей
Изобретение может принимать форму в различных компонентах и конфигурациях компонентов и в различных этапах и конфигурациях этапов. Чертежи приводятся лишь для целей иллюстрации предпочтительных вариантов осуществления и не должны толковаться как ограничивающие изобретение.
Фиг.1 иллюстрирует систему мобильных датчиков, которая использует сервер настройки для конфигурирования материала ключей во множестве датчиков во время фазы предварительного применения.
Фиг.2 иллюстрирует способ для обеспечения безопасной передачи данных между парой беспроводных датчиков, используя уникальные парные ключи.
Фиг.3 также показывает, как использовать идентификатор датчика в системе мобильных датчиков, например системе на фиг.1.
Фиг.4 иллюстрирует другой способ для идентификации датчика в системе мобильных датчиков, например в системе на фиг.1. Фиг.4 также показывает, как использовать идентификатор датчика в системе мобильных датчиков, например в системе на фиг.1.
Фиг.5 иллюстрирует способ обнаружения общей части t-полиномиального множества.
Фиг.6 иллюстрирует способ для извлечения точки вычисления части t-полиномиального множества.
Фиг.7 иллюстрирует систему мобильных датчиков, которая использует сервер настройки для конфигурирования материала ключей во множестве датчиков во время фазы предварительного применения.
Фиг.8 иллюстрирует систему мобильных датчиков, которая использует сервер безопасности и базовые станции, чтобы делать возможной безопасную передачу данных между множеством датчиков и соответствующими сетями датчиков на теле в системе мобильных датчиков во время фазы последующего применения.
Фиг.9 иллюстрирует способ предварительного распределения ключей, который использует симметричную схему Блома предварительного распределения ключей.
Фиг.10 иллюстрирует способ предварительного распределения ключей, который использует схему Блундо для предварительного распределения ключей.
Фиг.11 иллюстрирует способ для сертификации предварительно распределенных ключей.
Фиг.12 иллюстрирует способ управления предварительно распределенными ключами.
Фиг.13 иллюстрирует способ управления предварительно распределенными ключами.
Фиг.14 иллюстрирует способ управления предварительно распределенными ключами.
Фиг.15 иллюстрирует способ управления предварительно распределенными ключами.
Подробное описание предпочтительных вариантов осуществления
Система детерминистического предварительного распределения парных ключей (DPKPS) и способы
Фиг.1 иллюстрирует систему 2 мобильных датчиков, которая включает в себя сервер 4 настройки, множество беспроводных датчиков 6, 8, 10, 12, 14, 16, 18 и 20 и множество сетей 22, 24 и 26 датчиков на теле. Сервер 4 настройки является выделенным сервером безопасности, который активно участвует в безопасности лишь до применения датчиков. Беспроводные датчики 6-20 соединяются с сервером 4 настройки в начальной фазе конфигурирования (например, предварительного применения) до того, как используются датчики 6-20. Сервер 4 настройки обычно постоянно находится в пределах физически защищенного периметра, доступный лишь авторизованному персоналу. Во время фазы применения беспроводные датчики не имеют никакого средства соединения с сервером настройки. Обычно участок применения публично доступен. Беспроводные датчики 6-20 являются узлами, отвечающими за сбор и перемещение медицинских данных пациентов. Любой из датчиков 6-20 устанавливает беспроводные передачи данных с одним или более датчиков 6-20. Узлы датчиков имеют ограничения памяти, аккумуляторов и центрального процессора (CPV). Сети 22-26 датчиков на теле (BSN) являются множеством беспроводных сетевых узлов датчиков, которые могут присоединяться к одному или более пациентам (не показаны). BSN 22-26 обычно ограничены по пропускной способности из-за большого числа узлов в системе. Например, в среде больницы могут быть сотни или тысячи BSN (например, одна для каждого пациента).
Применение BSN требует ключей из logq бит. Согласно варианту осуществления 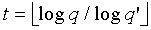 , при этом t≥1. При фиксированном q для требуемого уровня безопасности (например, 64 бита), полиномы в Fq' могут вычисляться и применяют оптимизацию полиномов Лиу и др. для получения ключа из logq бит. Объединенное множество из t двумерных полиномов
, при этом t≥1. При фиксированном q для требуемого уровня безопасности (например, 64 бита), полиномы в Fq' могут вычисляться и применяют оптимизацию полиномов Лиу и др. для получения ключа из logq бит. Объединенное множество из t двумерных полиномов 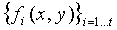 степени λ с коэффициентами над Fq' упоминается как t-полиномиальное множество
степени λ с коэффициентами над Fq' упоминается как t-полиномиальное множество 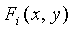 . T-полиномиальное множество
. T-полиномиальное множество 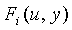 , вычисленное в точке u, в дальнейшем является частью t-полиномиального множества.
, вычисленное в точке u, в дальнейшем является частью t-полиномиального множества.
Фиг.2 иллюстрирует способ 30, который состоит из способа 32 настройки, способа 34 предварительного применения ключей, способа 36 обнаружения частей t-полиномиального множества и способа 38 установки ключей, используемого для установки уникальных парных ключей между датчиками, например, с помощью системы 2, приведенной выше. В 32, сервер настройки формирует части t-полиномиального множества и комбинаторную схему, которая может использоваться, чтобы вмещать N датчиков, где N является размером группы узлов, имеющих возможность взаимодействовать, и является целым числом, большим, чем или равным единице. В 34 сервер настройки распределяет части t-полиномиального множества в каждый датчик согласно комбинаторному распределению. Если были применены на 36, два произвольных датчика u и v обнаруживают, какую часть t-полиномиального множества они имеют совместно. На 38 два произвольных датчика u и v формируют уникальный парный ключ Kuv с помощью вычисления их общей части t-полиномиального множества.
Один аспект настоящего варианта осуществления увеличивает масштабируемость KPS на основе t-полиномиальных множеств без снижения ее устойчивости при поддержке оптимального узлового уровня производительности. В одном подходе n+1 t-полиномиальных множеств распределяются в каждый узел u, следуя FPP (n2+n+1, n+1, 1), т.е. с помощью ассоциирования N'/(n+1) отдельных частей каждого t-полиномиального множества 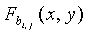 с каждым элементом
с каждым элементом 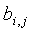 , j=1…n+1, принадлежащим блокам Bi, i=n2+n+1, плоскости FPP. Из-за свойств FPP два произвольных узла u и v относительно n+1 частей t-полиномиальных множеств, распределяемых согласно элементам различных блоков Bi,
, j=1…n+1, принадлежащим блокам Bi, i=n2+n+1, плоскости FPP. Из-за свойств FPP два произвольных узла u и v относительно n+1 частей t-полиномиальных множеств, распределяемых согласно элементам различных блоков Bi, 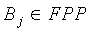 , i≠j, совместно используют одно t-полиномиальное множество Fk(x,y), которое они могут использовать для вычисления уникального парного ключа из logq бит. Аналогично, два узла с соответствующими n+1 частями t-полиномиального множества, распределяемыми согласно элементам одного и того же блока
, i≠j, совместно используют одно t-полиномиальное множество Fk(x,y), которое они могут использовать для вычисления уникального парного ключа из logq бит. Аналогично, два узла с соответствующими n+1 частями t-полиномиального множества, распределяемыми согласно элементам одного и того же блока 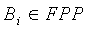 , имеют n+1 частей t-полиномиального множества совместно. Таким образом, узлы могут использовать любую из n+1 частей t-полиномиального множества для вычисления уникального парного ключа из logq бит.
, имеют n+1 частей t-полиномиального множества совместно. Таким образом, узлы могут использовать любую из n+1 частей t-полиномиального множества для вычисления уникального парного ключа из logq бит.
Этот способ разрешает увеличивать масштабируемость схем KPS Блундо и др., а также Кемтепа и Йенера без какой-либо потери в сетевой устойчивости и в то время как сохраняют вычислительную производительность на оптимуме и вероятность единица совместного использования уникального парного ключа. Кроме того, подобный подход решает проблему существования плоскости FPP схемы KPS Кемтепа и Йенера без понижения в сетевой устойчивости или прямом надежном соединении.
В 32 сервер настройки случайно формирует множество 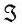 из
из 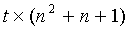
 двумерных полиномов
двумерных полиномов 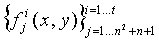 степени λ над Fq'. Впоследствии для j=1…n2+n+1 сервер настройки последовательно выбирает полиномы из
степени λ над Fq'. Впоследствии для j=1…n2+n+1 сервер настройки последовательно выбирает полиномы из 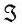 и формирует n2+n+1 t-полиномиальных множеств Fj(x,y). Затем он формирует FPP (n2+n+1, n+1, 1) с элементами, которые принадлежат множеству S, где │S│=n2+n+1. Множество S ассоциировано связано с полиномиальной совокупностью, т.е. каждый элемент j в S ассоциирован с отдельным t-полиномиальным множеством Fj(x,y). Дополнительно, каждый блок FPP ассоциирован с полиномиальным кольцом. Свойства FPP гарантируют, что любая пара полиномиальных колец (блоков FPP) имеет одно t-полиномиальное множество Fk(x,y) (элемент к) совместно.
и формирует n2+n+1 t-полиномиальных множеств Fj(x,y). Затем он формирует FPP (n2+n+1, n+1, 1) с элементами, которые принадлежат множеству S, где │S│=n2+n+1. Множество S ассоциировано связано с полиномиальной совокупностью, т.е. каждый элемент j в S ассоциирован с отдельным t-полиномиальным множеством Fj(x,y). Дополнительно, каждый блок FPP ассоциирован с полиномиальным кольцом. Свойства FPP гарантируют, что любая пара полиномиальных колец (блоков FPP) имеет одно t-полиномиальное множество Fk(x,y) (элемент к) совместно.
В 34 каждый узел u датчика принимает от сервера настройки n+1 частей 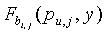 t-полиномиального множества, где
t-полиномиального множества, где 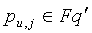 ,
, 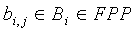 и j=1…n+1. Точка pu,j должна браться из конечного поля Fq'. Это ограничивает pu,j до q'-1 различных возможных значений. Однако число датчиков N для вмещения может быть больше, чем q'-1. Для того, чтобы гарантировать уникальность парных ключей, два различных датчика u и v не могут иметь то же самое t-полиномиальное множество Fk(x,y), вычисляемое в той же самой точке pk. Так как каждое t-полиномиальное множество Fj(x,y), j=1…n2+n+1, может быть вычислено в N'=q'-1 различных точках и индекс j от Fj(x,y) появляется в n+1 блоках FPP, то каждый из этих блоков (где встречается j) используется для предварительного распределения отдельных частей Fj(x,y) не в более чем N'/(n+1) различных датчиках. Процесс предварительного распределения ключей для смещения N≤N'n(1-1/(n+1))+N' узлов использует следующие этапы:
и j=1…n+1. Точка pu,j должна браться из конечного поля Fq'. Это ограничивает pu,j до q'-1 различных возможных значений. Однако число датчиков N для вмещения может быть больше, чем q'-1. Для того, чтобы гарантировать уникальность парных ключей, два различных датчика u и v не могут иметь то же самое t-полиномиальное множество Fk(x,y), вычисляемое в той же самой точке pk. Так как каждое t-полиномиальное множество Fj(x,y), j=1…n2+n+1, может быть вычислено в N'=q'-1 различных точках и индекс j от Fj(x,y) появляется в n+1 блоках FPP, то каждый из этих блоков (где встречается j) используется для предварительного распределения отдельных частей Fj(x,y) не в более чем N'/(n+1) различных датчиках. Процесс предварительного распределения ключей для смещения N≤N'n(1-1/(n+1))+N' узлов использует следующие этапы:
1. Начиная с первого блока B1 плоскости FPP с элементами 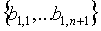 первый узел (u1) принимает части
первый узел (u1) принимает части 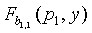 по
по 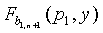 t-полиномиального множества, вычисленные в точке p1 из Fq'; второй датчик (u2) принимает
t-полиномиального множества, вычисленные в точке p1 из Fq'; второй датчик (u2) принимает 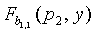 по
по 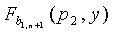 , вычисленные в точке p2; и так далее; до тех пор, когда N'/(n+1)-ый датчик (uN'/(n+1)) принимает
, вычисленные в точке p2; и так далее; до тех пор, когда N'/(n+1)-ый датчик (uN'/(n+1)) принимает 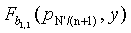 по
по 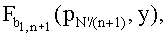 вычисленные в точке pN'/(n+1).
вычисленные в точке pN'/(n+1).
2. Следуя со вторым блоком B2 из FPP с элементами 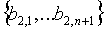 , предположим, что
, предположим, что 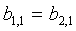 , датчик u1+N'/(n+1) принимает
, датчик u1+N'/(n+1) принимает 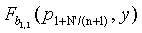 , которая вычисляется в точке p1+N'/(n+1) (так как
, которая вычисляется в точке p1+N'/(n+1) (так как 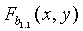 уже вычислено в нижних точках для датчиков u1 … uN'/(n+1)), и
уже вычислено в нижних точках для датчиков u1 … uN'/(n+1)), и 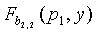 по
по 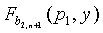 вычислены в точке p1; и так далее, и
вычислены в точке p1; и так далее, и
3. Повтор первого и второго этапов, чтобы вместить N узлов системы, используя все блоки FPP.
В 36 обнаруживаются части t-полиномиального множества. После применения до установки парного ключа каждый узел u датчика должен обнаружить, какое t-полиномиальное множество он совместно использует с его соседним узлом v. Для этого узлы u и v обмениваются своими идентификаторами (ID), которые явно содержат индексы n+1 частей t-полиномиального множества, которые они несут с собой и точки 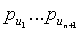 ,
, 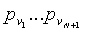 , где вычисляются соответствующие n+1 частей t-полиномиального множества. В конечном итоге, они находят индекс к (соответствующий общему t-полиномиальному множеству Fk(x,y) и соответствующие точки pu и pv вычисления.
, где вычисляются соответствующие n+1 частей t-полиномиального множества. В конечном итоге, они находят индекс к (соответствующий общему t-полиномиальному множеству Fk(x,y) и соответствующие точки pu и pv вычисления.
В 38 устанавливается ключ. Для того, чтобы вычислить парный ключ Kuv, узел u вычисляет t двумерных полиномов 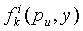 степени λ (включенных в Fk(pu,y) для i=1…t в точке pv (т.е.
степени λ (включенных в Fk(pu,y) для i=1…t в точке pv (т.е. 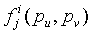 для получения t частичных ключей. Затем узел u усекает упомянутые t частичных ключей до logq' бит и конкатенирует t сегментов ключей для образования конечного парного ключа Kuv из logq бит.
для получения t частичных ключей. Затем узел u усекает упомянутые t частичных ключей до logq' бит и конкатенирует t сегментов ключей для образования конечного парного ключа Kuv из logq бит.
Простой ID датчика
Фиг.3 иллюстрирует способ 50, который определяет датчик u в DPKPS. В 52 n+1 индексов bi,1,…bi,n+1 n+1 частей t-полиномиального множества, которые он несет, конкатенируются с n+1 точками 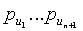 , где они вычисляются. В 54 такой ID однозначно определяет датчик u и в 56 делает возможным очень простое обнаружение общих частей t-полиномиального множества и точки вычисления части t-полиномиального множества.
, где они вычисляются. В 54 такой ID однозначно определяет датчик u и в 56 делает возможным очень простое обнаружение общих частей t-полиномиального множества и точки вычисления части t-полиномиального множества.
В 58 общая часть t-полиномиального множества обнаруживается с помощью использования простого ID датчика, два датчика u и v находят, какой индекс является общим в соответствующих ID, например индекс k. В 60 точка части t-полиномиального множества вычисления выводится получением k-той точки, включенной в простой ID датчика.
Оптимизированный ID датчика
Так как использование простых ID датчика значительно увеличивает затраты на хранение и передачу данных DPKPS, когда возрастает n, может применяться альтернативный способ оптимизированного ID датчика с помощью использования свойств FPP, основанных на взаимно ортогональных латинских квадратах (MOLS). Этот оптимизированный способ строит ID датчиков с очень короткой длиной для фактических значений n.
Фиг.4 показывает способ 70, используемый для идентификации датчика в системе мобильных датчиков, например системе 2 выше.
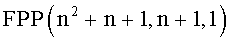 выводится из множества n-1 взаимно ортогональных латинских квадратов (MOLS) порядка n. Латинский квадрат является квадратной n×n матрицей L, элементы которой состоят из n символов так, что каждый символ появляется точно один раз в каждой строке и каждом столбце. Символы используются как целые значения от 1…n. Очень простым способом построить L является размещение целых чисел 1,2,…n в их обычном порядке в первой строке и для последовательных строк с помощью циклического вращения предыдущей строки вправо.
выводится из множества n-1 взаимно ортогональных латинских квадратов (MOLS) порядка n. Латинский квадрат является квадратной n×n матрицей L, элементы которой состоят из n символов так, что каждый символ появляется точно один раз в каждой строке и каждом столбце. Символы используются как целые значения от 1…n. Очень простым способом построить L является размещение целых чисел 1,2,…n в их обычном порядке в первой строке и для последовательных строк с помощью циклического вращения предыдущей строки вправо.
В 72 выводятся взаимно ортогональные латинские квадраты (MOLS). Два латинских квадрата 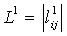 и
и 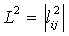 по n символам 1,2…n являются ортогональными, если при наложении каждая из n2 пар символов
по n символам 1,2…n являются ортогональными, если при наложении каждая из n2 пар символов 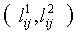 , i=1,2…n; j=1,2…n появляется точно один раз. Множество латинских квадратов L1, L2,…Lt одного и того же порядка n, каждый из которых является ортогональным соквадратом каждого из других, называется множеством квадратов MOLS. Множество n-1 MOLS порядка n является полным множеством.
, i=1,2…n; j=1,2…n появляется точно один раз. Множество латинских квадратов L1, L2,…Lt одного и того же порядка n, каждый из которых является ортогональным соквадратом каждого из других, называется множеством квадратов MOLS. Множество n-1 MOLS порядка n является полным множеством.
При заданной паре ортогональных латинских квадратов 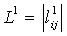 и
и 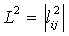 , ячейки в первом квадрате содержат один конкретный символ l1. Из-за свойств латинских квадратов имеется только одна из этих ячеек в каждой строке и каждом столбце. Из-за ортогональности n вхождений в ячейках ортогонального соквадрата, которые соответствуют ячейкам в первом квадрате, формируют трансверсаль в ортогональном соквадрате, например, n вхождений содержат каждый символ, точно один, и каждая из этих ячеек находится в разных строках и столбцах.
, ячейки в первом квадрате содержат один конкретный символ l1. Из-за свойств латинских квадратов имеется только одна из этих ячеек в каждой строке и каждом столбце. Из-за ортогональности n вхождений в ячейках ортогонального соквадрата, которые соответствуют ячейкам в первом квадрате, формируют трансверсаль в ортогональном соквадрате, например, n вхождений содержат каждый символ, точно один, и каждая из этих ячеек находится в разных строках и столбцах.
Для простой степени n множество полиномов формы fa(x,y)=ax+y, a≠0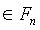 представляет полное множество n-1 MOLS порядка n. Это приводит к очень простому способу построения: допустим e1, e2, … en являются элементами Fn, т.е. целыми числами 1…n. Тогда для каждого элемента em, m=1,2,…n, элементы
представляет полное множество n-1 MOLS порядка n. Это приводит к очень простому способу построения: допустим e1, e2, … en являются элементами Fn, т.е. целыми числами 1…n. Тогда для каждого элемента em, m=1,2,…n, элементы 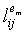 матрицы
матрицы 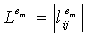 последовательно вычисляются с помощью:
последовательно вычисляются с помощью:
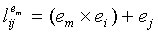 (Уравнение 1)
(Уравнение 1)
Параметры n и em достаточны для воспроизведения конкретного ортогонального латинского квадрата 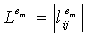 .
.
В 74 конечная проективная плоскость (FPP) строится из MOLS. Пусть L1, L2,…Ln-1 будет полным множеством MOLS порядка n и M n×n матрица. Первоначально матрица M должна строиться посредством размещения n2 целых чисел 1…n2 в их обычном порядке с первой по n-ю строку. Во-вторых, аффинная плоскость AG(2,n) порядка n формируется из MOLS следующим образом: (i) первые n блоков являются строками M, (ii) вторые n блоков являются столбцами M и (iii) оставшиеся n2-n блоков формируются с помощью последовательного наложения каждого  на M, и беря в качестве блоков элементы M, которые соответствуют единственному символу
на M, и беря в качестве блоков элементы M, которые соответствуют единственному символу  в каждом
в каждом 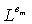 . Так как каждый
. Так как каждый 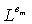 содержит n разных символов, каждая суперпозиция
содержит n разных символов, каждая суперпозиция 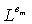 :M дает n блоков. В конечном счете, чтобы получить FPP(n2+n+1,n+1,1), необходимо (i) добавить новое целое число n2+1 к первым n блокам аффинной плоскости, (ii) добавить новое целое число n2+2 ко вторым n блокам, (iii) добавить целое число n2+2+em к n блокам, построенным из каждого
:M дает n блоков. В конечном счете, чтобы получить FPP(n2+n+1,n+1,1), необходимо (i) добавить новое целое число n2+1 к первым n блокам аффинной плоскости, (ii) добавить новое целое число n2+2 ко вторым n блокам, (iii) добавить целое число n2+2+em к n блокам, построенным из каждого 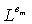 , и (iv) добавить новый блок к схеме, который содержит n+1 новых добавленных целых чисел.
, и (iv) добавить новый блок к схеме, который содержит n+1 новых добавленных целых чисел.
Пусть даны n и i, легко воспроизвести блок 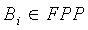 , 1<i≤2n. Например, для n=3 блок B4 строится из первого столбца M3×3 и целого числа 11, т.е. B4=(1,4,7,11). Для блока
, 1<i≤2n. Например, для n=3 блок B4 строится из первого столбца M3×3 и целого числа 11, т.е. B4=(1,4,7,11). Для блока 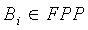 , 2n <i≤n2+n, индекс i также явно идентифицирует индекс em, 1≤em≤n-1, латинского квадрата
, 2n <i≤n2+n, индекс i также явно идентифицирует индекс em, 1≤em≤n-1, латинского квадрата 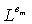 , из которого формируется Bi. Например, для n=3 блок B12 формируется из L2. Для того чтобы воспроизвести один из этих блоков Bi, 2n <i≤n2+n, дополнительно необходим элемент
, из которого формируется Bi. Например, для n=3 блок B12 формируется из L2. Для того чтобы воспроизвести один из этих блоков Bi, 2n <i≤n2+n, дополнительно необходим элемент 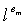 .
.
В 76 датчик u идентифицируется конкатенацией трех чисел i, ip и 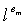 , где 1≤i≤n2+n+1, 1≤ ip ≤N'/(n+1) и 1≤em≤n. Первое, i, идентифицирует блок
, где 1≤i≤n2+n+1, 1≤ ip ≤N'/(n+1) и 1≤em≤n. Первое, i, идентифицирует блок 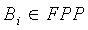 , согласно которому выбираются части t-полиномиального множества для u, второе, преобразование ip в распределении частей t-полиномиального множества датчику u в пределах Bi и третье, элемент латинского квадрата Li, из которого выводится Bi. Такой ID однозначно определяет датчик u и делает возможным намного более эффективное обнаружение общих частей t-полиномиального множества и точки t-полиномиального множества вычисления, чем с помощью простого ID.
, согласно которому выбираются части t-полиномиального множества для u, второе, преобразование ip в распределении частей t-полиномиального множества датчику u в пределах Bi и третье, элемент латинского квадрата Li, из которого выводится Bi. Такой ID однозначно определяет датчик u и делает возможным намного более эффективное обнаружение общих частей t-полиномиального множества и точки t-полиномиального множества вычисления, чем с помощью простого ID.
В 78 часть t-полиномиального множества обнаруживается для оптимизированного ID датчика. В 80 точка вычисления t-полиномиального множества выводится для оптимизированного ID датчика.
Фиг.5 показывает способ 100 для обнаружения общей части t-полиномиального множества с помощью использования информации, содержащейся в оптимизированном ID датчика. В 102 оптимизированный ID датчика позволяет узлу u датчика вычислить индексы своих собственных частей t-полиномиального множества и индексы узла-партнера v. В 104 с помощью сопоставления этой информации узел u может выводить индекс k, 1≤k≤n2+n+1, общей части t-полиномиального множества Fk(pu,y) с узлом v.
Индексы частей t-полиномиального множества 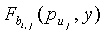 , j=1…n+1, которые несет датчик u, являются один к одному соответствующими элементам
, j=1…n+1, которые несет датчик u, являются один к одному соответствующими элементам 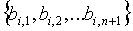 из
из 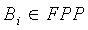 . Как отмечено выше, при заданных n, индексе i Bi и целом числе
. Как отмечено выше, при заданных n, индексе i Bi и целом числе 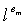 , является возможным однозначно воспроизвести
, является возможным однозначно воспроизвести 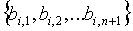 =Bi. Здесь мы должны различать два случая: в 106 блоки Bi, 1≤i≤2n, и
=Bi. Здесь мы должны различать два случая: в 106 блоки Bi, 1≤i≤2n, и 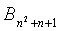 , чье воспроизведение является тривиальным. Альтернативно в 108 блоки Bi, 2n<i≤n2+n, чье воспроизведение является также простым, но требует последующего анализа. В 108 известно по этапу (iii) построения аффинных плоскостей (на этапе 54 из фиг.3а), что элементы
, чье воспроизведение является тривиальным. Альтернативно в 108 блоки Bi, 2n<i≤n2+n, чье воспроизведение является также простым, но требует последующего анализа. В 108 известно по этапу (iii) построения аффинных плоскостей (на этапе 54 из фиг.3а), что элементы 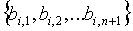 из Bi берутся из позиций в M, отмеченных с помощью 2n координат
из Bi берутся из позиций в M, отмеченных с помощью 2n координат 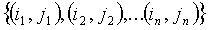 , где
, где 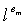 появляется в
появляется в 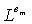 . Таким образом, определяя эти координаты, мы получим элементы Bi. В 110 из индекса i непосредственно выводится em, которое определяет латинский квадрат
. Таким образом, определяя эти координаты, мы получим элементы Bi. В 110 из индекса i непосредственно выводится em, которое определяет латинский квадрат 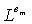 , используемый для выбора n из элементов Bi. В 112 позиции элемента
, используемый для выбора n из элементов Bi. В 112 позиции элемента 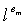 определяют трансверсаль в
определяют трансверсаль в 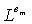 , тогда
, тогда 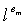 появляется один раз в каждой строке
появляется один раз в каждой строке 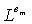 . Таким образом,
. Таким образом, 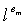 появляется в позициях
появляется в позициях 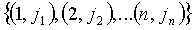 . Предполагая
. Предполагая 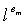 и em известными, используя уравнение 1, имеем:
и em известными, используя уравнение 1, имеем:
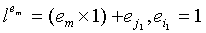
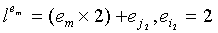
…
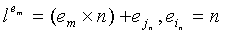
В 114 решаем эти уравнения, что дает вектор V из n отдельных значений 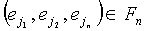 . Как отмечено, элементы e1,e2,…en из Fn последовательно используются для вычисления каждого элемента
. Как отмечено, элементы e1,e2,…en из Fn последовательно используются для вычисления каждого элемента 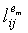 матрицы
матрицы 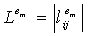 , т.е. элемент e1 используется для вычисления элементов в позициях
, т.е. элемент e1 используется для вычисления элементов в позициях 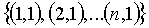 , элемент e2 используется для вычисления элементов в позициях
, элемент e2 используется для вычисления элементов в позициях 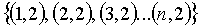 и так далее. Иначе говоря, каждое значение
и так далее. Иначе говоря, каждое значение 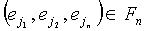 определяет координаты
определяет координаты 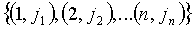 , где появляется
, где появляется 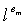 , например, если i3=3, ej3=2, то j3=2 (
, например, если i3=3, ej3=2, то j3=2 (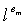 появляется в
появляется в 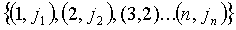 ).
).
В конечном итоге, в 116 эти координаты сопоставляются с элементами матрицы M, теперь можно непосредственно определить n из n+1 элементов Bi. Теперь имеется блок аффинной плоскости. Добавляя целое значение n2+2+em в блок, мы получаем блок 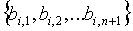 =Bi. Формирование блока из FPP с помощью этого способа требует (самое большее) n сложений и n умножений в Fn.
=Bi. Формирование блока из FPP с помощью этого способа требует (самое большее) n сложений и n умножений в Fn.
Фиг.6 иллюстрирует способ 130 для извлечения точки вычисления t-полиномиального множества. Для извлечения точки pv, где узел u вычисляет свою часть Fk(pu,y) для формирования ключа Kuv, узел u должен следовать простому процессу, который возможен благодаря свойствам FPP.
Как отмечено выше, ip является порядком узла v в распределении частей t-полиномиального множества согласно блоку 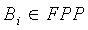 , 1≤i≤n2+n+1. Предположим, что часть t-полиномиального множества Fk(x,y) распределена v. Процесс, описанный ниже, дает возможность извлечения точки
, 1≤i≤n2+n+1. Предположим, что часть t-полиномиального множества Fk(x,y) распределена v. Процесс, описанный ниже, дает возможность извлечения точки 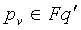 , где вычисляется часть Fk(pv,y) узла v. Предполагается, что
, где вычисляется часть Fk(pv,y) узла v. Предполагается, что 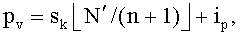 где sk определяет число появлений Fk(x,y) в блоках
где sk определяет число появлений Fk(x,y) в блоках  , j=1…i.
, j=1…i.
В 132, так как FPP строится из MOLS, его первые n2 элементов появляются один раз в каждой группе n последовательных блоков B1+t, B2+t,…Bn+t, t=0,n,2n,3n…n×n. Затем в 134, при заданном индексе i блока, 1≤i≤n2+n, и индексе k t-полиномиального множества, k≤n2, извлечение счетчика sk его появления является тривиальным, т.е. 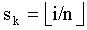 . Каждый элемент вида k=n2+j, j=1…n+1, появляется n раз в группе блоков Bi+n(j-1), i=1…n. В этом случае sk=i-n(j-1). В 136 элементы k= n2+j, j=1…n+1, блока
. Каждый элемент вида k=n2+j, j=1…n+1, появляется n раз в группе блоков Bi+n(j-1), i=1…n. В этом случае sk=i-n(j-1). В 136 элементы k= n2+j, j=1…n+1, блока 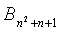 появляются в n+1-й раз в FPP. Таким образом, при заданном индексе k t-полиномиального множества, индексе i блока и порядке n FPP, можно непосредственно извлечь для узла u точку pv, чтобы вычислить его общую часть Fk(pu,y) с узлом v.
появляются в n+1-й раз в FPP. Таким образом, при заданном индексе k t-полиномиального множества, индексе i блока и порядке n FPP, можно непосредственно извлечь для узла u точку pv, чтобы вычислить его общую часть Fk(pu,y) с узлом v.
В отличие от предыдущих способов предварительного распределения случайных ключей, варианты осуществления дают возможность двум случайно выбранным узлам датчиков напрямую находить общий ключ для аутентификации, независимой от размера и плотности BSN (или окрестности соседства в терминах DSN). Кроме того, узлы датчиков могут перемещаться через различные BSN и все еще аутентифицировать и/или устанавливать безопасные передачи данных. Безопасность BSN функционирует без необходимости активного или сознательного участия пользователя-человека BSN.
Функциональное управление ключами
Фиг.7 и 8 иллюстрируют систему 150, которая включает в себя сервер 152 безопасности, сервер 154 настройки, множество беспроводных датчиков 156, 158, 160, 162, 164, 166, 168, 170, множество сетей 172, 174, 176 датчиков на теле и мобильные базовые станции 178 и 180. Фиг.7 показывает систему 150 до применения датчиков 156-170. Фиг.8 показывает систему 150 после применения датчиков. В одном примере сервер 152 безопасности и/или сервер 154 настройки являются выделенными серверами, используемыми для безопасности. Сервер 152 безопасности является выделенным сервером безопасности, который активно участвует в безопасности до и после применения датчиков. Сервер 154 настройки является выделенным сервером безопасности, который активно участвует в безопасности только до применения датчиков. После применения датчиков 156-170 и базовых станций 178, 180, он имеет непрерывное или спорадическое соединение исключительно с мобильными базовыми станциями. Как проиллюстрировано на фиг.8, один раз примененные, датчики 156-170 не соединяются с сервером безопасности 152. Как проиллюстрировано на фиг.7, мобильные базовые станции 178, 180 и датчики 156-170 могут соединяться с сервером 154 настройки только в фазе предварительного применения, т.е. в начальной фазе конфигурации до того, как используются устройства.
Беспроводные датчики 156-170 отвечают за сбор и передачу медицинских данных пациентов. В одном примере датчик 156 может устанавливать беспроводные соединения со вторым произвольным датчиком 158 и/или с базовой станцией 180. Узлы датчиков ограничены по памяти, аккумулятору и центральному процессору (CPV). В больнице могут быть тысячи датчиков. Одна или более BSN являются совокупностью беспроводных сетевых узлов датчиков. Узлы BSN могут быть присоединены к одному или более пациентам. BSN обычно ограничены по пропускной способности. В больнице могут быть сотни или тысячи сетей BSN (например, одна для каждого пациента). Мобильные базовые станции 178, 180 (BS) являются мобильными устройствами, используемыми для доступа к данным в и для конфигурирования сетей BSN. BS являются обычно устройствами с умеренными ресурсами и мощностью. В больнице могут быть сотни или тысячи BS.
Решение функционального управления ключами состоит из следующих способов.
1. Предварительное распределение ключей. Сервер настройки/безопасности распределяет основной материал ключей в каждый датчик, следуя основной схеме предварительного распределения ключей, и в каждую мобильную базовую станцию, следуя различным подходам. Это выполняется в фазе конфигурации до того, как применяются датчики или базовые станции в больнице.
2. Сертификация предварительно распределенных ключей. Произвольная BS осуществляет доступ к датчикам, формирующим произвольную BSN, для распределения сертификатов KCl ключей, которые проверяют достоверность предварительно распределенного материала ключей на предыдущем этапе для заданного будущего интервала Il.
3. Установка ключей. Два произвольных датчика u и v формируют уникальный парный ключ Kuv, с помощью использования предварительно распределяемого материала ключей и действительных сертификатов ключей.
Основные схемы предварительного распределения ключей
Могут применяться различные способы для реализации симметричных схем предварительного распределения ключей (например, Блома, Блундо и др. или DPKPS), которые могут использоваться как принципиальная основа схем, здесь описанных.
Фиг.9 иллюстрирует способ 230 предварительного распределения, который использует симметричную схему Блома предварительного распределения ключей. Схема Блома позволяет любой паре узлов в сети выводить парный секретный ключ. На основе работы Ду (Du) и др.

были добавлены некоторые незначительные изменения в исходную схему Блома согласно варианту осуществления, чтобы сделать ее подходящей для BSN.
Схема Блома может использоваться следующим образом. Во время фазы предварительного применения в 232 сервер настройки строит (λ+1)×N матрицу G над конечным полем Fq, где N является размером группы имеющих возможность взаимодействия узлов, которая потенциально встречается в различных BSN, и q является достаточно большим числом, чтобы вмещать криптографический ключ. G рассматривается как публичная информация, т.е. любой датчик может знать содержимое G, включая потенциально недобросовестных пользователей. В 234 сервер настройки строит случайную секретную симметричную (λ+1)×(λ+1) матрицу D над Fq, и в 236 вычисляет N×(λ+1) матрицу A=(DG)T, где (DG)T является транспонированной из матрицы DG. Так как D является симметричной, K=AG является симметричной матрицей. Следовательно, Kuv=Kvu, где Kuv является элементом, расположенным в K в u-той строке и v-том столбце. Kuv (или Kvu) используется как парный ключ между узлом u и узлом v. В конечном счете, для k=1,2,…N, сервер настройки распределяет:
1. в 238 k-тую строку матрицы A в узел k, и
2. в 240, k-тый столбец матрицы G в узел k. Альтернативно, чтобы сохранить требования памяти, начальное число G(k) для формирования k-того столбца матрицы G может быть распределено в узел k.
В 242 определяется, были ли распределены начальные числа. Если нет, то после фазы применения, в 242, когда узлам u и v необходимо найти парный ключ между ними, они сперва обмениваются своими столбцами из G. Альтернативно в 244, если начальные числа распределены, узлы u и v обмениваются начальными числами и вычисляют другой столбец G узла. Затем в 246, используя свои частные строки из A, узлы u и v могут соответственно вычислить Kuv и Kvu. Так как G является публичной информацией, ее столбцы (или начальные числа) могут передаваться незашифрованным текстом.
Альтернативно, как проиллюстрировано на фиг.10, способ 250 использует схему Блундо для предварительного распределения ключей. Блундо и др. предлагает протокол предварительного распределения ключей на основе полиномов для извлечения групповых ключей. Для групп из двух пользователей схема Блундо является конкретным случаем схемы Блома с единственным преимуществом: нет коммуникационных накладных расходов во время процесса установки парных ключей. Конкретный случай установки парных ключей на основе полиномов в контексте BSN рассматривается ниже.
В 252 сервер настройки случайно формирует двумерный полином 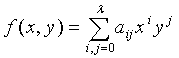 степени λ над конечным полем Fq, где q является достаточно большим простым числом для вмещения криптографического ключа, из условия, что он имеет свойство f(x,y)=f(y,x). Предполагается, что каждый датчик имеет уникальный идентификатор (ID). В 254 сервер настройки вычисляет и распределяет полиномиальную часть f(x,y) для каждого датчика u, т.е. f(u,y).
степени λ над конечным полем Fq, где q является достаточно большим простым числом для вмещения криптографического ключа, из условия, что он имеет свойство f(x,y)=f(y,x). Предполагается, что каждый датчик имеет уникальный идентификатор (ID). В 254 сервер настройки вычисляет и распределяет полиномиальную часть f(x,y) для каждого датчика u, т.е. f(u,y).
В 256 для любых двух узлов u и v датчиков узел u может вычислять общий ключ Kuv=f(u,v) с помощью вычисления f(u,y) в точке v, и узел v может вычислять тот же самый ключ Kvu=f(v,u)=f(u,v) с помощью вычисления f(v,y) в точке u. Доказательство безопасности в Блундо и др. гарантирует, что эта схема является безусловно безопасной и стойкой к " λ-сговору". То есть объединение не более чем λ взломанных узлов датчиков ничего не знает о парном ключе между любыми двумя невзломанными узлами.
Как предпочтительная альтернатива, DPKPS может использоваться для первоначального предварительного распределения парных ключей в датчики.
Упреждающие способы используются для увеличения надежности и управления использования ключей, предварительно распределенных в помощью любой из основных схем предварительного распределения ключей, и таким образом снижения эффекта взломанных узлов.
Будем предполагать, что время действия всех узлов датчиков разделено на n+1 общих длинных интервалов продолжительностью T, обозначаемых как I0, I1, I2,… и In, т.е. узлы датчиков все слабо синхронизированы с глобальным начальным моментом времени, даже когда соединены в различных BSN.
Фиг.11 иллюстрирует способ 260 для сертификации предварительно распределенных ключей и является итогом способов сертификации ключей на фиг.12-15 ниже. В 262 во время каждого временного интервала Il-1 мобильные базовые станции (BS) время от времени связываются с датчиками (где бы они не находились) и, в 264, после проверки целостности датчиков, в 266, распределяют сертификат KCl ключа в каждый невзломанный узел датчика. В 268 сертификат KCl ключа проверяет достоверность целостности предварительно распределяемых ключей датчиков для единственного интервала Il, т.е. предварительно распределяемые ключи достоверны для временного интервала Il. Аналогично в 270 взломанный узел u не принимает сертификат KCl ключа и, таким образом, его предварительно распределяемые ключи аннулируются.
В дальнейшем представлена последовательность способов 280, 310, 330 и 370; каждая последующая схема улучшает предыдущую, устраняя некоторые из ее ограничений. Разница между способами 280, 310, 330 и 370 находится на уровне соединения среди базовых станций и между базовыми станциями и сервером безопасности. Эти способы также различаются в том, как сертификат ключа формируется или согласовывается.
Фиг.12 иллюстрирует способ 280, используемый для централизованной выдачи глобальных сертификатов ключей. В этой части сервер безопасности находится в безопасном месте, отличном от области применения BSN. Как отмечено выше, сервер безопасности является выделенным сервером безопасности, который активно участвует в безопасности до и после применения датчиков. Сервер настройки является выделенным сервером безопасности, который активно участвует в безопасности только до применения датчиков. Следовательно, сервер настройки остается в отключенном от сети состоянии после того, как датчики применены. Также предполагается, что одна или более мобильных базовых станций присутствуют спорадически и кратковременно в BSN. Базовые станции также спорадически соединяются с сервером безопасности. Так как базовые станции являются дорогостоящими узлами, используют устойчивое к внешним воздействиям аппаратное обеспечение и не ограничиваются в вычислительной мощности или памяти. Таким образом, число мобильных базовых станций намного меньше числа узлов датчиков. Так как базовые станции обычно не оставляются без обслуживания, и они лишь спорадично представлены в области применения BSN, их не склонны захватывать или взламывать.
Так как узлы датчиков являются мобильными, нельзя предполагать, что базовая станция будет всегда в беспроводной области BSN (например, пациент с парой датчиков, присоединенных к его телу, который прогуливается в саду больницы). Тем не менее, так как целью BSN является сбор данных, которые необходимо доставить конечному пользователю, предполагается, что BSN спорадически будут находиться в беспроводной области базовой станции. Это важное требование для BSN, иначе информация, собранная с помощью узлов, может быть утеряна из-за ограничения объема памяти в узлах датчиков. Ограничения статичных выделенных серверов для сетевой безопасности датчиков хорошо известны. Например, недобросовестное лицо может попытаться совершить атаки «отказ от обслуживания» (DoS) на выделенные серверы. Такие ограничения исчезают, если выделенные серверы является дублированными, мобильными и не всегда присутствуют в BSN. В средах BSN предполагается существование мобильных базовых станций. Например, в одном подходе доктор загружает данные из BSN пациента в саду. В дальнейшем термины базовые станции относятся к мобильным базовым станциям, которые могут использоваться для безопасности.
Следуя любой из базовых схем предварительного распределения ключей (например, Блома, Блундо и др., DPKPS) до применения, в 282 узлы датчиков инициализируются с помощью уникального идентификатора и данных безопасности. Основные схемы предварительного распределения ключей не используются для предоставления парных ключей между узлами датчиков и базовыми станциями, чтобы избежать риска, что объединение λ взломанных узлов может выдавать себя за базовую станцию. Кроме того, групповой ключ не предлагается для совместного использования между базовой станцией BSi и узлами датчиков, так как взлом единичного узла сделает возможным взлом безопасности оставшихся узлов и, таким образом, приведет базовую станцию в нефункциональное состояние в отношении безопасности. Вместо этого, в 284, следуя тривиальной схеме предварительного распределения ключей, для каждой базовой станции BSi =1,…,M и каждого узла u датчика, u=1,…,N, N>>M, сервер безопасности случайно выбирает и распределяет парный ключ 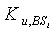 . Эта схема дает возможность каждому узлу датчика безопасно осуществлять связь с базовой станцией BSi. Это безусловно безопасно и дополнительный объем памяти, необходимый в узлах, равен лишь M×logq. В конечном итоге, в 286 сервер безопасности формирует цепочку ключей из n+1 элементов K0, K1,…,Kn с помощью случайного выбора секретного Kn и формирования Kk =F(Kk+1) для k=0,1,…,n-1, где F является псевдослучайной функцией. В 288 сервер безопасности распределяет начальный элемент последовательности ключей K0 в каждый узел u датчика, u=1,…,N. С помощью псевдослучайной функции F, при заданном Kk в последовательности ключей, любой узел датчиков может вычислить все предыдущие ключи Km; 0≤m≤k, но последующие ключи Km; k+1≤m≤n не могут быть вычислены. Таким образом, с помощью знания начального ключа K0 узел датчика может аутентифицировать любой ключ в последовательности ключей с помощью простого выполнения операций псевдослучайной функции. Второй элемент цепочки ключей K1 начально распределяется в каждую базовую станцию BSi.
. Эта схема дает возможность каждому узлу датчика безопасно осуществлять связь с базовой станцией BSi. Это безусловно безопасно и дополнительный объем памяти, необходимый в узлах, равен лишь M×logq. В конечном итоге, в 286 сервер безопасности формирует цепочку ключей из n+1 элементов K0, K1,…,Kn с помощью случайного выбора секретного Kn и формирования Kk =F(Kk+1) для k=0,1,…,n-1, где F является псевдослучайной функцией. В 288 сервер безопасности распределяет начальный элемент последовательности ключей K0 в каждый узел u датчика, u=1,…,N. С помощью псевдослучайной функции F, при заданном Kk в последовательности ключей, любой узел датчиков может вычислить все предыдущие ключи Km; 0≤m≤k, но последующие ключи Km; k+1≤m≤n не могут быть вычислены. Таким образом, с помощью знания начального ключа K0 узел датчика может аутентифицировать любой ключ в последовательности ключей с помощью простого выполнения операций псевдослучайной функции. Второй элемент цепочки ключей K1 начально распределяется в каждую базовую станцию BSi.
Базовые станции имеют аналогичную роль делегированным центрам сертификации инфраструктуры публичных ключей с сервером безопасности в качестве доверенного корня. В 290 базовая станция выпускает сертификат ключа (KC) в невзломанный узел, который подтверждает достоверность ее предварительно распределяемых ключей для ограниченного интервала времени T. После временного интервала T предварительно распределяемые ключи более не достоверны. Элементы цепочки ключей K0, K1,…,Kn используются последовательно как сертификат ключа для каждого интервала I1, I2,… и In. В последующем элементы цепочки ключей упоминаются как сертификаты ключей KC0, KC1,…,KCn.
В 292 в течение временного интервала Il каждая и любая базовая станция BSi спорадически связывается с сервером безопасности. Так как базовые станции и серверы безопасности являются мощными узлами, они могут использовать криптографию с открытым ключом для обеспечения безопасности их передач данных. Сервер безопасности распределяет следующий сертификат KCl+1 ключа в каждую базовую станцию BSi, BSi=1,…,M. Следует заметить, что в невероятном событии взлома базовой станции раскрывается только один сертификат без риска будущих раскрытий сертификатов ключей, т.е. взломанная базовая станция сама по себе не может вычислить следующий сертификат ключа. Взлом базовой станции легко обнаружить, так как она не будет обращаться к серверу безопасности в следующем временном интервале Il+1. Таким образом, раскрытая базовая станция не получит сертификатов ключей в последующие интервалы за интервалом взлома. Однако в подобном событии оставшиеся базовые станции должны информировать все узлы датчиков об идентификационной информации, взломанной базовой станции BSi. Каждый узел u датчика сотрет его совместно используемый ключ 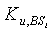 с BSi и, таким образом, удалит BSi из своего списка надежных базовых станций.
с BSi и, таким образом, удалит BSi из своего списка надежных базовых станций.
В 294 в течение временного интервала Il, по меньшей мере, одна произвольная базовая станция BSi спорадически и кратковременно обращается к BSN. В 296, используя соответствующие ключи 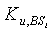 , базовая станция BSi аутентифицирует и устанавливает безопасную связь с каждым невзломанным узлом датчика, формирующим часть BSN. В 298 в каждый аутентифицированный узел датчика базовая станция распределяет сертификат KCl+1 ключа, соответствующий временному интервалу Il+1. В-третьих, узел датчика проверяет, что h(Kl+1) равняется сохраненному Kl. В отрицательном случае узел датчика может определенно сделать вывод, что базовая станция BSi была взломана и, таким образом, отвергнуть поддельный сертификат KC'l+1 ключа.
, базовая станция BSi аутентифицирует и устанавливает безопасную связь с каждым невзломанным узлом датчика, формирующим часть BSN. В 298 в каждый аутентифицированный узел датчика базовая станция распределяет сертификат KCl+1 ключа, соответствующий временному интервалу Il+1. В-третьих, узел датчика проверяет, что h(Kl+1) равняется сохраненному Kl. В отрицательном случае узел датчика может определенно сделать вывод, что базовая станция BSi была взломана и, таким образом, отвергнуть поддельный сертификат KC'l+1 ключа.
В 300 устанавливается ключ. Если двум узлам необходимо установить парный ключ, они сначала выводят парный ключ, как объяснено выше. Затем проверяют, чтобы оба имели действительный сертификат ключа от базовой станции BSi. Процесс проверки достоверности сертификата ключа, выполняемый двумя узлами u и v датчиков, должен быть безопасным для предотвращения получения недобросовестным пользователем действительного сертификата ключа. Следовательно, этот процесс не может требовать изначального обмена соответствующими сертификатами ключей и затем проверки достоверности сертификатов ключей с помощью внутренней проверки, что они были выпущены для текущего временного интервала Il и что они могут быть аутентифицированы с помощью начального ключа K0 (или извлеченных аутентифицированных ключей Km; m<l) последовательности ключей. Вместо этого оба узла датчиков выполняют протокол нулевого знания (ZK), чтобы доказать, что оба имеют действительный сертификат без его действительного показа. Протокол ZK указан ниже:
(Nu││Nv)
(Nv││Nu)
В (1) узел u отсылает самосформированный для данного случая элемент Nu в узел v. В (2) узел v отсылает самосформированный для данного случая элемент Nv в узел u. В (3) u использует сертификат KCl и оба для данного случая элемента Nu и Nv для вычисления кода аутентификации сообщения (MAC). Оба элемента для данного случая должны быть включены в сообщение (3) и (4) для избежания атак отражения, т.е. v, в случае, если он не знает KCl, обманом добивается от u вычислений KZNP, что v может затем использовать для успешного запуска протокола ZK с третьим узлом w. Вычисленный MAC составляет ключ для протокола ZK KZNPuv. С помощью аналогичной процедуры в (4) v вычисляет тот же самый ключ KZNPvu протокола ZK. Заметим, что KZNPuv≠KZNPvu. Оба ключа протокола ZK должны быть разными, чтобы избежать, что v, в случае, если он не знает KCl, лишь повторно воспроизводит сообщение (7) для успешного исполнения протокола ZK. В (5) u вычисляет MAC KZNPuv, используя парный ключ Kuv. В (6) v вычисляет MAC KZNPvu, используя парный ключ Kvu. Эти два этапа необходимы для ассоциирования сообщения KCl с u и v соответственно. Они также противостоят против перехвата сообщений злоумышленником, которыми обмениваются на (7) и (8). В конечном итоге, u проверяет действительность, что v известно KCl: следуя этапам, которые v выполняет в (4) и (7), u может вычислить часть информации для сравнения с информацией, принятой от v в (8). Узел v может следовать аналогичной процедуре для проверки действительности знания u о KCl. Следует заметить, что так как обмениваемые сообщения (7) и (8) являются MAC, вычисляемыми с помощью информации, хранящейся внутри узлов u и v, соответственно, и никакой дополнительной информации не раскрывается, никакая информация о KCl не открывается.
Фиг.13 иллюстрирует способ 310 для предоставления централизованно согласованных глобальных сертификатов ключей. Способ 280 из фиг.12 имеет важный недостаток для некоторых приложений: требование от базовой станции BSi осуществлять связь с сервером безопасности может быть невыполнимо в таких приложениях. Однако во многих приложениях базовые станции будут иметь взаимное спорадическое соединение некоторое время до следующего визита в BSN. Например, для глобального обмена информацией, собранной в различных BSN. В способе 310 мы используем такой факт.
В способе 310 мы делаем предположение об автономном сервере настройки, который находится в безопасном месте, отличном от области применения BSN. Также предполагаем существование множества мобильных базовых станций BSi, BSi=1,…,M, присутствующих спорадически и кратковременно в BSN. Однако в способе 310 базовые станции не обращаются спорадически к серверу настройки после фазы применения. Вместо этого они спорадически и кратковременно взаимно связываются. Оставшиеся предположения для базовых станций, обсужденные в способе 280, содержатся в способе 310.
В 312, следуя какой-либо из базовых схем предварительного распределения ключей, до применения, узлы датчиков инициализируются с уникальным идентификатором и данными безопасности. В 314, следуя тривиальной схеме предварительного распределения ключей, для каждой базовой станции BSi=1,…,M, и каждого узла датчика u=1,…,N, N>>M, сервер безопасности случайно выбирает и распределяет парный ключ 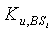 .
.
Базовые станции имеют аналогичную роль перекрестно связанным центром сертификации инфраструктуры публичных ключей. В 316 базовая станция выпускает сертификат ключа в невзломанный узел, который проверяет достоверность его предварительно распределяемых ключей для ограниченного периода T времени. После периода T времени предварительно распределяемые ключи узла более не достоверны. В 318 во время временного интервала Il-1 каждая и любая базовая станция BSi спорадически взаимно соединяются. Так как базовые станции являются мощными узлами, они могут использовать криптографию с открытым ключом для обеспечения безопасности своих передач данных. В 320 базовые станции согласовывают сертификат ключа KCl+1, соответствующий временному интервалу Il+1.
В течение временного интервала Il, по меньшей мере, одна произвольная базовая станция BSi спорадически и кратковременно обращается к BSN. В 322, используя соответствующие ключи 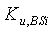 , базовая станция BSi аутентифицирует и устанавливает безопасную связь с каждым невзломанным узлом датчика, формирующим часть BSN. В 324 каждому аутентифицированному узлу датчика базовая станция распределяет сертификат KCl+1 ключа, соответствующий временному интервалу Il+1.
, базовая станция BSi аутентифицирует и устанавливает безопасную связь с каждым невзломанным узлом датчика, формирующим часть BSN. В 324 каждому аутентифицированному узлу датчика базовая станция распределяет сертификат KCl+1 ключа, соответствующий временному интервалу Il+1.
После временного интервала Il каждая базовая станция BSi отбрасывает сертификат ключа Kl+1. Следовательно, максимум базовая станция BSi сохранит сертификат ключа KCl+1 два временных интервала Il-1 и Il. Следует заметить, что в маловероятном событии взлома базовой станции, только два сертификата ключей KCl и KCl+1 раскрываются без риска будущих раскрытий сертификатов ключей, т.е. взломанная базовая станция не может предвидеть следующий сертификат ключа за KCl+1. Взлом базовой станции легко обнаружить, так как она не обращается к оставшимся базовым станциям в следующем временном интервале Il+1. Хотя в подобном событии оставшиеся базовые станции должны информировать все узлы датчиков об идентификационной информации взломанной базовой станции BSi и, если возможно, распределять обновленный сертификат KCобновленный l+1 ключа для в настоящий момент текущего временного интервала Il+1. Каждый узел u датчика стирает свой совместно используемый ключ Ku,BSi с BSi и, таким образом, удаляет BSi из своего списка надежных базовых станций.
В 326 устанавливается ключ. Если двум узлам необходимо установить парный ключ, они сначала выводят парный ключ, как объяснено выше. Затем они проверяют, что оба имеют действительный сертификат ключа с помощью исполнения протокола ZK, как объясняется в способе 280.
Фиг.14 иллюстрирует способ 330, который позволяет локально согласовывать глобальные сертификаты ключей. Способ 300 имеет важный недостаток для некоторых приложений: требование взаимного соединения всех базовых станций BSi в течение временного интервала Il может быть невыполнимо или непрактично в этих приложениях. Кроме того, базовые станции определенно спорадически соединяются в малых множествах за некоторое время до следующего визита в BSN. Например, для обмена информацией, собранной в различных BSN. В способе 330 используется такой факт.
В 332, следуя какой-либо основной схеме предварительного распределения ключей, до применения, узлы датчиков инициализируются с помощью уникального идентификатора и данных безопасности. В 334 следуя тривиальной схеме предварительного распределения ключей, для каждой базовой станции Bsi=1,…,M, и каждого узла u датчика, u=1,…,N, N>>M, сервер настройки случайно выбирает и распределяет парный ключ Ku,Bsi. В 336 сервер безопасности формирует секретное S. В 338, следуя пороговой схеме (t,M) (t≤M), сервер настройки формирует M частей S1, S2,…,SM из секретного S, и безопасно распределяет Si в каждую базовую станцию BSi. Любые t или более базовых станций, объединяющие свои части, легко восстанавливают S, но любая группа базовых станций, знающая только t-1 или менее частей, не может. Следует заметить, что в конкретном случае t=1, каждая базовая станция BSi сохраняет действительное секретное S.
В этом конкретном подходе базовые станции имеют аналогичную роль с перекрестно связанными полномочиями сертификации инфраструктуры публичного ключа. В 340 базовая станция выпускает сертификат ключа в невзломанный узел, который проверяет действительность ее предварительно распределяемых ключей для ограниченного периода времени T. После временного периода T предварительно распределяемые ключи узла более не действительны.
В 342 в течение временного интервала Il-1, каждая и любая базовая станция BSi спорадически безопасно соединяются, создавая малые несвязанные группы Gg, G1, G2… g<M. Каждая базовая станция BSi соединяется с, по меньшей мере, одной группой Gg. Следовательно, число членов каждой группы равно │Gg│≥M/g, где  является самым большим натуральным числом y, меньшим, чем или равным x. Группа Gg может быть представлена как Gg={Gg1,…,Ggk; k=│Gg│}. Например, с M=7 базовых станций и g=3, тогда │Gg│≥2 и расположение групп может быть G1={BS2, BS3, BS6} и G2={BS1, BS4, BS5} и G3={BS1, BS7}. Следует заметить, что для группы G3 │G3│=2 и Gg1=BS1 и Gg2=BS7. Необходимым условием для того, что сейчас последует, является то, что │Gg│≥t для всех g. В 344 члены Gg1,…,Ggk группы Gg объединяют и части
является самым большим натуральным числом y, меньшим, чем или равным x. Группа Gg может быть представлена как Gg={Gg1,…,Ggk; k=│Gg│}. Например, с M=7 базовых станций и g=3, тогда │Gg│≥2 и расположение групп может быть G1={BS2, BS3, BS6} и G2={BS1, BS4, BS5} и G3={BS1, BS7}. Следует заметить, что для группы G3 │G3│=2 и Gg1=BS1 и Gg2=BS7. Необходимым условием для того, что сейчас последует, является то, что │Gg│≥t для всех g. В 344 члены Gg1,…,Ggk группы Gg объединяют и части  …
… для вычисления S. Затем каждый член группы независимо вычисляет сертификат KCl+1 ключа для интервала Il+1 с помощью вычисления KCl+1=F(S,l+1). В конечном итоге, каждый член группы отбрасывает S.
для вычисления S. Затем каждый член группы независимо вычисляет сертификат KCl+1 ключа для интервала Il+1 с помощью вычисления KCl+1=F(S,l+1). В конечном итоге, каждый член группы отбрасывает S.
В течение временного интервала Il, по меньшей мере, одна произвольная базовая станция BSi спорадически и кратковременно обращается к BSN. В 346, используя соответствующие ключи 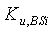 базовая станция аутентифицирует и устанавливает безопасную связь с каждым невзломанным узлом датчика, формирующим часть BSN. В 348 в каждый аутентифицированный узел датчика базовая станция распределяет сертификат KCl+1 ключа для временного интервала Il+1. Как в способе 300, после временного интервала Il каждая базовая станция BSi отбрасывает сертификат KCl+1 ключа.
базовая станция аутентифицирует и устанавливает безопасную связь с каждым невзломанным узлом датчика, формирующим часть BSN. В 348 в каждый аутентифицированный узел датчика базовая станция распределяет сертификат KCl+1 ключа для временного интервала Il+1. Как в способе 300, после временного интервала Il каждая базовая станция BSi отбрасывает сертификат KCl+1 ключа.
В 350 устанавливается ключ. Если двум узлам необходимо установить парный ключ, они сначала выводят парный ключ, как объясняется в способе 300. Затем они проверяют, что оба имеют действительный сертификат ключа с помощью выполнения протокола ZK, как объясняется в способе 270.
Фиг.15 иллюстрирует способ 370, который позволяет локально согласовывать отдельные сертификаты ключей. Способ 330 имеет значительное функциональное улучшение относительно способов 270 и 300: каждая малая часть базовых станций может управлять сертификатами ключей независимо и без необходимости обращения к серверу настройки. Более того, в маловероятном событии взлома базовой станции безопасность всех BSN не взламывается для оставшихся временных интервалов.
Предыдущие схемы имеют важное преимущество: все узлы датчиков могут взаимно аутентифицировать и/или устанавливать безопасные передачи данных в течение временного интервала Il, независимо от их мобильности, т.е. в течение временного интервала Il узел датчика может перемещаться по различным BSN и он все еще может безопасно передавать данные во всех из них. Другими словами, способы 270, 300 и 330 дают возможность логического безопасного соединения узлов в различных BSN через единственную защищаемую зону. Это, в свою очередь, имеет противоречивый эффект для безопасности: необнаруженный взломанный узел может все еще соединяться с BSN в оставшееся время интервала Il взлома, потому что он сохраняет KCl и, возможно, также в следующем интервале Il+1, если он уже имеет KCl+1. Следует принять во внимание, что взломанный узел не может обмануть базовую станцию. Таким образом, единственным способом взломанного узла получить Kl+1 - это принять его до того, как его взломают.
В некоторых приложениях датчиков, однако, степень защищенности системы менее важна. Мы ссылаемся здесь на приложения, где датчики имеют очень низкую мобильность. Представим, например, множество датчиков, присоединенных к человеческому телу. Тело естественно мобильно, но прикрепленные датчики не двигаются в отношении друг друга.
В способе 370 BSN не являются логически безопасно связанными тем, что совместно используют тот же самый сертификат KCl ключа. Скорее в данном варианте осуществления, разные BSN могут иметь разные сертификаты KC1 l, KC2 l…KCm l ключей, выделяя узлы датчиков, принадлежащие некоторой BSN из оставшихся узлов, принадлежащих сетям BSN с другими сертификатами ключей KCi l и KCj l, i≠j. Другими словами, множество датчиков теперь принадлежит разным и динамичным защищаемым зонам, причем каждая защищаемая зона определяется сертификатом ключа исключительно согласованного группой базовых станций. Два узла датчиков могут безопасно передавать данные, если и только если они принадлежат к одной и той же защищаемой зоне в заданный временной интервал Il.
В 372 ключ предварительно распределяется, как описано в способе 330. В 374 предварительно распределяется сертификация ключей. Базовые станции имеют аналогичную роль корневым центрам сертификации инфраструктуры публичных ключей. В 376 базовая станция выпускает сертификат ключа в невзломанный узел, который проверяет достоверность его предварительно распределенных ключей для ограниченного периода времени T. После временного периода T предварительно распределяемые ключи узла более недействительны. Сертификаты KCBSi l и KCBSj l ключей от различных базовых станций BSi и BSj, i≠j, не могут быть равными.
В 378 в течение временного интервала Il-1, каждая и любая базовая станция BSi спорадически безопасно соединяется, создавая малые несвязанные группы Gg,G1,G2…g<M. Каждая базовая станция BSi соединяется, по меньшей мере, с одной группой Gg. В 380 члены Gg1,…,Ggk группы Gg объединяют свои части 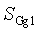 …
…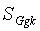 для вычисления S. В 382 каждый член группы независимо вычисляет сертификат KCg l+1 для интервала Il+1 с помощью вычисления
для вычисления S. В 382 каждый член группы независимо вычисляет сертификат KCg l+1 для интервала Il+1 с помощью вычисления 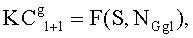 где
где 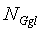 является элементом для данного случая единственным для группы Gg для интервала Il+1. В 384 каждый член группы отбрасывает S.
является элементом для данного случая единственным для группы Gg для интервала Il+1. В 384 каждый член группы отбрасывает S.
В 386 в течение временного интервала Il, по меньшей мере, одна произвольная базовая станция BSi спорадически и кратковременно обращается к BSN. В 388, используя соответствующие ключи Ku,Bsi, базовая станция BSi аутентифицирует и устанавливает безопасную передачу данных с каждым невзломанным узлом датчика, формирующим часть BSN. В 390 в каждый аутентифицированный узел датчика базовая станция распределяет сертификат KCg l+1 для временного интервала Il+1. Как и в предыдущих схемах, после временного интервала Il каждая базовая станция BSi отбрасывает сертификат KCg l+1 ключа.
Существует три отдельных случая в способе 370: первоначально, если каждой базовой станции BSi разрешается присоединиться только один раз к группе Gg, то она выводит единственный сертификат KCg l+1 ключа. Результатом становится столько разных защищаемых зон, сколько групп Gg. В конкретном случае t=1, каждая базовая станция BSi создает свою собственную группу Gi и, таким образом, результатом становится столько разных защищаемых зон, сколько базовых станций BSi. Во-вторых, если базовой станции BSi разрешено присоединяться к n различным группам G1,G2…Gn, 1<n≤g, то она выводит n разных сертификатов ключей KC1 l+1, KC2 l+1, KCn l+1. Результатом становится наличие разных защищаемых зон, некоторые из которых логически соединены. В-третьих, если все базовые станции соединяются с одной и той же и единственной группой, то они все согласовывают один и тот же сертификат ключа и, таким образом, результатом является глобальная защищаемая зона, как в способе 330.
В 392 устанавливается ключ. Если двум узлам необходимо установить парный ключ, они сначала выводят парный ключ, как объясняется в способе 300. Затем они проверяют, что оба имеют действительный сертификат ключа с помощью выполнения протокола ZK, как объясняется в способе 270. Два узла датчиков с разными сертификатами ключей не могут установить ключ.
В способе 370 взломанные узлы датчиков не могут использоваться для атаки на датчики с другими сертификатами ключей, нежели сертификат, хранимый взломанным узлом. Однако используя способ 370, узлы датчиков с разными сертификатами ключей не могут безопасно передавать данные в одной той же BSN. Эта система управления ключами улучшила устойчивость в отношении захватов узлов без опоры на какие-либо глобальные ID для сетей BSN и использует немного больше памяти датчиков, чем это необходимо основным схемам предварительного распределения ключей.
Изобретение описано со ссылкой на предпочтительные варианты осуществления. Модификации и изменения могут возникать для других при прочтении и понимании предшествующего подробного описания. Подразумевается, что изобретение следует толковать как включающее все подобные модификации и изменения в такой мере, как они попадают в объем прилагаемой формулы изобретения или ее эквивалентов.
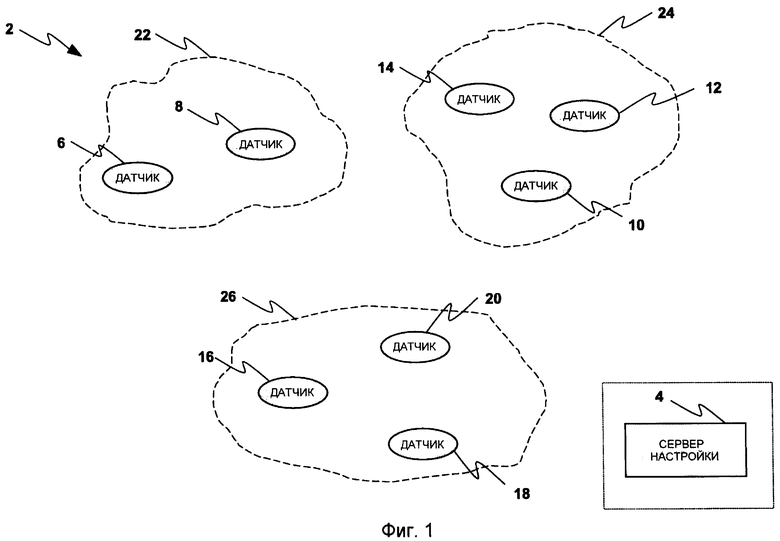
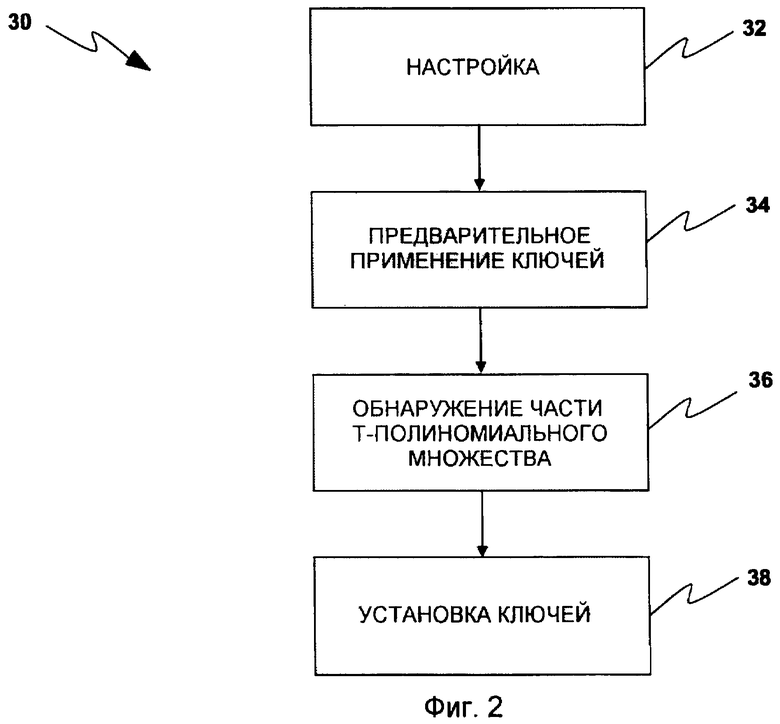
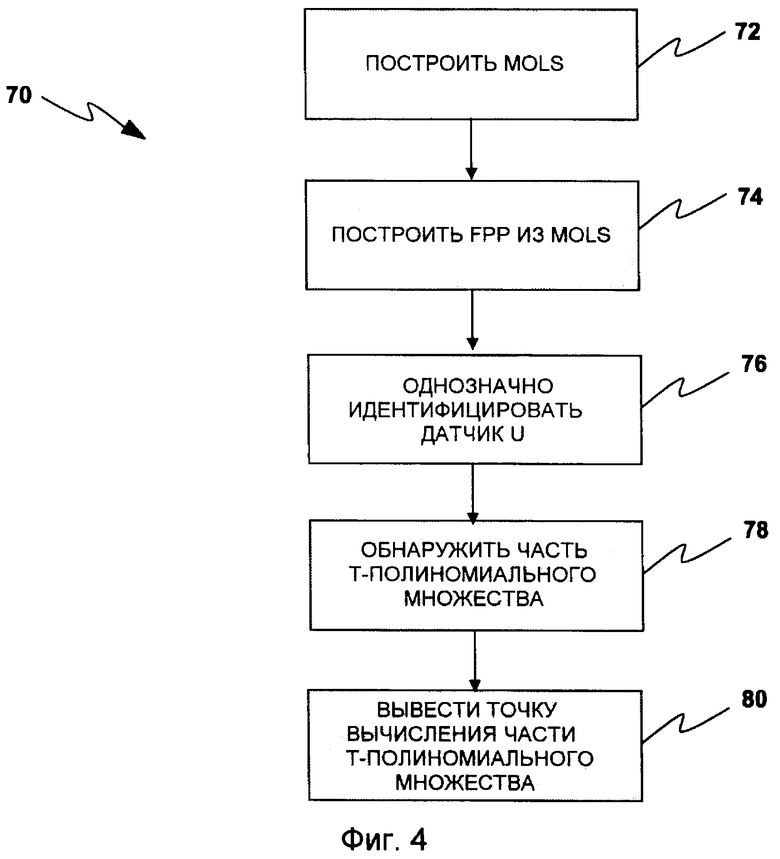
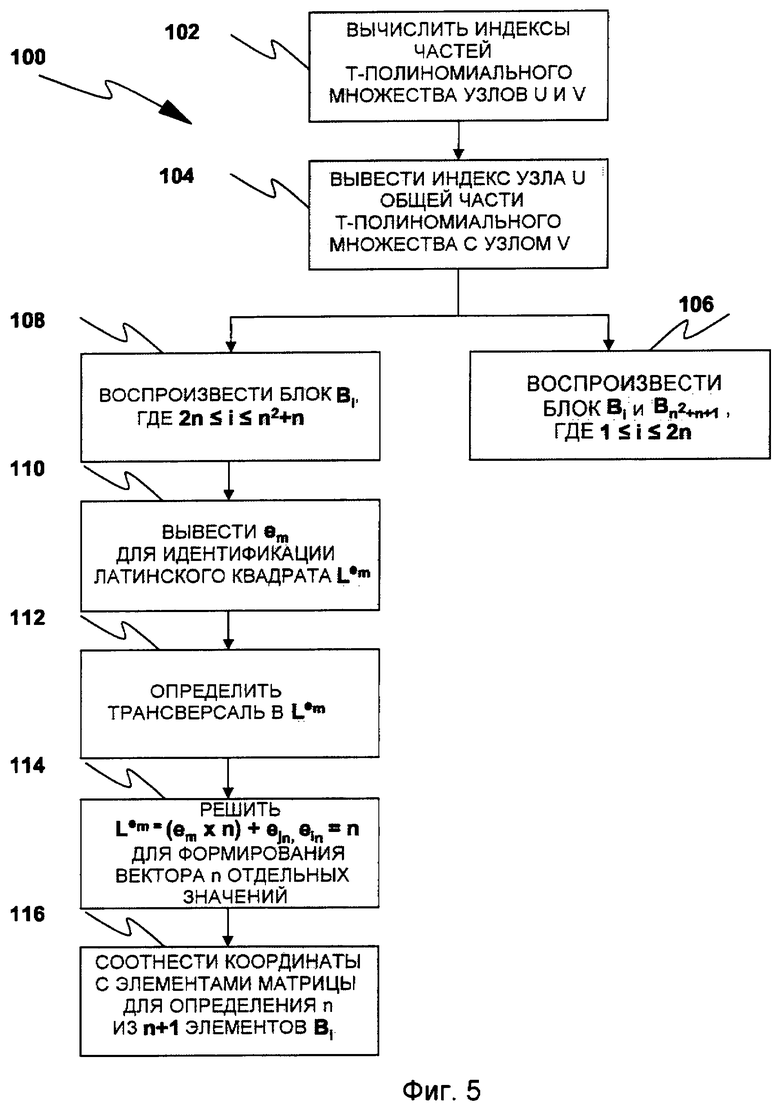
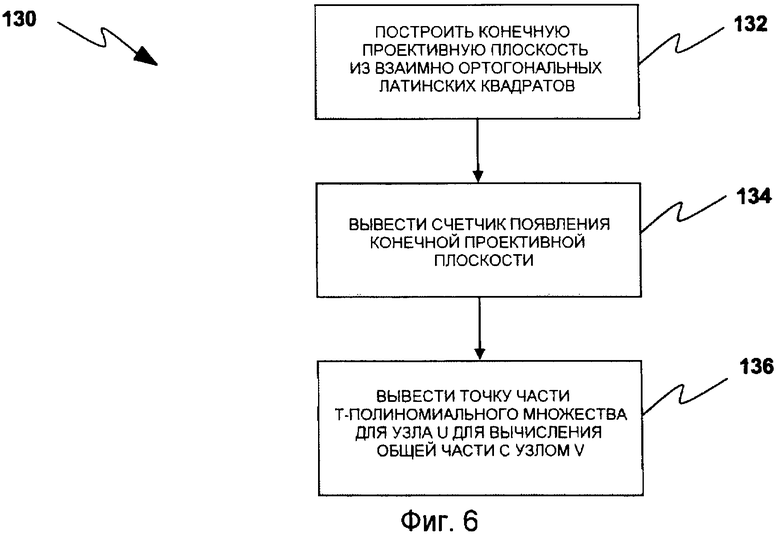

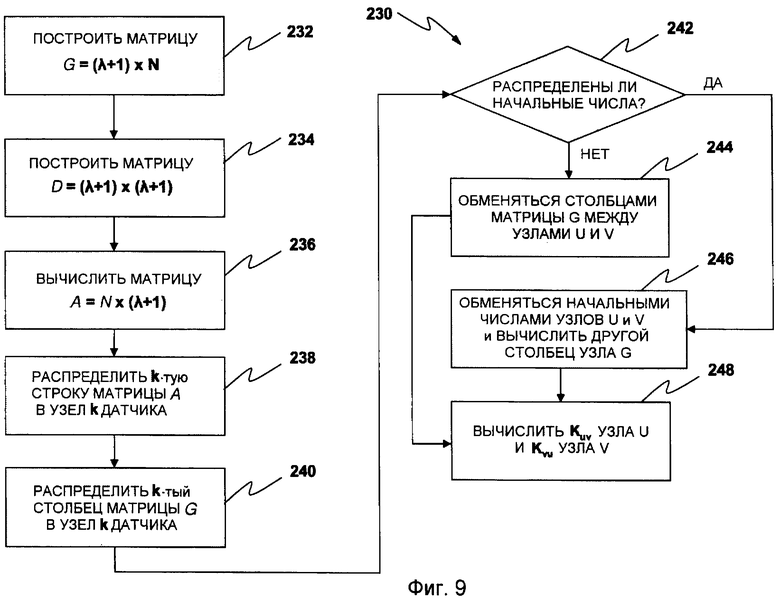
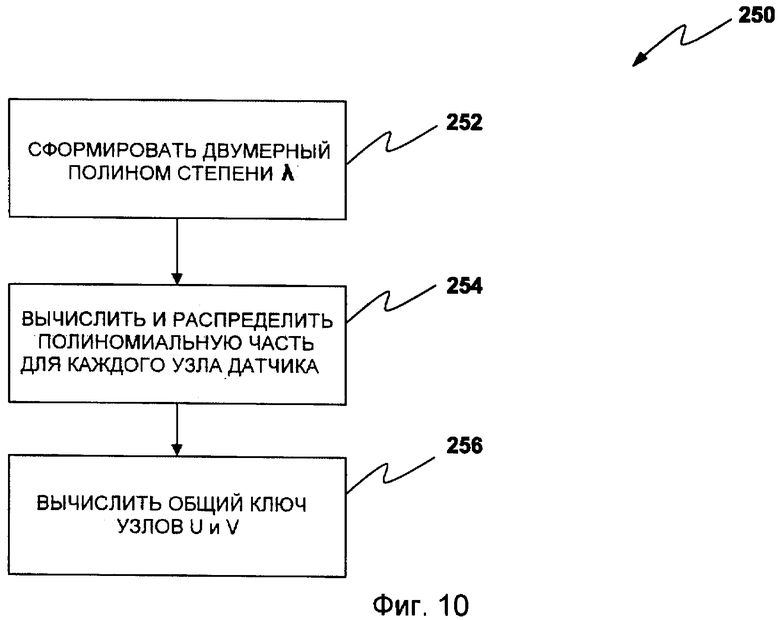
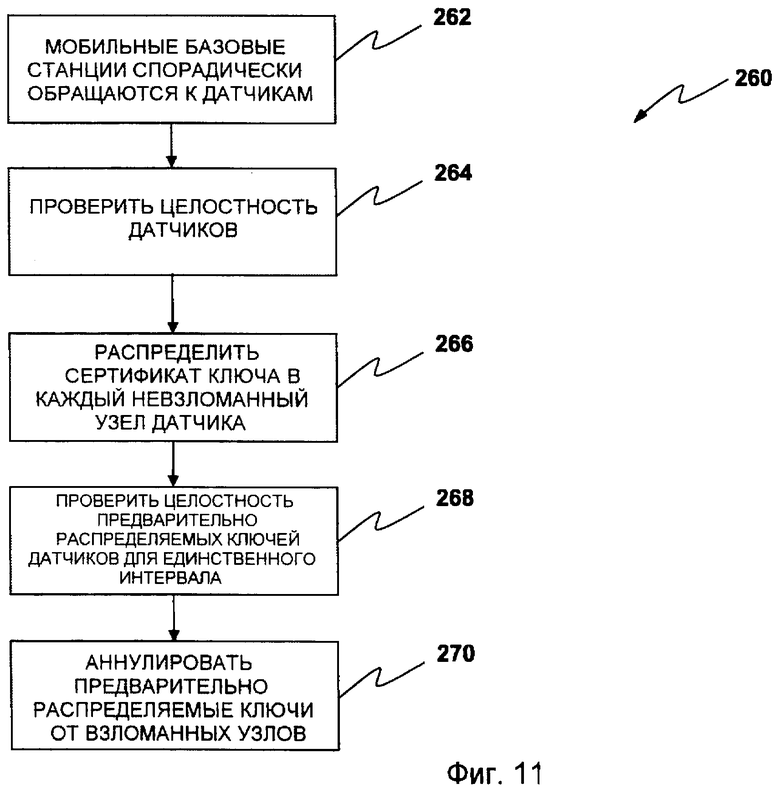
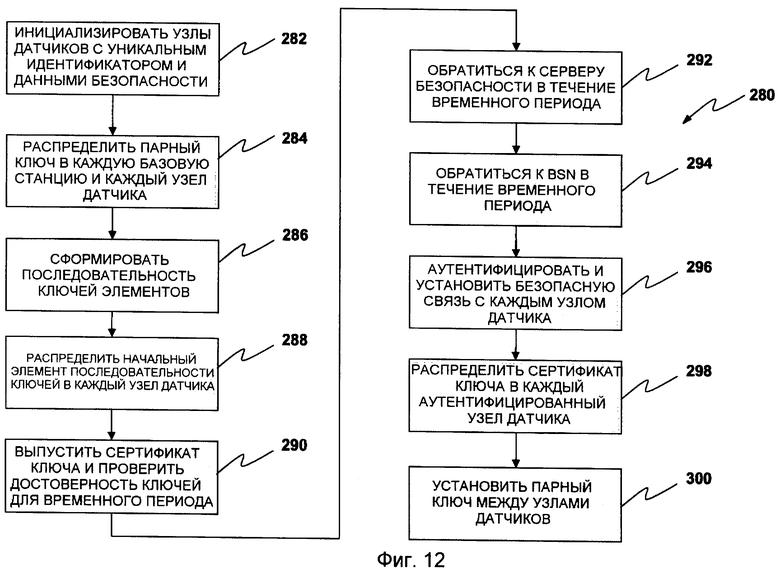
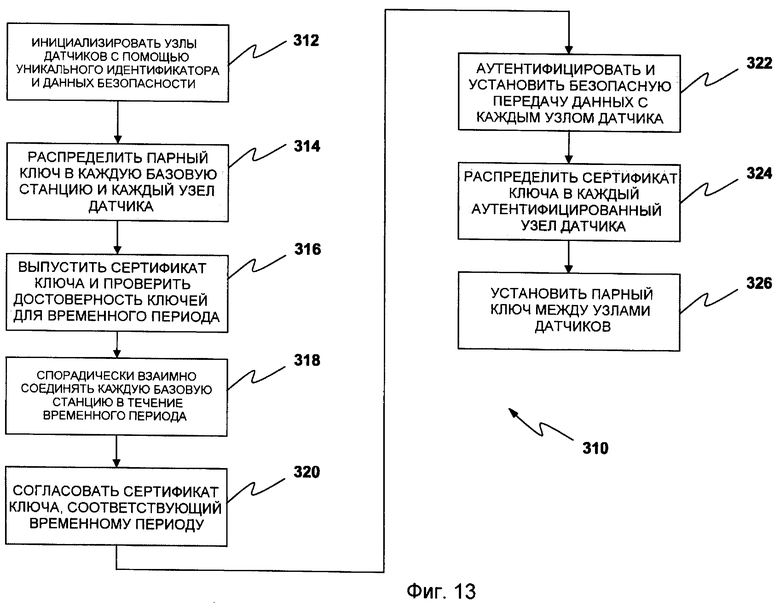
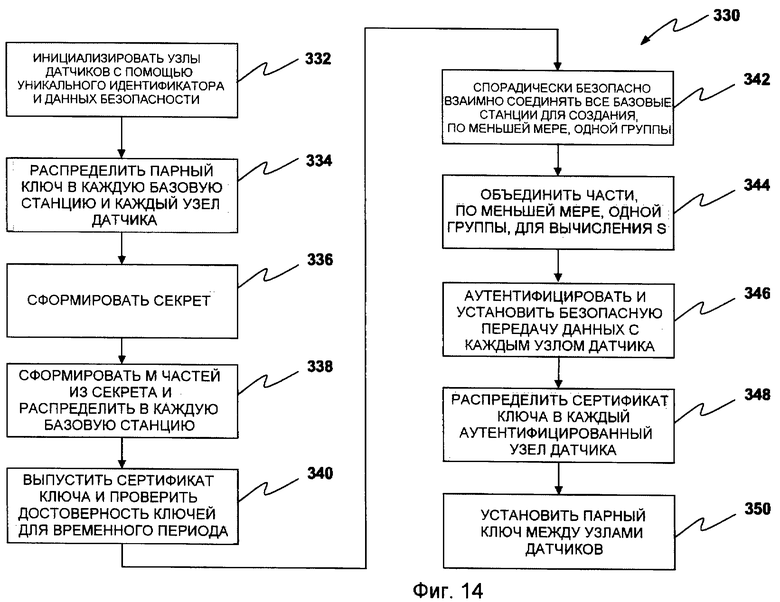
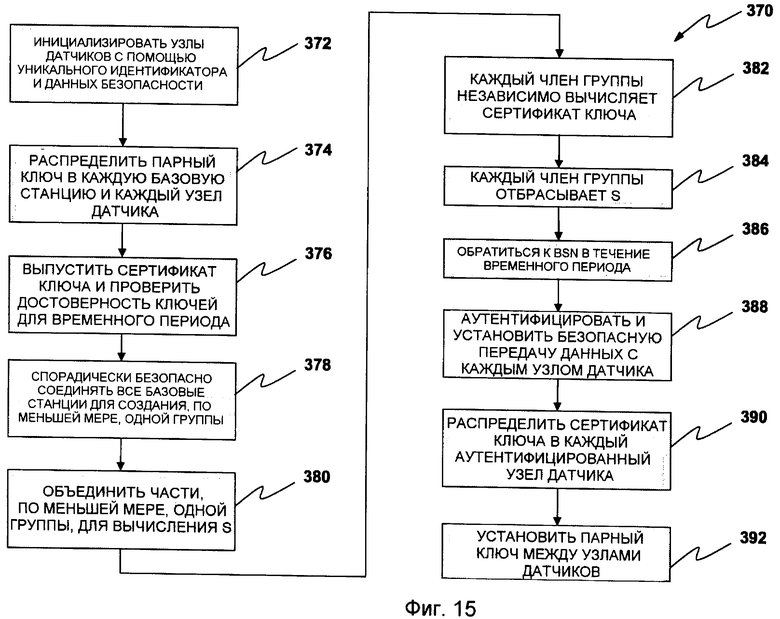
Изобретение относится к области беспроводных сетей связи. Технический результат заключается в улучшении безопасности соединения. Сущность изобретения заключается в том, что беспроводная сеть для мониторинга пациента включает в себя сеть датчиков на теле, которая включает в себя один или более беспроводных датчиков, подсоединенных к пациенту, которые собирают и передают информацию, относящуюся к здоровью пациента, в беспроводную сеть. Сервер настройки конфигурирует один или более беспроводных датчиков с материалом ключей до того, как один или более датчиков применяются в беспроводной сети. Базовая станция распределяет сертификат ключа в один или более датчиков, ассоциированных с сетью датчиков на теле из условия, чтобы два датчика формировали уникальный парный ключ, основываясь, по меньшей мере, частично на предварительно распределенном материале ключей и сертификате ключа, распределяемом базовой станцией. 4 н. и 19 з.п. ф-лы, 15 ил.
1. Беспроводная сеть (2, 150) для мониторинга пациента, причем беспроводная сеть (2, 150) содержит:
сеть датчиков на теле (22, 24, 26, 172, 174, 176), которая включает в себя один или более беспроводных датчиков (6, 8, 10, 12, 14, 16, 18, 20, 156, 158, 160, 162, 164, 166, 168, 170), работоспособно подсоединенных к пациенту, которые собирают и передают информацию, относящуюся к здоровью пациента, в беспроводную сеть (2, 150);
сервер (4, 154) настройки, который конфигурирует один или более беспроводных датчиков (6, 8, 10, 12, 14, 16, 18, 20, 156, 158, 160, 162, 164, 166, 168, 170) с материалом ключей до того, как один или более датчиков (6, 8, 10, 12, 14, 16, 18, 20, 156, 158, 160, 162, 164, 166, 168, 170) применяются в беспроводной сети (2,150); и
базовую станцию (178, 180), которая распределяет сертификат ключа в один или более датчиков (6, 8, 10, 12, 14, 16, 18, 20, 156, 158, 160, 162, 164, 166, 168, 170), ассоциированных с сетью (22, 24, 26, 172, 174, 176) датчиков на теле, из условия, чтобы два датчика формировали уникальный парный ключ на основе, по меньшей мере, частично предварительно распределенного материала ключей и сертификата ключа, распределяемого базовой станцией (178, 180).
2. Система по п.1, в которой сервер (4,154) настройки случайно
формирует множество ℑ из t×(n2+n+1) двумерных полиномов 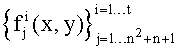 степени λ над Fq' и для j=1…n2+n+1, сервер настройки последовательно выбирает t из полиномов из ℑ и формирует n2+n+1 t-полиномиальных множеств Fj(x,y), где λ является числом узлов в беспроводной сети и является целым числом, большим, чем единица, n является простой степенью, t является целым числом, большим или равным единице, и Fq' является конечным полем, где q' является простым числом, достаточно большим для вмещения криптографического ключа.
степени λ над Fq' и для j=1…n2+n+1, сервер настройки последовательно выбирает t из полиномов из ℑ и формирует n2+n+1 t-полиномиальных множеств Fj(x,y), где λ является числом узлов в беспроводной сети и является целым числом, большим, чем единица, n является простой степенью, t является целым числом, большим или равным единице, и Fq' является конечным полем, где q' является простым числом, достаточно большим для вмещения криптографического ключа.
3. Система по п.2, в которой сервер (4, 154) настройки формирует конечную проективную плоскость (n2+n+1, n+1, 1) с элементами, принадлежащими множеству S, где |S|=n2+n+1, и множество S ассоциировано из условия, чтобы каждый элемент в S ассоциировался с отдельным элементом из t-полиномиального множества Fj(x,y), где n является простой степенью.
4. Система по п.3, в которой каждый узел датчика принимает от сервера (4, 154) настройки n+1 частей 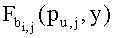 t-полиномиального множества, где pu,j∈Fq', bi,j∈Вi∈ конечной проективной плоскости, и j=1…n+1, при этом n является простой степенью.
t-полиномиального множества, где pu,j∈Fq', bi,j∈Вi∈ конечной проективной плоскости, и j=1…n+1, при этом n является простой степенью.
5. Система по п.4, в которой первый блок B1 конечной проективной плоскости имеет элементы {b1,1,…b1,n+1} и узел (ua) датчика принимает части 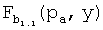 по
по 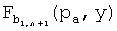 t-полиномиального множества, вычисленные в точке ра из Fq', при этом а находится между 1 и N'/(n+1), где N является размером группы узлов, имеющих возможность взаимодействовать, которое потенциально находится в различных беспроводных сетях и является целым числом, большим или равным единице, и n является простой степенью.
t-полиномиального множества, вычисленные в точке ра из Fq', при этом а находится между 1 и N'/(n+1), где N является размером группы узлов, имеющих возможность взаимодействовать, которое потенциально находится в различных беспроводных сетях и является целым числом, большим или равным единице, и n является простой степенью.
6. Система по п.5, в которой второй блок В2 конечной проективной плоскости имеет элементы 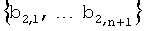 и b1,1=b2,1, и узел u1+N'/(n+1) датчика принимает части
и b1,1=b2,1, и узел u1+N'/(n+1) датчика принимает части 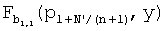 t-полиномиального множества, вычисленные в точке p1+N'/(n+1), и части
t-полиномиального множества, вычисленные в точке p1+N'/(n+1), и части 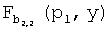 по
по 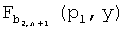 t-полиномиального множества, вычисленные в точке p1, где N является размером группы узлов, имеющих возможность взаимодействовать, которое потенциально находится в различных беспроводных сетях и является целым числом, большим или равным единице, и n является простой степенью.
t-полиномиального множества, вычисленные в точке p1, где N является размером группы узлов, имеющих возможность взаимодействовать, которое потенциально находится в различных беспроводных сетях и является целым числом, большим или равным единице, и n является простой степенью.
7. Система по п.6, в которой узлы датчиков обмениваются своими ID, причем каждый из ID содержит индексы n+1 частей t-полиномиального множества, переносимых с помощью ID, и точки 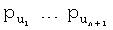 ,
, 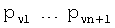 , в которых вычисляются соответствующие n+1 части t-полиномиального множества, где n является целым числом, большим или равным единице.
, в которых вычисляются соответствующие n+1 части t-полиномиального множества, где n является целым числом, большим или равным единице.
8. Система по п.7, в которой каждый узел датчика находит индекс k, соответствующий общему t-полиномиальному множеству Fk(x,y) и соответствующие точки pu и pv вычисления.
9. Система по п.8, в которой узел u вычисляет t двумерных полиномов 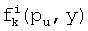 степени λ для i=1…t в точке pv (т.е.
степени λ для i=1…t в точке pv (т.е. 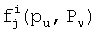 ) для получения t частичных ключей и усекает t частичных ключей до logq' бит и конкатенирует t сегментов ключей для установки конечного парного ключа Kuν из logq бит, где t является положительным целым числом.
) для получения t частичных ключей и усекает t частичных ключей до logq' бит и конкатенирует t сегментов ключей для установки конечного парного ключа Kuν из logq бит, где t является положительным целым числом.
10. Система по п.1, в которой распределение сертификатов ключей включает в себя:
инициализацию одного или более беспроводных датчиков;
распределение парного ключа в базовую станцию и один или более беспроводных датчиков;
формирование последовательности элементов ключа;
распределение начального элемента последовательности ключей в один или более беспроводных датчиков;
выпуск действительного сертификата ключа и проверку действительности ключей для временного периода, обращение к серверу безопасности в течение временного периода;
обращение к сети датчиков на теле в течение временного периода;
аутентификацию и установку безопасной передачи данных с каждым одним или более из беспроводных датчиков;
распределение сертификата ключа в каждый аутентифицированный узел датчика и
установку парного ключа между одним или более беспроводными датчиками.
11. Система по п.1, в которой сервер настройки инициализирует один или более беспроводных датчиков с помощью уникального идентификатора и данных безопасности, случайно выбирает и распределяет парный ключ для базовой станции и одного или более беспроводных датчиков, и базовая станция выпускает сертификат ключа в невзломанный узел, который проверяет действительность его предварительно распределяемых ключей для ограниченного периода времени.
12. Система по п.11, в которой в течение временного интервала I1-1 базовая станция спорадически соединяется с одной или более другими базовыми станциями и согласует сертификат ключа, соответствующий временному интервалу I1+1, где 1 является положительным целым числом, где после временного интервала I1 каждая базовая станция отбрасывает сертификат ключа и ключ устанавливается между одним или более беспроводными датчиками.
13. Система по п.1, в которой один или более беспроводных датчиков инициализируются с помощью уникального идентификатора и данных безопасности, случайно выбирает и распределяет парный ключ в один или более беспроводных датчиков и дополнительно включает в себя:
сервер безопасности, который формирует секретное S, формирует М частей S1, S2,…,SM из секретного S, следуя пороговой схеме, и защищенно распределяет секретное S в базовую станцию и одну или более других базовых станций в сети, где М является положительным целым числом.
14. Система по п.13, в которой в течение временного интервала I1-1 одна или более базовых станций спорадически защищенно соединяются, создавая малые несвязанные группы Gg, G1, G2…g<Mi, при этом каждая базовая станция соединяется с, по меньшей мере, одной группой Gg, где g и 1 являются положительными целыми числами, и каждый член группы независимо вычисляет сертификат ключа для интервала I1+1 с помощью вычисления KCg 1+1=F(S,NGgl), где NGgl является элементом для данного случая, единственным в группе Gg для интервала I1+1, и затем каждый член группы отбрасывает S.
15. Система по п.14, в которой в течение временного интервала I1, по меньшей мере, одна базовая станция:
спорадически и кратковременно обращается к сети датчиков на теле,
аутентифицирует и устанавливает безопасную передачу данных с каждым невзломанным беспроводным датчиком, формирующим часть сети датчиков на теле, используя, по меньшей мере, один ключ, и
распределяет сертификат KC1+1 ключа для временного интервала I1+1 в каждый аутентифицированный узел датчика и устанавливает ключ между одним или более беспроводными датчиками.
16. Беспроводная сеть (2, 150), которая содержит:
сеть (22, 24, 26, 172, 174, 176), которая включает в себя один или более беспроводных узлов (6, 8, 10, 12, 14, 16, 18, 20, 156, 158, 160, 162, 164, 166,168,170);
сервер (4, 154) настройки, который конфигурирует один или более беспроводных узлов (6, 8, 10, 12, 14, 16, 18, 20, 156, 158, 160, 162, 164, 166, 168, 170) с материалом ключей до того, как один или более узлов (6, 8, 10, 12, 14, 16, 18, 20, 156, 158, 160, 162, 164, 166, 168, 170) применяются в беспроводной сети (2,150); и
базовую станцию (178, 180), которая распределяет сертификат ключа в один или более узлов (6, 8, 10, 12, 14, 16, 18, 20, 156, 158, 160, 162, 164, 166, 168, 170), ассоциированных с сетью (22, 24, 26, 172, 174, 176), из условия, чтобы два узла формировали единственный парный ключ, основываясь, по меньшей мере, частично на предварительно распределенном материале ключей и сертификате ключа, распределенном базовой станцией (178, 180).
17. Способ для идентификации первого датчика в системе мобильных датчиков, содержащий этапы, на которых:
строят конечную проективную плоскость (n2+n+1, n+1, 1) из множества n-1 взаимно ортогональных латинских квадратов порядка n, где n является простой степенью;
обнаруживают общую часть t-полиномиального множества из конечной проективной плоскости и
выводят точку вычисления части t-полиномиального множества вторым датчиком из идентификатора первого датчика.
18. Способ по п.17, в котором для n вхождений в ячейках ортогонального соквадрата 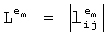 взаимно ортогональных латинских квадратов, для каждого элемента em, m=1, 2,…n, последовательно вычисляют элементы
взаимно ортогональных латинских квадратов, для каждого элемента em, m=1, 2,…n, последовательно вычисляют элементы 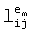 ортогональной матрицы.
ортогональной матрицы.
19. Способ по п.17, в котором конечные проективные плоскости конструируются с помощью построения матрицы М размещением n2 целых чисел от 1 до n2 в их обычном порядке от первой до n-й ее строки, где n является простой степенью.
20. Способ по п.17, дополнительно содержащий этапы, на которых:
выводят точку pv, в которой узел, и вычисляет свою часть Fk(рu,у) части t-полиномиального множества для формирования ключа Кuv;
конструируют конечную проективную плоскость из взаимно ортогонального латинского квадрата из условия, чтобы первые n2 элементов конечной проективной плоскости появлялись один раз в каждой группе n последовательных блоков В1+t, В2+t,…Вn+t, t=0,n,2n,3n…n×n; и
выводят счетчик sk появления из индекса i блока, 1≤i≤n2+n, и индекса k t-полиномиального множества, k≤n2, где k является положительным целым числом и n является простой степенью.
21. Способ по п.18, в котором индексы частей 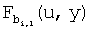 ,
, 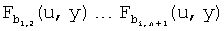 t-полиномиального множества, которые несет датчик u, являются соответствием один к одному элементам
t-полиномиального множества, которые несет датчик u, являются соответствием один к одному элементам 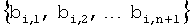 из В∈FPP, где 1≤i≤n2+n+1 и где n является простой степенью.
из В∈FPP, где 1≤i≤n2+n+1 и где n является простой степенью.
22. Способ по п.19, в котором аффинная плоскость AG(2,n) порядка n формируется из взаимно ортогональных латинских квадратов, в которых: (i) первые из n блоков Вi являются строками матрицы М, (ii) вторые n блоков являются столбцами матрицы М и (iii) оставшиеся n2-n блоков формируются с помощью последовательного наложения каждой из матриц 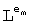 на М, и беря как блоки элементы матрицы М, которые соответствуют единственному элементу
на М, и беря как блоки элементы матрицы М, которые соответствуют единственному элементу 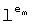 в каждой из матриц
в каждой из матриц 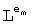 , где n является простой степенью.
, где n является простой степенью.
23. Способ для максимизации масштабируемости, устойчивости и производительности беспроводной системы, содержащий этапы, на которых:
вычисляют части t-полиномиального ассоциированного множества с узлами в беспроводной системе;
распределяют части t-полиномиального множества в вычисленные узлы в беспроводной системе и
предварительно распределяют ключ безопасности через сервер настройки в первый узел и второй узел, которые не взломаны, и передают данные по беспроводной системе.
| Станок для намотки катушек электрических аппаратов | 1984 |
|
SU1220501A1 |
| МАШИНА ДЛЯ ОБРАЗОВАНИЯ РАЗГРУЗОЧНОЙ ЩЕЛИ В ВЫБРОСООПАСНЫХ ПОРОДАХ | 1972 |
|
SU421765A1 |
| СПОСОБ АУТОТРАНСПЛАНТАЦИИ СЕЛЕЗЕНОЧНОЙ ТКАНИ | 1992 |
|
RU2067449C1 |
| JP 2004363883 A, 24.12.2004 | |||
| Пломба | 1930 |
|
SU36900A1 |
Авторы
Даты
2011-06-10—Публикация
2006-05-31—Подача