Изобретение относится к области геофизики, в частности к способам и устройствам определения ускорения силы тяжести (УСТ), и может быть использовано для выполнения морской гравиметрической съемки акватории континентального шельфа.
Известен способ определения УСТ на движущемся объекте, включающий измерения УСТ гравиметром, неподвижно установленным на объекте-носителе, определение широты места, пути и абсолютной скорости объекта навигационным средством, вычисление по полученным данным поправки за эффект Этвеша [1].
Также известен способ определения УСТ в море, включающей измерение УСТ гравиметром, неподвижно установленным на подвижном основании, определение широты места, пути объекта и абсолютной скорости гравиметра навигационным средством, вычисление по полученным данным поправки на эффект Этвеша и искомого УСТ [2].
Известное устройство для осуществления способа содержит функционально соединенные и расположенные на стабилизированной в горизонте платформе чувствительную систему, блок управления, навигационное средство, вычислитель и регистратор.
Недостаток известных способов и устройства заключаются в том, что они имеют недостаточно высокую точность определения УСТ на движущемся объекте при выполнении морской гравиметрической съемки. Это объясняется тем, что при их использовании имеют место существенная погрешность 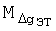 определения поправки на эффект Этвеша и 20 существенная погрешность
определения поправки на эффект Этвеша и 20 существенная погрешность 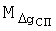 определения УСТ на движущемся объекте, обусловленная искажением гравитационного поля, которое возникает за счет значительной (от 3 до 6 мин) постоянной времени низкочастотного фильтра гравиметра, и скоростью изменения гравитационного поля, в котором движется объект. Погрешность
определения УСТ на движущемся объекте, обусловленная искажением гравитационного поля, которое возникает за счет значительной (от 3 до 6 мин) постоянной времени низкочастотного фильтра гравиметра, и скоростью изменения гравитационного поля, в котором движется объект. Погрешность 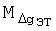 возникает при использовании известных способов и устройства из-за того, что поправку на эффект Этвеша вычисляют по формуле [1]
возникает при использовании известных способов и устройства из-за того, что поправку на эффект Этвеша вычисляют по формуле [1]
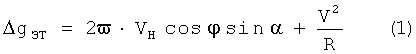
если Земля представлена в виде шара, или по формуле
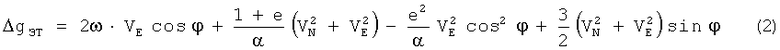
если Земля представляется в виде эллипсоида, где в формулах (1) и (2):
φ - широта места объекта,
α - путевой угол объекта,
R - радиус Земли,
а, е - большая полуось и эксцентриситет земного эллипсоида,
ω - угловая скорость вращения Земли,
VH - абсолютная скорость движения объекта-носителя гравиметра (абсолютная скорость движения чувствительной системы гравиметра),
VN,VE - соответственно северная и восточная составляющие VH.
При определении УСТ в море на движущемся объекте траектория чувствительной системы гравиметра ρ, как правило (в большинстве случаев), не совпадает с поверхностью моря или земного эллипсоида, так как поверхность моря или океана изменяется как во времени, так и в пространстве под воздействием тектонических, гидрометеорологических и других факторов. В результате этого радиус кривизны траектории движения гравиметра может принимать значения от А до ∞ и от -∞ до -А, а угол β между вектором абсолютной скорости гравиметра и плоскостью горизонта может принимать значения от 0 до β.
Погрешность поправки отвеса MΔgβ из-за не учета угла β можно вычислить по формуле
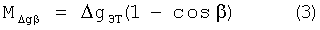
Например, когда β=5° и ΔgЭТ=100 мГал, то погрешность MΔgβ может достигать 8,7 мГал. Погрешность поправки Этвеша MΔgβ, обусловленную использованием в формулах (1) и (2) вместо радиуса кривизны траектории движения объекта ρ радиуса Земли или большую полуось и эксцентриситет земного эллипсоида, оценивают по формуле
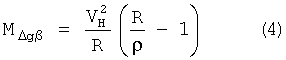
Например, когда VH=9 м/с, ρ=106 м при R=6378155 м, погрешность составляет 6,8 мГал. При этом необходимо учесть, что принятое для расчета погрешности значение ρ не является экстремальным для существующей динамики объекта носителя, движущегося по морской поверхности или удерживающего постоянную глубину погружения при съемке. Так, преобладающий период колебаний подводного объекта составляет 30-120 с, а амплитуда вертикальных перемещений - 2..3 м (Попов Е.И. Определение силы тяжести на подвижном основании. М.: Наука, 1967, с.178).
Отсюда следует, что значение ρ может достигать 3 км, что не учитывается в настоящее время при вычислении поправки Этвеша.
Погрешность М искажения гравиметрического поля, обусловленная наличием постоянной времени гравиметра и скорости движения носителя, можно оценить следующим образом. Известно (Аппаратура и методы экспериментальных исследований по гравиметрии. М.: Наука, 1965, с.103), что погрешность 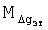 растет с увеличением постоянной времени гравиметра и скорости изменения гравитационного поля, в котором движется объект - носитель гравиметра, и ее можно вычислить по формуле
растет с увеличением постоянной времени гравиметра и скорости изменения гравитационного поля, в котором движется объект - носитель гравиметра, и ее можно вычислить по формуле
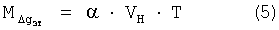
где α - скорость изменения гравитационного поля, в котором движется объект-носитель гравиметра,
VH - абсолютная скорость объекта-носителя гравиметра,
Т - постоянная времени низкочастотного фильтра гравиметра.
Например, когда α=0,8 мГал (средняя скорость изменения в средних широтах по меридиану УСТ (см. там же), VH=9,25 м/с (допустимая скорость движения объекта-носителя аппаратуры при проведении гравиметрической съемки в океане (Единые технические требования по Мировой гравиметрической съемке. Часть IV. Инструкция по морской гравиметрической съемке (ИГ-78). Л.: Изд. ГУНиО МО СССР, 1979, с.6, 7), Т=3 мин или Т=6 мин - значения постоянной времени у современных гравиметров [1], то погрешность 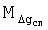 составит 1,3 мГал или 2,6 мГал соответственно.
составит 1,3 мГал или 2,6 мГал соответственно.
Однако допустимая погрешность определения УСТ в океане в соответствии с действующими нормативными документами по гравиметрической съемке (Единые технические требования по Мировой гравиметрической съемке. Часть IV. Инструкция по морской гравиметрической съемке (ИГ-78). Л.: Изд. ГУНиОМО СССР, 1979, с.6, 7) не должна превышать 1 мГал. Кроме того, для определения абсолютного значения УСТ необходимо использование опорных гравиметрических пунктов (ОГП), что значительно уменьшает эффективность съемки в связи с необходимостью периодического перемещения объекта-носителя в район ОГП.
Известен также способ [3] определения ускорения силы тяжести на движущемся объекте, включающий измерение ускорения (α0) неподвижным относительно объекта гравиметром (акселерометром по вертикали), определение широты места φ, путевого угла α, абсолютной скорости VH чувствительной системы гравиметра навигационным средством и вычисление по полученным данным искомого абсолютного значения ускорения силы тяжести (g0), в котором дополнительно определяют угол β между вектором абсолютной скорости чувствительной системы гравиметра и плоскостью горизонта, радиус кривизны ρ траектории движения чувствительной системы, а искомое абсолютное значение ускорения силы тяжести вычисляют по формуле
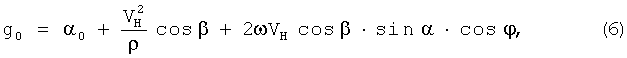
где ω - угловая скорость вращения Земли,
дополнительно измеряют вертикальную Vzi и горизонтальные составляющие Vxi, Vyi вектора абсолютной скорости чувствительной системы гравиметра в моменты времени ti и t(i+1) в точках траектории движения чувствительной системы, а значения β и ρ вычисляют по формулам
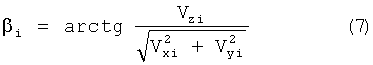
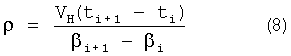
Измерение вертикальных и горизонтальных составляющих вектора абсолютной скорости чувствительной системы гравиметра и их последующий учет в результатах измерений по сравнению с известными способами [1, 2] повышает точность измерений в условиях спокойного моря. Однако недостаток данного способа выполнения гравиметрической съемки заключается в том, что он не обеспечивают необходимой точности определения УСТ на движущемся судне. Это объясняется тем, что при его использовании имеет место существенная погрешность измерения УСТ гравиметром, обусловленная наличием на движущемся судне ускорений, воздействующих на чувствительную систему гравиметра, возникающих в результате качки, пульсаций скорости движения и рыскания судна, которые имеют место в условиях волнения моря, изменчивости скорости и направления течений воды и ветра. Данная погрешность может достигать 5-7 мГал (Ситроев П.А. Гравиметрические исследования в Тихом океане // Морские гравиметрические исследования. М., 1982, с.70).
Известен также способ определения силы тяжести на морском опорном пункте [4], включающий измерения силы тяжести морскими гравиметрами на опорном пункте при прохождении его судном, движущимся последовательно по нескольким прямолинейным галсам, проложенным через опорный пункт, в котором для повышения точности определения силы тяжести, измерения производят гравиметрами на прямых и обратных курсах по n-парам галсов с углом смещения 40-50 градусов в пределах опорной зоны с радиусом 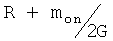 , где mon - погрешность значения силы тяжести на опорном пункте, G - градиент силы тяжести в пределах опорной зоны, вычисляют опорное значение силы тяжести для гравиметров как среднеарифметическое из значений по n-парным прохождениям в точках, максимально приближенных к опорному пункту. Ввиду того что измерения производят двумя противоположными ориентированными гравиметрами, а опорное значение силы тяжести и осредненный нуль-пункт вычисляют для каждой пары приборов, можно повысить точность определения силы тяжести. Однако технический результат достигается только в пределах рабочей зоны в точках, максимально приближенных к опорному пункту.
, где mon - погрешность значения силы тяжести на опорном пункте, G - градиент силы тяжести в пределах опорной зоны, вычисляют опорное значение силы тяжести для гравиметров как среднеарифметическое из значений по n-парным прохождениям в точках, максимально приближенных к опорному пункту. Ввиду того что измерения производят двумя противоположными ориентированными гравиметрами, а опорное значение силы тяжести и осредненный нуль-пункт вычисляют для каждой пары приборов, можно повысить точность определения силы тяжести. Однако технический результат достигается только в пределах рабочей зоны в точках, максимально приближенных к опорному пункту.
Общим недостатком известных способов гравиметрической съемки и обработки ее результатов является то, что они не обеспечивают требуемое качество гравиметрической съемки акватории. Это объясняется тем, что при их использовании не выявляются локальные аномалии гравитационного поля Земли (ГПЗ), расположенные в полосе между смежными галсами, обусловленные поднятием (рельефом дна) между смежными галсами, а следовательно, не представляется возможным определить искомые значения УСТ в полосе между смежными галсами по значениям только лишь УСТ, вычисленным вдоль смежных галсов, так как отсутствует дополнительная информация о глубинах в полосе между смежными галсами.
Известно, что аномалии УСТ, обусловленные локальными поднятиями дна акватории, достигают 20-40 мГал при периодах порядка 20-40 км (см. Баграмянц В.О., Бережная Л.Т., Тележен М.А. О результатах гравиметрических исследований в Индийском океане в 7-м рейсе НИС "Дмитрий Менделеев" // Морские гравиметрические исследования. М., 1982, с.123).
При выполнении гравиметрической съемки с междугалсовым расстоянием порядка 30 км в соответствии с требованием нормативного документа по морской гравиметрической съемки указанные локальные аномалии ГПЗ, расположенные в полосе между смежными галсами, не выявляются.
Кроме того, качество площадной морской гравиметрической съемки оценивается средней квадратичной погрешностью интерполяции (см. например: Сорокин А.И. Теоретические основы гидрографических исследований. - Л., ГУНиО МО, 1972. - 196 с.). Однако эта величина не в полной мере характеризует точность съемки. Чтобы решить ряд прикладных задач, таких как оценка качества полигона для географической навигации, оценка точности определения уклонения отвесной линии и другие задачи, необходимо знать ковариацию погрешностей интерполяции значений ускорения УСТ между съемочными галсами.
Задачей настоящего технического является повышение достоверности при измерениях УСТ в море.
Поставленная задача решается за счет того, что в способе определения ускорения силы тяжести на движущемся объекте, включающий измерение ускорения (α0) неподвижным относительно объекта гравиметром (акселерометром по вертикали), определение широты места φ, путевого угла α, абсолютной скорости VH чувствительной системы гравиметра навигационным средством и вычисление по полученным данным искомого абсолютного значения ускорения силы тяжести (g0), в котором дополнительно определяют угол β между вектором абсолютной скорости чувствительной системы гравиметра и плоскостью горизонта, радиус кривизны ρ траектории движения чувствительной системы, а искомое абсолютное значение ускорения силы тяжести вычисляют по формуле
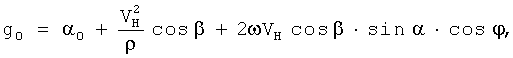
где ω - угловая скорость вращения Земли,
дополнительно измеряют вертикальную Vzi и горизонтальные составляющие Vxi, Vyi вектора абсолютной скорости чувствительной системы гравиметра в моменты времени ti и t(i+1) точках траектории движения чувствительной системы, а значения β и ρ вычисляют по формулам
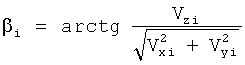
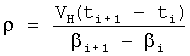 ,
,
в котором измеренные значения УСТ на двух галсах, расстояние между которыми равно L, определяют как разность между истинными значениями на двух галсах и случайными погрешностями измерения УСТ на этих же двух галсах, рассчитывают интерполированные значения УСТ на этих же галсах в точках, расположенных на двух перпендикулярных к съемочным галсам и удаленных от первого галса на расстояние l1 и l2 соответственно путем линейной интерполяции, определяют погрешности интерполированных значений УСТ, вычисляют истинные значения УСТ в точках, удаленных от первого галса на расстояние l1 и l2 соответственно, определяют корреляционную функцию УСТ путем обработки гравиметрических измерений на контрольных галсах, определяют ковариацию погрешностей измерения УСТ на галсе и между галсами, при этом ковариацию погрешностей измерения УСТ на галсе определяют путем обработки результатов гравиметрических измерений, полученных на контрольных галсах, при этом определяют пространственное положение вектора гравитационного поля, по отношению составляющих которого определяют наклонение вектора магнитного поля.
Для достижения требуемой точности создания эталонного гравитационного поля на акватории предлагается выполнение гравиметрической съемки на 1-2 профилях (контрольных галсах) с выполнением избыточных измерений УСТ в пунктах, расположенных вдоль эталонного галса. Данные избыточные измерения получают путем многократного прохождения съемочным судном вдоль эталонного галса.
По полученным результатам измерений с помощью уравнивания избыточных измерений можно не только получить вероятнейшие значения УСТ, но и определять технические параметры гравиметра, цену деления, величины вышеуказанных погрешностей, которые характеризуются как величины постоянной (систематической) и регулярной (медленно меняющейся) погрешностей.
Кроме того, определение пространственного положения вектора гравитационного поля, позволяет по отношению составляющих определить наклонение вектора магнитного поля, что при отдельных видах исследований позволит исключить необходимость использования магнитометра.
Сущность заявляемого технического решения поясняется чертежами.
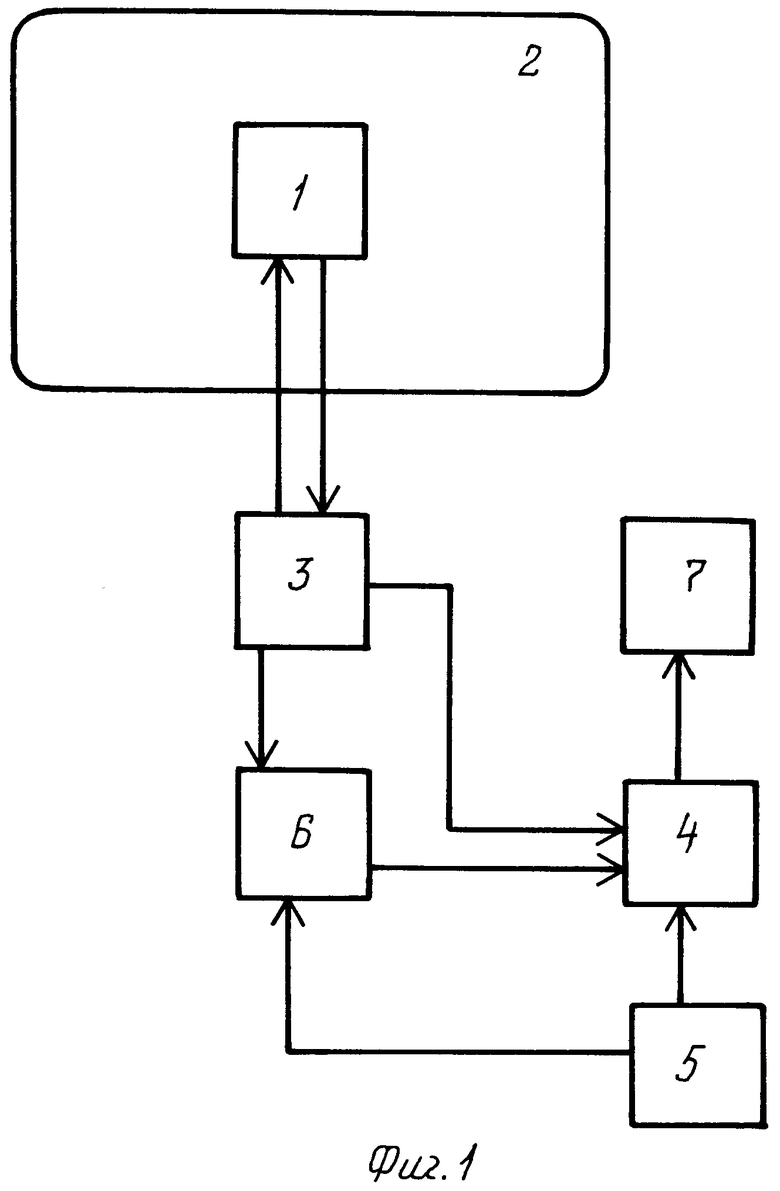
Фиг.1. Структурная схема устройства для реализации заявляемого способа.
Устройство содержит чувствительную систему гравиметра 1, установленную на стабилизированной платформе 2, выход которой соединен через блок управления 3 с входом вычислителя 4, навигационное модуль 5, предназначенный для определения широты места, путевого угла и вычисления абсолютной скорости чувствительной системы гравиметра 1 для определения угла β между вектором абсолютной скорости чувствительной системы 1 и платформой 2, а также радиуса кривизны ρ траектории движения чувствительной системы 1, выход которой через блок управления 3 подключен к входу вычислителя 4, выход которого подключен к регистратору 7, блок измерения абсолютной скорости 6.
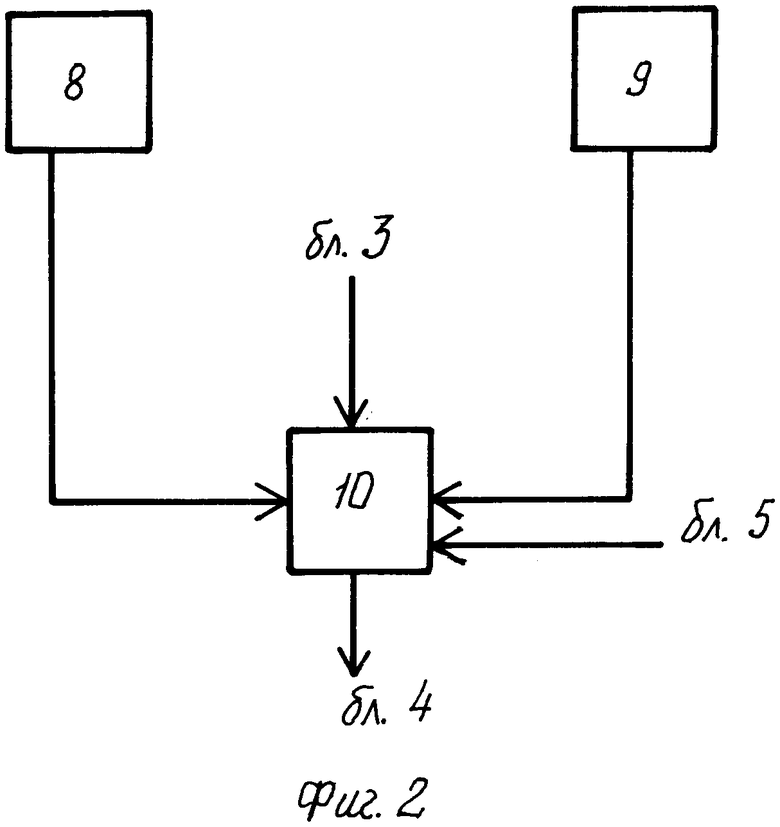
Фиг.2. Блок измерения абсолютной скорости 6 содержит трехкомпонентный измеритель абсолютной скорости 8, в качестве которого использован штатный судовой гидроакустический лаг, измеряющий скорость и угол дрейфа судна относительно морского дна по четырем лучам, измеритель времени 9 и вычислитель 10, реализующий формульные зависимости (7) и (8), к входу которого подключены выходы трехкомпонентного измерителя абсолютной скорости 8 и измерителя времени 9.
Фиг.3. Схема реализации способа, которая включает стабилизированную платформу 2, чувствительную систему 1, ω - угловая скорость вращения Земли, α - путевой угол судна, φ - широта места, ρ - траектория чувствительной системы гравиметра, Vн - северная составляющая абсолютной скорости движения судна, Ve - восточная составляющая абсолютной скорости движения судна, β - угол между вектором абсолютной скорости чувствительной системы 1 гравиметра и плоскостью горизонта, Vн - абсолютная скорость судна, Vx, Vy - продольная и поперечная составляющие абсолютной скорости соответственно.
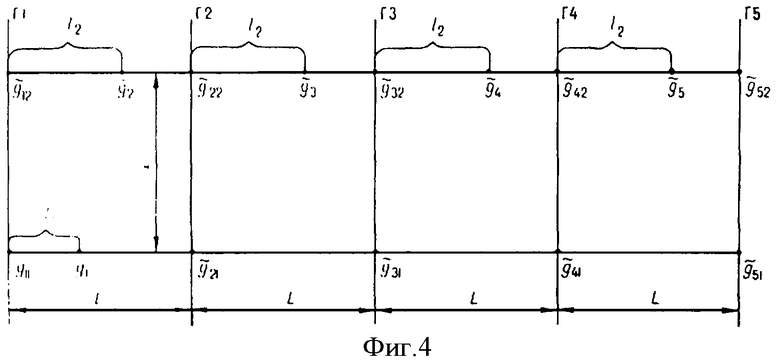
Фиг.4. Схема расположения галсов для определения УСТ.
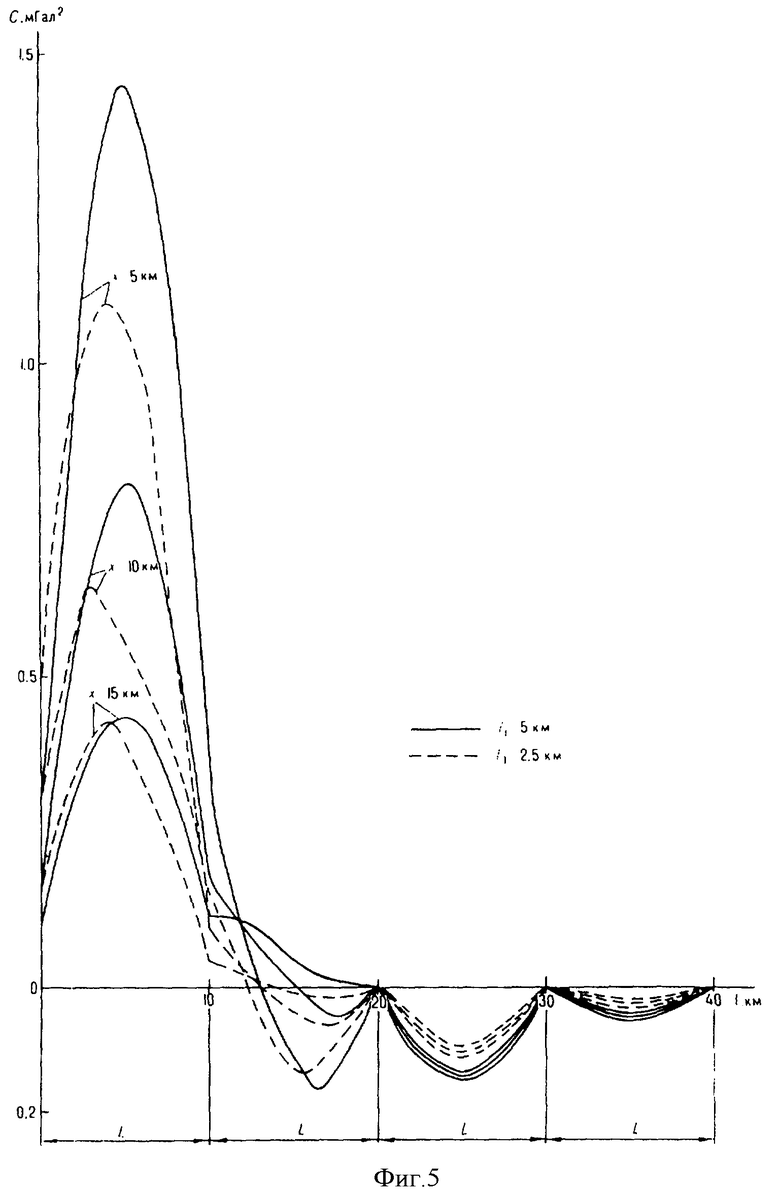
Фиг.5. График изменения ковариации на галсах.
Гравиметр 1 представляет собой гравиметр, построенный по асимметричной схеме, что позволяет исключить кросс-каплинг эффект, возникающий при волнении моря. Программное обеспечение технической реализации заявляемого способа позволяет использовать как морской гравиметр типа BGM 3, представляющего собой конструкцию принудительно уравновешенного акселерометра, в котором рабочая масса поддерживается в нулевом положении с помощью механизма обратной связи (струнный гравиметр), так и трехтензорный градиометр типа 3 - DFTG.
Стабилизированная платформа 2 представляет собой двухосную гироплатформу с коррекцией от акселерометров, что обеспечивает возможность выполнения измерений при возмущающих ускорениях до 150-200 Гал, с динамической погрешностью при небольших возмущающих ускорениях менее 1 мГал. При этом погрешность стабилизации не превышает 1 минуту, углы прокачки составляют 30-40 градусов, что обеспечивает возможность выполнения измерений при возмущающих ускорениях до 150-200 Гал.
Вычислитель 4 включает процессор Pentium 166 МГц, ОЗУ на 32 Мбайт, плату SVGA с памятью 1 Мбайт, дополнительную плату с двумя последовательными портами с FIFO памятью (UAR116550 - совместимая).
Блок управления 3 состоит из ПЗУ микрокоманд, ПЗУ управления выбором адреса, БИС микропрограммного управления, двух микропроцессоров, ПЗУ, ОЗУ, схемы формирования переносов, трех буферных регистров и магистралей адреса, микрокоманд, приема информации от судовых навигационных средств и предназначен для выработки и трансляции команд и информационных файлов с принимаемой от внешних источников информации, а также информации, находящейся в ПЗУ.
Определение УСТ на движущемся судне выполняется следующим образом.
При движении объекта-носителя заданным курсом по управляющим электрическим сигналам, формирующимся в блоке управления 3, чувствительная система 2 вырабатывает электрические сигналы, пропорциональные УСТ без учета поправки Этвеша, которые поступают в вычислитель 4.
От навигационного средства 5 сигналы, пропорциональные абсолютной скорости Vн пути а и широты места объекта-носителя, поступают в блок 6 измерения абсолютной скорости и вычислитель 4.
Блок 6 измерения абсолютной скорости вырабатывает электрические сигналы, пропорциональные углу β между вектором абсолютной скорости чувствительной системы 1 и плоскостью горизонта, а также радиусу кривизны ρ траектории ее движения, которые в виде пропорциональных им электрических сигналов поступают в вычислитель 4. По управляющим электрическим сигналам, формулирующимся в блоке управления 3, от трехкомпонентного измерителя абсолютной скорости 8 и измерителя времени 9 электрические сигналы, пропорциональные соответственно текущим значениям вертикальной Vz и горизонтальных Vx, Vy составляющих вектора абсолютной скорости движения чувствительной системы 1 и моментам времени ti их измерений в i-x точках траектории движения объекта (фиг.3), поступают в вычислитель 10, где по формулам (7) и (8) вычисляются значения ρ и β, которые поступают в вычислитель 4.
Сущность заявляемого способа заключается в следующем.
На галсах Г1 и Г2 (фиг.4), расстояние между которыми равно L, измеряют значения
УСТ 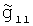 ,
, 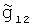 ,
, 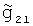 ,
, 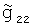 , расстояние между которыми по галсу равно х.
, расстояние между которыми по галсу равно х.
При этом измеренные значения УСТ выражаются зависимостями 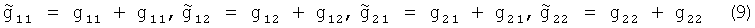 , где
, где 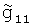 ,
, 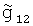 ,
, 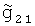 ,
, 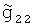 - истинные значения УСТ на галсах Г1 и Г2 соответственно, g11, g12, g21, g22 - случайные погрешности измерения УСТ на галсах Г1 и Г2 соответственно.
- истинные значения УСТ на галсах Г1 и Г2 соответственно, g11, g12, g21, g22 - случайные погрешности измерения УСТ на галсах Г1 и Г2 соответственно.
Путем линейной интерполяции между измеренными значениями УСТ на галсах Г1 и Г2 рассчитывают два интерполированных значения УСТ 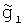 и
и 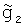 в точках, расположенных на двух перпендикулярных к съемочным галсам и удаленных от галса Г1 на расстояние 11 и 12 соответственно. С учетом выражения (9) погрешности g1 и g2 интерполированных значений УСТ будут равны:
в точках, расположенных на двух перпендикулярных к съемочным галсам и удаленных от галса Г1 на расстояние 11 и 12 соответственно. С учетом выражения (9) погрешности g1 и g2 интерполированных значений УСТ будут равны:
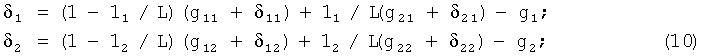
где g1 и g2 - истинные значения УТС в точках, удаленных от галса Г1 на расстояние 11 и 12 соответственно.
Ковариация погрешностей интерполяции равна (см., например: Мориц Г. Современная физическая геодезия. - Л.: Недра, 1983. - 392 с.):
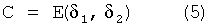 , где Е - оператор определения математического ожидания.
, где Е - оператор определения математического ожидания.
Подставив формулы (4) в равенство (5), после преобразований получим
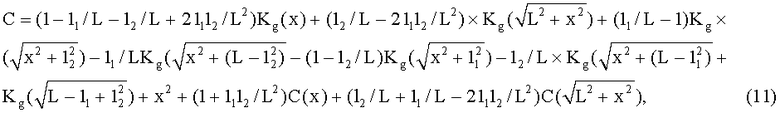
где Kg(S) - корреляционная функция УСТ при аргументе S, который принимает значения x,
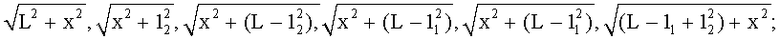 ;
;
C(x) - ковариация погрешностей измерения УСТ на галсе и между галсами при аргументе X, который принимает значения x, √L2+x2.
В варианте, когда второе значение УСТ, равное 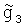 , получено путем интерполяции между значениями УСТ g11 g21, тогда ковариация погрешностей интерполяции определяется по формуле
, получено путем интерполяции между значениями УСТ g11 g21, тогда ковариация погрешностей интерполяции определяется по формуле
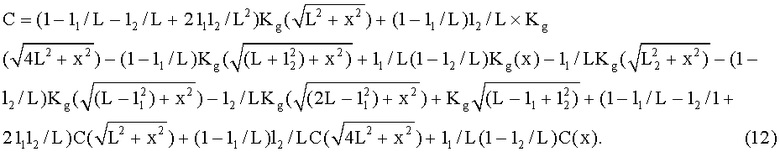
В формуле (12) величина 12 является расстоянием между точками со значениями УСТ 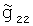 и
и 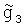 . Аналогичным образом получают формулу ковариации при использовании в качестве второго значения УСТ интерполированных значений
. Аналогичным образом получают формулу ковариации при использовании в качестве второго значения УСТ интерполированных значений 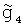 и
и 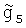 в точках, удаленных от галсов Г3 и Г4 соответственно на расстояние 12.
в точках, удаленных от галсов Г3 и Г4 соответственно на расстояние 12.
Для значения 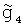 :
:
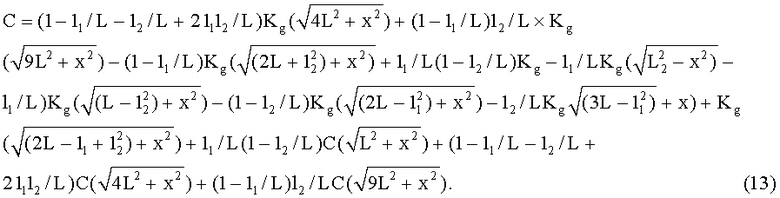
Для значения 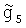 :
:
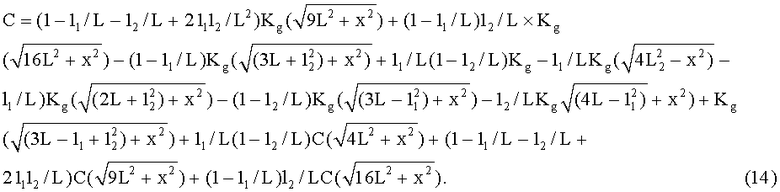
Ковариационную функцию УСТ получают при обработке гравиметрических измерений на контрольных галсах в соответствии с зависимостью (см., например: Iordan S.K. Effects of geodesic uncertainties on a damped inertial navigation system. IEEE Transactions on aerospace and electronic system. - 1973. - V. AES - 9, №5). Для Марковского процесса второго порядка корреляционная функция УСТ Kg(S) выражается зависимостью
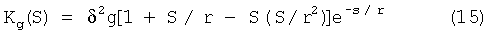 , где δg - стандарт УСТ, r - радиус корреляции.
, где δg - стандарт УСТ, r - радиус корреляции.
Ковариацию погрешностей измерения УСТ на галсе С(х) получают при обработке результатов гравиметрических измерений на контрольных галсах определяют в соответствии с зависимостью:
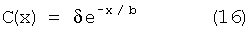 , где δ - средняя квадратическая погрешность измерения УСТ на галсе, b - коэффициент затухания.
, где δ - средняя квадратическая погрешность измерения УСТ на галсе, b - коэффициент затухания.
При апробации заявляемого способа и устройства для его реализации было получено несколько вариантов реализации по определению погрешностей интерполяции в зависимости от расположения точек 11 и 12 между галсами и расстояния Х между двумя перпендикулярными съемочными галсами. Расстояния Х имели значения 5, 10 и 15 км, расстояние 11 соответственно 2,5 и 5 км, радиус корреляции r=20 км, расстояние L=10 км, средняя квадратическая погрешность измерения УСТ на галсе - 1 км, стандарт УСТ - 10 км. Полученные результаты приведены на фиг.4 в виде зависимости ковариации погрешностей интерполяции С от расстояния l=(n-1)L+l2, где n - номер полосы между съемочными галсами. На фиг.5 показан характер изменения ковариации. Модуль экстремальных значений ковариации уменьшается при увеличении номера полосы. Наибольшее значение относится к первой полосе между галсами Г1 и Г2. В первой полосе ковариация положительная, во второй - принимает как положительные, так и отрицательные значения. В третьей и четвертой полосах ковариация имеет только отрицательные значения. Ковариация равна нулю на галсах Г3, Г4 и Г5. При увеличении расстояния Х модуль ковариации уменьшается.
По измеренным значениям характеристик УСТ и погрешности ее измерения на галсах в вычислителе 10 по зависимостям (11)-(16) определяются значения ковариации погрешностей интерполяции между галсами, которые учитываются при окончательном определение УСТ, что позволяет решить такие практические задачи, как оценка качества полигона для геофизической навигации и оценка точности уклонения отвесной линии.
Как известно (см., например: Гравиразведка. / Справочник геофизика. Под ред. Е.А.Мудрецовой, К.Е.Веселова. М., Недра, 1990, - 606 с.; Магниторазведка. / Справочник геофизика. Под ред. В.Е.Никитского, Ю.С.Глебовского. М., Недра, 1990 - 470 с.), гравитационное поле и аномальное магнитное поле Земли являются потенциальными и имеют следующие общие свойства:
- описываются уравнением Пуассона;
- связь между магнитными и гравитационными потенциалами для однородных масс описываются формулой Пуассона;
- магнитный и гравитационный потенциалы при выполнении измерений вне источников полей описываются уравнением Лапласа;
- аналитические зависимости моделей однородных источников в форме шара или кругового цилиндра по выбранным для вычисления производной ускорения силы тяжести и составляющих геомагнитного поля совпадают с точностью до постоянных коэффициентов.
Связь параметров магнитного и гравитационных полей подтверждена на практике (см., например: В.Н.Луговенко, А.В.Пчелкин, И.В.Луговенко. Сравнение аномальных геофизических полей и их интерпретация. / Геомагнитизм и аэрополия, 1999, т.39, №2, с.137-140) на основе сравнения их автокорреляционных функций (табл.1), где:
U, V - скалярный потенциал магнитного и гравитационного полей;
H, Z - горизонтальная и вертикальная составляющие вектора магнитного поля;
G - постоянная тяготения;
X, ξ - положение точки в плоскостной системе координат;
M, m - магнитная и гравитационная масса;
Р(ρ) - распределение плотности тяготеющих масс;
λ - эффективная масса единицы длины;
J, Jx, Jy, Jz - напряженность (интенсивность) намагничения и ее составляющие;
Xs, Ys, Zs - результаты измерения магнитного поля на судне.
Выражение из четвертой строки табл.1 равно: 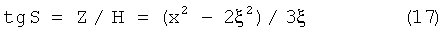 .
.
Для определения пространственного вектора гравитационного поля введен аналогичный угол гравитационного наклонения 9. Тогда в соответствии с выражениями (строки 4 и 5 табл.1) следует, что для произвольного шара (цилиндра) аналитическая зависимость магнитного и гравитационного наклонения в одной системе координат совпадает, т.е.
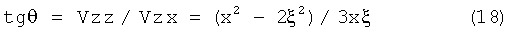 .
.
Из формул (17) и (18) следует, что tgθ=tgJ.
Следовательно, по результатам измерений наклонения вектора магнитного поля может быть определено отношение составляющих гравитационного поля Vzz и Vzx.
Общность аналитических зависимостей описания геомагнитного и гравитационного полей с точностью до постоянных наблюдается для шаровидных и цилиндрических объектов. Для объектов сложной формы совпадение аналитических зависимостей не наблюдается. Однако практические измерения как магнитного, так и гравитационного полей показывают, что модели шара и цилиндра при расстояниях, удаленных от источника (примерно на расстояние, превышающее размер источника), применимы и к реальным источникам с незначительной погрешностью.
Решая обратную задачу, определяют пространственное положение вектора гравитационного поля, по отношению составляющих которого определяют наклонение вектора магнитного поля.
Реализация заявляемого способа технической трудности не представляет, так как реализуется посредством штатных судовых средств измерения.
Источники информации
1. Юзефич А.П., Огородова Л.В. Гравиметрия. - М.: Недра, с.160-164.
2. Авторское свидетельство SU №1419347.
3. Патент RU №1760875.
4. Патент RU №2324207.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ МОРСКОЙ ГРАВИМЕТРИЧЕСКОЙ СЪЕМКИ | 2010 |
|
RU2440592C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СТАЦИОНАРНОГО ГЕОМАГНИТНОГО ПОЛЯ ПРИ ПРОВЕДЕНИИ МОРСКОЙ МАГНИТНОЙ СЪЕМКИ | 2010 |
|
RU2433427C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СТАЦИОНАРНОГО ГЕОМАГНИТНОГО ПОЛЯ ПРИ ПРОВЕДЕНИИ МОРСКОЙ МАГНИТНОЙ СЪЕМКИ | 2010 |
|
RU2433429C2 |
| СПОСОБ ГРАВИМЕТРИЧЕСКОЙ СЪЕМКИ АКВАТОРИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2575316C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ НА ДВИЖУЩЕМСЯ ОБЪЕКТЕ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2550161C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ НА ДВИЖУЩЕМСЯ ОБЪЕКТЕ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2006 |
|
RU2324207C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ НА ДВИЖУЩЕМСЯ ОБЪЕКТЕ И УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ НА ДВИЖУЩЕМСЯ ОБЪЕКТЕ | 2010 |
|
RU2479859C2 |
| СПОСОБ ГИДРОМЕТЕОРОЛОГОАКУСТИЧЕСКОГО НАБЛЮДЕНИЯ ЗА АКВАТОРИЕЙ МОРСКОГО ПОЛИГОНА | 2005 |
|
RU2304794C2 |
| Способ измерения гравитационного поля Земли | 2020 |
|
RU2737034C1 |
| СПОСОБ СЪЕМКИ РЕЛЬЕФА ДНА АКВАТОРИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2010 |
|
RU2434246C1 |
Изобретение относится к области геофизики, в частности к способам и устройствам определения ускорения силы тяжести (УСТ), и может быть использовано для выполнения морской гравиметрической съемки акватории континентального шельфа. По измеренным значениям характеристик УСТ и погрешности ее измерения на галсах определяют значения ковариации погрешностей интерполяции между галсами, которые учитывают при окончательном определении УСТ. Благодаря этому могут быть решены такие практические задачи, как оценка качества полигона для геофизической навигации и оценка точности уклонения отвесной линии. При этом определяют пространственное положение вектора гравитационного поля, по отношению составляющих которого определяют наклонение вектора магнитного поля. 1 табл., 5 ил.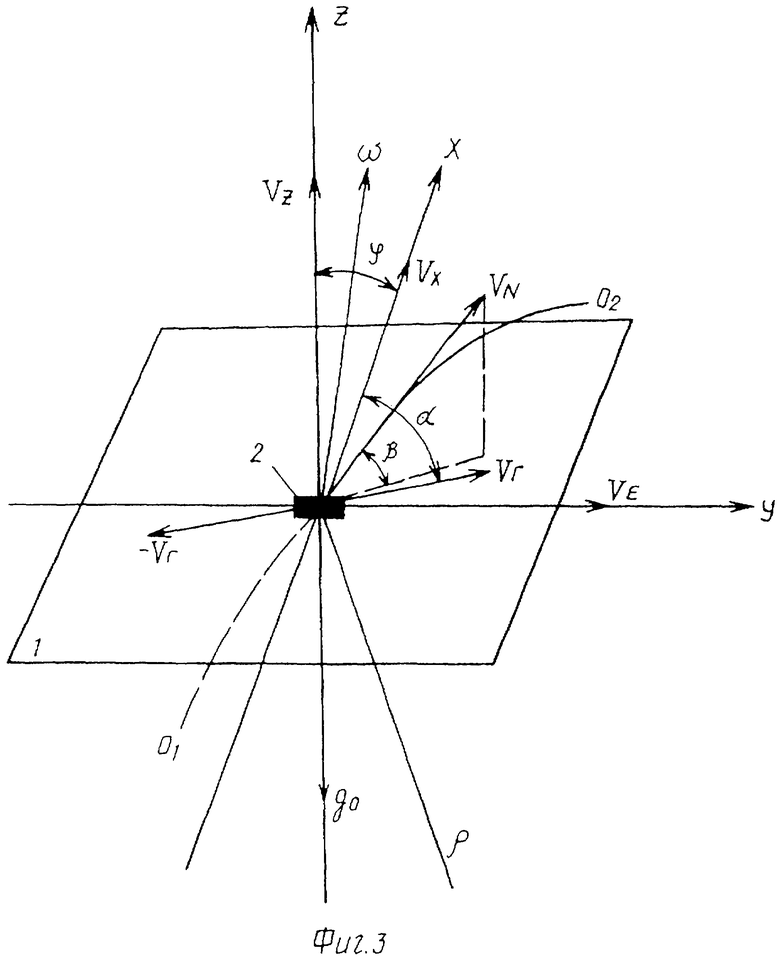
Способ определения ускорения силы тяжести (УСТ) на движущемся объекте, включающий измерение ускорения (α0) неподвижным относительно объекта гравиметром (акселерометром по вертикали), определение широты места φ, путевого угла α, абсолютной скорости VH чувствительной системы гравиметра навигационным средством и вычисление по полученным данным искомого абсолютного значения ускорения силы тяжести (g0), в котором дополнительно определяют угол β между вектором абсолютной скорости чувствительной системы гравиметра и плоскостью горизонта, радиус кривизны ρ траектории движения чувствительной системы, а искомое абсолютное значение ускорения силы тяжести вычисляют по формуле
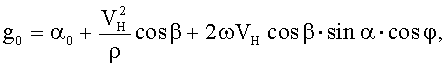
где ω - угловая скорость вращения Земли,
дополнительно измеряют вертикальную Vzi и горизонтальные составляющие Vxi, Vyi, вектора абсолютной скорости чувствительной системы гравиметра в моменты времени ti и t(i+1) в точках траектории движения чувствительной системы, а значения β и ρ вычисляют по формулам
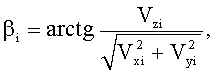
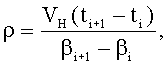
отличающийся тем, что измеренные значения УСТ на двух галсах, расстояние между которыми равно L, определяют как разность между истинными значениями на двух галсах и случайными погрешностями измерения УСТ на этих же двух галсах, рассчитывают интерполированные значения УСТ на этих же галсах в точках, расположенных на двух перпендикулярных к съемочным галсам и удаленных от первого галса на расстояние l1 и l2 соответственно путем линейной интерполяции, определяют погрешности интерполированных значений УСТ, вычисляют истинные значения УСТ в точках, удаленных от первого галса на расстояние l1 и l2 соответственно, определяют корреляционную функцию УСТ путем обработки гравиметрических измерений на контрольных галсах, определяют ковариацию погрешностей измерения УСТ на галсе и между галсами, при этом ковариацию погрешностей измерения УСТ на галсе определяют путем обработки результатов гравиметрических измерений, полученных на контрольных галсах, при этом определяют пространственное положение вектора гравитационного поля, по отношению составляющих которого определяют наклонение вектора магнитного поля.
| СПОСОБ ОПРЕДЕЛЕНИЯ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ НА ДВИЖУЩЕМСЯ ОБЪЕКТЕ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2006 |
|
RU2324207C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СИЛЫ ТЯЖЕСТИ НА МОРСКОМ ОПОРНОМ ПУНКТЕ | 1990 |
|
RU1760875C |
| Юзефич А.П., Огородова Л.В., Гравиметрия | |||
| - М., 1980, с.160-164 | |||
| УСТРОЙСТВО И СПОСОБ ДЛЯ ИЗМЕРЕНИЯ ГРАВИТАЦИИ | 1995 |
|
RU2144686C1 |
| ВЕРТОЛЕТНЫЙ ГРАВИМЕТРИЧЕСКИЙ КОМПЛЕКС | 1995 |
|
RU2128851C1 |
| ГРАВИИЗМЕРИТЕЛЬНЫЙ КОМПЛЕКС | 1998 |
|
RU2150132C1 |
| ВИНТОВОЙ НАГНЕТАТЕЛЬНЫЙ ВЕНТИЛЯТОР | 1925 |
|
SU4015A1 |
| НАВИГАЦИОННЫЙ КОМПЛЕКС | 1990 |
|
RU2016383C1 |
| US 3803916 А, 16.04.1974 | |||
| US 4550601 А, 05.11.1985. | |||
Авторы
Даты
2011-08-10—Публикация
2010-01-28—Подача