ГРАВИИЗМЕРИТЕЛЬНЫЙ КОМПЛЕКС Российский патент 2000 года по МПК G01V7/16 

Изобретение относится к приборам для гравиинерциальных измерений.

Известно устройство для измерения на подвижном основании ускорения силы тяжести гравиметром, установленным на гидростабилизированной платформе (1).

Недостатком этого устройства является низкая точность гравиметра из-за влияния ускорения движения объекта (9,81 мГл при j - 20 см/с²).

Наиболее близким к изобретению является аэрогравиметрический комплекс (2). Недостатком такого устройства является необходимость включения в комплекс, помимо гравиметра, инерциальной навигационной системы и спутниковой системы навигации, несколько измерителей высоты и вертикальной скорости полета высокой точности. При этом, однако, точность гравиинерциальных измерений не превышает 0,5 - 1мГл на подвижном основании, т.к. содержит достаточно большую методическую ошибку измерения.

Техническая задача, решаемая изобретением, заключается в повышении точности гравиинерциальных измерений на подвижном основании.

Указанная задача решается за счет того, что в известное устройство, содержащее гравиметр, инерциальную навигационную систему (ИНС) или только ИНС, спутниковую систему навигации, высотомер и вычислитель, работающих в диалоговом режиме, дополнительно введены вторая инерциальная навигационная система, удаленная от первой инерциальной системы вдоль продольной оси вертолета, ИНС могут содержать гравиметры, а вычислитель может содержать бинарный фильтр для оценки гравиинерциальных измерений и может быть подсоединен к блоку точного висения вертолета, радиомодемному блоку и иметь накопитель информации. Радиомодемный блок служит для передачи гравиинерциальных измерений в наземный комплекс создания гравиметрических карт.

Кроме того, вычислитель может содержать фильтр Калмана для оценки ошибок первой и второй инерциальных систем с использованием спутниковой системы навигации и одновременно бинарный фильтр оценки гравиинерциальных измерений.

На чертеже схематически показан предлагаемый гравиметрический комплекс.

Комплекс содержит две разобщенные инерциальные навигационные системы 1 и 2, каждая из которых может иметь гравиметры 3 и 4 и следящие системы 5 и 6 для обработки гравиметров в направлении вертикали.

На первый 7 и второй 8 входы вычислителя 9 подаются с выходов гравиметров 3 и 4 или ИНС. Одновременно, соответственно, выходы с первой и второй инерциальных систем по скорости 10 и 11, а также по вертикали 12 и 13 подаются на входы сумматоров 14 и 15, с выхода которых разностные сигналы по скорости 16 и по вертикали 17 поступают на входы 18 и 19 вычислителя 9, на 20 и 21 входы которого поступают сигналы с выхода системы спутниковой навигации 23 и высотомера 24. В вычислителе 9 функционируют фильтры 25 Калмана и бинарный фильтр 26. С выхода фильтра 25 Калмана, соответственно, оценки ошибок по скорости 27 и 28 и вертикали 29 и 30 поступают на первую ИНС 1 и вторую ИНС 2 для компенсации ошибок. С выходов бинарного фильтра 26 в блоке 9 оценки гравиинерциальных измерений 31 и 32 подаются на входы блока системы стабилизации висения вертолета 33, а также на радиомодемный блок 34 для передачи их на наземный комплекс создания гравиметрических карт 35.

Гравиизмерительный комплекс работает следующим образом.

После включения обычного режима выставки инерциальных навигационных систем 1 и 2, с помощью следящих систем 5 и 6, гравиметры 3 и 4 устанавливаются по вертикали в направлении ускорения силы тяжести, при этом физически гравиметры 3 и 4 находятся на удалении L друг от друга. Подключение гравиметров 3 и 4 к входам 7 и 8 вычислителя 9 вызывает гравитационный режим работы фильтров Калмана 25, обеспечивающий, соответственно, демпфирование ошибок первой 1 и второй 2 ИНС по скорости и вертикали. Одновременно подключаются спутниковая система навигации 23 и высотомер 24 к входам 20 и 21 вычислителя 9, которые вызывают координатный режим работы фильтра Калмана 25 для прецизиционной оценки и коррекции ошибки инерциальных навигационных систем 1 и 2 по скорости, вертикали и высоте полета, а также оценивания и компенсаций их инструментальных погрешностей (акселерометров и гироскопов). На этом режим прецизионной (точной) коррекции инерциальных навигационных систем 1 и 2 заканчивается, вступает в работу бинарный фильтр 26, имеющий следующие два режимы работы: гравитационный и гравиинерциальный. В результате достигается поставленная цель - повышение точности гравиинерциальных измерений на подвижном основании.

В самом деле, для гравитационного режима бинарного фильтра 26 уравнения гравиметров 3 и 4 можем записать в виде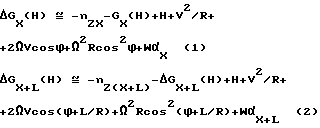

где W - горизонтальное ускорение вертолета;
V - скорость вертолета относительно Земли;
Ω - условная скорость вращения Земли;
H - вертикальное ускорение вертолета;
ϕ - широта места;
R - модуль радиуса вектора центра масс вертолета;
α_X, α_X+L - ошибки вертикали, соответственно в точках X и X+L;
L - расстояние между гравиметрами 3 и 4;
X - место расположения гравиметра 3 относительно центра масс вертолета (x=0);
n_Z(X, n_Z(X+L) - показания гравиметров, соответственно, в точках X и X+L;
ΔG_X(H), ΔG_X+L(H) - аномальная часть производной гравитационного потенциала, соответственно, для центра масс вертолета и на удалении L от центра масс вертолета;
G_x(H) - нормальная первой часть производной гравитационного потенциала - ускорение силы тяжести для центра масс вертолета на поверхности эллипсоида;
G_X+L(H) - нормальная часть первой производной гравитационного потенциала - ускорение силы тяжести удаленной на L от центра масс вертолета;
Анализ уравнений 1 и 2 показывает, что погрешность гравитационных измерений в значительной степени определяется ошибками траекторных измерений центров масс вертолета, т.е. вертикального ускорения (H), широты места (φ), горизонтальной скорости полета (V) и вертикали (α). Положив δV = = 0,05 м/с, V = 100-150 км/ч, δϕ = 1 угл.сек из (1), суммарная ошибка гравиинерциальных измерений, только для погрешностей δV и δϕ, составит не менее 0,4-0,5 мГл.

Таким образом, в одинарном гравитационном комплексе, если широта известна с точностью до 30 м, а линейная скорость до 5 см/с, ошибка гравиметра составит не менее 0,4-0,5 мГл.

В предлагаемом бинарном гравитационном комплексе уравнение фильтра, на основании разности уравнений (1) и (2), примет вид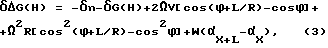

где δΔG(H) = ΔG_X+L(H)-ΔG_X(H);
δn = n_X+L-n_X;
δG(H) = G_X+L(H)-G_X(H).
После преобразований в (3), в первом приближении, уравнение бинарного гравитационного комплекса можем получить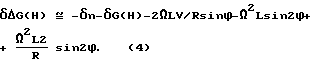

Сравнительный анализ уравнений (1) и (4) показывает, что погрешность гравитационных измерений в бинарном гравитационном комплексе из-за ошибки траекторного измерения существенно снижена и, главное, нет составляющей вертикального ускорения, которая приводила к необходимости иметь в комплексе высотомер и измеритель вертикальной скорости весьма высокой точности.

В таблице приведена сравнительная оценка ошибок из-за погрешности траекторных измерений для V = 30 м/с;
δV = 5•10^-2; δϕ = 5•10^-6; L = 10 м.

На основании данных, приведенных в таблице, ошибками в траекторных измерении в бинарном гравитационном комплексе можно пренебречь, при этом соотношение (4) примет вид
δΔG(H) ≅ -δn.
Аппроксимируя выражение δΔG(H) в (5) для x = Vt, запишем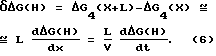

На основании (5) и (6) имеем
, (7)
где δn - разность показаний гравиметров, расположенных в точках X + L и X;
градиент аномальной части ΔG(H).
Из (7) следует, что чем больше L/V, тем чувствительность к выше.

Уравнения ошибок для бинарного гравитационного комплекса составим на основании разностных сигналов по скорости и вертикали от инерциальных систем 1 и 2, расположенных на расстоянии L друг от друга.

Уравнения ошибок для одноконтурных идеальных (прецизионных) инерциальных навигационных систем 1 и 2 имеют вид




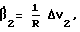
где ΔV_1,2 - погрешность определения скорости первой и второй ИНС;
β_1,2/- погрешность определения вертикали первой и второй ИНС
На основании (8) уравнение для бинарного гравитационного фильтра 26 будет иметь вид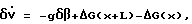


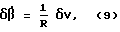
где δV = ΔV₂-ΔV₁;
δβ = β₂-β₁.
Аппроксимируя в (9) ΔG(x+L)-ΔG(x) для x = Vt, получим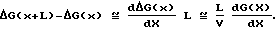

При этом выражение (9) примет вид


Решая соотношение (10) в бинарном фильтре 26, получим для относительных переменных δV и δβ:


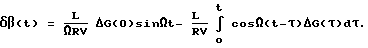
Из (11) следует, поскольку δV(t) и δβ(t) не входят показатели интегралов свертки, и то чем больше величина L/V, тем точнее могут быть определены интегралы свертки и, следовательно, выше точность гравиинерционных измерений на подвижном основании.

Из (11), в первом приближении, имеем

где L/V - коэффициент, представляющий собой период задержки времени, необходимый для перемещения второй ИНС на точку на земной поверхности, в которой в настоящее время находится первая ИНС;
ΔG(t) - аномальная часть под действием силы тяжести.

Из (12) следует, что степень положительного влияния гравитационных измерений ΔG(t) бинарном фильтре 26 пропорциональна периоду времени задержки L/V, поэтому наиболее предпочтительным для гравиинерциального режима бинарного фильтра является использование медленно движущегося вертолета, т.е. режим висения вертолета, когда скорость перемещения центра масс вертолета V не превышает 0,1-0,2 м/с.

Поскольку из конструктивных соображений, на вертолете инерциальные навигационные системы 1 и 2 не могут быть разнесены на расстояние L более чем на 5-10 м, тогда для V = 0,1 м/с, коэффициент L/V будет равен 50 и 100 секундам. Это эквивалентно увеличению чувствительности слабых гравитационных сигналов в 50-100 раз.

Заметим, что согласно (12) при L=0 эффект гравиинерциальных измерений пропадает, что отражает сущность функционирования бинарных гравиинерциальных комплексов.

Заметим, что гравиинерциальный комплекс может работать без гравиметров, их роль выполняют инерциальные системы 1 и 2.

Следует также отметить, что с экономических позиций, на первый взгляд, предлагаемый бинарный гравиинерциальный комплекс примерно в два раза дороже обычного гравитационного комплекса.

Однако он быстро окупается за счет реализации гравитационных карт. Так, 1 км² гравитационной карты с 1 мГл (обычный гравитационный комплекс) стоит 100 долларов США, а 1 км² гравитационной карты с 0,1 мГл (предлагаемый бинарный гравиинерциальный комплекс) стоит не менее 1,5 тысячи долларов США.

Источники информации
1. Приборы для гравиинерционных измерений, изд. "НАУКА", М., 1978 г.

2. Патент РФ N 2090911, от 10.09.97 г.

Использование: приборы для гравиизмерений. Сущность: две инерциальные навигационные системы (ИНС) выходами соединены с входами вычислителя, который другими входами соединен с системой спутниковой навигации и высотомером. В вычислителе функционируют фильтр Калмана и бинарный фильтр. С выхода фильтра оценки ошибок по скорости и вертикали поступают на ИНС для компенсации ошибок. Технический результат: повышение точности гравиинерциальных измерений на подвижном основании. 7 з.п. ф-лы, 1 ил., 1 табл.

1. Гравиметрический комплекс, содержащий инерциальную навигационную систему, спутниковую систему навигации и высотометр, соединенные с соответствующими входами вычислителя, отличающийся тем, что снабжен второй инерциальной навигационной системой, удаленной от первой инерциальной системы вдоль оси измерения летательного аппарата, при этом вычислитель своими четырьмя выходами непосредственно, а двумя входами через соответствующие сумматоры связан с входами и соответствующими выходами инерциальных навигационных систем. 2. Комплекс по п.1, отличающийся тем, что в качестве летательного аппарата использован вертолет. 3. Комплекс по п.1 или 2, отличающийся тем, что каждая инерциальная навигационная система включает гравиметр, каждый из которых соединен с соответствующим входом вычислителя. 4. Комплекс по п.2 или 3, отличающийся тем, что снабжен блоком стабилизации висения вертолета, вход которого связан с выходом вычислителя. 5. Комплекс по любому из пп.2 - 4, отличающийся тем, что снабжен радиомодемным блоком, вход которого связан с выходом вычислителя. 6. Комплекс по любому из пп.1 - 3, отличающийся тем, что вычислитель включает в себя фильтр Калмана. 7. Комплекс по любому из пп.4 - 6, отличающийся тем, что вычислитель включает в себя бинарный фильтр для оценки гравитационных измерений. 8. Комплекс по любому из пп.1 - 7, отличающийся тем, что вычислитель снабжен накопителем информации.