Изобретение относится к области радиотехники и может быть использовано при формировании ансамблей псевдослучайных бинарных последовательностей, используемых в качестве сигнатур при кодовом разделении широкополосных сигналов в спутниковых навигационных системах, а также при кодовом разделении каналов в широкополосных телекоммуникационных системах и системах многоканальной связи.
Кодовое разделение сигналов, применяемое в спутниковых навигационных системах, состоит в том, что сигналы, излучаемые навигационными космическими аппаратами (НКА), модулируются индивидуальными псевдослучайными бинарными периодическими последовательностями (кодовыми последовательностями), позволяющими на приемной стороне идентифицировать и разделять широкополосные сигналы разных НКА, передаваемые на одной несущей частоте. Это позволяет осуществлять навигационные измерения, основанные на измерениях псевдодальностей до соответствующих НКА, которые заключаются в определении запаздывания, имеющего место в процессе распространения широкополосных сигналов от НКА до приемника. При этом используются методы корреляционной обработки, основанные на сравнении кодовых последовательностей, относящихся к принятым сигналам, с их локальными, сдвигаемыми по времени копиями, формируемыми в приемнике.
Исходя из стоящих перед приемником задач по измерению запаздывания и временного разрешения принимаемых широкополосных сигналов вытекают требования к автокорреляционным функциям (АКФ) сигналов и, соответственно, модулирующим их кодовым последовательностям, а именно: АКФ должны иметь достаточно острый центральный пик и по возможности низкий уровень боковых лепестков. При этом ансамбль кодовых последовательностей, используемых для кодового разделения сигналов, должен быть достаточно объемным, чтобы удовлетворить все возрастающим требованиям по количеству разделяемых сигналов, а аппаратура, осуществляющая кодирование и декодирование, должна быть как можно проще исходя из требований практической реализации.
Простейшим из известных генераторов псевдослучайных бинарных последовательностей является генератор бинарных m-последовательностей, реализация которого описана, например, в книгах: [1] - М.Д.Венедиктов, С.А.Даниэлян, В.В.Марков, Г.С.Эйдус. Многостанционный доступ в спутниковых системах связи. М., Связь, 1973, с.81-83, рис.6.3, [2] - Глобальная спутниковая радионавигационная система ГЛОНАСС. Под ред. В.Н.Харисова, А.И.Перова, В.А.Болдина. М., ИПРЖ, 1998, с.64-66, рис.5.1, а также в патентах: [3] - SU 375769 A1, G06F 7/58, 01.01.1973, [4] - RU 2223593 C1, H03B 29/00, G06F 7/58, 10.02.2004. Рассматриваемый генератор бинарных m-последовательностей построен по принципу регистра сдвига с линейной обратной связью. Регистр сдвига состоит из n последовательно соединенных двоичных ячеек памяти (разрядов), каждая из которых имеет два возможных состояния. Состояние разрядов передается (сдвигается) на последующие разряды под действием тактовых импульсов, вырабатываемых средствами тактовой синхронизации. Начальная установка разрядов (загрузка регистра) осуществляется с помощью соответствующих средств начальной загрузки. Обратная связь реализуется с помощью блока обратной связи, который осуществляет логические операции над содержимым разрядов регистра сдвига и передает полученный результат на вход первого разряда. Логические операции заключаются в умножении выходных сигналов регистров на коэффициенты (константы), определяемые характеристическим полиномом, и их последующем сложении по модулю два. При этом практически умножение на единицу реализуется как простое соединение выхода соответствующего разряда регистра с входом сумматора, а умножение на нуль - как отсутствие соединения. Выходным сигналом генератора бинарных m-последовательностей является бинарная {0,1} последовательность импульсов, снимаемая с выхода последнего разряда регистра сдвига. Эта последовательность представляет собой линейную рекуррентную последовательность длины L=2n-1, которая называется последовательностью максимальной длины или m-последовательностью.
Характеристические полиномы, используемые при формировании бинарных m-последовательностей, выбираются из ансамблей примитивных полиномов, составляющих подкласс неприводимых полиномов. Примитивные полиномы известны, подробно описаны и табулированы, см., например, книгу [5] - У.Питерсон, Э.Уэлдон. Коды, исправляющие ошибки. М., Мир, 1976. Для каждого значения n существует определенный набор примитивных полиномов и, соответственно, ансамбль бинарных m-последовательностей.
Дискретные широкополосные сигналы, основанные на бинарных m-последовательностях, благодаря простоте формирования и обработки широко используются в информационных системах для измерения времени, в качестве обучающих сигналов и т.п. Например, в 2G стандарте мобильной связи cdmaOne (IS-95) бинарные m-последовательности различной длины используются как пилот-сигналы начальной синхронизации и зондирования каналов, а также как коды мультиплексирования сигналов базовых станций и скремблирования данных.
В случае асинхронного кодового разделения применяются более сложные по своей структуре псевдослучайные бинарные последовательности, обладающие лучшими взаимно корреляционными характеристиками, например последовательности Голда и Касами.
Общие принципы построения генератора последовательностей Голда описаны, в частности, в книге [6] - В.П.Ипатов. Широкополосные системы и кодовое разделение сигналов. Принципы и приложения. М., Техносфера, 2007, с.304-307, рис.7.18, а пример конкретной реализации генератора последовательностей Голда, предназначенного для формирования С/А кода, используемого для разделения сигналов НКА в глобальной спутниковой навигационной системе GPS, представлен в книге [7] - Бортовые устройства спутниковой радионавигации. И.В.Кудрявцев, И.Н.Мищенко, А.И.Волынкин и др. Под ред. B.C.Шебшаевича. М., Транспорт, 1988, с.15-16, рис.5.
Обобщенная структурная схема генератора последовательностей Голда содержит первый и второй n-разрядные двоичные регистры сдвига с линейной обратной связью, блок задержки, осуществляющий задержку на k тактов, и выходной сумматор по модулю два, выход которого образует выход генератора. К первому входу выходного сумматора по модулю два подключен выход первого регистра сдвига с линейной обратной связью, а к его второму входу - через блок задержки - выход второго регистра сдвига с линейной обратной связью.
Каждый из регистров сдвига за счет действия блока обратной связи формирует бинарную m-последовательность, соответствующую своему характеристическому полиному. Работа регистров сдвига синхронизирована тактовыми импульсами, вырабатываемыми средствами тактовой синхронизации. В результате сложения в выходном сумматоре по модулю два первой бинарной m-последовательности и сдвинутой на определенное количество тактов (k) второй бинарной m-последовательности формируется псевдослучайная бинарная последовательность, называемая последовательностью Голда. Меняя в блоке задержки величину тактовой задержки k, получают сигнатурный ансамбль последовательностей Голда.
Ансамбль последовательностей Голда характеризуется, как указано в [6, с.312, таблица 7.1], длиной последовательностей L=2n-1, объемом K=L+2=2n+1, квадратами максимума корреляции 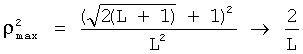 (n нечетное) и
(n нечетное) и 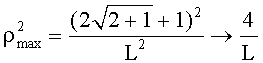 (n четное).
(n четное).
Ансамбли последовательностей Голда имеют широкое применение. Кроме указанной глобальной спутниковой навигационной системы GPS, где последовательности Голда используются для разделения сигналов НКА, эти последовательности используются также в 3G системе мобильной связи стандарта WCDMA в качестве скремблирующих CDMA кодов (code division multiple access).
По принципу построения к генератору последовательностей Голда примыкает генератор последовательностей Касами, описанный, в частности, в [6, с.307-310, рис.7.19, с.215-221], принятый в качестве прототипа.
Структурная схема генератора последовательностей Касами содержит первый и второй регистры сдвига с линейной обратной связью, блок задержки и выходной сумматор по модулю два, выход которого образует выход генератора.
Первый регистр сдвига с линейной обратной связью содержит n, где n - четное, последовательно соединенных двоичных ячеек памяти, каждая из которых имеет р=2 возможных состояний, и блок обратной связи, осуществляющий логические операции умножения и сложения по модулю два над содержимым ячеек памяти в соответствии с первым характеристическим полиномом и передающий полученный результат в виде двоичного сигнала обратной связи на вход первой ячейки памяти. Этот регистр формирует «длинную» бинарную m-последовательность. Его выход подключен к первому входу выходного сумматора по модулю два.
Второй регистр сдвига с линейной обратной связью содержит n/2 последовательно соединенных двоичных ячеек памяти, каждая из которых имеет р=2 возможных состояний, и блок обратной связи, осуществляющий логические операции умножения и сложения по модулю два над содержимым ячеек памяти в соответствии со вторым характеристическим полиномом и передающий полученный результат в виде двоичного сигнала обратной связи на вход первой ячейки памяти. Этот регистр формирует «короткую» бинарную m-последовательность. Его выход подключен к второму входу выходного сумматора по модулю два через блок задержки, осуществляющий задержку «короткой» бинарной m-последовательности на k тактов.
Генератор последовательностей Касами содержит также средства начальной загрузки ячеек памяти, средства тактовой синхронизации, обеспечивающие синхронизацию операций сдвига состояний ячеек памяти в каждом из регистров сдвига с операциями, осуществляемыми в блоках обратной связи и выходном сумматоре по модулю два, а также средства, обеспечивающие хранение коэффициентов характеристических полиномов, служащих множителями при осуществлении операций умножения в блоках обратной связи.
Принцип построения блоков обратной связи в генераторе последовательностей Касами такой же, как и в рассмотренных выше генераторах последовательностей Голда и бинарных m-последовательностей. В соответствии с выполняемыми функциями блоки обратной связи содержат элементы умножения и сложения по модулю два. При этом, как и ранее, умножение на единицу реализуется соединением сумматора по модулю два с выходом соответствующей ячейки регистра сдвига, а умножение на нуль - отсутствием такового. Элементы сложения по модулю два образуют в каждом из блоков обратной связи схему сложения, осуществляющую сложение по модулю два выходных сигналов элементов умножения с формированием выходного сигнала блока обратной связи.
Выходной сумматор по модулю два суммирует «длинную» бинарную m-последовательность, поступающую с выхода первого регистра сдвига с линейной обратной связью, с «короткой» бинарной m-последовательностью, поступающей с выхода второго регистра сдвига с линейной обратной связью через блок задержки, осуществляющий задержку на k тактов. В результате такого суммирования формируется псевдослучайная бинарная последовательность, называемая последовательностью Касами. Меняя в блоке задержки величину тактовой задержки k получают сигнатурный ансамбль последовательностей Касами.
Ансамбль последовательностей Касами характеризуется, как указано в [6, с.312, таблица 7.1], длиной последовательностей L=2n-1, где n - четное, объемом 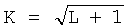 и квадратом максимума корреляции
и квадратом максимума корреляции 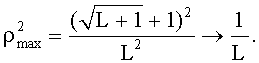
Сравнение характеристик ансамбля последовательностей Касами с ансамблем последовательностей Голда той же длины показывает существенный выигрыш ансамбля последовательностей Касами в уровне корреляционного пика по сравнению с ансамблем последовательностей Голда, что, однако, достигается за счет значительно меньшего (примерно в 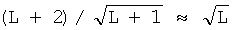 раз) числа сигнатур К.
раз) числа сигнатур К.
Технической задачей, на решение которой направлено изобретение, является разработка генератора псевдослучайных бинарных последовательностей, способного формировать сигнатурный ансамбль псевдослучайных бинарных последовательностей с примерно теми же корреляционными характеристиками, что и в прототипе, но существенно большего объема.
Сущность изобретения заключается в следующем. Генератор псевдослучайных бинарных последовательностей содержит регистр сдвига, состоящий из n последовательно соединенных ячеек памяти, каждая из которых имеет р возможных состояний, сумматор по модулю два, связанный с n-ой ячейкой памяти, блок обратной связи, осуществляющий логические операции умножения и сложения над содержимым ячеек памяти для формирования согласно характеристическому полиному сигнала обратной связи, передаваемого на сигнальный вход первой ячейки памяти, средства начальной установки регистра сдвига, средства тактовой синхронизации, обеспечивающие синхронизацию операций сдвига состояний ячеек памяти с операциями, осуществляемыми в блоке обратной связи и сумматоре по модулю два, а также средства, обеспечивающие хранение коэффициентов характеристического полинома, служащих множителями при осуществлении операций умножения в блоке обратной связи. В отличие от прототипа, каждая из n ячеек памяти регистра сдвига, где n - нечетное, выполнена в виде четверичной ячейки памяти, имеющей р=4 возможных состояния и состоящей из двух двоичных ячеек памяти, сигнальные входы и выходы которых образуют соответственно сигнальный вход и выход четверичной ячейки памяти, а блок обратной связи выполнен с использованием элементов умножения и сложения по модулю четыре, обеспечивающих выполнение логических операций умножения и сложения по модулю четыре над содержимым четверичных ячеек памяти в соответствии с четверичным характеристическим полиномом и передачу полученного результата в виде четверичного сигнала обратной связи на вход первой четверичной ячейки памяти, при этом выход старшей из двоичных ячеек памяти, входящей в состав n-ой четверичной ячейки памяти, образует первый выход генератора псевдослучайных бинарных последовательностей, соединенный с первым входом сумматора по модулю два, выход которого образует второй выход генератора псевдослучайных бинарных последовательностей, при этом второй вход сумматора по модулю два соединен с выходом генератора меандра, формирующего последовательность сигналов «нулей» и «единиц» …01010…, чередующихся с тактом работы регистра сдвига.
Сущность изобретения и возможность его осуществления поясняются иллюстративными материалами, представленными на фиг.1 и 2, где:
на фиг.1 представлена обобщенная структурная схема заявляемого генератора псевдослучайных бинарных последовательностей;
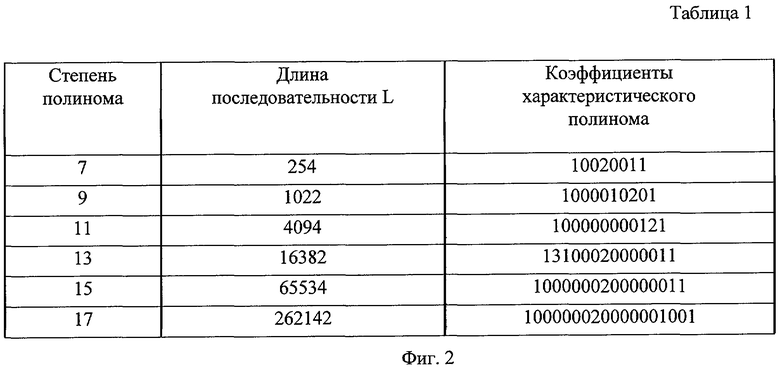
на фиг.2 - таблица четверичных характеристических полиномов.
Генератор псевдослучайных бинарных последовательностей содержит, см. фиг.1, регистр сдвига 1, состоящий из n последовательно соединенных ячеек памяти 2 (21, 22÷2n-1, 2n), где n - нечетное. Каждая ячейка памяти 2 представляет собой четверичную ячейку памяти, имеющую р=4 возможных состояния, и состоит из двух двоичных ячеек памяти 3 (старшей 31 и младшей 32), сигнальные входы и выходы которых образуют соответственно сигнальный вход и выход ячейки памяти 2. Входы установки двоичных ячеек памяти 3, образующие входы установки ячеек памяти 2, связаны с выходами соответствующих ячеек памяти блока 4 начальной установки регистра сдвига 1.
Выход старшей ячейки памяти 31, входящей в состав n-ой ячейки памяти 2n, образует первый выход генератора псевдослучайных бинарных последовательностей. Этот выход соединен с первым входом сумматора 5 по модулю два, выход которого образует второй выход генератора псевдослучайных бинарных последовательностей.
Второй вход сумматора 5 по модулю два соединен с выходом генератора меандра 6, формирующего последовательность сигналов «нулей» и «единиц» …01010…, чередующихся с тактом работы регистра сдвига 1. В простейшем случае генератор меандра 6 может быть реализован в виде счетного триггера, изменяющего свое состояние синхронно с изменением состояния ячеек памяти 2 в регистре сдвига 1 под действием тактовых импульсов, формируемых генератором тактовых импульсов (на фиг.1 не показан).
В состав генератора псевдослучайных бинарных последовательностей входит блок 7 обратной связи, осуществляющий логические операции умножения и сложения по модулю четыре над содержимым ячеек памяти 2 в соответствии с четверичным характеристическим полиномом с формированием четверичного сигнала обратной связи, передаваемого на сигнальный вход первой ячейки памяти 21.
В соответствии с выполняемыми функциями блок 7 обратной связи содержит элементы 8 умножения по модулю четыре и элементы 9 сложения по модулю четыре. Элементы 8 умножения по модулю четыре образуют схему 10 умножения, осуществляющую умножение по модулю четыре содержимого ячеек памяти 2 на коэффициенты четверичного характеристического полинома, хранящиеся в соответствующих ячейках памяти блока 11 коэффициентов характеристического полинома. Элементы 9 сложения по модулю четыре образуют схему 12 сложения, осуществляющую сложение по модулю четыре выходных сигналов, формируемых элементами 8 умножения по модулю четыре, с получением выходного четверичного сигнала блока 7 обратной связи. Операции, осуществляемые в блоке 7 обратной связи, синхронизированы с осуществляемыми в регистре сдвига 1 операциями по сдвигу состояний ячеек памяти 2. Синхронизация осуществляется с помощью обычных средств тактовой синхронизации, основанных на применении генератора тактовых импульсов (на фиг.1 не показан).
Четверичные характеристические полиномы, используемые в заявляемом генераторе псевдослучайных бинарных последовательностей, выбираются из ансамблей полиномов, математический аппарат построения которых представлен в работе [8] - А.А.Нечаев. Код Кердока в циклической форме // Дискретная математика, 1989, т.1, вып.4, с.123-139. Для нахождения четверичного характеристического полинома необходимо взять примитивный двоичный полином f(x)=xn+fn-1xn-1+f1x+1 той же степени n, где fi=0,1 для всех i=1, 2, …, n-1. Как уже указывалось, подобные полиномы подробно табулированы и представлены, в частности, в [5]. Отделив четные степени переменной х в f(x) от нечетных, двоичный полином можно представить как f(x)=F1(x2)+xF2(x2). Если теперь построить полином G(x) как G(x)=x[F2(x)]2-[F1(x)]2, где все операции выполняются по модулю четыре, искомым четверичным характеристическим полиномом окажется полином F(x)=G(3x). Поскольку для каждого значения n существует ряд двоичных примитивных полиномов, все они приводят к различным четверичным характеристическим полиномам. Любой из таких полиномов пригоден для заявляемого генератора псевдослучайных бинарных последовательностей, однако наиболее удобны те из них, в которых большое количество коэффициентов равно нулю. Дело в том, что умножение на нуль отвечает отсутствию соединения между соответствующей ячейкой памяти 2 регистра сдвига 1 и блоком 7 обратной связи, и поэтому большое число нулевых коэффициентов характеристического полинома упрощает реализацию заявляемого генератора псевдослучайных бинарных последовательностей. Для примера в таблице, представленной на фиг.2, приведено по одному четверичному характеристическому полиному для каждого значения n от семи до семнадцати, соответствующему диапазону длин L бинарных последовательностей от 254 до 262142, охватывающему нужды как любых навигационных, так и многих других приложений. Полиномы представлены набором четверичных коэффициентов начиная со старшего.
В своей основе принцип работы заявляемого генератора псевдослучайных бинарных последовательностей аналогичен рассмотренному выше генератору m-последовательностей. После начальной установки регистра сдвига 1 (установки начального состояния ячеек памяти 2) состояние ячеек памяти 2 сдвигается по тактам вдоль регистра сдвига 1. При этом состояние первой ячейки памяти 21 (состояние составляющих ее двоичных элементов памяти 31 и 32) определяется сигналом, поступающим с выхода блока 7 обратной связи. В результате совместной работы регистра сдвига 1 и блока 7 обратной связи в регистре сдвига 1 формируется четверичная линейная последовательность, индивидуальный код которой (индивидуальная структура) определяется начальной установкой регистра сдвига 1 и характеристическим полиномом.
Считывая состояние старшего двоичного элемента памяти 31, входящего в состав n-ой ячейки памяти 2n, получают псевдослучайную бинарную последовательность с алфавитом {0,1}, который, при необходимости, путем стандартного преобразования может быть изменен на алфавит {±1}: 0→1, 1→-1. Еще одна псевдослучайная бинарная последовательность снимается с выхода сумматора 5 по модулю два, складывающего вышеназванную последовательность с меандром (т.е. с последовательностью нулей и единиц …010110…, чередующихся с тактом работы регистра сдвига 1), формируемым генератором меандра 6.
Меняя начальное состояние регистра сдвига 1, получают сигнатурный ансамбль псевдослучайных бинарных последовательностей, которые характеризуются длиной последовательностей L=2(2n-1), где n - нечетное, объемом 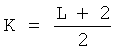 и квадратом максимума корреляции
и квадратом максимума корреляции 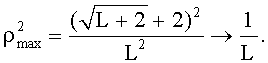 Для рассматриваемых применений имеют смысл «длинные» последовательности, характеризующиеся значениями n, равными или большими семи.
Для рассматриваемых применений имеют смысл «длинные» последовательности, характеризующиеся значениями n, равными или большими семи.
Из сравнения характеристик ансамбля псевдослучайных бинарных последовательностей, получаемых с помощью заявляемого генератора, с характеристиками ансамбля псевдослучайных бинарных последовательностей, получаемых с помощью прототипа - генератора последовательностей Касами, видно, что для сопоставимых длин последовательностей и при близких корреляционных свойствах объем ансамбля псевдослучаиных бинарных последовательностей 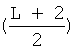 , который можно получить с помощью заявляемого генератора, многократно превышает объем ансамбля псевдослучайных бинарных последовательностей
, который можно получить с помощью заявляемого генератора, многократно превышает объем ансамбля псевдослучайных бинарных последовательностей 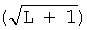 , который можно получить с помощью прототипа. Так, например, объем ансамбля псевдослучайных бинарных последовательностей длины L=4094, получаемых с помощью заявляемого генератора при n=11, составляет величину К=2048, что более чем на порядок превосходит аналогичный показатель (К=64) для ансамбля псевдослучайных бинарных последовательностей примерно той же длины L=4095, получаемых с помощью прототипа.
, который можно получить с помощью прототипа. Так, например, объем ансамбля псевдослучайных бинарных последовательностей длины L=4094, получаемых с помощью заявляемого генератора при n=11, составляет величину К=2048, что более чем на порядок превосходит аналогичный показатель (К=64) для ансамбля псевдослучайных бинарных последовательностей примерно той же длины L=4095, получаемых с помощью прототипа.
Таким образом, рассмотренное показывает, что заявляемое изобретение осуществимо и обеспечивает достижение технического результата, заключающегося в разработке генератора псевдослучайных бинарных последовательностей, способного формировать сигнатурный ансамбль псевдослучайных бинарных последовательностей с примерно теми же корреляционными характеристиками, что и в прототипе - генераторе последовательностей Касами, но существенно большего объема. С учетом сравнительно простой реализации указанная особенность заявляемого генератора псевдослучайных бинарных последовательностей делает его перспективным для решения актуальных задач в области широкополосной передачи и кодового разделения сигналов, связанных с увеличением числа каналов и расширением номенклатуры сигналов, в том числе в спутниковых навигационных системах.
Источники информации
1. М.Д.Венедиктов, С.А.Даниэлян, В.В.Марков, Г.С.Эйдус. Многостанционный доступ в спутниковых системах связи. М., Связь, 1973, с.81-83, рис.6.3.
2. Глобальная спутниковая радионавигационная система ГЛОНАСС. Под ред. В.Н.Харисова, А.И.Перова, В.А.Болдина. М., ИПРЖ, 1998, с.64-66, рис.5.1.
3. SU 375769 A1, G06F 7/58, опубл. 01.01.1973.
4. RU 2223593 C1, H03B 29/00, G06F 7/58, опубл. 10.02.2004.
5. У.Питерсон, Э.Уэлдон. Коды, исправляющие ошибки. М., Мир, 1976.
6. В.П.Ипатов. Широкополосные системы и кодовое разделение сигналов. Принципы и приложения. М., Техносфера, 2007, с.215-221, 304-310, рис.7.18, 7.19, с.312, табл.7.1.
7. Бортовые устройства спутниковой радионавигации. / И.В.Кудрявцев, И.Н.Мищенко, А.И.Волынкин и др. Под ред. B.C.Шебшаевича. М., Транспорт, 1988, с.15-16, рис.5.
8. А.А.Нечаев. Код Кердока в циклической форме // Дискретная математика, 1989. т.1, вып.4, с.123-139.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ тестирования оперативных запоминающих устройств | 2017 |
|
RU2660607C1 |
| ГЕНЕРАТОР СИНГУЛЯРНЫХ АНСАМБЛЕЙ ОПТИМАЛЬНЫХ ДИСКРЕТНЫХ СИГНАЛОВ | 2010 |
|
RU2447479C1 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ СИГНАЛОВ | 2009 |
|
RU2416157C1 |
| СПОСОБ ТЕСТИРОВАНИЯ ОПЕРАТИВНЫХ ЗАПОМИНАЮЩИХ УСТРОЙСТВ | 2009 |
|
RU2455712C2 |
| Генератор периодических псевдослучайных двоичных последовательностей сложной структуры | 2018 |
|
RU2690765C1 |
| Генератор псевдослучайных чисел | 1981 |
|
SU1013955A1 |
| Сигнатурный анализатор | 1989 |
|
SU1756890A1 |
| Генератор псевдослучайных чисел | 1985 |
|
SU1256161A1 |
| УСТРОЙСТВО И СПОСОБ ВЫРАБОТКИ ЧЕТВЕРИЧНОГО КОМПЛЕКСНОГО КВАЗИОРТОГОНАЛЬНОГО КОДА И РАСШИРЕНИЯ СИГНАЛА ПЕРЕДАЧИ С ИСПОЛЬЗОВАНИЕМ КВАЗИОРТОГОНАЛЬНОГО КОДА В СИСТЕМЕ СВЯЗИ МДКР | 1999 |
|
RU2193282C2 |
| Генератор псевдослучайных последовательностей | 1988 |
|
SU1636993A1 |
Изобретение относится к области радиотехники и может быть использовано при формировании ансамблей псевдослучайных бинарных последовательностей, используемых в качестве сигнатур при кодовом разделении широкополосных сигналов в спутниковых навигационных системах, в широкополосных телекоммуникационных системах и системах многоканальной связи. Техническим результатом является увеличение объема ансамбля псевдослучайных бинарных последовательностей с теми же корреляционными характеристиками, что и в прототипе. Устройство содержит регистр сдвига, состоящий из n последовательно соединенных четверичных ячеек памяти, где n - нечетное, каждая из которых состоит из двух двоичных ячеек памяти, блок начальной установки, сумматор по модулю два, генератор меандра, формирующего последовательность сигналов «нулей» и «единиц», блок обратной связи, осуществляющий логические операции умножения и сложения над содержимым ячеек памяти для формирования согласно характеристическому полиному сигнала обратной связи, средства тактовой синхронизации, средства, обеспечивающие хранение коэффициентов характеристического полинома, служащих множителями при осуществлении операций умножения в блоке обратной связи. 2 ил.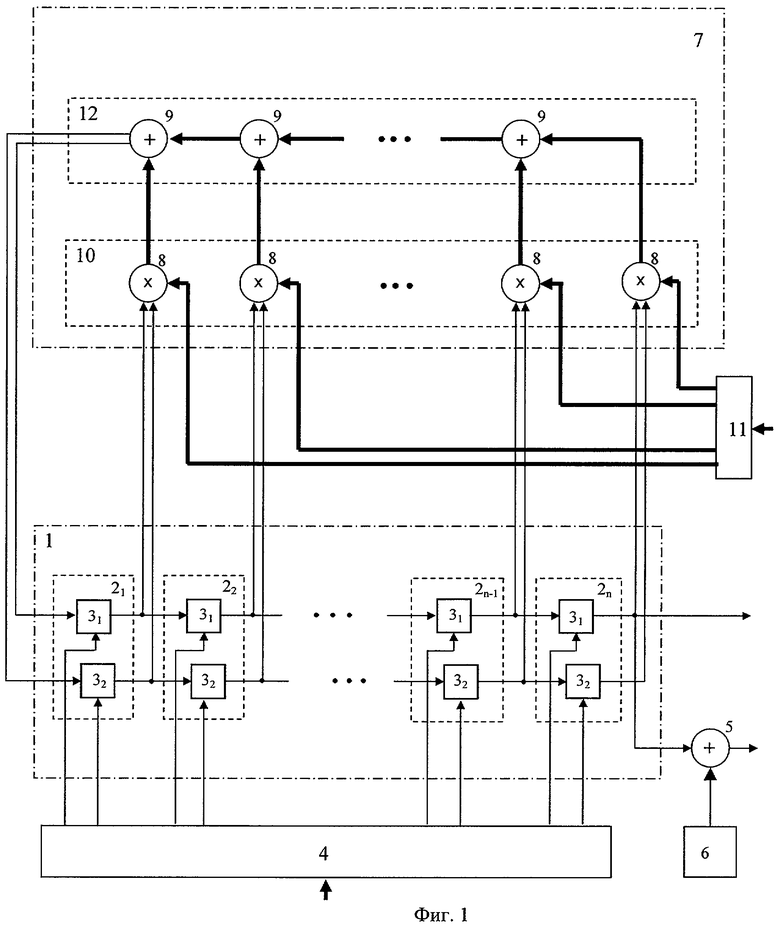
Генератор псевдослучайных бинарных последовательностей, содержащий регистр сдвига, состоящий из n последовательно соединенных ячеек памяти, каждая из которых имеет р возможных состояний, сумматор по модулю два, связанный с n-й ячейкой памяти, блок обратной связи, осуществляющий логические операции умножения и сложения над содержимым ячеек памяти для формирования согласно характеристическому полиному сигнала обратной связи, передаваемого на сигнальный вход первой ячейки памяти, средства начальной установки регистра сдвига, средства тактовой синхронизации, обеспечивающие синхронизацию операций сдвига состояний ячеек памяти с операциями, осуществляемыми в блоке обратной связи и сумматоре по модулю два, а также средства, обеспечивающие хранение коэффициентов характеристического полинома, служащих множителями при осуществлении операций умножения в блоке обратной связи, отличающийся тем, что каждая из n ячеек памяти регистра сдвига, где n - нечетное, выполнена в виде четверичной ячейки памяти, имеющей р=4 возможных состояния и состоящей из двух двоичных ячеек памяти, сигнальные входы и выходы которых образуют соответственно сигнальный вход и выход четверичной ячейки памяти, а блок обратной связи выполнен с использованием элементов умножения и сложения по модулю четыре, обеспечивающих выполнение логических операций умножения и сложения по модулю четыре над содержимым четверичных ячеек памяти в соответствии с четверичным характеристическим полиномом и передачу полученного результата в виде четверичного сигнала обратной связи на вход первой четверичной ячейки памяти, при этом выход старшей из двоичных ячеек памяти, входящей в состав n-й четверичной ячейки памяти, образует первый выход генератора псевдослучайных бинарных последовательностей, соединенный с первым входом сумматора по модулю два, выход которого образует второй выход генератора псевдослучайных бинарных последовательностей, при этом второй вход сумматора по модулю два соединен с выходом генератора меандра, формирующего последовательность сигналов «нулей» и «единиц»…01010…, чередующихся с тактом работы регистра сдвига.
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ | 2002 |
|
RU2223593C1 |
| 0 |
|
SU375769A1 | |
| Генератор последовательностей Голда | 1980 |
|
SU951671A1 |
| JP 11136101 A, 21.05.1999 | |||
| US 6363107 В1, 26.03.2002. | |||
Авторы
Даты
2011-08-27—Публикация
2009-10-19—Подача