Изобретение относится к радиотехнике и может быть использовано в системах передачи дискретной информации (СПДИ) для формирования групповых носителей информации со свойством «не более одного совпадения» любой длины и сложных частотно-фазоманипулированных сигналов на их основе, характерной особенностью которых является возможность формирования автокорреляционной функции (АКФ) с единичным уровнем боковых лепестков.
Известны устройства для формирования сигналов с хорошими автокорреляционными свойствами, например, на основе линейных рекуррентных последовательностей максимальной длины (МЛРП), характеризующиеся тем, что боковые пики АКФ сигналов, образованных МЛРП, равны 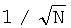 , где N - ее период [3, стр.202].
, где N - ее период [3, стр.202].
Наиболее близким к заявляемому устройству является генератор МЛРП представленный в [2, стр.203]. К недостаткам данного устройства относится высокий (неединичный) уровень боковых лепестков АКФ.
Целью изобретения является генерация сингулярного ансамбля дискретных сигналов, каждый из которых (сигналов), кроме периодической составляющей, обладает единичным уровнем боковых лепестков автокорреляционной функции независимо от длины. Такие сигналы принято называть «оптимальные дискретные сигналы» [3].
Поставленная цель достигается тем, что в устройство формирования МЛРП, состоящее из сдвигающего регистра с кольцом обратной связи и сумматора по модулю 2, дополнительно включены ячейки сдвига для формирования цуговых структур, а также инверторы, в которых инвертирование осуществляется по закону простого перебора всевозможных комбинаций с выходами на соответствующие схемы логического умножения и сами схемы логического умножения И, на выходе которых формируется сингулярный ансамбль оптимальных дискретных сигналов (СА ОДС).
На фиг.1 представлена структурная схема генератора СА ОДС.
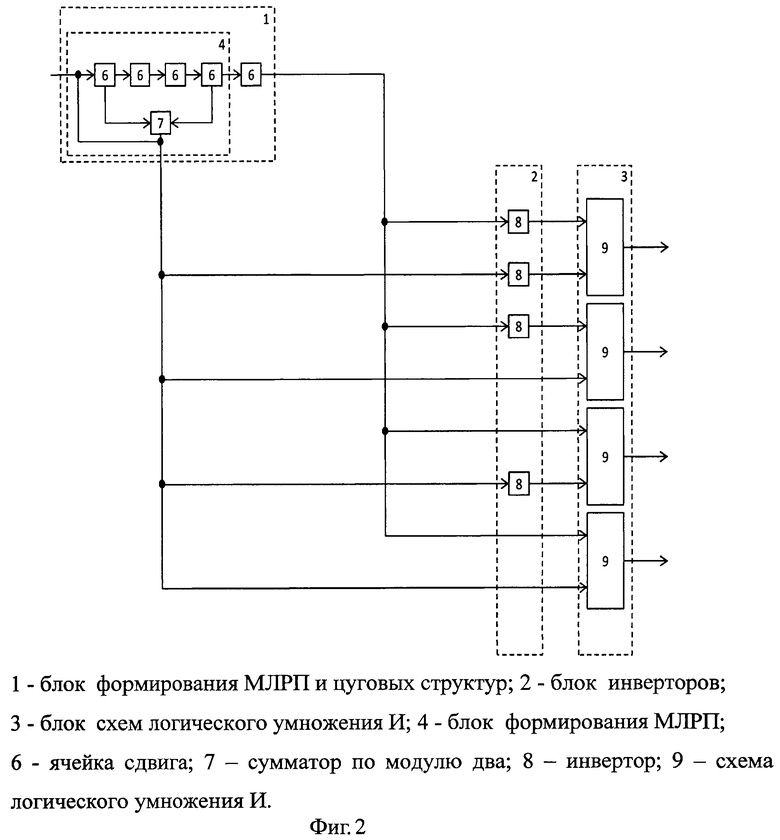
На фиг.2 представлена структурная схема генератора СА ОДС для рассматриваемого примера с образующим полиномом f(x)=х4 ⊕ х ⊕ 1.
На фиг.3 а), б), в), г) - иллюстрация процесса формирования СА ОДС на входах и выходах схем логического умножения И для рассматриваемого примера.
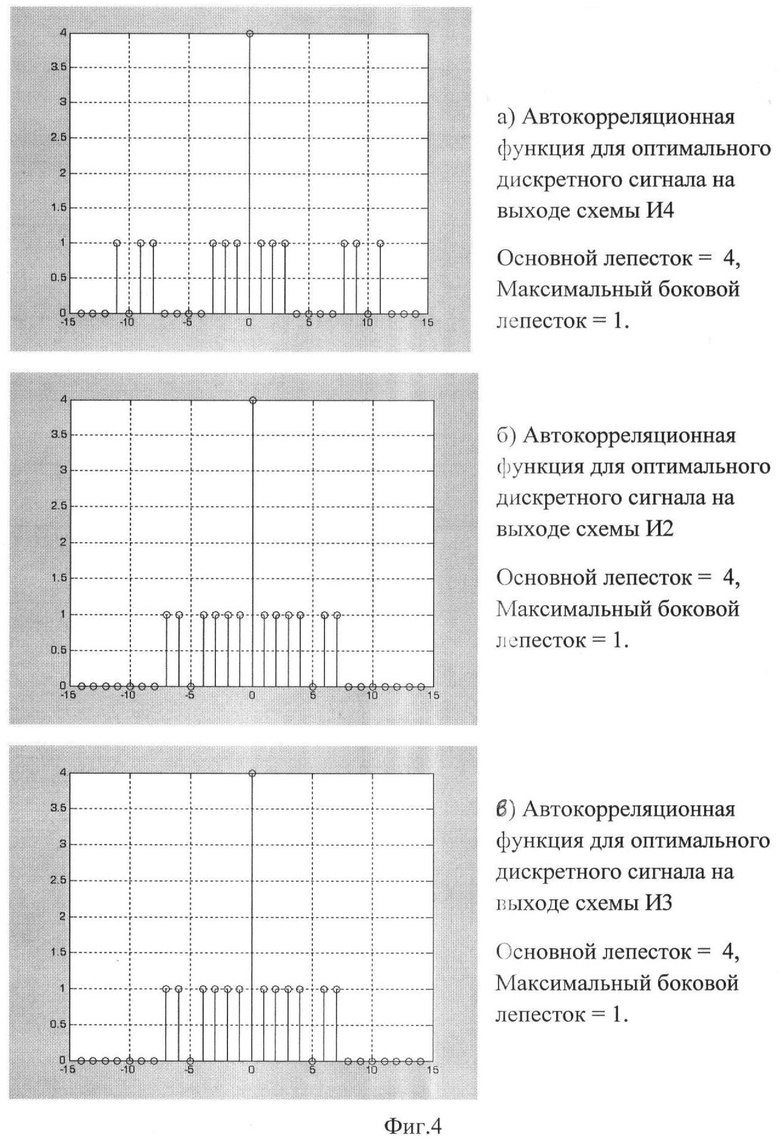
На фиг.4 а), б), в) - АКФ составляющих сингулярный ансамбль оптимальных дискретных сигналов для рассматриваемого примера.
Устройство для формирования СА ОДС имеет один вход, являющийся входом устройства, и m=2r, где r≥2 выходов, составляющих сформированный СА ОДС, и включает в себя (Фиг.1):
Блок 1 формирования МЛРП и цуговых структур имеет один вход и k=n/2·2n/2, где n - степень образующего МЛРП полинома выходов на блок инверторов и содержит блок формирования МЛРП, дополненный ячейками сдвига до длины цуга, дополнительные ячейки сдвига, образующие последующие цуговые структуры МЛРП.
Блок 2 инверторов содержит k=n/2·2n/2 входов и столько же выходов на блок 3 схем логического умножения И.
Блок 3 схем логического умножения И содержит z=n/2 входов на каждую схему логического умножения и m=2r выходов. Выходы блока 3 являются выходами генератора, который формирует СА ОДС.
Блок 1 формирования МЛРП и цуговых структур представляет собой линию задержки (сдвигающий регистр) с кольцом обратной связи и сумматором по модулю два для формирования бинарной МЛРП, дополненный ячейками сдвига до размера одного цуга, а также дополнительные ячейки сдвига, образующие последующие цуги МЛРП.
Блок 1 формирования МЛРП и последующих путовых структур содержит L·l ячеек сдвига, где L - длина одного цуга, а l - количество включаемых в генератор цугов и k=n/2·2n/2 выходов-отводов на блок 2 инверторов. Количество ячеек сдвига L определяется длиной цуга формируемой бинарной МЛРП:
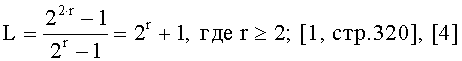
количество включаемых в генератор цуговых структур
l=n/2-2, где n - степень образующего МЛРП полинома.
Количество отводов на сумматор и законы их распределения определяются рекуррентным правилом формирования МЛРП на основе образующего полинома степени n.
Выходы-отводы на блок 2 инверторов берутся с крайних ячеек сдвига, образующих цуги МЛРП и с сумматора по модулю 2.
Блок 2 инверторов имеет k=n/2·2n/2 входов и столько же выходов на блок 3 схем логического умножения.
Правило инвертирования формируется по закону простого перебора всевозможных комбинаций выходов-отводов на блок 3 схем логического умножения.
Блок 3 схем логического умножения имеет
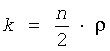 ,
,
где ρ=2n/2-количество включенных в устройство схем И входов и m=2r, где r≥2 выходов, которые являются выходом устройства, формирующего СА ОДС. Каждая схема И имеет z=n/2 входов, которые распределены в группы, обеспечивающие полный перебор возможных вариантов инвертирования.
Количество выходов в устройстве, а значит, и количество составляющих сингулярный ансамбль ОДС равно m=2r, где r≥2. Количество ненулевых компонент (импульсов) в каждом из ОДС N0=2r.
Работа предлагаемого устройства рассматривается для случая, когда код М-последовательности формируется на основе образующего полинома f(х)=х4 ⊕ х ⊕ 1 и соответствующего этому полиному рекуррентного правила a
i=a
i-4 ⊕ a
i-1 с периодом N=24-1=15. Длина цуга 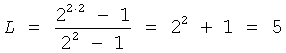 .
.
Количество включаемых в устройство цугов l=4/2-2=0. В рассматриваемом примере нет необходимости в дополнительных цуговых структурах (Фиг.2).
Для образующих код МЛРП полиномов более высоких степеней количество дополнительных цуговых структур составляет:
f(х)=х6 ⊕ х ⊕ 1, l=6/2-2=1;
f(х)=х8 ⊕ х7 ⊕ х5 ⊕ х3 ⊕ х ⊕ 1, l=8/2-2=2 и так далее.
Начальной комбинацией для формирования МЛРП в примере произвольно выбрана 1011 (4 элемента согласно степени образующего полинома). Генератор МЛРП автоматически дополняется одним элементом задержки до длины цуга L=5. Количество отводов на сумматор и их распределение, определяемые рекуррентным правилом, берутся соответственно с 1 и 4 ячеек сдвига.
Результат суммирования и значение крайней ячейки задержки цуга поступают на инвертор, имеющий k=n/2·2n/2=4/2·24/2=2·4=8 входов и столько же выходов на блок схем логического умножения И. Законы инвертирования определены следующим образом (Фиг.2, фиг.3).
Количество выходов-отводов с инвертора на каждую схему логического умножения И z=n/2=4/2=2, а количество включаемых схем логического умножения И - ρ=2n/2=22=4. Общая структурная схема генератора СА ОДС для рассматриваемого примера представлена на фиг.2.
Анализ известного и предложенного устройства показывает, что в рамках оценки уровня боковых лепестков АКФ любой из последовательностей, составляющих сингулярный ансамбль, кроме периодической, их уровень единичный и не зависит от длины самой последовательности (Фиг.4).
ЛИТЕРАТУРА
1. Амиантов И.Н. Избранные вопросы статистической теории связи. - М.: Сов. радио, 1971.
2. Варакин Л.Е. Теория сложных сигналов. - М.: Сов. радио, 1970.
3. Свердлик М.Б. Оптимальные дискретные сигналы. - М.: Сов. радио, 1975.
4. Щетинин В.И., Притчина Л.С. Сингулярные ансамбли оптимальных дискретных сигналов. 10-я Международная конференция и выставка: «Цифровая обработка сигналов и ее применение» // Труды Российского научно-технического общества радиотехники, электроники и связи им. А.С.Попова. 2008. Серия: Цифровая обработка сигналов и ее применение. Вып. Х-1, с.23-26.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ЦИФРОВОЙ ОБРАБОТКИ ПОЛИФАЗНЫХ ОРТОГОНАЛЬНЫХ ФАЗОКОДОМАНИПУЛИРОВАННЫХ СИГНАЛОВ | 2006 |
|
RU2346324C2 |
| УСТРОЙСТВО РАЗРЕШЕНИЯ ФАЗОКОДОМАНИПУЛИРОВАННЫХ СИГНАЛОВ | 2007 |
|
RU2371865C2 |
| ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ БИНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ | 2009 |
|
RU2427886C2 |
| РЕЦИРКУЛЯЦИОННЫЙ КОРРЕЛЯТОР РАЗРЕШЕНИЯ ФАЗОКОДОМАНИПУЛИРОВАННЫХ СИГНАЛОВ | 2005 |
|
RU2283541C1 |
| УСТРОЙСТВО ДЛЯ СИНХРОНИЗАЦИИ М-ПОСЛЕДОВАТЕЛЬНОСТИ | 2013 |
|
RU2550563C1 |
| Автокорреляционный измеритель параметров псевдослучайного фазоманипулированного сигнала | 1984 |
|
SU1197102A2 |
| Автокорреляционный измеритель параметров псевдослучайного фазоманипулированного сигнала | 1987 |
|
SU1518894A2 |
| Способ передачи дискретных сообщений и система для его осуществления | 2022 |
|
RU2794517C1 |
| Способ передачи дискретных сообщений с шифрованием кодов и система для его осуществления | 2022 |
|
RU2819142C1 |
| Способ передачи дискретных сообщений с синхронизируемым шифрованием и система для его осуществления | 2024 |
|
RU2832595C1 |

Изобретение относится к радиотехнике и может быть использовано в системах передачи дискретной информации для формирования групповых носителей информации со свойством «не более одного совпадения» любой длины и сложных частотно-фазоманипулированных сигналов на их основе, характерной особенностью которых является возможность формирования автокорреляционной функции с единичным уровнем боковых лепестков. Техническим результатом является генерация сингулярного ансамбля оптимальных дискретных сигналов, каждый из которых, кроме периодической составляющей, обладает единичным уровнем боковых лепестков автокорреляционной функции независимо от длины. Устройство содержит генератор линейных рекуррентных последовательностей максимальной длины, состоящий из сумматора по модулю два и ячеек сдвига, дополнительных ячеек сдвига, позволяющих формировать цуговые структуры, блок инверторов, блок схем логического умножения, на выходе которых формируется сингулярный ансамбль оптимальных дискретных сигналов. 4 ил.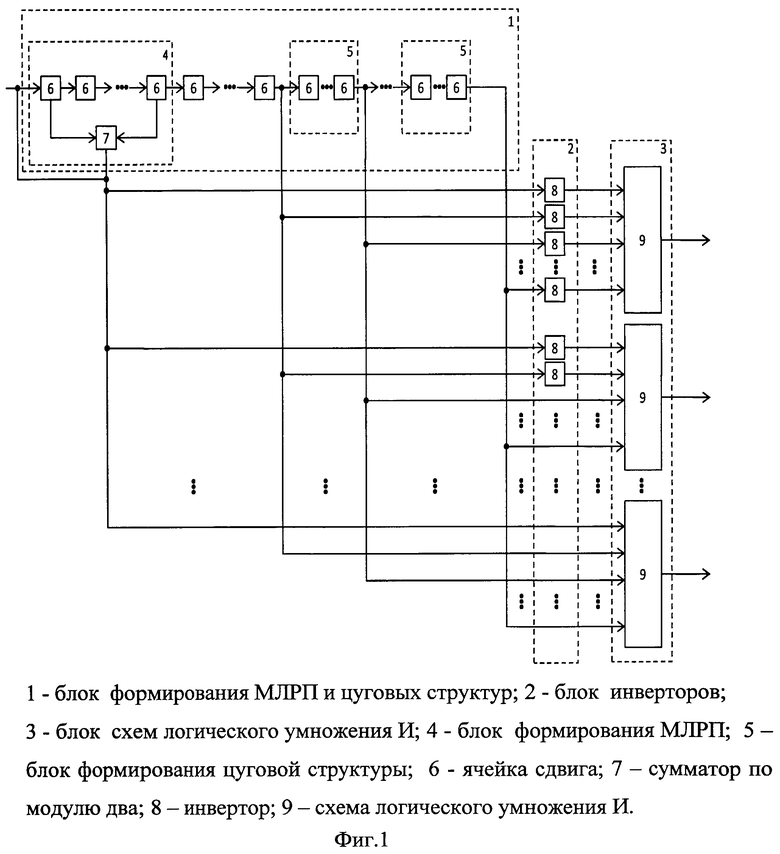
Генератор сингулярных ансамблей оптимальных дискретных сигналов, состоящий из генератора линейных рекуррентных последовательностей максимальной длины, являющийся входом устройства, включающий n ячеек сдвига и сумматора по модулю два с кольцом обратной связи, отличающийся тем, что в него введены дополнительные ячейки сдвига с целью формирования цуговых структур длины L, блок инверторов и блок схем логического умножения И, причем k-выходов с крайних ячеек сдвига, образующих цуговые структуры и с сумматора по модулю два соединены с соответствующими k-входами блока инверторов, z-комбинаций-выходов которого соединены с соответствующими входами р-схем логического умножения И, m-выходы с которых являются выходами генератора сингулярного ансамбля оптимальных дискретных сигналов.
| Устройство для формирования импульсных кодов псевдослучайных последовательностей | 1973 |
|
SU734870A1 |
| Генератор рекуррентной последовательности с самоконтролем | 1989 |
|
SU1656512A1 |
| Вальцевый макаронный агрегат | 1949 |
|
SU92270A1 |
| US 2009204656 А1, 13.08.2009 | |||
| US 7475102 В2, 06.01.2009. | |||
Авторы
Даты
2012-04-10—Публикация
2010-11-01—Подача