СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ ЮНГА И КОЭФФИЦИЕНТА ПУАССОНА ЛИТЫХ ДЕТАЛЕЙ Российский патент 2011 года по МПК G01N3/32 

Изобретение относится к области машиностроения (литейное производство), более конкретно к способам определения механических свойств материалов литых стержневых деталей, а именно к способам определения динамических: модуля упругости Юнга и коэффициента Пуассона.

Из уровня техники известны способы определения статического модуля упругости Юнга (Авторское свидетельство СССР №954850, МПК G01N 3/08, 1982; Авторское свидетельство СССР №957054, МПК G01N 3/42, 1982; патент РФ №2292029, МПК G01N 3/08, 2006), основанные на растяжении и сжатии образцов.

Однако эти способы не предназначены для определения динамических: модуля упругости Юнга и коэффициента Пуассона.

Наиболее близко к заявляемому техническому решению, принятому за прототип, относится способ определения динамического модуля упругости Юнга [ГОСТ 25095-82 «Метод определения модуля упругости (модуля Юнга)»]. Способ основан на испытаниях образцов с круглым сечением диаметром 6 мм или прямоугольным сечением 6×8 мм и длиной 60-65 мм, установленных в приспособление между двумя пьезоэлементами, определении самой низкой резонансной частоты образца анализатором при плавном изменении частоты генератора, определении плотности и вычислении модуля Юнга по известной формуле.

Недостатком указанного способа является то, что он не учитывает влияния технологии изготовления стержневых литых деталей на величину динамического модуля упругости Юнга, а также не позволяет определить динамический коэффициент Пуассона.

Задача изобретения состоит в устранении указанных недостатков, а именно получении способа определения динамических: модуля упругости Юнга и коэффициента Пуассона стержневых литых деталей.

Поставленная задача решается расчетно-экспериментальным способом. Сущность этого способа состоит в том что образец в виде толстостенного кольца изготавливают по технологии реальной литой стержневой детали, образец изготавливают по технологии реальной литой стержневой детали, подвешивают на упругой подвеске через центральное отверстие и импульсным силовым воздействием, последовательно по боковой и торцевой поверхности образца возбуждают в нем собственные формы колебаний, причем акустический сигнал, исходящий от образца, воспринимает микрофон и через предусилитель передает в анализатор, при помощи которого экспериментально определяют, по крайней мере, пять резонансных частот, после чего создают конечно-элементную динамическую модель, рассчитывают пять собственных частот и форм колебаний образца и методом аппроксимации определяют значения динамических: модуля упругости Юнга и коэффициента Пуассона.

Кроме того, отличие состоит в том, что в качестве упругой подвески, на которую подвешивают испытываемый образец, используют, например, резиновый шнур.

Отличие состоит также в том, что в качестве импульсного силового воздействия используют 10 ударов молотка весом 3 кг.

Еще одно отличие состоит в том, что исходными данными конечно-элементной динамической модели образца являются: геометрические размеры и экспериментально полученная плотность образца, а также табличные значения модуля упругости Юнга и коэффициента Пуассона для сплава.

Отличием также является то, что сначала задают диапазоны изменения динамических: модуля упругости Юнга и коэффициента Пуассона, а затем с помощью метода аппроксимации определяют их значения, при которых пять рассчитанных резонансных частот совпадают с экспериментальными в пределах 0,1%.

Технический результат, который получают от использования данного способа, заключается в том, что на стадии проектирования литых стержневых деталей при создании их динамической математической модели для оптимизации динамических и прочностных характеристик используют уточненные значения динамического модуля упругости Юнга и динамического коэффициента Пуассона. В результате получают отливки с заданными физико-механическими характеристиками.

Предложенное изобретение иллюстрируется чертежами, на которых изображено:

на фиг.1 - блок-схема испытания толстостенного образца;

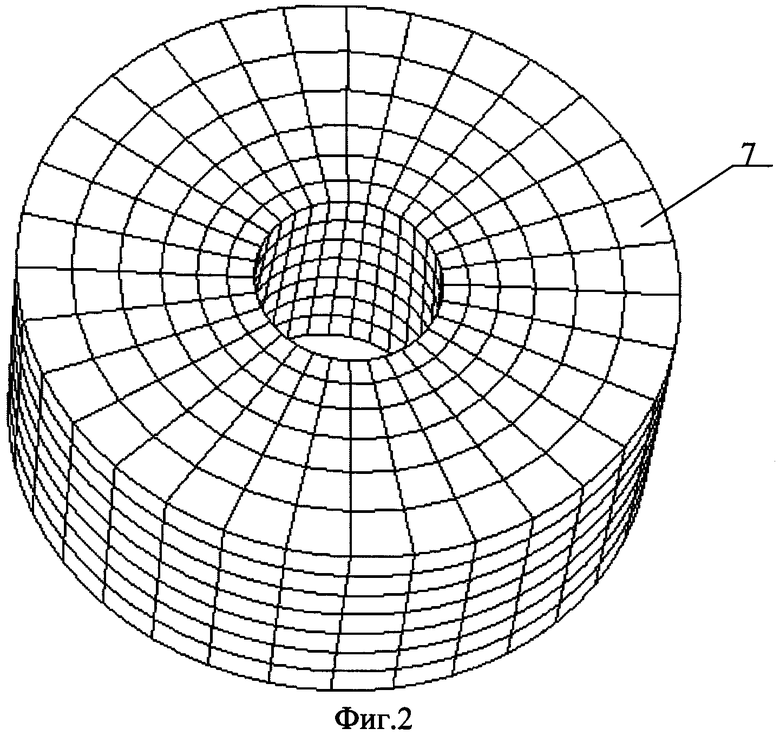
на фиг.2 - конечно-элементная модель образца в виде толстостенного кольца.

Динамические: модуль упругости Юнга и коэффициент Пуассона по предлагаемому способу определяют расчетно-экспериментальным методом в следующей последовательности:

1. Выбирают форму образца в виде толстостенного кольца 1.

2. Образец изготавливают с применение формовочных смесей и режимов заливки как при изготовлении реальной литой стержневой детали (общий вид литейной формы приведен в приложении 1).

3. Образец подвешивают (см. приложение 2) через центральное отверстие на упругой подвеске 2 (резиновый шнур), подобная упругая подвеска практически не оказывает влияния на резонансные формы колебаний образца, а колебания возбуждают последовательно по боковой и торцевой поверхности образца путем импульсного силового воздействия ударами молотка 3 (по крайней мере 10 ударов по 10 кг каждый).

4. Акустический сигнал от образца воспринимает микрофон 4 и через предусилитель 5 передает на анализатор (БПФ) 6, который определяет пять собственных частот, которые отражены в таблице 1.

Таблица 1 Сравнение измеренных и рассчитанных пяти собственных частот образца при различных значениях модуля упругости Юнга и коэффициента Пуассона Физические параметры Измерено Расчет Отклонение Физические параметры Измерено Расчет Отклонение 1 2 3 4 5 6 7 8 м. Юнга 1.0430Е+05 к. Пуассона 0.3364 плотность 8.708Е-06 2651 2615 1.38% м. Юнга 1.0600Е+05 к. Пуассона 0.3446 плотность 8.708Е-06 2678 2669 0.34% 3357 3294 1.91% 3395 3347 1.43% 4379 4378 0.02% 4438 4437 0.02% 5488 5489 -0.02% 5543 5547 -0.07% 5491 5908 -7.06% 5548 5963 -6.96%   1 2 3 4 5 6 7 8 м. Юнга 1.0470Е+05 к. Пуассона 0.3403 плотность 8.708Е-06 2668 2642 0.98% м. Юнга 1.0390Е+05 к. Пуассона 0.3328 плотность 8.708Е-06 2654 2615 1.49% 3380 3320 1.81% 3359 3294 1.97% 4413 4408 0.11% 4377 4378 -0.02% 5524 5519 0.09% 5491 5489 0.04% 5524 5937 -6.96% 5498 5908 -6.94%   1 2 3 4 5 6 7 8 м. Юнга 1.0880Е+05 к. Пуассона 0.3387 плотность 8.708Е-06 2684 2669 0.56% м. Юнга 1.0520Е+05 к. Пуассона 0.37 плотность 8.708Е-06 2615 2615 0.00% 3399 3347 1.55% 3327 3294 1.00% 4437 4437 0.00% 4379 4378 0.02% 5556 5547 0.16% 5403 5489 -1.57% 5557 5963 -6.81% 5432 5908 -8.06%

5. По ГОСТ 20018 «Метод определения плотности» определяют экспериментальным путем реальную плотность образца с погрешностью не более 0,01 г/см³.

6. Создают конечно-элементную динамическую модель образца в виде толстостенного кольца (фиг.2, где 7- I-ый конечный элемент) исходными данными которой являются:

- геометрические размеры образца, уточненные после его отливки;

- экспериментально по ГОСТ 20018 полученная плотность образца;

- табличные значения модуля упругости Юнга и коэффициента Пуассона для сплава.

7. Рассчитывают, по крайней мере, пять форм и пять собственных частот колебаний образца 1 (см. приложение 3) и методом аппроксимации, в заданных диапазонах изменения значений модуля упругости Юнга и коэффициента Пуассона, определяют значения динамических: модуля упругости Юнга и коэффициента Пуассона, при которых рассчитанные частоты совпадают с экспериментальными в пределах 0,1%.

Таким образом, использование предложенного способа определения модуля упругости Юнга и коэффициента Пуассона стержневых литых деталей позволяет определить значения динамического модуля упругости Юнга и динамического коэффициента Пуассона стержневых литых деталей.

Полученные таким способом уточненные значения динамического модуля упругости Юнга и динамического коэффициента Пуассона могут быть использованы в динамических математических моделях при разработке компьютерной технологии проектирования литых стержневых деталей с заданными физико-механическими характеристиками (колокола, картер двигателя автомобиля, блок цилиндров, клапанные крышки и др.).

Впервые в мире без дополнительной доводки (настройки) получены сверхтяжелые колокола, образующие музыкальный аккорд, т.е. каждый колокол с точностью менее 1,3% совпадает с заданной нотой, что отражено в таблице 2.

Достоверность полученных этим способом значений динамического модуля упругости Юнга и динамического коэффициента Пуассона бронзовых стержневых литых деталей была подтверждена при воссоздании тяжелых колоколов Троице-Сергеевой Лавры (Царь-колокол - 72 т, Благовест - 37 т, Первенец - 27 т).

Таблица 2 Акустические характеристики тяжелых колоколов Свято-Троицкой Сергиевой Лавры Царь колокол 72 тонны Частота (Гц) F1 F2 F3 F4 F5 Частота [Гц], нота 46,9 Фа # 91,3 Фа # 112,8 Ля 155,2 Ре # 195,3 Соль Отклонение [%]   1,3       "Благовестник" 35,5 тонн Частота (Гц) F1 F2 F3 F4 F5 Частота [Гц], нота 62,0 Си 125,2 Си 155,8 Ре # 201,0 Соль 273,0 До # Отклонение [%]   0,8       "Первенец" 27 тонн Частота (Гц) F1 F2 F3 F4 F5 Частота [Гц], нота 75,8 Ре # 154,3 Ре # 191,5 Соль 268,0 До 342,0 Фа Отклонение [%]   0,8      

Настоящее изобретение относится к способам определения механических свойств материалов литых деталей, изготовленных литьем в стержневые формы, а именно к способам определения динамических: модуля упругости Юнга и коэффициента Пуассона. Сущность: определяют плотность образца, образец изготавливают по технологии реальной литой детали, подвешивают на упругой подвеске через центральное отверстие и импульсным силовым воздействием, последовательно по боковой и торцевой поверхности образца возбуждают в нем собственные формы колебаний. Акустический сигнал, исходящий от образца, воспринимает микрофон и через предусилитель передает в анализатор, при помощи которого экспериментально определяют, по крайней мере, пять резонансных частот. Создают конечно-элементную динамическую модель, рассчитывают пять собственных частот и форм колебаний образца. Методом аппроксимации определяют значения динамических: модуля упругости Юнга и коэффициента Пуассона. Технический результат: возможность получения способа определения динамических: модуля упругости Юнга и коэффициента Пуассона литых деталей. 5 з.п. ф-лы, 2 ил., 2 табл.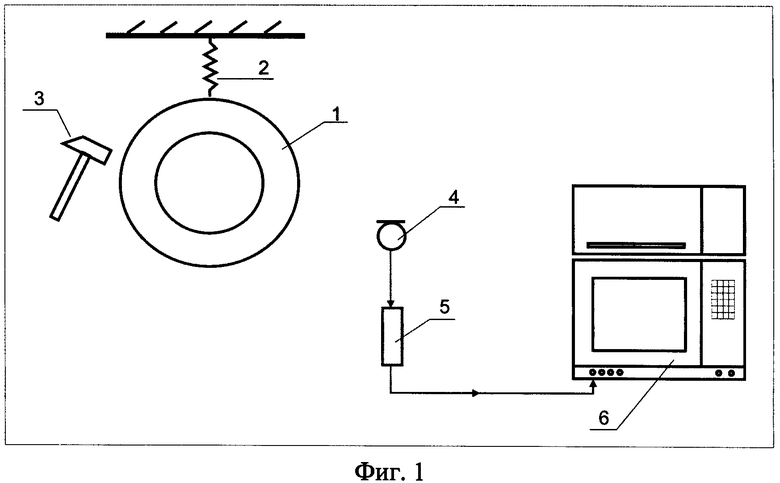

1. Способ определения модуля упругости Юнга и коэффициента Пуассона литых деталей, включающий испытание образца, установленного в приспособление, возбуждение собственной формы колебаний, определение, по крайней мере, одной резонансной частоты анализатором, определение плотности образца и вычисление статического значения модуля упругости Юнга по известной формуле, отличающийся тем, что образец изготавливают по технологии реальной литой детали, подвешивают на упругой подвеске через центральное отверстие и импульсным силовым воздействием последовательно по боковой и торцевой поверхности образца возбуждают в нем собственные формы колебаний, причем акустический сигнал, исходящий от образца, воспринимает микрофон и через предусилитель передает в анализатор, при помощи которого экспериментально определяют, по крайней мере, пять резонансных частот, после чего создают конечно-элементную динамическую модель, рассчитывают пять собственных частот и форм колебаний образца и методом аппроксимации определяют значения динамических: модуля упругости Юнга и коэффициента Пуассона.

2. Способ по п.1, отличающийся тем, что образец изготавливают в виде толстостенного кольца.

3. Способ по п.1, отличающийся тем, что в качестве упругой подвески, на которую подвешивают испытываемый образец, используют, например, резиновый шнур.

4. Способ по п.1, отличающийся тем, что в качестве импульсного силового воздействия используют 10 ударов молотка весом 3 кг.

5. Способ по п.1, отличающийся тем, что исходными данными конечно-элементной динамической модели образца являются: геометрические размеры и экспериментально полученная плотность образца, а также табличные значения модуля упругости Юнга и коэффициента Пуассона для сплава.

6. Способ по п.1, отличающийся тем, что сначала задают диапазоны изменения динамических: модуля упругости Юнга и коэффициента Пуассона, а затем с помощью метода аппроксимации определяют их значения, при которых пять резонансных рассчитанных частот совпадают с экспериментальными в пределах 0,1%.