Изобретение относится к способам определения механических свойств материалов путем приложения растягивающих или сжимающих нагрузок, а именно к способам определения статического модуля упругости Юнга (ниже модуль упругости).
Известен способ определения модуля упругости [Авторское свидетельство СССР №954850, кл. G 01 N 3/08, 1982], основанный на том, что нагружают растяжением образец материала, имеющий площадь F сечения, с установленным на нем датчиком деформации, измеряют сигнал ΔR с датчика, соответствующий изменению напряжения в рабочем сечении. Используют образец эталонного материала, имеющий площадь FЭ сечения и модуль упругости ЕЭ с установленным на нем датчиком деформации, который размещают последовательно с образцом исследуемого материала и нагружают одновременно с ним, измеряют сигнал ΔRЭ с датчика, установленного на образце эталонного материала, и рассчитывают модуль упругости Е материала.
Недостатками указанного способа определения модуля упругости являются: невозможность его применения к образцам материалов с непостоянной площадью сечения, например шарообразных образцов, а также необходимость использования эталонного материала.
Наиболее близким к заявляемому техническому решению, принятым за прототип, является способ определения модуля упругости, основанный на том, что в материал внедряют цилиндрический индентор без сцепления его с материалом и измеряют глубину внедрения, затем внедряют индентор с сцеплением с материалом при той же нагрузке. Определяют отношение глубин внедрения, по которым судят о модуле упругости [Авторское свидетельство СССР №957054, кл. G 01 N 3/42, 1982].
Недостатком указанного способа определения модуля упругости является сложность его реализации в образцах материалов малых размеров, меньших 100 нм.
Задача изобретения - устранение указанных недостатков, а именно получение способа определения модуля упругости для шарообразных наночастиц.
Способ определения модуля упругости включает в себя два этапа.
1. Задача решается с помощью экспериментального сжатия шарообразной наночастицы сосредоточенной силой. Находят перемещение в точке действия силы на наночастицу. Сравнивают экспериментальное значение перемещения в точке приложения силы к наночастице со значением перемещения в этой точке, вычисленной по аналитическому решению зависимости перемещений от радиуса упругого шара, сжимаемого сосредоточенными силами, приложенными в противоположные концы диаметра и направленными параллельно, для справочных значений модуля упругости и коэффициента Пуассона (ниже коэффициент поперечных деформаций) исследуемого материала. При этом радиус упругого шара равен радиусу наночастицы, прикладываемые расчетные силы к упругому шару равны прикладываемой силе к наночастице. Изменяя модуль упругости, находят такое его значение для справочного коэффициента поперечных деформаций, при котором совпадают экспериментальное перемещение, замеренное в точке приложения силы к наночастице с расчетным значением перемещения в этой точке, вычисленным по аналитическому решению зависимости перемещений от радиуса упругого шара, сжимаемого сосредоточенными силами.
2. Методом молекулярной динамики, с помощью компьютерного эксперимента, проводят расчет сжатия шарообразной наночастицы сосредоточенными силами, приложенными к противоположным концам диаметра и направленными параллельно. Сравнивают полученную зависимость перемещений от радиуса наночастицы вдоль оси приложения сил с соответствующей аналитической зависимостью перемещений от радиуса упругого шара, сжимаемого сосредоточенными силами, для справочных значений модуля упругости и коэффициента поперечных деформаций исследуемого материала. При этом радиус упругого шара равен радиусу наночастицы, прикладываемые силы к упругому шару равны прикладываемым силам к наночастице. Изменяя модуль упругости, находят такое его значение для справочного коэффициента поперечных деформаций, при котором совпадают (из расчета минимальной среднеквадратичной ошибки) зависимость перемещений от радиуса наночастицы вдоль оси приложения сил, полученная с помощью компьютерного моделирования, с соответствующей аналитической зависимостью перемещений от радиуса упругого шара, сжимаемого сосредоточенными силами.
Вычисляют модуль упругости как среднеарифметическое значение модулей упругости, полученных при совпадении экспериментального перемещения, замеренного в точке приложения силы к наночастице с аналитическим решением зависимости перемещений от радиуса упругого шара, сжимаемого сосредоточенными силами, в этой же точке и зависимости перемещений от радиуса сжимаемой сосредоточенными силами наночастицы, полученной с помощью компьютерного моделирования с аналитическим решением зависимости перемещений от радиуса упругого шара, сжимаемого сосредоточенными силами.
На фиг.1 представлена схема сжатия шарообразной наночастицы после приложения сосредоточенной силы.
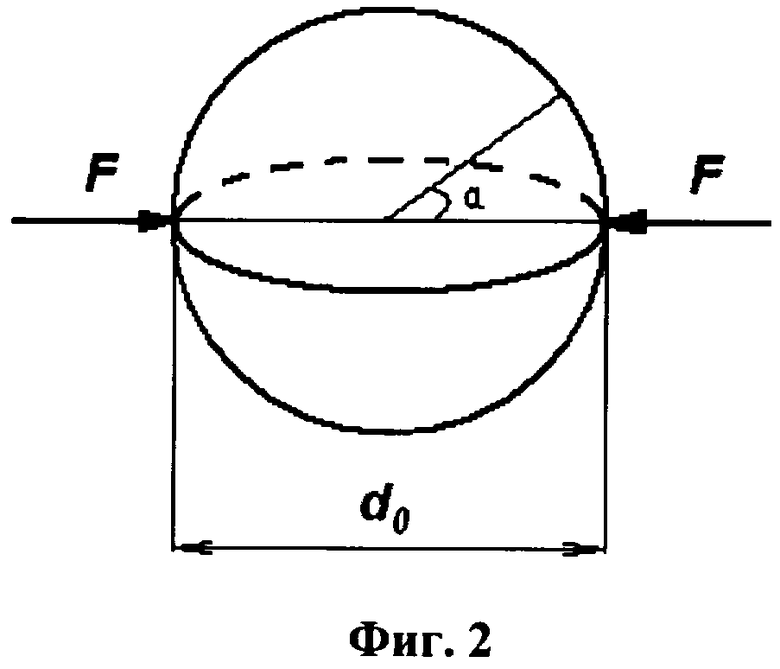
На фиг.2 представлен упругий шар, сжимаемый сосредоточенными силами F, приложенными в противоположные концы его диаметра d0.
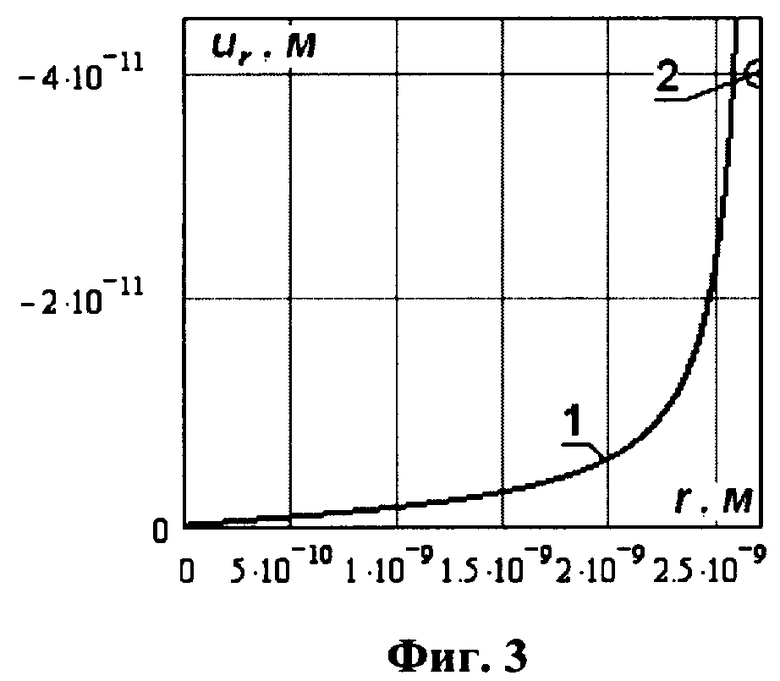
На фиг.3 представлена зависимость перемещений от радиуса упругого шара (1) при его сжатии сосредоточенными силами, приложенными в противоположные концы диаметра для E=1.3·1011 Па, ν=0.34 и экспериментальное перемещение (2) наночастицы с числом атомов 9258 в точке действия силы. Диаметр упругого шара и наночастицы одинаков и равен d0=53.8·10-10 м.
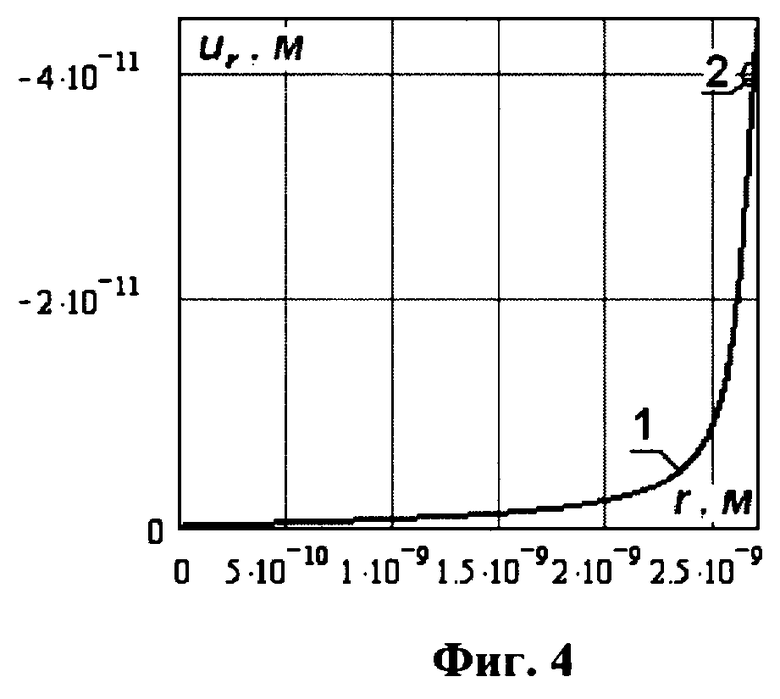
На фиг.4 представлена зависимость перемещений от радиуса упругого шара (1) при его сжатии сосредоточенными силами, приложенными в противоположные концы диаметра для E=E00=3.38·1011 Па, ν=0.34 и экспериментальное перемещение (2) наночастицы с числом атомов 9258 в точке действия силы.
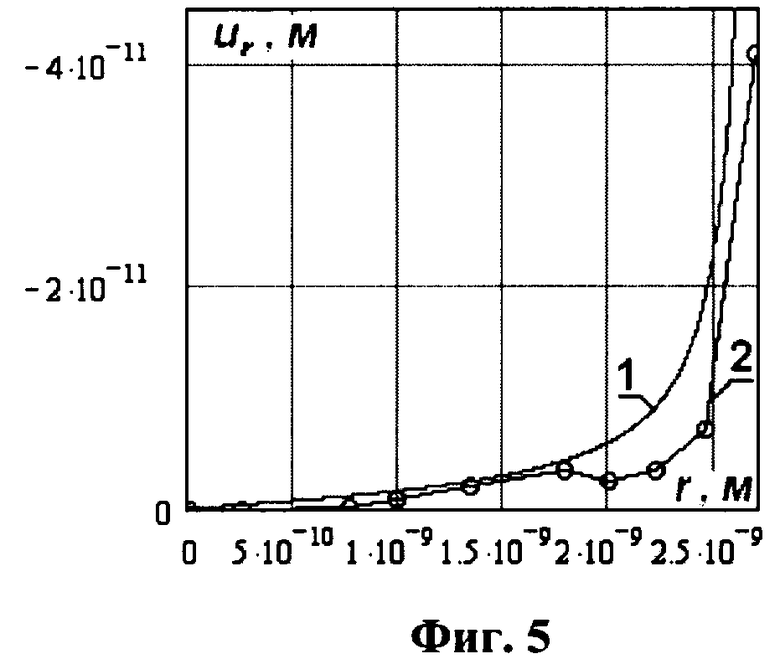
На фиг.5 представлены зависимости перемещений от радиуса при сжатии сосредоточенными силами, приложенными в противоположные концы диаметра вдоль оси приложения сил; (1) - для упругого шара при E=1.3·1011 Па, ν=0.34, (2) - для наночастицы с количеством атомов 9258.
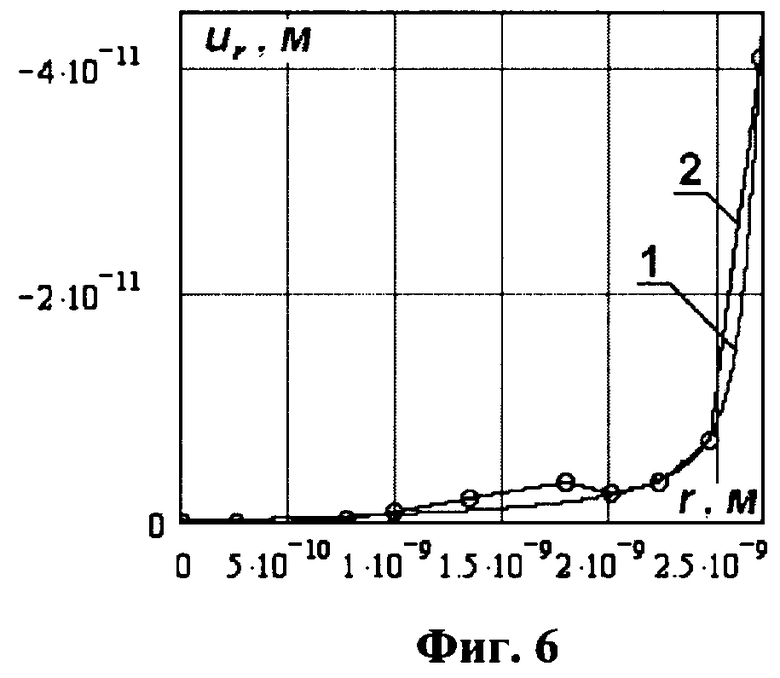
На фиг.6 представлены зависимости перемещений от радиуса при сжатии сосредоточенными силами, приложенными в противоположные концы диаметра вдоль оси приложения сил; (1) - для упругого шара при Е=E01=3.33·1011 Па, ν=0.34, (2) - для наночастицы с количеством атомов 9258.
Способ реализуется, используя сканирующий зондовый микроскоп JSPM-4610 [http://www.tokyo-boeki.ru/science/pdfs/JSPM-4610.pdf], имеющий разрешение по вертикали 0.01·10-9 м, следующим образом. С помощью пьезодвигателей 1 зонд 2 приближают к поверхности наночастицы 3. Таким образом, осуществляют экспериментальное сжатие наночастицы сосредоточенной силой F. Величину силы F взаимодействия определяют при помощи сенсора 4. Вычисляют перемещение в точке приложения силы к наночастице по формуле: 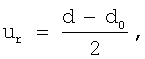 где d0 - начальный диаметр наночастицы, d - диаметр наночастицы после сжатия. Исследуемым материалом в описании примера применения способа является медь. Для наночастицы меди, состоящей из N=9258 атомов, начальный диаметр d0=53.8·10-10 м, d=53.0·10-10 м, соответственно ur=-0.4·10-10 м.
где d0 - начальный диаметр наночастицы, d - диаметр наночастицы после сжатия. Исследуемым материалом в описании примера применения способа является медь. Для наночастицы меди, состоящей из N=9258 атомов, начальный диаметр d0=53.8·10-10 м, d=53.0·10-10 м, соответственно ur=-0.4·10-10 м.
Справочные значения модуля упругости и коэффициента поперечных деформаций для меди равны E=1.3·1011 Па, ν=0.34.
В вычислениях с помощью компьютерного эксперимента между атомами в наночастице действует потенциал парного взаимодействия в форме Леннарда-Джонса, со следующими для меди параметрами: ε=-9.436 ккал/моль - глубина потенциальной ямы, rmin=2.624·10-10 м - расстояние, при котором потенциал Леннарда-Джонса достигает минимума. Сила, прикладываемая к наночастице F=1.4·10-9 H.
Строят аналитическое решение зависимости перемещений от радиуса упругого шара r0, сжимаемого сосредоточенными силами F, направленными параллельно и приложенными в противоположные концы его диаметра d0, вдоль оси приложения сил, для справочных значений модуля упругости Е и коэффициента поперечных деформаций ν по формуле (1)
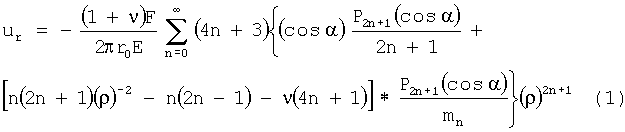
где r0 - радиус шара, P2n(cosα) - полином Лежандра, ρ=r/r0<1, mn - функция, зависящая от ν и n [Блох В.И. Теория упругости: Издательство Харьковского Университета, 1964, с.463].
Изменяя модуль упругости Е, находят такое его значение E00=3.38·1011 Па, при котором совпадают зависимость перемещений от радиуса упругого шара при его сжатии сосредоточенными силами с перемещением в точке приложения силы к наночастице, полученным экспериментально. Коэффициент поперечных деформаций ν остается неизменным.
Изменяя модуль упругости Юнга Е, находят такое его значение Е01=3.33·1011 Па, при котором совпадают зависимость перемещений от радиуса наночастицы, полученная с помощью компьютерного моделирования, и аналитическая зависимость перемещений от радиуса упругого шара при их сжатии сосредоточенными силами, приложенными в противоположные концы диаметра вдоль оси приложения сил.
Вычисляют модуль упругости по формуле (2):
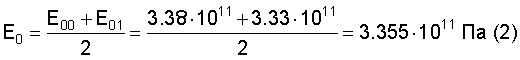
Благодаря предложенному способу стало возможным определять модуль упругости в шарообразных наночастицах.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ ЮНГА МАТЕРИАЛОВ | 2005 |
|
RU2296972C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ ЮНГА МАТЕРИАЛА МИКРО- И НАНОЧАСТИЦ | 2012 |
|
RU2494038C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СВОЙСТВ МАТЕРИАЛА НАНОИНДЕНТИРОВАНИЕМ | 2013 |
|
RU2551263C2 |
| Устройство для проведения инструментального индентирования с возможностью экспериментального наблюдения области контакта индентора с поверхностью образца в реальном времени | 2022 |
|
RU2796200C1 |
| Устройство 3D визуализации деформационного состояния поверхности материала в области упругих деформаций | 2019 |
|
RU2714515C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ ЮНГА И КОЭФФИЦИЕНТА ПУАССОНА МАТЕРИАЛА МИКРО- И НАНОЧАСТИЦ | 2005 |
|
RU2297617C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ ДЕФОРМАЦИИ | 1998 |
|
RU2145655C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИОННЫХ И ПРОЧНОСТНЫХ СВОЙСТВ МАТЕРИАЛОВ ПРИ БОЛЬШИХ ДЕФОРМАЦИЯХ И НЕОДНОРОДНОМ НАПРЯЖЕННО-ДЕФОРМИРОВАННОМ СОСТОЯНИИ | 2006 |
|
RU2324162C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ ДЕФОРМАЦИИ МАТЕРИАЛЬНОЙ СРЕДЫ | 2014 |
|
RU2566400C1 |
| Способ определения механических характеристик оболочки | 1989 |
|
SU1742661A1 |
Изобретение относится к способам определения механических свойств материалов. Сущность: проводят экспериментальное сжатие шарообразной наночастицы сосредоточенной силой. Вычисляют перемещение в точке действия силы на наночастицу. Проводят расчет зависимости перемещений от радиуса наночастицы при ее сжатии сосредоточенными силами, приложенными в противоположные концы диаметра и направленными параллельно вдоль оси приложения сил с помощью компьютерного эксперимента методом молекулярной динамики. Сравнивают экспериментальную зависимость перемещения в точке действия силы на наночастицу и зависимость перемещений от радиуса наночастицы, полученную с помощью компьютерного эксперимента с аналитическим решением зависимости перемещений от радиуса упругого шара, сжимаемого сосредоточенными силами, приложенными в противоположные концы диаметра и направленными параллельно, для справочных значений модуля упругости и коэффициента поперечных деформаций исследуемого материала. Изменяя модуль упругости Юнга, находят такие его значения, при которых совпадают экспериментальная зависимость перемещения в точке действия силы на наночастицу и полученная с помощью компьютерного моделирования зависимость перемещений от радиуса наночастицы с аналитической зависимостью перемещений от радиуса упругого шара, сжимаемого сосредоточенными силами. Вычисляют модуль упругости как среднеарифметическое значение, полученное из двух сравнений. Технический результат: возможность определения модуля упругости для шарообразных наночастиц. 6 ил.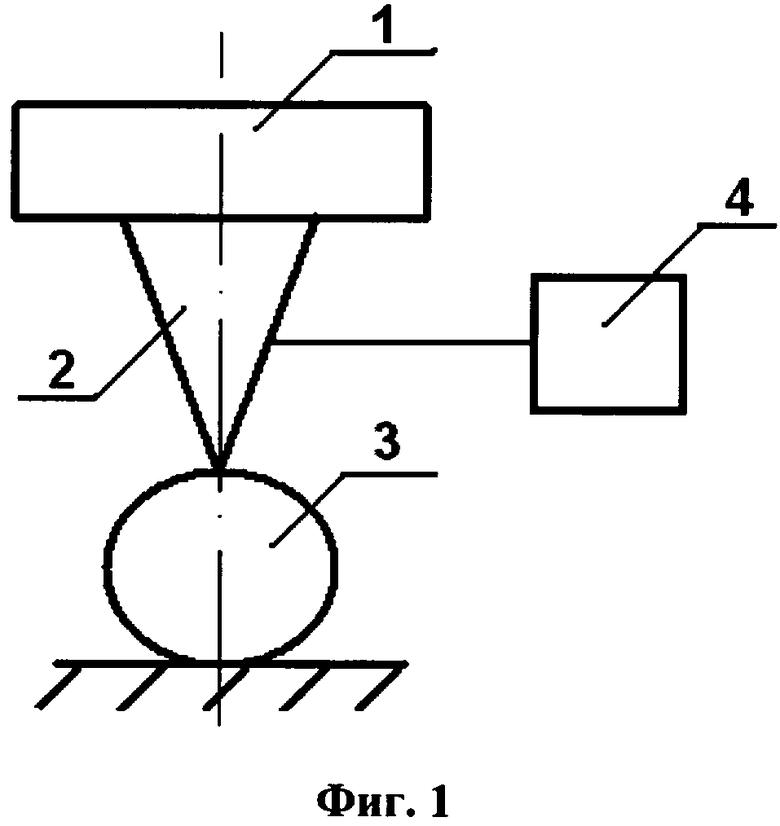
Способ определения модуля упругости Юнга материалов путем приложения сжимающих нагрузок, отличающийся тем, что проводят экспериментальное сжатие шарообразной наночастицы сосредоточенной силой, вычисляют перемещение в точке действия силы на наночастицу; проводят расчет зависимости перемещений от радиуса наночастицы при ее сжатии сосредоточенными силами, приложенными в противоположные концы диаметра и направленными параллельно вдоль оси приложения сил с помощью компьютерного эксперимента методом молекулярной динамики; сравнивают экспериментальную зависимость перемещения в точке действия силы на наночастицу и зависимость перемещений от радиуса наночастицы, полученную с помощью компьютерного эксперимента с аналитическим решением зависимости перемещений от радиуса упругого шара, сжимаемого сосредоточенными силами, приложенными в противоположные концы диаметра и направленными параллельно, для справочных значений модуля упругости и коэффициента поперечных деформаций исследуемого материала; изменяя модуль упругости Юнга, находят такие его значения, при которых совпадают экспериментальная зависимость перемещения в точке действия силы на наночастицу и полученная с помощью компьютерного моделирования зависимость перемещений от радиуса наночастицы с аналитической зависимостью перемещений от радиуса упругого шара, сжимаемого сосредоточенными силами; вычисляют модуль упругости как среднеарифметическое значение, полученное из двух сравнений.
| Способ определения модуля упругости материала | 1980 |
|
SU957054A1 |
| Способ определения модуля упругости материала | 1990 |
|
SU1758475A1 |
| Способ определения динамического модуля Юнга материалов | 1982 |
|
SU1019279A1 |
| DE 4329051 A1, 02.03.1995. | |||
Авторы
Даты
2007-01-20—Публикация
2005-05-06—Подача