Область техники, к которой относится изобретение
Изобретение относится к радиоспектроскопии ядерного магнитного (ЯМР), ядерного квадрупольного (ЯКР), электронного парамагнитного (ЭПР) резонансов и может быть использовано при анализе структуры и динамики молекул, процессов обмена, переноса намагниченности, интенсивности и характерных траекторий движения.
Уровень техники
Многомерная радиоспектроскопия существенно расширила возможности методов при анализе сложных спектров, вместе с тем традиционная многомерная спектроскопия является одним из наиболее трудоемких методов, где эксперимент длится много часов.
Известен способ получения многомерных спектров путем регистрации сигнала в виде функции G(t1, t2, …, tn), где t1 - обычно текущее время, t2-tn - интервалы времени в используемой импульсной последовательности, дискретно с постоянным шагом и независимо меняющиеся в процессе эксперимента. Период повторения импульсной последовательности Т0>T1 (T1 - время спин-решеточной релаксации) и, как правило, в каждой точке требуется накопление сигнала. После применения алгоритма быстрого n-мерного Фурье-преобразования по всем временам получают n-мерный спектр G(ω1, ω2, …, ωn) [1].
Данный способ имеет недостатки: 1) требует очень больших затрат времени (например, двухмерный эксперимент может длиться около суток); 2) максимальное расстояние между двумя соседними точками согласно теореме Найквиста не может быть больше величины, обратной предполагаемой ширине спектра. Если теорема Найквиста не выполняется, то появляются ложные сигналы. С другой стороны, разрешение спектра тем выше, чем больше длина выборки. В результате при сохранении неизменного количества измерительных точек невозможно увеличить разрешение спектра без уменьшения ширины наблюдаемого спектрального диапазона.
Известен также способ нерегулярных, случайных выборок во временной области, предложенный для регистрации многомерных спектров ЯМР. Здесь шаг дискретизации задается по случайному закону с равномерным или нормальным распределением. Многомерное Фурье-преобразование для получения n-мерного спектра из-за неравномерного временного шага выполняется численным интегрированием. Метод не дает определенного предела для ширины наблюдаемого спектра, позволяет без увеличения количества регистрируемых точек увеличивать длину выборки сигнала, а следовательно, и повышать разрешение спектра [2]. Он взят за прототип. Данный способ имеет недостаток - он сопровождается неизбежным наличием артефактов, уровень которых увеличивается при уменьшении количества точек. Увеличить количество точек на этапе обработки и сделать их эквидистантными могла бы интерполяция сигнала полиномом, однако аппроксимация таких функций полиномом даже высокой степени дает грубое приближение, что приводит к не меньшим артефактам. Артефакты, как и выборки, носят случайный характер, зависящий от реализации случайной величины временного интервала. Наличие артефактов в большей степени связано с неравными расстояниями между точками, чем с неточностью интегрирования. Численное интегрирование для набора данных неравномерной выборки не позволяет получить спектр без артефактов. Хорошие результаты с минимальным уровнем артефактов могут быть получены только в случае избыточной выборки при большой средней плотности измерительных точек.
Сущность изобретения
Целью данного изобретения является разработка способа быстрой регистрации многомерных спектров в радиоспектроскопии при сохранении высокого разрешения линий и низкого уровня артефактов.
Эта задача решается с помощью существенных признаков, указанных в формуле изобретения: общих с прототипом - способ сокращения времени измерения n-мерной интерферограммы сигнала за счет уменьшения количества измеряемых точек на временных интервалах, с неравномерно следующими выборками; получение многомерного спектра путем n-мерного Фурье-преобразования численным интегрированием, которое для одного (n-ного) можно записать как: 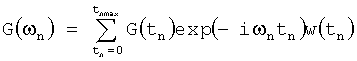 , где w(tn) - весовой множитель, определяемый характером распределения неравномерных длительностей tn и отличительных от наиболее близкого аналога существенных признаков - при измерении используется адаптивная дискретизация сигнала в каждой размерности времени tn по специальному алгоритму, так что шаг дискретизации тем меньше, чем больше амплитуда сигнала. Ниже раскрывается наличие причинно-следственной связи с совокупностью существенных признаков заявляемого изобретения с достигаемым результатом.
, где w(tn) - весовой множитель, определяемый характером распределения неравномерных длительностей tn и отличительных от наиболее близкого аналога существенных признаков - при измерении используется адаптивная дискретизация сигнала в каждой размерности времени tn по специальному алгоритму, так что шаг дискретизации тем меньше, чем больше амплитуда сигнала. Ниже раскрывается наличие причинно-следственной связи с совокупностью существенных признаков заявляемого изобретения с достигаемым результатом.
Во-первых, впервые предложен способ быстрой регистрации многомерных спектров в радиоспектроскопии, не приводящий к искажению спектров артефактами.
Во-вторых, предложенный способ позволяет работать с сигналами, имеющими невысокое отношение сигнал/шум.
В-третьих, способ с адаптацией шага дискретизации к сигналу не требует сортировки данных перед n-мерным Фурье-преобразованием.
Анализ всех отличительных признаков предлагаемого изобретения показал, что изобретательский уровень высок - раньше такие приемы не использовались для решения данной задачи.
Рассмотрим реализацию предлагаемого изобретения на примере 2М-нутационного спектра ЯКР для ядер со спином I=3/2 (η=0.2) в порошке. В простейшем случае, здесь экспериментально необходимо измерить сигнал индукции G(t, tw) после р.ч. импульса переменной длительности tw. По текущему времени t затраты времени несущественны и дискретизация здесь равномерная, с любым необходимым шагом и количеством точек. Основные временные затраты на получение зависимости сигнала от tw, обусловленные периодом повторения Т0>T1 импульсной последовательности и необходимостью накопления сигнала. Сначала задаем ширину наблюдаемого спектра νmax (100 кГц) и определяем максимальный шаг дискретизации спектра 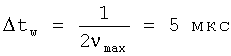 , задаем длину выборки twmax (500 мкс), предполагая разрешение линий 1 кГц. Таким образом, минимальное количество точек при равномерной дискретизации будет Nmin=100. Устанавливаем длительность tw=5 мкс и измеряем сигнал G(t, tw), определяем стандартное отклонение σ амплитуды шума в конце выборки по текущему времени t. Сравниваем величину сигнала G(0, tw) с сигналом G(0, 0)=0 в предыдущий момент времени tw=0. Если изменение сигнала по абсолютной величине больше 2σ, то следующее измерение выполняется для tw=2Δtw, в противном случае величина шага для tw увеличивается. На фиг.1 приведен алгоритм адаптивной дискретизации временного интервала tw, который используется при реализации способа. При tw=twmax измерения заканчиваются, определяется число точек адаптивной выборки Nад<Nmin и выполняется Фурье-преобразование сигнала методом численного интегрирования.
, задаем длину выборки twmax (500 мкс), предполагая разрешение линий 1 кГц. Таким образом, минимальное количество точек при равномерной дискретизации будет Nmin=100. Устанавливаем длительность tw=5 мкс и измеряем сигнал G(t, tw), определяем стандартное отклонение σ амплитуды шума в конце выборки по текущему времени t. Сравниваем величину сигнала G(0, tw) с сигналом G(0, 0)=0 в предыдущий момент времени tw=0. Если изменение сигнала по абсолютной величине больше 2σ, то следующее измерение выполняется для tw=2Δtw, в противном случае величина шага для tw увеличивается. На фиг.1 приведен алгоритм адаптивной дискретизации временного интервала tw, который используется при реализации способа. При tw=twmax измерения заканчиваются, определяется число точек адаптивной выборки Nад<Nmin и выполняется Фурье-преобразование сигнала методом численного интегрирования.
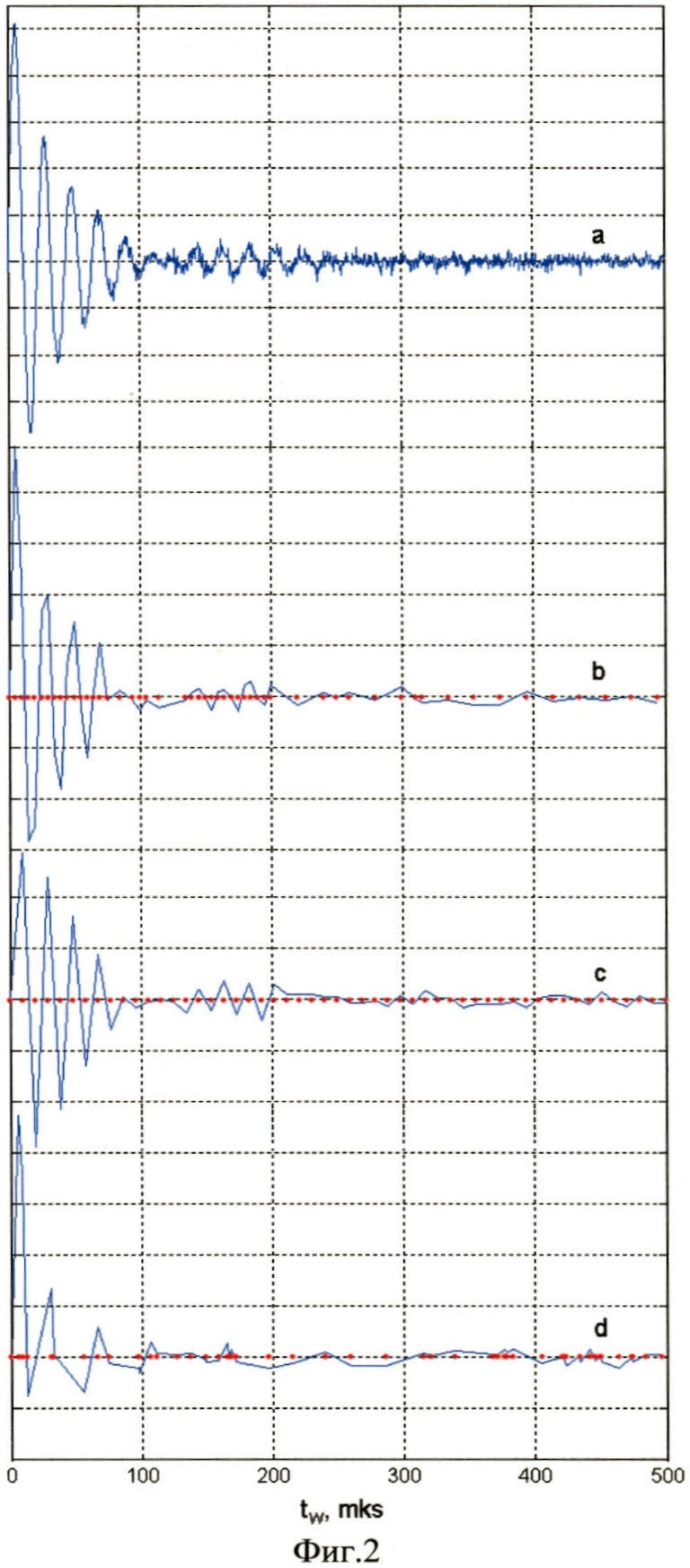
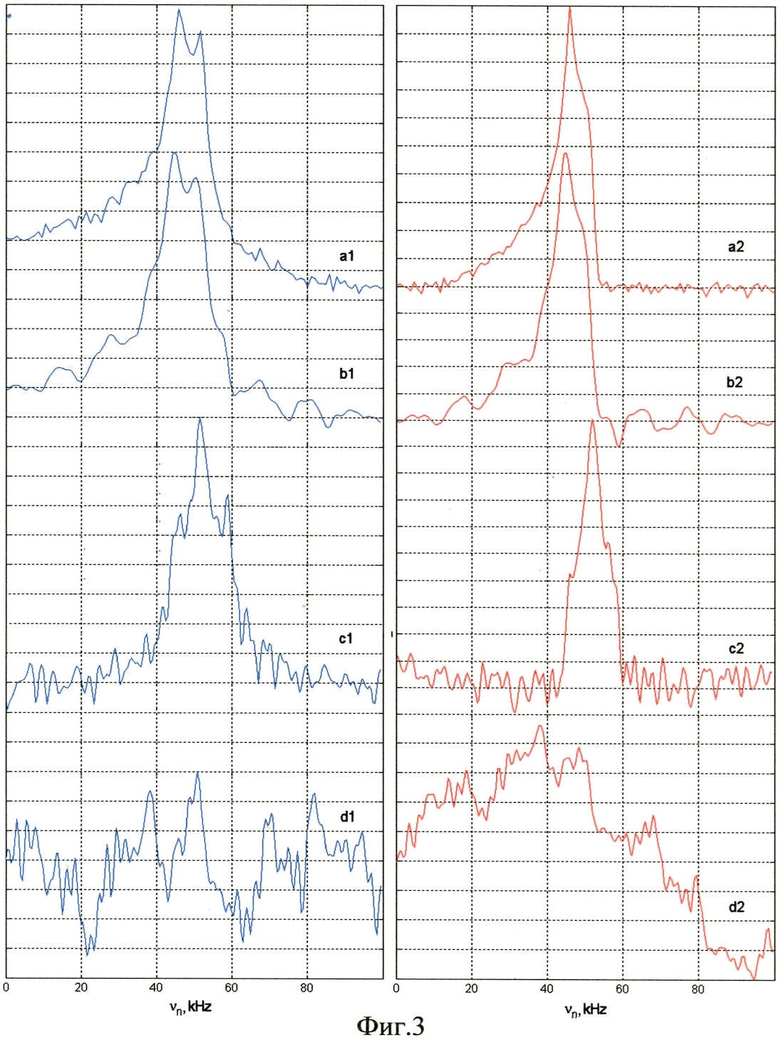
На фиг.2 приведены смоделированные сигналы ЯКР G(0, tw) для I=3/2 (η=0.2) в порошке при равномерной выборке N=1000 точек (а), адаптивной дискретизации Nад=52 (b), равномерной дискретизации N=52 (с) и дискретизации по случайному закону N=52 (d). На фиг.3 для сравнения показаны спектры мощности сигналов, представленных на фиг.2, при равномерной выборке N=1000 точек (а1), адаптивной дискретизации Nад=52 (b1), равномерной дискретизации N=52 (с1) и дискретизации по случайному закону N=52 (d1). Соответствующие действительные величины спектров обозначены а2, b2, с2 и d2. При адаптивной выборке (b1, b2) нутационный спектр воспроизводится без искажений, обеспечивая выигрыш во времени Nmin/Naд=2 раза (в одной временной размерности), в то время как при равномерной выборке с таким же количеством точек (с1, с2) наблюдаются недопустимые искажения спектра. При случайной выборке с таким же количеством точек (d1, d2) нутационный спектр из-за сильных артефактов вообще не наблюдается. Таким образом, данный способ позволяет значительно сократить время регистрации многомерных спектров при сохранении высокого разрешения.
Источники информации
1. Р.Эрнст, Дж.Боденхаузен, А.Вокаун. ЯМР в одном и двух измерениях. - М.: Мир, 1990.
2. К.Kazimierczuk, A.Zawadzka, W.Kozminski & I.Zhukov // Random sampling of evolution time space and Fourier transform processing // J. Biomol. NMR (2006), 36, 157-168, /3/ - K.Kazimierczuk, A.Zawadzka, W.Kozminski & I.Zhukov // Lineshapes and Artifacts in Multidimensional Fourier Transform of Arbitrary Sampled NMR Data Sets // J. Magn. Reson., 188 (2007), 344-356 (прототип).
Использование для быстрой регистрации многомерных спектров в радиоспектроскопии. Сущность заключается в том, что осуществляют воздействие на образец импульсной последовательностью с независимо изменяющимися временными интервалами, уменьшают количество измеряемых точек на временных интервалах за счет неравномерно следующих выборок без уменьшения длины выборки, выполняют многомерное Фурье-преобразование численным интегрированием, при этом дискретизацию временных переменных выполняют адаптивно к амплитуде сигнала, увеличивая шаг выборки с уменьшением интенсивности регистрируемого сигнала. Технический результат: сокращение времени регистрации многомерных спектров при сохранении высокого разрешения. 3 ил.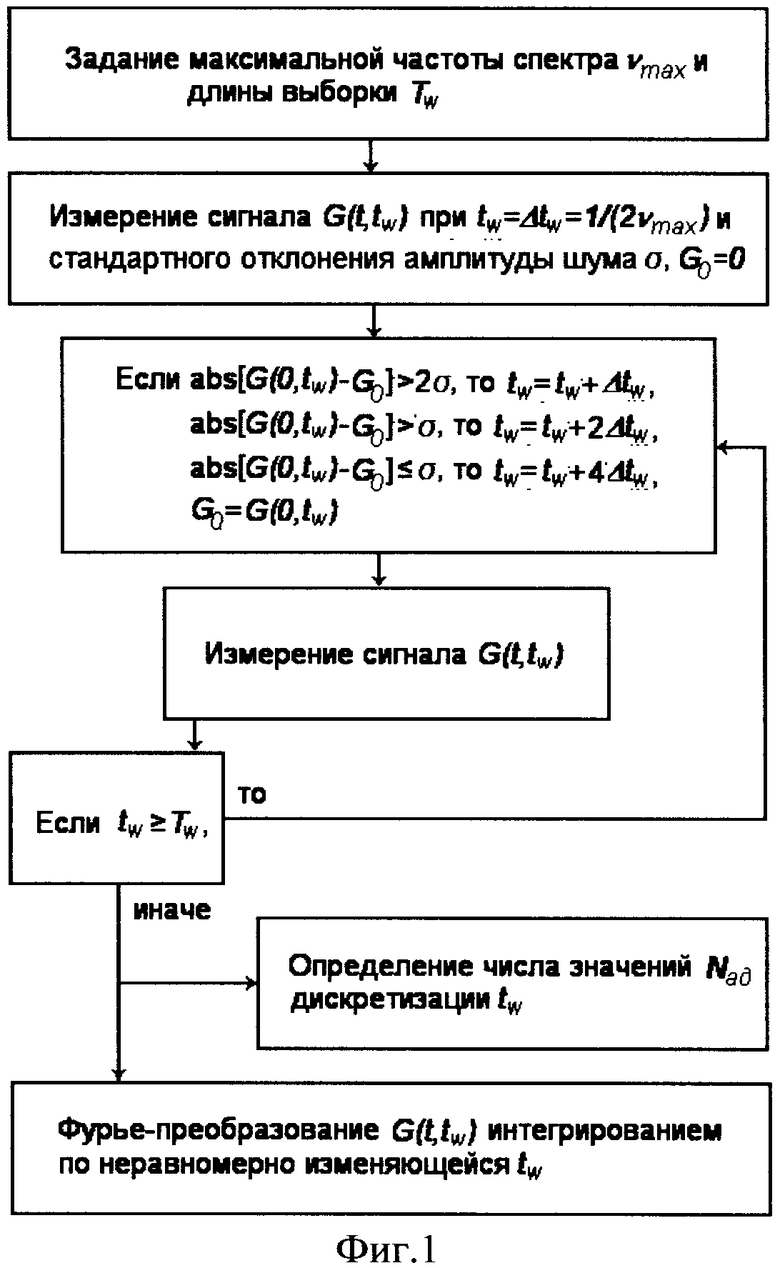
Способ быстрой регистрации многомерных спектров в радиоспектроскопии, включающий воздействие на образец импульсной последовательности с независимо изменяющимися временными интервалами, уменьшение количества измеряемых точек на временных интервалах за счет неравномерно следующих выборок без уменьшения длины выборки, многомерное Фурье-преобразование численным интегрированием, отличающийся тем, что дискретизацию временных переменных выполняют адаптивно к амплитуде сигнала, увеличивая шаг выборки с уменьшением интенсивности регистрируемого сигнала.
| K.Kazimierczuk, A.Zawadzka, W.Kozminski & I.Zhukov, Lineshapes and Artifacts in Multidimensional Fourier Transform of Arbitrary Sampled NMR Data Sets, J | |||
| Magn | |||
| Reson., 188, 2007, c.344-356 | |||
| Способ измерения времени спин-решеточной релаксации | 1989 |
|
SU1728750A1 |
| Способ регистрации сигнала резонансного взаимодействия вещества с электромагнитным излучением (ЭМИ) и устройство для его осуществления | 1987 |
|
SU1566275A1 |
| Способ томографии на основе ядерного магнитного резонанса | 1986 |
|
SU1467476A1 |
| JP 3007141 A, 14.01.1991 | |||
| US 6704594 В1, 09.03.2004. | |||
Авторы
Даты
2011-11-27—Публикация
2010-06-22—Подача