Перекрестная ссылка на родственные заявки
В данной заявке PCT заявлен приоритет в соответствии с (1) предварительной заявкой № 60/855064 на патент США под названием "SYSTEMS, METHODS AND APPARATUS FOR PARTICLE DETECTION AND ANALYSIS AND FIELD DEPLOYMENT OF THE SAME", поданной 27 октября 2006 г., и (2) заявкой № 11/771169 на патент США под названием "RADIATION PORTAL MONITOR SYSTEM AND METHOD", поданной 29 июня 2007 г.
Раскрытия упомянутых выше двух заявок приведены здесь в качестве ссылочного материала.
Заявление в отношении федеральных прав
Данное изобретение было выполнено при поддержке Правительства в соответствии с контрактом № DE-AC52-06NA25396, предоставленным Департаментом энергетики Соединенных Штатов Америки. Правительство обладает определенными правами в отношении данного изобретения.
Область техники, к которой относится изобретение
Варианты воплощения относятся к областям детектирования частиц, анализа, управления и, более конкретно, но не исключительно, к способам и системам анализа данных, полученных из системы детектирования заряженных частиц, имеющих множество датчиков, чувствительных к положению, и предназначенным для реконструкции траектории заряженной частицы, такой как мю-мезон космических лучей, пролетающей через систему детектирования заряженных частиц.
Уровень техники
Томография заряженных частиц основана на рассеянии заряженных частиц. Одна из форм томографии заряженных частиц представляет собой томографию космических лучей, которая основана на рассеянии мю-мезонов космических лучей. Прилетающие из открытого космоса стабильные частицы, в основном протоны, постоянно бомбардируют Землю. Эти частицы взаимодействуют с атомами в верхней атмосфере, формируя ливни частиц, которые включают в себя множество короткоживущих пи-мезонов, которые распадаются и формируют долгоживущие мю-мезоны. Мю-мезоны взаимодействуют с веществом, в основном, через кулонову силу без ядерного взаимодействия и при значительно меньшем излучении, чем электроны. Они теряют энергию только медленно в результате электромагнитного взаимодействия. Следовательно, множество мю-мезонов достигает поверхности Земли как обладающее высокой степенью проникающей способности излучение заряженных частиц. Поток мю-мезонов на уровне моря составляет приблизительно один мю-мезон на см2 в минуту.
По мере того, как мю-мезоны пролетают через материал, кулоново рассеяние зарядов внутриатомных частиц нарушает их траекторию. Полное отклонение зависит от нескольких свойств материала, но доминирующие параметры представляют собой атомное число Z ядра и плотность материала.
Существует потребность в разработке улучшенного способа и системы для реконструирования, представляющего интерес объема, на основе мю-мезонов или других заряженных частиц, пролетающих через этот объем.
Сущность изобретения
Следующий раздел "Сущность изобретения" представлен с тем, чтобы облегчить понимание некоторых технических свойств, относящихся к технологиям, устройству и системам детектирования частиц, таких как заряженные частицы типа мю-мезонов, и статистической реконструкции профилей плотности рассеяния в предметном объеме по томографическим данным заряженных частиц, и не предназначен для представления полного описания. Полное понимание различных аспектов изобретения будет получено при рассмотрении всего описания, формулы изобретения, чертежей и реферата в целом.
Упомянутые выше аспекты изобретения и другие цели и преимущества могут быть теперь достигнуты, как описано ниже.
В соответствии с одним аспектом, описана система детектирования, предназначенная для детектирования предметного объема с использованием заряженных частиц, пролетающих через этот предметный объем. Эта система включает в себя первый набор детекторов, чувствительных к положению, расположенных на первой стороне предметного объема, для измерения положений и углов падающих заряженных частиц в направлении предметного объема; второй набор детекторов, чувствительных к положению, расположенных на второй стороне предметного объема, противоположной первой стороне, для измерения положения и углов заряженных частиц, вылетающих из объема объекта; и модуль обработки сигналов для приема данных измеренных сигналов из первого набора чувствительных к положению детекторов и измеренных сигналов из второго набора чувствительных к положению детекторов. Модуль обработки сигнала обрабатывает принятые данные для получения статистической реконструкции распределения плотности рассеяния в предметном объеме.
Модуль обработки сигнала может быть выполнен с возможностью: (a) получать томографические данные заряженных частиц, соответствующие углам рассеяния, и оценивать импульсы заряженных частиц, пролетающих через предметный объем; (b) предоставлять распределение вероятности плотности рассеяния заряженных частиц на основе множества статистических моделей рассеяния; (c) определять, по существу, оценку наибольшего правдоподобия плотности рассеяния предметного объема, используя алгоритм максимизации ожидания (ML/EM); и (d) выводить реконструированную плотность рассеяния предметного объема на основе, по существу, оценки наибольшего правдоподобия.
В соответствии с другим аспектом, способ детектирования предметного объема по томографическим данным заряженных частиц, полученным из предметного объема, содержит: (a) получают заданные томографические данные заряженных частиц, соответствующие углам рассеяния и оцениваемым импульсам заряженных частиц, пролетающих через предметный объем; (b) предоставляют распределение вероятности рассеяния заряженных частиц на основе статистической модели множественного рассеяния; (c) определяют, по существу, оценку наибольшего правдоподобия плотности рассеяния предметного объема, используя алгоритм максимизации ожидания (ML/EM); (d) выводят реконструированную плотность рассеяния предметного объема; и, в случае необходимости, (e) принимают решение на основе реконструированной плотности рассеяния предметного объема.
Способ позволяет пользователю идентифицировать наличие и/или тип объекта, занимающего объем, представляющий интерес, по реконструированному профилю плотности рассеяния объема. Различные варианты применения включают в себя томографию мю-мезонов космических лучей для различных вариантов применения при инспекции для национальной безопасности, в которых можно сканировать транспортные средства или грузы с использованием системы слежения за мю-мезонами.
Томографические данные заряженных частиц могут содержать томографические данные, собранные по заряженным частицам, таким как мю-мезоны, генерируемые космическими лучами или некоторым другим источником.
Принятие решения на основе реконструированной плотности рассеяния предметного объема может содержать принятие решения по, по меньшей мере, одному из (1) наличия и (2) типа целевого объекта в предметном объеме на основе реконструированной плотности рассеяния предметного объема.
Представление распределения вероятности рассеяния заряженных частиц для использования в алгоритме максимизации ожидания (ML/EM) может содержать (g), получают двумерное распределение вероятности для заряженной частицы на основе заданной плотности рассеяния однородного объекта; (h) получают трехмерное распределение вероятности для заряженной частицы на основе двумерного распределения вероятности; (i) получают распределение вероятности для рассеяния множества заряженных частиц через неоднородный предметный объем, характеризуемый через основные функции; и (j) получают распределение вероятности для множественного рассеяния на основе его определения и результатов измерения рассеяния и импульса заряженных частиц.
Получение двумерного распределения вероятности для заряженной частицы на основе заданной плотности рассеяния однородного объекта может содержать (k), определяют плотность рассеяния материала как ожидаемое среднеквадратичное рассеяние заряженных частиц через единицу глубины материала; (l) аппроксимируют распределение рассеяния заряженной частицы на основе гауссовой модели; и (m) аппроксимируют рассеяние и смещение лучей заряженных частиц на основе коррелированного двумерного гауссова распределения.
Получение трехмерного распределения вероятности для заряженной частицы на основе двумерного распределения вероятности может содержать добавление координаты и определение трехмерной длины пути; расчет трехмерного смещения; и определение трехмерной ковариационной матрицы.
Получение распределения вероятности для рассеяния множества заряженных частиц через неоднородный предметный объем, характеризуемый через основные функции, может содержать установление трехмерной решетки на основе функций, представляющих дискретные оценки плотности рассеяния; определение ковариационной матрицы рассеяния/смещения для каждого индивидуального мю-мезона как функции пути луча и оценки плотности рассеяния; и определение распределения вероятности для множества заряженных частиц как произведение вероятностей отдельных заряженных частиц.
Определение, по существу, максимальной оценки вероятности плотности рассеяния предметного объема с использованием алгоритма максимизации ожидания (ML/EM) может содержать сбор результатов измерений рассеяния и импульса для каждой заряженной частицы; оценку пространственной структуры взаимодействия каждой заряженной частицы с каждой основной функцией статистической модели рассеяния; для каждой пары основной функции заряженной частицы определяют матрицу весов: Wij; инициализируют плотность рассеяния каждой основной функции на основе предположения; и итеративно находят приблизительное решение наибольшего правдоподобия для содержания предметного объема, в котором итеративный процесс останавливают через заданное количество итераций, или когда решение изменяется меньше, чем заданное допустимое значение.
Определение, по существу, максимальной оценки вероятности плотности рассеяния предметного объема с использованием алгоритма максимизации ожидания (ML/EM) может содержать: собирают результаты измерения рассеяния и импульса для каждой заряженной частицы от i=1 до i=М. (Δθx, Δθy, Δx, Δy, p2 r)i, получают оценку пространственной структуры взаимодействия каждого мю-мезона с каждым вокселем от j=1 до j=N: (L, T)ij; для каждой пары заряженная частица - воксель рассчитывают матрицу весов: Wij, как 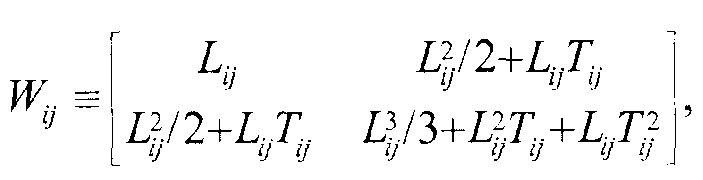 , инициализируют предположение о плотности λj,old рассеяния в каждом вокселе; и используют обработку критерия остановки для установки λj,old=λj,new для всех вокселей.
, инициализируют предположение о плотности λj,old рассеяния в каждом вокселе; и используют обработку критерия остановки для установки λj,old=λj,new для всех вокселей.
Алгоритм максимизации ожидания (ML/EM) может включать в себя правило обновления среднего значения или правило обновления медианы.
В соответствии с еще одним аспектом, выполняемый компьютером способ детектирования предметного объема по томографическим данным заряженных частиц, полученных из предметного объема, содержит: (a) получают томографические данные заряженных частиц, соответствующие углам рассеяния и оценкам импульсов заряженных частиц, пролетевших через предметный объем; (b) предоставляют распределение вероятности плотности рассеяния заряженных частиц для использования в алгоритме максимизации ожидания (ML/EM), причем распределение вероятности основано на статистической модели множественного рассеяния; (c) определяют, по существу, оценку наибольшего правдоподобия плотности рассеяния предметного объема, используя алгоритм максимизации ожидания (ML/EM); и (d) выводят реконструированную плотность рассеяния предметного объема. Может быть принято решение на основе реконструированной плотности объема рассеяния объекта.
В соответствии с еще одним другим аспектом компьютерный программный продукт содержит используемый компьютером носитель данных, на котором записаны инструкции, которые при выполнении их компьютером обеспечивают выполнение компьютером способа статистической реконструкции профилей распределения плотности предметного объема по томографическим данным заряженных частиц, способ содержит: (a) получают заданные томографические данные заряженных частиц, соответствующие углам рассеяния и оценкам импульсов заряженных частиц, пролетающих через предметный объем; (b) предоставляют распределение вероятности рассеяния заряженных частиц для использования в алгоритме максимизации ожидания (ML/EM), причем распределение вероятности основано на статистической модели множественного рассеяния; (c) определяют, по существу, оценку наибольшего правдоподобия плотности предметного объема, используя алгоритм максимизации ожидания (ML/EM); и (d) выводят реконструированную плотность рассеяния предметного объема.
Краткое описание чертежей
Приложенные чертежи, на которых одинаковыми номерами ссылочных позиций обозначены идентичные или функционально аналогичные элементы на всех отдельных видах, и которые приведены в описании и формируют часть описания, дополнительно иллюстрируют настоящее изобретение и, вместе с подробным описанием изобретения, используются для пояснения принципов настоящего изобретения.
На фиг. 1 иллюстрируется один пример концепции мю-мезонной томографии;
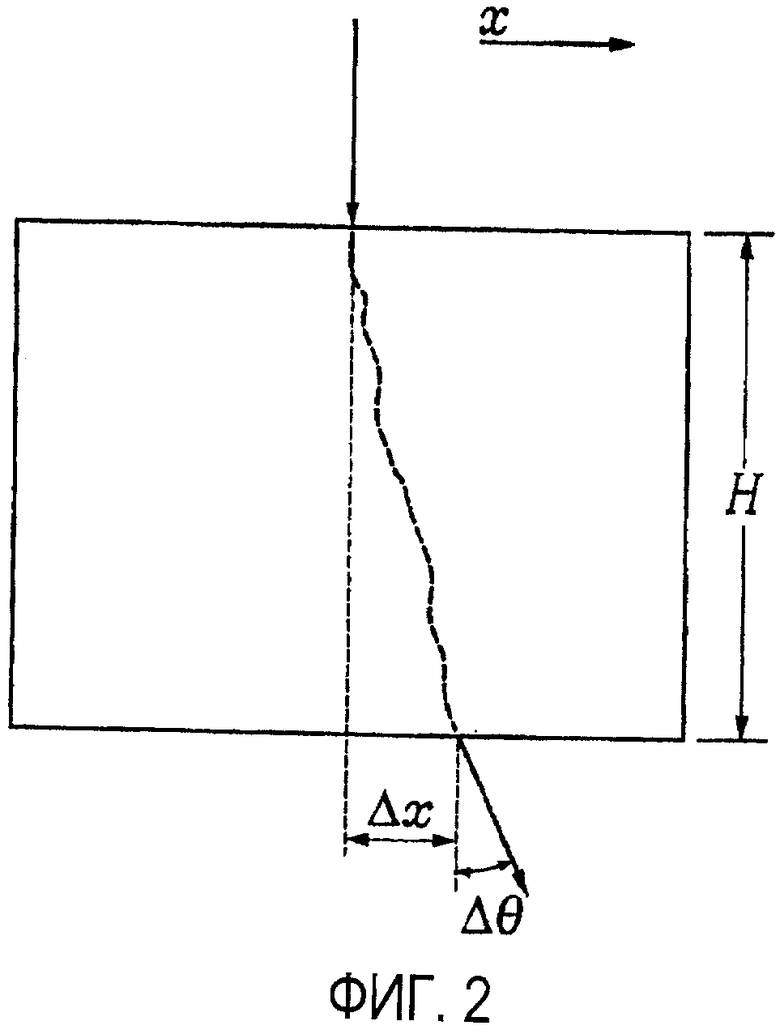
на фиг. 2 иллюстрируется двумерная проекция рассеяния и смещения, используемая для определения кулонова рассеяния;
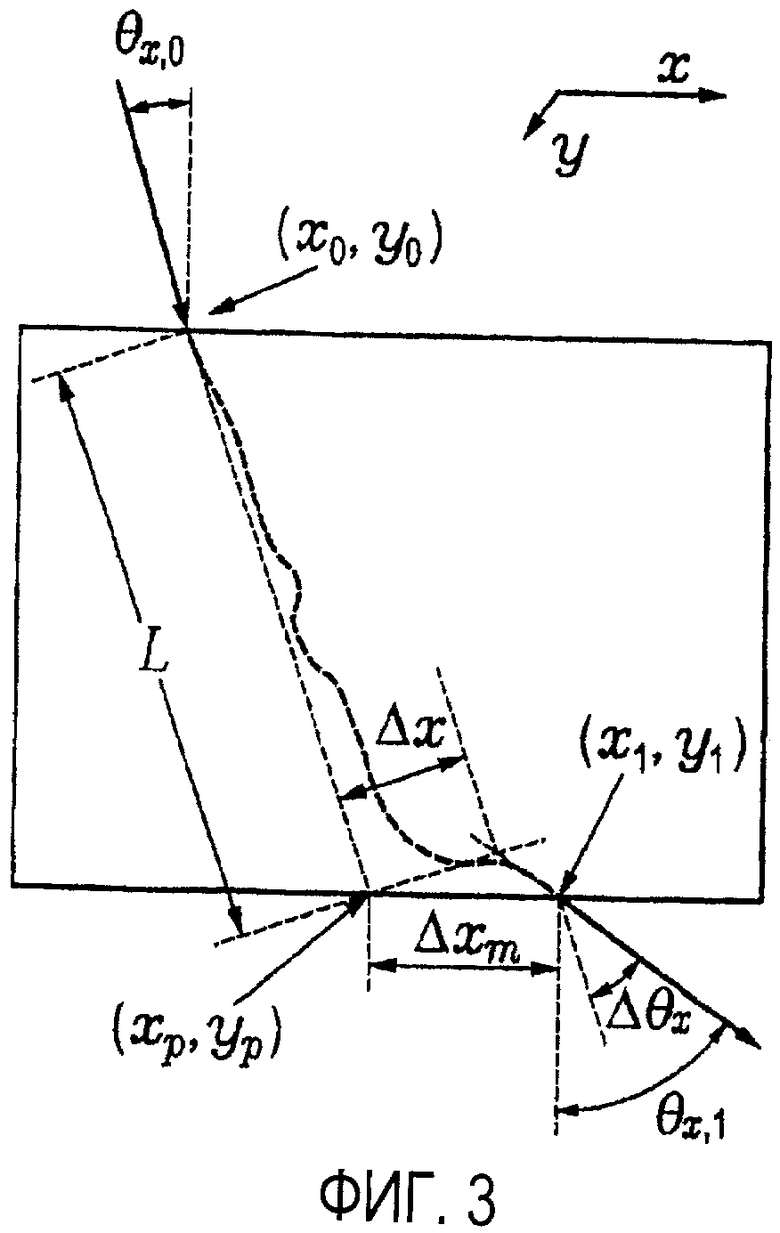
на фиг. 3 иллюстрируются параметры двумерной проекции и рассеяния, и смещения, используемые для регулировки модели трехмерного рассеяния;
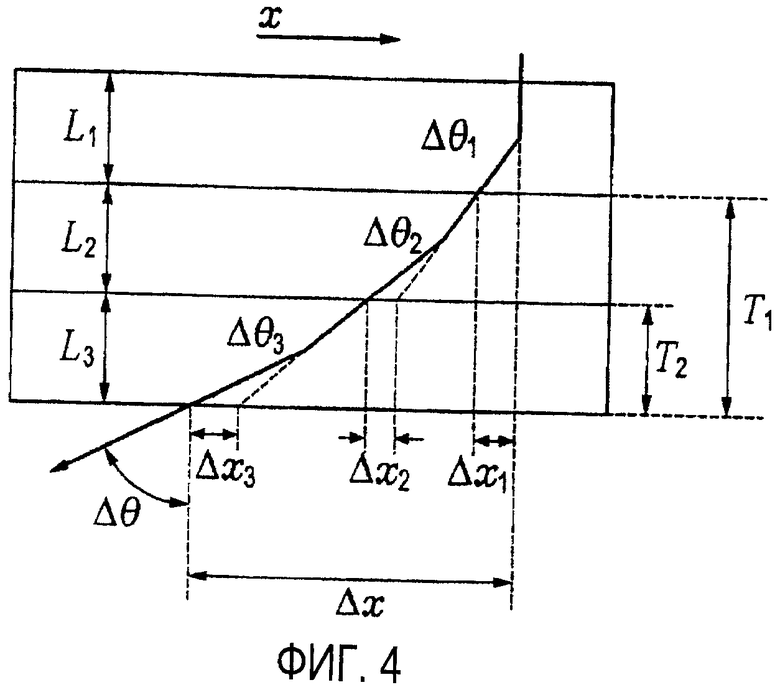
на фиг. 4 иллюстрируется рассеяние через множество слоев материала;
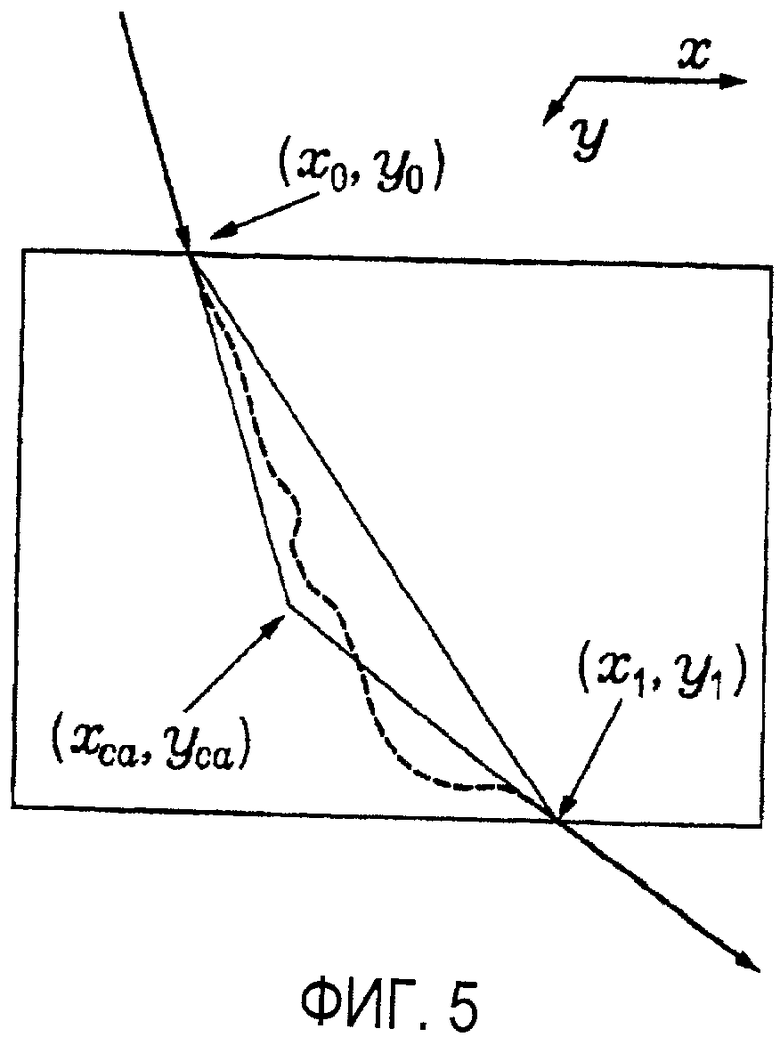
на фиг. 5 иллюстрируется точка использования ближайшего приближения для расчетов длины пути проекции, показанной на фиг.3;
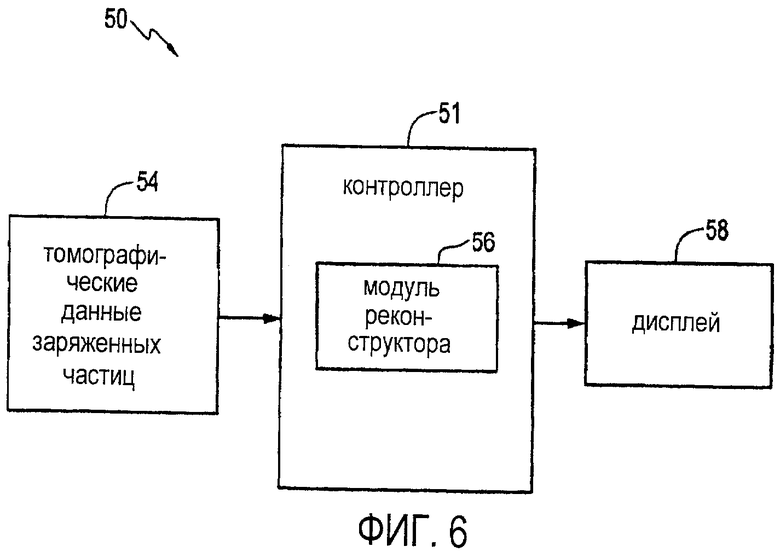
на фиг. 6 иллюстрируется автоматизированная система для статистической реконструкции профилей плотности рассеяния в объеме для мю-мезонной томографии;
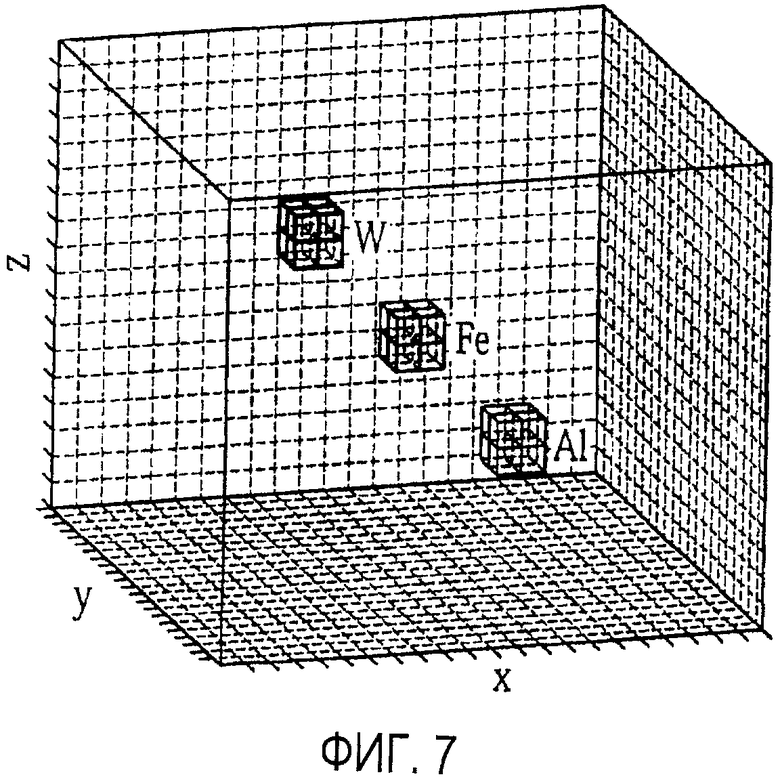
на фиг. 7 иллюстрируется вид в перспективе моделируемых объектов;
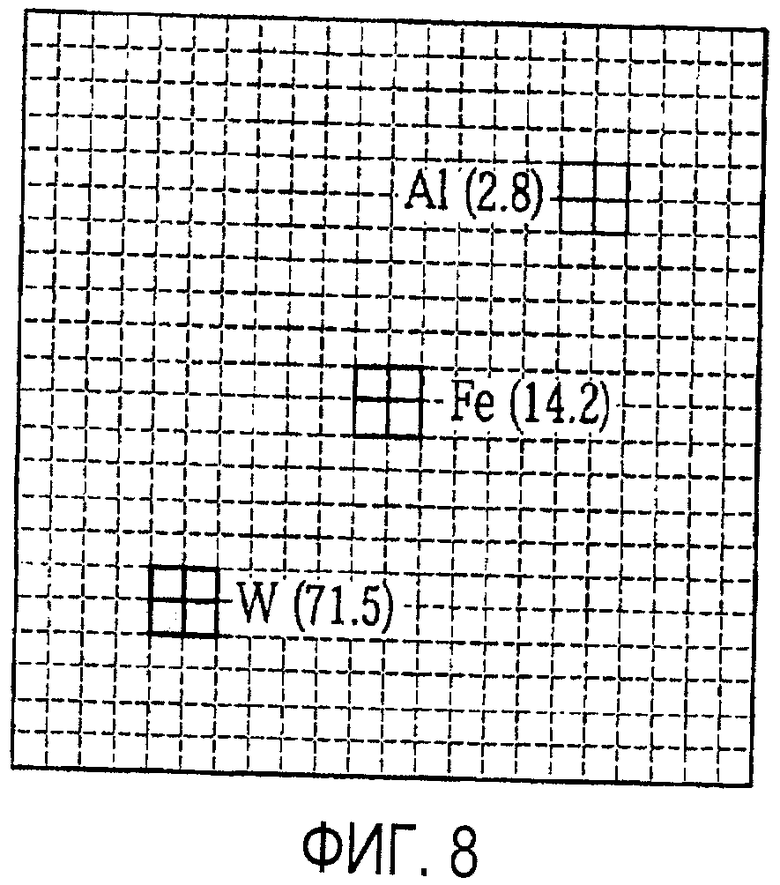
на фиг. 8 иллюстрируется вид сверху моделируемых объектов;
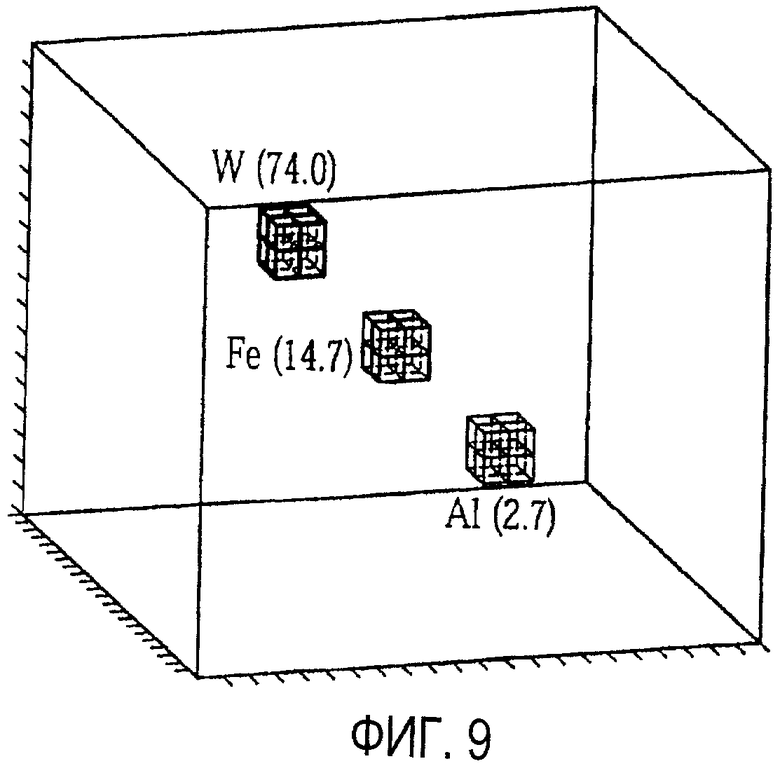
на фиг. 9 иллюстрируется реконструкция моделирования гауссова рассеяния с длинами пути, оценка которых была получена на основе предположения двух линий, соединенных в точке PoCA;
на фиг. 10 иллюстрируется реконструкция моделируемых данных с использованием рассеяния с негауссовыми хвостами;
на фиг. 11 иллюстрируется реконструкция моделируемых данных с использованием рассеяния с негауссовыми хвостами при применении способа медианы;
на фиг. 12 иллюстрируются основные объекты в моделируемом пассажирском микроавтобусе;
на фиг. 13 иллюстрируется реконструкция для моделируемой мю-мезонной экспозиции в течение 1 минуты пассажирского микроавтобуса с использованием способа средних значений;
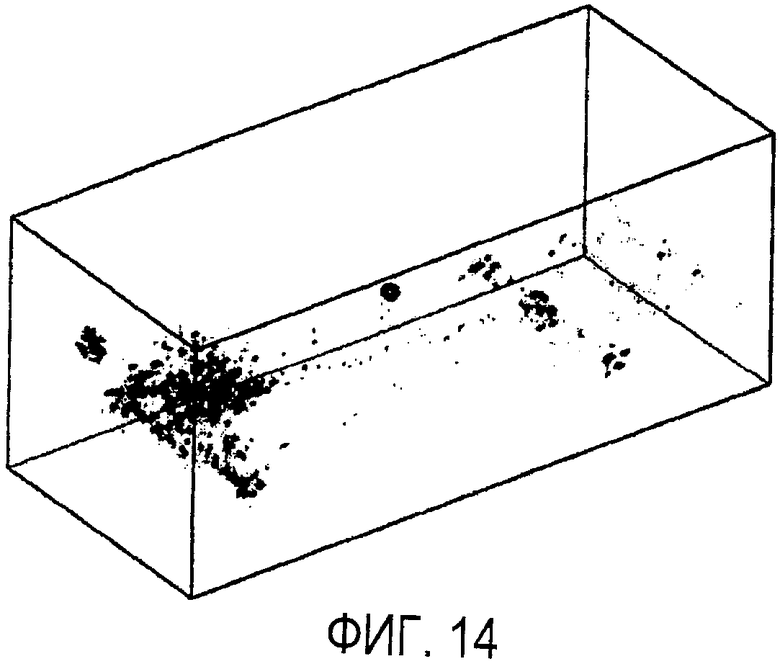
на фиг. 14 иллюстрируется реконструкция сцены пассажирского микроавтобуса с использованием способа медианы;
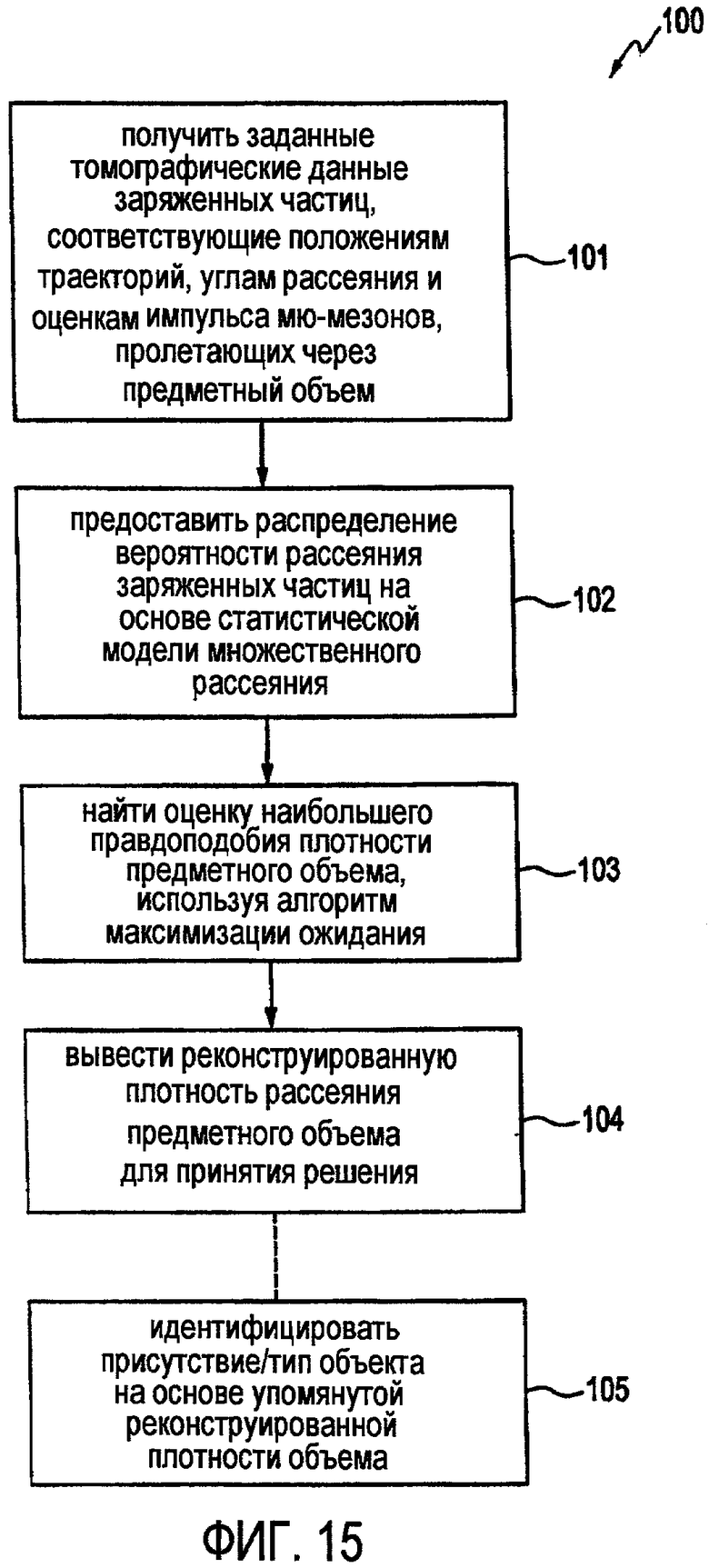
на фиг. 15 иллюстрируется блок-схема последовательности операций, в общем, представляющая способ статистической реконструкции профилей распределения плотности рассеяния в объеме для томографии заряженных частиц в соответствии с одним вариантом осуществления;
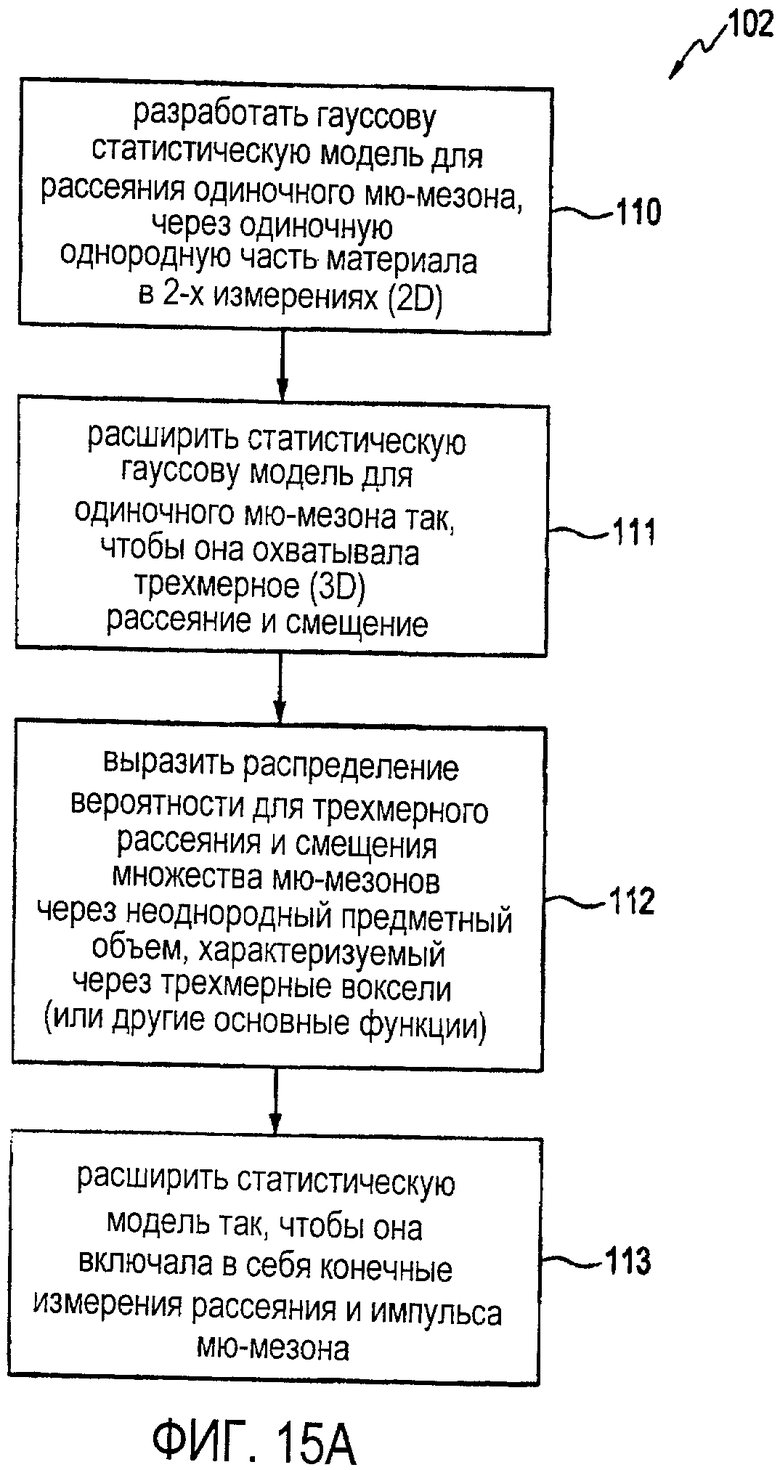
на фиг. 15A иллюстрируется блок-схема последовательности операций, представляющая пример обработки оценки распределения вероятности рассеяния мю-мезона, пролетающего через предметный объем, с использованием множества моделей статистического рассеяния в соответствии с одним вариантом осуществления;
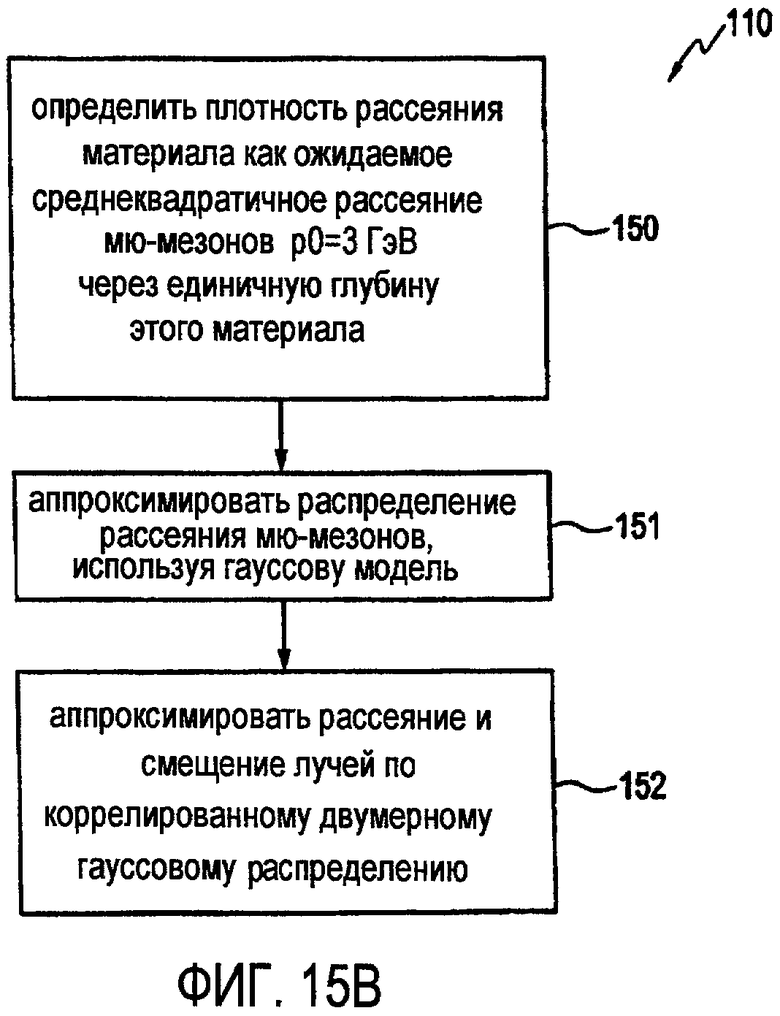
на фиг. 15B иллюстрируется блок-схема последовательности операций, представляющая пример обработки оценки ожидаемого распределения вероятности двумерного рассеяния для одного мю-мезона на основе заданной плотности рассеяния объекта в соответствии с одним вариантом осуществления;
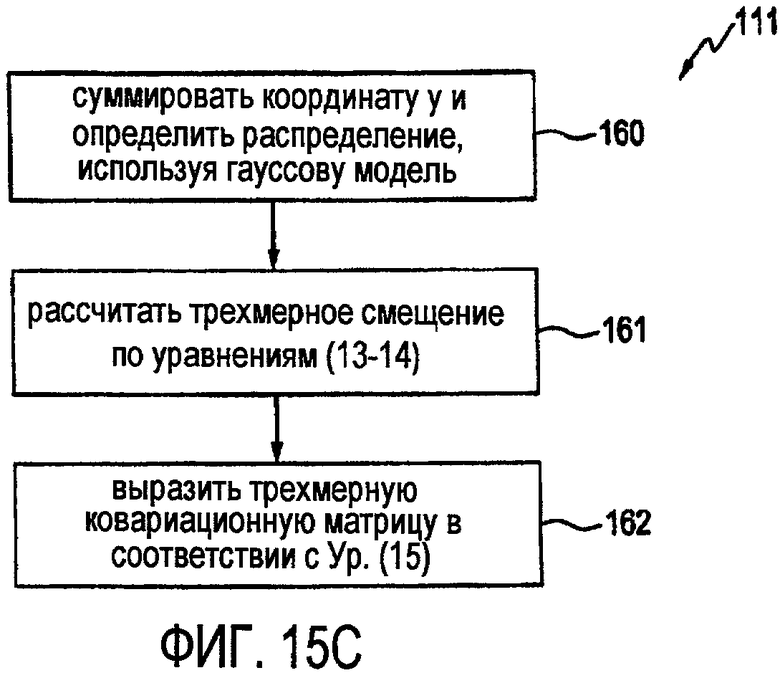
на фиг. 15C иллюстрируется блок-схема последовательности операций, представляющая пример обработки расширения статистической модели до трехмерной модели в соответствии с одним вариантом осуществления;
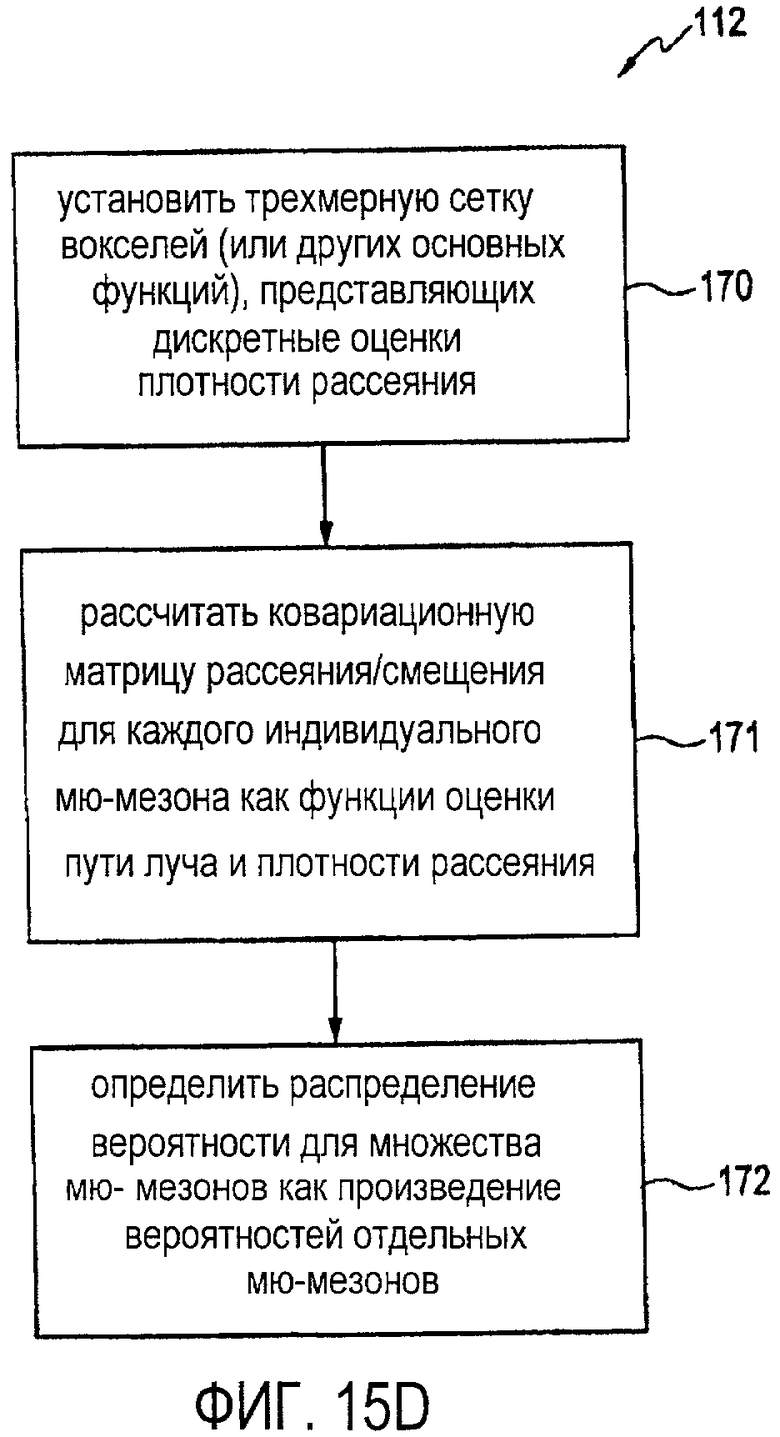
на фиг. 15D иллюстрируется блок-схема последовательности операций, представляющая пример обработки определения распределения вероятности для рассеяния и смещения множества мю-мезонов через неоднородные материалы в соответствии с одним вариантом осуществления; и
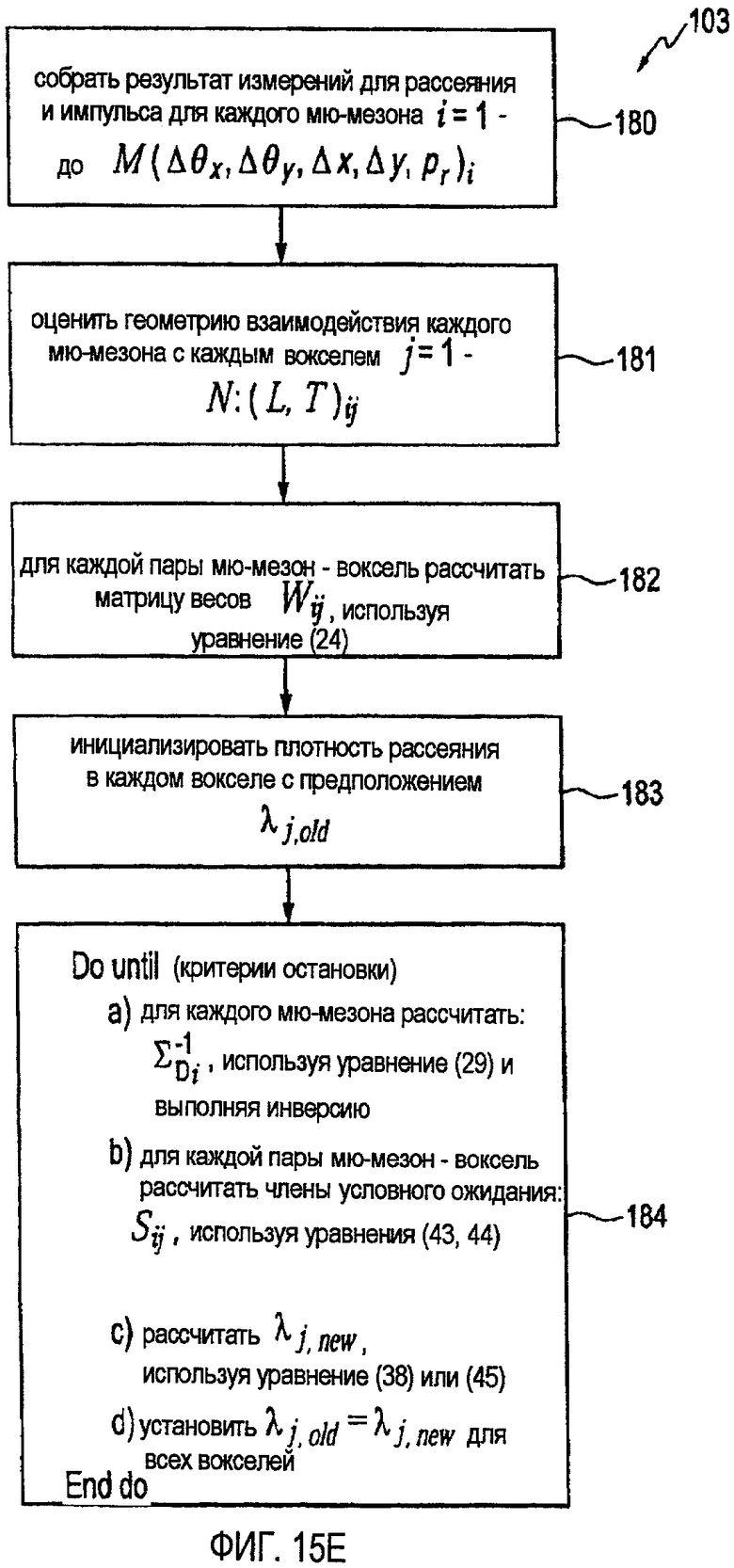
на фиг. 15E иллюстрируется блок-схема последовательности операций, представляющая пример обработки максимизации вероятности оценки профилей распределения плотности предметного объема, с использованием алгоритма максимизации ожидания в соответствии с одним вариантом осуществления.
Подробное описание изобретения
Конкретные значения и конфигурации, описанные в этих неограничительных примерах, могут изменяться, и они приведены здесь только для иллюстрации, по меньшей мере, одного варианта осуществления настоящего изобретения и не предназначены для ограничения объема изобретения.
Технические свойства, описанные в данной заявке, можно использовать для построения различных систем детектирования частиц. Например, система детектирования частиц, предназначенная для детектирования мю-мезонов как заряженных частиц, может включать в себя область удержания объекта, предназначенную для размещения в ней инспектируемого объекта, первый набор детекторов мю-мезонов, чувствительных к положению, размещенных на первой стороне области удержания объекта для измерения положения и углов падающих мю-мезонов в направлении области удержания объекта, второй набор детекторов мю-мезонов, чувствительных к положению, расположенных на второй стороне области удержания объекта, противоположной первой стороне, для измерения положения и углов вылетающих мю-мезонов, которые вылетают из области удержания объекта, и модуль обработки сигналов, который может включать в себя, например, микропроцессор, предназначенный для приема данных измеряемых сигналов падающих мю-мезонов из первого набора детекторов мю-мезонов, чувствительных к положению, и измеренных сигналов вылетающих мю-мезонов по второму набору детекторов мю-мезонов, чувствительных к положению. В качестве примера, каждый из первого и второго наборов детекторов частиц может быть воплощен так, что он будет включать в себя трубки дрейфа, расположенные так, что они обеспечивают, по меньшей мере, проведение трех измерений положения заряженных частиц в первом направлении и, по меньшей мере, трех измерений положения заряженных частицах во втором направлении, которое отличается от первого направления. Модуль обработки сигнала выполнен с возможностью анализировать поведение рассеяния мю-мезонов, связанное с рассеянием мю-мезонов в материалах в пределах области удержания объекта на основе измерения положений и углов падающих и вылетающих мю-мезонов для получения томографического профиля или пространственного распределения центров рассеяния внутри области удержания объекта. Полученный томографический профиль или пространственное распределение центров рассеяния можно использовать для выявления наличия или отсутствия одного или больше объектов в области удержания объектов, таких как материалы с высокими атомными числами, включающие в себя ядерные материалы или устройства. Каждый из чувствительных к положению детекторов мю-мезонов может быть выполнен в различных конфигурациях, включающих в себя дрейфовые ячейки, такие как дрейфовые трубки, заполненные газом, который может быть ионизирован мю-мезонами. Такую систему можно использовать для использования естественных мю-мезонов космических лучей в качестве источника мю-мезонов для детектирования одного или больше объектов в области удержания объекта.
В одном варианте осуществления способ и система для статистической реконструкции профилей плотности рассеяния объема для томографии заряженных частиц в соответствии с иллюстрируемыми вариантами осуществления предусматривают подход, при котором можно реконструировать изображение или модель объекта на основе рассеяния заряженных частиц космических лучей, пролетающих через объект.
Специальные ядерные материалы (SNM, СЯМ), которые обеспечивают хорошее экранирование гамма-лучей (такие как свинец и вольфрам), в большей степени влияют на траекторию, чем материалы, которые составляют более обычные объекты (такие как вода, пластик, алюминий и сталь). Для заряженных частиц космических лучей и, в частности для мю-мезонов космических лучей, каждый мю-мезон переносит информацию об объектах, через которые он проник, и путем измерения рассеяния множества мю-мезонов можно определить свойства этих объектов. В частности, можно детектировать объекты с высоким числом Z среди более типичных веществ с малым и средним числом Z.
Для того, чтобы пояснить различные технические свойства статистической реконструкции профилей плотности объема для томографии заряженных частиц в соответствии с иллюстрируемыми вариантами осуществления, вначале будет сделана ссылка на пример концепции мю-мезонной томографии, которая представлена на фиг.1.
Наборы детекторов 10, чувствительных к положению, установлены выше и ниже предметного объема 11, изображения которого формируют для получения положений и углов траекторий 12, как падающих, так и вылетающих заряженных частиц (показаны сплошными линиями со стрелками). Два или больше наборов детекторов 10, чувствительных к положению, расположенных выше объема, изображение которого формируют, обеспечивают положение и углы траекторий падающих заряженных частиц. Такие детекторы измеряют положение заряженной частицы в двух ортогональных или не ортогональных координатах. Другой набор детекторов 10, чувствительных к положению, записывает положения и углы вылетающих заряженных частиц. Боковые детекторы (не показаны) можно использовать для детектирования более горизонтально ориентированных траекторий заряженных частиц. Угол рассеяния каждой траектории заряженной частицы рассчитывают по совпадению падающих и вылетающих измерений. Импульс заряженной частицы оценивают по слабому рассеянию, возникающему в самих детекторах или в слоях рассеивателей с известными свойствами, помещенных между двумя наборами плоскостей детекторов, чувствительных к положению.
Один пример детекторов заряженных частиц, чувствительных к положению, представляет собой дрейфовую трубку, заполненную рабочим газом. Дрейфовая трубка может представлять собой цилиндрическую трубку и заполнена газом детектора, таким как аргон-изобутан, который обеспечивает возможность детектирования заряженных частиц космических лучей, таких как мю-мезоны. Положительное высокое напряжение приблизительно 2-3 кВ прикладывают к проводу центрального анода, продолжающемуся вдоль длины цилиндрической трубки с заземленной внешней поверхностью трубки таким образом, что присутствует статическое поле с высоким напряжением. Когда заряженная частица взаимодействует с атомами газа, множество электронов высвобождается из этих атомов на прямой линии через хорду трубки. Статическое поле приводит к тому, что "цепочка" электронов будет дрейфовать в направлении положительно заряженного анодного провода, который считывают электронным способом с использованием TDCS (ПВЦ, преобразователей значений времени в цифровую форму) электронного средства сбора данных. Каждый набор детекторов может быть выполнен как дрейфовые трубки, расположенные так, что они обеспечивают, по меньшей мере, возможность трех измерений положения заряженных частиц в первом направлении и, по меньшей мере, трех измерений положений заряженных частиц во втором направлении, которое отличается от первого направления и может быть ортогональным первому направлению.
Модуль обработки сигнала, например компьютер, предусмотрен в системе по фиг. 1 для приема данных измеренных сигналов падающих мю-мезонов, полученных с помощью детекторов, расположенных над предметным объемом, и вылетающих мю-мезонов, полученных с помощью детекторов, расположенных под предметным объемом. Такой модуль обработки сигнала выполнен с возможностью анализа поведения рассеяния мю-мезонов, связанного с рассеянием в объеме на основе измеряемых падающих и вылетающих положений, и углов мю-мезонов для получения томографического профиля или пространственного распределения центров рассеяния в этом объеме. Полученный томографический профиль или пространственное распределение центров рассеяния в объеме может раскрывать наличие или отсутствие объекта в этом объеме. В некоторых вариантах воплощения дополнительные детекторы в виде дрейфовой трубки могут быть выполнены по сторонам объема для формирования коробки или четырехсторонней структуры, в которую можно помещать упаковку, транспортное средство или грузовой контейнер для сканирования с помощью системы. Таким образом, множественное рассеяние мю-мезонов космических лучей можно использовать для избирательного детектирования материала с высоким значением z на фоне нормального груза. Предпочтительно, такая технология является пассивной, она не привносит какую-либо дозу облучения выше фонового значения и является избирательной в отношении плотных материалов с большим значением числа z. Часть томографической обработки модуля обработки сигнала может быть выполнена на основе установленного здесь же компьютера, который находится в том же месте, где и детекторы 10. В качестве альтернативы, часть томографической обработки модуля обработки сигналов может быть выполнена в удаленном компьютере, который подключен к компьютерной сети, такой как частная сеть, или в сеть общего пользования, такую как Интернет.
В иллюстрируемом на фиг. 1 варианте осуществления заряженные частицы представляют собой мю-мезоны космических лучей или другие заряженные частицы космических лучей, и детекторы 10, чувствительные к положению, представляют собой дрейфовые ячейки, заполненные рабочим газом, для определения заряженных частиц. Дрейфовые ячейки могут быть выполнены, например, с помощью дрейфовых трубок с центральным анодным проводом, продолжающимся вдоль продольного направления каждой трубки. Однако другие заряженные частицы, кроме мю-мезонов, можно детектировать, используя другие, чувствительные к положению датчики, кроме дрейфовых ячеек. Кроме того, заряженные частицы могут генерироваться с помощью другого источника, кроме космических лучей. Например, мю-мезоны могут быть сгенерированы как луч с низкой интенсивностью из ускорителя.
Мю-мезоны, проникающие через плотный объект (черные траектории), рассеиваются значительно сильнее, чем мю-мезоны, проникающие через воздух (серые траектории). По множеству измерений траекторий можно реконструировать как геометрию объекта, так и плотность электронов материала. Мю-мезоны, пролетающие через объем, рассеиваются в зависимости от материалов, через которые они пролетают.
Обработка результатов измерений для мю-мезонов космических лучей в инспектируемом объеме (например, пакете, контейнере или транспортном средстве) с помощью модуля обработки для системы, показанной на фиг. 1, может включать в себя реконструирование траектории мю-мезона через объем, измерение импульса падающего мю-мезона на основе сигналов от детекторов на каждой стороне объема и определение пространственного распределения плотности рассеяния в объеме. Эти и другие результаты обработки можно использовать для построения томографического профиля и измерения различных свойств объема, таких как детектирование целевого объекта.
Например, реконструирование траектории заряженной частицы, пролетающей через детекторы 10, имеющие набор дрейфовых ячеек, может включать в себя: (a) получают сигналы попадания, представляющие идентификаторы дрейфовых ячеек, в которые попали заряженные частицы, и соответствующие импульсы времени попадания; (b) группируют дрейфовые ячейки с одновременным попаданием, идентифицированные как ассоциированные с траекторией определенной заряженной частицы, пролетающей через упомянутый детектор; (c) выполняют первоначальную оценку нулевого значения времени для импульса времени, в который упомянутая конкретная заряженная частица попала в дрейфовую ячейку; (d) определяют радиусы дрейфа на основе оценок значений нулевого времени, данных преобразования времени дрейфа и времени попадания; (e) сопоставляют линейные траектории с радиусами дрейфа, соответствующими определенному нулевому значению времени; и (f) выполняют поиск и выбор нулевого значения времени, ассоциированного с наилучшими попаданиями траекторий, выполненными для определенной заряженной частицы, и проводят расчет ошибки в нулевой импульс времени и параметров отслеживания. Такая реконструкция траектории на основе нулевого времени попадания обеспечивает реконструированную линейную траекторию заряженной частицы, пролетающей через детектор заряженных частиц, без необходимости использования быстрых детекторов (таких как трубки фотоумножителей со сцинтилляционными лопатками) или некоторого другого быстрого детектора, который детектирует пролет мю-мезона через устройство до ближайших нескольких наносекунд для обеспечения нулевого времени.
Также, например, обработка по измерению импульса падающего или вылетающего мю-мезона, на основе сигналов от детекторов 10 на фиг. 1, может включать в себя: (a) конфигурируют множество детекторов, чувствительных к положению, для рассеяния заряженной частицы, пролетающей через них; (b) измеряют рассеяние заряженной частицы в детекторах, чувствительных к положению, в которой измерение рассеяния содержит: получают, по меньшей мере, три измерения положения рассеиваемой заряженной частицы; (c) определяют, по меньшей мере, одну траекторию заряженной частицы по измерениям положения; и (d) определяют, по меньшей мере, один результат измерения импульса заряженной частицы, по меньшей мере, по одной траектории. Такую технологию можно использовать для определения импульса заряженной частицы на основе траектории заряженной частицы, которую определяют по рассеянию заряженной частицы в самих детекторах, чувствительных к положению, без использования дополнительных металлических пластин в детекторе.
Ниже приведены детали примерных систем и способов для статистической реконструкции профилей плотности рассеяния предметного объема по томографическим данным заряженных частиц.
Пример автоматизированной системы для статистической реконструкции профилей плотности рассеяния объема для томографии заряженных частиц в соответствии с одним вариантом осуществления представлен в виде блок-схемы на фиг. 6. Автоматизированная система 50 имеет контроллер 51, выполненный с возможностью и установленный для приема томографических данных 54 заряженных частиц. Томографические данные заряженных частиц могут представлять собой, например, томографические данные мю-мезонов, определенные по результатам измерений мю-мезонов, с использованием детектора 1 заряженных частиц по фиг. 1 или, в качестве альтернативы, любого другого детектора заряженных частиц, имеющего детекторы, чувствительные к положению, выполненные с возможностью отслеживания пролета заряженных частиц через объем. В результате томографические данные мю-мезонов или других заряженных частиц можно использовать для выделения или определения углов рассеяния и оценки импульсов мю-мезонов или других заряженных частиц, пролетающих через предметный объем.
Автоматизированная система 50 включает в себя модуль 56 статистического реконструктора, содержащийся в контроллере. Модуль 56 реконструктора отвечает за статистическую реконструкцию профилей плотности рассеяния объема для мю-мезонной томографии или томографии других заряженных частиц. Модуль 56 может быть выполнен как программный модуль или аппаратный модуль.
В представленном варианте выполнения автоматизированной системы 50 по фиг. 6 контроллер 51 сформирован с использованием системы с одним или больше функционально соединенных компьютерных модулей обработки (CPU, ЦПУ), таких как компьютер (PC, ПК), или другой системы на основе микропроцессора, такой как система на основе цифрового процессора сигналов. Контроллер может представлять собой одиночный стандартный компьютер, но для получения результатов в режиме реального времени контроллер типично включает в себя ферму параллельных обрабатывающих компьютеров (не показаны), количество которых достаточно для обеспечения вычислительных возможностей, необходимых для получения результатов в режиме реального времени. Например, контроллер может включать в себя, допустим, 20 ЦПУ. Чем больше объем сканирования детекторов мю-мезонов и чем выше требуемая разрешающая способность, тем большую ферму обрабатывающих компьютеров требуется применять.
Операционная система работает в контроллере 51 и может представлять собой коммерчески доступную операционную систему или операционную систему из открытого источника, включающую в себя, но без ограничений, операционную систему Apple, Windows, Linux или Unix, или другие, которые могут быть разработаны в будущем. Инструкции для операционной системы и приложений или программ сохраняют в устройствах-накопителях, таких как привод жесткого диска. Кроме того, в автоматизированной системе 50 модуль 56 реконструкции траектории представляет собой программное обеспечение в форме используемого компьютером носителя данных, на котором содержатся инструкции, которые при выполнении их контроллером обеспечивают выполнение контроллером способа статистической реконструкции профилей плотности рассеяния в объеме для томографии заряженных частиц в соответствии с представленными вариантами осуществления. Модуль может быть установлен локально в контроллере, как обозначено на фиг. 6, или может работать в удаленном местоположении через сеть, подключенную к контроллеру. Для специалистов в данной области техники будет понятно, что существует множество способов выполнения такого модуля.
Автоматизированная система 50 также включает в себя дисплей 58, функционально соединенный с контроллером 51, предназначенный для отображения изображений пользователя или данных профилей плотности объекта, реконструируемых системой, в соответствии с необходимостью. Интерфейс пользователя (не показан) может быть функционально соединен с системой обработки для обеспечения возможности для оператора - человека выполнять манипуляции с системой обработки, в соответствии с необходимостью.
Для специалистов в данной области техники будет понятно, что иллюстрация, показанная на фиг. 6, представляет собой всего лишь представление одного примера вариантов осуществления автоматизированной системы 50, и что варианты осуществления не ограничиваются этим. Например, некоторые или все функции модуля реконструктора могут быть выполнены как аппаратные средства, такие как аналоговые или цифровые схемы, без использования микропроцессора.
На фиг. 15 приведена блок-схема последовательности операций, в общем, представляющая способ статистической реконструкции профилей плотности объема для томографии заряженных частиц, в соответствии с одним вариантом осуществления. Способ 100 инициализируют при получении заданных томографических данных заряженных частиц, соответствующих положениям траектории, углам рассеяния и импульсам рассеяния заряженных частиц, пролетающих через предметный объем, как обозначено на этапе 101 обработки. Заданные томографические данные заряженных частиц могут быть получены, например, из детектора по фиг. 1. После этого предоставляют распределение вероятности для рассеяния множества заряженных частиц, пролетающих через предметный объем, представленное пространственным распределением плотности рассеяния (которое будет определено ниже), на основе множества статистических моделей рассеяния, как обозначено на этапе 102 обработки. Оценку наибольшего правдоподобия профиля плотности рассеяния предметного объема затем определяют, используя алгоритм максимизации ожидания, как обозначено на этапе 103 обработки. Реконструированный профиль плотности рассеяния объемного рассеяния затем выводят для принятия решения (этап 104 обработки). Процесс принятия решения является необязательным и может представлять собой процесс идентификации присутствия и/или типа объекта, занимающего объем, как обозначено на этапе 105 обработки. Процесс принятия решения может включать в себя интерпретацию человеком реконструированного профиля плотности, представляющего изображение предметного объема, и/или автоматизированное принятия решения с помощью дополнительных алгоритмов.
Способы и автоматизированные системы в соответствии с вариантами осуществления обеспечивают возможность дискретной томографической реконструкции представляющего интерес объема, которую выполняют на основе данных, предоставляемых по множеству заряженных частиц. Пример итерационного алгоритма максимизации ожидания (EM, МО) используют для поиска максимальных оценок вероятности профилей плотности объектов. Способ и системы в соответствии с вариантами воплощения обеспечивают для пользователя возможность идентификации присутствия и/или типа объекта, занимающего представляющий интерес объем, по реконструированному профилю плотности объема. Различные приложения включают в себя томографию на основе мю-мезонов космических лучей для различных вариантов применения при инспекции в области национальной безопасности, при которой транспортные средства или грузы можно сканировать с использованием мю-мезонного устройства слежения. Полученные в результате мю-мезонные томографические данные можно использовать для реконструирования и отображения профилей распределения плотности транспортных средств или груза, с использованием способа и автоматизированных систем в соответствии с представленными в качестве иллюстрации вариантами осуществления, что позволяет идентифицировать любые, представляющие угрозу объекты.
В то время как максимальную вероятность используют при реконструировании медицинских изображений, в частности для реконструирования PET (ТПЭ, томография на основе позитронной эмиссии) и SPECT (ОФЭКТ, однофотонная эмиссионная компьютерная томография), несколько важных различий не позволяют использовать стандартные способы, разработанные для этих вариантов применения. Во-первых, измеренный сигнал, представляющий угол рассеяния, является стохастическим, что означает равный нулю и имеющий среднеквадратическое отклонение, определенное по свойствам материала, через который были пропущены лучи. Во-вторых, мю-мезоны космических лучей не поступают из определенных дискретных направлений или углов, а скорее имеют широкое, непрерывное угловое распределение вокруг зенита и продолжаются практически до горизонта. Наконец, траектории мю-мезонов не являются прямыми; при этом изгиб обеспечивает возможность поиска приблизительного местоположения сильно рассеивающего объекта. EM алгоритм является гибким и эффективным при вычислениях, и его применение в комплексных структурах может быть проиллюстрировано.
Этапы 102-104 обработки будут описаны ниже в соответствии с одним вариантом осуществления, в котором данные представляют собой томографические данные мю-мезонов космических лучей, полученные из детекторов по фиг. 1, которые измеряют мю-мезоны, пролетающие через объем.
Процесс обеспечения оценки распределения вероятности при рассеянии мю-мезонов, пролетающих через предметный объем, с использованием множественной статистической модели рассеяния (этап 102 обработки), в соответствии с одним вариантом осуществления, представлен в общих чертах в виде блок-схемы последовательности операций на фиг. 15A. Как обозначено на этапах 110-113 обработки, процесс имеет четыре основных компонента. Вначале оценивают двумерное распределение вероятности для одного мю-мезона на основе заданной плотности рассеяния однородного объекта (этап 110 обработки). Затем двумерное распределение расширяют до трехмерного (этап 111 обработки). После этого, на этапе 112 обработки, неоднородный предметный объем выражают с использованием функции на основе вокселей и выражают распределение вероятности для рассеяния множества мю-мезонов на основе заданной по вокселям плотности рассеяния. Наконец, выражение распределения вероятности расширяют до конечной точности рассеяния мю-мезонов и результатов измерений импульса (этап 113 обработки).
Этапы 110-113 обработки выполняют с использованием статистической модели с множественным рассеянием, которая будет вначале описана со ссылкой на рассеяние в одном слое однородного материала и затем в неоднородном материале.
Мю-мезон космических лучей, пролетающий через материал, испытывает множество кулоновых рассеяний, как представлено на фиг. 2, на которой показана двумерная проекция рассеяния и смещение, используемое для описания множества кулоновых рассеяний. На этом и других чертежах величина рассеяния сильно преувеличена с целью иллюстрации. Траектория вылета мю-мезона может характеризоваться углом рассеяния и смещением относительно ориентации и положения падающего мю-мезона. Типичные углы рассеяния составляют несколько десятков миллирадиан (1 миллирадиан приблизительно равен 0,06 градуса), и углы рассеяния более чем несколько градусов встречаются очень редко. Распределение центральных 98% углов рассеяния может быть приблизительно описано как гауссова функция с нулевым средним значением
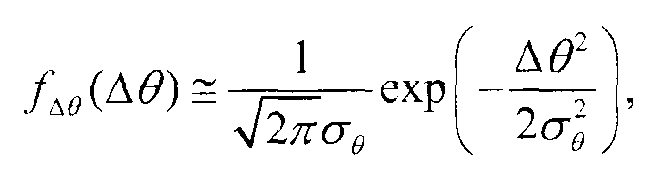 Уравнение (1)
Уравнение (1)
хотя фактическое распределение имеет более тяжелые или крупные хвосты, чем гауссово распределение. Ширина распределения может быть выражена приблизительно с учетом свойств материала. Многие исследователи представили эмпирически разработанные выражения для рассеяния как функцию различных свойств материала, как рассмотрено в публикации S. Eidelman et al., "Review of particle physics," Phys. Lett., vol. B592, p. 1, 2004, раскрытие которой приведено здесь в качестве ссылочного материала. В частности, простая форма может быть представлена как
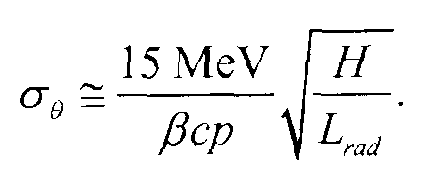 Уравнение (2)
Уравнение (2)
Здесь ρ представляет собой импульс частицы в МэВ/c, H представляет собой глубину материала, и Lrad представляет собой глубину излучения материала, βc представляет скорость (c представляет скорость света), и используется аппроксимация I для β=1. Длина излучения уменьшается по мере того, как атомное число и плотность материала увеличиваются. Авторы установили номинальный импульс мю-мезона ρ0 и определили плотность рассеяния материала при длине излучения Lrad как
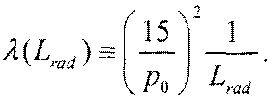 Уравнение (3)
Уравнение (3)
Плотность рассеяния, λ, материала, таким образом, представляет среднеквадратичное значение угла рассеяния мю-мезонов с номинальным импульсом, пролетающих через единицу глубины этого материала. Значения плотности рассеяния в миллирадианах2 на сантиметр для некоторых материалов представляют: например, приблизительно 3 для алюминия, 14 для железа и 78 для урана. Таким образом, дисперсия рассеяния мю-мезона с импульсом p, который пролетает через материал с плотностью λ рассеяния и глубиной H, может быть представлена как
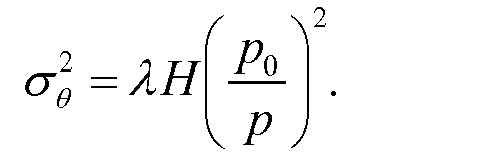 Уравнение (4)
Уравнение (4)
Пусть
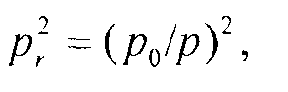 Уравнение (5)
Уравнение (5)
тогда
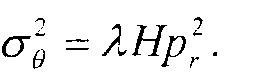 Уравнение (6)
Уравнение (6)
Смещение Δx скоррелировано с углом Δθ рассеяния. При совместном учете угол рассеяния и смещение предоставляют информацию, по которой можно определить положение локальных факторов рассеяния в большом объеме, как можно предположить по "изгибам" путей, показанных на фиг. 1. Распределение угла рассеяния и смещения может быть охарактеризовано как совместная гауссова функция с нулевым средним значением
и
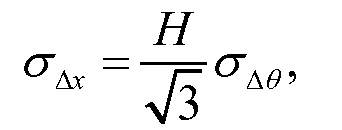 Уравнение (7)
Уравнение (7)
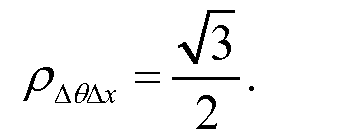 Уравнение (8)
Уравнение (8)
Можно выразить ковариационную матрицу как
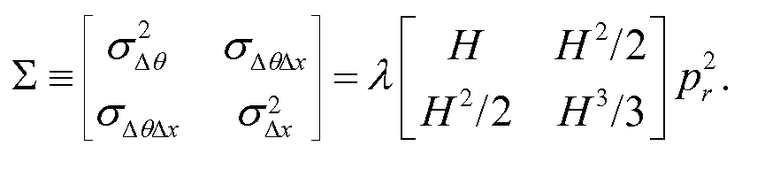 Уравнение (9)
Уравнение (9)
Пусть
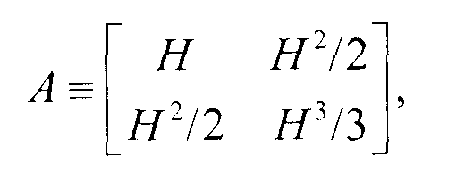 Уравнение (10)
Уравнение (10)
тогда
Σ=λAp2 r.Уравнение (11)
С учетом описанного выше, получение двумерного распределения вероятности рассеяния для рассеяния одиночного мю-мезона (этап 110 обработки) в соответствии с одним вариантом осуществления может быть описано, как представлено в блок-схеме последовательности операций, показанной на фиг. 15B. Как обозначено на этапе 150 обработки, плотность рассеяния материала определена как ожидаемое среднеквадратичное значение рассеяния ρ0=3GeV/c мю-мезона через единицу глубины данного материала в соответствии с уравнением (3). Затем гауссово приближение получают как среднеквадратичную величину рассеяния, как обозначено на этапе 151 обработки уравнения (1, 5, 6). Наконец, рассеяние лучей и распределение смещения аппроксимируют по коррелированному двумерному гауссовому распределению с нулевым средним значением, как обозначено на этапе 152 обработки, который описан уравнениями (10, 11).
В трех измерениях рассеяние характеризуют с учетом координаты y, которая ортогональна x, и при этом ссылаются на углы Δθx и Δθy рассеяния и смещения Δx и Δy. Отклонения в плоскости x и y являются независимыми и идентично распределенными (см. публикацию Eidelman и др.). Представленное выше описание основано на системе координат, которая ориентирована ортогонально направлению падающего мю-мезона. В 3-мерной модели необходимо учитывать длину 3-мерного пути и проецировать результаты измерения смещения на плоскость, ортогональную пути падения мю-мезона. На фиг. 3, на которой иллюстрируются параметры, используемые для регулировки модели для 3-мерного рассеяния, представлен мю-мезон, падающий с проецируемым углом θx,0 от вертикали.
Для того чтобы помочь в понимании такого трехмерного рассеяния, полезно представить ассоциированный проецируемый угол θy,0 в ортогональной координате y, которая направлена из плоскости страницы. Продолжение в виде прямой линии пути мю-мезона через слой до проецируемой (не рассеянной) точки (xp, yp) (то есть, длина 3-мерного пути) составляет
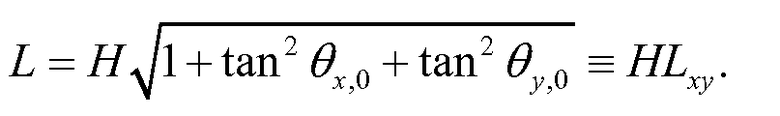 Уравнение (12)
Уравнение (12)
Определим положение x и угол вылетающего мю-мезона как (x1, θx,1), затем пусть
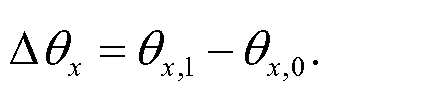 Уравнение (13)
Уравнение (13)
Измеренное смещение x может быть рассчитано как xm=x1-xp, но этот результат измерения следует повернуть в плоскость, ортогональную пути луча, и отрегулировать для 3-мерного пути. Определяют смещение как
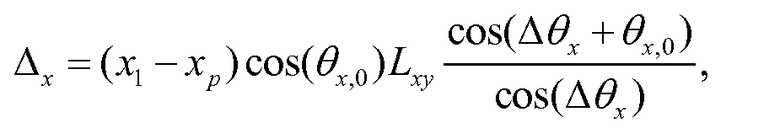 Уравнение (14)
Уравнение (14)
где два средних члена учитывают 3-мерный путь, и последний член проецирует измерение на правильную ориентацию.
В конечном итоге, переопределяют веса ковариантности как
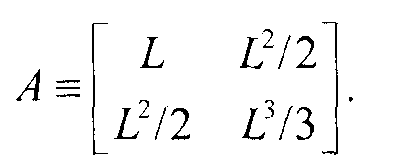 Уравнение (15)
Уравнение (15)
Затем необходимо продолжить аналогичную обработку для рассеяния и смещения, и уравнение (11) определяет ковариационную матрицу для обоих этих параметров и рассеяние координат. Измерения рассеяния выполняют независимо в двух ортогональных горизонтальных координатах. Для упрощения системы обозначений авторы разработали анализ только для одной координаты. Комбинирование информации по двум координатам будет описано ниже. Следует отметить, что эта модель действительна для "малых" углов рассеяния и смещений. Члены второго порядка, которые были отброшены при выводе модели, могут стать существенными для больших углов рассеяния.
В отношении описанного выше, получили статистическую модель, расширенную до 3D (этап 111 обработки), как представлено в блок-схеме последовательности операций на фиг. 15C в соответствии с одним вариантом осуществления. Вначале координату y суммировали и определили длину пути в трех измерениях (этап 160 обработки, уравнение (12)). Затем, на этапе 161 обработки, рассчитали 3D смещение в соответствии с уравнениями (13-14). Наконец, в соответствии с уравнением (15), выразили 3D ковариационную матрицу (этап 162 обработки).
Для неоднородного объема материала профиль плотности был представлен с целью реконструкции в виде линейной 3D комбинации основных функций {φ1, …, φj, φN} с коэффициентами {ν1,…, νj, νN}, то есть,
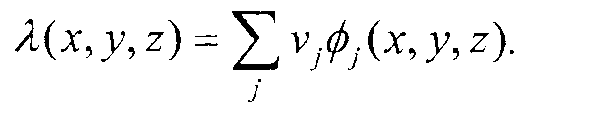 Уравнение (16)
Уравнение (16)
Хотя существует широкий выбор основных функций, внимание здесь направлено на прямоугольные 3D воксели. λj использовали для обозначения коэффициента j-й основной функции, то есть, плотности рассеяния j-го вокселя. На фиг. 4 показаны три слоя (или вокселя) с лучом, пролетающим через этот набор, который передает наблюдаемую информацию Δθ и Δx. "Скрытое" рассеяние и смещение в j-м вокселе обозначено как Δθj и Δxj, соответственно. И снова, магнитуда рассеяния преувеличена на чертеже. Наблюдаемые и скрытые данные можно сопоставить, используя выражение
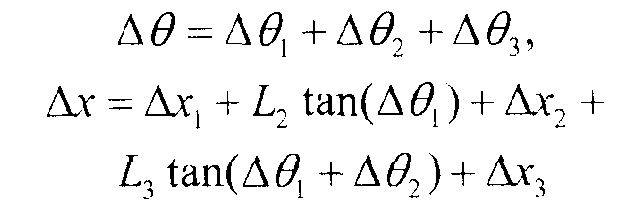 Уравнение (17)
Уравнение (17)
 Уравнение (18)
Уравнение (18)
Здесь заявители полагались на предположение малых углов рассеяния во втором уравнении и определили Tj как 3D длину пути луча от точки выхода j-го вокселя до точки выхода из объема реконструкции. В более общем случае, для луча, пролетающего через набор вокселей χ,
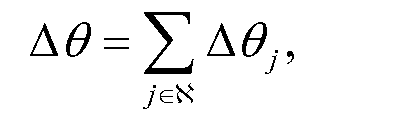 Уравнение (19)
Уравнение (19)
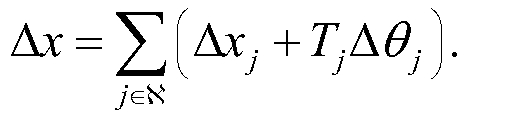 Уравнение (20)
Уравнение (20)
Наконец, можно выразить ковариантность совокупного рассеяния/смещения для i-го луча, таким образом, отметив вначале, что для j-го вокселя
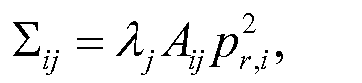 Уравнение (21)
Уравнение (21)
где
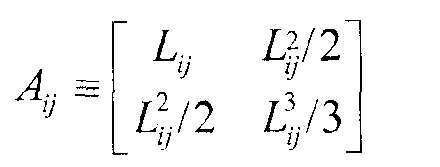 Уравнение (22)
Уравнение (22)
и Li,j представляет собой длину пути i-го луча через j-й воксель, определенную как равную нулю для вокселей, в которые не "попал" луч. Комбинируя уравнения (19)-(22), можно записать
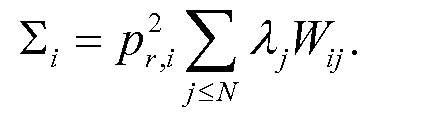 Уравнение (23)
Уравнение (23)
Здесь N представляет собой общее количество вокселей, и авторы определяют матрицу весов
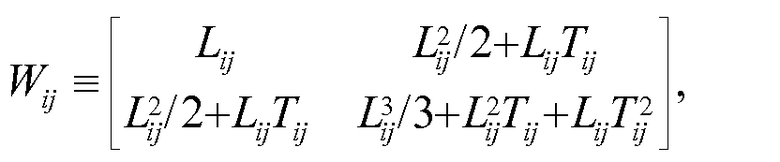 Уравнение (24)
Уравнение (24)
на основе простого, но длительного расчета для элементов.
Некоторые предположения были сделаны в отношении неизвестного пути мю-мезона для того, чтобы оценить длины путей лучей через воксели. Как показано на фиг. 5, аппроксимация начинается с расчета точки ближайшего приближения (PoCA, ТоБП) падающих и вылетающих траекторий (xcα, ycα). Затем вход PoCA соединяют с выходными точками для оценки длины пути вокселя.
Наконец, определяют вектор данных
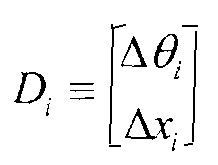 Уравнение (25)
Уравнение (25)
и пусть D обозначает все измерения по М мю-мезонам. Запишем вероятность данных на основе профиля λ плотности следующим образом:
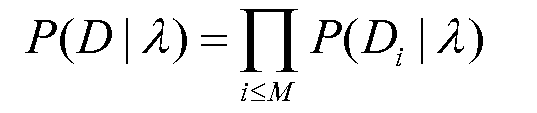 Уравнение (26)
Уравнение (26)
с коэффициентами
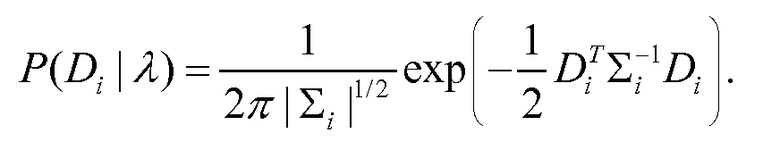 Уравнение (27)
Уравнение (27)
Учитывая описанное выше, можно получить распределение вероятности для рассеяния и смещения множества мю-мезонов через неоднородный материал (этап 112 обработки) в соответствии с одним вариантом осуществления, как представлено на фиг. 15D. Вначале устанавливают 3D сетку вокселей (или других основных функций) (этап 170 обработки). Затем в ходе обработки на этапе 171 рассчитывают ковариационную матрицу для рассеяния/смещения для каждого мю-мезона, в соответствии с уравнениями (23, 24). Наконец, рассчитывают общее распределение вероятности для всех мю-мезонов, на основе пути лучей и плотности рассеяния вокселей, в соответствии с уравнениями (25-27), что представлено как этап 172 обработки.
После описания статистической модели множественного рассеяния рассмотрим теперь расширение модели для экспериментальных эффектов (этап 113 обработки). Реальные детекторы мю-мезонов проявляют конечную разрешающую способность положения. Падающие и вылетающие траектории мю-мезонов характеризуются углами и положениями, выводимыми по попаданию траекторий для множества положений измерения. Ошибки измерения, таким образом, распространяются для угла рассеяния и измерений смещения, которые составляют набор данных для томографии мю-мезонов. Точность заданного детектора характеризуется среднеквадратичной ошибкой ep. Для конкретной компоновки детекторов может быть определена матрица ошибок
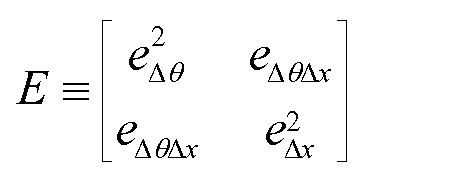 Уравнение (28)
Уравнение (28)
на основе того, как распространяется ошибка. С такой ошибкой относительно просто работать с использованием итерационных способов реконструкции. В нашем случае можно учитывать ошибку детектора путем дополнения ковариационной матрицы в соответствии с уравнением (23)
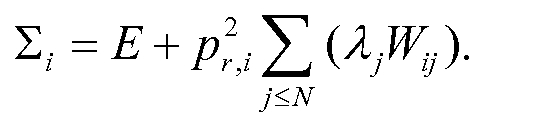 Уравнение (29)
Уравнение (29)
Таким образом, уменьшают шум, который в противном случае мог бы появиться в реконструкциях, из-за ошибок детектора. Более точная модель для ошибки детектора должна учитывать зависимость импульса, поскольку один источник ошибки отслеживания представляет собой рассеяние в самих детекторах, и рассеяние уменьшается при увеличении импульса частицы. Если доступна оценка импульса индивидуального мю-мезона 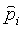 , тогда может быть получена оценка матрицы Ei(
, тогда может быть получена оценка матрицы Ei(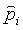 ) ошибки для каждого луча. Как можно видеть из уравнения (2), ширина множественного кулонова рассеяния зависит от импульса частицы. Различный импульс мю-мезона учитывают для ввода коэффициента p2 r в уравнение (5). На практике импульс мю-мезона точно не известен, но оценка импульса отдельного мю-мезона может быть получена по результатам измерений рассеяния в известном рассеивателе, таком как известный спектр мю-мезонов космических лучей. Здесь предполагается, что была получена хорошая оценка
) ошибки для каждого луча. Как можно видеть из уравнения (2), ширина множественного кулонова рассеяния зависит от импульса частицы. Различный импульс мю-мезона учитывают для ввода коэффициента p2 r в уравнение (5). На практике импульс мю-мезона точно не известен, но оценка импульса отдельного мю-мезона может быть получена по результатам измерений рассеяния в известном рассеивателе, таком как известный спектр мю-мезонов космических лучей. Здесь предполагается, что была получена хорошая оценка 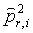 для каждого мю-мезона.
для каждого мю-мезона.
Оценка наибольшего правдоподобия плотности предметного объема может быть определена с использованием алгоритма максимизации ожидания (этап 103 обработки способа 100). Алгоритм EM основан на выражении вероятности "неполных" данных на основе "полных" данных, то есть, наблюдаемых данных вместе со скрытыми данными. В нашем случае наблюдаемые данные D={Di:1≤i≤М} представляют собой измеренное рассеяние. Скрытые данные H={Hij:1≤i≤М и 1≤j≤N} представляют собой угол рассеяния и смещение i-го мю-мезона j-м вокселем. В публикации Dempster, N. Laird and D. Rubin, "Maximum likelihood from incomplete data via the EM algorithm," J. Roy. Statist. Soc. B, vol. 39, pp. 1-78, 1977, раскрытие которой приведено здесь в качестве ссылки, описан алгоритм в виде следующей вспомогательной функции:
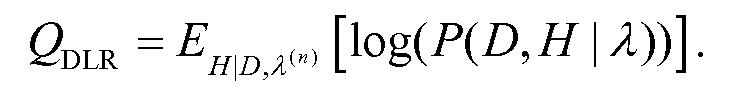 Уравнение (30)
Уравнение (30)
Эта функция представляет собой ожидаемое значение логарифма вероятности регистрации как наблюдаемых, так и не наблюдаемых данных, на основе вектора λ параметра в отношении распределения H координат заданного вектора и вектора параметра λ(n). Каждая итерация алгоритма состоит из следующих двух этапов.
этап E: оценить или характеризовать P(H|D,λ(n)) условное распределение скрытых данных;
этап М: максимизировать вспомогательную функцию Q, которая представляет собой ожидаемое значение в отношении распределения, охарактеризованного на этапе E.
В нашем случае, поскольку скрытые данные уникально определяют наблюдаемые данные, используя более простую вспомогательную функцию
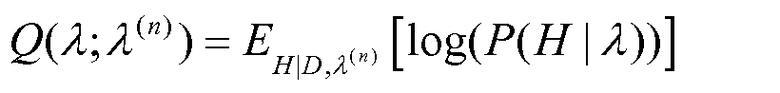 Уравнение (31)
Уравнение (31)
получаем ту же последовательность оценок 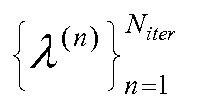 , которую можно было бы получить, используя QDLR. По оценке параметра λ(n), итерация алгоритма позволяет получить новую оценку, в соответствии с
, которую можно было бы получить, используя QDLR. По оценке параметра λ(n), итерация алгоритма позволяет получить новую оценку, в соответствии с
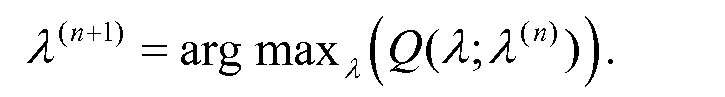 Уравнение (32).
Уравнение (32).
Начнем с того, что отметим, что распределение вероятности для рассеяния одиночного мю-мезона через одиночный воксель получают просто по статистической модели для одиночного слоя.
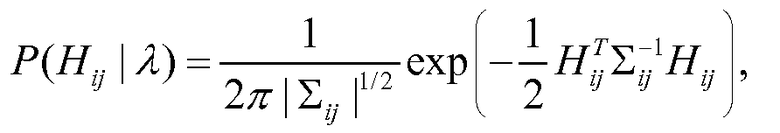 Уравнение (33)
Уравнение (33)
где ∑ij=λjAijp2 r,i определено в уравнении (21). Поскольку безусловное распределение рассеяния в каждом вокселе не зависит от рассеяния в других вокселях, вероятность обобщенного набора скрытых данных представляет собой произведение вероятности каждого элемента. Поэтому логарифм вероятности может быть записан как
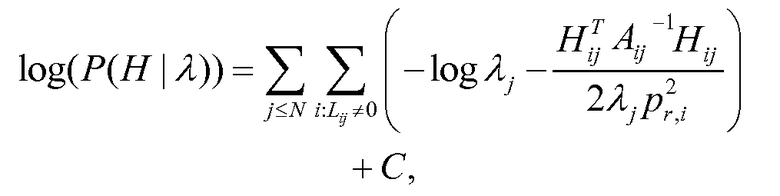 Уравнение (34)
Уравнение (34)
где C представляет собой член, не содержащий λ. На основе условного ожидания запишем функцию Q как
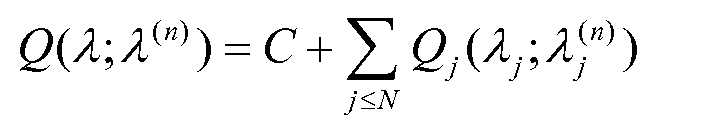 Уравнение (35)
Уравнение (35)
со слагаемыми
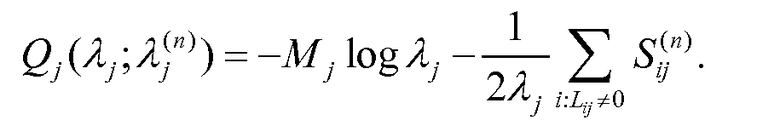 Уравнение (36)
Уравнение (36)
Здесь Mj представляет собой количество лучей, для которых Lij≠0 (то есть, количество лучей, попадающих в j-й воксель, и Sij (n) определено как
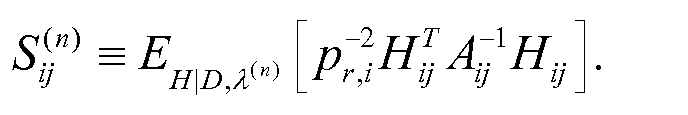 Уравнение (37)
Уравнение (37)
Устанавливая производную в отношении λj по уравнению (36) равной нулю, находим следующую итерационную формулу для максимизации вспомогательной функции (этап М)
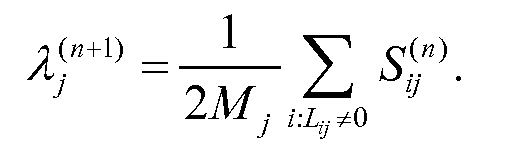 Уравнение (38)
Уравнение (38)
Квадратичная форма Sij гарантирует то, что λ(n+1) будет положительной. Остается рассчитать условные ожидания Sij. Пусть X обозначают случайную величину Hij|Di. Ожидаемое значение квадратичной формы XTA-1X может быть представлено как
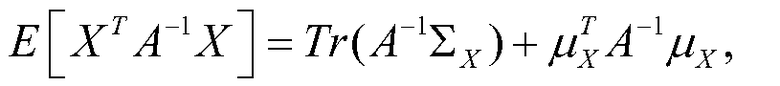 Уравнение (39)
Уравнение (39)
где μX и ∑X представляют собой среднее значение и ковариантность X, соответственно. Поскольку Di линейно зависит от Hij, они совместно представляют собой гауссову функцию. Условное распределение Hij для заданного Di также представляет собой гауссову функцию, в соответствии с теорией многомерного распределения. Используя эту теорию и тот факт, что каждый из Hij и Di имеет нулевое среднее значение, находим
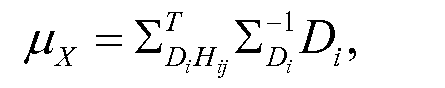 Уравнение (40)
Уравнение (40)
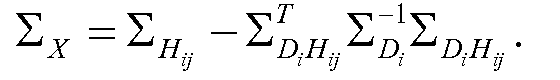 Уравнение (41)
Уравнение (41)
Здесь ∑Di, ковариантность наблюдаемых данных, определяют по уравнению (29), и ∑Hij, ковариантность элемента скрытых данных, может быть выражена через уравнение (21). Вместо записи ковариантности наблюдаемых - скрытых данных, ∑DiHij однозначно, можно выполнить простой (хотя и длинный) расчет матрицы для того, чтобы показать, что
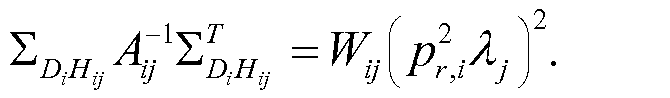 Уравнение (42)
Уравнение (42)
Подставляя результаты из уравнений (39)-(42) в уравнение (37), определяем, что
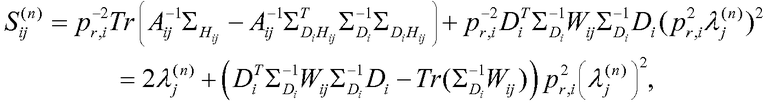 Уравнение (43)
Уравнение (43)
где использовали Tr (AB)=Tr (BA) на последнем этапе. Наконец, для того чтобы подставить данные рассеяния по обеим координатам x и y, просто используем среднее значение
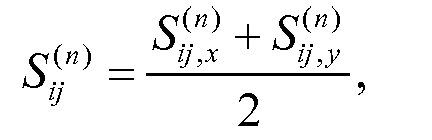 Уравнение (44)
Уравнение (44)
в обновленном уравнении (38).
Следует отметить, что уравнение (38) представляет среднее значение по лучам, попавшим в воксель. Использование такого уравнения будет называться ниже способом среднего. Ниже будет показано, что альтернативная форма такого обновленного уравнения полезна при уменьшении шумов для данных по изолированным мю-мезонам. Способ медианного алгоритма определен по измененному уравнению обновления
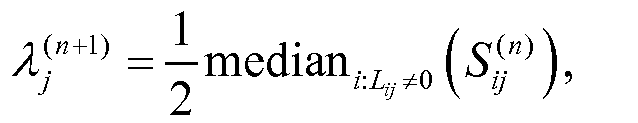 Уравнение (45)
Уравнение (45)
Учитывая приведенное выше, обработка максимизации вероятности оценки профилей плотности предметного объема, в которой используют алгоритм максимизации ожидания (этап 103 обработки способа 100), представлен на фиг. 15E. Как показано на этапе 180 обработки, измерения рассеяния и импульса объединяют для каждого мю-мезона i = от 1 до М (Δθx, Δθy, Δx, Δy, p2 r)i. Оценивают геометрию взаимодействия каждого мю-мезона с каждым вокселем j = от 1 до N: (L, T)ij (этап 181 обработки). Для каждой пары мю-мезон - воксель рассчитывают матрицу весов: Wij, используя уравнение (24) (этап 182 обработки). Плотность рассеяния в каждом вокселе инициализируют на основе предположения: λj,old (этап 183 обработки). Критерии остановки представляют на этапе 184 обработки следующим образом. Для каждого мю-мезона рассчитывают ∑-1 Di, используя уравнение (29), и получают инверсную величину для каждой пары мю-мезон - воксель, члены условного ожидания: Sij рассчитывают, используя уравнения (43, 44), λj,new рассчитывают, используя уравнение (38) или уравнение (45), и λj,old=λj,new устанавливают для всех вокселей.
Для того чтобы дополнительно проиллюстрировать способ 100, рассмотрим числовой пример. Разработали модель установки, аналогичной показанной на фиг. 1. При первой проверке пригодности использовали простую модель, разработанную так, чтобы она близко соответствовала модели множественного статистического рассеяния. Одиночные плоскости детектора (вместо 3 плоскостей, показанных на чертеже), имели размеры 2×2 м2, и вертикальное разделение между верхним и нижним детекторами составило 1,1 м. Эти детекторы идеально записали положения мю-мезонов и углы. Использовали упрощенный спектр мю-мезонов с мю-мезонами с равномерным распределением импульсов от 500-10000 МэВ/c. Частицы, попавшие в объем на верхней плоскости детекторов под проецируемыми углами, равномерно охватывали пространство от вертикали.
Множественное рассеяние и смещение мю-мезона оценивали в соответствии с этапами 110-113 обработки. Объекты размещали в центральном участке объема размером 1,1×1,1×1,1 м3, как показано на фиг. 7 и 8. Моделировали три куба размером 10×10×10 см3 из таких материалов, как вольфрам (W), железо (Fe) и алюминий (Al), с плотностью рассеяния 71,5, 14,2 и 2,8 мрад2/см, соответственно. В модели учитывали 400000 мю-мезонов, попадавших на верхней слой детекторов, что соответствовало приблизительно 10 минутам экспозиции. Приблизительно 160000 этих мю-мезонов не попали на нижнюю плоскость детекторов, в результате чего осталось 240000 мю-мезонов для реконструкции. Размер вокселя 5×5×5 см3 использовали для реконструкции и выполняли с использованием способа средних, описанного выше, предполагая точно известный импульс для каждого мю-мезона. Моделирование начали с объема, заполненного воздухом, и выполнили 100 итераций алгоритма (достаточных для сходимости блочных свойств). Результат показан на фиг. 9. Средние значения реконструированных значений для 8 вокселей, соответствующих каждому из трех объектов, составили (74,0, 14,7, 2,7) для блоков (W, Fe, Al), соответственно. Фракционный разброс (СКО/среднее) этих 8 вокселей, составляющих каждый куб, составил (12,6%, 13,2%, 12,1%). Этот результат подтверждает алгоритм инверсии и выполнения, учитывая соответствие между моделями имитации и инверсии.
Реконструкция выглядит идентичной сцене с объектом. Средние значения реконструированных значений для этих 8 вокселей, соответствующих каждому из трех объектов, составили (74,0, 14,7, 2,7) для блоков из (W, Fe, Al), соответственно. Фракционный разброс (СКО/среднее) для 8 вокселей, составляющих каждый куб, составил (12,6%, 13,2%, 12,1%). Этот результат подтверждает алгоритм инверсии и воплощение, учитывая соответствие между моделями имитации и инверсии.
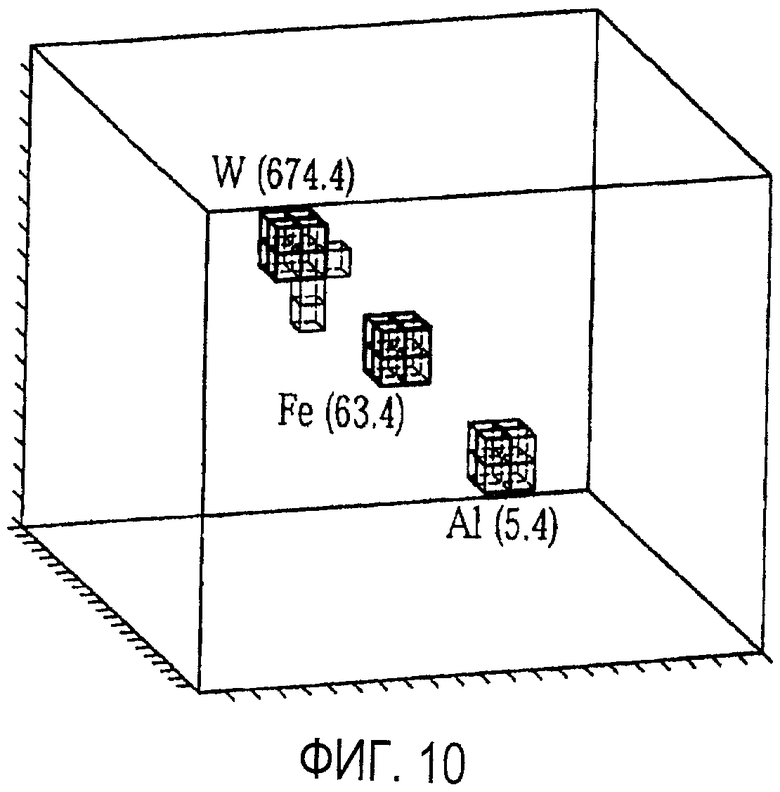
Затем ту же сцену повторно моделировали, используя пакет GEANT4 Монте-Карло. Подробное описание GEANT4 можно найти в публикации J. Allison, "Geant4 developments and applications," IEEE Trans. Nucl.Sci., vol. 53, no. 1, pp. 270-278, Feb. 2006, раскрытие которой приведено здесь в качестве ссылки. GEANT4 реализует более полную, точную и проверенную модель для множественного рассеяния. Эта модель включает в себя более точный расчет ширины центрального гауссова участка распределения рассеяния, воплощение тяжелых хвостов и моделирование потери энергии мю-мезонов при их прохождении через материал. Также использовали генератор события мю-мезона, который имитировал распределение углов и импульсов на уровне моря для мю-мезонов космических лучей. Предполагалось, что детекторы в этой модели были идеальными, с точным знанием импульса каждого мю-мезона, при этом электроны космических лучей или вторичные частицы траекторий не были включены. Результаты показаны на фиг. 10. Средние значения для вокселей, соответствующие блокам (W, Fe, Al), составили (674,4, 63,4, 5,4), соответственно.
Величины вокселя слишком велики, и очевидна неправильная классификация некоторых сред с низкими областями Z. Нормализация реконструкции путем деления всех значений вокселей приблизительно на 4 для получения правильной средней величины вокселей для вокселей со средним значением Z не позволяет получить правильные значения для высоких и низких значений Z вокселей или устранить всю неправильную классификацию. Причина этого эффекта состоит в малом проценте рассеяния мю-мезонов, что плохо описывается гауссовой моделью. Центральные 98% проецируемого углового распределения рассеяния, как считается, хорошо аппроксимируются гауссовым распределением. Приблизительно 2% всех мю-мезонов рассеиваются по углам, которые велики относительно описанной здесь статистической модели, то есть, гораздо больше, чем можно найти для гауссова распределения. Поскольку квадрат углов рассеяния определяет попадание, этот эффект может быть весьма существенным. Рассеяния мю-мезонов, которые попадают в эти хвосты, приводит к получению слишком большой оценки плотности рассеяния.
Кроме того, другие процессы, такие как распад мю-мезонов в инструменте по фиг. 1 или существенные ошибки детектора, могут быть ошибочно записаны как события очень большого угла рассеяния (хотя эти источники не присутствовали в нашей модели). Это может происходить в любом месте в объеме и проявляет тенденцию генерирования отдельных вокселей с необоснованно большой плотностью рассеяния. Такие события следует устранить, поскольку они дают фальшивые положительные показания SNM.
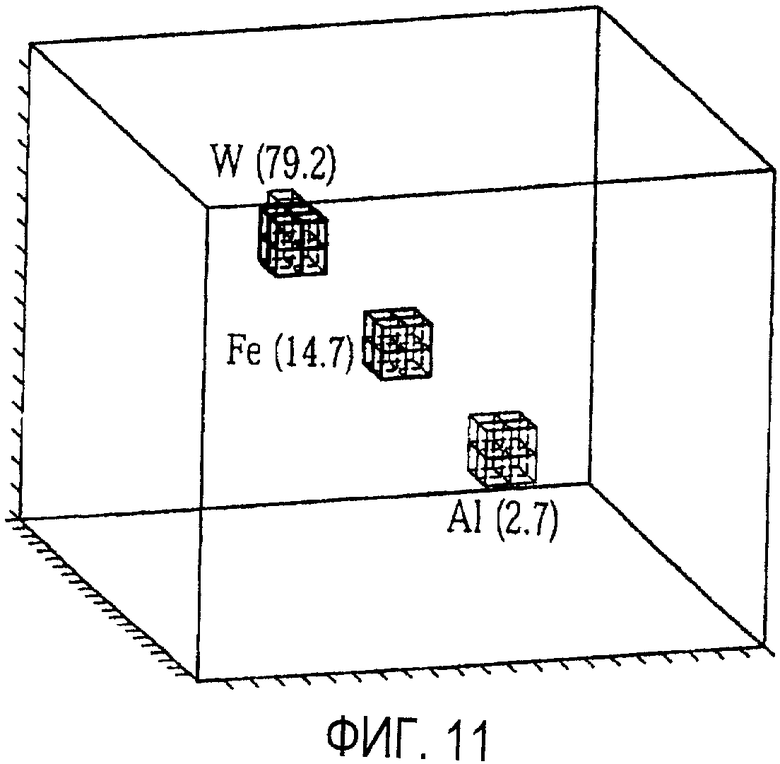
Для того чтобы сделать алгоритм EM толерантным к негауссовым данным, правило обновления среднего по уравнению (38) может быть заменено уравнением (45), то есть, можно использовать способ медианы.
Результаты использования способа медианы показаны на фиг. 11. Средние значения вокселей для областей (W, Fe, Al) составляют (79,2, 14,2, 2,1), соответственно, с фракционным разбросом (21,5%, 26,3%, 23,2%). Очевидно, что использование правила обновления медианы улучшает устойчивость алгоритма инверсии.
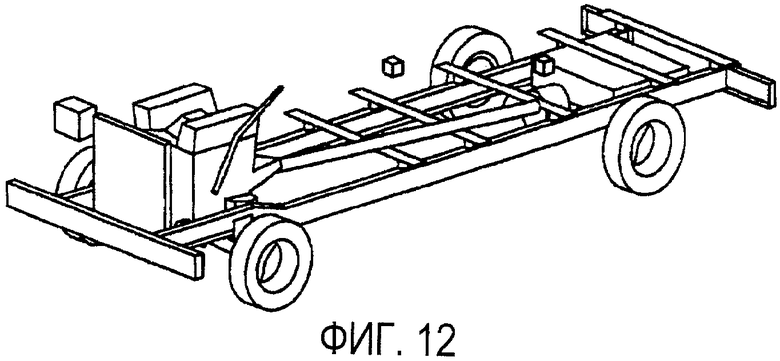
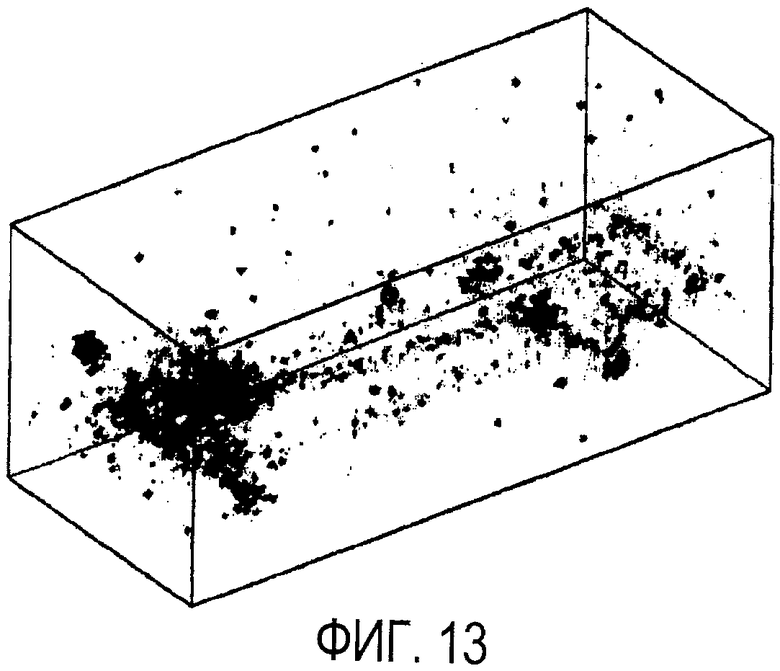
Более практичный пример реконструированных профилей плотности показан на фиг. 12, на которой иллюстрируется подробная GEANT4 модель пассажирского микроавтобуса. Иллюстрация основных компонентов разреза корпуса микроавтобуса показана на фиг. 12. Красный блок в центре иллюстрации представляет твердый кусок вольфрама размером 10×10×10 см3, который представляет объект обработки с высоким значением Z. В этом случае авторы использовали имитируемые плоскости детектора, расположенные по четырем длинным сторонам сцены, для того, чтобы получить преимущество более горизонтально ориентированных мю-мезонов. Имитировали экспозицию длительностью 1 минута для мю-мезонов космических лучей и выполнили реконструкцию по данным с использованием вокселей размером 5×5×5 см3, в соответствии со способом среднего и способом медианы. На фиг. 13 и 14, соответственно, показаны визуализации реконструкций, выполненных с использованием способа EM среднего и способа EM медианы. Эффект негауссовых данных весьма очевиден на этой сцене в реконструкции способа среднего, который представлен более темными пятнами, рассеянными по изображению. В реконструкции способа медианы эти помехи изображения полностью исчезли, и более плотные компоненты микроавтобуса (двигатель, аккумулятор, трансмиссия) проявились как (малое значение Z) или (среднее значение Z), в то время как объект обработки выделен как более темный (высокое значение Z). Использование способа медианы позволяет получить результаты, которые проявляют тенденцию устойчивости к фальшивым положительным проявлениям, получаемым в результате негауссова распределения рассеяния и других аномальных событий.
Варианты выполнения и примеры, представленные здесь, показаны для того, чтобы лучше всего пояснить настоящее изобретение и его практическое применение и чтобы, таким образом, обеспечить для специалиста в данной области техники возможность использовать изобретение. Для специалистов в данной области техники, однако, будет понятно, что приведенное выше описание и примеры были представлены только с целью иллюстрации и примера.
Другие варианты и модификации (такие как регуляризация процесса реконструкции) в соответствии с настоящим изобретением будут понятны для специалистов в данной области техники, и предполагается, что назначение приложенной формулы изобретения состоит в том, чтобы охватить все такие варианты и модификации.
Предполагается, что приведенное выше описание не является исчерпывающим и не ограничивает объем изобретения. Множество модификаций и вариантов возможны с учетом приведенного выше описания, без выхода за пределы объема следующей формулы изобретения. Предполагается, что при использовании настоящего изобретения в него могут быть включены компоненты, имеющие другие характеристики.
Изобретение относится к областям детектирования частиц. Сущность изобретения заключается в том, что детектирование заряженных частиц включает в себя профили плотности рассеяния статистической реконструкции предметного объема по томографическим данным заряженных частиц для определения распределения вероятности рассеяния заряженных частиц, используя статистическую модель множественного рассеяния, и определения, по существу, оценки наибольшего правдоподобия плотности рассеяния предметного объема с использованием алгоритма максимизации ожидания (ML/EM) для реконструирования плотности рассеяния предметного объема. Присутствие и/или тип объекта, занимающего объем, представляющий интерес, могут быть идентифицированы по реконструированному профилю плотности объемного рассеяния. Томографические данные заряженной частицы могут представлять собой томографические данные мю-мезонов космических лучей, полученные из устройства слежения за мю-мезонами, для сканирования упаковок, контейнеров, транспортных средств или грузов. Технический результат - повышение качества детектирования частиц. 4 н. и 19 з.п. ф-лы, 15 ил.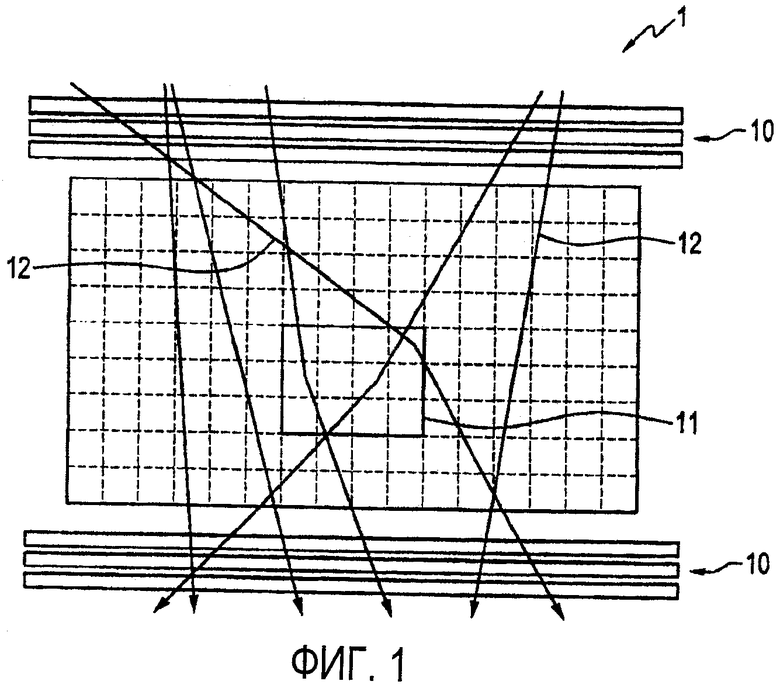
1. Способ детектирования предметного объема по томографическим данным заряженных частиц, полученным из предметного объема, содержащий этапы, на которых
(a) получают заранее заданные томографические данные заряженных частиц, соответствующие углам рассеяния и оцениваемым импульсам заряженных частиц, пролетающих через предметный объем;
(b) предоставляют распределение вероятности рассеяния заряженной частицы для использования в алгоритме максимизации ожидания (ML/EM), причем упомянутое распределение вероятности основано на статистической модели множественного рассеяния, причем упомянутое предоставление распределения вероятности содержит этапы, на которых
- получают двумерное распределение вероятности для заряженной частицы на основе заданной плотности рассеяния однородного объекта;
- получают трехмерное распределение вероятности для упомянутой заряженной частицы на основе упомянутого двумерного распределения вероятности;
- получают распределение вероятности для рассеяния множества заряженных частиц через неоднородный предметный объем, характеризуемый через базисные функции; и
- получают распределение вероятности для множественного рассеяния на основе упомянутого его определения и результатов измерения рассеяния и импульса упомянутых заряженных частиц;
(c) определяют оценку, по существу, наибольшего правдоподобия плотности рассеяния предметного объема, используя упомянутый алгоритм максимизации ожидания (ML/EM); и
(d) выводят реконструированную плотность рассеяния предметного объема на основе оценки, по существу, наибольшего правдоподобия.
2. Способ по п.1, содержащий этапы, на которых принимают решение по, по меньшей мере, одному из (1) наличия и (2) типа целевого объекта в предметном объеме на основе упомянутой реконструированной плотности рассеяния предметного объема.
3. Способ по п.1, в котором получение двумерного распределения вероятности для заряженной частицы на основе заданной плотности рассеяния однородного объекта содержит этапы, на которых
(k) определяют плотность рассеяния материала как ожидаемое среднеквадратичное рассеяние упомянутых заряженных частиц через единичную глубину упомянутого материала;
(l) аппроксимируют распределение рассеяния заряженных частиц на основе гауссовой модели; и
(m) аппроксимируют рассеяние и смещение лучей заряженных частиц на основе коррелированного двумерного гауссова распределения.
4. Способ по п.1, в котором получение трехмерного распределения вероятности для упомянутой заряженной частицы на основе упомянутого двумерного распределения вероятности содержит этапы, на которых
суммируют координату и определяют длину трехмерного пути;
рассчитывают трехмерное смещение; и
определяют трехмерную ковариационную матрицу.
5. Способ по п.4, в котором получение распределения вероятности для рассеяния множества заряженных частиц через неоднородный предметный объем, характеризуемый через базисные функции, содержит этапы, на которых устанавливают трехмерную сетку базисных функций, представляющих дискретные оценки плотности рассеяния;
определяют ковариационную матрицу рассеяния/смещения для каждого отдельного мю-мезона как оценки функции пути луча и плотности рассеяния; и
определяют распределение вероятности для множества заряженных частиц как произведение вероятностей отдельных заряженных частиц.
6. Способ по п.1, в котором определение оценки, по существу, наибольшего правдоподобия плотности рассеяния предметного объема с использованием упомянутого алгоритма максимизации ожидания (ML/EM) содержит этапы, на которых
собирают измерения рассеяния и импульса для каждой заряженной частицы;
оценивают геометрию взаимодействия каждой заряженной частицы с каждой базисной функцией упомянутой статистической модели рассеяния;
для каждой пары заряженной частицы и базисной функции определяют матрицу весов Wij;
инициализируют плотность рассеяния в каждой базисной функции с предположением; и
итерационно находят решение для приблизительного решения наибольшего правдоподобия для содержимого предметного объема;
в котором итерационный процесс останавливают после заданного количества итераций или когда решение изменяется менее, чем на заданное допустимое значение.
7. Способ по п.1, в котором определение оценки, по существу, наибольшего правдоподобия плотности рассеяния предметного объема с использованием упомянутого алгоритма максимизации ожидания (ML/EM) содержит этапы, на которых
собирают результаты измерения рассеяния и импульса для каждой заряженной частицы i=1 до М 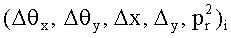 ;
;
получают оценку геометрии взаимодействия каждого мю-мезона с каждым векселем j=1 до N:(L,T)ij;
для каждой пары заряженная частица - вексель рассчитывают матрицу весов Wij
как 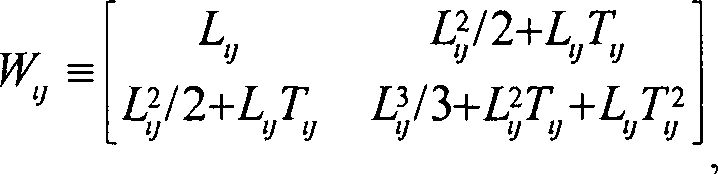
инициализируют предположение о плотности рассеяния λj,old в каждом векселе; и
используют обработку критерия остановки для установки λj,old=λj,new для всех векселей.
8. Способ по п.1, в котором упомянутый алгоритм максимизации ожидания (ML/EM) включает в себя правило обновления среднего значения или правило медианы обновления значения.
9. Способ по п.1, в котором упомянутые томографические данные заряженных частиц содержат томографические данные мю-мезонов космических лучей.
10. Способ по п.9, в котором определение оценки, по существу, наибольшего правдоподобия плотности рассеяния предметного объема с использованием упомянутого алгоритма максимизации ожидания (ML/EM) содержит этапы, на которых
собирают результаты измерения рассеяния и импульса для каждой заряженной частицы от i=1 до i=М 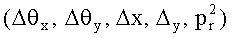 ;
;
оценивают геометрию взаимодействия каждой заряженной частицы с каждым векселем от j=i до j=N:(L,T)ij;
для каждой пары заряженная частица - вексель рассчитывают матрицу весов Wij
как,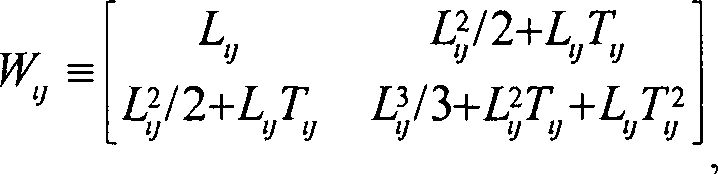
инициализируют предположение плотности рассеяния λj,old в каждом векселе;
используют обработку критерия остановки для установки λj,old=λj,new для всех векселей.
11. Способ по п.10, в котором упомянутая обработка критериев остановки содержит для каждой заряженной частицы вычисление 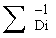 , используя
, используя 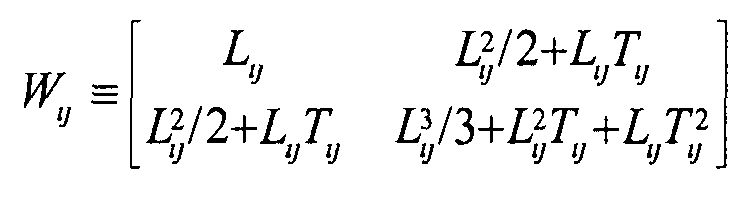 , и выполняя инверсию для каждой пары заряженная частица - вексель, вычисляют члены условного ожидания: Sij, используя
, и выполняя инверсию для каждой пары заряженная частица - вексель, вычисляют члены условного ожидания: Sij, используя
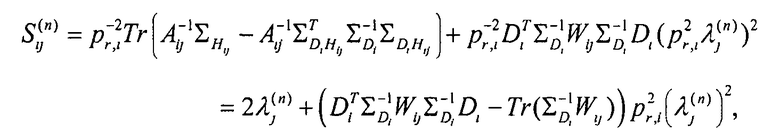
где Tr (AB)=Tr (BA) на последнем этапе;
и подставляют данные рассеяния обеих координат x и y, используя
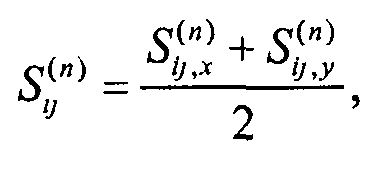
в правиле обновления.
12. Способ по п.11, в котором упомянутые заряженные частицы являются мю-мезонами.
13. Способ по п.11, в котором упомянутый алгоритм ML/EM включает в себя правило обновления среднего значения, определенное как 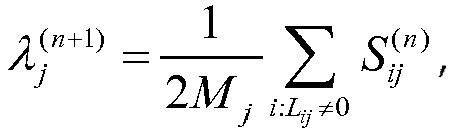 или правило обновления медианы, определенное как
или правило обновления медианы, определенное как 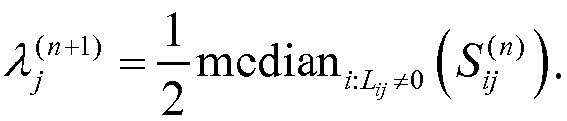
14. Компьютерно-реализуемый способ детектирования предметного объема по томографическим данным заряженных частиц, полученным из предметного объема, упомянутый способ содержит этапы, на которых
(а) получают томографические данные заряженных частиц, соответствующие углам рассеяния и оценкам импульсов заряженных частиц, пролетевших через предметный объем;
(b) предоставляют распределение вероятности плотности рассеяния заряженной частицы для использования в алгоритме максимизации ожидания (ML/EM), причем упомянутое распределение вероятности основано на статистической модели множественного рассеяния, причем упомянутое предоставление распределения вероятности содержит этапы, на которых
- получают двумерное распределение вероятности для заряженной частицы на основе заданной плотности рассеяния однородного объекта;
- получают трехмерное распределение вероятности для упомянутой заряженной частицы на основе упомянутого двумерного распределения вероятности;
- получают распределение вероятности для рассеяния множества заряженных частиц через неоднородный предметный объем, характеризуемый через базисные функции; и
- получают распределение вероятности для множественного рассеяния на основе упомянутого его определения и результатов измерения рассеяния и импульса упомянутых заряженных частиц;
(c) определяют оценку, по существу, наибольшего правдоподобия плотности рассеяния предметного объема, используя упомянутый алгоритм максимизации ожидания (ML/EM); и
(d) выводят реконструированную плотность рассеяния предметного объема.
15. Способ по п.14, дополнительно содержащий этап, на котором принимают решение на основе упомянутой реконструированной плотности рассеяния предметного объема.
16. Способ по п.14, в котором упомянутые томографические данные заряженных частиц содержат томографические данные заряженных частиц космических лучей.
17. Способ по п.16, в котором оценка двумерного распределения вероятности для заряженной частицы на основе заданной плотности рассеяния однородного объекта содержит этапы, на которых определяют плотность рассеяния материала как ожидаемое среднеквадратичное рассеяние заряженных частиц космических лучей с номинальным импульсом ρ0=3 ГэВ через единичную глубину этого материала;
аппроксимируют распределение рассеяния заряженных частиц космических лучей, используя гауссову модель; и
аппроксимируют рассеяние и смещение космических лучей посредством коррелированного двумерного гауссова распределения;
в котором получение трехмерного распределения вероятности для упомянутой заряженной частицы на основе упомянутого двумерного распределения вероятности содержит этапы, на которых суммируют координату и определяют длину трехмерного пути;
рассчитывают трехмерное смещение; и
определяют трехмерную ковариационную матрицу, и
в котором получение распределения вероятности для рассеяния множества заряженных частиц через неоднородный предметный объем, характеризуемый базисными функциями, содержит этапы, на которых
устанавливают трехмерную сетку базисных функций, представляющую дискретные оценки плотности рассеяния;
определяют ковариационную матрицу рассеяния/смещения для каждой отдельной заряженной частицы космических лучей как функцию пути луча и оценок плотности рассеяния; и
определяют распределение вероятности для множества заряженных частиц космических лучей как произведение отдельных вероятностей заряженных частиц.
18. Способ по п.16, в котором определение оценки, по существу, наибольшего правдоподобия плотности рассеяния предметного объема с использованием упомянутого алгоритма максимизации ожидания (ML/EM) содержит этапы, на которых
собирают результаты измерения рассеяния и импульса для каждой заряженной частицы космических лучей;
выполняют оценку пространственной структуры взаимодействия каждой заряженной частицы с каждой базисной функцией упомянутой статистической модели множественного рассеяния;
для каждой пары заряженной частицы и базисной функции определяют матрицу весов Wij,
инициализируют плотность рассеяния в каждой базисной функции с предположением;
итеративно находят решение для аппроксимации решения наибольшего правдоподобия для содержания предметного объема;
где итеративный процесс останавливают после заданного количества итераций, или когда решение изменяется менее, чем на заданное допустимое значение.
19. Используемый компьютером носитель данных, на котором записаны инструкции, которые, при выполнении с помощью компьютера, обеспечивают выполнение компьютером способа для статистической реконструкции профилей плотности предметного объема по томографическим данным заряженных частиц, причем способ содержит этапы, на которых
(a) получают заданные томографические данные заряженных частиц, соответствующие углам рассеяния и оценкам импульсов заряженных частиц, пролетающих через предметный объем;
(b) предоставляют распределение вероятности рассеяния заряженной частицы для использования в алгоритме максимизации ожидания (ML/EM), причем упомянутое распределение вероятности основано на статистической модели множественного рассеяния, причем упомянутое предоставление распределения вероятности содержит этапы, на которых
- получают двумерное распределение вероятности для заряженной частицы на основе заданной плотности рассеяния однородного объекта;
- получают трехмерное распределение вероятности для упомянутой заряженной частицы на основе упомянутого двумерного распределения вероятности;
- получают распределение вероятности для рассеяния множества заряженных частиц через неоднородный предметный объем, характеризуемый через базисные функции; и
- получают распределение вероятности для множественного рассеяния на основе упомянутого его определения и результатов измерения рассеяния и импульса упомянутых заряженных частиц;
(c) определяют оценку, по существу, наибольшего правдоподобия плотности рассеяния предметного объема, используя упомянутый алгоритм максимизации ожидания (ML/EM); и
(d) выводят реконструированную плотность рассеяния предметного объема.
20. Система детектирования, предназначенная для детектирования предметного объема с использованием заряженных частиц, пролетающих через предметный объем, содержащая:
первый набор детекторов, чувствительных к положению, расположенных на первой стороне предметного объема, для измерения положения и углов падения заряженных частиц в направлении предметного объема;
второй набор детекторов, чувствительных к положению, расположенных на второй стороне предметного объема, противоположной первой стороне, для измерения положения и углов выходящих заряженных частиц, вылетающих из предметного объема; и
модуль обработки сигнала, предназначенный для приема данных измеренных сигналов из первого набора детекторов, чувствительных к положению, и измеренных сигналов из второго набора детекторов, чувствительных к положению, в котором модуль обработки сигнала обрабатывает принятые данные для получения статистической реконструкции распределения плотности рассеяния объема в предметном объеме, причем модуль обработки сигнала выполнен с возможностью предоставлять распределение вероятности плотности рассеяния заряженной частицы на основе статистической модели множественного рассеяния, причем упомянутое предоставление распределения вероятности содержит этапы, на которых
- получают двумерное распределение вероятности для заряженной частицы на основе заданной плотности рассеяния однородного объекта;
- получают трехмерное распределение вероятности для упомянутой заряженной частицы на основе упомянутого двумерного распределения вероятности;
- получают распределение вероятности для рассеяния множества заряженных частиц через неоднородный предметный объем, характеризуемый через базисные функции; и
- получают распределение вероятности для множественного рассеяния на основе упомянутого его определения и результатов измерения рассеяния и импульса упомянутых заряженных частиц.
21. Система по п.20, в которой модуль обработки сигнала выполнен с возможностью:
(a) получать томографические данные заряженных частиц, соответствующие углам рассеяния, и оцениваемые импульсы заряженных частиц, пролетающих через предметный объем;
(b) определять оценку, по существу, наибольшего правдоподобия плотности рассеяния предметного объема, используя алгоритм максимизации ожидания (ML/EM); и
(c) выводить реконструированную плотность рассеяния предметного объема, на основе оценки, по существу, наибольшего правдоподобия.
22. Система по п.20, в которой:
каждый из первого и второго наборов детекторов частиц включает в себя дрейфовые трубки, расположенные с возможностью выполнения по меньшей мере трех измерений положения заряженной частицы в первом направлении и по меньшей мере трех измерений положения заряженной частицы во втором направлении, которое отличается от первого направления.
23. Система по п.20, в которой заряженные частицы представляют собой естественные мю-мезоны космических лучей, попадающие в предметный объем, и модуль обработки сигнала выполнен с возможностью индикации, присутствует ли целевой объект в предметном объеме, на основе статистической реконструкции плотности распределения объемного рассеяния в предметном объеме.
| BOROZDIN K | |||
| ЕТ AL.: "INFORMATION EXTRACTION FROM MUON RADIOGRAPHY DATA", INTERNATIONAL CONFERENCE ON CYBERNETICS AND INFORMATION TECHNOLOGIES, SYSTEMS AND APPLICATIONS: CITSA 2004, PAGES 1-5 | |||
| JP 2006284329 A, 19.10.2006 | |||
| СПОСОБ ТОМОГРАФИЧЕСКОГО КОНТРОЛЯ КРУПНОГАБАРИТНЫХ ГРУЗОВ | 1993 |
|
RU2072513C1 |
| ШТАНГЕНЦИРКУЛЬ | 1935 |
|
SU46363A1 |
Авторы
Даты
2012-11-27—Публикация
2007-10-26—Подача