СПОСОБ ПРОКАТА ДВУТАВРОВОГО ПРОФИЛЯ СЕЧЕНИЯ ИЗ НИЗКОЛЕГИРОВАННОЙ СТАЛИ Российский патент 2013 года по МПК B21B1/00 B21B1/08 

Предлагаемое изобретение относится к совершенствованию горячекатаных двутавровых профилей и к металлическим конструкциям промышленных и гражданских зданий с балочными перекрытиями и каркасами, а также к мостовым конструкциям из таких профилей.

Известен двутавровый прокатный профиль Гост 26020-83 [1]. Сортамент горячекатаных двутавров с параллельными гранями полок. Примем этот профиль за аналог. В аналоге пропорции сечения не зависят от того, из какой стали прокатывается двутавровый профиль: малоуглеродистой или низколегированной.

Недостаток аналога в том, что гибкость стенки профиля (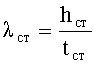 $${\lambda }_{ст}=\frac{h_{ст}}{t_{ст}}$$ , где h_ст - высота стенки; t_ст - толщина стенки) переменная и колеблется для разных номеров двутавров. Кроме того, материалоемкость стенки отличается от оптимальной материалоемкости 50%, например

Двутавр I Гибкость стенки λ_ст Материалоемкость стенки К W_x, см³ J_x, см⁴ I 100 Б1 59,25 0,52 9011 446000 I 100 Б2 55,76 0,49 10350 516400 I 100 Б3 52,67 0,519 11680 597700 I 100 Б4 48,6 0,562 12940 655400

I 100Б4-h=101,3 см, t_п=3,25 см, t_ст=1,95 см, h_ст=94,8 см, 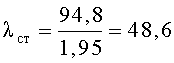$${\lambda }_{ст}=\frac{94,8}{1,95}=48,6$$

Известен двутавровый прокатный профиль для прокатных балок (из малоуглеродистой стали), предложенный К.К.Неждановым и разработанный с аспирантами [2, RU №2383401]. Примем этот профиль за прототип.

В прототипе разработан сортамент новых прокатных профилей из малоуглеродистой стали С255 (В Ст3 Сп5, Гост 27772-88).

Однако двутавровые прокатные профили из низколегированной стали должны иметь другие параметры. Сортамент двутавровых профилей из низколегированной стали не разработан.

В настоящее время прокатные профили из малоуглеродистой и низколегированной стали имеют одинаковое очертание поперечного сечения, что ошибочно, так как гибкости стенки для профилей из легированных сталей имеют значение меньше, чем предельная гибкость стенки, а именно λ_{ст. пред}=65.

По действующим нормам [2, с.27] устойчивость стенок балок не требуется проверять, если условная гибкость стенок 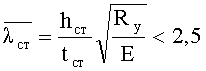$$\overline{{\lambda }_{ст}}=\frac{h_{ст}}{t_{ст}}\sqrt{\frac{R_{у}}{E}}<2,5$$ , где значение 2,5 - при наличии местных напряжений в профиле.

Для низколегированных сталей, например 12Г2Сгр1, ТУ 14-1-43 23-88, 09Г2С, 14Г2, 15ХСНД по Гост 19282-73* [2, с.64], с расчетным сопротивлением R_у=300 МПа при толщине t=20…40 мм и модулем упругости Е=206000 МПа приведенная гибкость 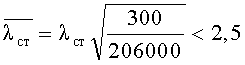$$\overline{{\lambda }_{ст}}={\lambda }_{ст}\sqrt{\frac{300}{206000}}<2,5$$ , отсюда предельная гибкость, когда не требуется постановка промежуточных ребер жесткости, равна λ_{ст пред}=2,5×26,204=65,51.

С некоторым запасом назначим предельную гибкость стенки двутаврового прокатного профиля равной λ_{ст пред}=65.

Оптимальное распределение материала по сечению балки

Значительное снижение материалоемкости двутаврового прокатного профиля может быть достигнуто оптимальным распределением металла по сечению балок. Поставим задачу прокатать балку наибольшей прочности, то есть с максимальным моментом сопротивления max W_x из заготовки площадью поперечного сечения А см².

Очевидно, что уменьшение толщины стенки t_ст приводит к увеличению высоты балки h и увеличению момента сопротивления W_x. Материал сечения должен быть оптимально распределен между стенкой и поясами балки. Введем коэффициент K, определяющий материалоемкость стенки.

Тогда $$A_{ст}=K\cdot A\text{ (1)}$$

Введем постоянный коэффициент гибкости стенки:

$${\lambda }_{ст}=\frac{h}{t_{ст}}=\frac{h\cdot t_{ст}}{t_{ст}^2}=\frac{K\cdot A}{t_{ст}^2}=const\text{ (2)}$$

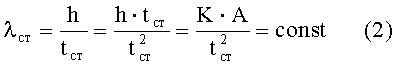
Отсюда

$$t_{ст}=\sqrt{\frac{A}{{\lambda }_{ст}}}\cdot K^{\mathrm{0,5}}\text{ (3)}$$

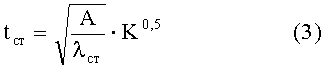
Тогда расстояние между центрами тяжести поясов h_цц будет зависеть только от коэффициента материалоемкости стенки К:

$$h_{цц}=t_{ст}\cdot {\lambda }_{ст}=\sqrt{A\cdot {\lambda }_{ст}}\cdot K^{\mathrm{0,5}}\text{ (4)}$$

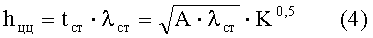
Площадь поперечного сечения двух поясов

$$2A_{п}=A-A_{ст}=A\cdot (1-K)\text{ (5)}$$

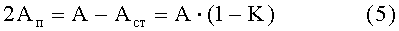
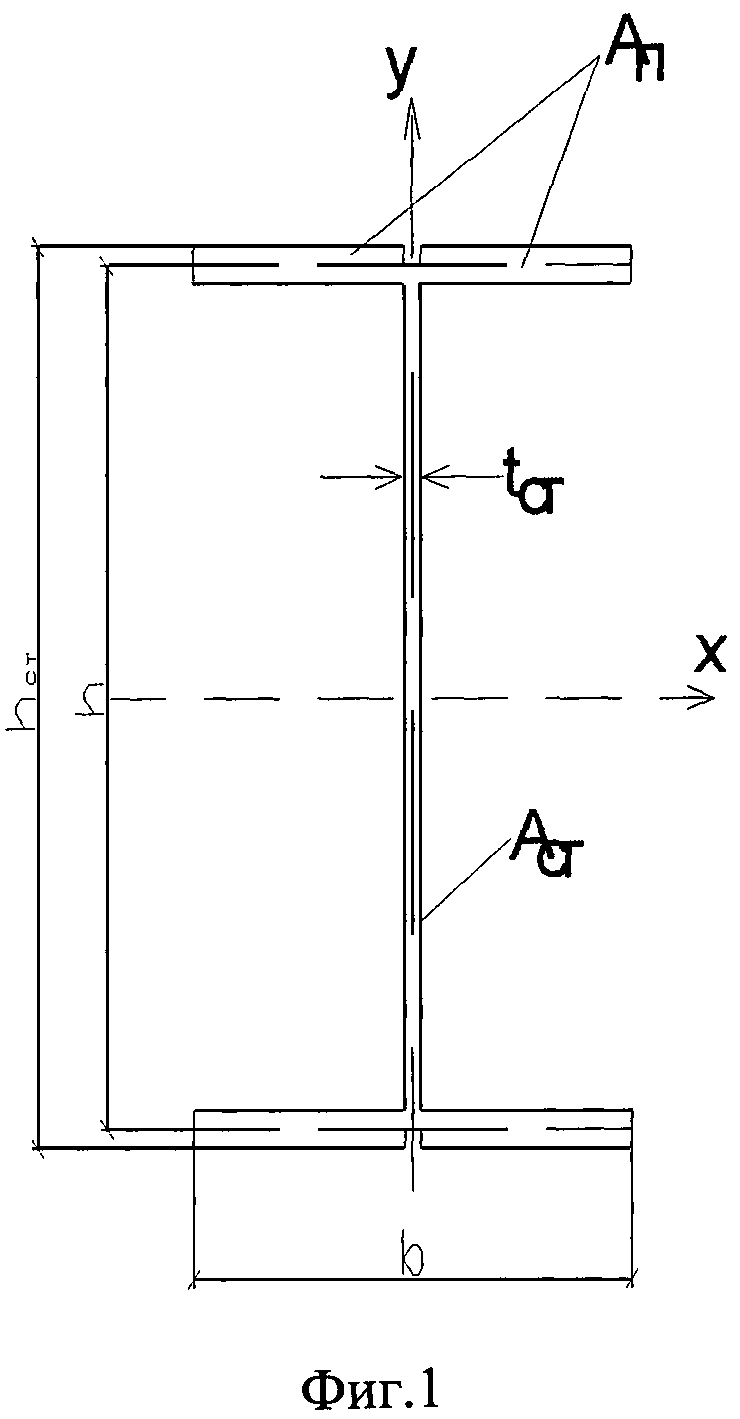
Пренебрегая собственными моментами инерции поясов балки, запишем главным момент инерции (см. фиг.1)

$$J_x=2A_{п}{\left(\frac{h_{цц}}{2}\right)}^2+A_{ст}\frac{h_{цц}^2}{12}\text{ (6)}$$

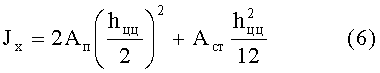
Поделив (6) на 0,5·h_цц, найдем момент сопротивления W_x на высоте центров тяжести поясов:

$$W_x=\frac{h}{2}\left(2A_{п}+\frac{A_{ст}}{3}\right)=\frac{1}{2}A\sqrt{A\cdot {\lambda }_{ст}}\cdot K^{\mathrm{0,5}}(1-\frac{2}{3}K)\text{ (7)}$$

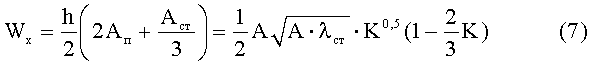
Итак, момент сопротивления зависит только от материалоемкости K стенки. Определим экстремум W_x, взяв производную по K.

$$\frac{d{W}_X}{dK}=\frac{1}{2}A\sqrt{A\cdot {\lambda }_{ст}}\left[\frac{1}{2}{K}^{\mathrm{0,5}}(1-\frac{2}{3}K)-\frac{2}{3}{K}^{\mathrm{0,5}}\right]=\text{0 (8)}$$

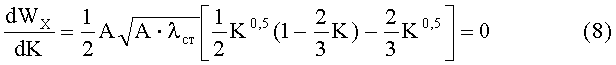
Отсюда K=0,5.

Следовательно, при K=0,5 материалоемкость стенки составляет 50% от материалоемкости всего сечения балки.

Тогда оптимальная высота сечения равна

$$h_{опт}=\frac{\mathrm{0,5}A}{t_{ст}}\text{ (9)}$$

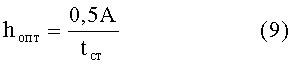
Этой высоте соответствует наибольший момент сопротивления, равный

$$W_x^2=\frac{A^3{\lambda }_{ст}}{18},\text{ (11)}$$

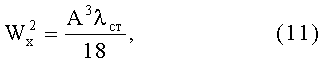
и соответствующая гибкость стенки

$${\lambda }_{ст}=\frac{\mathrm{0,5}A}{t_{ст}^2}.\text{ (12)}$$

Подставив (12) в (11), получим W_x в зависимости от А и t_ст

$$W_X=\frac{A^2}{6\cdot t_{ст}}$$

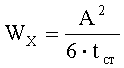
и соответствующую минимальную площадь сечения балки

$$A=\sqrt{6\cdot W_X\cdot t_{ст}},\text{ (13)}$$

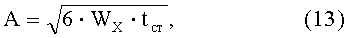
или в зависимости от гибкости стенки

$$A=\sqrt[3]{\frac{18W_X^2}{{\lambda }_{ст}}}\text{ (14)}$$

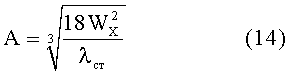
Из (11) и (12) получим

$$t_{ст}=\sqrt[3]{\frac{\mathrm{1,5}{W}_X}{{\lambda }_{ст}^2}},\text{ (15)}$$

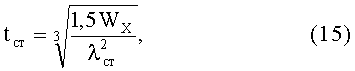
легко убедиться, что радиус ядра сечения r в этом случае будет равен

r=h/3.

Проанализируем материалоемкость и гибкость стенки аналога. Например, для двутавров с высотой сечения 100 см по Гост 26020-83.

Таблица 1 Размеры в см, площади в см²   h b t_ст t_п h_ст A A_ст λ_ст К 100 Б1 99 32 1,6 2,1 94,8 293,82 151,68 59,25 0,52 100 Б2 99,8 32 1,7 2,5 94,8 328,9 161,16 55,76 0,49 100 Б3 100,6 32 1,8 2,9 94,8 364 170,64 52,67 0,519 100 Б4 101,3 32 1,95 3,25 94,8 400,6 184,86 48,62 0,562

Анализ показывает, что материалоемкость стенки отличается от оптимальной Л=0,5, а гибкость стенки для низколегированной стали меньше предельной величины λ_{ст пред}=65.

Таким образом, имеются резервы для снижения материалоемкости профиля.

Технологическая задача изобретения - максимальное снижение материалоемкости двутаврового прокатного профиля, при его прокате, путем оптимального распределения материала между поясами и стенкой профиля, обеспечивающего достижение моментом сопротивления сечения профиля относительно главной оси Х своего максимального значения.

Технологическая задача по реализации способа распределения стали по сечению двутаврового профиля, содержащего полки с параллельными гранями и соединяющую их стенку, решена следующим образом.

Отличие в том, что при прокате на прокатном стане двутаврового профиля гибкость стенки балки назначают предельной для данной низколегированной марки стали, обеспечивающей устойчивость стенки без ребер жесткости. Блюм разогревают до температуры 600…650°C и обжимают его в клети валками на прокатном стане с четырех сторон, деформируют сечение в двутавровый профиль, содержащий полки с параллельными гранями и стенку, монолитно соединяющую полки, с образованием двутавра, при прокате из низколегированной стали (например, 12Г2Сгр1, ТУ14-1-4323-88, расчетным сопротивлением R_у=300 МПа и толщине проката 20…40 мм)

Площадь сечения профиля при прокате распределяют по сечению в следующей пропорции: 50% - на стенку профиля и по 25% на каждый из поясов.

Толщину стенки профиля определяют из уравнения

$$t_{ст}=\sqrt{\frac{0,5А}{{\lambda }_{ст}}}$$

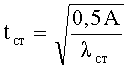
где А - площадь поперечного сечения профиля;

λ_ст - предельная гибкость стенки профиля, обеспечивающая устойчивость ее без постановки ребер жесткости.

Высоту стенки находят из формулы h_ст=λ_ст·t_ст, где ширину полки и толщину ее назначают такой, чтобы отношение ширины полки к ее толщине не превышало предельное отношение, обеспечивающее местную устойчивость плоского пояса.

Главный момент инерции профиля определяют по формуле

$$J_x=\frac{b\cdot h^3-(b-t_{ст})\cdot h_{ст}^3}{12}$$

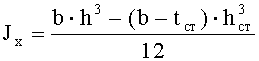
где b - ширина полки профиля;

h - высота поперечного сечения профиля.

Момент сопротивления вычисляют по формуле 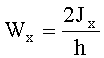$$W_x=\frac{2J_x}{h}$$

На фиг.1 показано поперечное сечение двутаврового прокатного профиля. Полки имеют ширину b. Толщина полки t_п. Высота сечения профиля равна h. Стенка имеет высоту h_ст. Толщина стенки равна t_ст.

Площадь сечения каждой из полок равна А_п=b·t_п.

Площадь сечения стенки равна А_ст=h_ст·t_ст.

Площадь всего сечения равна А=2А_п+А_ст.

Пример конкретной реализации

Повысим прочность двутавра I100Б4 по ГОСТ 26020-83 [1]. Основные размеры профиля и его характеристики приведены в табл.1.

Вычисления производим в следующей последовательности.

1. По формуле 12 находим необходимую толщину стенки нового двутаврового профиля при заданной его площади сечения А=400,6 см² и предельной гибкости стенки 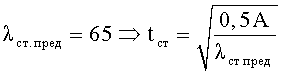$${\lambda }_{ст.пред}=65\Rightarrow t_{ст}=\sqrt{\frac{0,5А}{{\lambda }_{стпред}}}$$

2. Находим площадь сечения стенки А_ст=0,5А.

3. Затем высоту стенки 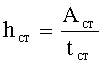$$h_{ст}=\frac{{А}_{ст}}{t_{ст}}$$ , округляем ее.

4. Фактическую площадь сечения стенки А_{ст ф}=h_ст·t_ст.

5. Находим площадь сечения полки А_п=0,25·А.

6. Определяем толщину полки 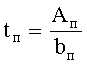$$t_{п}=\frac{{А}_{п}}{b_{п}}$$ , при заданной ширине полки b_п, и округляем ее.

7. Затем фактическую площадь сечения полки А_пф=b_п·t_п.

8. Определяем высоту сечения балки h=h_ст+2t_п.

9. Фактическую площадь сечения А=2А_пф+А_ст.

10. Определяем главный момент инерции 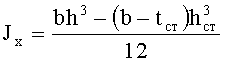$$J_x=\frac{b{h}^3-\left(b-t_{ст}\right)h_{ст}^3}{12}$$

11. Момент сопротивления сечения 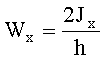$$W_x=\frac{2J_x}{h}$$

Например, по сортаменту для двутавра I100Б4 площадь сечения А=400,6 см². Назначаем гибкость стенки λ_{ст пред}=65.

1. Находим необходимую толщину стенки нового двутаврового профиля при заданной его площади сечения и гибкости стенки

$${\lambda }_{ст}=\frac{\mathrm{0,5}А}{t_{ст}^2}\Rightarrow t_{ст}=\sqrt{\frac{\mathrm{0,5}А}{{\lambda }_{ст\text{ пред}}}}=\sqrt{\frac{\mathrm{0,5}\cdot \mathrm{400,6}}{65}}=\mathrm{1,7554.}$$ Принимаем t_ст=1,76 см.

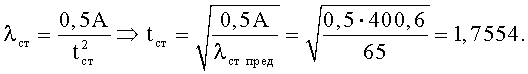
2. Находим площадь сечения стенки А_ст=0,5А=200,3 см².

3. Затем высоту стенки 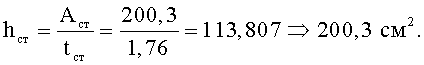$$h_{ст}=\frac{{А}_{ст}}{t_{ст}}=\frac{\mathrm{200,3}}{\mathrm{1,76}}=\mathrm{113,807}\Rightarrow \mathrm{200,3}{\text{ см}}^{\text{2}}.$$

4. Фактическую площадь сечения стенки А_стф=h_ст·t_ст=113,8·1,76=200,288 см².

5. Находим площадь сечения полки А_п=0,25·А=0,25·400,6=100,15 см².

Оставляем ширину полки b_п=32, тогда

6. $$t_{п}=\frac{\mathrm{100,15}}{32}=\mathrm{3,1297}\Rightarrow \mathrm{3,13}\text{ см}\text{.}$$

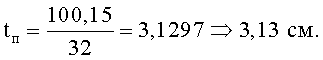
7. Затем фактическую площадь сечения полки А_пф=b_п·t_п=32·3,13=100,16 см².

8. Определяют высоту сечения балки

9. h=h_ст+2t_п=113,8+2·3,13=120,06 см.

10. Фактическая площадь сечения А=2А_пф+А_ст=2·100,16+113,8·1,76=400,608 см².

11. Определяют главный момент инерции 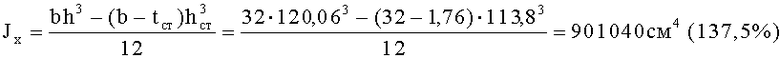$$J_x=\frac{b{h}^3-(b-t_{ст})h_{ст}^3}{12}=\frac{32\cdot {\mathrm{120,06}}^3-(32-\mathrm{1,76})\cdot {\mathrm{113,8}}^3}{12}=901040{\text{ см}}^{\text{4}}\text{ (137}\text{,5\%)}$$

12. Было J_x=655400 см⁴ (100%).

13. Момент сопротивления 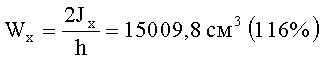$$W_x=\frac{2J_x}{h}=\mathrm{15009,8}{\text{ см}}^{\text{3}}\left(\text{116\%}\right)$$

14. Было W_x=12940 см³ (100%).

Список литературы

1. Двутавры стальные горячекатаные с параллельными гранями полок. Сортамент. Гост 26020-83. Переиздание. Октябрь 1998, 9 с.

2. СНиП 11-23-81. Стальные конструкции, Госстрой СССР, Москва, 1999, 96 с.

3. Васильченко В.Т. и др. Справочник конструктора металлических конструкций, Киев, «Будiвельник», 1980, 288 с.

4. Писаренко Г.С. и др. Справочник по сопротивлению материалов, Киев, «Наукова думка», 1975, 704 с.

5. Нежданов К.К., Нежданов А.К., Эйдлин A.M. Двутавровый прокатный профиль. Патент России №2383401, B21B 1/08 (2006.01). Заявка №2007 136405/02. Публикация заявки 10.04.2009. Опубликовано 10.03.2010. Бюл. №7.

Изобретение предназначено для снижения материалоемкости двутаврового прокатного профиля. Двутавровый профиль выполнен из низколегированной стали и имеет полки с параллельными гранями и стенку, где рациональное распределение стали по сечению балки обеспечивается за счет того, что гибкость его стенки, равная отношению высоты стенки к ее толщине, не превышает предельную величину гибкости λ_{ст пред}, обеспечивающую устойчивость стенки без промежуточных ребер жесткости, и составляет 65, а толщина, высота стенки, ее предельная гибкость регламентируются математическими зависимостями, при этом площадь сечения профиля распределена в пропорции: 50% - стенка профиля, 25% - каждая из полок, кроме того, отношение ширины полки к ее толщине не превышает предельное отношение, обеспечивающее местную устойчивость полки, что обеспечивает повышенную прочность, то есть происходит увеличение момента сопротивления W_x см³ и жесткости. 1 ил., 2 табл.

Способ прокатки профиля двутаврового сечения из низколегированной стали с расчетным сопротивлением R_у=300, включающий разогрев блюма толщиной 20-40 мм до температуры 600-650°C и обжим его в клети валками на прокатном стане с четырех сторон, деформирование в двутавровый профиль, имеющий полки с параллельными гранями в виде плоских поясов и стенку, монолитно соединяющую их, отличающийся тем, что стенку профиля прокатывают с предельной гибкостью, равной отношению высоты стенки к ее толщине, не превышающей предельную величину гибкости λ_{ст пред}, составляющей 65 и обеспечивающей устойчивость стенки без промежуточных ребер жесткости, профиль трансформируют при горячей прокатке путем обжима его валками и принудительного распределения площади по сечению в пропорции 50% на стенку профиля и по 25% на каждый из плоских поясов, при этом толщину стенки профиля t_ст определяют из уравнения
$$t_{ст}=\sqrt{\mathrm{0,5}A/{\lambda }_{ст\text{ пред}}}$$ ,
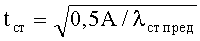
где A - площадь поперечного сечения профиля;
λ_{ст пред} - предельная гибкость стенки профиля, обеспечивающая ее устойчивость без промежуточных ребер жесткости;
причем высоту стенки h_ст определяют из уравнения
h_ст=λ_{ст пред}·t_ст,
где полку прокатывают такой, чтобы отношение ширины полки к ее толщине не превышало предельное отношение, обеспечивающее местную устойчивость плоского пояса, а главный момент инерции профиля J_x определяют по формуле
$$J_x=\left[b\cdot h^3-(b-t_{ст})\cdot h_{ст}^3\right]/12$$ ,
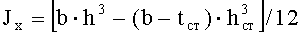
где b - ширина полки двутаврового профиля;
h - высота поперечного сечения двутаврового профиля,
а максимальный момент сопротивления определяют по формуле:
W_x=2J_x/h.