Предлагаемое изобретение относится к металлическим конструкциям промышленных и гражданских зданий с балочными перекрытиями и каркасами, а также к мостовым конструкциям.
Известен двутавровый прокатный профиль Гост 26020-83 [1]. Сортамент горячекатаных двутавров с параллельными гранями полок. Примем этот профиль за прототип.
Недостаток профилей прототипа в том, что гибкость стенки профиля (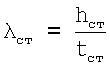 , где hст - высота стенки; tст - толщина стенки) переменная и колеблется для разных номеров двутавров.
, где hст - высота стенки; tст - толщина стенки) переменная и колеблется для разных номеров двутавров.
Так для двутавра I 90 Б1 - λст=57,
I 60 Б1 - λст=53,5,
I 100 Б1 - λст=57,8,
I 100 Б4 - λст=48,6.
Для двутавра I 100 Б4 высота сечения h=101,3, толщина полки его tп=3,25, толщина стенки tcт=1,95, высота стенки hcт=94,8, гибкость стенки λст=94,8/1,95=48,6.
По действующим нормам устойчивость стенок балок не требуется проверять, если условная гибкость стенок 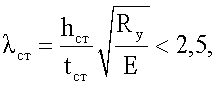 где 2,5 - при наличии местных напряжений в профиле [2, с.27].
где 2,5 - при наличии местных напряжений в профиле [2, с.27].
Для малоуглеродистой стали В Ст3 Сп5, Гост 2-777-2-88 при толщинах t=20…40 мм, расчетное сопротивление равно Ry=230 МПа, модуль упругости Е=206000 МПа.
Тогда условная гибкость стенки 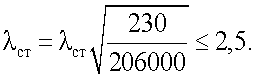
Отсюда предельная гибкость стенки, когда не требуется укрепление ее промежуточными ребрами жесткости, будет равна λст.пред.=2,5·29,927=74,8.
С некоторым запасом для малоуглеродистой стали назначаем гибкость стенки двутаврового прокатного профиля равной λст=70.
Для легированных сталей, например 09Г2С, 14Г2, 15ХСНД по Гост 19282-73* [2, с.64], расчетное сопротивление равно Rу=300 МПа.
Тогда условная гибкость стенки 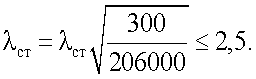 Отсюда предельная гибкость для легированных сталей равна λст.пред.=2,5·26,2=65,5.
Отсюда предельная гибкость для легированных сталей равна λст.пред.=2,5·26,2=65,5.
С некоторым запасом назначаем гибкость λст для легированных сталей равную λст.=60.
Оптимальное распределение материала по сечению балки
Значительное снижение материалоемкости двутаврового прокатного профиля достигнуто рациональным распределением металла по сечению балок. Поставим задачу прокатать балку (фиг.1) наибольшей прочности, то есть с максимальным моментом сопротивления max Wx из заготовки площадью поперечного сечения А см2 такой же, как у прототипа.
Очевидно, что уменьшение толщины стенки tст приводит к увеличению высоты балки h и увеличению момента сопротивления Wx. Материал должен быть оптимально распределен между стенкой и поясами балки.
Введем коэффициент К, определяющий материалоемкость стенки.

Введем постоянный коэффициент гибкости стенки:
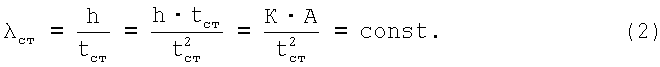
Где h - расстояние между центрами тяжести поясов; tcт - толщина стенки; Аст=h tcт - площадь сечения стенки; Аn - площадь сечения одного пояса; А=2Аn+Аст - площадь всего сечения.
Отсюда 
Тогда высота сечения h (расстояние между центрами тяжести поясов) будет зависеть только от коэффициента материалоемкости стенки К:
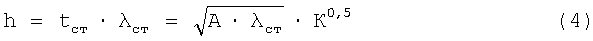
Площадь поперечного сечения двух поясов
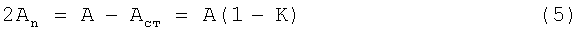
Пренебрегая собственными моментами инерции поясов балки, запишем главный момент инерции относительно оси X (см. фиг.1)

Поделив (6) на h/2, найдем момент сопротивления Wx на высоте центра тяжести пояса:
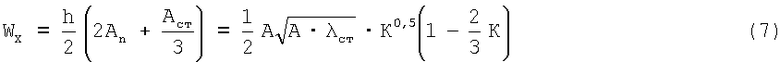
Итак, момент сопротивления зависит только от материалоемкости К стенки. Определим экстремум Wx, взяв производную по К.
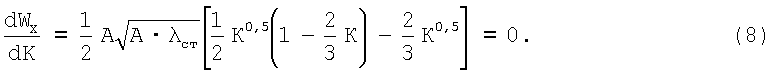
Отсюда 
Следовательно, при материалоемкости стенки 50% К=0,5 оптимальная высота сечения равна

Этой высоте соответствует наибольший момент сопротивления, равный

и соответствующая гибкость стенки

Подставив (12) в (11), получим момент сопротивления в зависимости от tст и А

и соответствующую минимальную площадь всего сечения балки

Или в зависимости от гибкости стенки

Тогда толщина стенки
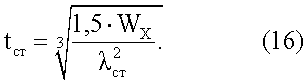
Легко убедиться, что радиус ядра сечения r в этом случае будет равен ρ=h/3.
Проанализируем материалоемкость профиля и гибкость стенки прототипа. Например, для двутавров по Гост 26020-83 с высотой сечения 100 см. Размеры в табл.1 даны в см, а площади в см2.
Анализ показывает, что материалоемкость стенки отличается от оптимальной К=0,5, а гибкость стенки меньше предельной λст<70.
Таким образом, имеются резервы для снижения материалоемкости.
Технологическая задача изобретения - максимальное снижение материалоемкости двутаврового прокатного профиля путем оптимального распределения материала между поясами и стенкой профиля, обеспечивающего достижение моментом сопротивления сечения профиля относительно главной оси X своего максимального значения.
Техническая задача решена тем, что двутавровый прокатный профиль содержит полки с параллельными гранями и стенку, соединяющую полки.
Отличие в том, что каждый из профилей выполнен с постоянной гибкостью стенки, не превышающей ее предельную величину: для малоуглеродистой стали назначим гибкость стенки, равную 70, а для легированной стали - гибкость стенки, равную 60. Причем площадь сечения профиля распределена по сечению балки в следующей пропорции: 50% - на стенку профиля по 25% на каждый из поясов, при этом толщина стенки профиля определяется из уравнения
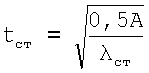 ,
,
где А - площадь поперечного сечения профиля, λст - гибкость стенки балки, обеспечивающая устойчивость ее без постановки промежуточных ребер жесткости.
Высота стенки находится из формулы
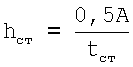
Ширина полки и толщина ее назначается такой, чтобы отношение ширины полки к ее толщине не превышало предельное отношение, обеспечивающее местную устойчивость плоского пояса. Главный момент инерции профиля относительно оси X определяется по формуле
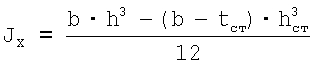 ,
,
где b - ширина полки профиля;
h - высота поперечного сечения профиля;
tст - толщина стенки;
hcт - высота стенки;
а главный момент сопротивления равен
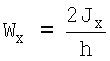 .
.
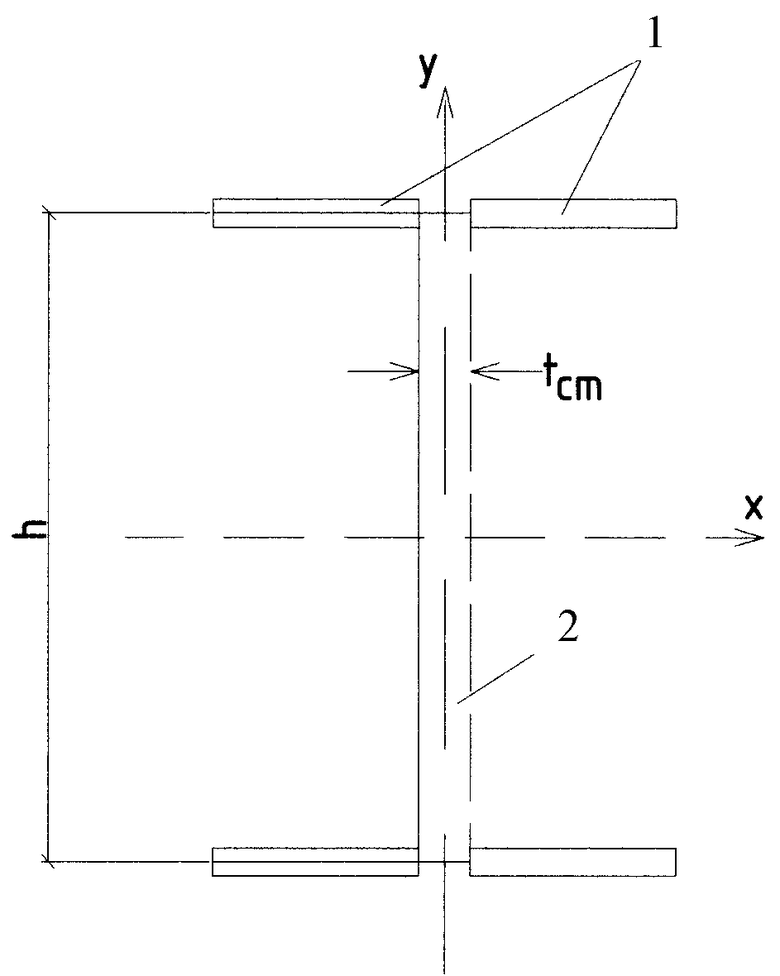
На чертеже показано поперечное сечение двутаврового прокатного профиля, содержащего полки 1 с параллельными гранями и соединяющую их стенку 2.
Полки 1 имеют ширину b. Толщина полки tn. Высота сечения профиля равна h. Стенка 2 имеет высоту hcт. Толщина стенки равна tст. Площадь сечения каждой из полок равна An=b·tn. Площадь сечения стенки равна Acт=hcт·tcт. Площадь всего сечения равна А=2Аn+Аст.
Пример конкретной реализации
Повысим прочность двутавра I 100 Б4 по Гост 26020-83 [1]. Основные размеры профиля и его характеристики приведены в табл.1. По формуле 12 найдем необходимую толщину стенки нового двутаврового профиля.
Находим 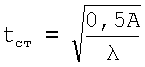 . Примем гибкость стенки такой же, как в действующем СНиП II-23-81* [2] λ=70.
. Примем гибкость стенки такой же, как в действующем СНиП II-23-81* [2] λ=70.
Площадь сечения оставляем неизменной А=400,6 см2.
Находим площадь сечения стенки Аст=0,5А.
Затем 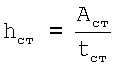 округляем
округляем 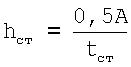 .
.
Находим Аст ф=hст·tст.
Находим площадь сечения одной полки Аn=0,25·А.
Ширину полки оставляем такой же bn.
Находим толщину полки 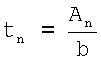 и округляем ее.
и округляем ее.
Находим фактическую площадь сечения полки и высоту сечения балки
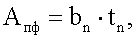
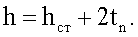
Находим суммарную площадь сечения балки ΣA=2Апф+Aст.
Находим главный момент инерции 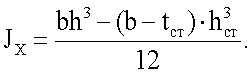
Находим момент сопротивления 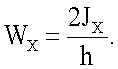
По сортаменту I 100 Б4 A=400,6 см2.
Назначаем λ=70.
Находим толщину стенки 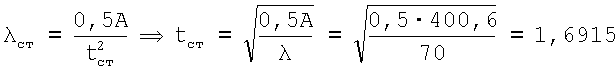 .
.
Принимаем tст=1,69 см. На стенку 50% площади Аст=0,5А=200,3 см2.
Тогда 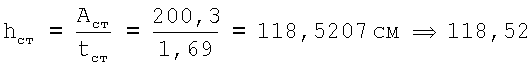 .
.
Принимаем hст=118,52.
Тогда Аст ф=118,52·1,69=200,3 см2.
Аn=0,25·А.
Оставляем ширину пояса bn=32, тогда 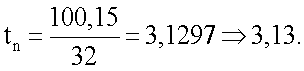
Вся высота балки h=hст+2tn=118,52+2·3,13=124,78.
Главный момент инерции нового профиля
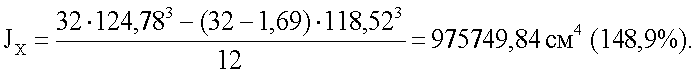
У прототипа главный момент инерции был Jx=655400 см4 (100%).
Момент сопротивления 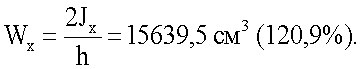
У прототипа главный момент был 12940 см3 (100%).
Из той же заготовки ΣА=200,3+2·32·3,13=400,62 см2 получен двутавр, имеющий главный момент инерции на 48,9% больший, чем раньше, то есть жесткость повышена на 48,9%. А момент сопротивления на 20,9% больший, чем раньше, то есть прочность при изгибе повышена на 20,9%.
Гибкость стенки 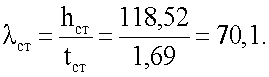
Список литературы
1. Двутавры стальные горячекатаные с параллельными гранями полок. Сортамент. Гост 26020-83. Переиздание. Октябрь 1998, 9 с.
2. СНиП II-23-81*. Стальные конструкции, Госстрой СССР, М., 1999, 96 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПРОКАТА ДВУТАВРОВОГО ПРОФИЛЯ СЕЧЕНИЯ ИЗ НИЗКОЛЕГИРОВАННОЙ СТАЛИ | 2011 |
|
RU2486972C2 |
| ПРОКАТНАЯ БАЛКА | 2001 |
|
RU2227069C2 |
| БАЛКА | 2002 |
|
RU2232125C2 |
| ДВУТАВРОВЫЙ ГОРЯЧЕКАТАНЫЙ КОЛОННЫЙ ПРОФИЛЬ | 2009 |
|
RU2411091C1 |
| РЕЛЬСОБАЛОЧНЫЙ БЛОК КОНСТРУКЦИЙ ДЛЯ ПАРАЛЛЕЛЬНЫХ РЕЛЬСОВЫХ ПУТЕЙ | 2005 |
|
RU2288886C2 |
| ПРОКАТНАЯ БАЛКА | 1995 |
|
RU2140477C1 |
| ВЫСОКОРЕСУРСНАЯ ПОРТАЛЬНАЯ ДВУХСТЕНЧАТАЯ ПОДКРАНОВАЯ БАЛКА | 2016 |
|
RU2677375C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ НЕСИММЕТРИЧНОЙ В СЕЧЕНИИ ПОДКРАНОВОЙ КОНСТРУКЦИИ | 1998 |
|
RU2196100C2 |
| ЗЕТОБРАЗНЫЙ ПРОФИЛЬ И СПОСОБ ЕГО ИЗГОТОВЛЕНИЯ | 1995 |
|
RU2108279C1 |
| СПОСОБ ПОВЫШЕНИЯ НЕСУЩЕЙ СПОСОБНОСТИ ЦИЛИНДРИЧЕСКОЙ ТРУБЫ НА ИЗГИБ | 2005 |
|
RU2304479C2 |
Изобретение предназначено для снижения материалоемкости двутаврового прокатного профиля. Двутавровый профиль выполнен из стали и содержит полки с параллельными гранями и стенку. Рациональное распределение стали по сечению балки обеспечивается за счет того, что гибкость его стенки, равная отношению высоты стенки к ее толщине, не превышает предельную величину гибкости λст, обеспечивающую устойчивость стенки без промежуточных ребер жесткости, и составляет 70 для малоуглеродистой стали и 60 для легированной стали, толщина, высота стенки, ее предельная гибкость регламентируются математическими зависимостями, площадь сечения профиля распределена по сечению в пропорции: 50% - стенка профиля, 25% - каждая из полок, отношение ширины полки к ее толщине не превышает предельное отношение, обеспечивающее местную устойчивость полки, при этом главный момент инерции профиля и главный момент сопротивления регламентированы, 1 ил., 1 табл.
Двутавровый прокатный профиль из стали, содержащий полки с параллельными гранями и стенку, соединяющую полки, отличающийся тем, что гибкость его стенки, равная отношению высоты стенки к ее толщине, не превышает предельную величину гибкости λст, обеспечивающую устойчивость стенки без промежуточных ребер жесткости, и составляет 70 для малоуглеродистой стали и 60 для легированной стали, толщина стенки tct равна
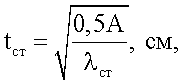
где А - площадь поперечного сечения профиля, см2;
λст - предельная гибкость стенки профиля,
высота стенки равна
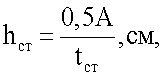
площадь сечения профиля распределена по сечению в пропорции: 50% - стенка профиля, 25% - каждая из полок, отношение ширины полки к ее толщине не превышает предельное отношение, обеспечивающее местную устойчивость полки, при этом главный момент инерции профиля Jx относительно оси X равен
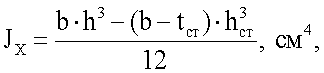
где b - ширина полки профиля, см;
h - высота поперечного сечения профиля, см;
tст - толщина стенки, см;
hст - высота стенки, см,
а главный момент сопротивления Wx равен
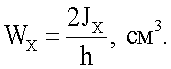
| Двутавровый профиль | 1977 |
|
SU801909A1 |
| Двутавровый профиль | 1989 |
|
SU1692693A1 |
| Способ изготовления двутавров | 1982 |
|
SU1045961A1 |
| WO 8404263 А1, 08.11.1984 | |||
| УСТРОЙСТВО для ОПРЕДЕЛЕНИЯ УДЛИНЕНИЯ ИЗВИТОЙНИТИ | 0 |
|
SU348913A1 |
Авторы
Даты
2010-03-10—Публикация
2007-10-01—Подача